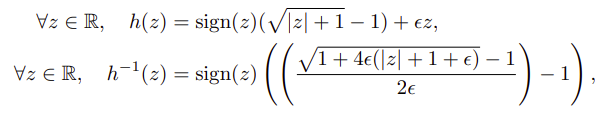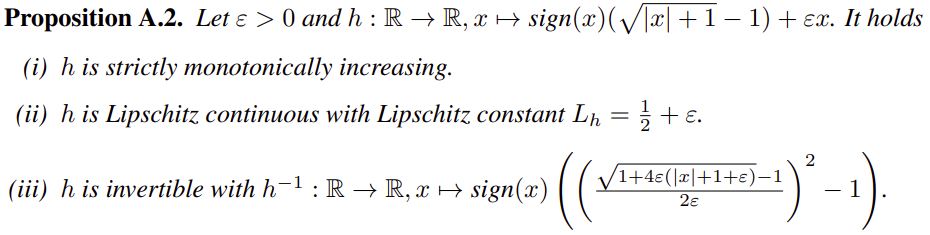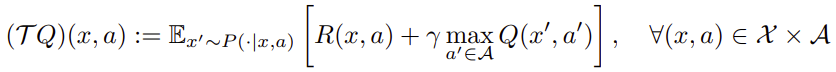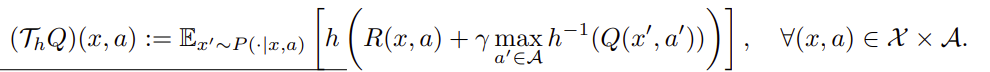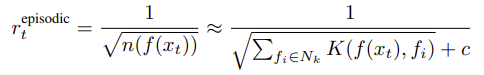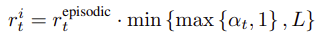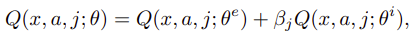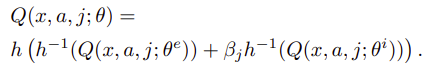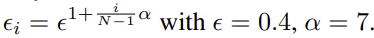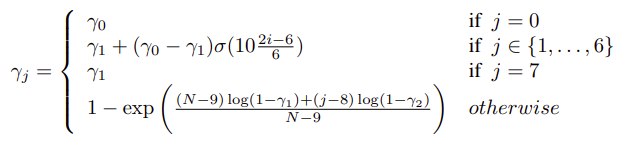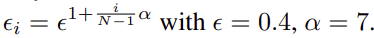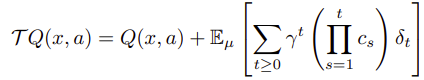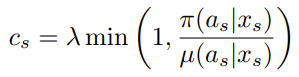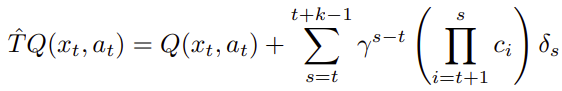Agent57までにいろいろなテクニックが使われてきましたが理解を深めるためにテーブル形式の強化学習手法として実装してみました。
※ネット上の情報をかき集めて自分なりに実装しているので正確ではないところがある点はご了承ください
はじめに
Agent57は過去の記事も参照してください。
ここではテーブル形式の環境に限ってQ学習の手法を適用してみたいと思います。
本記事のコード
テクニックについて
今回Q学習に追加実装するテクニックは以下です。
| テクニック | 内容 | 実装について | 備考 | |
|---|---|---|---|---|
| DQN | window_length | 数stepの状態を入力状態とする | × | 状態が増える機能は実装しません |
| Target Network | Q関数を2つ作り学習を安定化 | 〇 | ||
| Delay update Target Network | Target Networkの更新を遅らせる | 〇 | ||
| Huber loss function | - | ニューラルネット特有のテクニック | ||
| Experience Replay | 経験を保存し、その中からランダムに学習する | 〇 | ||
| Frame skip | 学習の間隔をあけ、学習効率を上げる手法 | × | Atariに特化したテクニックなので実装しません | |
| Annealing e-greedy | 探索の目安となるεを最初は高く最後は低くする手法 | × | コードをシンプルにするために見送ります | |
| Reward clip | 報酬を[-1,1]にクリップ | × | 報酬設計は環境側を尊重したいと思います | |
| Image preprocessor | 画像の前処理 | × | Atariに特化したテクニックなので実装しません | |
| Rainbow | Double DQN | Target Networkの更新方法を改善 | 〇 | |
| Priority Experience Replay | Experience Replayに優先順位をつけて効率化 | 〇 | ||
| Dueling Network | - | ニューラルネット特有のテクニック | ||
| Multi-Step learning | 報酬を数step先まで見る | × | コードをシンプルにするために見送ります | |
| Noisy Network | - | ニューラルネット特有のテクニック | ||
| Categorical DQN | - | ニューラルネット特有のテクニック | ||
| DRQN | LSTM | - | ニューラルネット特有のテクニック | |
| Ape-X | 分散学習 | × | コードをシンプルにするために見送ります | |
| R2D2 | Value function rescaling | 価値関数をrescalingで丸める | 〇 | |
| NGU | Intrinsic Reward | 内部報酬を実装し探索を効率化 | 〇 | |
| UVFA | - | ニューラルネット特有のテクニック | ||
| Retrace | オフポリシー強化学習の学習改善手法 | 〇 | ||
| Agent57 | Meta controller | メタコントローラーによる探索の効率化 | 〇 | |
| Intrinsic Reward split | 内部報酬の分割 | 〇 |
各インターフェース
実装にあたってインターフェースを整理したいと思います。
環境側
今回はテーブル形式の環境を扱うので、以下の形式で固定します。
| 形式 | 例 | |
|---|---|---|
| アクション | 離散値(int) | 2 |
| 状態 | 離散値の配列(list[int]) | (1,2,3) |
stateはnumpy配列として扱っています。
クラスとしては以下のイメージです。
from abc import ABCMeta, abstractmethod
class Env(metaclass=ABCMeta):
@property
@abstractmethod
def action_space(self) -> gym.spaces.Space:
raise NotImplementedError()
@property
@abstractmethod
def observation_space(self) -> gym.spaces.Space:
raise NotImplementedError()
@abstractmethod
def reset(self) -> np.ndarray:
raise NotImplementedError()
@abstractmethod
def step(self, action: int) -> tuple[np.ndarray, float, bool, dict]:
raise NotImplementedError()
基本は OpenAI gym で提供されている環境を意識してあります。
アクション・状態が連続値である環境は出来る限り変換して使えるようにしています。
アクションが連続値の場合は10分割し(アクション数10)、
状態が連続値の場合は1つの次元に対して50分割しています。
変換用のコードは長くなるので Google Colab の EnvForRL のコードを見てください。
Agent側
上記Envを元に学習するAgentは以下となります。
from abc import ABCMeta, abstractmethod
class RL(metaclass=ABCMeta):
@abstractmethod
def init_by_env(self, env: EnvForRL) -> None:
"""
環境を元に初期化します
"""
raise NotImplementedError()
@abstractmethod
def on_reset(self, state: np.ndarray, training: bool) -> None:
"""
毎エピソードの最初に実行されます。
このエピソードでトレーニングするかどうかが training に入っています。
"""
raise NotImplementedError()
@abstractmethod
def policy(self, state: np.ndarray) -> tuple[int, Any]: # (env_action, agent_action)
"""
state を元にアクションを返します。
戻り値の env_action は実際に環境に渡されるアクションで、
agent_action は次の on_step で受け取るアクションです。
"""
raise NotImplementedError()
@abstractmethod
def on_step(
self,
state: np.ndarray,
agent_action: Any,
new_state: np.ndarray,
reward: float,
done: bool,
) -> None:
"""
毎step実行されます。
"""
raise NotImplementedError()
実行部分
上記を元に以下のような実行を想定しています。
import gym
# 環境を作成し、EnvForRLでラップする
env = EnvForRL(gym.make("FrozenLake-v1"))
# agent
agent = RL()
agent.init_by_env(env)
# 学習するかどうか
training = True
# エピソードの初期化
done = False
step = 0
total_reward = 0
state = env.reset()
agent.on_reset(state, training)
# 1エピソード
while not done:
# action
env_action, agent_action = agent.policy(state)
# step
new_state, reward, done, _ = env.step(env_action)
step += 1
total_reward += reward
agent.on_step(state, agent_action, new_state, reward, done)
state = new_state
Q学習(ベースライン)
ベースとなるQ学習は以下です。
このクラスを元に機能を追加していきます。
@dataclass
class QL(RL):
"""Q learning"""
# ハイパーパラメータ
epsilon: float = 0.1
test_epsilon: float = 0.0
gamma: float = 0.9 # 割引率
lr: float = 0.1 # 学習率
def init_by_env(self, env: EnvForRL) -> None:
# アクション情報
self.nb_actions = env.action_space.n
# Qテーブル
self.Q = {}
def on_reset(self, state: np.ndarray, training: bool) -> None:
self.training = training
def policy(self, state: np.ndarray) -> Tuple[int, Any]:
s = str(state.tolist())
if self.training:
epsilon = self.epsilon
else:
epsilon = self.test_epsilon
if random.random() < epsilon:
# epsilonより低いならランダムに移動
action = random.randint(0, self.nb_actions - 1)
elif s not in self.Q:
action = random.randint(0, self.nb_actions - 1)
else:
# Q値が最大のアクションを実行
q = np.asarray(self.Q[s])
action = random.choice(np.where(q == q.max())[0])
return action, action
def on_step(
self,
state: np.ndarray,
action: int,
new_state: np.ndarray,
reward: float,
done: bool,
) -> None:
s = str(state.tolist())
n_s = str(new_state.tolist())
# Qテーブルにない状態を初期化
if s not in self.Q:
self.Q[s] = [0 for a in range(self.nb_actions)]
if n_s not in Q:
self.Q[n_s] = [0 for a in range(self.nb_actions)]
# Q値の計算
if done:
gain = reward
else:
gain = reward + self.gamma * max(self.Q[n_s])
td_error = gain - self.Q[s][action]
self.Q[s][action] += self.lr * td_error
Experience Replay & Priority Experience Replay
Experience Replay(経験再生)は環境から得た経験($(s_t,a_t,r_t,s_{t+1},d_t)$の組)(サンプルや遷移,traceなどとも言ったり)を一時的に Replay Memory に保存しておき、
学習時には Replay Memory からランダムに取得した経験を元に学習する手法です。
これによりサンプルの学習効率が上がります。
またニューラルネットではミニバッチ学習が適用できるという利点もあるかと思います。
Experience Replay ではランダムに経験を取り出していましたが、経験に優先順位をつけて取り出す手法が Priority Experience Replay(優先順位付き経験再生) です。
Priority Experience Replayの詳細は以前に記事を書いているので省きます。
主要部分のコードのみ書きます。
# メモリのIF
class Memory(metaclass=ABCMeta):
@abstractmethod
def add(self, exp: Any, priority: int = 0) -> None:
"""
メモリに経験をpriorityで追加する
"""
raise NotImplementedError()
@abstractmethod
def update(self, idx: int, exp: Any, priority: int) -> None:
"""
インデックス(idx)にある経験(exp)をpriorityで更新する
"""
raise NotImplementedError()
@abstractmethod
def sample(self, batch_size: int, steps: int) -> tuple[list, list, list]:
"""
バッチサイズ分の経験をランダムに選び返す
戻り値の weights はIS用
"""
raise NotImplementedError()
# return (indexes, batchs, weights)
# --- ハイパーパラメータ
memory = Memory() # メモリの種類を選んで作成
warmup_size = 10 # ウォームアップサイズ
# --- 毎step
def on_step(self, state: np.ndarray, action: Any, new_state: np.ndarray, reward: float, done: bool):
s = str(state.tolist())
n_s = str(new_state.tolist())
# 経験
batch = {
"state": s,
"action": action,
"n_state": n_s,
"reward": reward,
"done": done,
}
# メモリに経験を追加し、一定数貯まるまで学習はしない
self.memory.add(batch)
if len(self.memory) < self.warmup_size:
return
# メモリからランダムに取得
(indexes, batchs, weights) = self.memory.sample(1, self.train_count)
# batchで学習
s = batch[0]["state"]
action = batch[0]["action"]
n_s = batch[0]["n_state"]
reward = batch[0]["reward"]
done = batch["done"]
Q[s][action] = (学習)
# 学習時の更新ですが、weight をtd_errorに掛ける必要があります
# Q[s][action] += lr * td_error
# ↓↓↓
# Q[s][action] += lr * td_error * weights[0]
# priorityを計算し、メモリを更新
priority = np.abs(td_error) + 0.0001
self.memory.update(indexes[0], batchs[0], priority)
Target Network & Double DQN
ニューラルネットに使われる手法ですが、Qテーブルにも適用できそうだったので実装してみました。
Q関数と同じ構造のTargetQ関数を追加し、Q値の更新ではTargetQ関数を使う手法です。
TargetQ関数は一定step毎にQ関数と同期します。
これにより、状態の過大評価を緩和する効果があるそうです。
コードは以下です。
# --- ハイパーパラメータ
enable_double_dqn: bool = True # DoubleDQNを使うか
target_model_update_interval: int = 100 # 更新間隔
# --- 全体の初期化
def init_by_env(self, env: EnvForRL) -> None:
self.Q = {}
self.Q_target = {} # TargetQ
# --- 毎ステップ
def on_step(self, state: np.ndarray, action: Any, new_state: np.ndarray, reward: float, done: bool):
s = str(state.tolist())
n_s = str(new_state.tolist())
# TargetQとQテーブルは同じ構造
if s not in self.Q:
self.Q[s] = [0 for a in range(self.nb_actions)]
self.Q_target[s] = [0 for a in range(self.nb_actions)]
if n_s not in Q:
self.Q[n_s] = [0 for a in range(self.nb_actions)]
self.Q_target[n_s] = [0 for a in range(self.nb_actions)]
# --- 学習
if self.enable_double_dqn:
# 次のアクションは、今のQ値の最大値indexを使用
n_act_idx = np.argmax(self.Q[n_s])
else:
# 次のアクションは、TargetQ値の最大値indexを使用
n_act_idx = np.argmax(self.Q_target[n_s])
if done:
gain = reward
else:
# TargetQ値を用いて更新する
gain = reward + self.gamma * self.Q_target[n_s][n_act_idx]
td_error = gain - self.Q[s][action]
self.Q[s][action] += self.lr * td_error
# 一定間隔でTargetQに重さをコピー
if self.train_count % self.target_model_update_interval == 0:
for k, v in self.Q.items():
self.Q_target[k] = v
self.train_count += 1
Value function rescaling
様々な密度やスケールの報酬に対してもうまく学習できるように導入した関数が、rescaling 関数となります。
rescaling 逆関数ですが、Agent57の論文で書かれている式が違っていました。
正しくは以下のようです。(2乗があります)
以下の論文とgithubのコードを参考にしています。
- 論文: Observe and Look Further: Achieving Consistent Performance on Atari
- github: google-research/seed_rlagents/r2d2/learner.py
- github: horoiwa/deep_reinforcement_learning_gallery/R2D2/atari/util.py
コードは以下です。
def rescaling(x, eps=0.001):
return np.sign(x) * (np.sqrt(np.abs(x) + 1.0) - 1.0) + eps * x
def inverse_rescaling(x, eps=0.001):
n = np.sqrt(1.0 + 4.0 * eps * (np.abs(x) + 1.0 + eps)) - 1.0
n = n / (2.0 * eps)
return np.sign(x) * ((n ** 2) - 1.0)
rescaling関数について
DQNでは報酬を[-1,1]にクリップしていました。
これは学習を安定させましたが、好ましい学習ができているかは別問題でした。
例えばボーリングにて、ピンを1本倒すのと10本倒すのが同じ扱いになる問題があります。
そこでこの論文では価値関数のスケールを縮小する関数 $h$ を導入しこの問題に対処しました。
Q学習のベルマン最適化演算子は以下です。(ベルマン方程式とベルマン演算子について:What is the Bellman operator in reinforcement learning?)
$h$ を用いると以下になります。
rescaling関数の可視化
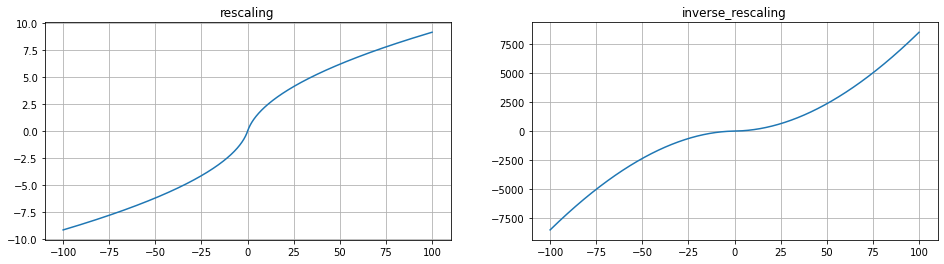
まずは関数直接です。
-100から100の範囲で描画してみました。
| -100 | -10 | -1 | 0 | 1 | 10 | 100 | |
|---|---|---|---|---|---|---|---|
| rescale | -9.150 | 2.327 | -0.415 | 0 | 0.415 | 2.327 | 9.150 |
| inverse_rescaling | -8546.626 | -117.430 | -2.988 | 0 | 2.988 | 117.430 | 8546.626 |
逆rescalingは値を大きく、rescalingは値を小さく丸める役割を持っていますね。
次に報酬を加味した状況を見てみます。
$$ h( r + h^{-1}(x) )$$
$r$ が報酬、$x$ がQ値となります。
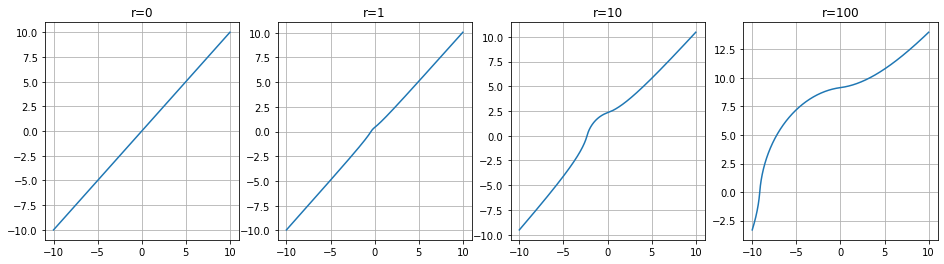
報酬を固定し、Q値を変えたグラフを見てみます。(負は反転しただけになるので省略)
r=0ではちゃんと線形ですね(例えば10の出力に対して10)。
r=100の時が顕著ですが、100(報酬) + 10(Q値)の結果が13あたりになっています。
報酬の結果がかなり抑えられて反映されている印象を受けますね。
実装コード
Q値を更新する箇所に対して適用させます。
if done:
gain = reward
else:
gain = reward + self.gamma * max(self.Q[n_s])
td_error = gain - self.Q[s][action]
self.Q[s][action] += self.lr * td_error
# ↓↓↓
if done:
gain = reward
else:
gain = reward + self.gamma * inverse_rescaling(max(self.Q[n_s])) # 変更
td_error = rescaling(gain) - self.Q[s][action] # 変更
self.Q[s][action] += self.lr * td_error
内部報酬(Intrinsic Reward)
NGUで追加された手法で、従来の報酬(外部報酬:Extrinsic Reward)に内部報酬(Intrinsic Reward)を加えた報酬を真の報酬とする手法です。
内部報酬の役割は主に以下です。
- 1エピソード内で同じ状態を訪れないようにする(強め)
- トレーニング全体で同じ状態を訪れないようにする(弱め)
- エージェントの行動に関係なく変化する状態を無視する
内部報酬は生涯記憶部(life long novelty module)とエピソード記憶部episodic novelty module)から成ります。
エピソード記憶部(episodic novelty module)
エピソード記憶部では1エピソード内で同じ状態を訪れないように報酬を決めます。
$\approx$ より右辺はニューラルネットの為の近似化なので以下をそのまま使います。
$$ r^{episode}_t = \frac{1}{ \sqrt{ n(f(x _{t})) } }$$
$n(f(x_t))$ が訪問回数を表します。
埋め込み関数 $f(x_t)$ は今回見送り、$n(x_t)$としています。
# --- エピソードの開始時
def on_reset(self, state: np.ndarray, training: bool) -> None:
# エピソード内での訪問回数
self.episodic_C = {}
def _calc_episodic_reward(self, state):
state = str(state.tolist())
if state not in self.episodic_C:
self.episodic_C[state] = 0
# 0回だと無限大になるので1回は保証する
reward = 1 / np.sqrt(self.episodic_C[state] + 1)
# 数える
self.episodic_C[state] += 1
return reward
埋め込み関数
埋め込み関数の役割はエージェントの行動に関係なく変化する状態を無視する事です。
NGUではこれを Siamese Network で学びます。
しかしテーブル型の状態に対して学ぶいい方法が考えつかなかったので今回は見送ります。
生涯記憶部(life long novelty module)
生涯記憶部での役割はトレーニング全体で同じ状態をなるべく訪れないようにする事です。
同じ状態の訪問回数をAgent57では RND(Random Network Distillation) を用いて表現しています。
RNDは同じモデルの2つのニューラルネットを用いて2つのモデルの出力差で訪問回数を表現します。
片方をもう片方に近づけるように学習する事で、誤差が大きい→訪問回数が少ない、誤差が少ない→訪問回数が多いとなるわけです。
2つのモデルの出力差は平均2乗誤差で計算します。
$$ err(x_t) = || \hat{g}(x_t;\theta) - g(x_t)||^2$$
次に標準化(平均1、分散1)します。
$$ \alpha_t = 1 + \frac{ err(x_t) - \mu_e }{ \sigma_e }$$
ここで $\sigma_e$ は $err(x_t)$ の標準偏差、$\mu_e$ は $err(x_t)$ の平均になります。
最後に1~L(=5)の範囲でクリップします。
$$ \min(\max(\alpha_t,1), L)$$
テーブル形式に対応
Q学習は状態がテーブル形式なので状態の近似が不要になります。
数を数えてもいいですが、RNDと同じ考えで実装したいと思います。
アルゴリズムは同じ状態を訪れるたびに少しずつ減少していく形です。
Agent57と合わせて値の範囲は1~Lとします。
# ハイパーパラメータ
self.lifelong_reward_L = 5.0
self.lifelong_decrement_rate = 0.999 # 減少割合
# local val
self.lifelong_C = {} # 状態を数える用
def _calc_lifelong_reward(self, state):
state = str(state.tolist())
# RNDと同じ発想で、回数を重ねると0に近づくようにする
if state not in self.lifelong_C:
self.lifelong_C[state] = self.lifelong_reward_L - 1.0 # 初期値
lifelong_reward = self.lifelong_C[state]
# 0に近づける
self.lifelong_C[state] *= self.lifelong_decrement_rate
return lifelong_reward + 1.0
内部報酬の計算
内部報酬は以下で計算されます。
$r^i_t$ が内部報酬、$r^{episode}_t$ がエピソード記憶部、$\alpha _{t}$ が生涯記憶部です。
$ min ( max ( \alpha _{t}, 1 ), L ) $ のスケール部分は calc_lifelong_reward 内で実装しているのでコード上は掛けるだけです。
episodic_reward = self._calc_episodic_reward(state)
lifelong_reward = self._calc_lifelong_reward(state)
int_reward = episodic_reward * lifelong_reward
可視化
以下のようなコードで可視化してみました。
states = []
states.extend([16] * 20)
states.extend([1] * 50)
states.extend([32] * 30)
states.extend([1] * 50)
lifelong_C = {}
episodic_C = {}
rewards1 = []
rewards2 = []
rewards3 = []
for state in states:
r1 = _calc_lifelong_reward(lifelong_C, state)
r2 = _calc_episodic_reward(episodic_C, state)
rewards1.append(r1)
rewards2.append(r2)
rewards3.append(r1 * r2)
plt.figure(figsize=(16,8))
plt.plot(rewards1, label="lifelong")
plt.plot(rewards2, label="episodic")
plt.plot(rewards3, label="intrinsic")
plt.legend()
plt.show()
状態として、[16]が20step、[1]が50step…と来た場合の報酬をグラフ化しています。
同じ状態が続く場合は小さくなり、新しい状態が来た場合は高くなっていますね。
Intrinsic Reward split(内部報酬の分割)
NGUの結果、外部報酬と内部報酬を同時に学習するのが難しい事が分かり、Agent57ではQ関数を分ける手法を提案しています。
($\theta^e$ は外部報酬用のパラメータで、$\theta^i$ は内部報酬用のパラメータです)
更に rescaling 関数を適用した場合は以下となります。
Agent57の論文では rescaling 関数の適用はパフォーマンス的にはあまり重要な役割を果たしていなそうとの記載がありました。(3.1.の最後の部分)
アクションを決める際は外部報酬と内部報酬を合わせた報酬を使用します。
しかし、学習ではそれぞれのQ関数を学習させます。
以下、コードとなります。
# --- ハイパーパラメータ
beta = 0.3 # 内部報酬の反映率
ext_lr = 0.01 # 外部報酬Q関数の学習率
int_lr = 0.01 # 内部報酬Q関数の学習率
# --- 全体の初期化
def init_by_env(self):
# Qテーブル
self.Q_ext = {} # 外部報酬用
self.Q_int = {} # 内部報酬用
# --- アクションの選択
def policy(self, state: np.ndarray) -> tuple[int, Any]:
s = str(state.tolist())
if random.random() < epsilon:
# epsilonより低いならランダムに移動
action = random.randint(0, self.nb_actions - 1)
else:
# 外部報酬と内部報酬
q_ext = np.asarray(self.Q_ext[s])
q_int = np.asarray(self.Q_int[s])
# Q値
q = q_ext + self.beta * q_int
# 最大値を選ぶ(複数あればランダム)
action = random.choice(np.where(q == q.max())[0])
return action, action
# --- 毎ステップ
def on_step(self, state: np.ndarray, action: Any, new_state: np.ndarray, reward: float, done: bool):
s = str(state.tolist())
n_s = str(new_state.tolist())
# 外部報酬
ext_reward = reward
# 内部報酬
episodic_reward = self._calc_episodic_reward(new_state) # エピソード記憶部
lifelong_reward = self._calc_lifelong_reward(new_state) # 生涯記憶部
int_reward = episodic_reward * lifelong_reward
def update_q(Q, reward, lr):
# Qテーブルにない状態を初期化
if s not in Q:
Q[s] = [0 for _ in range(self.nb_actions)]
if n_s not in Q:
Q[n_s] = [0 for _ in range(self.nb_actions)]
# Q値の計算
if done:
gain = reward
else:
gain = reward + self.gamma * max(Q[n_s])
td_error = gain - Q[s][action]
Q[s][action] += lr * td_error
return td_error
# それぞれで学習
td_error_ext = update_q(self.Q_ext, ext_reward, self.ext_lr)
td_error_int = update_q(self.Q_int, int_reward, self.int_lr)
内部報酬の正規化
これはこの記事独自の内容です。
内部報酬の役割ですがこれは未知のエリアの探索です。
ただこれを累積報酬和として扱うと少し不都合が起こりました。
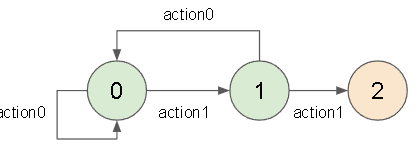
例えば以下のような環境を考えます。
この時以下のstepを踏んだとします。
(内部報酬は同じ状態を訪れると少なくなっていきます)
| step | state | action | 内部報酬 | 更新後のQ(割引率0.9) |
|---|---|---|---|---|
| 0 | 0 | 0 | (new)5.0 | 5.0+0.9*0.0=5.0 |
| 1 | 0 | 0 | 2.0 | 2.0+0.9*5.0=6.5 |
| 2 | 0 | 0 | 1.0 | 1.0+0.9*6.5=6.85 |
| 3 | 0 | 1 | (new)5.0 | 5.0+0.9*0.0=5.0 |
この状態でstate1でaction0とaction1の内部報酬を見てみます。
| state | action | new_state | 内部報酬 | 更新後のQ(割引率0.9) |
|---|---|---|---|---|
| 1 | 0 | 0 | 0.6 | 0.6+0.9*6.85=6.765 |
| 1 | 1 | 2 | (new)5.0 | 5.0+0.9*0.0=5.0 |
本当はaction1の方が新しい状態に遷移するので高くなってほしい所ですが、
既知の状態に遷移するaction0の方が高くなってしまっています。
これを解決するために内部報酬を学習回数で割って正規化してみました。
正規化すると以下になり新しい状態の方が高くなります。
| state | action | new_state | 内部報酬 | 更新後のQ(割引率0.9) |
|---|---|---|---|---|
| 1 | 0 | 0 | 0.6 | 0.6+0.9*(6.85/3)=2.655 |
| 1 | 1 | 2 | (new)5.0 | 5.0+0.9*0.0=5.0 |
多分訪問した状態に学習回数が依存するQ学習ならではの問題な気がします。
メタコントローラー(Meta controller)
Agent57で追加された手法で、探索の選択を多腕バンディット問題に見立てて効率よく探索する手法です。
Q学習では探索はε-greedy法によるεの値で制御していました。(εが高い→ランダムに動いて探索、εが低い→Q値を信じて探索しない)
DQNではε値を最初は高く、後半低くする事で探索の効率化を図っていました。(最初は探索し、後半は探索しない)
メタコントローラーではまずActor(探索者)を複数人用意し、Actor毎に違う探索の値を設定します。
そしてエピソードの開始時にActorを選び、そのActorの探索率で実際に経験を収集します。
Actorの決め方は多腕バンディット問題(MAB)に見立てて決定するという内容です。
MABのアルゴリズムとしては UCB が使われており、また元のMABと違い、結果(報酬の期待値)が動的に変化するため(元のMABは報酬の期待値は固定)直近の数エピソードのみを対象としています。
Actorで使う探索パラメータの可視化
論文内でActorが設定する値は3種類あります。
- ランダム探索率(ε)
- 割引率(γ: discount factor)
- 内部報酬探索率(β: exploration rate)
ランダム探索率(ε)
εの固定化は Ape-X で提案されており、その後ずっと使われているようです。(Agent57では $\alpha=8$ になってました)
コードは以下です。
def create_epsilon_list(policy_num: int, epsilon=0.4, alpha=8.0):
epsilon_list = []
for i in range(policy_num):
e = epsilon ** (1 + (i / (policy_num - 1)) * alpha)
epsilon_list.append(e)
return epsilon_list
割引率(γ:discount factor)
割引率はQ学習における割引率です。
未来の報酬ほど不確定になるのでその分価値を減らそうという考えです。
これですが、Agent57の論文に書かれている数式が多分間違っています。
その通りにグラフを作成するとおかしい形になりました。
多分正しくは以下です。(これで論文通りのグラフになりました)
\gamma_j = \left\{
\begin{array}{ll}
\gamma0 \qquad (j=0) \\
\gamma0 + (\gamma1 - \gamma0)\sigma(10 \frac{2i-6}{6} ) \qquad (j \in (1,...,6)) \\
\gamma1 \qquad (j=7) \\
1-exp(\frac{(N-9-(j-8))log(1-\gamma1) + (j-8)log(1-\gamma2)}{N-9}) \quad (otherwise)
\end{array}
\right.
コードは以下です。
def sigmoid(x, a=1):
return 1 / (1 + np.exp(-a * x))
def create_gamma_list(policy_num: int, gamma0=0.9999, gamma1=0.997, gamma2=0.99):
assert policy_num > 0
gamma_list = []
for i in range(policy_num):
if i == 0:
g = gamma0
elif 1 <= i and i <= 6:
g = gamma0 + (gamma1 - gamma0) * sigmoid(10 * ((2 * i - 6) / 6))
elif i == 7:
g = gamma1
else:
g = (policy_num - 9 - (i - 8)) * np.log(1 - gamma1) + (i - 8) * np.log(1 - gamma2)
g = 1 - np.exp(g / (policy_num - 9))
gamma_list.append(g)
return gamma_list
内部報酬探索率(β:exploration rate)
内部報酬(Intrinsic Reward)の反映率です。
論文内で exploration rate と言っているので探索率と訳しています。
内部報酬は主に効率的な探索を促すために追加されているので、βが高い=探索する、βが低い=探索しない、という感じになります。
コードは以下です。
def sigmoid(x, a=1):
return 1 / (1 + np.exp(-a * x))
def create_beta_list(policy_num: int, max_beta=0.3):
assert policy_num > 0
beta_list = []
for i in range(policy_num):
if i == 0:
b = 0
elif i == policy_num - 1:
b = max_beta
else:
b = 10 * (2 * i - (policy_num - 2)) / (policy_num - 2)
b = max_beta * sigmoid(b)
beta_list.append(b)
return beta_list
可視化
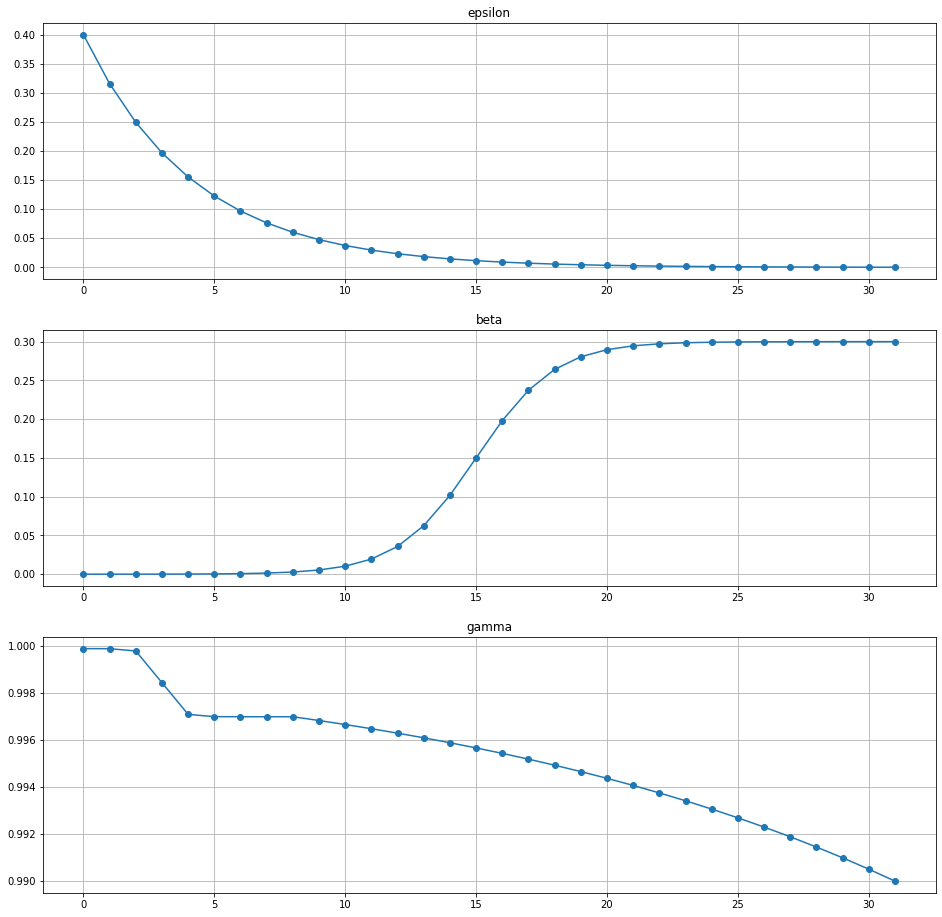
policy_num=32 で作成したリストは以下です。
| 0 | 5 | 15 | 25 | 32 | |
|---|---|---|---|---|---|
| epsilon | 0.4 | 0.122628 | 0.011525 | 0.001083 | 0.000262 |
| beta | 0 | 0.000381 | 0.15 | 0.299619 | 0.3 |
| gamma | 0.9999 | 0.997004 | 0.994378 | 0.992695 | 0.99 |
Actor0は内部報酬がない代わりにランダム探索が強く、報酬もあまり割り引かないですね。
Actor32ではランダム探索を少なくする代わりに内部報酬による探索が強くなっています。
sliding-window UCB
上記Actorに対して1エピソードで得た割引かない元の報酬でUCB値を計算します。
アルゴリズムは以前の記事で書いたものと同じです。(再掲)
$$ N_k(a) = \sum_{m=0}^{k-1} 1 (A_m = a) $$
\hat{\mu}_k(a) = \frac{1}{N_k(a)} \sum_{m=0}^{k-1} R_k(a)1 (A_m = a)
A_k = argmax_{1\leq a \leq N} \hat{\mu}_{k-1}(a) + \beta \sqrt{ \frac{ log(k-1) }{N_{k-1}(a)} }
$A$が各アームを表し、$k$がエピソード回数(windowサイズは超えない)で、$R$が報酬、$\beta$はUCBの定数です。
またεの確率で、UCB法で選択するかランダムに選択するかを選びます。
UCBメイン部分のコードは以下です。
# ハイパーパラメータ (160,0.5 or 3600,0.01)
ucb_window_size = 3600 # 上限
ucb_epsilon = 0.01 # εでUCBを使うか選択
policy_num = 32 # ポリシーの総数
ucb_beta = 1 # UCBのβ
# (sliding-window UCB)
def _calc_policy_index(self):
if not self.training:
# traningじゃない場合はpolicy0(=探索なし)
return 0
self.episode_count += 1
# UCB計算用に保存
if self.episode_count > 0:
self.ucb_data.append(
(
self.policy_index,
self.prev_episode_reward,
)
)
# 全て1回は実行
if self.episode_count < self.policy_num:
return self.episode_count
# ランダムでpolicyを決定
if random.random() < self.ucb_epsilon:
return random.randint(0, self.policy_num - 1)
# UCB値を計算
N = [1 for _ in range(self.policy_num)] # 回数
u = [0.0 for _ in range(self.policy_num)] # 報酬/回
for i, reward in self.ucb_data:
N[i] += 1
u[i] += reward
for i in range(self.policy_num):
u[i] /= N[i]
count = len(self.ucb_data)
ucb = [0.0 for _ in range(self.policy_num)]
for i in range(self.policy_num):
ucb[i] = u[i] + self.ucb_beta * np.sqrt(np.log(count) / N[i])
# UCB値最大のポリシー(複数あればランダム)
return random.choice(np.where(ucb == np.max(ucb))[0])
実行側は以下です。
import collections
# --- 全体の初期化
def init_by_env(self):
self.ucb_data = collections.deque(maxlen=ucb_window_size) # 履歴保存用
self.episode_count = -1 # エピソード数(先+のため-1スタート)
self.prev_episode_reward = 0.0 # 前エピソードの報酬
self.policy_index = 0 # 前エピソードのActor
self.training = True
# 各リスト
self.beta_list = create_beta_list(self.policy_num)
self.gamma_list = create_gamma_list(self.policy_num)
self.epsilon_list = create_epsilon_list(self.policy_num)
# --- エピソード前の初期化
def on_reset(self, state: np.ndarray, training: bool) -> None:
self.training = training
# エピソード毎に policy を決める
self.policy_index = self._calc_policy_index()
self.gamma = self.gamma_list[self.policy_index] # 割引率
self.beta = self.beta_list[self.policy_index] # 探索率
self.epsilon = self.epsilon_list[self.policy_index] # policy epsilon
# sliding-window UCB 用に報酬を保存
self.prev_episode_reward = 0.0
# --- 毎ステップ
def on_step(self, state: np.ndarray, action: Any, new_state: np.ndarray, reward: float, done: bool):
# 割引なしの報酬
self.prev_episode_reward += reward
可視化
UCBと報酬のの影響を見るために可視化してみました。
Actorは32人とし、以下 $\epsilon$ の確率でエピソードの報酬が手に入るとします。
1000回実行し、選んだポリシーを数えたいと思います。
概要をコードにすると以下です。
policy_num = 32
epsilon_list = create_epsilon_list(policy_num)
policy_list = []
for _ in range(1000):
policy_index = calc_policy_index()
# 選んだポリシーを数える
policy_list.append(policy_index)
# epsilonで報酬が手に入る
if random.random() < epsilon_list[policy_index]:
reward = # ここの報酬を変える
else:
reward = 0.0
- 報酬が1の場合
count reward ucb
0 151 0.36 0.5715
1 113 0.32 0.5658
2 74 0.26 0.5623
3 48 0.19 0.5669
4 29 0.07 0.5570
5 32 0.09 0.5584
6 29 0.07 0.5570
7 22 0.00 0.5603
8 25 0.04 0.5657
9 22 0.00 0.5603
10 25 0.04 0.5657
11 22 0.00 0.5603
12 22 0.00 0.5603
13 22 0.00 0.5603
14 22 0.00 0.5603
15 22 0.00 0.5603
16 22 0.00 0.5603
17 22 0.00 0.5603
18 22 0.00 0.5603
19 22 0.00 0.5603
20 22 0.00 0.5603
21 22 0.00 0.5603
22 22 0.00 0.5603
23 22 0.00 0.5603
24 22 0.00 0.5603
25 22 0.00 0.5603
26 22 0.00 0.5603
27 22 0.00 0.5603
28 22 0.00 0.5603
29 22 0.00 0.5603
30 22 0.00 0.5603
31 22 0.00 0.5603
- 報酬が100の場合
count reward ucb
0 958 37.47 37.5588
1 2 0.00 1.8585
2 2 0.00 1.8585
3 2 0.00 1.8585
4 5 20.00 21.1754
5 5 20.00 21.1754
6 2 0.00 1.8585
7 8 25.00 25.9292
8 2 0.00 1.8585
9 2 0.00 1.8585
10 2 0.00 1.8585
11 2 0.00 1.8585
12 2 0.00 1.8585
13 2 0.00 1.8585
14 2 0.00 1.8585
15 2 0.00 1.8585
16 2 0.00 1.8585
17 2 0.00 1.8585
18 2 0.00 1.8585
19 2 0.00 1.8585
20 2 0.00 1.8585
21 2 0.00 1.8585
22 2 0.00 1.8585
23 2 0.00 1.8585
24 2 0.00 1.8585
25 2 0.00 1.8585
26 2 0.00 1.8585
27 2 0.00 1.8585
28 2 0.00 1.8585
29 2 0.00 1.8585
30 2 0.00 1.8585
31 2 0.00 1.8585
報酬が大きいとUCB値の影響が小さくなります。
ハイパーパラメータの $\beta$ はこれを調整する値になります。
Retrace
追記:更にリベンジしました。
やっと理解できたと思うRetraceについて丁寧に解説【強化学習】
以下の内容は間違っている内容が含まれているので注意です。
リベンジです。
学習データの収集で使われる方策と学習したい方策が異なる強化学習をオフポリシー強化学習といいます。
Q学習は探索時はε-greedyの方策で、学習したい方策はgreedyな方策(Q値が最大の行動を選択)なのでオフポリシーな強化学習と言えます。
方策は確率分布なので、実際にサンプルする確率分布と求めたい確率分布が異なるという状況です。
こういう状況は一般的には重点サンプリング(IS)という手法を使い値を修正しますが、ISでは分散が大きすぎ(又は無限)たようです。(分散が大きいと学習が安定しません)
そこで上限を1に切り捨てるIS(Retrace)を導入しこの問題を解決したようです。
重点サンプリングについては過去に記事を書いているのでそちらもどうぞ。
- 論文: Safe and Efficient Off-Policy Reinforcement Learning
- 論文の日本語スライド: safe and efficient off policy reinforcement learning
- Safe and efficient off-policy reinforcement learning.
- github: Some_Projects/Python/Reinforcement Learning/project-RL-sim.ipynb
- DeepMindParis: off-policy deep RL
- NEVER GIVE UP: LEARNING DIRECTED EXPLORATION STRATEGIES
学習データの収集で使われる方策を $\mu$、学習したい方策を $\pi$ としています。
Retraceを考える上でのベルマン演算子は以下です。
$\delta$ はTD誤差で以下です。
Retrace は以下です。
$\lambda$は固定値($=1$)です。
オンライン(任意の時刻$t$から$k$ステップ後までの軌跡)では以下になります。
ベルマン演算子は以下のように解釈しました。
$$ NewQ値←Q値 + (割引率 \times Retrace \times TD誤差)_{k-stepの合計} $$
()の中が次の状態の価値(の期待値)を表し、Retrace で確率分布を補正、任意のkステップ先まで見ることができます。
(2step先以降は割引率を適用)
疑問点1
$\prod_{i=t+1}^{s}$ ですが、なぜ $i=t+1$ かが分かっていません。現在のアクションに対してなので $i=t$ な気がするのですが…
また $\mu(a_{t+1}|s_{t+1})$ を計算するのが少し大変な事もあり今回は $i=t$ で実装しています。
疑問点2
Retrace内の $\pi(a_s|x_s)$ と TD誤差内の $\pi(a_s|x_s)$ について同じ記号を使っていますが役割が違う気がします。
Retrace内は探索で使う(理想の)方策、TD誤差内は学習したい方策(テストで使う方策)だと思われます。
検証した結果を後述しています。
ε-greedy の各アクションの確率
Q値が最大のアクションとそうじゃないアクションを分けて考えます。
- Q値が最大値のアクションが選ばれる確率
ε以上とε以下で分けて考えます。
※$|A|$ : アクション数
※$|A_{max}|$ : Q値が最大のアクション数
$$
(1-\epsilon) \times \frac{1}{|A_{max}|} + \epsilon \frac{1}{|A|}
$$
- Q値が最大値じゃないアクションが選ばれる確率
$$
(1-\epsilon) \times 0 + \epsilon \frac{1}{|A|}
$$
実装コード
未来の報酬ですが元のQ学習にならって1step先だけにします。
# --- 確率の計算
def _calc_probs(self, state, epsilon):
# 未知の場所は一様分布
if state not in self.Q:
return [1 / self.nb_actions for _ in range(self.nb_actions)]
q = self.Q[state]
qmax = np.max(q)
qmax_num = q.count(qmax)
probs = []
for a in range(self.nb_actions):
prob = epsilon / self.nb_actions
if q[a] == qmax:
prob += (1 - epsilon) / qmax_num
probs.append(prob)
return probs
# --- アクションを決める箇所
def policy(self, state: np.ndarray) -> tuple[int, Any]:
s = str(state.tolist())
# 確率μ
probs = self._calc_probs(s, self.epsilon)
action = ε-greedy でアクションを決める
prob = probs[action]
return action, (action, prob)
# --- 学習時
def on_step(self, state: np.ndarray, action_: Any, new_state: np.ndarray, reward: float, done: bool):
action = action_[0]
mu_prob = action_[1]
s = str(state.tolist())
n_s = str(new_state.tolist())
# s : x_t
# n_s : x_t+1
# action : a_t
# mu_prob : μ(a_t|x_t)
# reward : r_t
# π(・|x_t)とπ(・|x_t+1)を計算
pi_probs = self._calc_probs(s, self.epsilon) # ε-greedy
n_pi_probs = self._calc_probs(n_s, 0) # greedy
# retrace
h = 1
c = h * np.minimum(1.0, pi_probs[action] / mu_prob)
# td_error
if done:
gain = reward
else:
# 方策πでの期待値
P = 0
for i in range(self.nb_actions):
P += n_pi_probs[i] * self.Q[n_s][i]
gain = reward + self.gamma * P
td_error = gain - self.Q[s][action]
# update , (self.gamma ** 0) = 1 だけど厳密に記載
self.Q[s][action] += self.lr * ((self.gamma ** 0) * c * td_error)
πの考察
表記を、Retrace内の $\pi(a_s|x_s)$ を $\pi_{retrace}$、TD誤差内の $\pi(a_s|x_s)$ を $\pi_{td}$ にします。
$\pi_{retrace}$ の役割は、確率分布 $\mu$ で得たデータに対して確率分布 $\pi_{retrace}$ で得たデータに変換する事です。
$\pi_{retrace}$ で得るべきデータは、探索に使用する方策で得る確率分布なので $\pi_{retrace}$=ε-greedyだと思われます。
次に$\pi_{td}$ですが、次の状態の期待値を計算する時の方策です。(ベルマン方程式の方策)
Q学習では最大値を得る方策なので $\pi_{td}$=greedyです。
CliffWalking-v0 による検証
CliffWalking-v0 はよくQ学習とSarasaを比較する際に使われる環境です。
参考:今さら聞けない強化学習(10): SarsaとQ学習の違い
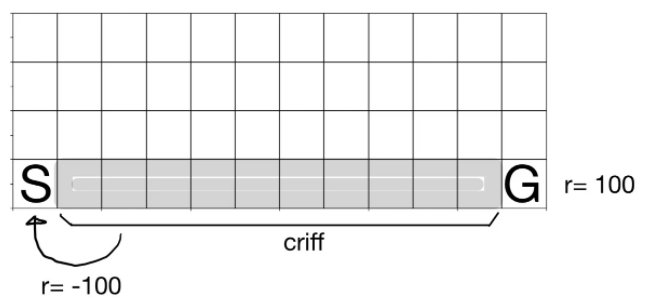
CliffWalking-v0は以下のような環境です
※参考の記事より引用しています
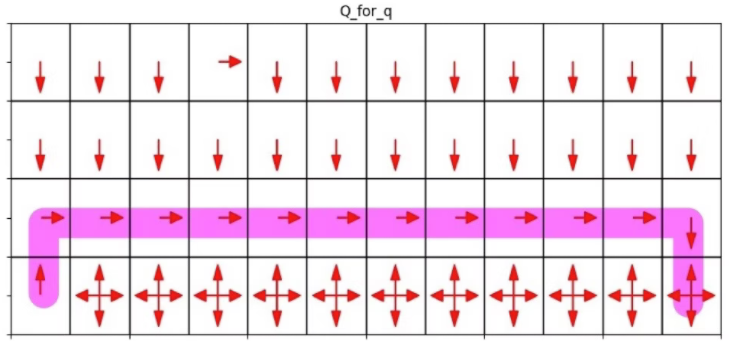
これをQ学習で学習すると以下のような経路になります。
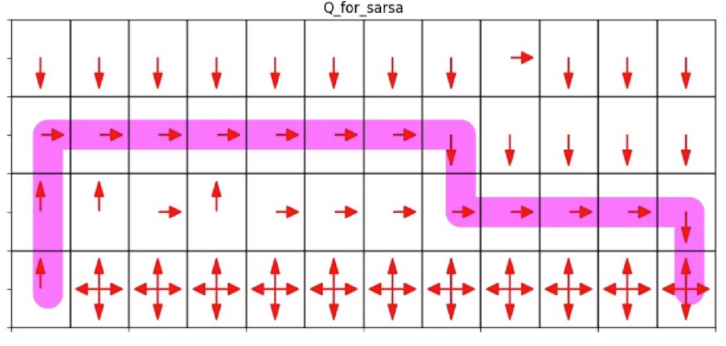
次にSarasaで学習すると以下です。
これらと比較してもらえればと思います。
コードですが、以下の場所のεの値を変えると方策を変更できます。
ε=0にすると greedy な方策です。
epsilon_retrace: float = pi_retraceの方策
epsilon_td: float = pi_tdの方策
pi_probs = self._calc_probs(s, epsilon_retrace)
n_pi_probs = self._calc_probs(n_s, epsilon_td)
結果は以下です。
切れていますが全容を見たい方は colab のコードを見てください。
- Q学習(ベースライン)
retraceを使わない場合です。
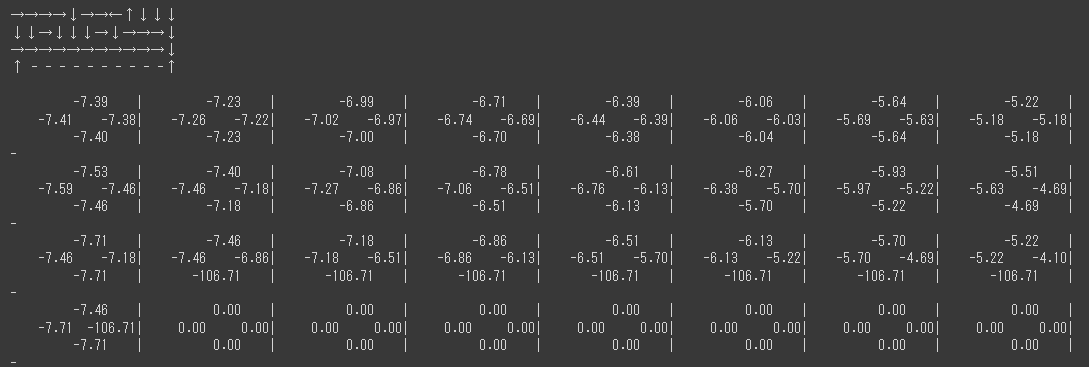
- epsilon_retrace=0, epsilon_td=0
探索の方策が greedy(に補正)、最終的な方策もgreedyなパターンです。
上の方の矢印が整っているのは greedy な探索結果からでしょう。
また、穴に近い場所の伝搬が-10でとどまっているのは2回目以降の伝搬が greedy な探索なため伝搬されなかったからだと思います。
- epsilon_retrace=0.9, epsilon_td=0
探索の方策が ε-greedy(に補正、ε=0.9)、最終的な方策がgreedyなパターンです。
探索はε-greedyに補正されますが、報酬の伝搬がgreedyなためベースラインのQ学習とあまり変わらないと思います。
(ε=0.1に比べε=0.9なのでよりざっくり値が調整されているはず?)
- epsilon_retrace=0, epsilon_td=0.9
探索の方策が greedy(に補正)、最終的な方策がε-greedyなパターンです。
Q学習の方策がε-greedyなパターンがSarasaになるので、Sarasaと同じ結果になりましたね。
報酬がマイナスの近くを避けて少し離れた経路になっています。
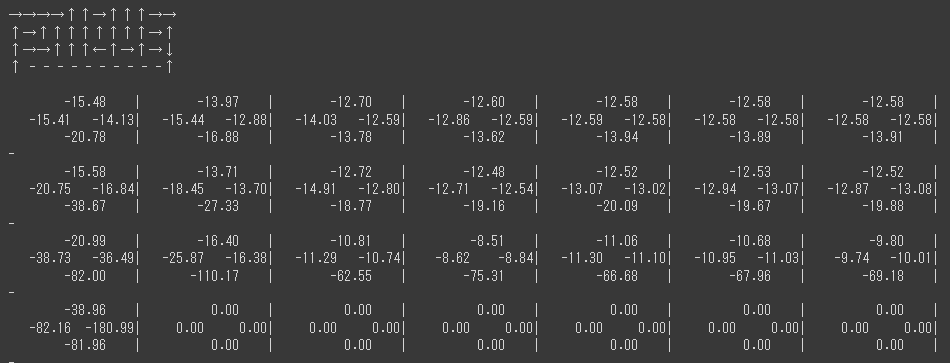
- epsilon_retrace=0.9, epsilon_td=0.9
探索の方策もε-greedy(に補正、ε=0.9)、最終的な方策もε-greedyなパターンです。
εが0.9と高いのでマイナス報酬をかなり避けていますね。
探索が逃げ腰かつ伝搬も逃げ腰なのでそもそもゴールまで経路を組めていません。
以上より、$\pi_{retrace}$ が探索に使いたい方策、$\pi_{td}$ が最終的に求めたい方策なような気がしています。
比較
Colabのコードでは以下の環境についても比較してみていますが、記事が長くなったので詳細は省略します。
- OneRoad(オリジナル)
- FrozenLake-v1(gym)
- CliffWalking-v0(gym)
- Taxi-v3(gum)
- MountainCarContinuous-v0(gym)
あとがき
今回色々調べましたが以前のAgent57も所々間違っていますね。
リベンジするかも知れません。