Actor-Criticの基礎的な手法の1つであるTRPOを実装してみました。
※ネット上の情報をかき集めて自分なりに実装しているので正確ではない可能性がある点はご注意ください
※ライブラリはTensowflow2.0(+Keras)を使っています。
コード全体
本記事で作成したコードは以下です。
TRPO(trust region policy optimization)
第2回で紹介した方策勾配法(Policy Gradient)は以下でした。
$$
\nabla J(\theta) \propto E_{\pi_\theta} [ log \pi_{\theta}(a|s) A^{\pi_\theta}(s,a) ]
$$
方策勾配法では方策パラメータ $\theta$ の更新方向を教えてくれましたが、更新幅までは分かりませんでした。
$\theta$ を大きく更新してしまうと方策が全く違うものになり、もし方策が劣化すると悪い経験を収集しさらに劣化するという負のスパイラルに陥ります。
逆に更新幅を小さくしてしまうと学習がなかなか進みません。
そこで、この更新幅をKL距離(Kullback-Leibler Distance)で制約をかけて更新する手法がTRPOとなります。
参考
TRPOの制約条件
以下が制約条件です。
\begin{align}
\underset{\theta}{\text{maximize}} L(\theta) \\
L(\theta) = E[ \frac{\pi_{\theta} (a|s)}{ \pi_{\theta_{old}}(a|s)} A^{\pi_\theta }(s,a) ]\\
subject \ to \ E [ D_{KL}(\pi_{\theta_{old}} || \pi_{\theta}) ] \leq \delta
\end{align}
制約ですが、更新前の行動分布 $\pi_{\theta_{old}}$ と更新後の行動分布 $\pi_{\theta}$ のKL距離 $D_{KL}$ が $\delta$ 以下になるように制約をかけます。($\delta$は任意の定数)
この制約下で Advantage $A^{\pi_\theta}(s,a)$ の期待値が最大となるように更新していきます。
また、Advantage は更新前後の変化に応じて重み $\frac{\pi_{\theta} (a|s)}{ \pi_{\theta_{old}}(a|s)}$ が掛けられます。
これは重点サンプリング(Importance Sampling)といい、求めたい期待値の確率分布とサンプリングされた際の確率分布が異なる場合、その差分を埋める手法となります。
今回ですとサンプル $A^{\pi_\theta}$ は $\pi_{\theta_{old}}$ から集まったサンプルになり、求める確率分布は $\pi_{\theta}$ になるのでISしています。
次にKL距離ですが、これは2つの確率分布の差異を図る尺度です。
このKL距離が $\delta$ 以下になるように制約をかけることで大きい方策の更新を抑えます。
重点サンプリング
重点サンプリングについては他でも結構でてくるのでもう少し見てみます。
参考
例としてある未知の関数 $f(x)$ の期待値 $E$ を計算する場合を考えます。
$$ E(X) = \int p(x) f(x) dx$$
ここで $p(x)$ は確率分布になります。
この時、期待値を求める方法の1つにモンテカルロ積分があります。
モンテカルロ積分は、確率分布 $p(x)$ から$N$個のサンプル($x_1, ...,x_N$)を生成し、以下の式で近似する手法です。
$$ E(X) \fallingdotseq \frac{1}{N} \sum_{n=1}^N f(x_n)$$
実際に見てみます。
\begin{align}
f(x) &= 2x \\
p(x) &= \frac{1}{a-b}(一様分布)\\
0 &\leqq x \leqq 2 \\
\end{align}
この場合の期待値は以下です。
\begin{align}
E(X) =& \int_0^{2} \frac{1}{2}2x dx \\
=& \begin{bmatrix} \frac{x^2}{2} \end{bmatrix}_0^{2} \\
=& 2 \\
\end{align}
これをモンテカルロ積分で解いてみます。
import numpy as np
import scipy.integrate
def f(x):
return 2 * x
def p(x):
# 範囲外をとる確率は0%
if x < 0 or 2 < x:
return 0
return 1/2
#--- 積分(真の期待値)
I = scipy.integrate.quad(lambda x: f(x) * p(x), -np.inf, np.inf)[0]
print("scipy.integrate: {}".format(I)) # 1.9999999999999938
#--- モンテカルロ積分
# サンプリング
samples = []
for _ in range(10000):
# 一様分布に従う0~2の乱数を出す
x = np.random.rand() * 2
# 未知の関数の結果を取得
samples.append(f(x))
# サンプル値の平均が期待値
print("MC: {}".format(np.mean(samples))) # 1.9869423645827053
ここでサンプリングする際の確率分布が違う場合の計算方法が重点サンプリングになります。
変える一番大きな理由はサンプリングの領域を変えたい場合などです。
例えば高次元空間において、本当に欲しいサンプルが狭い領域にある場合は一様分布でサンプリングすると、広範囲にまたがってしまい非常に効率が悪いです。
ですので、サンプリング範囲を狭める為に確率分布を変えたりする感じです。
強化学習ではサンプリング時の確率分布が変わってしまうので修正するって感じですけど。
重点サンプリングでは新しく重点関数 $g(x)$ を導入して以下の計算式を採用します。
$$ E(X) = \int g(x) \Bigl( \frac{p(x)}{g(x)} f(x) \Bigr) dx$$
$\frac{g(x)}{g(x)}$ を掛けただけです。
ここで $g(x)$ を元のモンテカルロ積分の確率分布、$\frac{p(x)}{g(x)} f(x)$ を未知の関数と考えます。
すると期待値は以下の通り近似できます。
$$ E(X) \fallingdotseq \frac{1}{N} \sum_{n=1}^N \frac{p(x)}{g(x)} f(x)$$
では先ほどの例で、サンプリング時の確率分布を標準正規分布に変更してみてみます。
# 正規分布
def normal(x, mean, stddev):
stddev = stddev ** 2
a1 = (2 * np.pi * stddev) ** (-1/2)
a2 = np.exp( - ((x - mean) ** 2) / (2 * stddev))
return a1 * a2
# サンプリング
samples = []
for _ in range(10000):
# 標準正規分布に従う乱数を出す
x = np.random.normal(0, 1)
# ISを計算
weight = p(x) / normal(x, 0, 1)
samples.append(weight * f(x))
# サンプル値の平均が期待値
print("IS: {}".format(np.mean(samples))) # 2.073728329238663
ちゃんと2に近い値になりましたね。
念のため未知の関数を $x^4$ に変更した場合も見てみました。(他の条件は同じ)
def f(x):
return x ** 4
#--- 積分(真の期待値)
I = scipy.integrate.quad(lambda x: f(x) * p(x), -np.inf, np.inf)[0]
print("scipy.integrate: {}".format(I)) # 3.2000000000000037
#--- モンテカルロ積分
samples = []
for _ in range(10000):
x = np.random.rand() * 2
samples.append(f(x))
print("MC: {}".format(np.mean(samples))) # 3.2414563258042945
#--- IS
samples = []
for _ in range(10000):
x = np.random.normal(0, 1)
samples.append(f(x) * p(x) / normal(x, 0, 1))
print("IS: {}".format(np.mean(samples))) # 3.2536320585828973
KLダイバージェンス(Kullback-Leibler divergence)
KL距離(KLダイバージェンス)は2つの確率分布の差の大きさを測る尺度です。
2つの確率分布 $p,q$ のKL距離は以下となります。
- 離散値
$$
KL(p||q) = \sum_x p(x) \log \frac{p(x)}{q(x)}
$$
コード例
def compute_kl_discrete(probs1, probs2):
return tf.reduce_sum(probs1 * tf.math.log(probs1 / probs2))
probs1 = tf.Variable([[0.25, 0.25], [0.25, 0.25]], dtype=tf.float32)
probs2 = tf.Variable([[0.25, 0.25], [0.2, 0.3]], dtype=tf.float32)
probs3 = tf.Variable([[0.25, 0.25], [0.25, 0.25]], dtype=tf.float32)
probs4 = tf.Variable([[0.25, 0.25], [0.1, 0.4]], dtype=tf.float32)
kl1 = compute_kl_discrete(probs1, probs2)
kl2 = compute_kl_discrete(probs3, probs4)
print(kl1) # 0.010205492377281189
print(kl2) # 0.1115717813372612
assert kl1.numpy() < kl2.numpy()
- 連続値
$$
KL(p||q) = \int_{-\infty}^{\infty} p(x) \log \frac{p(x)}{q(x)}dx
$$
今回連続値で扱う確率分布が正規分布になるので、その場合のKL距離を計算しておきます。
$p,q$ が正規分布の場合のKL距離は以下です。
\begin{align}
p(x) = N(\mu_1, \sigma_1^2) \\
q(x) = N(\mu_2, \sigma_2^2)
\end{align}
$$
KL(p||q) = \log( \frac{\sigma_2}{\sigma_1}) + \frac{\sigma_1^2 + (\mu_1 - \mu_2)^2}{2 \sigma_2^2} - \frac{1}{2}
$$
コード例
def compute_kl_discrete_normal(mean1, stddev1, mean2, stddev2):
a1 = tf.math.log(stddev2 / stddev1)
a2 = (tf.square(stddev1) + tf.square(mean1 - mean2)) / (2.0 * tf.square(stddev2))
a3 = -0.5
return a1 + a2 + a3
means1 = tf.Variable([0.], dtype=tf.float32)
stdevs1 = tf.Variable([1.], dtype=tf.float32)
means2 = tf.Variable([1.], dtype=tf.float32)
stdevs2 = tf.Variable([2.], dtype=tf.float32)
kl = compute_kl_discrete_normal(means1, stdevs1, means2, stdevs2)
print(kl) # [0.44314718]
参考:
制約付き最大化問題
ここの計算(途中の計算含む)や解説の詳細はハムスターでもわかるTRPOを参照してください。
TRPOは制約付き最大化問題を解くことになります。
解き方ですが、まず制約条件をテイラー展開します。
その結果が以下です。
\begin{align}
L(\theta) &\simeq g^T (\theta - \theta_{old})\\
D_{KL}(\pi_{\theta_{old}} || \pi_{\theta}) &\simeq \frac{1}{2} (\theta - \theta_{old})^T H(\theta - \theta_{old})
\end{align}
この式に対してラグランジュの未定乗数法(ある制約下で関数の最大化を求める手法)を使って計算した結果が以下です。
$$
\theta = \theta_{old} + \sqrt{ \frac{2 \delta}{s'^T Hs}} H^{-1}g
$$
各記号の数式は以下になり、$H$ はKLダイバージェンスの二階微分(ヘッセ行列:ヘシアン:Hessian)です。
\begin{align}
g =& \nabla_{\theta} \frac{\pi_{\theta} (a|s)}{ \pi_{\theta_{old}}(a|s)} A^{\pi_\theta }(s,a) \\
H =& \nabla_\theta^2 D_{KL}(\pi_{\theta_{old}} || \pi_{\theta}) \\
s' =& H^{-1}g
\end{align}
パラメータの更新式は上記ですが、テイラー展開により近似しているのでこの式通り更新しても、「KL制約を満たさない」または「$L(\theta)$が改善されない」可能性があります。
そこでTRPOではまず式の更新を行った後、「KL制約を満たす」と「$L(\theta)$が改善される」を確認し、満たさない場合は更新幅を満たすまで減少させます。
g の実装
上記数式の $g$ の実装例です。
policy_model = 方策モデル
value_model = 価値モデル
states = 状態
actions = アクション
v_vals = モンテカルロ法やGAE等で集めた割引報酬
# 更新前のアクションの確率or確率分布を計算 π_old(a|s)
prob_eval = policy_model(states)
old_pi = actionsとprob_evalからアクションの確率or確率分布を計算
# 勾配の計算式を定義
with tf.GradientTape() as tape:
prob_eval = policy_model(states, training=True)
new_pi = actionsとprob_evalからアクションの確率or確率分布を計算
# g の計算式
loss = (new_pi / old_pi) * advatage
# ミニバッチ処理
loss = tf.reduce_mean(loss)
# 勾配を計算 ∇ π(a|s) / π_old(a|s) A(s|a)
g = tape.gradient(loss, policy_model.trainable_variables)
s'とH の計算
計算するまでにヘシアンの計算、共役勾配法、ヘシアンとベクトルの積(Hessian vector product)を理解する必要があります。
ヘシアン(ヘッセ行列)の計算
ヘッセ行列はある関数において、パラメータすべてに対して二階偏微分した行列です。
$$ H(f)_{ij}(x) = \nabla_i \nabla_j f(x) $$
例として $f(x,y) = x^3 + x^2 y + y^2$ の場合は以下になります。(WolframAlpha計算知能の結果)
\nabla f(x, y) =
\begin{bmatrix}
3 x^2 + 2xy\\
x^2 + 2y\\
\end{bmatrix}
H f(x_1, x_2) =
\begin{bmatrix}
6x + 2y & 2x\\
2x & 2\\
\end{bmatrix}
$x=2,y=1$ の場合は以下です。
H f(2, 1) =
\begin{bmatrix}
14 & 4\\
4 & 2\\
\end{bmatrix}
tensorflow での実装はヤコビアンの計算例にヘシアンの計算があったので参考にしました。
TensorFlow > 学ぶ > TensorFlow Core > ガイド > 高度な自動微分
tensorflow では二階微分はネストを使って書く事ができます。
また、persistent=True にすることで複数回微分することができます。(自分で開放する必要あり)
愚直に書くと以下です。
def f(x):
return x[0] ** 3 + (x[0] ** 2) * (x[1]) + x[1] ** 2
x = tf.Variable([2.0, 1.0], dtype=tf.float32)
with tf.GradientTape(persistent=True) as t2:
with tf.GradientTape() as t1:
y = f(x)
dy1, dy2 = t1.gradient(y, x)
h11, h12 = t2.gradient(dy1, x)
h21, h22 = t2.gradient(dy2, x)
del t2
h = tf.convert_to_tensor([[h11, h12], [h21, h22]])
tf.print(h) # [[14 4] [4 2]]
ヤコビアンを使うと微分部分は以下のように書けます。
with tf.GradientTape() as t2:
with tf.GradientTape() as t1:
y = f(x)
dy = t1.gradient(y, x)
h = t2.jacobian(dy, x)
tf.print(h) # [[14 4] [4 2]]
共役勾配法
計算ではヘシアンの逆行列が必要です。
しかし、逆行列の計算はO(N^3)のコストがかかるため計算が大変です。
そこで共役勾配法を使い、逆行列の計算を回避します。
参考
$s' = H^{-1}g$ の式を以下のように変形します。
$$
H s' = g
$$
これは連立一次方程式 $Ax=b$ と同じ形です。
共役勾配法は $Ax=b$ に対して x の近似解を求めるアルゴリズムです。
これにより $H^{-1}$ を計算せずに $s'$ を求めます。
アルゴリズムの実装は英語版wikipediaの疑似コードを元に作成しました。
def solve_CG(A, b, iters=10):
x = tf.zeros_like(b)
r = b # r=b-A*x だけどx=0なのでr=b
p = r
# 反復法なので一定回数繰り返す
for i in range(iters):
Ap = tf.matmul(A, p)
rTr = tf.matmul(tf.transpose(r), r)
a = rTr / tf.matmul(tf.transpose(p), Ap)
x = x + a * p
r = r - a * Ap
new_rTr = tf.matmul(tf.transpose(r), r)
if tf.sqrt(new_rTr) < 1e-10:
break
b = new_rTr / rTr
p = r + b * p
return x
H = tf.Variable([[1,0,0],[0,2,0],[0,0,1]], dtype=tf.float32)
g = tf.Variable([[4],[5],[6]], dtype=tf.float32)
#--- Hの逆行列×ベクトル
invH = tf.linalg.inv(H)
invHg = tf.matmul(invH, g)
print(invHg) # [[4. ], [2.5], [6. ]]
#--- 共役勾配法
x = solve_CG(H, g)
print(x) # [[4. ], [2.5], [6. ]]
Hessian vector product
共役勾配法を用いてもヘシアンを計算する必要があります。(Ap = tf.matmul(A, p)の部分)
ただ計算上はヘシアンとベクトルの積(Hessian vector product:Fisher vector product)を計算すればよく、これは効率よく計算する方法があります。
参考:Efficiently Computing the Fisher Vector Product in TRPO
アルゴリズムはヘシアンの1次導関数ベクトルに対して対象ベクトルの積を計算し、その得られたスカラーに対して微分する方法です。
(数式は参考より引用)
$$ y_k = \sum_j H_{kj}x_j =
\frac{\partial}{\partial \theta_k}
\sum_j \frac{\partial D_{KL}}{\partial \theta_j} x_j$$
アルゴリズムの実装は上記参考のコードを参考にしました。
def compute_Hvp(f, x, v):
with tf.GradientTape() as t2:
with tf.GradientTape() as t1:
y = f(x)
grads = t1.gradient(y, x)
# matmulはバッチ処理もしているので1次元追加
grads = tf.reshape(grads, (1, -1))
grads_vector_product = tf.matmul(grads, v)
hvp = t2.gradient(grads_vector_product, x)
hvp = tf.reshape(hvp, (-1, 1)) # ベクトルとshapeを合わせる
return hvp + v * 1e-2 # 共役勾配法の安定化のために微小量を加える
ヘシアンの計算で確認した例と同じ例で確認してみます。
# ヘシアンの計算と同じ例です
def f(x):
return x[0] ** 3 + (x[0] ** 2) * (x[1]) + x[1] ** 2
x = tf.Variable([2.0, 1.0], dtype=tf.float32)
# 計算過程は省いて直接ヘシアンを作ります
h = tf.Variable([[14.0, 4.0], [4.0, 2.0]], dtype=tf.float32)
# 対象ベクトル
g = tf.convert_to_tensor([[3], [12], [6]], dtype=tf.float32)
#--- 積
tf.print(tf.matmul(h, g)) # [[58] [20]]
#--- HVP
hvp = compute_Hvp(f, x, g)
tf.print(hvp) # [[58.03] [20.04]]
実装
実装に関してはハムスターでもわかるTRPO ③tensorflow2での実装例を主に参考にさせてもらっています。
実装1、CartPole-v0
環境は gym.make("CartPole-v0") です。
| アクション | 状態価値の推定 | 方策価値の推定 |
|---|---|---|
| 離散 | Multistep-learning | Multistep-learning |
| ハイパーパラメータ | |
|---|---|
| 学習回数 | 500step |
| batch_size | 256 |
| 割引率 | 0.9 |
| KL制約閾値 | 0.01 |
価値推定方法
価値推定方法に関しては第3回を見てください。
今回は状態価値と方策価値両方とも Multistep lerning を採用しています。
$$ r_{t+1} + \gamma r_{t+2} ... + \gamma^{t+n-1} V(s_{t+n}) $$
また、ベースラインとして平均値を引いています。
コードは第3回とほぼ変わらないので省略します。
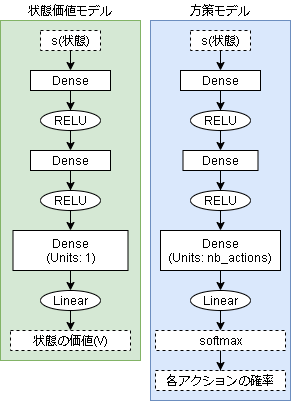
モデル
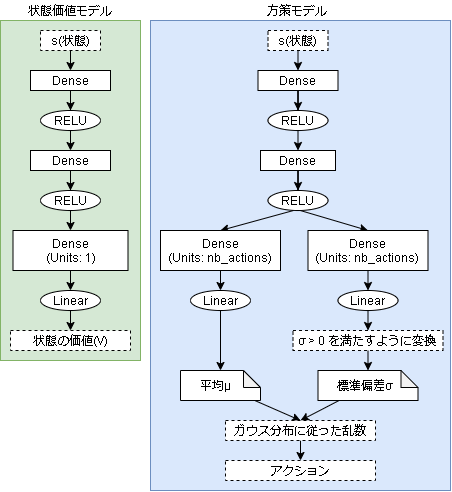
状態価値モデルと方策モデルの2つのモデルを使います。(なのでActor-Criticですね)
状態価値モデル
状態の価値を学習するだけのシンプルなモデルです。
更新式は以下です。
$$ V(s_t) \leftarrow V(s_t) + \alpha(推定価値 - V(s_t)) $$
#--- モデルの定義
obs_shape = env.observation_space.shape # 入力の状態shape
nb_actions = env.action_space.n # 出力のアクション数
c = input_ = keras.layers.Input(shape=obs_shape)
c = keras.layers.Dense(16, activation="relu")(c)
c = keras.layers.Dense(16, activation="relu")(c)
c = keras.layers.Dense(1, activation="linear")(c)
value_model = keras.Model(input_, c)
value_model.compile(optimizer=Adam(lr=0.01), loss="mse")
value_model.summary()
学習は以下です。
states = 状態
v_vals = 推定した価値
# 学習
value_model.train_on_batch(states, v_vals)
方策モデル
lossの計算だけではなく、重みの更新も自作します。
# 独自のモデルを定義
class PolicyModel(keras.Model):
def __init__(self, action_space):
super().__init__()
self.nb_actions = action_space.n
# 各レイヤーを定義
self.dense1 = keras.layers.Dense(16, activation="relu")
self.dense2 = keras.layers.Dense(16, activation="relu")
self.dense3 = keras.layers.Dense(self.nb_actions, activation="linear")
# Forward pass
def call(self, inputs, training=False):
x = self.dense1(inputs)
x = self.dense2(x)
x = self.dense3(x)
# softmaxで各アクションの確率を出す
x = tf.nn.softmax(x)
return x
# 確率に基づいてアクションを出力
def sample_action(self, state):
probs = self(state.reshape((1,-1)))
return np.random.choice(self.nb_actions, 1, p=probs[0].numpy())[0]
学習にあたりモデルの重みを直接操作します。
モデルの重みは階層構造になっており、そのままだと計算できないので平坦化⇔復元できる関数を用意しておきます。
# パラメーターをフラット化
def params_flatten(params):
params_list = [tf.reshape(layer, [1, -1]) for layer in params]
params_list = tf.concat(params_list, axis=1)
return tf.reshape(params_list, [-1])
# フラットなパラメータをモデルの構造に復元
from functools import reduce
def params_restore_shape(flat_params, model):
n = 0
weights = []
for layer in model.trainable_variables:
# shape のサイズを計算(各要素を掛け合わせる)
size = reduce(lambda a, b: a*b, layer.shape)
w = tf.reshape(flat_params[n:n+size], layer.shape)
weights.append(w)
n += size
return weights
# 適当なモデル
model = keras.Sequential([
keras.layers.Dense(2, activation="relu"),
keras.layers.Dense(3, activation="relu"),
keras.layers.Dense(1),
])
x = np.asarray([[0.5, 0.4]])
y = model(x)
params = model.trainable_variables
# (2, 2)
# (2,)
# (2, 3)
# (3,)
# (3, 1)
# (1,)
for param in params:
print(param.shape)
flat_params = params_flatten(params)
# (19,)
print(flat_params.shape)
restore_params = params_restore_shape(flat_params, model)
# (2, 2)
# (2,)
# (2, 3)
# (3,)
# (3, 1)
# (1,)
for param in restore_params:
print(param.shape)
# setしてみて確認
model.set_weights(restore_params)
restore_y = model(x)
assert y == restore_y # True
学習は以下です。
gamma = 0.9 # 割引率
MAX_KL = 0.01 # KL制約の閾値
states = 状態
actions = アクション
v_vals = 推定した価値
#--- pi(各アクションの確率)の計算
onehot_actions = tf.one_hot(actions, nb_actions)
old_action_probs = policy_model(states)
old_pi = tf.reduce_sum(onehot_actions * old_action_probs, axis=1, keepdims=True)
#--- g の計算
# g の計算式を定義
with tf.GradientTape() as tape:
new_action_probs = policy_model(states, training=True)
new_pi = tf.reduce_sum(onehot_actions * new_action_probs, axis=1, keepdims=True)
loss = (new_pi / old_pi) * v_vals
loss = tf.reduce_mean(loss) # ミニバッチ
# g を計算
g = tape.gradient(loss, policy_model.trainable_variables)
# gの形式を変更 params shape -> (flat size, 1)
g = tf.reshape(params_flatten(g), (-1, 1))
#--- s の計算
# Hessian vector product の定義
@tf.function
def hvp_func(v):
with tf.GradientTape() as t2:
with tf.GradientTape() as t1:
new_action_probs = policy_model(states, training=True)
# KL距離の計算
t = tf.math.log(old_action_probs / new_action_probs)
kl = tf.reduce_sum(old_action_probs * t, axis=1, keepdims=True)
mean_kl = tf.reduce_mean(kl) # ミニバッチ
grads = t1.gradient(mean_kl, policy_model.trainable_variables)
grads = tf.reshape(params_flatten(grads), (1, -1))
grads_vector_product = tf.matmul(grads, v)
hvp = t2.gradient(grads_vector_product, policy_model.trainable_variables)
hvp = tf.reshape(params_flatten(hvp), (-1, 1)) # ベクトルとshapeを合わせる
return hvp + v * 1e-2 # 共役勾配法の安定化のために微小量を加える
# 共役勾配法で s を計算
step_direction = solve_CG(hvp_func, g)
#--- 更新幅を計算
shs = tf.matmul(tf.transpose(step_direction), hvp_func(step_direction))
lm = tf.sqrt(2 * MAX_KL / shs)
fullstep = lm * step_direction
# 更新幅をモデルの構造に復元する
fullstep = params_restore_shape(fullstep, policy_model)
# 更新前の情報を保存
old_params = [var.numpy() for var in policy_model.trainable_variables]
old_loss = loss
#--- 条件を満たすように更新
# KL制約を満たすか、目的関数を改善するかをチェック
# そうでなければ更新幅を小さくしていく
for stepsize in [0.5 ** i for i in range(10)]:
# モデルを更新
new_params = [p + step * stepsize for p, step in zip(old_params, fullstep)]
policy_model.set_weights(new_params)
# 新しいpi
new_action_probs = policy_model(states)
new_pi = tf.reduce_sum(onehot_actions * new_action_probs, axis=1, keepdims=True)
# KL距離
kl = old_action_probs * tf.math.log(old_action_probs / new_action_probs)
kl = tf.reduce_sum(kl, axis=1, keepdims=True)
mean_kl = tf.reduce_mean(kl)
if mean_kl > MAX_KL:
continue # KL制約が満たせていないのでステップ縮小
# 新しいlossを計算
new_loss = (new_pi / old_pi) * v_vals
new_loss = tf.reduce_mean(new_loss)
if new_loss < old_loss:
continue # 目的関数が改善していないのでステップサイズ縮小
# 更新成功
break
else:
# 更新失敗
policy_model.set_weights(old_params)
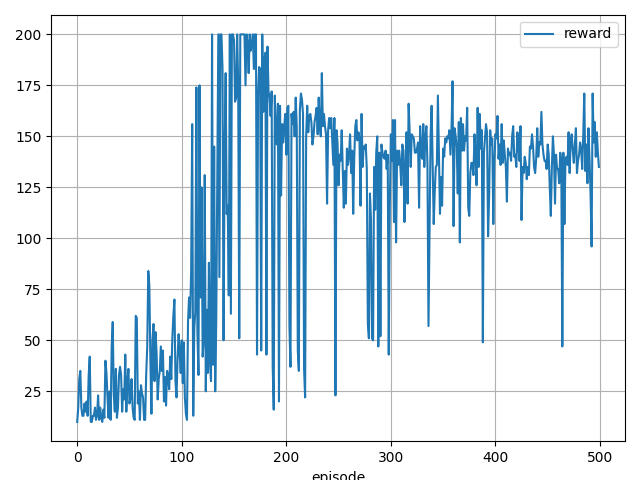
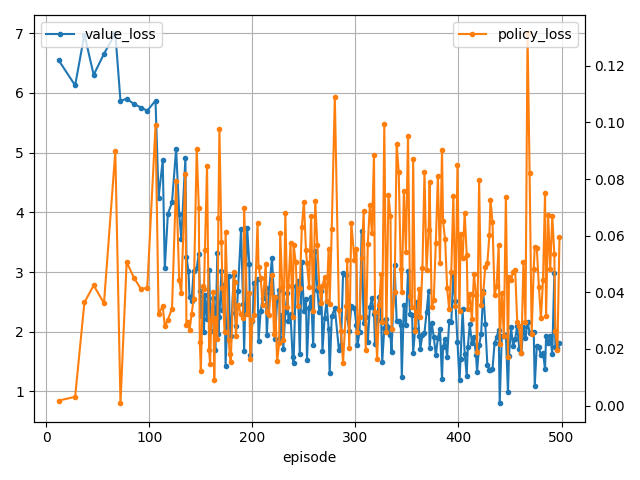
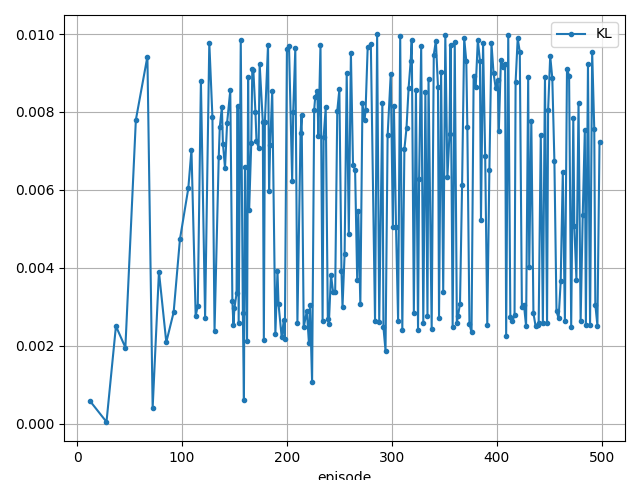
実行結果
172 step, reward: 172.0
142 step, reward: 142.0
191 step, reward: 191.0
155 step, reward: 155.0
136 step, reward: 136.0
実装2、Pendulum-v0
学習できたので連続値の学習としては Pendulum-v0 を試してみました。
Pendulum-v0 を簡単に言うと、左右に棒を動かして上側で棒を立たせ続ける環境です。
最初に棒を持ち上げるタスク、持ち上げた後に棒を維持するタスク、と2つのタスクを同時に学習する必要がありCartpoleより難易度が高い環境となります。
TRPOのパラメータは以下です。
| アクション | 状態価値の推定 | 方策価値の推定 |
|---|---|---|
| 連続 | Multistep-learning | GAE |
| ハイパーパラメータ | |
|---|---|
| 学習回数 | 1000step |
| batch_size | 512 |
| 割引率 | 0.9 |
| GAE割引率 | 0.98 |
| KL制約閾値 | 0.01 |
価値推定方法
方策モデルの価値推定はGAEを採用しています。(Multistep-learningより学習が安定したため)
状態価値モデルではGAEが使えない(方策勾配法ではない)ので、Multistep-learning を採用しています。
コードは第3回とほとんど変わらないので省略します。
モデル
状態価値モデルは変更ありません。
方策モデルは連続値用に変更しています。(ガウス分布です)
学習コードは実装1と比べて主に確率の計算が違うだけなのでそこだけ記載しておきます。
# 平均、分散、アクションから log(π(a|s))を計算する関数
def compute_logpi(mean, stddev, action):
a1 = -0.5 * np.log(2*np.pi)
a2 = -tf.math.log(stddev)
a3 = -0.5 * (((action - mean) / stddev) ** 2)
return a1 + a2 + a3
#--- log(π(a|s))の計算
means, stddevs = policy_model(states)
logpi = compute_logpi(means, stddevs, actions)
# KL距離の計算
def compute_kl_discrete_normal(mean1, stddev1, mean2, stddev2):
a1 = tf.math.log(stddev2 / stddev1)
a2 = (tf.square(stddev1) + tf.square(mean1 - mean2)) / (2.0 * tf.square(stddev2))
a3 = -0.5
return a1 + a2 + a3
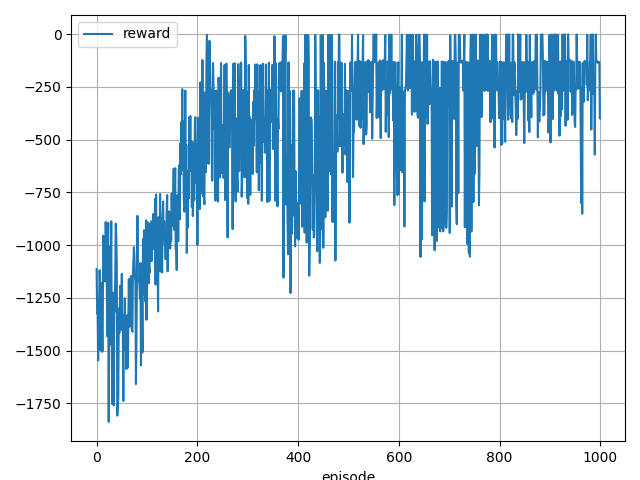
実行
200 step, reward: -1.477869693887614
200 step, reward: -377.33243182319256
200 step, reward: -276.0575733649071
200 step, reward: -131.04692614229117
200 step, reward: -274.1824092081488
あとがき
TRPOはバッチサイズが大きいほうが安定する気がします。
連続値でもかなり安定して学習できる印象です。
ただ、使われている手法が多く計算もかなり複雑でした…