はじめに
EMアルゴリズムに出てくるKLダイバージェンスがよくわからなかったので、正規分布間のKLダイバージェンスを求めることでイメージを掴みたいと思います。
KLダイバージェンス
Kullback-Leibler divergence ( KLダイバージェンス、KL情報量 )は、2つの確率分布がどの程度似ているかを表す尺度です。
定義は以下になります。
KL(p||q) = \int_{-\infty}^{\infty}p(x)\ln \frac{p(x)}{q(x)}dx
重要な特性が2点あります。
1つ目は、同じ確率分布では0となるということです。
KL(p||p) = \int_{-\infty}^{\infty}p(x)\ln \frac{p(x)}{p(x)}dx
= \int_{-\infty}^{\infty}p(x)\ln(1)dx
= 0
2つ目は、常に0を含む正の値となり、確率分布が似ていない程、大きな値となるということです
これらの特性について正規分布の実例を用いて見ていきます。
正規分布
正規分布の確率密度関数p(x)とq(x)を下記のように定義します。
p(x) = N(\mu_1,\sigma_1^2) = \frac{1}{\sqrt{2\pi\sigma_1^2}} \exp\left(-\frac{(x-\mu_1)^2}{2\sigma_1^2}\right) \\
q(x) = N(\mu_2,\sigma_2^2) = \frac{1}{\sqrt{2\pi\sigma_2^2}} \exp\left(-\frac{(x-\mu_2)^2}{2\sigma_2^2}\right)
正規分布間のKLダイバージェンス
上記2つの正規分布間のKLダイバージェンスを求めます。計算は省略します。
\begin{eqnarray}
KL(p||q)&=& \int_{-\infty}^{\infty}p(x)\ln \frac{p(x)}{q(x)}dx \\
&=& \cdots \\
&=& \ln\left(\frac{\sigma_2}{\sigma_1}\right) + \frac{\sigma_1^2+(\mu_1-\mu_2)^2}{2\sigma_2^2} - \frac{1}{2}
\end{eqnarray}
変数が4つもあると分かりにくいので、$p(x)$を平均0、分散1の標準正規分布$N(0,1)$とします。
p(x) =N(0,1)= \frac{1}{\sqrt{2\pi}} \exp\left(-\frac{x^2}{2}\right)
平均が変数のとき
まずは、$q(x)$の標準偏差$\sigma_2$を1として、平均$\mu_2$のみを変数とします。
q(x) =N(\mu_2,1)= \frac{1}{\sqrt{2\pi}} \exp\left(-\frac{(x-\mu_2)^2}{2}\right)
この時のKLダイバージェンスは、
\begin{eqnarray}
KL(p||q) &=& \ln\left(\frac{\sigma_2}{\sigma_1}\right) + \frac{\sigma_1^2+(\mu_1-\mu_2)^2}{2\sigma_2^2} - \frac{1}{2} \\
&=& \ln\left(\frac{1}{1}\right) + \frac{1^2+(\mu_1-0)^2}{2*1^2} - \frac{1}{2} \\
&=& \frac{\mu_2^2}{2}
\end{eqnarray}
となります。
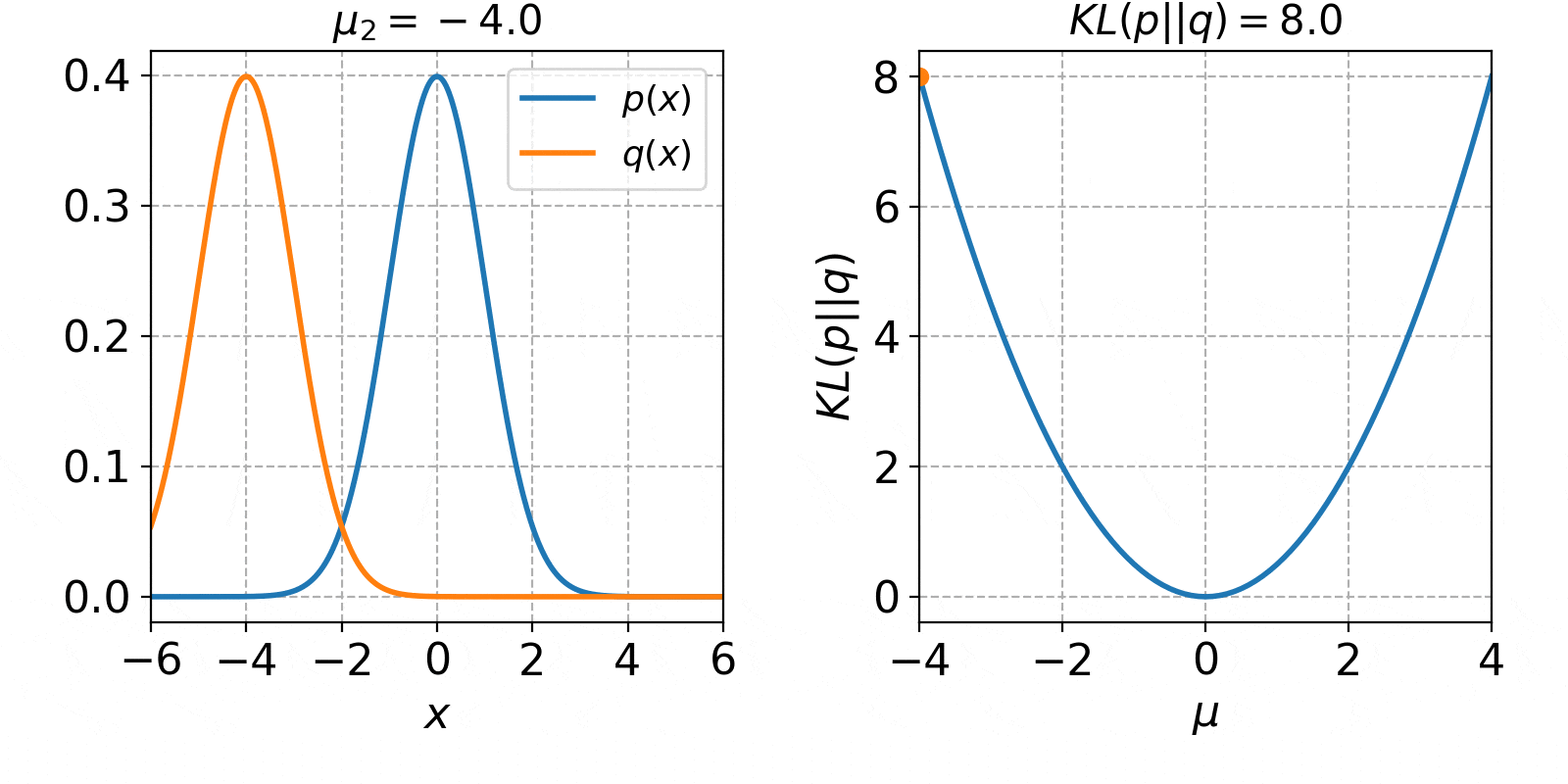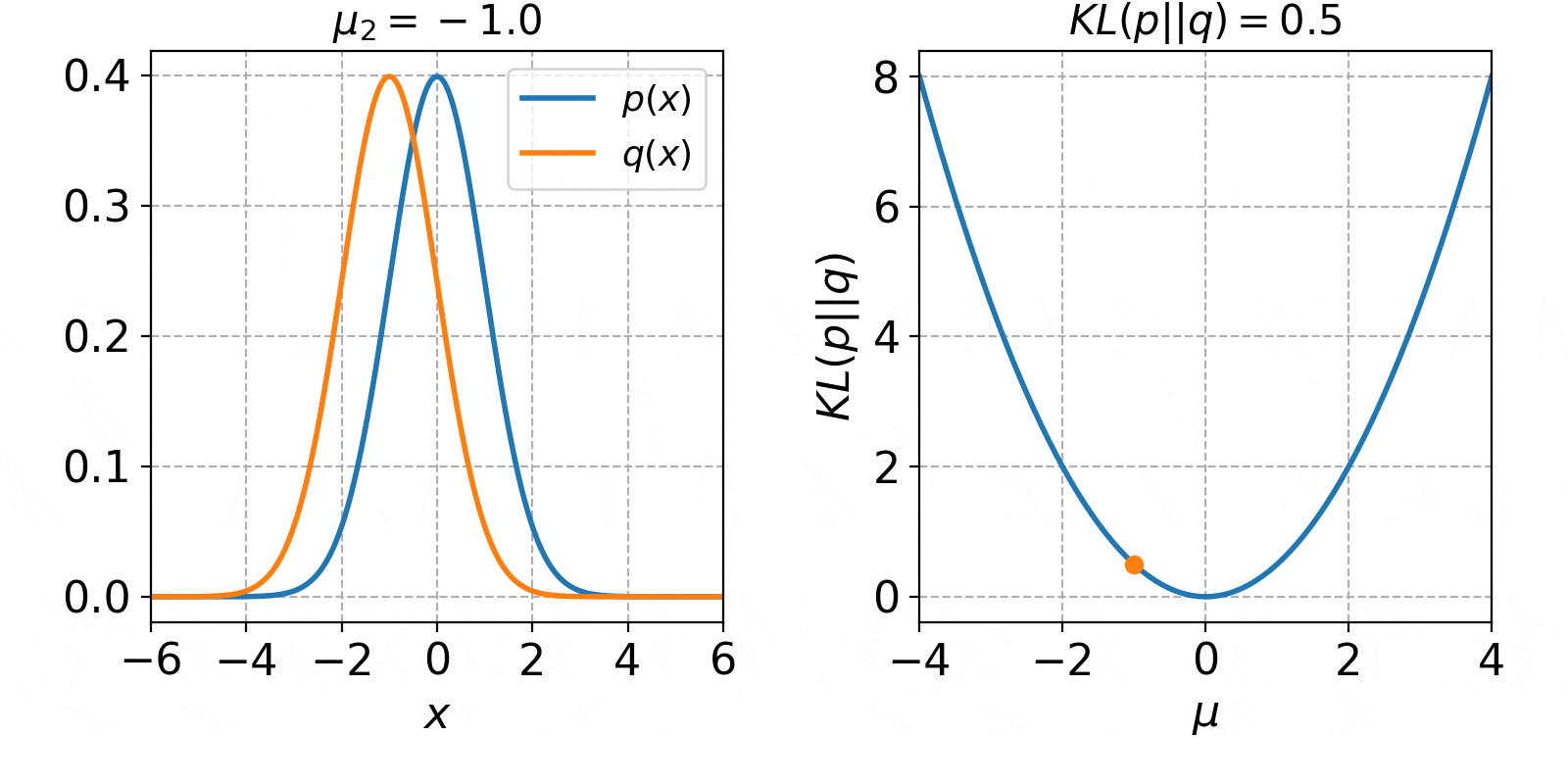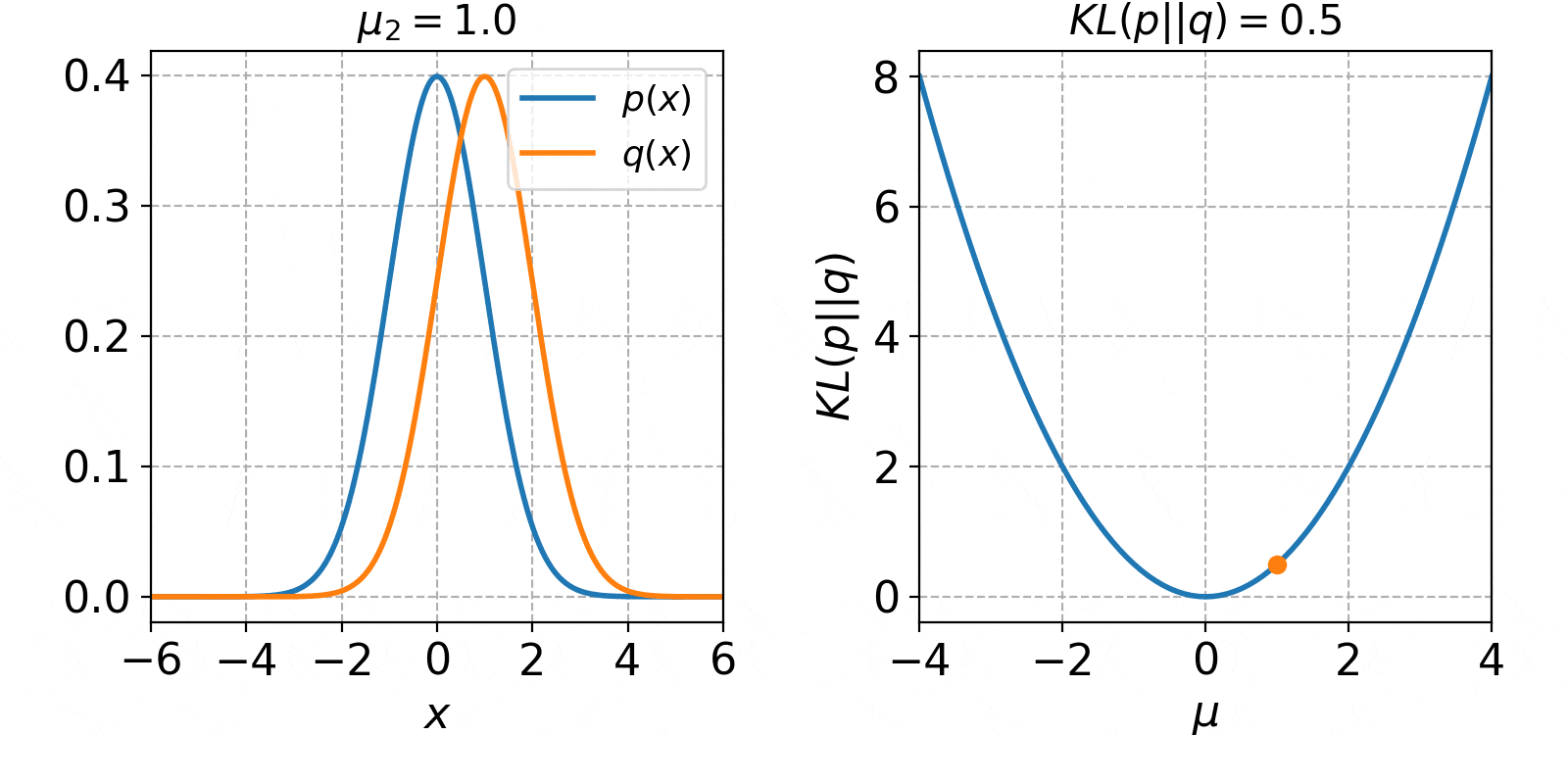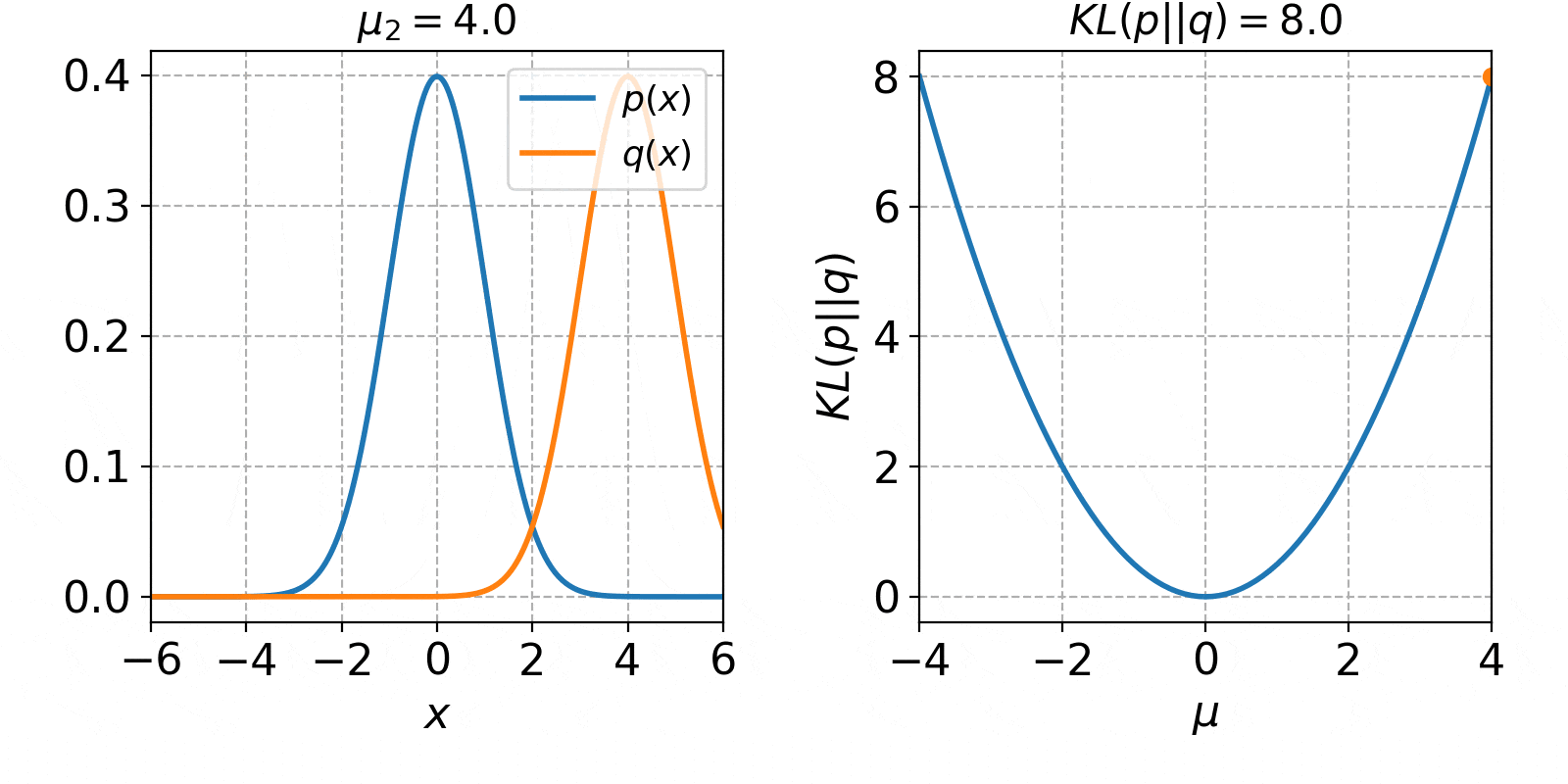
$\mu_2$の値を-4から4まで1ずつ増加させた時の、確率分布$q(x)$とKLダイバージェンス$KL(p||q)$の値は以下のようになります。
左側のオレンジ色の線が、平均$\mu_2$を変化させた時の$q(x)$です。右側の図は、平均$\mu_2$をx軸に取った時の図になります。青色の線が解析解で、オレンジ色の点が今のKLダイバージェンスの値になります。KLダイバージェンスは、$p(x)$と$q(x)$が完全に一致した時に0となり、離れる程増加していくことが確認できました。
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
# 正規分布
def gaussian1d(x,μ,σ):
y = 1 / ( np.sqrt(2*np.pi* σ**2 ) ) * np.exp( - ( x - μ )**2 / ( 2 * σ ** 2 ) )
return y
# 正規分布のKL divergence
def gaussian1d_KLdivergence(μ1,σ1,μ2,σ2):
A = np.log(σ2/σ1)
B = ( σ1**2 + (μ1 - μ2)**2 ) / (2*σ2**2)
C = -1/2
y = A + B + C
return y
# KL divergence
def KLdivergence(p,q,dx):
KL=np.sum(p * np.log(p/q)) * dx
return KL
# xの刻み
dx = 0.01
# xの範囲
xlm = [-6,6]
# x座標
x = np.arange(xlm[0],xlm[1]+dx,dx)
# xの数
x_n = len(x)
# Case 1
# p(x) = N(0,1)
# q(x) = N(μ,1)
# p(x)の平均μ1
μ1 = 0
# p(x)の標準偏差σ1
σ1 = 1
# p(x)
px = gaussian1d(x,μ1,σ1)
# q(x)の標準偏差σ2
σ2 = 1
# q(x)の平均μ2
U2 = np.arange(-4,5,1)
U2_n = len(U2)
# q(x)
Qx = np.zeros([x_n,U2_n])
# KLダイバージェンス
KL_U2 = np.zeros(U2_n)
for i,μ2 in enumerate(U2):
qx = gaussian1d(x,μ2,σ2)
Qx[:,i] = qx
KL_U2[i] = KLdivergence(px,qx,dx)
# 解析解の範囲
U2_exc = np.arange(-4,4.1,0.1)
# 解析解
KL_U2_exc = gaussian1d_KLdivergence(μ1,σ1,U2_exc,σ2)
# 解析解2
KL_U2_exc2 = U2_exc**2 / 2
#
# plot
#
# figure
fig = plt.figure(figsize=(8,4))
# デフォルトの色
clr=plt.rcParams['axes.prop_cycle'].by_key()['color']
# axis 1
# -----------------------
# 正規分布のプロット
ax = plt.subplot(1,2,1)
# p(x)
plt.plot(x,px,label='$p(x)$')
# q(x)
line,=plt.plot(x,Qx[:,i],color=clr[1],label='$q(x)$')
# 凡例
plt.legend(loc=1,prop={'size': 13})
plt.xticks(np.arange(xlm[0],xlm[1]+1,2))
plt.xlabel('$x$')
# axis 2
# -----------------------
# KLダイバージェンス
ax2 = plt.subplot(1,2,2)
# 解析解
plt.plot(U2_exc,KL_U2_exc,label='Analytical')
# 計算
point, = ax2.plot([],'o',label='Numerical')
# 凡例
# plt.legend(loc=1,prop={'size': 15})
plt.xlim([U2[0],U2[-1]])
plt.xlabel('$\mu$')
plt.ylabel('$KL(p||q)$')
plt.tight_layout()
# 軸に共通の設定
for a in [ax,ax2]:
plt.axes(a)
plt.grid()
# 正方形に
plt.gca().set_aspect(1/plt.gca().get_data_ratio())
# 更新
def update(i):
# 線
line.set_data(x,Qx[:,i])
# 点
point.set_data(U2[i],KL_U2[i])
# タイトル
ax.set_title("$\mu_2=%.1f$" % U2[i],fontsize=15)
ax2.set_title('$KL(p||q)=%.1f$' % KL_U2[i],fontsize=15)
# アニメーション
ani = animation.FuncAnimation(fig, update, interval=1000,frames=U2_n)
# plt.show()
# ani.save("KL_μ.gif", writer="imagemagick")
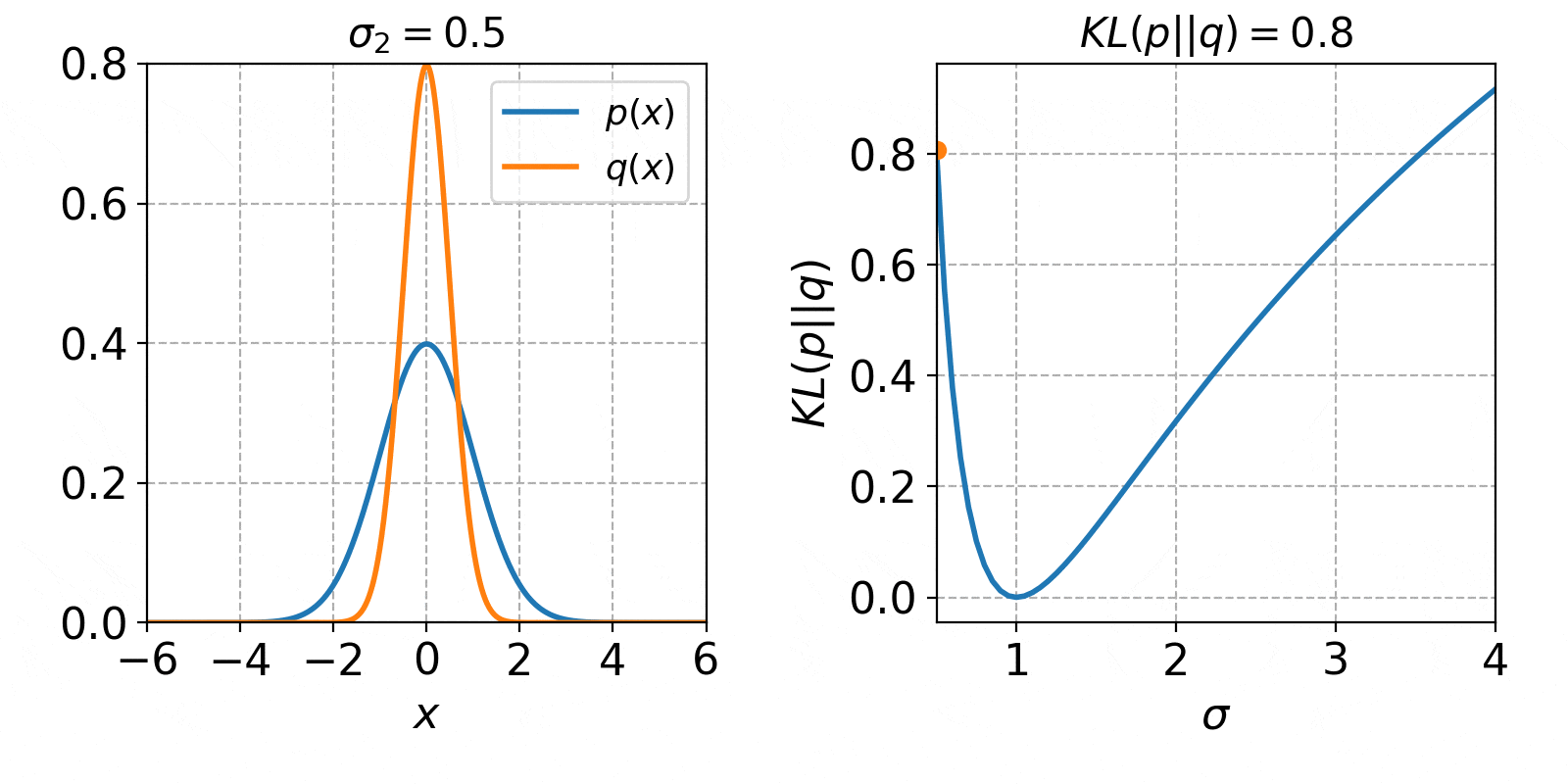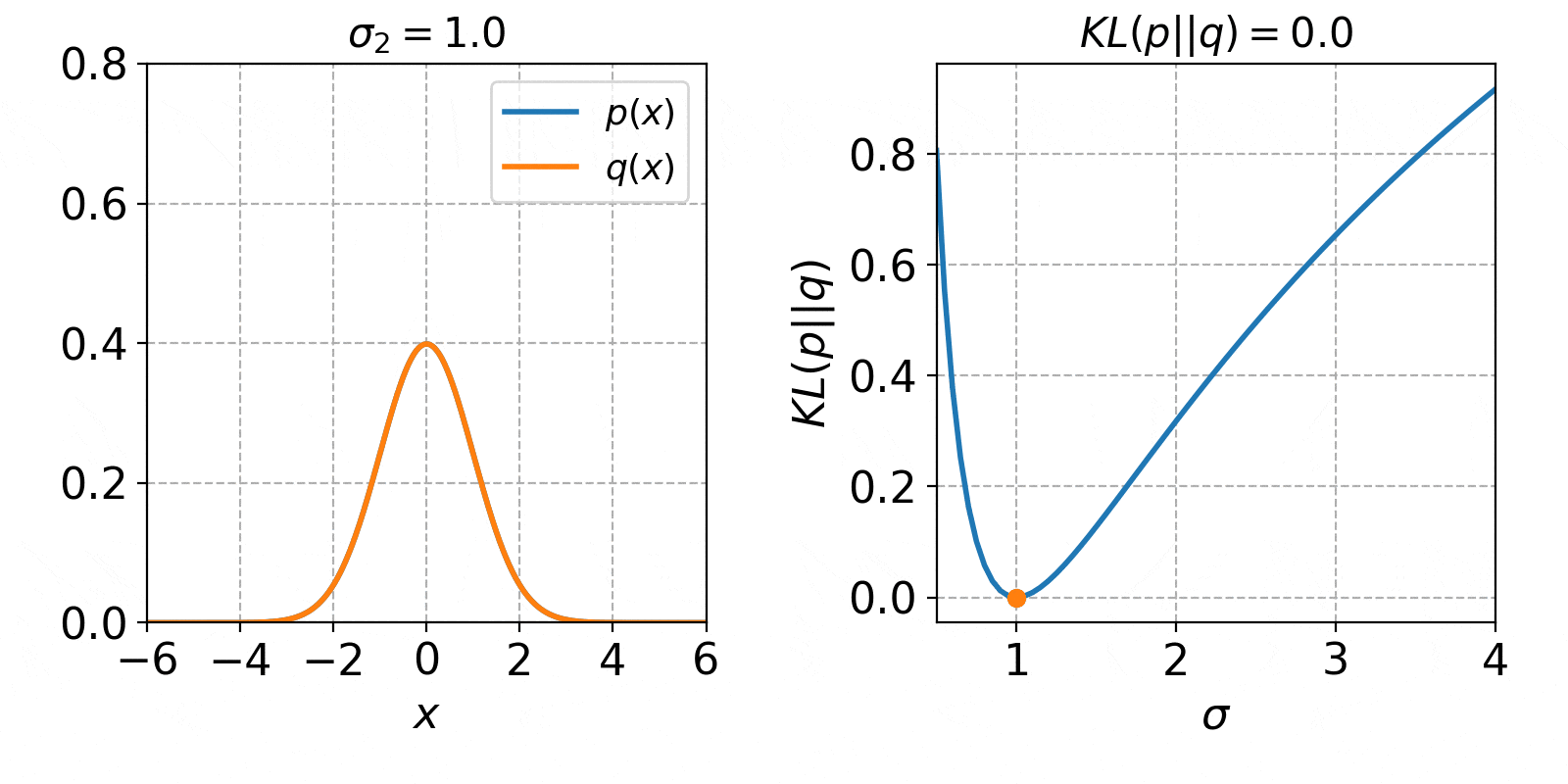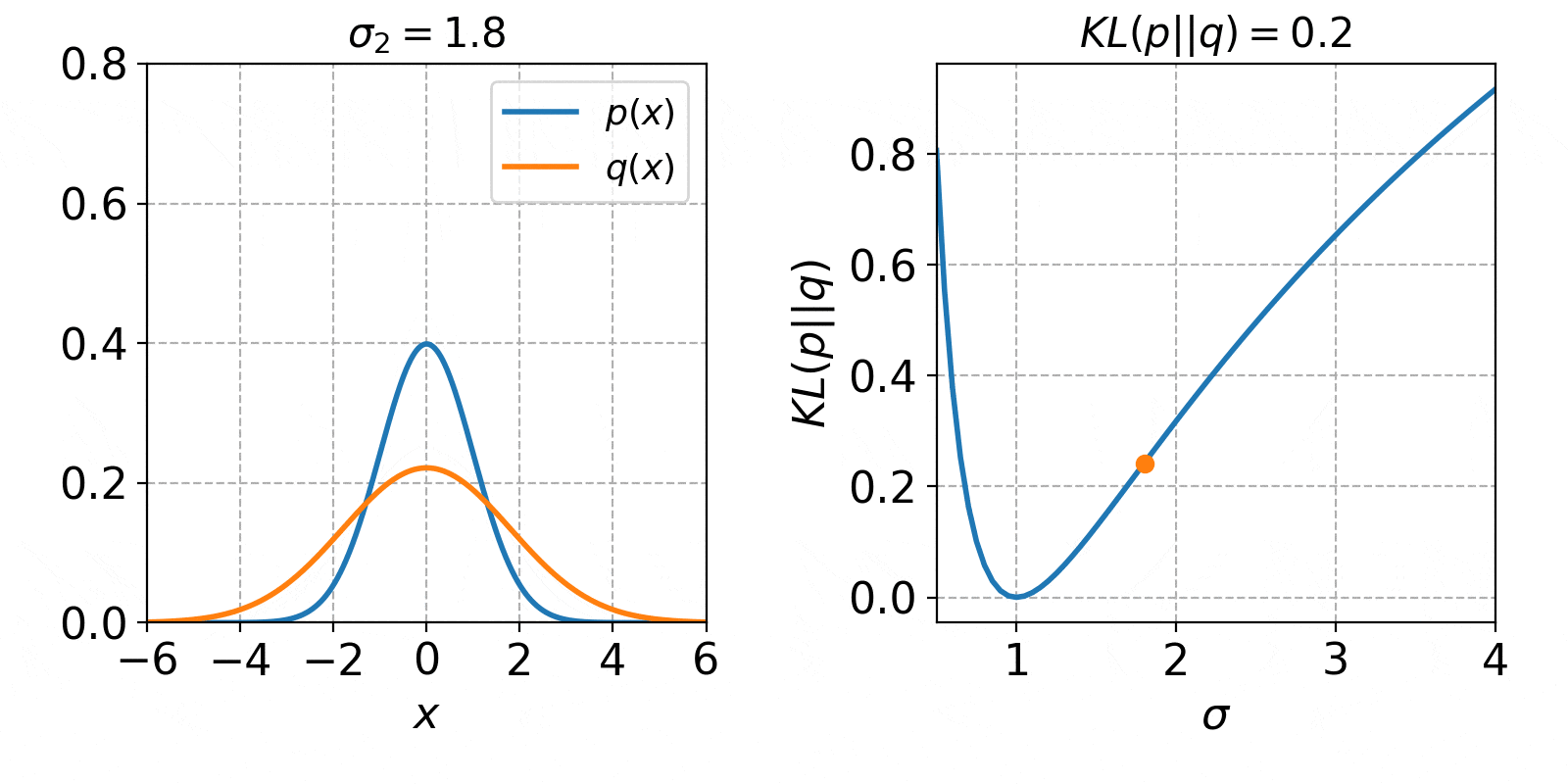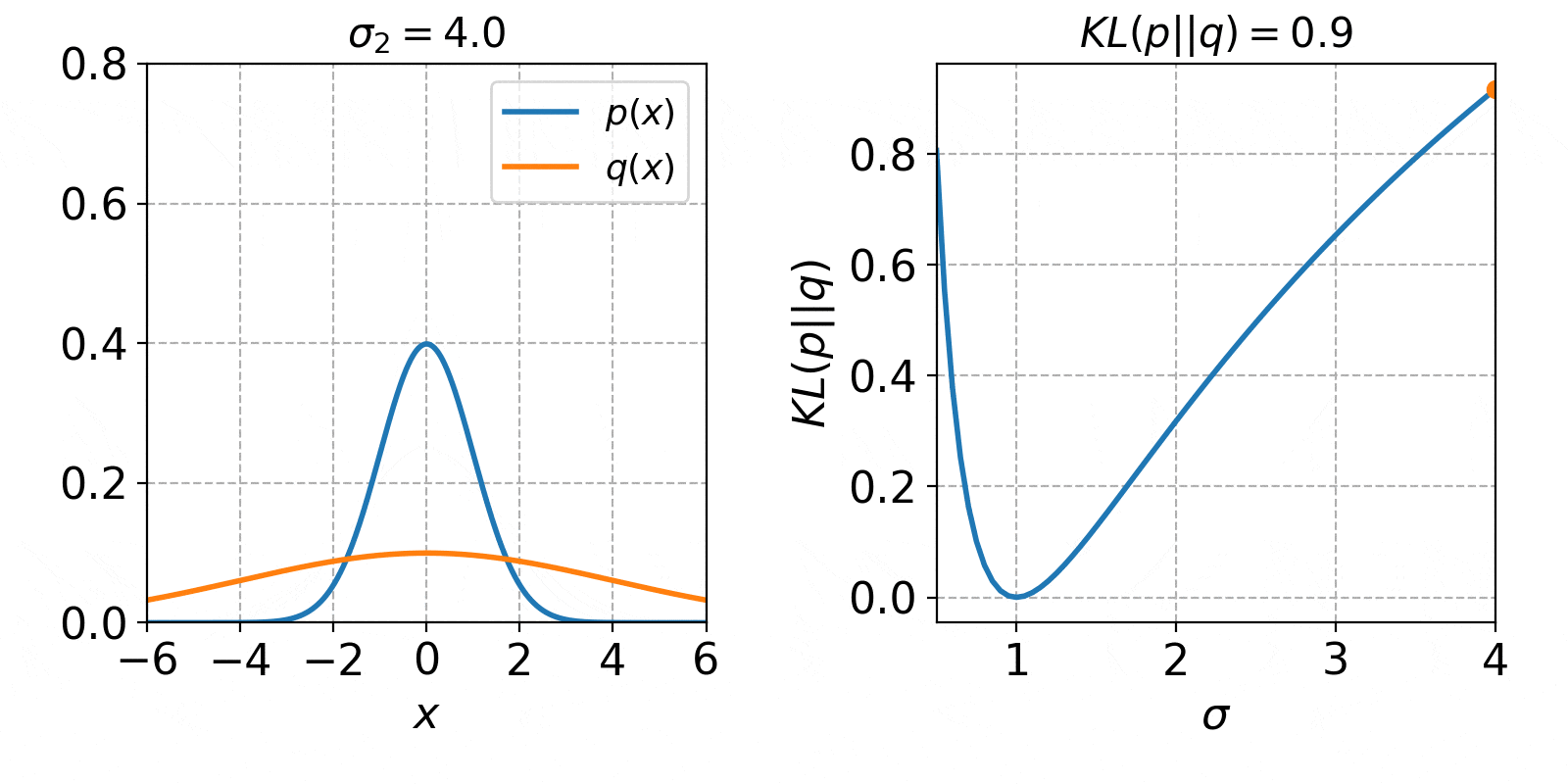
標準偏差が変数のとき
続いて$q(x)$の平均$\mu_2$を0として、標準偏差$\sigma_2$のみを変数とします。
q(x) =N(0,\sigma^2_2)= \frac{1}{\sqrt{2\pi\sigma_2^2}} \exp\left(-\frac{x^2}{2\sigma_2^2}\right)
この時のKLダイバージェンスは、
\begin{eqnarray}
KL(p||q) &=& \ln\left(\frac{\sigma_2}{\sigma_1}\right) + \frac{\sigma_1^2+(\mu_1-\mu_2)^2}{2\sigma_2^2} - \frac{1}{2} \\
&=& \ln\left(\frac{\sigma_2}{1}\right) + \frac{1^2}{2\sigma_2^2} - \frac{1}{2} \\
&=& \ln\left(\sigma_2\right) + \frac{1}{2\sigma_2^2} - \frac{1}{2} \\
\end{eqnarray}
となります。
$\sigma_2$の値を0.5から4まで変化させた時の、確率分布$q(x)$とKLダイバージェンス$KL(p||q)$の値は以下のようになります。
KLダイバージェンスの変化は、先程と同じく確率分布が一致した時に0となり、形状が異なる程増加していくという特徴が見られました。
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
# 正規分布
def gaussian1d(x,μ,σ):
y = 1 / ( np.sqrt(2*np.pi* σ**2 ) ) * np.exp( - ( x - μ )**2 / ( 2 * σ ** 2 ) )
return y
# 正規分布のKL divergence
def gaussian1d_KLdivergence(μ1,σ1,μ2,σ2):
A = np.log(σ2/σ1)
B = ( σ1**2 + (μ1 - μ2)**2 ) / (2*σ2**2)
C = -1/2
y = A + B + C
return y
# KL divergence
def KLdivergence(p,q,dx):
KL=np.sum(p * np.log(p/q)) * dx
return KL
# xの刻み
dx = 0.01
# xの範囲
xlm = [-6,6]
# x座標
x = np.arange(xlm[0],xlm[1]+dx,dx)
# xの数
x_n = len(x)
# Case 2
# p(x) = N(0,1)
# q(x) = N(0,σ**2)
# p(x)の平均μ1
μ1 = 0
# p(x)の標準偏差σ1
σ1 = 1
# p(x)
px = gaussian1d(x,μ1,σ1)
# q(x)の平均μ2
μ2 = 0
# q(x)の標準偏差σ2
S2 = np.hstack([ np.arange(0.5,1,0.1),np.arange(1,2,0.2),np.arange(2,4.5,0.5) ])
S2_n = len(S2)
# q(x)
Qx = np.zeros([x_n,S2_n])
# KLダイバージェンス
KL_S2 = np.zeros(S2_n)
for i,σ2 in enumerate(S2):
qx = gaussian1d(x,μ2,σ2)
Qx[:,i] = qx
KL_S2[i] = KLdivergence(px,qx,dx)
# 解析解の範囲
S2_exc = np.arange(0.5,4+0.05,0.05)
# 解析解
KL_S2_exc = gaussian1d_KLdivergence(μ1,σ1,μ2,S2_exc)
# 解析解2
KL_S2_exc2 = np.log(S2_exc) + 1/(2*S2_exc**2) - 1 / 2
#
# plot
#
# figure
fig = plt.figure(figsize=(8,4))
# デフォルトの色
clr=plt.rcParams['axes.prop_cycle'].by_key()['color']
# axis 1
# -----------------------
# 正規分布のプロット
ax = plt.subplot(1,2,1)
# p(x)
plt.plot(x,px,label='$p(x)$')
# q(x)
line,=plt.plot(x,Qx[:,i],color=clr[1],label='$q(x)$')
# 凡例
plt.legend(loc=1,prop={'size': 13})
plt.ylim([0,0.8])
plt.xticks(np.arange(xlm[0],xlm[1]+1,2))
plt.xlabel('$x$')
# axis 2
# -----------------------
# KLダイバージェンス
ax2 = plt.subplot(1,2,2)
# 解析解
plt.plot(S2_exc,KL_S2_exc,label='Analytical')
# 計算
point, = ax2.plot([],'o',label='Numerical')
# 凡例
# plt.legend(loc=1,prop={'size': 15})
plt.xlim([S2[0],S2[-1]])
plt.xlabel('$\sigma$')
plt.ylabel('$KL(p||q)$')
plt.tight_layout()
# 軸に共通の設定
for a in [ax,ax2]:
plt.axes(a)
plt.grid()
# 正方形に
plt.gca().set_aspect(1/plt.gca().get_data_ratio())
# 更新
def update(i):
# 線
line.set_data(x,Qx[:,i])
# 点
point.set_data(S2[i],KL_S2[i])
# タイトル
ax.set_title("$\sigma_2=%.1f$" % S2[i],fontsize=15)
ax2.set_title('$KL(p||q)=%.1f$' % KL_S2[i],fontsize=15)
# アニメーション
ani = animation.FuncAnimation(fig, update, interval=1000,frames=S2_n)
plt.show()
# ani.save("KL_σ.gif", writer="imagemagick")
平均、標準偏差が変数のとき
平均$\mu_2$と標準偏差$\sigma_2$の両方を変化させた時の、KLダイバージェンスの値をプロットしたのが下記になります。
## おまけ 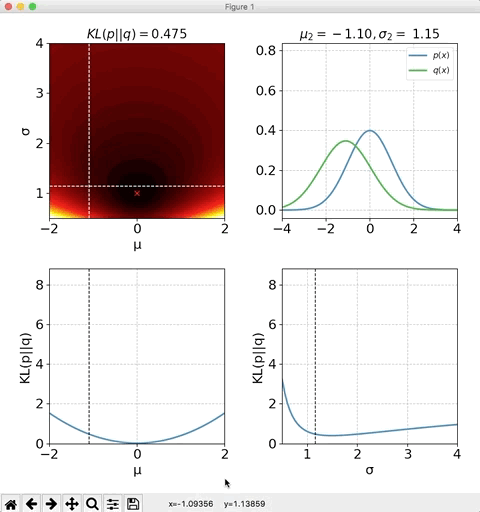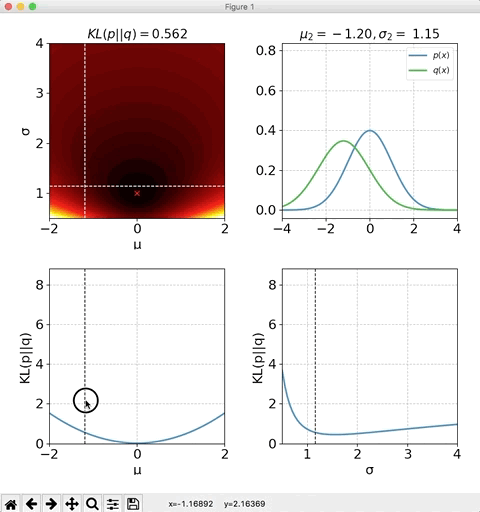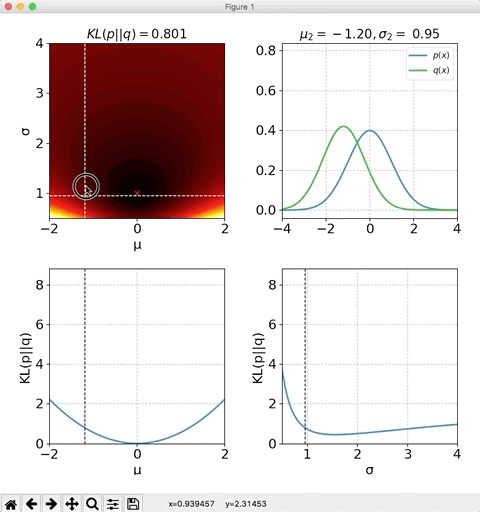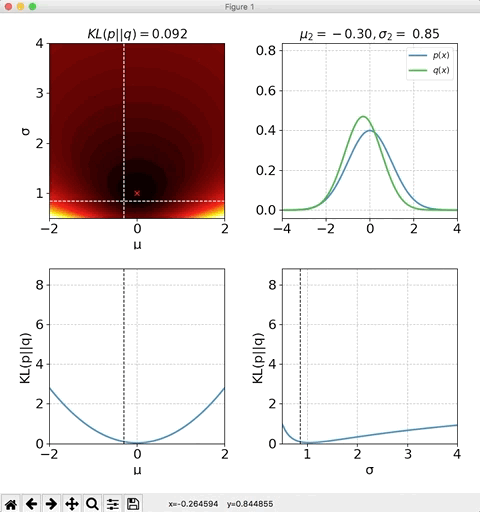import numpy as np
import matplotlib.pyplot as plt
# 正規分布
def gaussian1d(x,μ,σ):
y = 1 / ( np.sqrt(2*np.pi* σ**2 ) ) * np.exp( - ( x - μ )**2 / ( 2 * σ ** 2 ) )
return y
# 正規分布のKL divergence
def gaussian1d_KLdivergence(μ1,σ1,μ2,σ2):
A = np.log(σ2/σ1)
B = ( σ1**2 + (μ1 - μ2)**2 ) / (2*σ2**2)
C = -1/2
y = A + B + C
return y
# KL divergence
def KLdivergence(p,q,dx):
KL=np.sum(p * np.log(p/q)) * dx
return KL
def Motion(event):
global cx,cy,cxid,cyid
xp = event.xdata
yp = event.ydata
if (xp is not None) and (yp is not None):
gca = event.inaxes
if gca is axs[0]:
cxid,cx = find_nearest(x,xp)
cyid,cy = find_nearest(y,yp)
lns[0].set_data(G_x,Qx[:,cxid,cyid])
lns[1].set_data(x,Z[:,cyid])
lns[2].set_data(y,Z[cxid,:])
lnhs[0].set_ydata([cy,cy])
lnvs[0].set_xdata([cx,cx])
lnvs[1].set_xdata([cx,cx])
lnvs[2].set_xdata([cy,cy])
if gca is axs[2]:
cxid,cx = find_nearest(x,xp)
lns[0].set_data(G_x,Qx[:,cxid,cyid])
lns[2].set_data(y,Z[cxid,:])
lnvs[0].set_xdata([cx,cx])
lnvs[1].set_xdata([cx,cx])
if gca is axs[3]:
cyid,cy = find_nearest(y,xp)
lns[0].set_data(G_x,Qx[:,cxid,cyid])
lns[1].set_data(x,Z[:,cyid])
lnhs[0].set_ydata([cy,cy])
lnvs[2].set_xdata([cy,cy])
axs[1].set_title("$\mu_2=%5.2f, \sigma_2=$%5.2f" % (cx,cy),fontsize=15)
axs[0].set_title('$KL(p||q)=$%.3f' % Z[cxid,cyid],fontsize=15)
plt.draw()
def find_nearest(array, values):
id = np.abs(array-values).argmin()
return id,array[id]
# xの刻み
G_dx = 0.01
# xの範囲
G_xlm = [-4,4]
# x座標
G_x = np.arange(G_xlm[0],G_xlm[1]+G_dx,G_dx)
# xの数
G_n = len(G_x)
# p(x)の平均μ1
μ1 = 0
# p(x)の標準偏差σ1
σ1 = 1
# p(x)
px = gaussian1d(G_x,μ1,σ1)
# q(x)の平均μ2
μ_lim = [-2,2]
μ_dx = 0.1
μ_x = np.arange(μ_lim[0],μ_lim[1]+μ_dx,μ_dx)
μ_n = len(μ_x)
# q(x)の標準偏差σ2
σ_lim = [0.5,4]
σ_dx = 0.05
σ_x = np.arange(σ_lim[0],σ_lim[1]+σ_dx,σ_dx)
σ_n = len(σ_x)
# KLダイバージェンス
KL = np.zeros([μ_n,σ_n])
# q(x)
Qx = np.zeros([G_n,μ_n,σ_n])
for i,μ2 in enumerate(μ_x):
for j,σ2 in enumerate(σ_x):
KL[i,j] = gaussian1d_KLdivergence(μ1,σ1,μ2,σ2)
Qx[:,i,j] = gaussian1d(G_x,μ2,σ2)
x = μ_x
y = σ_x
X,Y = np.meshgrid(x,y)
Z = KL
cxid = 0
cyid = 0
cx = x[cxid]
cy = y[cyid]
xlm = [ x[0], x[-1] ]
ylm = [ y[0], y[-1] ]
axs = []
ims = []
lns = []
lnvs = []
lnhs = []
# figure
# ----------------
plt.close('all')
plt.figure(figsize=(8,8))
# デフォルトの色
clr=plt.rcParams['axes.prop_cycle'].by_key()['color']
# フォントサイズ
plt.rcParams["font.size"] = 16
# 線幅
plt.rcParams['lines.linewidth'] = 2
# gridのlinestyleを点線に
plt.rcParams["grid.linestyle"] = '--'
# plot時の範囲のマージンをなくす
plt.rcParams['axes.xmargin'] = 0.
# ax1
# ----------------
ax = plt.subplot(2,2,1)
Interval = np.arange(0,8,0.1)
plt.plot(μ1,σ1,'rx',label='$(μ_1,σ_1)=(0,1)$')
im = plt.contourf(X,Y,Z.T,Interval,cmap='hot')
lnv= plt.axvline(x=cx,color='w',linestyle='--',linewidth=1)
lnh= plt.axhline(y=cy,color='w',linestyle='--',linewidth=1)
ax.set_title('$KL(p||q)=$%.3f' % Z[cxid,cyid],fontsize=15)
plt.xlabel('μ')
plt.ylabel('σ')
axs.append(ax)
lnhs.append(lnh)
lnvs.append(lnv)
ims.append(im)
# ax2
# ----------------
ax = plt.subplot(2,2,2)
plt.plot(G_x,px,label='$p(x)$')
ln, = plt.plot(G_x,Qx[:,cxid,cyid],color=clr[1],label='$q(x)$')
plt.legend(prop={'size': 10})
ax.set_title("$\mu_2=%5.2f, \sigma_2=$%5.2f" % (cx,cy),fontsize=15)
axs.append(ax)
lns.append(ln)
plt.grid()
# ax3
# ----------------
ax = plt.subplot(2,2,3)
ln,=plt.plot(x,Z[:,cyid])
lnv= plt.axvline(x=cx,color='k',linestyle='--',linewidth=1)
plt.ylim([0,np.max(Z)])
plt.grid()
plt.xlabel('μ')
plt.ylabel('KL(p||q)')
lnvs.append(lnv)
axs.append(ax)
lns.append(ln)
# ax4
# ----------------
ax = plt.subplot(2,2,4)
ln,=plt.plot(y,Z[cxid,:])
lnv= plt.axvline(x=cy,color='k',linestyle='--',linewidth=1)
plt.ylim([0,np.max(Z)])
plt.xlim([ylm[0],ylm[1]])
plt.grid()
plt.xlabel('σ')
plt.ylabel('KL(p||q)')
lnvs.append(lnv)
axs.append(ax)
lns.append(ln)
plt.tight_layout()
for ax in axs:
plt.axes(ax)
ax.set_aspect(1/ax.get_data_ratio())
plt.connect('motion_notify_event', Motion)
plt.show()