第4回 今更だけど基礎から強化学習を勉強する 連続行動空間編

今までは行動空間(アクション)は離散値を扱っていましたが、今回は連続値を扱いたいと思います。

第3回　価値推定編(TD法、モンテカルロ法、GAE)
第5回　TRPO編(IS、KL距離、ヘシアン、共役勾配法)

※ネット上の情報をかき集めて自分なりに実装しているので正確ではない可能性がある点はご注意ください
※ライブラリはTensowflow2.0(+Keras)を使っています。

※2021/5/15 分散に関して大きな間違いがあったのでそれに関する内容を最後に追記しています

コード全体

本記事で作成したコードは以下です。

• GoogleColaboratory
• 2021/5/15 修正後のGoogleColaboratory

環境(MyCartpole)

Cartpole-v0を使いますが今回は連続行動空間を扱いため少し手を加えます。
本当はPendulum-v0を使いたかったのですが学習難易度が高く、もう少し難易度を下げた環境を用意しました。

変更箇所は以下です。

• アクションを2値(0,1)からスカラー値(-10～10)に変更
• 200ターンで終了する処理を追加
• アクション値がnanの場合の例外処理を追加

from gym import spaces
from gym.envs.classic_control.cartpole import CartPoleEnv
import numpy as np
import math

# オリジナルのCartpoleを継承
class MyCartpole(CartPoleEnv):
    def __init__(self):
        super().__init__()

        # action_space を連続空間に変更
        self.action_space = spaces.Box(-self.force_mag, self.force_mag, shape=(1,), dtype=np.float32)

    def reset(self):
        # 終了ターン用
        self.step_count = 0
        return super().reset()

    def step(self, action):
        # 200ターンたったら終了する
        self.step_count += 1
        if self.step_count > 200:
            return np.array(self.state), 0.0, True, {}

        # 例外処理
        if np.isnan(action):
            return np.array(self.state), 0.0, True, {}

        # アクションをclipして force の値にする
        force = np.clip(action, -self.force_mag, self.force_mag)[0]

        #--- 以下オリジナルのstepコードをコピペ ---

        x, x_dot, theta, theta_dot = self.state
        costheta = math.cos(theta)
        sintheta = math.sin(theta)

        # For the interested reader:
        # https://coneural.org/florian/papers/05_cart_pole.pdf
        temp = (force + self.polemass_length * theta_dot ** 2 * sintheta) / self.total_mass
        thetaacc = (self.gravity * sintheta - costheta * temp) / (self.length * (4.0 / 3.0 - self.masspole * costheta ** 2 / self.total_mass))
        xacc = temp - self.polemass_length * thetaacc * costheta / self.total_mass

        if self.kinematics_integrator == 'euler':
            x = x + self.tau * x_dot
            x_dot = x_dot + self.tau * xacc
            theta = theta + self.tau * theta_dot
            theta_dot = theta_dot + self.tau * thetaacc
        else:  # semi-implicit euler
            x_dot = x_dot + self.tau * xacc
            x = x + self.tau * x_dot
            theta_dot = theta_dot + self.tau * thetaacc
            theta = theta + self.tau * theta_dot

        self.state = (x, x_dot, theta, theta_dot)

        done = bool(
            x < -self.x_threshold
            or x > self.x_threshold
            or theta < -self.theta_threshold_radians
            or theta > self.theta_threshold_radians
        )

        if not done:
            reward = 1.0
        elif self.steps_beyond_done is None:
            # Pole just fell!
            self.steps_beyond_done = 0
            reward = 1.0
        else:
            if self.steps_beyond_done == 0:
                logger.warn(
                    "You are calling 'step()' even though this "
                    "environment has already returned done = True. You "
                    "should always call 'reset()' once you receive 'done = "
                    "True' -- any further steps are undefined behavior."
                )
            self.steps_beyond_done += 1
            reward = 0.0

        return np.array(self.state), reward, done, {}

Google Colab上での描画に関して

ライブラリを作成している方を見つけたのでそちらを使わせてもらいました。
簡単で使いやすいです。

【強化学習】OpenAI Gym を Google Colab上で描画する方法 (2020.6版)

方策勾配法(連続行動空間)

方策勾配法に関しては第2回を見てください。
第2回では行動空間は離散値でしたがこれを連続値に置き換えてみます。
置き換え方は方策を変更します。

方策 $\pi$ はある状態 $s$ で行動 $a$ をとる確率でした。
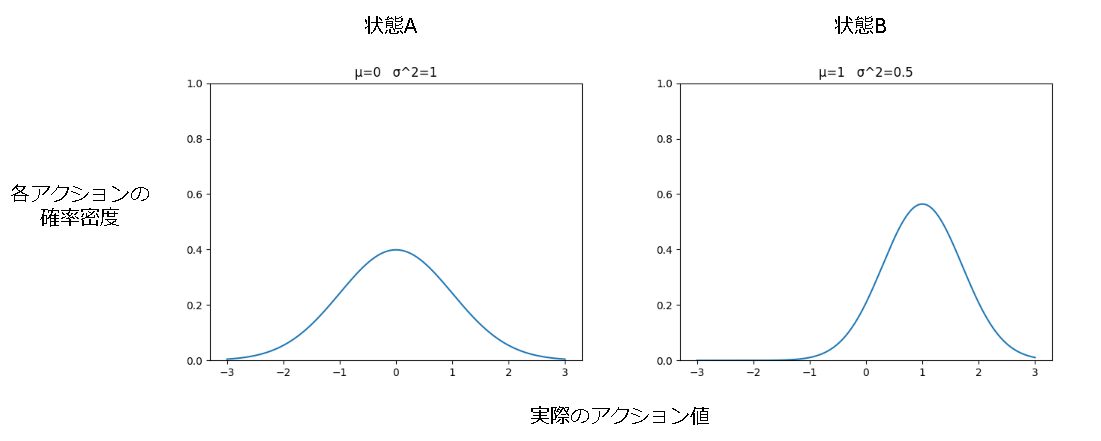
ここで行動をある確率密度分布に従うと仮定し、連続行動空間を表現します。
方策 $\pi$ をある状態 $s$ で行動 $a$ をとる確率密度に置き換えます。

図は行動がガウス分布(正規分布)に従うと仮定している場合に、状態Aの時に平均0,分散1、状態Bでは平均1,分散0.5 に従う方策の例です。

学習では状態に対する確率分布のパラメータを学習します。
ガウス分布だと学習するパラメータは平均と分散の値です。

参考

• Actor-Criticを連続行動空間へ拡張するには？
• ロボットの強化学習における状態一行動空間の汎化

確率と確率密度に関して

最初にはまったのですが、確率と確率密度は違うものです。
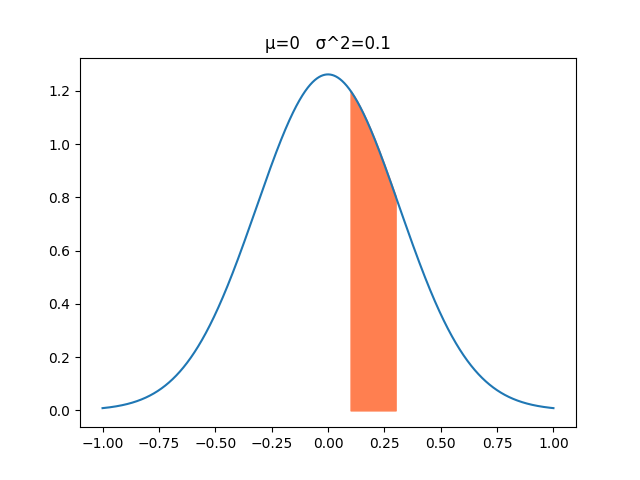
下図から分かる通り確率密度は1以上の値を取ります。
例えば平均0、分散0.1の0地点における確率密度は約1.26になります。

連続空間においてある一点の確率は0%です。
例えば0ピッタリになる確率はまずありえません。(0.00001になったり0.0002になったりとピッタリにはならない)

では連続空間の確率はというとある区間の面積に対して計算されます。
例えばアクション値が0.1～0.3の範囲になる確率は？という風に区間を設定すると計算できます。
図のオレンジ色が0.1～0.3の範囲に該当し、これを計算すると約20%になります。

方策勾配法は、方策 $\pi$ が確率を表しています。
これを連続行動空間では確率密度に変更していますがそれでいいかどうかは…、それに言及している内容は見つけられませんでした…。
まあ多分大丈夫なんでしょう。

参考：確率密度が1を超えるのはおかしいか？

ガウス分布による行動空間の学習

方策 $\pi$ がガウス分布に従う場合の手法を見ていきます。
ガウス分布は以下です。（平均 $\mu$ 、分散 $\sigma^2$）

$$
f(x) = \frac{1}{\sqrt{2 \pi \sigma^2 } }
exp(- \frac{(x - \mu)^2}{ 2 \sigma^2} )
$$

ガウス分布の学習では平均 $\mu$ と分散 $\sigma^2$ を学習します。

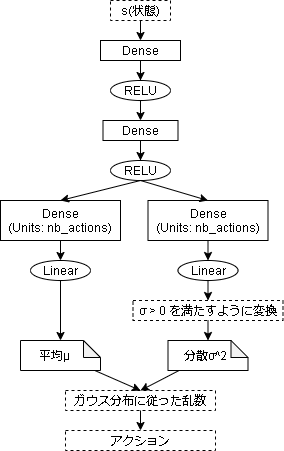
モデル側のコードは以下です。
今回は SubClass API でモデルを作成しています。

参考：TensorFlow > 学ぶ > TensorFlow Core > サブクラス化によるレイヤとモデルの新規作成

from tensorflow.python import keras
from tensorflow.keras.optimizers import Adam

# 独自のモデルを定義
class PolicyModel(keras.Model):
    def __init__(self, action_space):
        super().__init__()

        # 各レイヤーを定義
        self.dense1 = keras.layers.Dense(16, activation="relu")
        self.dense2 = keras.layers.Dense(16, activation="relu")
        self.pi_mean = keras.layers.Dense(action_space, activation="linear")
        self.pi_stddev = keras.layers.Dense(action_space, activation="linear")

        # optimizer もついでに定義しておく
        self.optimizer = Adam(lr=0.01)

    # Forward pass
    def call(self, inputs, training=False):
        x = self.dense1(inputs)
        x = self.dense2(x)
        mean = self.pi_mean(x)
        stddev = self.pi_stddev(x)

        # σ^2 > 0 になるように変換(指数関数)
        stddev = tf.exp(stddev)

        return mean, stddev

    # 状態を元にactionを算出
    def sample_action(self, state):
        # モデルから平均と分散を取得
        mean, stddev = self(state.reshape((1,-1)))

        # ガウス分布に従った乱数をだす
        sampled_action = tf.random.normal(tf.shape(mean), mean=mean, stddev=stddev)
        return sampled_action.numpy()[0]

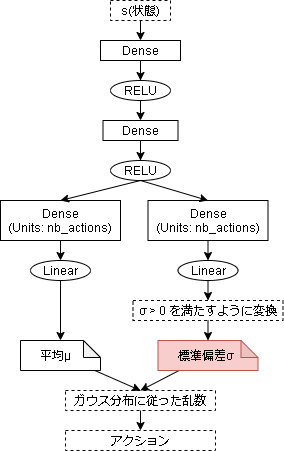
実際にアクションを出力する処理ですが、平均はそのまま線形で使います。
しかし、分散は $\sigma^2 > 0$ の条件があるのでそのままでは使えません。
ですので、指数関数で条件を満たすように変換しています。

変換方法はいくつかあるようで、シグモイド関数、Softplus関数、指数関数などがありました。

学習

学習するうえで $log \pi(a|s)$ が必要なので計算しておきます。
(数式がすぐでて来なかったので手動で計算しています)

計算過程

\begin{align}
log(f(x)) &= log (\frac{1}{\sqrt{2 \pi \sigma^2 } }
exp(- \frac{(x - \mu)^2}{ 2 \sigma^2} ) ) \\
&= log (\frac{1}{\sqrt{2 \pi \sigma^2 } }) + log(exp(- \frac{(x - \mu)^2}{ 2 \sigma^2} ) )
\\
&= log (1) - log({\sqrt{2 \pi \sigma^2 } }) - \frac{(x - \mu)^2}{ 2 \sigma^2}
\\
&= 0 - log({(2 \pi \sigma^2)^{ \frac{1}{2}} }) - \frac{(x - \mu)^2}{ 2 \sigma^2}
\\
&= 0 - \frac{1}{2} log({2 \pi \sigma^2 }) - \frac{(x - \mu)^2}{ 2 \sigma^2}
\end{align}

$$
log f(x) = -\frac{1}{2} log({2 \pi \sigma^2 }) - \frac{(x - \mu)^2}{ 2 \sigma^2}
$$

方策勾配法で更新し、経験の収集はモンテカルロ法で実装しています。
(方策勾配法は第2回、モンテカルロ法は第3回を見てください)

ほぼ過去の実装と同じですが、アクションだけ変更点があります。
今回アクションの範囲が-10～10と大きく、そのままでは学習できません。(安定しません)
ですのでアクションの学習は-1～1とし、環境に渡すときに-10～10に直しています。(逆正規化?)
アクションの最小値、最大値は環境から提供される情報なので、環境に依存したコードにはなっていません。

with MyCartpole() as env:

    # 出力用にactionの修正値を計算
    # アクションは-10～10の範囲をとるが、学習は-1～1の範囲と仮定し、
    # 出力時に-10～10に戻す
    action_centor = (env.action_space.high + env.action_space.low)/2
    action_scale = env.action_space.high - action_centor

    （略）

    # 学習ループ
    for episode in range(500):
        （略）

        # 1episode
        while not done:
            # アクションを決定
            action = model.sample_action(state)

            # 1step進める（アクション値を修正して渡す）
            n_state, reward, done, _ = env.step(action * action_scale + action_centor)

            （略）

経験収集後の方策勾配法の部分は以下です。

def train(model, experiences):

    ・収集した経験から学習用のデータを作成
    state_batch  = 状態
    action_batch = アクション
    v_vals       = モンテカルロ法で集めた割引報酬

    # baseline
    v_vals -= np.mean(v_vals)

    # 勾配を計算
    with tf.GradientTape() as tape:

        # モデルから値を取得
        mean, stddev = model(state_batch, training=True)

        # log(π(a|s))を計算
        a1 = -0.5 * tf.math.log(2 * np.pi * stddev)
        a2 = -((actions - mean) ** 2) / (2 * stddev)
        logpi = a1 + a2

        # log(π(a|s)) * Q(s,a) を計算
        policy_loss = logpi * v_vals

        # ミニバッチ処理
        loss = -tf.reduce_mean(policy_loss)

    # 勾配を元にoptimizerでモデルを更新
    gradients = tape.gradient(loss, model.trainable_variables)
    model.optimizer.apply_gradients(zip(gradients, model.trainable_variables))

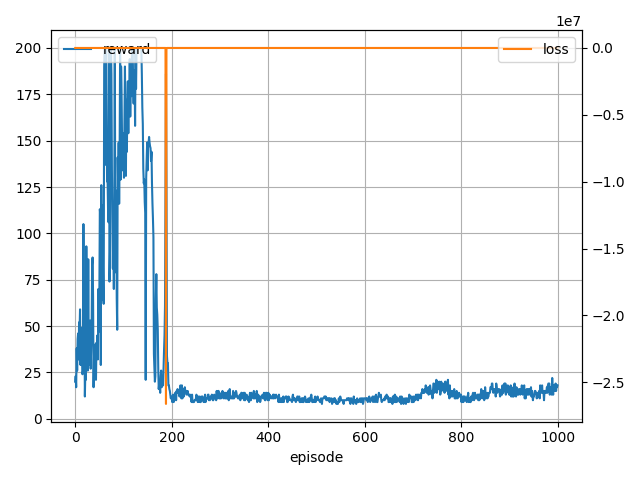
学習中の様子

0 (min,ave,max)reward 20.0 20.0 20.0, loss -1.16 -1.16 -1.16
100 (min,ave,max)reward 12.0 86.8 200.0, loss -1.74 -0.05 0.96
200 (min,ave,max)reward 11.0 114.8 200.0, loss -26611860.00 -266757.19 4.33
300 (min,ave,max)reward 9.0 11.9 18.0, loss -43.56 -3.34 -0.83
400 (min,ave,max)reward 9.0 12.0 16.0, loss -5.49 -3.55 -2.13
500 (min,ave,max)reward 9.0 10.6 13.0, loss -12.53 -4.66 -3.54
600 (min,ave,max)reward 8.0 10.1 12.0, loss -8.57 -4.86 -4.02
700 (min,ave,max)reward 8.0 10.6 14.0, loss -8.71 -4.75 -3.77
800 (min,ave,max)reward 9.0 14.5 21.0, loss -22.90 -2.89 -1.41
900 (min,ave,max)reward 9.0 13.4 19.0, loss -4.32 -3.34 -2.20

loss が下にはねた後学習に失敗していますね。
他にも loss が inf になったり nan になったりするパターンもありました。

一応200取れている場合もあるので学習は進んでいるようです。

学習失敗の原因に関して

上記の通り値がおかしくなり学習自体が失敗する場合があります。
いくつか原因がありましたが分からない部分も大きいです。
分かった範囲を書いておきます。

分散0問題

学習が進んでいくとガウス分布のグラフがだんだん尖ってくる形になる事が想像できると思います。
（学習されアクション値が決まってくるため）
そうなると分散が限りなく0に近づきます。
分散が0に近づくと確率密度が無限に近い値を取るため、pythonが処理しきれる桁を超えた時点で学習結果がinf/nanになり計算できなくなります。

愚直に解決するなら以下のように分散が0にならないように小さい値を足せばいいですが、それで問題ないかはちょっと分かりません。

class PolicyModel(keras.Model):
    def call(self, inputs, training=False):
        (略)
        # σ^2 > 0 になるように変形(指数関数)
        stddev = tf.exp(stddev)

        # 分散が0にならないように小さい値を追加
        stddev += 1e-10

        return mean, stddev

loss発散問題

時々 loss がものすごく跳ね上がるタイミングがあります。
これは憶測ですが、ガウス分布の取りえる値が -∞～∞ の間が原因な気がします。

アクション値は乱数なのでものすごく大きい値を引く可能性があります。
その場合計算過程でlossがおかしな値になっている気がします。
値によっては inf などになりそのまま学習に失敗する可能性もあります。

この後紹介する Squashed Gaussian Policy を適用することで防げるような気がしますが詳細は分かりません。

分散固定ガウス分布学習

こちらは本記事オリジナルです。（探せば既にあると思います）
思いついたのでやってみました。

上記問題において、分散に起因する問題が大きそうなので分散を固定して学習したほうが安定するのでは？
という発想からきています。

モデル部分は以下です。

# 独自のモデルを定義
class PolicyModel(keras.Model):
    def __init__(self, action_space, stddev=1.0):
        super().__init__()

        self.stddev = stddev

        # 各レイヤーを定義
        self.dense1 = keras.layers.Dense(16, activation="relu")
        self.dense2 = keras.layers.Dense(16, activation="relu")
        self.pi_mean = keras.layers.Dense(action_space.shape[0], activation="linear")

        # optimizer もついでに定義しておく
        self.optimizer = Adam(lr=0.01)

    # Forward pass
    def call(self, inputs, training=False):
        # 共通層
        x = self.dense1(inputs)
        x = self.dense2(x)

        # ガウス分布のパラメータ層(actor)
        mean = self.pi_mean(x)

        return mean

    # 状態を元にactionを算出
    def sample_action(self, state, is_train):
        # モデルから平均と分散を取得
        mean = self(state.reshape((1,-1)))

        if is_train:
            # 学習中はガウス分布に従った乱数をだす
            sampled_action = tf.random.normal(tf.shape(mean), mean=mean, stddev=self.stddev)
            action = sampled_action.numpy()[0]
            return action
        else:
            # テストはmeanを出す
            return mean.numpy()[0]

アクションの算出ですが、学習時は分散を固定して学習しています。
テスト時は分散が大きいと乱数による影響が大きくなってしまうので、平均値をそのまま出力する形にしています。
(平均値が一番いい数値と仮定しています)
(分散を低い値に変更して乱数を混ぜてもいいかもしれません)

次に学習箇所です。

def train(model, experiences):
    （略）

    # 勾配を計算
    with tf.GradientTape() as tape:

        # モデルから値を取得
        mean = model(state_batch, training=True)

        # log(π(a|s))を計算
        a1 = -0.5 * tf.math.log(2 * np.pi * model.stddev)
        a2 = -((actions - mean) ** 2) / (2 * model.stddev)
        logpi = a1 + a2

        （略）

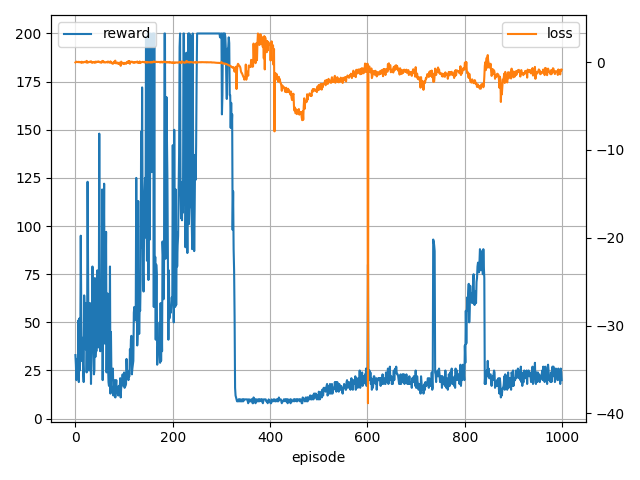
• 学習結果

0 (min,ave,max)reward 19.0 19.0 19.0, loss -0.26 -0.26 -0.26
100 (min,ave,max)reward 10.0 32.1 147.0, loss -0.90 -0.04 0.51
200 (min,ave,max)reward 59.0 175.6 200.0, loss -0.37 -0.01 0.19
300 (min,ave,max)reward 36.0 147.9 200.0, loss -0.29 -0.00 0.19
400 (min,ave,max)reward 94.0 180.1 200.0, loss -0.29 -0.02 0.20
500 (min,ave,max)reward 200.0 200.0 200.0, loss -0.28 -0.01 0.13
600 (min,ave,max)reward 122.0 173.3 200.0, loss -0.39 -0.00 0.22
700 (min,ave,max)reward 94.0 176.3 200.0, loss -0.33 -0.02 0.15
800 (min,ave,max)reward 113.0 161.2 200.0, loss -0.34 -0.02 0.20
900 (min,ave,max)reward 21.0 163.3 200.0, loss -0.35 0.00 0.17

• テスト結果

175 step, reward: 175.0
185 step, reward: 185.0
166 step, reward: 166.0
191 step, reward: 191.0
179 step, reward: 179.0

割と安定した気がします。
それでも長時間学習していると時々 nan になる場合があります。
(平均が無限に増える状況があるような・・・)

Squashed Gaussian Policy

Soft Actor-Criticで使われている手法です。(SACについてはそのうち…?)
追記：SAC編記事を書きました。

ガウス分布は-∞～∞の値を取りますが、実際のアクションは制限がある場合が多いです。
(今回ですと-10～10ですね)
SGPはガウス方策から出力されたアクションに tanh を適用することで-1から1に範囲を制限する手法です。

参考

• Soft Actor-Critic (SAC) ②tensorflow2による実装
• [論文解説] Soft Actor-Critic
• (OpenAI Spinning Up)Soft Actor-Critic
• [論文]Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor

アクションに tanh を適用するのでアクションの確率密度分布が変わります。
数式は以下です。(論文より)

$$
\pi(a|s) = \mu(u|s)
\begin{vmatrix}
det( \frac{da}{du} )
\end{vmatrix}^{-1}
$$

$$
log{\pi(a|s)} = log{\mu(u|s)} - \sum_{i=1}^D log(1 - tanh^2(u_i))
$$

$\mu(u|s)$ が-∞～∞の値を持つ分布になります。（論文ではガウス分布に限定していません）
コードは最初の「ガウス分布による行動空間の学習」をベースに変更箇所を記載しています。

class PolicyModel(keras.Model):
    def sample_action(self, state):
        # モデルから平均と分散を取得
        mean, stddev = self(state.reshape((1,-1)))

        # ガウス分布に従った乱数をだす
        actions = tf.random.normal(tf.shape(mean), mean=mean, stddev=stddev)

        # tanhを適用
        actions_squashed = tf.tanh(actions)

        # 学習にtanh適用前のaction値も欲しいのでそれも返す
        return actions_squashed.numpy()[0], actions.numpy()[0]

# 学習ループ
episode_rewards = []
for episode in range(1000):
     # 1episode
    while not done:

        # アクションを決定
        action, action_org = model.sample_action(state)

        # 1step進める
        n_state, reward, done, _ = env.step(action * action_scale + action_centor)

        （略）

        # 経験を追加
        experiences.append({
            "state": state,
            "action": action,
            "action_org": action_org,  # 追加
            "reward": reward,
            "n_state": n_state,
            "done": done,
        })

        （略）

def train(model, experiences):
    （略）

    action_org = np.asarray([e["action_org"] for e in batchs])

    （略）
    with tf.GradientTape() as tape:

        # モデルから値を取得
        mean, stddev = model(state_batch, training=True)

        # log(μ(a|s))を計算
        a1 = -0.5 * tf.math.log(2 * np.pi * stddev)
        a2 = -((action_org - mean) ** 2) / (2 * stddev)
        logmu = a1 + a2

        # log(π(a|s))を計算
        tmp = 1 - tf.tanh(action_org) ** 2
        tmp = tf.clip_by_value(tmp, 1e-10, 1.0)  # log(0)回避用
        logpi = logmu - tf.reduce_sum(tf.math.log(tmp), axis=1, keepdims=True)

        # log(π(a|s)) * Q(s,a) を計算
        policy_loss = logpi * v_vals

        （略）

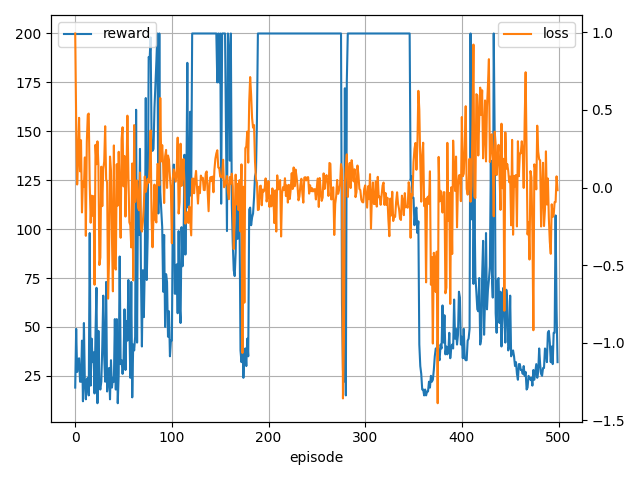
• 結果

0 (min,ave,max)reward 33.0 33.0 33.0, loss -0.03 -0.03 -0.03
100 (min,ave,max)reward 11.0 40.8 148.0, loss -0.41 -0.02 0.17
200 (min,ave,max)reward 16.0 82.0 200.0, loss -0.19 -0.00 0.13
300 (min,ave,max)reward 50.0 162.8 200.0, loss -0.10 -0.02 0.14
400 (min,ave,max)reward 8.0 51.0 200.0, loss -3.05 0.20 3.27
500 (min,ave,max)reward 8.0 9.9 14.0, loss -7.88 -3.37 2.38
600 (min,ave,max)reward 10.0 17.0 26.0, loss -3.12 -1.75 -0.15
700 (min,ave,max)reward 15.0 21.1 80.0, loss -38.85 -1.40 -0.13
800 (min,ave,max)reward 13.0 22.9 93.0, loss -3.15 -1.43 -0.06
900 (min,ave,max)reward 11.0 39.0 88.0, loss -4.53 -1.65 0.81

あとがき

本当はTRPOまで書く予定でしたが思ったより長くなったので分けます。

連続空間になったら学習が本当に安定しなくなりましたね…
実行する毎に結果が変わるのでコードがミスっているのかそもそもアルゴリズムがこの精度なのかハイパーパラメータが悪いのか判断がつきませんでした…。

ガウス分布における分散の取り扱い方の間違えについて(追記:2021/5/15)

上記3種類の手法で学習が安定しない理由は、モデルの出力の分散 $\sigma^2$ と標準偏差 $\sigma$ をごっちゃにしており、コードが間違っていた事が原因でした。

修正点は以下です。
まず、モデルからの出力を標準偏差 $\sigma$ に変更しています。

次に $log \pi(a|s)$ を以下のように変形しています。

計算過程

\begin{align}
log(f(x)) &= log (\frac{1}{\sqrt{2 \pi \sigma^2 } }
exp(- \frac{(x - \mu)^2}{ 2 \sigma^2} ) ) \\
&= log (\frac{1}{\sqrt{2 \pi \sigma^2 } }) + log(exp(- \frac{(x - \mu)^2}{ 2 \sigma^2} ) )
\\
&= log (1) - log(\sqrt{2 \pi \sigma^2 }) - \frac{(x - \mu)^2}{ 2 \sigma^2}
\\
&= 0 - log((2 \pi \sigma^2)^{ \frac{1}{2}}) - \frac{(x - \mu)^2}{ 2 \sigma^2}
\\
&= -\frac{1}{2} log(2 \pi \sigma^2) - \frac{(x - \mu)^2}{ 2 \sigma^2}
\\
&= -\frac{1}{2} (log(2 \pi) + log(\sigma^2)) - \frac{1}{2}( \frac{x - \mu}{\sigma} )^2
\\
&= -\frac{1}{2} (log(2 \pi) + 2log(\sigma)) - \frac{1}{2}( \frac{x - \mu}{\sigma} )^2
\end{align}

$$
log f(x) = -\frac{1}{2} log(2 \pi) - log(\sigma) - \frac{1}{2}( \frac{x - \mu}{\sigma} )^2
$$

def compute_logpi(mean, stddev, action):
    a1 = -0.5 * np.log(2*np.pi)
    a2 = -tf.math.log(stddev)
    a3 = -0.5 * (((action - mean) / stddev) ** 2)
    return a1 + a2 + a3

アクション取得部分は変わらず以下になります。

def sample_action(self, state):
    # モデルから平均と標準偏差を取得
    mean, stddev = self(state.reshape((1,-1)))

    # ガウス分布に従った乱数をだす
    # stddevの引数が分散ではなく標準偏差だったので以前のモデルでは学習が不安定になっていた
    sampled_action = tf.random.normal(tf.shape(mean), mean=mean, stddev=stddev)
    action = sampled_action.numpy()[0]
    return action

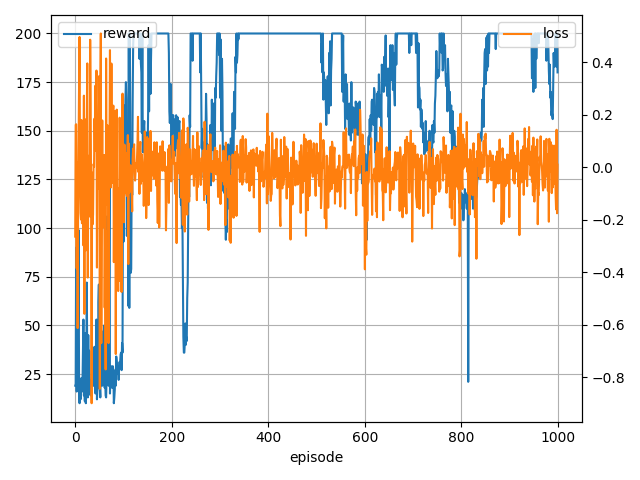
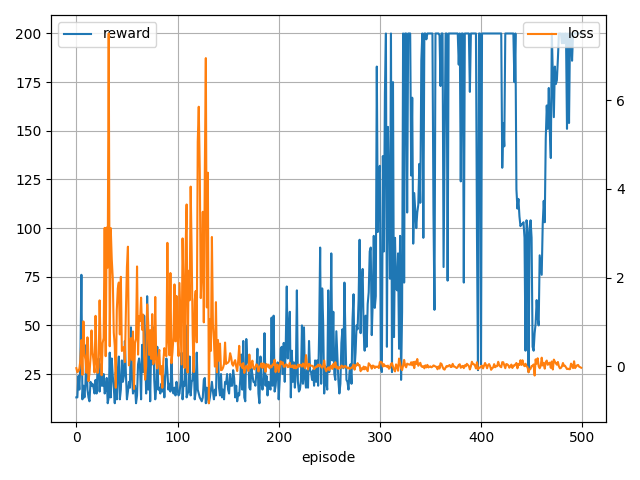
修正したコードで方策勾配法と(方策勾配法+tanh)を試した結果は以下になりました。

• 方策勾配法

0 (min,ave,max)reward 19.0 19.0 19.0, loss 0.99 0.99 0.99
100 (min,ave,max)reward 11.0 63.9 200.0, loss -0.72 0.00 0.58
200 (min,ave,max)reward 24.0 145.4 200.0, loss -1.07 0.03 0.71
300 (min,ave,max)reward 15.0 192.8 200.0, loss -1.36 -0.02 0.21
400 (min,ave,max)reward 15.0 118.4 200.0, loss -1.39 -0.10 0.62

• 方策勾配法+tanh

0 (min,ave,max)reward 13.0 13.0 13.0, loss -0.04 -0.04 -0.04
100 (min,ave,max)reward 10.0 23.2 76.0, loss -0.51 0.76 7.51
200 (min,ave,max)reward 10.0 21.4 55.0, loss -0.84 0.78 6.95
300 (min,ave,max)reward 13.0 44.0 183.0, loss -0.11 -0.00 0.25
400 (min,ave,max)reward 22.0 151.8 200.0, loss -0.12 0.01 0.17

学習はかなり安定しましたね・・・。
ただ、見てわかる通り学習し続けると失敗するケースやまれに学習自体に失敗するケースもありました。
（これはアクションが離散の場合でもありました）