第2回 今更だけど基礎から強化学習を勉強する ディープラーニング編(Q学習、方策勾配法/REINFORCE、A3C/A2C)

今回は基本的にモデルフリーの環境が前提となります。
モデルベースについてはいつかやるかも?

第1回　基礎編(動的計画法、Q学習、SARSA、Actor Critic)
第3回　価値推定編(TD法、モンテカルロ法、GAE)

※ネット上の情報をかき集めて自分なりに実装しているので正確ではない可能性がある点はご注意ください

ディープラーニングに使うライブラリですが、Tensowflow2.0(+Keras)を使います。
Tensowflow2.0から公式でKerasが取り入れられたようでそちらを使っていきます。

コード全体

本記事で作成したコードは以下です。

• GoogleColaboratory

環境

OpenAI gym で提供されている CartPole-v0 を使用します。

台座を右か左に動かして棒を立たせ続けるゲームです。
棒がある一定以上傾いたり、画面外に行くと終了します。

報酬は常に1手に入り、早く終了する=累計報酬が少なくなるという学習です。
200stepまで実行されるので最大報酬は200となります。

状態は[台座の位置,台座の速度,棒の角度,棒の速度]を返します。
アクションは台座を左に移動させる、右に移動させるの２つです。

GoogleColaboratoryによる Gym の描画

昔に書いた記事を参考にしています。
コメントにもある通り以下の部分が不要になったようです。(コメントありがとうございます)

※2021/6/3 編集
第4回で紹介していますが、もっといい手法があったのでそちらを紹介します。
とても簡単で使いやすいです。
【強化学習】OpenAI Gym を Google Colab上で描画する方法 (2020.6版)

価値関数の学習(Q学習)

Q学習の行動価値関数をニューラルネットワークで拡張してみます。

更新式

Q学習の更新式は以下でした。
（$\alpha$ は学習率、$\gamma$は割引率）

$$ Q(s_t,a_t) \leftarrow Q(s_t,a_t) + \alpha ( r_{t+1} + \gamma \max_a (Q(s_{t+1}, a)) - Q(s_t,a_t) ) $$

しかし、差分の計算はニューラルネットワーク内で計算されるので以下の式だけが必要になります。

$$ r_{t+1} + \gamma \max_a (Q(s_{t+1}, a))$$

また、エピソード終了時は次の状態がないため以下となり、報酬だけになります。

$$ r_{t+1}$$

価値関数モデルの定義

モデルは状態を入力とし、各アクションでの価値を出力します。

from tensorflow.python import keras
from tensorflow.keras.optimizers import Adam

# 環境の状態の形式(shape)
obs_shape = env.observation_space.shape

# 環境の取りうるアクション数
nb_actions = env.action_space.n

lr = 0.001  # 学習率

c = input_ = keras.layers.Input(shape=obs_shape)
c = keras.layers.Dense(10, activation="relu")(c)
c = keras.layers.Dense(10, activation="relu")(c)
c = keras.layers.Dense(nb_actions, activation="linear")(c)
model = keras.Model(input_, c)
model.compile(optimizer=Adam(learning_rate=lr), loss='mse', metrics=["mae"])
model.summary()

拡張性を優先してSequentialモデルではなくFunctionalAPIでモデルを作っています。
Dense層を2つ結合したシンプルなモデルです。
optimizerはAdamを使い、損失関数には平均二乗誤差(mse)を使っています。

メトリクスは確認用なので学習には関係ありません。

行動の決定

Epsilon-Greedy法を使います。
Tensorflow2.0での値の取り出し方の説明がメインです。
Tensorflowを使う場合はshape(次元数)を意識することが重要な気がします。

def EGreedyPolicy(model, state, nb_actions, epsilon):
    if np.random.random() < epsilon:
        # epsilonより低いならランダムに移動
        return np.random.randint(nb_actions)
    else:
        # Q値が最大のアクションを実行
        q = model(state.reshape(1,-1))[0].numpy()
        return np.argmax(q)

モデルからの値の取り出しは model(入力) で行います。
入力ですが、複数の結果も１回で取り出すことができるので次元数を1増やして与える必要があります。
今回ですと state は (4,) 次元（[位置,加速度,角度,速度]）なので reshape して (1,4) 次元（[[位置,加速度,角度,速度]]）に増やしています。

(1,4) で入力すると出力は (1, 出力結果) で返ってきます。
今回ですとアクション数が出力になるので(1,2)です。
ですので、[0] で0番目の結果を取得し、q には(2,)次元（[左アクションの価値,右アクションの価値]）が入ります。

また、model()で返ってくる値はTensor型なので numpy() で numpy 型に変換しています。

最後に、qから価値の高いほうのアクションをargmax関数で取得しています。

経験の収集（Experience Replay）と学習ループのコード

強化学習によるディープラーニングは基本オンライン学習になります。（反対はバッチ学習）
（いつかオンライン強化学習とオフライン強化学習まで触れられればいいなー）
オンライン学習は1データ毎にパラメータを更新するため学習が安定しにくいといった欠点があります。
それを補う手法としてミニバッチ学習という複数のデータでパラメータを更新する手法があります。

モデルフリーの強化学習ではデータ収集の仕方上どうしてもデータが時系列となり、データに偏りが生じてしまいます。
これでは学習が安定しないため、Experience Replay と呼ばれる手法を用いてバラバラの複数のデータからミニバッチ学習を実施しています。

データ(経験)を収集するコードは以下です。

import numpy as np
from collections import deque

epsilon = 0.1
batch_size = 32
buffer_size = 1024

# 収集する経験は上限を決め、古いものから削除する
experiences = deque(maxlen=buffer_size)

# 学習ループ
env = gym.make("CartPole-v0")
for episode in range(300):
    state = np.asarray(env.reset())
    done = False
    total_reward = 0

    # 1episode
    while not done:

        # アクションを決定
        action = EGreedyPolicy(model, state, nb_actions, epsilon)

        # 1step進める
        n_state, reward, done, _ = env.step(action)
        n_state = np.asarray(n_state)
        total_reward += reward

        # 経験を保存する
        experiences.append({
            "state": state,
            "action": action,
            "reward": reward,
            "n_state": n_state,
            "done": done,
        })

        state = n_state

        # 学習（中身は後述）
        train(model, experiences, batch_size, buffer_size)

学習

学習はまずある程度経験が貯まるまでまってから実行します。
コードはバッファサイズ分(1024)貯まるまで待っています。

貯まったらまず経験をランダムにバッチサイズ分取得します。
その後、更新式の通り計算して教師用のデータを作りモデルを学習させます。

import random
def  train(model, experiences, batch_size, buffer_size):
    # 経験が貯まるまで学習しない
    if len(experiences) < buffer_size:
        return

    gamma = 0.9  # 割引率

    # ランダムに経験を取得してバッチを作成
    batchs = random.sample(experiences, batch_size)

    # データ形式を変形
    state_batch = np.asarray([e["state"] for e in batchs])
    n_state_batch = np.asarray([e["n_state"] for e in batchs])

    # 現在の状態のQ値と次の状態のQ値を求める
    # (batch_size, nb_actions) ← (batch_size, state)
    # (32, 2) ← (32, 4)
    q = model(state_batch).numpy()
    n_q = model(n_state_batch).numpy()

    # 各バッチでQ値を計算
    for i, batch in enumerate(batchs):
        action = batch["action"]
        reward = batch["reward"]
        if batch["done"]:
            q[i][action] = reward
        else:
            q[i][action] = reward + gamma * np.max(n_q[i])

    # モデルをミニバッチ学習する
    model.train_on_batch(state_batch, q)

評価と結果の出力

強化学習では機械学習で使われる一般的なメトリクスの他に、1エピソードで取得できた合計報酬が重要となります。

報酬を基準に評価していいのですが、学習用に使ってるデータは探索用の行動が含まれているので少し正確ではない点に注意が必要です。(下振れします)

評価用のコードは以下です。

# 探索をやめてQ値が最高の行動のみにする
# 0 でもいいが、序盤に局所解に陥ってるとつまらないので少し乱数を混ぜて何回か見てみる
epsilon = 0.0001

# 5回テストする
for episode in range(5):
    tate = np.asarray(env.reset())
    env.render()
    done = False
    total_reward = 0

    # 1episode
    while not done:
        action = EGreedyPolicy(model, state, nb_actions, epsilon)
        n_state, reward, done, _ = env.step(action)
        state = np.asarray(n_state)
        env.render()
        step += 1
        total_reward += reward

    print("{} step, reward: {}".format(step, total_reward))

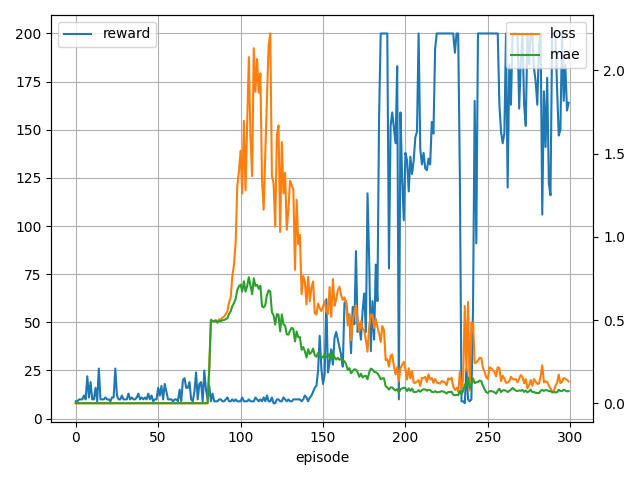
• 学習中の様子

メトリクスは1エピソードの平均値で表示しています。
学習は80エピソードあたりから始まっていますね。

• テスト結果

200 step, reward: 200.0
200 step, reward: 200.0
200 step, reward: 200.0
195 step, reward: 195.0
199 step, reward: 199.0

戦略関数の学習(Policy Gradient)

パラメータを持った戦略関数の更新

価値関数はそのまま実際の価値を教師データとして入力すればよかったですが、戦略関数はそうはいきません。
戦略関数から出力される行動確率は簡単には求められないからです。
ではどうするかというと期待値を計算し、それが最大化されるように戦略関数を学習します。

期待値 $J(\theta)$ は「(戦略に従い)状態に遷移する確率」×「行動確率」×「行動価値」から計算されます。

$$
J(\theta) \propto \sum_{s \in S} d^{\pi_\theta}(s) \sum_{a \in A} \pi_{\theta}(a|s) Q^{\pi_\theta}(s,a)
$$

$d^{\pi_\theta}(s)$ は戦略 $\pi_{\theta}$に従い状態$s$へ遷移する確率、$\pi_{\theta}(a|s)$ はそこで行動$a$をとる確率、$Q^{\pi_\theta}(s,a)$ は行動価値です。
また、$\propto$(propotional to)は比例関係を表す記号で期待値がエピソード長に比例することを表しています。

この式については導出が複雑らしく、詳細はググってください（え

この期待値 $J(\theta)$ を最大化する方法を考えます。
直感的には高い報酬が見込まれる行動には高い確率を、その逆には低い確率を割り当てる感じです。
これを最大化する手法として方策勾配法(Policy Gradient)があります。

方策勾配法(Policy Gradient)とREINFORCE

期待値 $J(\theta)$ の勾配は以下になるようです。

$$
\nabla J(θ) \propto \sum_{s \in S} d^{\pi_\theta}(s) \sum_{a \in A} \pi_{\theta}(a|s) \nabla log \pi_{\theta}(a|s) Q^{\pi_\theta}(s,a)
$$

この計算も結構複雑らしいので割愛します。
ここで、$d^{\pi_\theta}(s)$と$\pi_{\theta}(a|s)$が確率、$\nabla log \pi_{\theta}(a|s) Q^{\pi_\theta}(s,a)$が値と見ることができます。
なのでこれを期待値E[値]という形式で書くと以下となります。

$$
\nabla J(θ) \propto E_{\pi_\theta} [ log \pi_{\theta}(a|s) Q^{\pi_\theta}(s,a) ]
$$

戦略モデルの定義

モデルは状態を入力とし、各アクションを選択する確率(戦略)を出力します。

from tensorflow.python import keras
from tensorflow.keras.optimizers import Adam

# 環境の状態の形式(shape)
obs_shape = env.observation_space.shape

# 環境の取りうるアクション数
nb_actions = env.action_space.n

lr = 0.01  # 学習率

c = input_ = keras.layers.Input(shape=obs_shape)
c = keras.layers.Dense(10, activation="relu")(c)
c = keras.layers.Dense(10, activation="relu")(c)
c = keras.layers.Dense(nb_actions, activation="softmax")(c)
model = keras.Model(input_, c)
model.compile(optimizer=Adam(lr=lr))
model.summary()

出力層をsoftmaxにすることで各アクションの確率を出力するようにしています。
また損失関数は自作するので指定していません。

行動の決定

モデルが各アクションの選択確率を出力するのでそのまま確率に従って選ぶだけです。

def SoftmaxPolicy(model, state, nb_actions):
    action_probs = model(state.reshape((1,-1)))[0].numpy()
    return np.random.choice(nb_actions, 1, p=action_probs)[0]

経験の収集と学習ループのコード

経験の収集ですが、収集した時に使われていた戦略と学習する時の戦略が一致している必要があります。(On-policyのため)
ですのでモデルを更新すると過去の経験が使えなくなります。
これは Experience Replay と相性が悪く、今回の実装では Experience Replay は使わずにモンテカルロ法で実装しています。

また、経験と学習の戦略が一致していない場合は Off-policy となり、この差異を何かしら調整して学習する手法もあったります。
（今回は触れません）

経験収集と学習のループのコードは以下です。

# 学習ループ
env = gym.make("CartPole-v0")
for episode in range(300):
    state = np.asarray(env.reset())
    done = False
    total_reward = 0
    experiences = []

    # 1episode
    while not done:

        # アクションを決定
        action = SoftmaxPolicy(model, state, nb_actions)

        # 1step進める
        n_state, reward, done, _ = env.step(action)
        n_state = np.asarray(n_state)
        total_reward += reward

        # 経験を保存する
        experiences.append({
            "state": state,
            "action": action,
            "reward": reward,
            "n_state": n_state,
            "done": done,
        })

        state = n_state

    # 現在からエピソード最後までの報酬を計算
    for i,exp in enumerate(experiences):
        G = 0
        t = 0
        for j in range(i, len(experiences)):
            G += (gamma ** t) * experiences[j]["reward"]
            t += 1
        exp["G"] = G

    # 1エピソード毎に学習（中身は後述）
    train(model, experiences)

学習

更新式の通りに勾配を計算して更新する必要があるので損失関数は自作したものを用意する必要があります。

Tensorflow2.0 では GradientTape を用いると勾配を計算できるようです。(参考の公式チュートリアルが参考になりました)

from sklearn.preprocessing import StandardScaler

def  train(model, experiences):

    # データ形式を変形
    state_batch = np.asarray([e["state"] for e in experiences])
    action_batch = np.asarray([e["action"] for e in experiences])
    reward_batch = np.asarray([e["G"] for e in experiences])

    # アクションは one_hot ベクトルにする
    one_hot_actions = tf.one_hot(action_batch, nb_actions)

    # (a)報酬は正規化する
    # (正規化しないと学習が安定しませんでした)
    # (softmax層と相性が悪いから？)
    reward_batch = StandardScaler().fit_transform(reward_batch.reshape((-1, 1))).flatten()

    # 勾配を計算する
    with tf.GradientTape() as tape:
        # 現在の戦略を取得
        action_probs = model(state_batch, training=True)  # Forward pass

        # (1) 選択されたアクションの確率を取得
        selected_action_probs = tf.reduce_sum(one_hot_actions * action_probs, axis=1)

        # log(0) 回避用
        clipped = tf.clip_by_value(selected_action_probs, 1e-10, 1.0)

        # (2) 期待値「log( π(a|s) ) × Q」を計算
        loss = tf.math.log(clipped) * reward_batch

        # (3) experiences すべての期待値の合計が最大となるように損失を設定
        # 最大値がほしいので負の値にしています
        # 追記：ミニバッチ処理の場所になるので合計ではなく平均のほうが正しい
        loss = -tf.reduce_sum(loss)

    # 勾配を元にoptimizerでモデルを更新
    gradients = tape.gradient(loss, model.trainable_variables)
    model.optimizer.apply_gradients(zip(gradients, model.trainable_variables))

    return loss  # 確認用

(1)で $\pi_{\theta}(a|s)$ を計算しています。
(2)で $log \pi_{\theta}(a|s) Q^{\pi_\theta}(s,a)$ を計算しています。
(3)で計算した期待値を合計しています。

ベースライン(追記: 2021/4/20)

勾配の計算で用いられる価値 $Q^{\pi_\theta}(s,a)$ は関数 $b(s)$ を引くのが一般的らしいです。

$$
Q^{\pi_\theta}(s,a) - b(s)
$$

ですので以下の式になります。

$$
\nabla J(θ) \propto E_{\pi_\theta} [ log \pi_{\theta}(a|s) (Q^{\pi_\theta}(s,a) - b(s) ) ]
$$

価値Qのベースラインを変更していることから、この $b(s)$ はベースラインと呼ばれます。
$b(s)$ は勾配の分散を下げ、学習を安定させる目的で導入されています。
値としてはどんな値($b(s)=0$)でも問題ないですが、$V(s)$ が使われることが多いそうです。

また、$b(s)$ が報酬の平均をとる手法が REINFORCE となります。

コードの(a)で正規化しないと学習が安定しないというのはこのベースラインの影響ですね。
REINFORCE にするには以下のようにコードを変更すれば実現できます。
(追記内容なのでGoogleColaboratoryにはありません GoogleColaboratoryを更新しました)

//reward_batch = StandardScaler().fit_transform(reward_batch.reshape((-1, 1))).flatten()
reward_batch -= np.mean(reward_batch)  # 報酬の平均を引く

参考

• 強化学習 森村哲郎・著 シリーズ: 機械学習プロフェッショナルシリーズ
• 言語生成の強化学習をやっていく（手法紹介 REINFORCE編）

評価と結果の出力

戦略を学習しているのでテスト用に何かする必要はありません。
そのまま実行できます。

# 5回テストする
for episode in range(5):
    tate = np.asarray(env.reset())
    env.render()
    done = False
    total_reward = 0

    # 1episode
    while not done:
        action = SoftmaxPolicy(model, state)
        n_state, reward, done, _ = env.step(action)
        state = np.asarray(n_state)
        env.render()
        step += 1
        total_reward += reward

    print("{} step, reward: {}".format(step, total_reward))

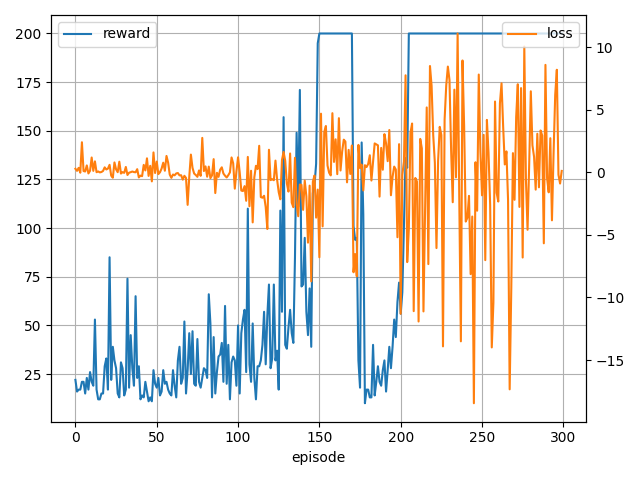
• 学習中の様子

• テスト結果

200 step, reward: 200.0
200 step, reward: 200.0
200 step, reward: 200.0
200 step, reward: 200.0
200 step, reward: 200.0

A3C/A2C

※2021/4/29 実装が間違っていたので見直しました。

Actor CriticのディープラーニングアルゴリズムとしてA2C(Advantage Actor Critic)を取り上げます。
A2Cの前にA3C(Asynchronous Advantage Actor Critic)があり、A3Cでは分散学習+Asynchronous(非同期)で学習する手法でした。
しかし、非同期がなくても同等以上の精度がでるといわれて提案された手法がA2Cらしいです。

ただ、今回の実装において分散学習は本質ではないのでそれを除外した実装を行います。
そうなるとA3CとA2Cで大きく実装の差異はないようです。

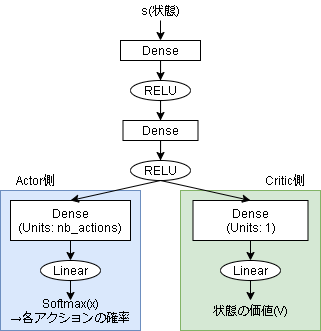
モデルの定義

A2Cのモデルでは状態の入力に対してActor側とCritic側の2つの出力を持ちます。

Dueling Networkに似てますね（もしかしたらこれが元ネタかも知れません）

from tensorflow.python import keras
from tensorflow.keras.optimizers import Adam

# 環境の状態の形式(shape)
obs_shape = env.observation_space.shape

# 環境の取りうるアクション数
nb_actions = env.action_space.n

lr = 0.01  # 学習率

c = input_ = keras.layers.Input(shape=obs_shape)
c = keras.layers.Dense(10, activation="relu")(c)
c = keras.layers.Dense(10, activation="relu")(c)
actor_layer = keras.layers.Dense(nb_actions, activation="linear")(c)
critic_layer = keras.layers.Dense(1, activation="linear")(c)

model = keras.Model(input_, [actor_layer, critic_layer])
model.compile(optimizer=Adam(lr=lr))
model.summary()

今回も損失関数は自作するので指定していません。

行動の決定

方策勾配法の時と同じですが出力が線形なのでsoftmax関数を経由して確率的に選ぶようにしています。

def LinearSoftmaxPolicy(model, state, nb_actions):
    action_eval, _ = model(state.reshape((1,-1)))
    probs = tf.nn.softmax(action_eval)
    return np.random.choice(nb_actions, 1, p=probs[0].numpy())[0]

モデルの出力が2つあるのでその処理も行っています。

経験の収集と学習ループのコード

経験の収集は方策勾配法の時と同じく同じ戦略の経験を集める必要があります。
なのでモンテカルロ法で実装しますが、Criticにより価値を見積もることもできるのでエピソード終了まで待つ必要はありません。
バッチサイズ分経験が貯まったらその都度計算していきます。

経験収集と学習のループのコードは以下です。

batch_size = 32
experiences = []

# 学習ループ
env = gym.make("CartPole-v0")
for episode in range(300):
    state = np.asarray(env.reset())
    done = False
    total_reward = 0

    # 1episode
    while not done:

        # アクションを決定
        action = LinearSoftmaxPolicy(model, state, nb_actions)

        # 1step進める
        n_state, reward, done, _ = env.step(action)
        n_state = np.asarray(n_state)
        total_reward += reward

        # 経験を保存する
        experiences.append({
            "state": state,
            "action": action,
            "reward": reward,
            "n_state": n_state,
            "done": done,
        })

        state = n_state

        # batch_size貯まるごとに学習する
        if len(experiences) == batch_size:
            train(model, experiences)
            experiences = []

勾配の計算

A2Cでは1つのネットワークで戦略と価値を出力しているのでロス関数も1つとなります。
更新式は以下に分けられます。

Total loss = -アドバンテージ方策勾配 + α Value loss - β 方策エントロピー

アドバンテージ方策勾配と方策エントロピーは最大値を求めたいのでマイナスをかけています。
αとβは割合を決めるハイパーパラメーターです。

アドバンテージ方策勾配

方策勾配で求める勾配は上記でも書いた通り以下になります。

$$ log \pi_{\theta}(a|s) Q^{\pi_\theta}(s,a) $$

アドバンテージ方策勾配は以下になります。

$$ log \pi_{\theta}(a|s) A^{\pi_\theta}(s,a) $$

QがAに変わっただけですね、Aは以下になります。

$$ A(s_t,a_t) = Q(s_t,a_t) - V(s_t) = r_{t+1} + V(s_{t+1}) - V(s_t) $$

方策勾配の重みづけに状態行動価値をそのまま使わずに現在の状態価値を引くことで分散が小さくなり学習が安定するそうです。
上記式では1stepのみ引いていますが、数ステップ先まで引く方法もあるようです。

Value loss

Q学習と変わらず次の状態の価値と今の状態の価値の差分です。
平均二乗誤差で損失を出します。

$$ \frac{ \sum(r + V(s_{t+1}) - V(s_t) )^2}{n} $$

方策エントロピー

方策エントロピーとはエントロピーが大きいほうが良い状態を指します。
例えばアクションが[50%,50%]と[70%,30%]の方策があった場合、後者のほうがエントロピーが大きい(乱雑である)といいます。
方策エントロピーが大きいほうが、学習が進んでおりいい方策になっていると考えられるため、これにボーナスを与える項がこの方策エントロピーになります。

数式は以下です。

$$ \sum_a \pi(a_t|s_t) log \pi(a_t|s_t) $$

方策エントロピー項の追加は、方策関数の正則化効果が期待できるようです。

学習

各経験に関して、状態価値関数が予測できるので、分かる部分に関しては実測値から、不明な部分は状態価値関数から予測して状態価値を計算しています。

def  train(model, experiences):

    gamma = 0.9  # 割引率

    # 現在からエピソード最後までの報酬を計算（後ろから計算）
    if experiences[-1]["done"]:
        # 最後が終わりの場合は全部使える
        G = 0
    else:
        # 最後が終わりじゃない場合は予測値vで補完する
        n_state = np.atleast_2d(experiences[-1]["n_state"])
        _, n_v = model(n_state)
        G = n_v[0][0].numpy()

    # 割引報酬を後ろから計算
    discounted_rewards = []
    for exp in reversed(experiences):
        if exp["done"]:
            G = 0
        G = exp["reward"] + gamma * G
        discounted_rewards.append(G)
    discounted_rewards.reverse()

    # 計算用にnp化して (batch_size,1) の形にする
    discounted_rewards = np.asarray(discounted_rewards).reshape((-1, 1))

    # ベースライン処理
    discounted_rewards -= np.mean(discounted_rewards)  # 報酬の平均を引く

    # データ形式を変形
    state_batch = np.asarray([e["state"] for e in experiences])
    action_batch = np.asarray([e["action"] for e in experiences])

    # アクションをonehotベクトルの形に変形
    onehot_actions = tf.one_hot(action_batch, nb_actions)

    #--- 勾配を計算する
    with tf.GradientTape() as tape:
        action_eval, v = model(state_batch, training=True)

        # π(a|s)を計算
        # 全アクションの確率をだし、選択したアクションの確率だけ取り出す
        # action_probs: [0.2, 0.8] × onehotアクション: [0 ,1] ＝ [0.8] になる
        action_probs = tf.nn.softmax(action_eval)
        selected_action_probs = tf.reduce_sum(onehot_actions * action_probs, axis=1, keepdims=True)

        #--- アドバンテージを計算
        # アドバンテージ方策勾配で使うvは値として使うので、
        # 勾配で計算されないように tf.stop_gradient を使う
        advantage = discounted_rewards - tf.stop_gradient(v)

        # log(π(a|s)) * A(s,a) を計算
        selected_action_probs = tf.clip_by_value(selected_action_probs, 1e-10, 1.0)  # 0にならないようにclip
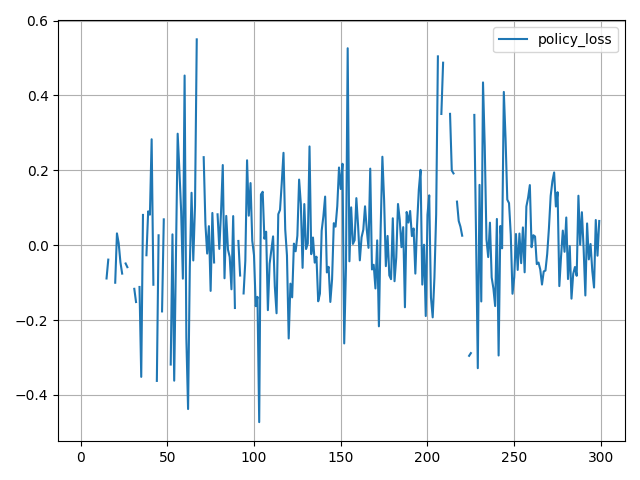
        policy_loss = tf.math.log(selected_action_probs) * advantage

        #--- Value loss
        # 平均二乗誤差で損失を計算
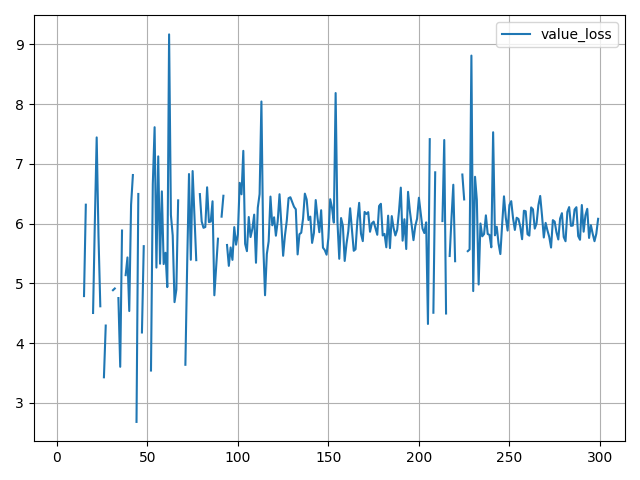
        value_loss = tf.reduce_mean((discounted_rewards - v) ** 2, axis=1, keepdims=True)

        #--- 方策エントロピー
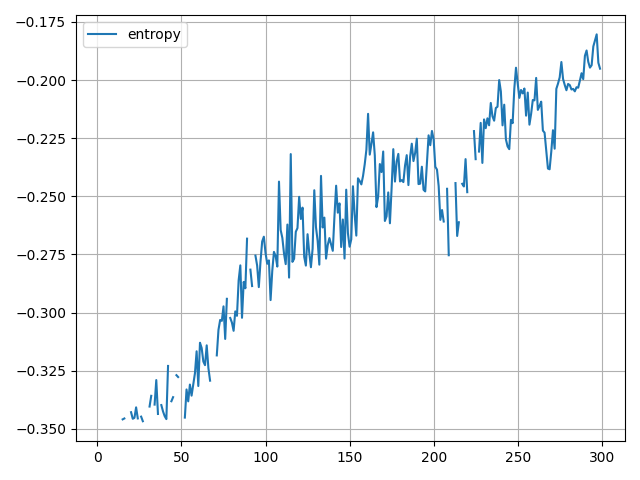
        entropy = tf.reduce_sum(tf.math.log(selected_action_probs) * selected_action_probs, axis=1, keepdims=True)

        #--- total loss
        value_loss_weight = 0.5
        entropy_weight = 0.1
        loss = -policy_loss + value_loss_weight * value_loss - entropy_weight * entropy

        # 全バッチのlossの平均(ミニバッチ処理?)
        loss = tf.reduce_mean(loss)

    # 勾配を計算し、optimizerでモデルを更新
    gradients = tape.gradient(loss, model.trainable_variables)
    model.optimizer.apply_gradients(zip(gradients, model.trainable_variables))

評価と結果の出力

方策勾配法と同じで戦略を学習しているのでテスト用に何かする必要はありません。
そのまま実行できます。

# 5回テストする
for episode in range(5):
    tate = np.asarray(env.reset())
    env.render()
    done = False
    total_reward = 0

    # 1episode
    while not done:
        action = LinearSoftmaxPolicy(model, state)
        n_state, reward, done, _ = env.step(action)
        state = np.asarray(n_state)
        env.render()
        step += 1
        total_reward += reward

    print("{} step, reward: {}".format(step, total_reward))

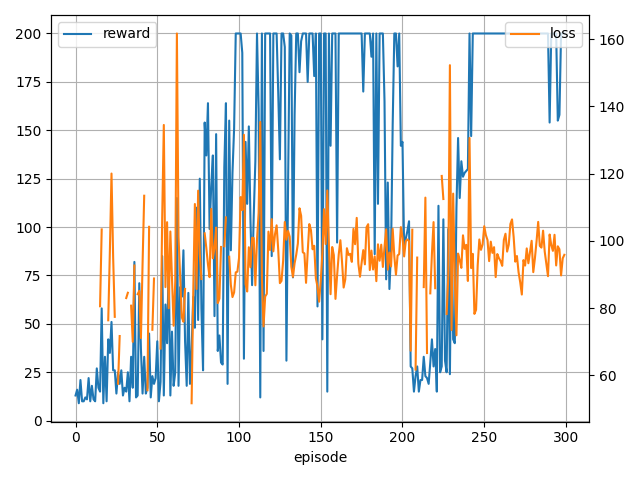
• 学習中の様子

• Policy loss
  

• Value loss
  

• エントロピー
  

• テスト結果

200 step, reward: 200.0
200 step, reward: 200.0
200 step, reward: 200.0
200 step, reward: 200.0
200 step, reward: 200.0

あとがき

ニューラルネットワークに反映するうえで重要なのは勾配の出し方ですね。
価値関数は簡単ですが、戦略関数の更新は計算が難しいですね…（まあ、計算結果だけを使えば問題ないですけど）

参考

• TensorFlow > 学ぶ > TensorFlow Core > ガイド基本的なトレーニングループ
• TensorFlow > 学ぶ > TensorFlow Core > ガイド > トレーニングループを最初から作成する
• 機械学習スタートアップシリーズ　Ｐｙｔｈｏｎで学ぶ強化学習　［改訂第２版］　入門から実践まで(amazonリンク)
• A3CでCartPole (強化学習)
• Policy Gradient Algorithms
• A3C(論文)
• A2C(論文)
• Advantage Actor Critic Tutorial: minA2C
• 【強化学習】実装しながら学ぶA3C【CartPoleで棒立て：1ファイルで完結】