今まで強化学習の記事をいくつかあげてきましたが強化学習をちゃんと勉強したときがありませんでした。
なので改めて基礎から勉強してみました。
第2回:ディープラーニング編(Q学習、方策勾配法、A3C/A2C)
コード全体
本記事で作成したコードは以下です。
強化学習の分類
強化学習を分類する上でよく見る要素をまとめてみました。
この分類に沿って見ていきたいと思います。
- モデル
- モデルベース
- モデルフリー
- 更新対象
- 価値関数(Valueベース)
- 方策関数(Policyベース)
- 両方(Actor-Critic)
- 学習に使う経験
- 実測値(モンテカルロ法)
- 予測値(TD法)
※方策は戦略と言ったりPolicyと言ったりします
モデル
まずは環境を定義します。(マルコフ決定過程と言われるやつです)
| 記号 | 備考 | |
|---|---|---|
| 状態 | $s$ | |
| 行動 | $a$ | |
| 即時報酬 | $r$ | |
| 遷移確率 | $P_a(s, s')$ | $s$にて$a$を実行した後に$s'$へ遷移する確率 |
| 状態遷移確率(遷移関数) | $P = T(s'|s, a)$ | $T$関数から$P$が出力される |
| 報酬関数 | $r = R(s, s')$ | $R$関数から$r$が出力される |
| エピソード時刻 | $0 ... t ... T$ |
状態遷移確率 $T(s'|s, a)$ は次の状態に遷移する遷移確率 $P_a(s, s')$を返す関数です。
モデルに関して、状態遷移確率 $T(s'|s, a)$ と即時報酬 $R(s, s')$ が分かっている事を前提にした学習をモデルベース、分からない事を前提にした学習をモデルフリーといいます。
次にある時刻tからエピソード最後までの報酬を定義しておきます。
$$ r_t + r_{t+1} + ... + r_{T} $$
t=0とすれば1エピソードで手に入れた全報酬です。
ただ、ある時刻 $t$ から見た未来の報酬は不確定要素が入るので未来の報酬には割引率 $\gamma$ を適用します。($\gamma$は0.9など1に近い定数)
ある時刻 $t$ における割引報酬 $G_t$ は以下になります。
$$ G_t = r_{t+1}+ \gamma r_{t+2} + \gamma^{2} r_{t+3} + ... + \gamma^{T-t-1} r_T$$
$$ G_t = \sum_{k=0}^{T-t-1}\gamma^k r_{t+k+1} \quad (\sumでまとめたもの)$$
$$ G_t = r_{t+1} + \gamma G_{t+1} \quad (漸化式ver)$$
3つ書きましたが全部同じです。
この割引報酬 $G_{t}$ は価値とも言い、学習するうえで重要な値となります。
更新対象
強化学習では何を学ぶのでしょうか?
ある時刻$t$で次にどのアクションを選択すればいいかを考えます。
選択できる全てのアクションで、アクション実行後に遷移した状態の価値 $G_{t+1}$ が最大となるアクションを選べばいいですね。
ただ、$G_{t+1}$ を求めるには未来で手に入る報酬を計算しないといけません。
しかし未来の報酬は実際に行動してみないと分かりません。
これは行動後の状態が確率的に遷移するためです。
(「コインを投げる」と行動した場合、表か裏のどちらがでるかは分からない)
$G_{t+1}$ を求めるのは難しいので代わりに期待値を求めることを考えます。
期待値を求めると何が嬉しいかというと、良い状態と悪い状態を比較できることです。
コインを例にすると、コインA(表75% 裏25%)とコインB(表60% 裏40%)があった場合、コインAを投げたほうが良さそうな結果になると思います。
(表の報酬が1、裏の報酬が-1とします)
これは以下のように期待値を計算すれば数字で比較することができます。
コインA: 0.75×1 + 0.25×-1 = 0.5
コインB: 0.6×1 + 0.4×-1 = 0.2
この期待値を比較することで、機械に良い悪いを判断してもらいいます。
次にいきなりですが方策 $\pi$ を定義します。
方策 $\pi$ において、状態 $s$ で行動 $a$ をとる確率を $\pi(a|s)$ と定義します。
方策 $\pi$ において、ある状態 $s$ の価値 $V_{\pi}(s)$ は以下です。
$$ V_{\pi}(s_t) = E_{\pi}[ r_{t+1} + \gamma V_{\pi}(s_{t+1}) ] $$
$E$ は期待値、$r_{t+1}$ は報酬、$\gamma$ は割引率です。
期待値は(確率×値)と計算できるので、期待値部分を展開すると以下になります。
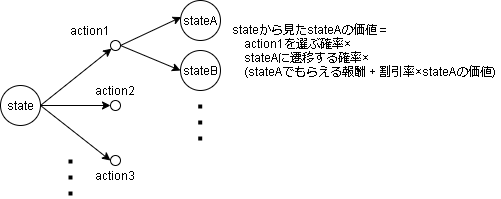
$$ V_{\pi}(s_t) = \sum_{a} \pi(a_t|s_t) \sum_{s'} T(s_{t+1}|s_t,a_t)(r_{t+1} + \gamma V_{\pi}(s_{t+1})) $$
日本語で簡単に言うと、(アクションを選ぶ確率×次の状態に遷移する確率×遷移後の状態の価値)の合計です。
図で書くと以下です。
コードだと以下みたいな感じです。
def policy(state): # pi
# ある方策において、引数stateの場合に各アクションがとる確率
pi = {
"状態A": {
"アクション1": 20%,
"アクション2": 50%,
"アクション3": 30%,
},
"状態B": ...
}
return pi[state]
def env_transitions_at(state, action): # T
# 引数(state, action)の場合に遷移する可能性のある状態と確率
trans = {
"状態A": {
"アクション1":{
"次の状態A": 20%,
"次の状態C": 80%,
},
...
},
"状態B": ...
}
return trans[state][action]
def env_reward_func(next_state): # R
# stateからnext_stateに遷移した時の報酬
r = {
"状態A": 10,
"状態B": 0,
...
}
return r[next_state]
def V_func(state): # ある状態(state)における価値
gamma = 0.9
action_probs = policy(state)
v = 0
for action in 全アクション:
q = 0
transition_probs = env_transitions_at(state, action)
for next_state, state_prob in transition_probs.items():
reward = env_reward_func(next_state)
# 価値を計算
# 終了処理をいれてないがエピソード終了まで再帰する
q += state_prob * (reward + gamma * V_func(next_state))
v += action_probs[action] * q
return v
この式は Bellman Equation (ベルマン方程式)といいます。
ベルマン方程式で問題なのは、未来の状態の価値も(再帰的に)見ているのでこのままでは求めることができない点です。
これを求めるために強化学習では大きく分けて、各状態の価値(状態価値$V$,行動価値$Q$)を学習する方法と、方策 $\pi$ を学習する方法があります。
また、価値と方策両方を学習する手法もあり、Actor-Critic と言います。
価値関数(状態価値関数/行動価値関数)
状態価値関数はベルマン方程式でだした $V_{\pi}(s)$ となります。
行動価値関数 $Q_{\pi}(s,a)$ はさらにアクションを選択した場合の価値となります。
$$ Q_{\pi}(s_t,a_t) = \sum_{s'} T(s_{t+1}|s_t,a_t)(r_{t+1} + \gamma V_{\pi}(s_{t+1})) $$
$Q$ と $V$ はアクションの差異だけなので以下の式が成り立ちます。
$$ V_{\pi}(s_t) = \sum_a \pi(a_t|s_t) Q_{\pi}(s_t,a_t) $$
$Q$ の式から $V$ を除いた式は以下です。
$$ Q_{\pi}(s_t,a_t) = \sum_{s'} T(s_{t+1}|s_t,a_t)(r_{t+1} + \gamma \sum_{a} \pi(a_{t+1}|s_{t+1}) Q_{\pi}(s_{t+1},a_{t+1}) ) $$
方策関数
価値関数 $V$ が分かっている場合、方策関数 $\pi$ を決めれば期待値が求まります。
その期待値が最大となるように方策を学習する手法がPolicyベースの学習となります。
これは On-policy な学習とも言ったりします。
(逆に価値関数を学習する手法は方策がないという意味で Off-policy と呼んだりします)
学習に使う経験
強化学習で価値を計算する場合、未来の報酬を知る必要があります。
(ベルマン方程式の $V_{\pi}(s_{t+1})$ の部分ですね)
これを計算する際、実測値で計算するか予測値で計算するかで違いがあります。
前者は1エピソード終わった後に1エピソードの情報を元に計算する手法でモンテカルロ法といいます。
後者は1step毎にアルゴリズム内の予測値を用いて更新する手法でTD法といいます。
(追記:ここについては第3回で詳細に取り上げています)
価値関数の更新を考えてみます。
現在の価値を予測してみた所ある状態での価値が $V(s_t)$ だったとします。
次に実際に1step進めてみた所、価値 $V'(s_t)$ は以下でした。
(報酬と次の状態が分かるので新しく予測できます)
$$ V'(s_t) = r_{t+1} + \gamma V(s_{t+1})$$
$r_{t+1}$ は報酬、$\gamma$ は割引率、$V(s_{t+1})$ は遷移先の状態の価値です。
現在予測している価値と実際に得られた価値の差異 $V'(s_t) - V(s_t)$ はTD誤差とよばれます。
価値関数の更新ではこれを元に価値を更新します。
\begin{align}
TD_{error} &= r_{t+1} + \gamma V(s_{t+1}) - V(s_t) \\
V(s_t) &\leftarrow V(s_t) + \alpha(TD_{error}) \\
\end{align}
$\alpha$ は機械学習でおなじみの学習率です。
上記の式で $V(s_{t+1})$ に予測値を使う方法がTD法で、エピソード最後まで展開する方法がモンテカルロ法です。
エピソード最後まで展開したモンテカルロ法の更新式は以下です。
\begin{align}
TD_{error} &= (r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} + ... + \gamma^{T-t-1} r_{r_{T-t}}) - V(s_t) \\
V(s_t) &\leftarrow V(s_t) + \alpha (TD_{error}) \\
\end{align}
実践
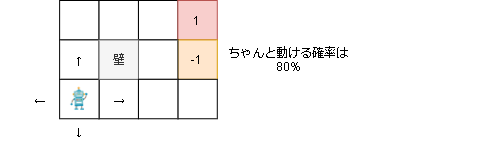
環境(GridEnv)
プレイヤーは上下左右に動け、右上のゴールにたどり着くと報酬1がもらえます。
しかし右真ん中のマスは報酬-1が入ってしまいます。
また、実際に動ける確率は80%で20%の確率で横方向に行ってしまいます。
(1ステップ毎に-0.04の報酬が手に入ります)
環境の実装コードはコード全体を見てください。
gym.Env を継承して作っているので動かす場合は以下になります。
env = GridEnv()
# ゲーム情報
print("action_space : " + str(env.action_space))
print("observation_space : " + str(env.observation_space))
print("reward_range : " + str(env.reward_range))
# エピソードループ
for episode in range(1):
env.reset() # ゲームの初期化
env.render() # ゲームの描画
total_reward = 0
# 最大 20 step 実行
for step in range(20):
# アクションをランダムに取得
action = env.action_space.sample()
# 1step 実行する。
# 戻り値は、環境,報酬,終了判定(done),情報
observe, reward, done, _ = env.step(action)
total_reward += reward
env.render() # 描画
# 終了判定がTrueなら1ゲーム終了
if done:
break
print("Episode {}: {:.2f} reward".format(episode, total_reward))
env.close()
(環境側)遷移関数、報酬関数
モデルベースの学習も試すため、環境側には遷移関数と報酬関数も実装します。
# 全アクション
actions = [Action.UP, Action.DOWN, Action.LEFT, Action.RIGHT]
# 各行動において、実際に行動する確率
move_prob = {
Action.UP: {
Action.UP: 0.8,
Action.DOWN: 0,
Action.RIGHT: (1 - 0.8) / 2,
Action.LEFT: (1 - 0.8) / 2,
},
Action.DOWN: ...
Action.RIGHT: ...
Action.LEFT: ...
}
# 遷移関数
def transitions_at(state, action):
transition_probs = {}
for a in actions:
# アクションが実行される確率
prob = move_prob[action][a]
# アクションを実行した後に遷移した状態
tmp_state = _move(state, a)
# 遷移後の状態に移行する確率を追加する
if tmp_state not in transition_probs:
transition_probs[tmp_state] = 0
transition_probs[tmp_state] += prob
return transition_probs
def _move(state, action):
stateにて、actionを実行した場合の次の状態を返す
return next_state
# 報酬関数
def reward_func(state):
stateで得る報酬を返す
return reward
動的計画法
価値反復法(Value Iteration)
モデルベースの状態価値関数を求めるアルゴリズムです。
| モデル | 更新対象 | 行動 |
|---|---|---|
| モデルベース | 状態価値関数 | 価値が最大となるアクションで固定(Off-policy) |
以下のように更新します。
$$ V(s_{t}) \leftarrow \max_a \Bigl( \sum_{s_{t+1}} T(s_{t+1}|s_{t}, a)(R(s) + \gamma V(s_{t+1}) ) \Bigr) $$
max は期待値が最大となるアクションを選ぶという意味にあたります。
コードは以下です。
# 価値関数の全状態を初期化
V = {s:0 for s in env.states}
# 割引率
gamma = 0.9
# 学習
for i in range(100): # for safety
delta = 0
# 全状態をループ
for s in env.states:
# アクションが実行できる状態のみ実施
if not env.can_action_at(s):
continue
# 各アクションでの報酬期待値を計算
expected_reward = []
for a in env.actions:
# 報酬期待値を計算
r = 0
transition_probs = env.transitions_at(s, a)
for next_state, prob in transition_probs.items():
reward,_ = env.reward_func(next_state)
r += prob * (reward + gamma * V[next_state])
expected_reward.append(r)
# 各アクションで最大の期待値となるアクションを採用
max_reward = max(expected_reward)
delta = max(delta, abs(V[s] - max_reward)) # 学習打ち切り用に差分を保存
V[s] = max_reward
# 更新差分が閾値以下になったら学習終了
if delta < 0.0001:
break
print("training end. train count: {}".format(i))
実際に実行した結果は以下です。
(説明用にアルファベットを入れています。)
training end. train count: 10
0.61044 0.76621(b) 0.92818(a) 0.00000(ゴール)
0.48720 0.00000(壁) 0.58493(c) 0.00000(穴)
0.37381 0.32662 0.42754 0.18882
学習自体は10回で終わっていますね。
出力は各状態における価値の値になっています。
ゴールに近い(a)が一番価値が高くなっています。
(b)と(c)はゴールへの距離は同じですが、穴に近い(c)の方が価値が低くなっています。
ちゃんと学習できていますね。
方策反復法(Policy Iteration)
モデルベースの方策関数を求めるアルゴリズムです。
価値反復法では行動は最大値を採用していましたが、方策反復法では方策から行動を決めます。
| モデル | 更新対象 |
|---|---|
| モデルベース | 方策関数(On-policy) |
更新は各アクションにて、期待値が最大となるアクションを選択する確率を100%に、それ以外のアクションを0%にします。
まずはポリシーにおける状態価値を返す関数を作成します。(価値反復法で計算)
価値反復法では行動は最大値を採用していましたが、方策反復法ではどのアクションを選ぶかはポリシー側が学習するためベルマン方程式通り合計値(期待値)を返します。
# ポリシーにおける状態の価値を価値反復法で計算
def estimate_by_policy(env, policy, gamma=0.9, threshold=0.0001):
V = {s:0 for s in env.states}
# 学習
for i in range(100): # for safety
delta = 0
# 全状態をループ
for s in env.states:
# アクションが実行できる状態のみ実施
if not env.can_action_at(s):
continue
# 各アクションでの報酬期待値を計算
expected_reward = []
for a in env.actions:
# ポリシーにおけるアクションの遷移確率
actoin_prob = policy[s][a]
# 報酬期待値を計算
r = 0
transition_probs = env.transitions_at(s, a)
for next_state, prob in transition_probs.items():
reward,_ = env.reward_func(next_state)
r += actoin_prob * prob * (reward + gamma * V[next_state])
expected_reward.append(r)
# 各アクションの期待値を合計する
value = sum(expected_reward)
delta = max(delta, abs(V[s] - value)) # 学習打ち切り用に差分を保存
V[s] = value
# 更新差分が閾値以下になったら学習終了
if delta < threshold:
break
return V
次に方策の学習部分です。
# 方策関数を初期化
policy = {}
for s in env.states:
policy[s] = {}
for a in env.actions:
# 最初は均等の確率
policy[s][a] = 1/len(env.actions)
# 割引率
gamma = 0.9
# 学習
for i in range(100): # for safety
update_stable = True
# 現policy状態での価値を計算
V = estimate_by_policy(env, policy)
# 全状態をループ
for s in env.states:
# アクションが実行できる状態のみ実施
if not env.can_action_at(s):
continue
# 各アクションにて、選択後の状態価値の期待値を計算
action_rewards = {}
for a in env.actions:
r = 0
transition_probs = env.transitions_at(s, a)
for next_state, prob in transition_probs.items():
reward,_ = env.reward_func(next_state)
r += prob * (reward + gamma * V[next_state])
action_rewards[a] = r
# 期待値が一番高いアクション
best_action = max(action_rewards, key=action_rewards.get)
# 現ポリシーで一番選ばれる確率の高いアクション
policy_action = max(policy[s], key=policy[s].get)
# ベストなアクションとポリシーのアクションが違う場合は更新
if best_action != policy_action:
update_stable = False
# ポリシーを更新する(greedy)
# ベストアクションの確率を100%にし、違うアクションを0%にする
for a in policy[s]:
if a == best_action:
prob = 1
else:
prob = 0
policy[s][a] = prob
# 更新しなくなったら学習終了
if update_stable:
break
print("training end. train count: {}".format(i))
実際に実行した結果は以下です。
training end. train count: 3
----------------------------------------------------
0.00 | 0.00 | 0.00 | 0.25 |
0.00 1.00|0.00 1.00|0.00 1.00|0.25 0.25|
0.00 | 0.00 | 0.00 | 0.25 |
----------------------------------------------------
1.00 | 0.25 | 1.00 | 0.25 |
0.00 0.00|0.25 0.25|0.00 0.00|0.25 0.25|
0.00 | 0.25 | 0.00 | 0.25 |
----------------------------------------------------
1.00 | 0.00 | 1.00 | 0.00 |
0.00 0.00|0.00 1.00|0.00 0.00|1.00 0.00|
0.00 | 0.00 | 0.00 | 0.00 |
----------------------------------------------------
・学習後のpolicyでのV
0.61044 0.76621 0.92818 0.00000
0.48720 0.00000 0.58493 0.00000
0.37381 0.32662 0.42754 0.18882
学習は3回で終わっています。
学習後の方策では確率が1になっているので出力されたVは価値反復法で出した値と同じになりましたね。
Q学習
モデルフリーの行動価値関数を求めるアルゴリズムです。
モデルフリーなので環境が提供する遷移関数と報酬関数は使わずに学習を行います。
ではどうやるかというと実際に動かして学習を行います。
| モデル | 更新対象 | 行動 | 学習に使う経験 |
|---|---|---|---|
| モデルフリー | 行動価値関数 | 価値が最大となるアクションで固定(Off-policy) | 予測値(TD法) |
まずは行動ですが、モデルフリーでは実際に行動する上で探索と活用のトレードオフを考えないといけません。
多腕バンディット問題等が有名ですね(以前記事を書いているのでよかったらどうぞ)
Q学習では Epsilon-Greedy 法を使って探索を行います。
コードだと以下です。
def EGreedyPolicy(Q, state, actions, epsilon):
if np.random.random() < epsilon:
# epsilonより低いならランダムに移動
return np.random.randint(len(actions))
elif np.sum(Q[state]) == 0:
# Q値が0は全く学習していない状態なのでランダム移動
return np.random.randint(len(actions))
else:
# Q値が最大のアクションを実行
return np.argmax(Q[state])
次に更新式ですが、以下となります。
$$ Q(s_t,a_t) \leftarrow Q(s_t,a_t) + \alpha ( r_{t+1} + \gamma Q_{max}(s_{t+1}) - Q(s_t,a_t) ) $$
$\alpha$ は学習率、$\gamma$は割引率です。
$Q_{max}(s_{t+1})$ が予測値となり以下のように $s_{t+1}$ における各アクションでの最大値を返します。
$$ Q_{max}(s_{t+1}) = \max_a (Q(s_{t+1}, a)) $$
import collections
# Q関数を初期化
Q = collections.defaultdict(lambda: [0] * len(env.actions))
gamma = 0.9 # 割引率
lr = 0.9 # 学習率
epsilon = 0.1
# 学習ループ
total_rewards = []
for episode in range(100):
state = env.reset()
done = False
total_reward = 0
# 1episode 最大20stepで終わりにする
for step in range(20):
# Epsilon-Greedy でアクションを決定
action = EGreedyPolicy(Q, state, env.actions, epsilon)
# 1step進める
n_state, reward, done, _ = env.step(action)
total_reward += reward
# Q値の計算
gain = reward + gamma * max(Q[n_state])
td = gain - Q[state][action]
Q[state][action] += lr * td
state = n_state
if done:
break
total_rewards.append(total_reward)
学習後のQ値は以下です。
-------------------------------------------------------
-0.01 | 0.67 | 0.07 | 0.00 |
-0.02 0.73| 0.07 0.85|-0.06 1.00| 0.00 0.00|
-0.01 | 0.02 | 0.00 | 0.00 |
-------------------------------------------------------
0.58 | 0.00 | 0.84 | 0.00 |
-0.11 -0.12| 0.00 0.00|-0.05 -1.00| 0.00 0.00|
0.32 | 0.00 | -0.90 | 0.00 |
-------------------------------------------------------
0.38 | -0.14 | 0.50 | -0.90 |
-0.11 -0.15|-0.16 -0.15|-0.15 -0.17|-0.17 -0.90|
0.18 | -0.14 | -0.17 | -0.15 |
-------------------------------------------------------
結果は毎回変わります。
学習はできていそうですね。
Q学習(モンテカルロ法)
Q学習の学習に使う経験が実測値のバージョンです。
| モデル | 更新対象 | 行動 | 学習に使う経験 |
|---|---|---|---|
| モデルフリー | 行動価値関数 | 価値が最大となるアクションで固定(Off-policy) | 実測値(モンテカルロ法) |
基本はTD法と一緒ですが、学習タイミングが1エピソード終わった後になります。
$$ Q(s_t,a_t) \leftarrow Q(s_t,a_t) + \alpha ( (r_{t+1} + \gamma r_{t+2} + ... + \gamma^{T-t-1} r_{r_{T-t}} ) - Q(s_t,a_t) ) $$
Q学習(TD法)と大きく違う部分を載せます。
(略)
# 学習ループ
for episode in range(100):
(略)
# 1episode
for step in range(20):
# Epsilon-Greedy でアクションを決定
action = EGreedyPolicy(Q, state, env.actions, epsilon)
# 1step進める
n_state, reward, done, _ = env.step(action)
total_reward += reward
# 学習用に経験を保存
experiences.append({
"state": state,
"action": action,
"reward": reward,
})
(略)
# 1エピソード終了後に学習
for i, exp in enumerate(experiences):
state = exp["state"]
action = exp["action"]
# 現在からエピソード最後までの報酬を計算
G = 0
t = 0
for j in range(i, len(experiences)):
G += (gamma ** t) * experiences[j]["reward"]
t += 1
# Q値を更新
td = G - Q[state][action]
Q[state][action] += lr * td
(略)
学習後のQ値は以下です。
-------------------------------------------------------
-0.25 | 0.64 | -0.09 | 0.00 |
-0.04 -0.19|-0.30 0.85|-0.08 1.00| 0.00 0.00|
-0.24 | -0.21 | -0.27 | 0.00 |
-------------------------------------------------------
-0.30 | 0.00 | 0.72 | 0.00 |
-0.66 -0.26| 0.00 0.00| 0.42 -0.90| 0.00 0.00|
-0.25 | 0.00 | -0.26 | 0.00 |
-------------------------------------------------------
-0.34 | -0.88 | -0.31 | -0.99 |
-0.35 -0.31|-0.34 -0.22|-0.92 -0.93|-0.29 -0.30|
-0.32 | -0.14 | -0.04 | -0.25 |
-------------------------------------------------------
SARSA
モデルフリーの方策関数を求めるアルゴリズムです。
| モデル | 更新対象 | 学習に使う経験 |
|---|---|---|
| モデルフリー | 方策関数(On-policy) | 予測値(TD法) |
$$ Q(s_t,a_t) \leftarrow Q(s_t,a_t) + \alpha ( r_{t+1} + \gamma Q(s_{t+1},a_{t+1}) - Q(s_t,a_t) ) $$
Q学習との違いは更新に使うQ値がmaxではなく、実際に選んだアクションのQ値で更新している点です。
選ぶアクション事態はQ学習と変わらず、価値が最大となるアクション+ε-greedy法です。
Q値の役割が行動価値関数ではなく方策関数となっており、方策自体を更新しているのでOn-policyになっていると思います。
(ここら辺は理解が怪しいです…)
(略)
# 学習ループ
for episode in range(100):
(略)
# エピソード前に初期アクションを生成
action = EGreedyPolicy(Q, state, env.actions, epsilon)
# 1episode
for step in range(20):
# 1step進める
n_state, reward, done, _ = env.step(action)
total_reward += reward
# 次のアクションを求める
n_action = EGreedyPolicy(Q, state, env.actions, epsilon)
# 次のアクションでQ値を計算
gain = reward + gamma * Q[n_state][n_action]
td = gain - Q[state][action]
Q[state][action] += lr * td
action = n_action
state = n_state
if done:
break
total_rewards.append(total_reward)
(略)
学習後のQ値は以下です。
-------------------------------------------------------
0.03 | 0.50 | 0.86 | 0.00 |
0.56 0.72|-0.33 0.86|-0.24 1.00| 0.00 0.00|
-0.52 | -0.73 | -0.94 | 0.00 |
-------------------------------------------------------
0.48 | 0.00 | -0.07 | 0.00 |
-0.43 -0.42| 0.00 0.00|-0.10 -1.00| 0.00 0.00|
-0.37 | 0.00 | -0.93 | 0.00 |
-------------------------------------------------------
0.27 | -0.29 | -0.46 | -0.93 |
-0.15 -0.48|-0.42 -0.70|-0.44 -0.88|-0.52 -0.95|
-0.16 | -0.49 | -0.41 | -0.50 |
-------------------------------------------------------
Q学習とSARSAでどちらのアルゴリズムが優れているといった事はありません。(学習対象の環境に左右される)
Q学習は常に最善の行動をとるため楽観的、SARSAは現在の方策に基づくため現実的といった感じらしいです。
Actor Critic
モデルフリーの価値関数と方策関数両方を学習する手法です。
| モデル | 更新対象 | 学習に使う経験 |
|---|---|---|
| モデルフリー | 状態価値関数、方策関数 | 予測値(TD法) |
まずは行動ですが、Softmaxによる確率選択で決定します。
ざっくりいうと各値に比例した確率でアクションが選択される選び方です。
アクション1が9、アクション2が1の場合、アクション1が90%、アクション2が10%で選ばれる感じです。
計算したらアクション1が1、アクション2が2の場合、アクション1が27%、アクション2が73%程でした。
def SoftmaxPolicy(Q, state, actions):
x = Q[state]
t = np.exp(x) / np.sum(np.exp(x), axis=0)
a = np.random.choice(len(actions), 1, p=t)[0]
return a
状態価値関数の更新式は以下です。
$$ V(s_{t}) \leftarrow V(s_t) + \alpha ( r_{t+1} + \gamma V(s_{t+1}) - V(s_t) ) $$
方策関数の更新式は以下です。
$$ Q(s_t,a_t) \leftarrow Q(s_t,a_t) + \alpha ( r_{t+1} + \gamma V(s_{t+1}) - V(s_t) ) $$
状態価値のTD誤差をもとに状態価値関数と方策関数を更新している点がポイントでしょうか。
# 初期化
Q = collections.defaultdict(lambda: [random.uniform(0, 1)] * env.action_space.n)
V = collections.defaultdict(float)
gamma = 0.9 # 割引率
lr = 0.9 # 学習率
# 学習ループ
total_rewards = []
for episode in range(100):
state = env.reset()
done = False
total_reward = 0
# 1episode
for step in range(20):
# アクションを決定
action = SoftmaxPolicy(Q, state, env.actions)
# 1step進める
n_state, reward, done, _ = env.step(action)
total_reward += reward
# 更新
gain = reward + gamma * V[n_state]
td = gain - V[state]
Q[state][action] += lr * td
V[state] += lr * td
state = n_state
if done:
break
total_rewards.append(total_reward)
(略)
学習後のQ値とV値です。
-------------------------------------------------------
-0.11 | -0.44 | 0.81 | 0.81 |
-0.61 3.55|-0.46 4.18| 0.75 5.18| 0.81 0.81|
-0.56 | -0.11 | -2.19 | 0.81 |
-------------------------------------------------------
2.99 | 0.40 | 0.02 | 0.60 |
0.14 -0.18| 0.40 0.40| 2.62 -1.31| 0.60 0.60|
-1.02 | 0.40 | -0.62 | 0.60 |
-------------------------------------------------------
3.48 | 0.30 | 0.57 | -0.36 |
0.40 -0.02| 0.92 -0.93| 2.27 -0.78| 0.37 0.65|
0.45 | 0.23 | 0.86 | 0.61 |
-------------------------------------------------------
0.73 0.83 1.00 0.00
0.61 0.00 -0.37 0.00
0.51 -0.22 -0.24 -1.00
あとがき
まずは環境や学習対象の関数がすべてテーブル形式での強化学習について扱いました。
次はテーブル形式ではなく関数の場合にどうなるかを見ていきたいと思います。