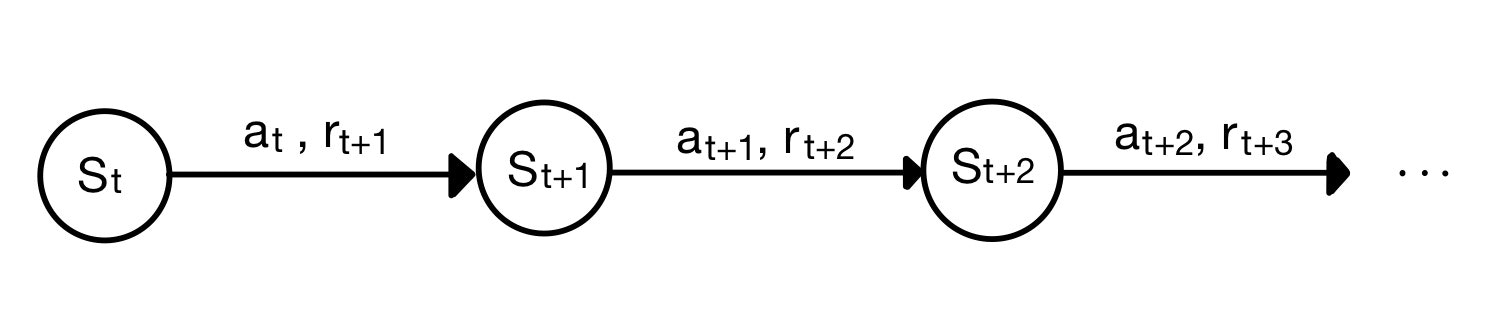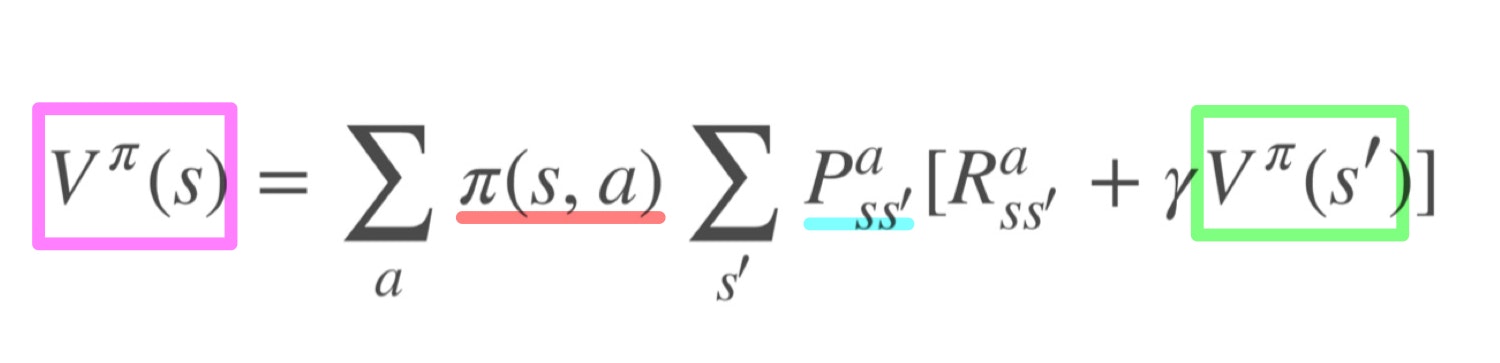はじめに
強化学習に対する参考書を読み進めて、深層強化学習のコードをgithubで落として一部改変して使ったりしています。しかし、肝心の理論に関するところが追いついていけません。
思うに、参考書を進めるうちになんとなくわかった気になったり、飛ばしたりするうちに不理解が蓄積していっているんだと思います。そのため、強化学習の基礎の基礎から、もう少し整理する必要があると思いました。シリーズものにして少しずつまとめていけたらと思います。
間違いや不明瞭なところなどありましたらどんどんご指摘いただけるとありがたいです。
参考書籍
Richard S. Sutton and Andrew G. Batro 著「強化学習」第1版 三上貞芳・皆川雅章訳、森北出版株式会社
現状
- 価値関数、方策、価値最適化、方策評価、Q関数など、なんとなくわかっているが、やはりなんとなくしかわかっていない。。
今回やったこと
- 状態価値関数$V^\pi(s)$の導出、理解
- 状態価値関数とは何か?イメージで理解する
- 格子世界に関する状態価値関数の計算(のための準備。実装は次回に回す)
格子世界(grid world)
まずは今回の設定から説明します。
5×5のグリッドの世界を考えます。このマス目の中をエージェントは上下左右好きな方向に動く事ができます。この問題設定は上記の参考書籍のP.77より引用しました。
x軸y軸は下図のようにとります。行列の指標番号に合わせた形にしています。
軸の交点が(0,0)になってないですが、表記上の問題です。お許しください。

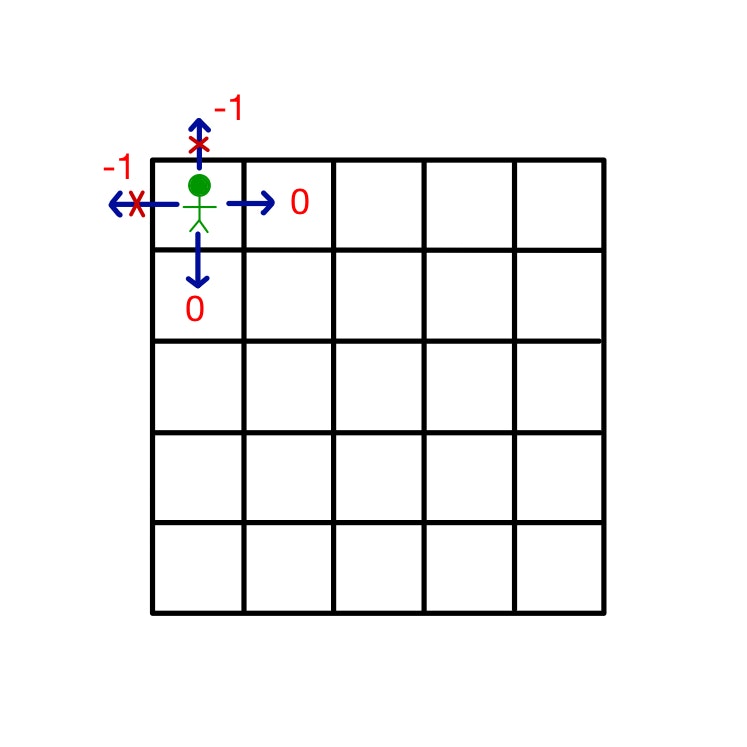
グリッドの外側の境界線を破って外に行く事はできません。例えば下図の状態では上と左に動くことはできず、そのような行動をとっても今の状態から動くことはできません。また、その場合、-1の報酬が支払われます。
下図のA,Bに到達した場合、その後どのアクションをとってもそれぞれA',B'の状態に移動し、それぞれ+10, +5の報酬が支払われます。その場所に到達するようなアクションを取った時ではなく、そこに到達した後のアクションに対して報酬が支払われる事に注意してください。

状態の価値
エージェントはあるポリシー$\pi$に従って行動するとします。
例えば「右に動いたあとは下には動かない」とか「3回続けて左には動かない」などです。また、上下左右の行動をある確率値にしたがって行動を決めるのもポリシーの一つです。
さて、この格子世界ではどの場所に位置することが価値が高いとみなされるでしょうか。直感的には報酬が高くもらえる所の近辺が価値が高いといえます。
例えばAにいる時は、どの行動を取ったとしても+10の報酬がもらえるので、ここにいることが他よりも価値が高いと推定されます。Bも同様です。
さらにAやBの付近も価値が高いでしょう。なぜならAやBに近いのでAやBに到達する可能性が高いからです。その中でもAの右の方がAの左よりも価値が高そうです。前者はAとBに隣接していますが、後者はAにしか隣接していません。またAの左の方が左側の壁にぶつかって減点される可能性があるからです。
このように、系のとる状態(この場合位置)に関して、なんとなくここが高そうだなと感じている価値を定量化するのが今回の目的です。
ここで強調したい点は、価値はポリシーによって変わる、ということです。
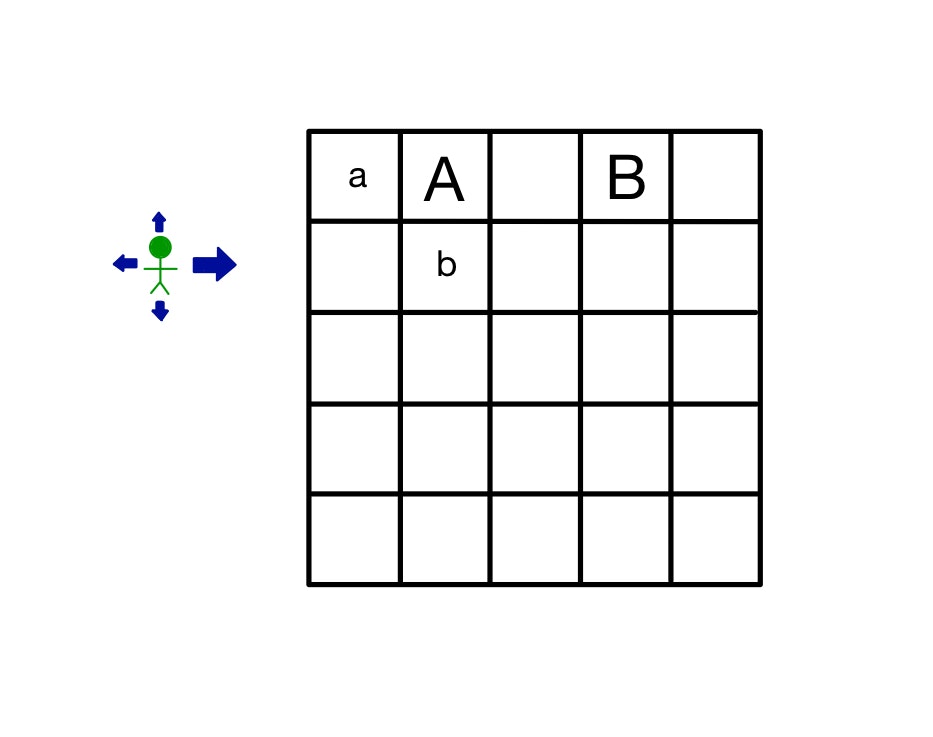
下図でaとbのどちらが高いかはポリシーによって変わってきます。緑のエージェントのポリシーが図のように右に動くことに重きを置くと、aの価値が高くなる方向に動きます。
ポリシー(方策)
ポリシーについて定式化しておきましょう。この場合、方策とはある状態sの時に行動aを取る確率として定義されます。
格子世界の例でいうと(ここからは座標の表記も併用します)、ある位置(x=2,y=3)において右に0.7、その他に0.1ずつの確率で移動する方策の場合
\pi(s, a) = \left\{
\begin{array}{}
0.7\quad (s = (2,3),\: a = right)\\
0.1\quad (s = (2,3),\: a = up)\\
0.1\quad (s = (2,3),\: a = left)\\
0.1\quad (s = (2,3),\: a = down)
\end{array}
\right.
となります。それぞれの状態sについて行動aそれぞれの確率を返すわけですから、方策を配列に格納しようとする場合はs×a= 25×4=100個の値が必要になります。これを$s \in S, a \in A, \pi \in S\times A$と表したりします。
もちろん、状態(場所)sによらずに常に同じ確率分布をとる。といったポリシーもあります。
これは自分でポリシーを設定するときに、各場所について決めるのはめんどくさいからざくっと決めるという時に使われます。
〜注意〜
この記事は格子世界に対して最適な方策を決める記事ではありません。ある(わかっている)方策のもとでの状態価値関数を算出するための記事です。
つまり方策最適化のための前段階の記事です。まだまだ道は長い。。。
価値の定量化
さて、これまでの問題設定で直感的に見積もった価値を定式化してみましょう。そのために価値関数と呼ばれる概念を導入します。
価値関数には2種類あり
- 状態価値関数
- $V^\pi(s)$ : 状態sにいることの価値
- 状態行動価値関数
- $Q^\pi(s,a)$ : 状態sにいて行動aを取る価値
です。←今回は状態の価値関数を扱います
しかし、状態sにいることの価値を具体的にどうやって定式化しましょう?エージェントが環境から受け取れるフィードバックは環境からの報酬$r$だけです。
まず、強化学習のシステムについて図示しましょう。
時刻$t$の時に状態$s_t$にいたとき、方策$\pi$に従って行動$a_t$を取った結果、時刻$t+1$の時に状態$s_{t+1}$に遷移し、報酬$r_{t+1}$をもらいます。(報酬は$r_t$ではなく$r_{t+1}$であることに注意)。これを時々刻々と繰り返していきます。
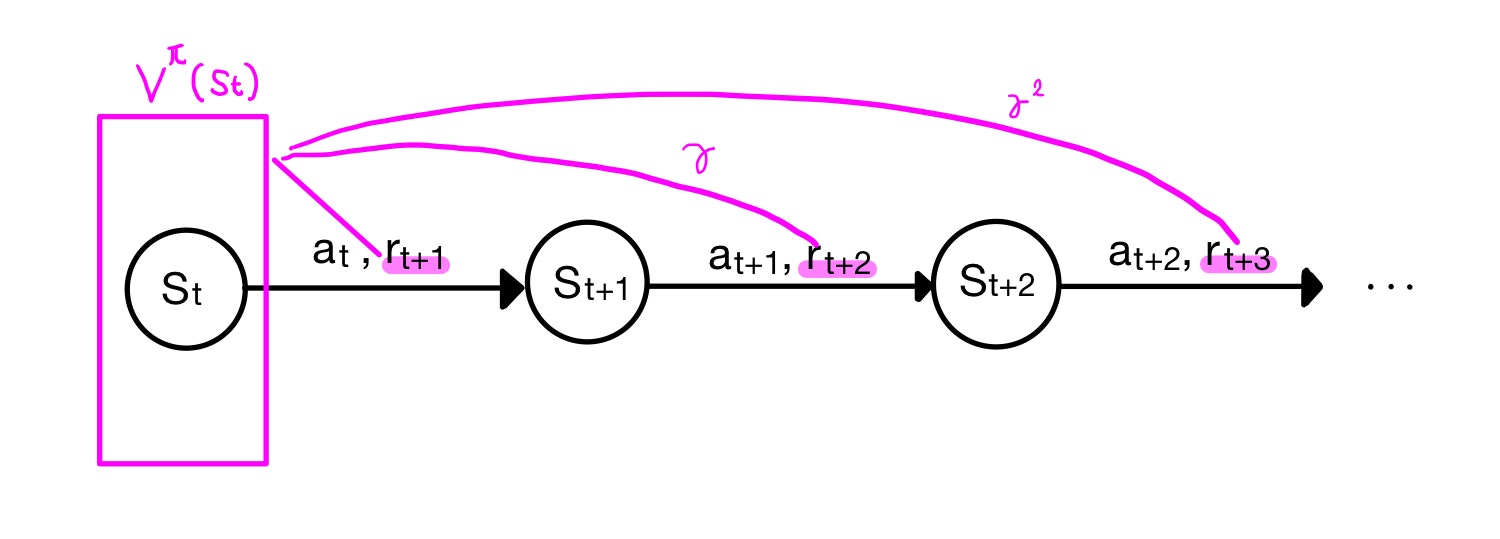
そこで、時刻tにおける状態$s_t$の状態価値$V^\pi(s_t)$を、
「状態$s_t$を起点に、方策$\pi$に従って行動をとり続けて行った時の報酬の合計(すなわち)収益」
というように定義します。
「とり続けて」、と書きましたがいつまで続けるのでしょうか?答えは「終わりが来るまで。来ないのなら永遠に」です。今回の格子世界では終わりを設定していないので、永遠に報酬を足し続けことになります。そうすると報酬の合計が発散して収束しないので、時間が経つにつれ報酬を割り引くための係数を掛けるようにしましょう。タイムステップが続くにつれて、係数が掛かっていくため、未来の報酬ほど値が減衰していきます。この係数を$\gamma$とおきます。$\gamma$の値を調整することで未来の値をどれだけ重視するかを決められます。
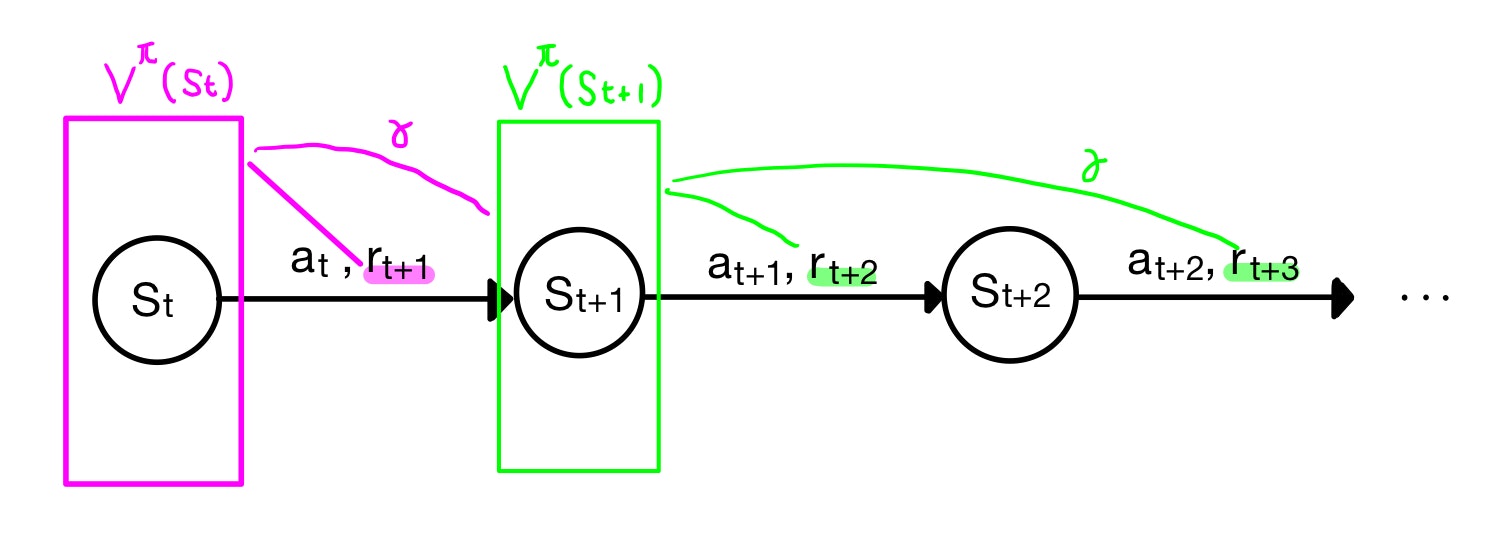
いま、時刻$t$起点での価値関数$V^\pi(s_t)$を考えましたが、視点を時刻$t+1$に進めて$V^\pi(s_{t+1})$も考えてみましょう(下図緑色)。上図を右に一つずらしただけです。なにも難しくないですね。
ふたたび視点を時刻$t$に戻します。
計算したいのは$V^\pi(s_t)$ですが、時刻$t+1$以降の報酬は$V^\pi(s_{t+1})$が合計してくれていますね。ただし時間が一つずれているため、$\gamma$の係数が一つずれていますのでそれを勘案する必要があります。それを補正すると
$$V^\pi(s_t) = r_{t+1} + \gamma V^\pi(s_{t+1})$$
と書けるような気がします。ある時刻における価値関数は、その先の時刻における価値関数の漸化式になっているようです。
さて、上で価値関数に関しての数式を初めてかきました。「書けるような気がします」。と書いたのは、厳密にはこの式は成り立たない、というか価値関数の性質を表すには不十分だからです。
正しい価値関数の導出
方策による枝分かれ
上図のダイアグラムではある重要なことを二つ見落としています。一つ目は
- ある状態$s$から方策$\pi$にしたがって取る行動$a$は一義的に決まらない(確率分布である)
ポリシー(方策)の項で、方策は、ある状態に対する行動を確率で返すことを説明しました。つまりなんらかの行動が確定的に一つ決まる訳ではなく、確率分布にしたがって複数の行動候補から実際の行動が決定されます。もちろん、ある行動だけを確率100%にしてしまえば確定的な行動をとることができますが、これは確率的な方策に内包されます。
そのため、上図のダイアグラムでは状態$s_t$に対する行動候補が枝分かれします。

もちろん、現実の行動としてはどれか一つをとるのですが、価値関数は未来の収益を考えるため、枝分かれの全ての選択肢を考慮する必要があります。
遷移確率による枝分かれ
未来の分岐についてもう一つ考える必要があります。
- 状態$s$の時に方策$\pi$に従って行動$a$をとったとき、それに対する結果、つまり対応する状態($s'$)は一義的に決まらない(確率分布である)
なんなのそれ、と思うかもしれません。右に行くって決めれば右のマスに確定的に行くんじゃないの?と思うかもしれません。もちろんそういうケースもあり、実際今回の格子世界では行動に対して確定的に状態が遷移します。しかし、現実問題では前に進もうとしても右に行く、ということが起こり得ます。例えば千鳥足の人とか。これを表すのが遷移確率(transition probability)です
任意の状態と行動、$s$と$a$が与えられたとして、次に可能な各状態s'の確率は、
P_{ss'}^a = Pr\{ s_{t+1} = s' | s_t=s, a_t =a\}
と表されます。またその際の報酬は$R_{ss'}^a$と表します。これを考慮したダイアグラムは以下のようになります。

さて、ようやく状態価値関数を表す準備ができました。
状態価値関数の導出とBellman方程式
さて、これまでに中途半端ながら価値関数の定義から、$V^\pi(s_t)$を漸化式を用いて
$$V^\pi(s_t) = r_{t+1} + V^\pi(s_{t+1})$$
で定義しましたね。
これに二つの枝分かれを考慮していきましょう。
二つの枝分かれ、つまり方策と遷移確率を考慮するためには、とりうる分岐全てを考慮して報酬を合計していく必要があります。その際、それぞれの枝の重みにその枝分かれがとる確率を当てはめます。つまりこれは期待値計算ですね。
これを考慮すると最終的な価値関数の表記は
となります。
これを日本語で表現すると
- 価値関数は、直近の報酬に1ステップ先の価値関数を足したものである。ただし、方策および遷移確率で未来のとりうる値は枝分かれするので、その期待値をとる
となります。色付けを図と対応させてあるのでイメージが湧かなければ確認してみてください。
このような漸化式を$V^\pi$に対するBellman方程式と呼びます。
数式
さて、Sutton本P.76に書いてある状態価値関数の導出を引用しておきます。
難しいことが書いてありますが結局やっていることはこれまでの図の話です。
この式変形を導く必要はなく、暗記する必要もなく、図のイメージを持てれば良いのではないかと思います。
\begin{align}
V^\pi(s) &= E_\pi\{R_t|s_t = s\} \\
&= E_\pi\{\sum_{k=0}^{\infty}\gamma^kr_{t+k+1}|s_t=s\} \\
&= E_\pi\{r_{t+1}+\gamma\sum_{k=0}^{\infty}\gamma^kr_{t+k+2}|s_t=s\} \\
&= \sum_a\pi(s,a)\sum_{s'}P_{ss'}^a[R_{ss'}^a + \gamma E_\pi\{\sum_{k=0}^\infty\gamma^kr_{t+k+2}|s_{t+1} = s'\}] \\
&= \sum_a\pi(s,a)\sum_{s'}P_{ss'}^a[R_{ss'}^a + \gamma V^{\pi}(s')]
\end{align}
最後に
格子世界を例に状態価値関数の導出について話ました。
実は本当にやりたかったのは、Pythonを用いて状態価値関数を計算したところなのですが、予想外に導出に分量がかかったので、一旦ここで分けようかと思います。