はじめに
前回の記事で状態価値関数$V^\pi$の導出をおこないました。今回はその際に説明した格子世界での状態価値関数をPython実装により計算してみたいと思います。
コードは[github] (https://github.com/triwave33/reinforcement_learning)に公開しています。
修正:コードに一部バグがあったので修正しました。(180719)
参考文献(設定問題の該当箇所)
Richard S. Sutton and Andrew G. Barto 「強化学習」、森北出版、P.77
前回の要約
状態価値関数
状態$s$のときに、方策$\pi$の元で行動$a$をとり続けていったときの報酬の合計(すなわち収益)の期待値を$V^\pi(s)$とする。ただし、報酬には1タイムステップごとに割引率$\gamma$を適用する。
$V^\pi(s)$は以下のように表される。
V^\pi(s) = E_\pi\{R_t|s_t = s\} = \sum_a\pi(s,a)\sum_{s'}P_{ss'}^a[R_{ss'}^a + \gamma V^{\pi}(s') \quad (1)
ただし、
- $\pi(s,a)$ は方策と呼ばれ、状態$s$のときに各行動$a$をとる確率
- $P_{ss'}^a$ は状態$s$で行動$a$を取った時に状態$s'$に遷移する確率
- $R_{ss'}^a$ は状態$s$で行動$a$を取り状態$s'$に遷移した時の報酬
とする。

格子世界(grid world)
5*5のグリッド上の世界を考える
- エージェントは、状態$s$によらず上下左右等確率の方策で(つまりランダムに)移動する。
- $\pi(any, right)$ = $\pi(any, up)$ = $\pi(any, left)$ = $\pi(any, down)$ = 0.25
- 遷移確率は確定的。つまり右に移動しようとしたときには必ず右に移動する。
- 壁際にいる時、外に出る方向に移動しようとすると-1点の報酬、その際、位置は変わらない
- Aの位置に到着したあとは、上下左右どの方向に移動しても+10点の報酬。さらにA'に移動する
- Bも同様だが報酬は+5点
- その他は0点


Pythonによる実装
格子世界
まず、格子世界をさまようエージェントをAgentクラスで表現します。
class Agent():
## クラス変数定義
# アクションと移動を対応させる辞書
actions = ['right', 'up', 'left', 'down']
act_dict = {'right':np.array([0,1]), 'up':np.array([-1,0]),\
'left':np.array([0,-1]), 'down':np.array([1,0])}
num_action = len(actions) # 4
# 上下左右全て等確率でランダムに移動する
pi_dict1 = {'right':0.25, 'up':0.25,'left':0.25, 'down':0.25}
def __init__(self, array_or_list):
# 入力はリストでもnp.arrayでも良い
if type(array_or_list) == list:
array = np.array(array_or_list)
else:
array = array_or_list
assert (array[0] >=0 and array[0] < 5 and \
array[1] >=0 and array[1] <5)
self.pos = array
# 現在位置を返す
def get_pos(self):
return self.pos
# 現在位置をセットする
def set_pos(self, array_or_list):
if type(array_or_list) == list:
array = np.array(array_or_list)
else:
array = array_or_list
assert (array[0] >=0 and array[0] < 5 and \
array[1] >=0 and array[1] <5)
self.pos = array
クラス変数として、エージェントの移動をactionとして定義します。acionを具体的な座標情報として表すためのact_dict変数、さらに方策$\pi$を決定するためのデータ格納テーブルであるpi_dict1を定義します。
次に、コンストラクタメソッドですが、Agentクラスのインスタンスを発生させる際は、x,y座標のどの位置で生まれるかを指定するようにしています。
また、現在位置を返すget_posメソッド、現在位置を強制的にセットするset_posメソッドを定義します。
次に、エージェントの移動を定義します。
# 現在位置から移動
def move(self, action):
# 辞書を参照し、action名から移動量move_coordを取得
move_coord = Agent.act_dict[action]
# A地点
if (self.get_pos() == np.array([0,1])).all():
pos_new = [4,1]
# B地点
elif (self.get_pos() == np.array([0,3])).all():
pos_new = [2,3]
else:
pos_new = self.get_pos() + move_coord
# グリッドの外には出られない
pos_new[0] = np.clip(pos_new[0], 0, 4)
pos_new[1] = np.clip(pos_new[1], 0, 4)
self.set_pos(pos_new)
エージェントの現在位置にactionによる差分を加えた位置をset_posメソッドに渡しています。ただし、グリッドの外には出られないようnp.clip関数でクリップしています。
次は、状態$s$で行動$a$を取った時の報酬$r$をrewardメソッドで定義します。rewardメソッドはエージェントの現在位置(つまりself.get_pos)だけでなく、指定した任意の状態の報酬を計算したいため、state変数を切り出して用いています。
# 現在位置から移動することによる報酬。この関数では移動自体は行わない
def reward(self, state, action):
# A地点
if (state == np.array([0,1])).all():
r = 10
return r
# B地点
if (state == np.array([0,3])).all():
r = 5
return r
# グリッドの境界にいて時に壁を抜けようとした時には罰則
if (state[0] == 0 and action == 'up'):
r = -1
elif(state[0] == 4 and action == 'down'):
r = -1
elif(state[1] == 0 and action == 'left'):
r = -1
elif(state[1] == 4 and action == 'right'):
r = -1
# それ以外は報酬0
else:
r = 0
return r
方策$\pi$についても定義します。今回、方策は状態$s$によらず、どの位置でも上下左右ランダムに移動するようにします。辞書型pi_dict1変数を参照して、状態$s$, 行動$a$の時の確率を引っ張ってきます。もちろんstate引数を定義する必要はありませんが、一般化のために敢えて加えています。
def pi(self, state, action):
# 変数としてstateを持っているが、実際にはstateには依存しない
return Agent.pi_dict1[action]
状態価値関数
式(1)を再掲しましょう。
V^\pi(s) = E_\pi\{R_t|s_t = s\} = \sum_a\pi(s,a)\sum_{s'}P_{ss'}^a[R_{ss'}^a + \gamma V^{\pi}(s') \quad (1)
この式は、$V^\pi$に対する漸化式になっています。そのため実装でも再帰関数を用いて$V^\pi$を実装するのが自然でしょう。
def V_pi(self, state, n, out, iter_num):
#print('\nnow entering V_pi at n=%d, state=%s' %(n, str(state)))
# state:関数呼び出し時の状態
# n:再帰関数の呼び出し回数。関数実行時は1を指定
# out:返り値用の変数。関数実行時は0を指定
if n==iter_num: # 終端状態
for i, action in enumerate(Agent.actions):
out += self.pi(state, action) * self.reward(state,action)
#print("terminal condition")
return out
else:
for i, action in enumerate(ACTIONS):
#print("action: %s" % action)
out += self.pi(state, action) * self.reward(self.get_pos(),action) # 報酬
#print("before move, pos:%s" % str(self.get_pos()))
self.move(action) # 移動してself.get_pos()の値が更新
#print("after move, pos:%s" % str(self.get_pos()))
## 価値関数を再帰呼び出し
# state変数には動いた先の位置、つまりself.get_pos()を使用
out += self.pi(self.get_pos(), action) * \
self.V_pi(self.get_pos(), n+1, 0, iter_num) * GAMMA
agent.set_pos(state) # 再帰先から戻ったらエージェントを元の地点に初期化
#print("agent pos set to %s, at n:%d" % (str(state), n))
return out
この状態価値関数 $V^\pi$メソッドについて説明します。まずは引数から。
-
まず引数として、任意の状態stateを取れるようにしておきます。これは、エージェント(インスタンス)がV_piメソッドを呼び出すと、どんどん枝分かれのなかを進んで(つまりメソッドを再帰的に読み出して)いきます。呼び出す度に、自分の位置(self.get_pos)は移動していくのですが、期待値をとる際に枝分かれの根元に戻る必要があります。そのための変数として切り出しておきます。
-
次の引数nは、メソッドを再帰呼び出ししているなかで今何回めの呼び出しなのかを保持しておく変数です。最初のメソッドの呼び出し時にはn=1を指定しておき、関数が再帰的に呼び出されるたびに1ずつ加算されていきます。
-
引数outは、価値関数の値を保持しておく変数です。
-
引数iter_numは、再帰呼び出しの上限値を指定します。つまり、何ステップ先まで未来(枝分かれ)を増やすかを指定します。
次に関数の中身を説明します。
if文の最初は終端状態を記述していますが、これはあとで説明します。
終端状態でない場合は、式(1)の定義通りにout変数に加算していきます。
forループで、アクションの組み合わせ(上下左右)だけ回しています。これは式(1)の一番左のΣに対応します。今回、状態$s$の時に行動$a$を取った時の遷移状態$s'$はただ一つに確定的に決まります。そのため、右のΣはありません。定義に従って、報酬$R_{ss'}^a$を計算して、out変数に足しこみます。
その後、とった行動$a$にしたがって現在位置を移動させます。
次に割引率$\gamma$を掛けた状態価値関数を足します。この部分が再帰的になっているため、メソッド自身であるV_piを定義の中で再び呼び出しています。指定する状態は移動後のエージェントの位置、nは1ステップ進んだn+1を指定します。
outには0を入れるところが注意点です。呼び出し先の状態関数をout変数に足しこみたいので、ここはまっさらな状態の0を指定しておいて、帰ってきた値をoutに足しています。
最後に終端状態ですが、$V^\pi$=0とみなして、報酬だけを返すようにしています。
結果
11ステップ先までを考慮した状態価値関数を以下に示します。コードはgithubに公開しています。

Aの位置での価値関数の値は8.9で報酬10よりも低くなっています。この理由はAから格子の端に入りこみやすいA'へと連れて行かれるからと考えられます
逆にBの価値関数は報酬5よりも高くなっています。これは、B'が端から離れていること、またB'から端へいって-1の報酬を得るよりも、AやBへ行って正の報酬を得ることが期待されるからです。
正解(無限ステップ)との比較
sutton本(Richard S. Sutton and Andrew G. Barto 「強化学習」 第1版) P.78には、状態価値関数の正解値(無限ステップ)が掲載されています。それを以下に示します。上述のPythonによる計算値と小数点第1桁で異なるところを赤字で示しています。

11ステップまでの結果は±0.1の間に収まっていますが、なおそれだけの誤差が残っています。これは、状態価値関数の推定が、11ステップの枝分かれでは不十分であることを示しています。
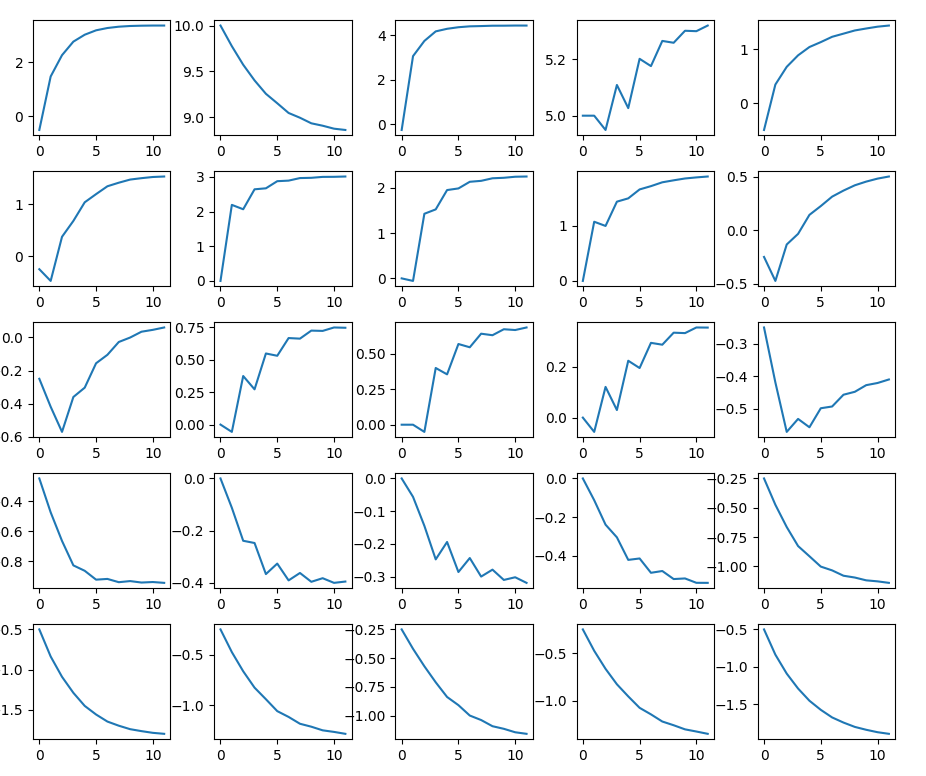
各グリッドについて、推定した状態価値関数を縦軸に、タイムステップを横軸としたプロットを以下に示します。
やはり11ステップでは値が収束しているとは言い難いですね。
それもそのはずで、未来の報酬の寄与度を与える$\gamma$を考えてみましょう。11ステップ先の報酬の寄与率は
$$\gamma^{11} \simeq 0.31$$
で、未だに30%の寄与度を持っています。ステップ数が足りないのは明らかです。
それではもう少しステップ数を増やせば?と考えますが、逆に枝分かれがどれくらいになっているかを考えてみます。actionは4通りなので、
$$4^{11} = 4,194,304$$
400万通りになります。「いけなくもないな」という数ですが、今回、状態遷移確率は確定的(1通り)にしていましたが、これも分岐すると考えると組み合わせが爆発的に増えてしまいます。
おわりに
今回は、格子世界に対して状態価値関数を計算してみました。定義に従い再帰関数を実装して、状態価値関数を計算することはできましたが、このような単純な問題でもたかだか10ステップ超を考えるだけで組み合わせ爆発の問題が起きてしまいます。
- 組み合わせ爆発を回避するような近似方法は?
- ある状態$s$についての価値関数$V^{\pi}$(s)を求めたが、ある状態$s$である行動$a$を取った時の価値は?
- 方策がわかっている上で価値関数を求めたが、そもそも方策が不明な状態から価値関数をもとに最適な方策を決めるには?
これらの問題に対してさらに考察を深めて行きたいと思います。