今回はモデルフリーの環境における価値の推定(評価)手法の話がメインとなります。
第2回 ディープラーニング編(Q学習、方策勾配法/REINFORCE、A3C/A2C)
第4回 連続行動空間編
※ネット上の情報をかき集めて自分なりに実装しているので正確ではない可能性がある点はご注意ください
※ライブラリはTensowflow2.0(+Keras)を使っています。
コード全体
本記事で作成したコードは以下です。
環境(CartPole-v0)
第2回と同じ CartPole-v0を使っていきます。
学習コード概要
第2回のA3C/A2Cアルゴリズムをベースに価値関数の評価(推定)手法を見ていきます。
まずはメインとなるコードを作成し、手法に影響ある部分だけを変えて実装していきます。
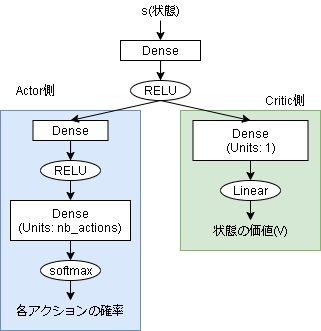
今回のモデルは以下です。
Actor側の出力を softmax にしています。
そのままだと学習がうまくいかなかったので前段階にDense層をはさみました。
学習のメインコードは以下です。
import gym
import numpy as np
import tensorflow as tf
from tensorflow.python import keras
from tensorflow.keras.optimizers import Adam
# softmaxでアクションを決定
def SoftmaxPolicy(model, state, nb_actions):
action_probs, _ = model(state.reshape((1,-1)))
return np.random.choice(list(range(nb_actions)), size=1, p=action_probs[0].numpy())[0]
with gym.make("CartPole-v0") as env:
nb_actions = env.action_space.n
obs_shape = env.observation_space.shape
# モデルの定義
c = input_ = keras.layers.Input(shape=obs_shape)
c = keras.layers.Dense(10, activation="relu")(c)
c1 = keras.layers.Dense(10, activation="relu")(c)
actor_layer = keras.layers.Dense(nb_actions, activation="softmax")(c1)
critic_layer = keras.layers.Dense(1, activation="linear")(c)
model = keras.Model(input_, [actor_layer, critic_layer])
model.compile(optimizer=Adam(lr=0.01))
# 経験バッファ用
experiences = []
# 学習ループ
for episode in range(300):
state = np.asarray(env.reset())
done = False
total_reward = 0
# 1episode
while not done:
# アクションを決定
action = SoftmaxPolicy(model, state, nb_actions)
# 1step進める
n_state, reward, done, _ = env.step(action)
n_state = np.asarray(n_state)
total_reward += reward
# 経験を追加
experiences.append({
"state": state,
"action": action,
"reward": reward,
"n_state": n_state,
"done": done,
})
state = n_state
※(a)1step毎に学習する場合の処理を記載
※(b)1episode毎に学習する場合の処理を記載
print("episode: {}, reward: {}".format(episode, total_reward))
各手法において、毎ステップ学習する手法の場合は(a)に、1エピソード毎に学習する手法は(b)にコードを記載します。
次にモデル学習側のメインコードです。
(c)に各手法での推定価値の計算を記述します。
その後、推定価値は正規化をおこなっています。
正規化は強化学習の話ではなく機械学習全般の話ですね。
ここでは平均0、分散1になるように正規化しています。
def train(model, experiences):
※(c) 各手法で、推定価値(v_val)を計算
# 推定価値の正規化(平均0,分散1)
std = v_val.std()
if std != 0:
v_val = (v_val - v_val.mean()) / std
# データ整形
states = np.asarray([e["state"] for e in experiences])
actions = np.asarray([e["action"] for e in experiences])
# actionをonehot化
onehot_actions = tf.one_hot(action_batch, nb_actions)
# 勾配を計算
with tf.GradientTape() as tape:
action_probs, v = model(state_batch, training=True)
# π(a|s)を計算
selected_action_probs = tf.reduce_sum(onehot_actions * action_probs, axis=1, keepdims=True)
# log(π(a|s)) * Q(s,a) を計算
selected_action_probs = tf.clip_by_value(selected_action_probs, 1e-10, 1.0) # 0にならないようにclip
policy_loss = tf.math.log(selected_action_probs) * advantage
# Value loss
value_loss = tf.reduce_mean((v_val - v) ** 2, axis=1, keepdims=True)
#--- 方策エントロピー
entropy = tf.math.log(selected_action_probs) * selected_action_probs
entropy = tf.reduce_sum(entropy, axis=1, keepdims=True)
#--- total loss
value_loss_weight = 1.0
entropy_weight = 0.1
loss2 = -policy_loss + value_loss_weight * value_loss - entropy_weight * entropy
# ミニバッチ処理(平均をlossに)
loss = tf.reduce_mean(loss2)
# 勾配を元にoptimizerでモデルを更新
gradients = tape.gradient(loss, model.trainable_variables)
model.optimizer.apply_gradients(zip(gradients, model.trainable_variables))
価値関数の推定の仕方
第1回でも話しましたが強化学習は現在の価値を推定し、その差分を価値関数または方策関数という形で学習していく手法となります。
現在の価値の推定にはベルマン方程式が使われますが、未来の報酬 $V_\pi(s_{t+1})$ がありそのままでは計算できません。
今回はこの価値の推定方法についてまとめてみました。
TD法
1step進めた結果を元に価値を予測する手法です。
ExperienceMemoryと相性がよく、Q学習でよく使われる手法ですね。
現在の価値は以下の式で推定されます。
$$ V(s_t) = r_{t+1} + \gamma V(s_{t+1}) $$
次の状態の価値 $V(s_{t+1})$ が推定値となり、現在の価値関数から予測した値となります。
コードは以下です。
batch_size = 16
# 学習ループ
experiences = []
for episode in range(300):
# 1episode
while not done:
(略)
experiences.append(経験)
# (a) batchサイズたまったら学習
if len(experiences) >= batch_size:
train_TD(model, experiences)
# On-policyアルゴリズムは学習毎に方策が変わるので、経験は学習毎に初期化する
experiences = []
(略)
def train_TD(model, experiences):
gamma = 0.9
# 次の状態の推定価値を取得
_, n_v = model(np.asarray([e["n_state"] for e in experiences]))
n_v = n_v.numpy()
# 各経験毎に価値を推定
v_vals = []
for i, e in enumerate(experiences):
if e["done"]:
# 終了時は次の状態がないので報酬のみ
r = e["reward"]
else:
r = e["reward"] + gamma * n_v[i][0]
v_vals.append(r)
v_vals = np.asarray(v_vals).reshape((-1, 1)) # 整形
(以下、学習コード)
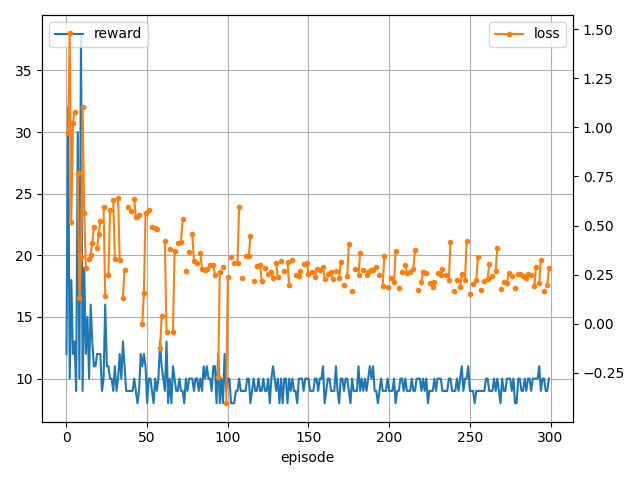
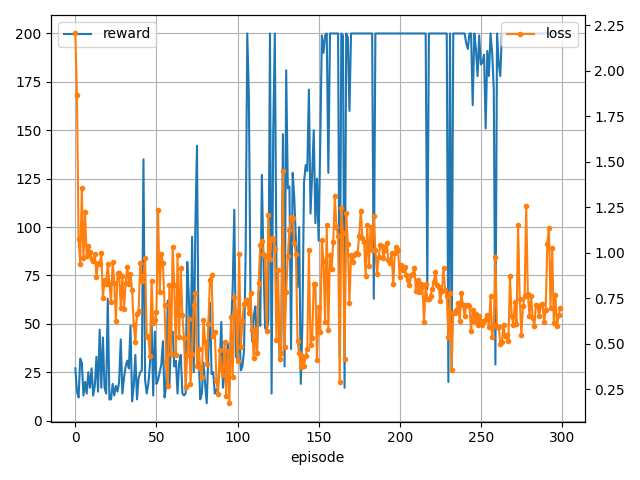
学習結果です。
On-policy 手法とは相性が悪く学習できていませんね。
モンテカルロ法
1エピソードの結果を元に価値を推定する手法です。
推定といっていますが、実際に観測した報酬を使って推定しています。
TD法であった次の状態価値の推定値 $V(s_{t+1})$ が無くなっているのが特徴です。
$$ V(s_t) = r_{t+1} + \gamma r_{t+2} ... + \gamma^{T-t-1} r_{T-t} $$
# 学習ループ
experiences = []
for episode in range(300):
# 1episode
while not done:
(略)
experiences.append(経験)
# (b) 1episode毎に処理する
if len(experiences) >= batch_size:
train_MC(model, experiences)
# On-policyアルゴリズムは学習毎に方策が変わるので、経験は学習毎に初期化する
experiences = []
(略)
def train_MC(model, experiences):
gamma = 0.9
# 各経験毎に価値を推定、後ろから計算
v_vals = []
r = 0
for e in reversed(experiences):
if e["done"]:
# 終了時は次の状態がないので報酬のみ
r = e["reward"]
else:
r = e["reward"] + gamma * r
v_vals.append(r)
v_vals.reverse() # 反転して元に戻す
v_vals = np.asarray(v_vals).reshape((-1, 1)) # 整形
(以下、学習コード)
価値の計算は後ろから計算する事で計算しやすくなります。
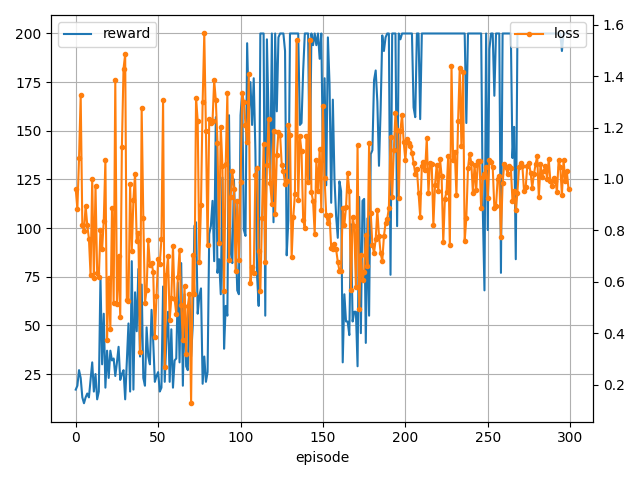
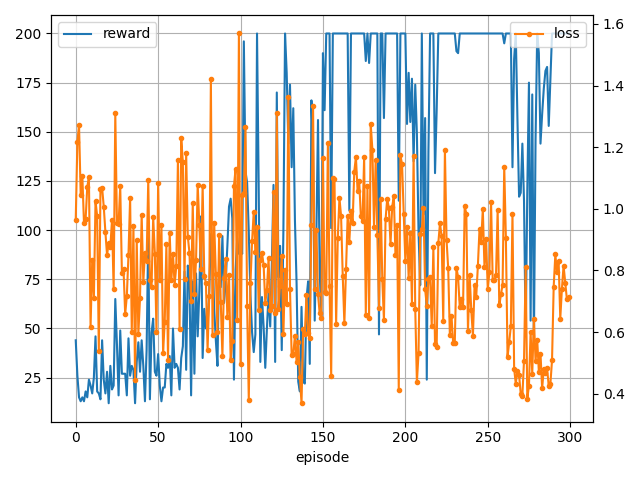
学習結果です。
Multistep lerning
モンテカルロ法では1エピソード全ての経験が対象でしたが、n-step先を対象に価値を推定する手法が Multistep lerning です。
1-stepの場合はTD法と同じになり、エピソード長と同じステップならモンテカルロ法と同じになります。
$$ V(s_t) = r_{t+1} + \gamma r_{t+2} ... + \gamma^{t+n-1} V(s_{t+n}) $$
n_step = 16
# 学習ループ
experiences = []
for episode in range(300):
# 1episode
while not done:
(略)
experiences.append(経験)
# (a) N step毎に処理する
if len(experiences) >= n_step:
train_ML(model, experiences)
# On-policyアルゴリズムは学習毎に方策が変わるので、経験は学習毎に初期化する
experiences = []
(略)
def train_ML(model, experiences):
gamma = 0.9
# 各経験毎に価値を推定、後ろから計算
if experiences[-1]["done"]:
# 最後が終わりの場合は全部使える
r = 0
else:
# 最後が終わりじゃない場合は予測値vで補完する
_, n_v = model(np.atleast_2d(experiences[-1]["n_state"]))
r = n_v[0][0].numpy()
v_vals = []
for e in reversed(experiences):
if e["done"]:
r = 0
r = e["reward"] + gamma * r
v_vals.append(r)
v_vals.reverse() # 反転して元に戻す
v_vals = np.asarray(v_vals).reshape((-1, 1)) # 整形
(以下、学習コード)
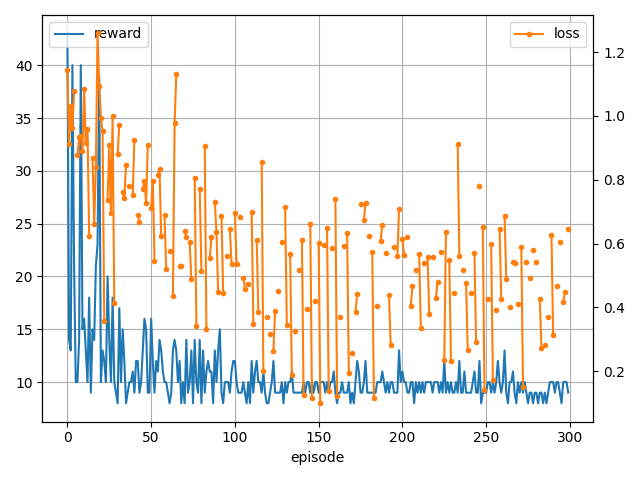
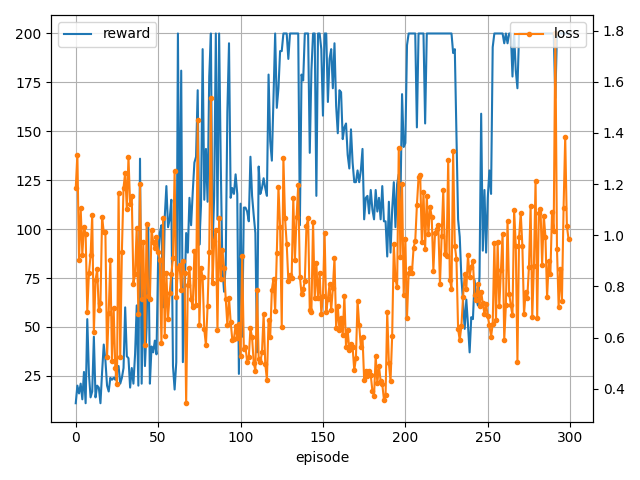
学習結果です。
TD(λ)法
上記3つの手法における各stepでの推定価値ですが、本質的には同じ価値を推定しているので重みを使って平均化することができます。
どういうことかというとあるタイミングの価値はTD法だと (1-step価値)、モンテカルロ法だと (エピソード最後までの価値) ですが、全stepを足した平均 (1-step価値 + 2-step価値 + ... + エピソード最後までの価値) を使っても問題ないという考えです。
各step $n$毎の推定価値 $G_t^n$ は以下です。
\begin{align}
1step &: \ G_t^1 = r_{t+1} + \gamma V(s_{t+1}) \\
2step &: \ G_t^2 = r_{t+1} + \gamma r_{t+2} + \gamma^2 V(s_{t+2}) \\
nstep &: \ G_t^n = r_{t+1} + \gamma r_{t+2} + ... + \gamma^{n-1} r_{t+n} + \gamma^n V(s_{t+n}) \\
episode end &: \ G_t^{T-n} = r_{t+1} + \gamma r_{t+2} + ... + \gamma^{T-t} r_{T-t} \\
\end{align}
TD(λ)法ではこれら各stepに $\lambda^{n-1}$ に比例して重みづけをします。
$$ G_t^1 + \lambda G_t^2 + \lambda^2 G_t^3 ... $$
ここで $1 + \lambda + \lambda^2 + ... \to \frac{1}{1-\lambda}$ なので正規化するために $1-\lambda$ を掛けます。
すると以下となります。
$$ G_t^\lambda = (1-\lambda)(G_t^1 + \lambda G_t^2 + ... + \lambda^{T-n-2} G_t^{T-n-1}) + \lambda^{T-n-1} G_t^{T-n}$$
エピソード最後の $G_t^{T-n}$ に $1-\lambda$ がかかっていないのは、
$$(1-\lambda)(1 + \lambda + \lambda^2 + ... + \lambda^{T-t-2}) = 1- \lambda^{T-t-1}$$
になるからです。
各stepの重み $\lambda$ ですが $\lambda=0$ の場合TD法と同じになり、$\lambda=1$ の場合モンテカルロ法と同じになります。
コードは以下です。
# 学習ループ
experiences = []
for episode in range(300):
# 1episode
while not done:
(略)
experiences.append(経験)
# (b) 1エピソード毎に処理する
if len(experiences) >= n_step:
train_TDh(model, experiences)
# On-policyアルゴリズムは学習毎に方策が変わるので、経験は学習毎に初期化する
experiences = []
(略)
def train_TDh(model, experiences):
gamma = 0.9
td_lambda = 0.9
# 次の状態の推定価値を出しておく
_, n_v = model(np.asarray([e["n_state"] for e in experiences]))
n_v = n_v.numpy()
v_vals = []
for i in range(len(experiences)):
# 各step
r = 0
t = 0
G = 0
for j in range(i, len(experiences)-1):
# 割引報酬を計算
r += (gamma ** t) * experiences[j]["reward"]
t += 1
# 推定価値を計算
G = (td_lambda ** (t-1)) * (r + (gamma ** t) * n_v[j][0])
# G全体の計算とエピソード最後の報酬
G = (1 - td_lambda) * G + (r + (gamma ** t) * experiences[-1]["reward"])
v_vals.append(G)
v_vals = np.asarray(v_vals).reshape((-1, 1)) # 整形
(以下、学習コード)
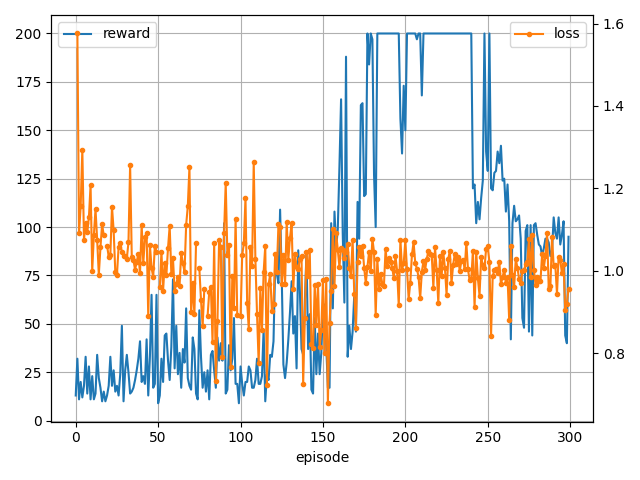
学習結果です。
方策勾配法における価値関数の推定
方策勾配法では行動価値 $Q^{\pi_\theta}(s,a)$ を推定する必要があります。
$$
\nabla J(θ) \propto E_{\pi_\theta} [ log \pi_{\theta}(a|s) Q^{\pi_\theta}(s,a) ]
$$
基本的にこの推定方法はTD法等上記で紹介した方法で推定しても問題ありません。
ただ、より学習を安定するためにいくつか手法がるようです。
参考
Baseline
方策勾配法では分散を小さくすることが重要となります。(機械学習全般にいえますが)
分散が大きいと学習後の方策が大きく異なってしまい、性能が大きく向上する可能性もありますが大きく低下する可能性もあります。
分散を小さくする手法の1つがBaseline $b(s_t)$ の導入です。
$$
\nabla J(θ) \propto E_{\pi_\theta} [ log \pi_{\theta}(a|s) (Q^{\pi_\theta}(s,a) - b(s_t))]
$$
Baseline $b(s_t)$ はどんな値をつかってもいいのですが、実装では価値の平均を採用しています。
コードは以下です。
経験の収集はモンテカルロ法で実装しています。
# 学習ループ
experiences = []
for episode in range(300):
# 1episode
while not done:
(略)
experiences.append(経験)
# (b) 1エピソード毎に処理する
if len(experiences) >= n_step:
train_B(model, experiences)
# On-policyアルゴリズムは学習毎に方策が変わるので、経験は学習毎に初期化する
experiences = []
(略)
def train_B(model, experiences):
gamma = 0.9
# 各経験毎に価値を推定、後ろから計算
v_vals = []
r = 0
for e in reversed(experiences):
if e["done"]:
# 終了時は次の状態がないので報酬のみ
r = e["reward"]
else:
r = e["reward"] + gamma * r
v_vals.append(r)
v_vals.reverse() # 反転して元に戻す
v_vals = np.asarray(v_vals).reshape((-1, 1)) # 整形
# ベースラインとして平均を引く
v_vals -= np.mean(v_vals)
(以下、学習コード)
学習結果です。
Advantage function
Advantage functionは以下で定義されます。
$$
A^{\pi}(s,a) = Q^{\pi}(s,a) - V^{\pi}(s)
$$
この Advantage function を用いて更新する手法となります。
$$
\nabla J(θ) \propto E_{\pi_\theta} [ log \pi_{\theta}(a|s) A^{\pi}(s,a)]
$$
Baselineの $b(s)$ を $V^{\pi}(s)$ にした物と同じですね。
コードは以下です。
経験の収集はモンテカルロ法で実装しています。
# 学習ループ
experiences = []
for episode in range(300):
# 1episode
while not done:
(略)
experiences.append(経験)
# (b) 1エピソード毎に処理する
if len(experiences) >= n_step:
train_Adv(model, experiences)
# On-policyアルゴリズムは学習毎に方策が変わるので、経験は学習毎に初期化する
experiences = []
(略)
def train_Adv(model, experiences):
gamma = 0.9
# 各経験毎に価値を推定、後ろから計算
v_vals = []
r = 0
for e in reversed(experiences):
if e["done"]:
# 終了時は次の状態がないので報酬のみ
r = e["reward"]
else:
r = e["reward"] + gamma * r
v_vals.append(r)
v_vals.reverse() # 反転して元に戻す
v_vals = np.asarray(v_vals).reshape((-1, 1)) # 整形
# Vを引く
_, v = model(np.asarray([e["state"] for e in experiences]))
v_vals -= v.numpy()
(以下、学習コード)
学習結果です。
GAE
Advantage function でも未来の価値をどう推定するかは決まっていませんでした。(上記実装ではモンテカルロ法で推定しています)
GAE(Generalized Advantage Estimator)では未来の価値をTD誤差を元に推定する方法となります。
TD誤差 $\delta_t^V$ は以下です。
$$ \delta_t^V = r_t + \gamma V(s_{t+1}) - V(s_t)$$
これを元にTD(λ)法のように各ステップをλで重みづけした手法がGAEとなります。
\hat{A}_t^{GAE(\gamma, \lambda)} = (1 - \lambda)(\delta_t^V + \lambda (\delta_t^V + \gamma \delta_{t+1}^V) + \lambda^2 (\delta_t^V + \gamma \delta_{t+1}^V + \gamma^2 \delta_{t+2}^V) + ... )
この式を解くと以下になります。
\hat{A}_t^{GAE(\gamma, \lambda)} = \sum^{\infty}_{l=0}( \gamma \lambda)^l \delta^V_{t+l}
- High-Dimensional Continuous Control Using Generalized Advantage Estimation(論文)
- Notes on the Generalized Advantage Estimation Paper
- 一般化報酬による高次元の強化学習の論文を読む
- OpenAIのSpinning Upで強化学習を勉強してみた その4
n_step = 16
# 学習ループ
experiences = []
for episode in range(300):
# 1episode
while not done:
(略)
experiences.append(経験)
# (a) n-step毎に処理する
if len(experiences) >= n_step:
train_GAE(model, experiences)
# On-policyアルゴリズムは学習毎に方策が変わるので、経験は学習毎に初期化する
experiences = []
(略)
def train_GAE(model, experiences):
gamma = 0.9
gae_lambda = 0.9
# 推定価値をだす
_, v = model(np.asarray([e["state"] for e in experiences]))
_, n_v = model(np.asarray([e["n_state"] for e in experiences]))
v = v.numpy()
n_v = n_v.numpy()
# 逆から計算する
last = 0
v_vals = []
for i in reversed(range(len(experiences))):
e = experiences[i]
if e["done"]:
delta = e["reward"] - v[i]
last = 0
else:
delta = e["reward"] + gamma * n_v[i] - v[i]
last = delta + gamma * gae_lambda * last
v_vals.append(last)
v_vals.reverse()
v_vals = np.asarray(v_vals).reshape((-1, 1)) # 整形
(以下、学習コード)
学習結果です。
あとがき
結果ですが、環境側の報酬や使うアルゴリズムによってかなり性能が変わります。
参考程度ですね。
価値推定方法は各手法に既知として組み込まれている場合が多く理解するまでに苦労しました。。。
Baseline についてちょっとだけ追記
他の実装をいくつか見た中から Baseline の実装について紹介しておきます。
こういう実装があるっていうだけで比較等は行いません(対象の環境にかなり左右されるので比較が難しい)
また、GAEは基本Baselineと合わせて使う事が多いようです。(GAEの結果からさらにBaselineを引く)
- 平均
本記事の実装ですね。推定価値の平均を引く手法です。
v_vals = v_vals - np.mean(v_vals)
- 状態価値
Advantage function です。
予測状態価値を引くやり方です。
状態価値モデルが実装されている手法しか適用できません。
v = value_model(states) # 状態価値モデルから現状の価値を予測
v_vals = v_vals - v # 推定した価値から予測した価値を引く
- 標準正規分布に正規化
標準正規分布に正規化する方法です。
v_vals = (v_vals - np.mean(v_vals)) / (np.std(v_vals) + 1e-8)
- 分散を1に正規化
平均は無視して分散のみ正規化する方法です。
v_vals = v_vals / (np.std(v_vals) + 1e-4)