第8回 今更だけど基礎から強化学習を勉強する SAC編(連続行動空間)

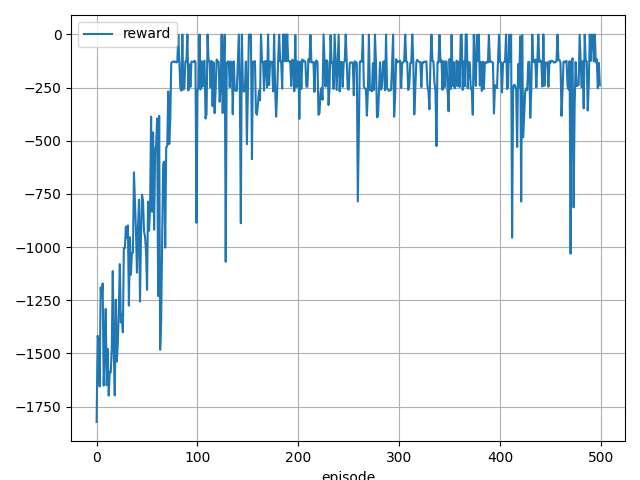
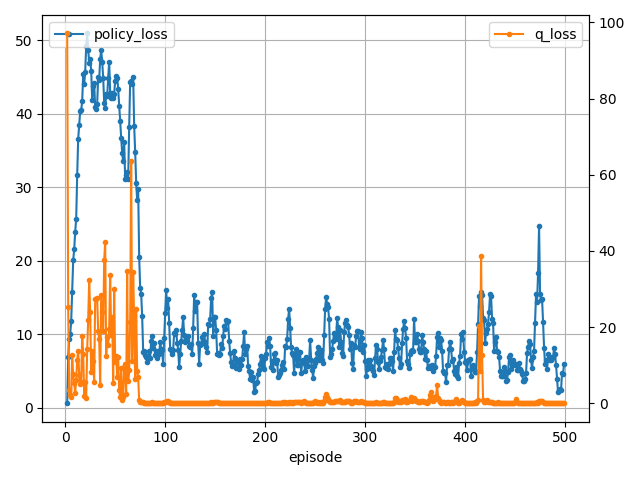
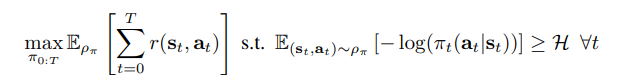今回はSACを実装してみました。
方策を学習する手法はいったんこれが最後になると思います。

第7回　DDPG/TD3編
第9回　遺伝的アルゴリズム編（閑話）

※ネット上の情報をかき集めて自分なりに実装しているので正確ではない可能性がある点はご注意ください
※ライブラリはTensowflow2.0(+Keras)を使っています。

コード全体

本記事で作成したコードは以下です。

• GoogleColaboratory

追記：自作フレームワークを作成しています。そちらにも実装があります。

SAC(Soft-Actor-Critic)

強化学習のアルゴリズムは大きくOn-policyなアルゴリズム(A2CやTRPO,PPO等)とOff-policyなアルゴリズム(Q学習やDDPG等)に分かれます。
On-policyなアルゴリズムはモデルが更新するたびに方策が変わるので、過去の経験が利用できなくなる欠点がありました。
(PPOは重点サンプリングにより再利用できますね)
Off-policyなアルゴリズムはハイパーパラメータに敏感で調整が難しいという欠点がありました。

SAC(Soft-Actor-Critic)の理論的背景はSoft-Q学習からきており、従来の目的関数に方策エントロピー項を加え、より多様な探索を可能にした手法です。
エントロピー項は正則化の役割を持っており、ポリシーは価値とエントロピーのトレードオフの最大化を学習します。
すなわちエントロピーが大きい領域は探索が不十分な領域、小さい領域はよく探索された領域として、価値が大きいけど未探索な点（価値があまり信用できない）・価値が大きく探索も十分（価値が信用できる）が分かるように数式に取り入れている手法です。

参考

• [OpenAI Spininng Up]Soft Actor-Critic
• Soft-Actor-Critic (SAC) ①Soft-Q学習からSACへ
• [論文解説] Soft Actor-Critic
• Soft Actor-Critic Algorithms and Applications(論文)
• Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor(論文)

方策エントロピー

従来の目的関数は以下の式の通り、価値(総報酬)の最大化が目的でした。

$$
J(\pi) = E_{\pi}
\begin{bmatrix}
\sum^T_{t=0} R(s_t, a_t)
\end{bmatrix}
$$

$R$ は即時報酬、$E$ は期待値で、目的関数 $J$ はある方策 $\pi$ における総報酬の期待値です。
Soft-Q学習では以下のように方策エントロピーを足した値を目的関数とし、これを最大化することを目的とします。

$$
J(\pi) = E_{\pi}
\begin{bmatrix}
\sum^T_{t=0} R(s_t, a_t) + \alpha H(\pi(.|s_t))
\end{bmatrix}
$$

$H(\pi(.|s_t))$ が方策エントロピー、$\alpha$ はエントロピー項の反映率です。
これを元にベルマン方程式を導出すると以下になります。

$$
Q_{\pi}(s_t,a_t) = E_{\pi}
\begin{bmatrix}
r_{t+1} + \gamma (Q_{\pi}(s_{t+1}, a_{t+1}) + \alpha H(\pi(.|s_{t+1})))
\end{bmatrix}
$$

$Q$は行動価値関数、$r$ は即時報酬、$\gamma$ は割引率です。

エントロピー（情報量）

エントロピーについて見ていきます。(分かる人は飛ばしてください)

エントロピーを簡単に言うとある事象の起こりにくさで、期待値を取ると乱雑さを表す尺度となります。
※エントロピー自体は熱力学や統計力学等ほかの分野でも使われる用語で、ここでは情報理論におけるエントロピーを指しています

ある事象 $E$ が起こる確率を $P(E)$ とすると、事象 $E$ が起こった後の情報量 $I(E)$ は以下です。

$$
I(E) = -log P(E)
$$

※一般的にはlogの底は2を使い、底が2の時の情報量をbitといいます

例としてAとBのコインを用意します。
それぞれのコインの確率は以下です。

A: 表90%、裏10%
B: 表60%、裏40%

それぞれのエントロピーを計算してみます。

\begin{align}
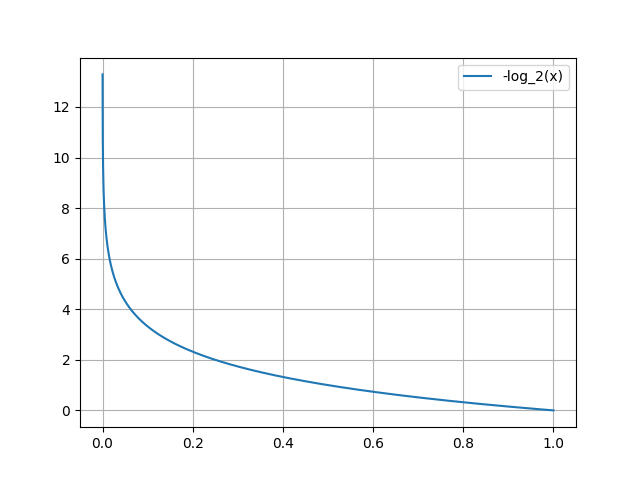
A(表) = -log_{2}(0.9) \fallingdotseq 0.152 \\
A(裏) = -log_{2}(0.1) \fallingdotseq 3.322 \\
B(表) = -log_{2}(0.6) \fallingdotseq 0.737 \\
B(裏) = -log_{2}(0.4) \fallingdotseq 1.322 \\
\end{align}

この場合A(表)は、エントロピーが小さい=事象が起きやすい、と解釈できます。
また、参考までに0～100%の場合をグラフにしてみました。(0%で∞、100%で0になります。)

次にAとBのコインのエントロピーを見てみます。
すべての事象の情報量の期待値を平均情報量(または情報エントロピー等)といい、これが一般的なエントロピー(乱雑さを表す尺度)で使われます。

$$
H = - \sum_{E \in \Omega} P(E) log P(E)
$$

$\Omega$ は起こりうる全事象になります。
実際に計算してみると以下です。

\begin{align}
A = -( 0.9 log_{2}(0.9) + 0.1 log_{2}(0.1) ) \fallingdotseq 0.469 \\
B = -( 0.6 log_{2}(0.6) + 0.4 log_{2}(0.4) ) \fallingdotseq 0.971
\end{align}

A は情報エントロピーが低い=取りえる値が偏る(表が多い)=乱雑ではない、
B は情報エントロピーが高い=いろんな値を取る可能性がある=乱雑である
となります。
(ちなみに確率50%の時、情報エントロピーは1(1bit)になります)

参考

• エントロピー
• 情報量(wikipedia)
• 情報理論 #2
• 情報エントロピー（平均情報量）の求め方とその取りうる値域の証明

方策エントロピー項と方策の更新

方策エントロピー項とそれを代入した後の目的関数は以下です。

$$
H(\pi(.|s)) = E_{a \sim \pi}
\begin{bmatrix}
-log{\pi(a | s) }
\end{bmatrix}
$$

$$
Q_{\pi}(s_t,a_t) = E_{\pi}
\begin{bmatrix}
r_{t+1} + \gamma (Q_{\pi}(s_{t+1}, a_{t+1}) - \alpha log{\pi(a_{t+1} | s_{t+1})}
\end{bmatrix}
$$

方策関数 $\pi$ ですが、Soft-Q学習ではsoftmax方策を採用していました。
これはQ値によって選択される確率が変わる方策で、離散値と相性がいい方策です。
ただ、連続値では計算が複雑になるという問題がありました。

そこで、SACでは方策関数がsoftmax方策の厳密な近似器である必要はなく、任意の方策を使用しても問題ない事を証明し、シンプルなactor-critic型のSoft-Q学習を提案したとの事です。

DDPG/TD3との違い

基本となる実装はDDPG/TD3と同じです。
DDPG/TD3から引き続き使用しているテクニックは以下です。(リンクは第7回の説明です)

• Replay buffer
  経験をメモリー上に保存し、その中からランダムにミニバッチ学習する手法です。
• Target Network
  Target Networkを別途作成し推定価値に使うモデルの学習を遅らせる手法です。
  一定間隔毎に同期する場合を Hard-Target といい、少しずつ近づける場合を Soft-Target といいます。
• Clipped Double Q learning
  アクションの選択と推定で別のモデルを使うことで過大評価を防ぐ手法です。

逆にPPDG/TD3とは違う手法は以下です。

• 探索ノイズ
  DDPGは決定論的方策なため探索にノイズを含めていたが、SACは確率論的な方策のため不要になっています。
• Target Policy Smoothing
  Target Policyから予測された次の状態のアクションにノイズを混ぜてQ関数をなめらか(smooth)にする手法です。
  SACでは、Target Policy ではなく現状のPolicyからアクションを取得し、ノイズも混ぜません。

Squashed Gaussian Policy

ガウス分布から生成されるアクションですが、取りえる値が-∞～∞なので tanh を適用し-1～1 に範囲に押し込めるという手法です。

第4回ですでに書いているので詳細はそちらを参照してください。

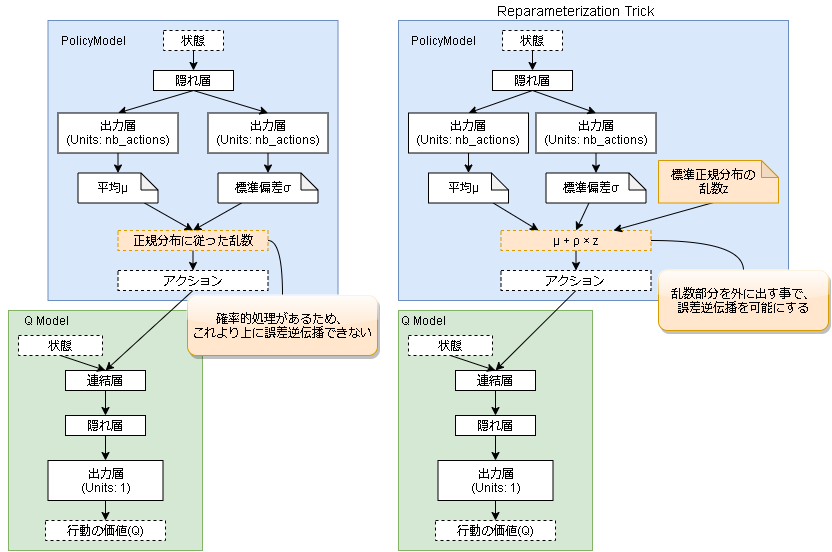
Reparameterization trick

VAE（Variational Auto Encoder）でも使われているテクニックです。
誤差逆伝搬をする上で通り道に確率的処理が入ると微分できません。
そこで確率的処理を通り道がら追い出すことで誤差逆伝搬を可能にする手法です。

コードは以下です。

@tf.function
def sample_actions(self, states):
    # 方策モデルから平均と標準偏差を出す
    mean, stddev = self(states)

    # 標準正規分布に従った乱数をだす
    normal_random = tf.random.normal(mean.shape, mean=0., stddev=1.)

    # Reparameterization trick
    action_org = mean + stddev * normal_random

    # Squashed Gaussian Policy
    action = tf.tanh(action_org)

    return (
      action,     # tanhで-1～1にしたアクション、envに使用 
      action_org  # tanh適用前のアクション、学習で使用
    )

参考：Variational Autoencoder徹底解説

方策エントロピーパラメータαの自動調整

エントロピー項の反映率を表すパラメータ $\alpha$ ですが、最適な数値は学習の進みぐあいで変化するのでそれを自動調整します。
(SAC初期の論文ではハイパーパラメータだったらしいです)

調整の仕方ですが、エントロピー下限値の制約付き報酬累積和の最大化問題として解きます。
(数式はSACの論文より)

解き方の詳細は論文を参照してください。
最終的には次式を最小化するようにパラメータ $\alpha$ を調整します。

$$
J(\alpha) = E_{a_t \sim \pi_t}
\begin{bmatrix}
-\alpha log \pi_t(a_t|s_t) - \alpha \bar{H}
\end{bmatrix}
$$

$\bar{H}$ は望ましい最小のエントロピー値でありハイパーパラメータです。(-1×アクション数が推奨値らしい)
コード例は以下です。

# H
target_entropy = -1 * env.action_space.shape[0]

# α値
# 勾配を計算して更新するのでtensorflow型に、またメンダコブログの方の実装を参考に出力をlog形式にしています。
log_alpha = tf.Variable(0.0, dtype=tf.float32)

# モデルを更新する箇所
def update_model():
    # log_alphaをalphaに変換
    alpha = tf.math.exp(log_alpha)

    （alphaを用いてポリシーモデルとQモデルを学習）
    logpi = ポリシーモデルから logπ(a|s) を計算

    #--- alphaの更新
    with tf.GradientTape() as tape:
        # -a logpi - a H
        loss = -tf.exp(log_alpha) * (logpi + target_entropy)
        log_alpha_loss = tf.reduce_mean(loss)

    # 勾配を計算し、log_alpha を更新
    grad = tape.gradient(log_alpha_loss, log_alpha)
    q_model.optimizer.apply_gradients([(grad, log_alpha)])

実装

環境は Pendulum-v0 です。

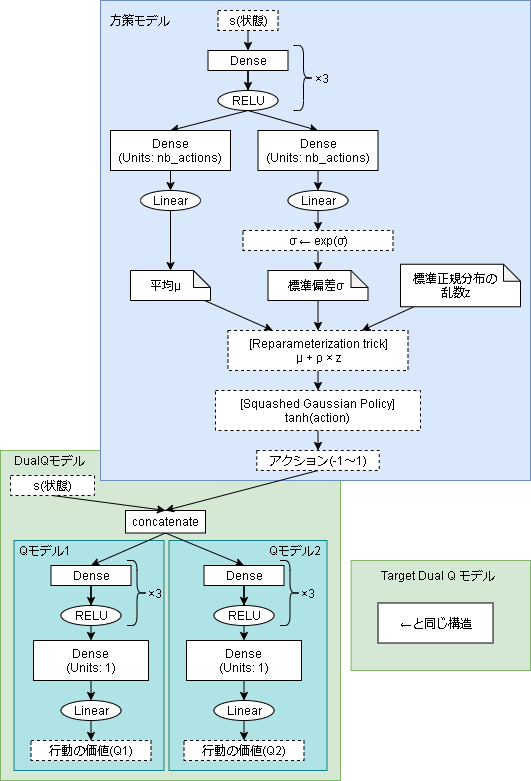
モデル

• 方策モデル

class PolicyModel(keras.Model):
    def __init__(self, action_space):
        super().__init__()

        self.action_space = action_space

        # Envアクション用
        self.action_centor = (action_space.high + action_space.low)/2
        self.action_scale = action_space.high - self.action_centor

        # 各レイヤーを定義
        self.dense1 = keras.layers.Dense(64, activation="relu")
        self.dense2 = keras.layers.Dense(64, activation="relu")
        self.dense3 = keras.layers.Dense(64, activation="relu")
        self.pi_mean = keras.layers.Dense(action_space.shape[0], activation="linear")
        self.pi_stddev = keras.layers.Dense(action_space.shape[0], activation="linear")
        
        # optimizer
        self.optimizer = Adam(learning_rate=0.003)

    # Forward pass
    def call(self, inputs, training=False):
        x = self.dense1(inputs)
        x = self.dense2(x)
        x = self.dense3(x)

        mean = self.pi_mean(x)
        stddev = self.pi_stddev(x)

        # σ > 0 になるように変換(指数関数)
        stddev = tf.exp(stddev)

        return mean, stddev

    # 学習(自動勾配内)でも使う箇所
    @tf.function
    def sample_actions(self, states, training=False):
        mean, stddev = self(states, training)

        # Reparameterization trick
        normal_random = tf.random.normal(mean.shape, mean=0., stddev=1.)
        action_org = mean + stddev * normal_random

        # Squashed Gaussian Policy
        action = tf.tanh(action_org)
        
        return action, mean, stddev, action_org

    # 学習以外で使う箇所(1アクションを返す)
    def sample_action(self, states, training=False):
        action, mean, _, _ = self.sample_actions(states.reshape(1, -1), training)
        action = action.numpy()[0]

        # 環境に渡すアクションを計算
        env_action = action * self.action_scale + self.action_centor
        
        if training:
            return env_action, action
        else:
            # テスト時には平均を使うと乱数の影響が無くなるので少し良くなるとの事
            return mean.numpy()[0] * self.action_scale + self.action_centor
            #return env_action

• QNetwork

class QNetwork(keras.Model):
    def __init__(self):
        super().__init__()

        # 各レイヤーを定義
        self.dense1 = keras.layers.Dense(64, activation="relu")
        self.dense2 = keras.layers.Dense(64, activation="relu")
        self.dense3 = keras.layers.Dense(64, activation="relu")
        self.value1 = keras.layers.Dense(1, activation="linear")
        self.dense4 = keras.layers.Dense(64, activation="relu")
        self.dense5 = keras.layers.Dense(64, activation="relu")
        self.dense6 = keras.layers.Dense(64, activation="relu")
        self.value2 = keras.layers.Dense(1, activation="linear")

        # optimizer
        self.optimizer = Adam(learning_rate=0.003)

    # Forward pass
    def call(self, states, actions, training=False):
        x = tf.concat([states, actions], axis=1)
        x1 = self.dense1(x)
        x1 = self.dense2(x1)
        x1 = self.dense3(x1)
        q1 = self.value1(x1)
        x2 = self.dense4(x)
        x2 = self.dense5(x2)
        x2 = self.dense6(x2)
        q2 = self.value2(x2)
        return q1, q2

学習

Actorの学習とCriticの学習があります。

# 方策が正規分布時の logπ(a|s)
@tf.function
def compute_logpi(mean, stddev, action):
    a1 = -0.5 * np.log(2*np.pi)
    a2 = -tf.math.log(stddev)
    a3 = -0.5 * (((action - mean) / stddev) ** 2)
    return a1 + a2 + a3

# Squashed Gaussian Policy時の logπ(a|s)
@tf.function
def compute_logpi_sgp(mean, stddev, action):
    logmu = compute_logpi(mean, stddev, action)
    tmp = 1 - tf.tanh(action) ** 2
    tmp = tf.clip_by_value(tmp, 1e-10, 1.0)  # log(0)回避用
    logpi = logmu - tf.reduce_sum(tf.math.log(tmp), axis=1, keepdims=True)
    return logpi

def update_model(
        policy_model, 
        q_model, 
        target_q_model,
        experiences,
        batch_size,
        gamma,
        log_alpha,
        soft_target_tau,
        hard_target_interval,
        target_entropy,
        all_train_count,
    ):

    # 方策エントロピーの反映率αを計算
    alpha = tf.math.exp(log_alpha)

    # ランダムに経験を取得してバッチを作成
    batchs = random.sample(experiences, batch_size)

    # データ整形
    states = np.asarray([e["state"] for e in batchs])
    n_states = np.asarray([e["n_state"] for e in batchs])
    actions = np.asarray([e["action"] for e in batchs])
    rewards = np.asarray([e["reward"] for e in batchs]).reshape((-1, 1))
    dones = np.asarray([e["done"] for e in batchs]).reshape((-1, 1))

    # ポリシーより次の状態のアクションを取得
    n_actions, n_means, n_stddevs, n_action_orgs = policy_model.sample_actions(n_states)
    # 次の状態のアクションのlogpiを取得(Squashed Gaussian Policy時)
    n_logpi = compute_logpi_sgp(n_means, n_stddevs, n_action_orgs)

    # 2つのQ値から小さいほうを採用(Clipped Double Q learning)してQ値を計算
    # (reward if done else (reward + gamma * n_qval)) - (alpha * H)
    n_q1, n_q2 = target_q_model(n_states, n_actions)
    q_vals = rewards + (1 - dones) * gamma * tf.minimum(n_q1, n_q2) - (alpha * n_logpi)

    #--- Qモデルの学習 MSEで学習
    with tf.GradientTape() as tape:
        q1, q2 = q_model(states, actions, training=True)
        loss1 = tf.reduce_mean(tf.square(q_vals - q1))
        loss2 = tf.reduce_mean(tf.square(q_vals - q2))
        q_loss = loss1 + loss2
    
    grads = tape.gradient(q_loss, q_model.trainable_variables)
    q_model.optimizer.apply_gradients(zip(grads, q_model.trainable_variables))

    #--- ポリシーの学習
    with tf.GradientTape() as tape:
        # アクションを出力
        selected_actions, means, stddevs, action_orgs = policy_model.sample_actions(states, training=True)
        
        # logπ(a|s) (Squashed Gaussian Policy)
        logpi = compute_logpi_sgp(means, stddevs, action_orgs)

        # Q値を出力、小さいほうを使う
        q1, q2 = q_model(states, selected_actions)
        q_min = tf.minimum(q1, q2)
        
        # alphaは定数扱いなので勾配が流れないようにする
        policy_loss = q_min - (tf.stop_gradient(alpha) * logpi)

        policy_loss = -tf.reduce_mean(policy_loss)  # 最大化
    
    grads = tape.gradient(policy_loss, policy_model.trainable_variables)
    policy_model.optimizer.apply_gradients(zip(grads, policy_model.trainable_variables))

    
    #--- 方策エントロピーαの自動調整
    _, means, stddevs, action_orgs = policy_model.sample_actions(states, training=True)
    logpi = compute_logpi_sgp(means, stddevs, action_orgs)

    with tf.GradientTape() as tape:
        loss = -tf.exp(log_alpha) * (logpi + target_entropy)
        log_alpha_loss = tf.reduce_mean(loss)

    grad = tape.gradient(log_alpha_loss, log_alpha)
    q_model.optimizer.apply_gradients([(grad, log_alpha)])  # optimizerはq_modelを代用(新規作成をめんどくさがっただけです)


    #--- soft target update
    target_q_model.set_weights(
        (1 - soft_target_tau) * np.array(target_q_model.get_weights(), dtype=object)
        + (soft_target_tau) * np.array(q_model.get_weights(), dtype=object))


    #--- hard target update
    if all_train_count % hard_target_interval == 0:
        target_q_model.set_weights(q_model.get_weights())

全体の流れ

env = gym.make("Pendulum-v0")

# ハイパーパラメータ
buffer_size = 1000   # キューの最大容量
warmup_size = 500    # 最低限キューに入れる数
train_interval = 10  # 学習間隔
batch_size = 32      # バッチサイズ
gamma = 0.9          # 割引率
soft_target_tau = 0.02      # Soft Target network の近づく割合
hard_target_interval = 100  # Hard Target network の同期する間隔

# エントロピーαの目標値、-1×アクション数が良いらしい
target_entropy = -1 * env.action_space.shape[0]

# モデルの定義
policy_model = PolicyModel(env.action_space)
q_model = DualQNetwork()
target_q_model = DualQNetwork()

# モデルは一度伝搬させないと重みが作成されない
dummy_state = np.random.normal(0, 0.1, size=(1,) + env.observation_space.shape)
dummy_action  = np.random.normal(0, 0.1, size=(1,) + env.action_space.shape)
q_model(dummy_state, dummy_action)
target_q_model(dummy_state, dummy_action)
target_q_model.set_weights(q_model.get_weights())

# エントロピーα自動調整用
log_alpha = tf.Variable(0.0, dtype=tf.float32)

# 収集する経験は上限を決め、古いものから削除する
experiences = deque(maxlen=buffer_size)

all_step_count = 0
all_train_count = 0

# 学習ループ
for episode in range(500):
    state = np.asarray(env.reset())
    done = False
    total_reward = 0
    step = 0

    # 1episode
    while not done:
        
        # アクションを決定
        env_action, action = policy_model.sample_action(state, True)

        # 1step進める
        n_state, reward, done, _ = env.step(env_action)
        n_state = np.asarray(n_state)
        step += 1
        total_reward += reward

        experiences.append({
            "state": state,
            "action": action,
            "reward": reward,
            "n_state": n_state,
            "done": done,
        })
        state = n_state

        # warmup貯まったら train_interval 毎に学習する
        if len(experiences) >= warmup_size and all_step_count % train_interval == 0:
            # モデルの更新
            update_model(
                policy_model, 
                q_model, 
                target_q_model, 
                experiences, 
                batch_size, 
                gamma,
                log_alpha,
                soft_target_tau,
                hard_target_interval,
                target_entropy,
                all_train_count,
            )
            all_train_count += 1
        all_step_count += 1

#--- 5回テストする例
for episode in range(5):
    state = np.asarray(env.reset())
    env.render()
    done = False
    total_reward = 0
    step = 0

    # 1episode
    while not done:
        action = actor_model.sample_action(state)
        n_state, reward, done, _ = env.step(action)
        env.render()
        state = np.asarray(n_state)
        step += 1
        total_reward += reward

    print("{} step, reward: {}".format(step, total_reward))

env.close()

学習結果

200 step, reward: -128.83854766172155
200 step, reward: -131.89505697415248
200 step, reward: -126.30291875355188
200 step, reward: -246.97134159900398
200 step, reward: -126.01479919292069

あとがき

DDPGでせっかく決定論的方策を実現したのにSACで確率的方策に戻った感じがしましたが、性能はすごくいいですね。
DDPGよりさらに性能が上がって、安定しているように感じます。
これで方策ベースの主なアルゴリズムは実装できたと思います。

次は何をやろうかな。