第9回 今更だけど基礎から強化学習を勉強する 遺伝的アルゴリズム編（閑話）

息抜きに遺伝的アルゴリズムでCartpole-v0を解いてみました。

第8回　SAC編
第10回　モデルベース編

※ネット上の情報をかき集めて自分なりに実装しているので正確ではない可能性がある点はご注意ください
※ライブラリはTensowflow2.0(+Keras)を使っています。

コード全体

本記事で作成したコードは以下です。

• GoogleColaboratory

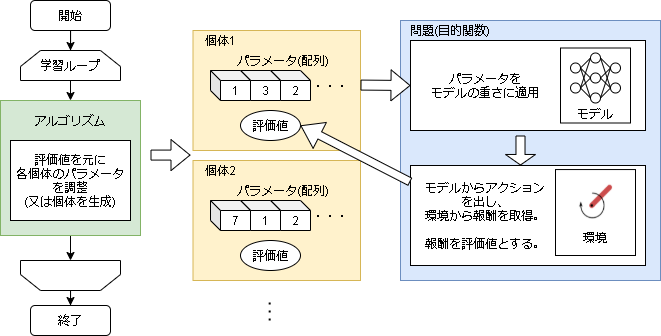
遺伝的アルゴリズムの適用

今までのディープラーニングの最適化手法は確率的勾配降下法が使われていました。
勾配降下法は、関数は微分すると勾配になる事を利用して、勾配=0=最小値を求める手法です。

最適化手法は確率的勾配降下法以外にもいろいろあり、その中の一つ遺伝的アルゴリズムを使ってみました。
最適化手法に関しては以前に記事にまとめているのでよかったらどうぞ。（最適化アルゴリズムを実装していくぞ（概要））

適用イメージ

ニューラルネットワークはモデルの重さ(とバイアス)で結果が一意に決まります。
各個体がニューラルネットワークの重さ(別々のモデル)を持っているイメージです。
個体毎に環境で実際の性能を評価し、できるだけ良い個体を生成することが最終ゴールです。

実装

基本的な実装は最適化アルゴリズムを実装していくぞ（概要）とほぼ同じです。

個体データクラス

パラメータと評価値を持つ個体データのクラスです。
評価値はキャッシュさせます。

class ProblemData():
    def __init__(self, problem, size):
        self.problem = problem    # 環境情報(下限値や上限値などの情報用)
        self.size = size          # パラメータのサイズ
        self.np_arr = np.zeros(self.size)  # パラメータ
        self.score = None         # 評価値

    def copy(self):
        o = ProblemData(self.problem, self.size)
        o.np_arr = self.np_arr.copy()
        o.score = self.score
        return o

    # パラメータを取得
    def getArray(self):
        return self.np_arr.copy()
    
    # パラメータを設定する
    def setArray(self, np_arr):
        # パラメータは下限値と上限値でま止めて設定する
        np_arr = np.where(np_arr < self.problem.MIN_VAL, self.problem.MIN_VAL, np_arr)
        np_arr = np.where(np_arr > self.problem.MAX_VAL, self.problem.MAX_VAL, np_arr)
        self.np_arr = np_arr
        self.score = None  # scoreが変わるのでNone

    # 評価値を返す
    def getScore(self):
        if self.score is not None:
            return self.score
        # 評価値がない場合は評価する
        self.score = self.problem.eval(self.np_arr)
        return self.score

ニューラルネットワークの重さのフラット化

ニューラルネットワークの重さを配列に変換/戻す動作が必要なので関数を用意しておきます。

# パラメーターをフラット化
def params_flatten(params):
    params_list = [tf.reshape(layer, [1, -1]) for layer in params]
    params_list = tf.concat(params_list, axis=1)
    return tf.reshape(params_list, [-1]).numpy()

# フラットなパラメータをモデルの構造に復元
from functools import reduce
def params_restore_shape(flat_params, model):
    n = 0
    weights = []
    for layer in model.trainable_variables:
        # shape のサイズを計算(各要素を掛け合わせる)
        size = reduce(lambda a, b: a*b, layer.shape)
        w = tf.reshape(flat_params[n:n+size], layer.shape)
        weights.append(w)
        n += size
    return weights

問題クラス

問題(目的関数)を管理するクラスです。
個体データの生成も行います。

ニューラルネットワークの重さですが、-∞～∞だと範囲が広すぎるのである程度制限させます。
今回は-2～2の範囲としています。

class GymProblem():
    def __init__(self, ENV_ID, model):
        self.ENV_ID = ENV_ID  # gym envの名前
        self.model = model    # 求めるNNのモデル
        
        # モデルのパラメータを配列化
        params = params_flatten(model.get_weights())
        self.size = len(params)  # モデルのパラメータ数

        # 重さの最小値・最大値（任意の範囲）
        self.MIN_VAL = -2
        self.MAX_VAL = 2

    # 個体データを生成
    # 引数にパラメータが設定されている場合はその値で、Noneならランダムで生成
    def create(self, arr=None):
        o = ProblemData(self, self.size)
        if arr is None:
            arr = np.random.uniform(self.MIN_VAL, self.MAX_VAL, self.size)
        else:
            arr = np.asarray(arr)
        o.setArray(arr)
        return o

    # 1パラメータのランダムな値を返す
    def randomVal(self):
        return self.MIN_VAL + random.random() * (self.MAX_VAL - self.MIN_VAL)

    # パラメータを元に評価値を返す
    def eval(self, arr):

        # パラメータをモデルにセットする
        self.model.set_weights(params_restore_shape(arr, self.model))

        # 何回か回して平均値を評価値にする
        scores = []
        for episode in range(10):
            with gym.make(self.ENV_ID) as env:
                # 1episode回す、gym_playは後述
                score = gym_play(env, self.model)
            scores.append(score)
        return np.mean(scores)

1episode実行関数

モデルを元に1episode実行します。
アクションの決め方はGreedy法で実装しています。

def gym_play(env, model, is_render=False):
    state = np.asarray(env.reset())
    if is_render:
        env.render()
    done = False
    total_reward = 0
    while not done:

        # アクションは最大のQ値を採用
        q = model(state.reshape(1,-1))[0].numpy()
        action = np.argmax(q)

        n_state, reward, done, _ = env.step(action)
        if is_render:
            env.render()
        n_state = np.asarray(n_state)
        total_reward += reward
        state = n_state
    return total_reward

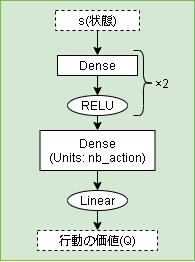
モデル

状態を入力すると行動価値を出力するシンプルなモデルです。

def build_model(env):
    c = input_ = keras.layers.Input(shape=env.observation_space.shape)
    c = keras.layers.Dense(16, activation="relu")(c)
    c = keras.layers.Dense(16, activation="relu")(c)
    c = keras.layers.Dense(env.action_space.n, activation="linear")(c)
    model = keras.Model(input_, c)
    model.compile()
    return model

アルゴリズム(パラメーターフリーGA)

アルゴリズムはパラメーターフリー遺伝的アルゴリズムを使います。
詳細は以前の記事をどうぞ

class PfGA():
    def __init__(self, mutation=0.1):
        self.mutation = mutation

    def init(self, problem):
        self.problem = problem
        self.count = 0
        self.individuals = []  # 局所集団(local genes)
        for _ in range(2):
            self.individuals.append(problem.create())

    def getMaxElement(self):
        self.sort()
        return self.individuals[-1]

    def getElements(self):
        return self.individuals

    def sort(self):
        self.individuals.sort(key=lambda x: x.getScore())

    def step(self):

        # 2以下なら追加
        if len(self.individuals) < 2:
            self.individuals.append(self.problem.create())

        # ランダムに2個取り出す
        p1 = self.individuals.pop(random.randint(0, len(self.individuals)-1))
        p2 = self.individuals.pop(random.randint(0, len(self.individuals)-1))

        # 子を作成
        c1, c2 = self._cross(p1, p2)

        if p1.getScore() < p2.getScore():
            p_min = p1
            p_max = p2
        else:
            p_min = p2
            p_max = p1
        if c1.getScore() < c2.getScore():
            c_min = c1
            c_max = c2
        else:
            c_min = c2
            c_max = c1

        if c_min.getScore() >= p_max.getScore():
            # 子2個体がともに親の2個体より良かった場合
            # 子2個体及び適応度の良かった方の親個体計3個体が局所集団に戻り、局所集団数は1増加する。
            self.individuals.append(c1)
            self.individuals.append(c2)
            self.individuals.append(p_max)
        elif p_min.getScore() >= c_max.getScore():
            # 子2個体がともに親の2個体より悪かった場合
            # 親2個体のうち良かった方のみが局所集団に戻り、局所集団数は1減少する。
            self.individuals.append(p_max)
        elif p_max.getScore() >= c_max.getScore() and p_min.getScore() <= c_max.getScore():
            # 親2個体のうちどちらか一方のみが子2個体より良かった場合
            # 親2個体のうち良かった方と子2個体のうち良かった方が局所集団に戻り、局所集団数は変化しない。
            self.individuals.append(c_max)
            self.individuals.append(p_max)
        elif c_max.getScore() >= p_max.getScore() and c_min.getScore() <= p_max.getScore():
            # 子2個体のうちどちらか一方のみが親2個体より良かった場合
            # 子2個体のうち良かった方のみが局所集団に戻り、全探索空間からランダムに1個体選んで局所集団に追加する。局所集団数は変化しない。
            self.individuals.append(c_max)
            self.individuals.append(self.problem.create())
        else:
            raise ValueError("not comming")

    def _cross(self, o1, o2):
        arr1 = o1.getArray()
        arr2 = o2.getArray()
        
        # 一様交叉
        new_arr1 = []
        new_arr2 = []
        for i in range(len(arr1)):
            r = random.random()
            if r < 0.5:
                val1 = arr1[i]
                val2 = arr2[i]
            else:
                val1 = arr2[i]
                val2 = arr1[i]

            # 突然変異
            r = random.random()
            if r < self.mutation:
                val1 = self.problem.randomVal()
                val2 = self.problem.randomVal()
                
            new_arr1.append(val1)
            new_arr2.append(val2)

        new_o1 = self.problem.create(new_arr1)
        new_o2 = self.problem.create(new_arr2)
        self.count += 2
        return new_o1, new_o2

    def getScores(self):
        return [x.getScore() for x in self.getElements()]

    def getMaxScore(self):
        return self.getMaxElement().getScore()

実行

# 環境
ENV_ID = "CartPole-v0"

# モデルを作成
with gym.make(ENV_ID) as env:
    model = build_model(env)

# 問題の作成
problem = GymProblem(ENV_ID, model)

# アルゴリズム
alg = PfGA()
alg.init(problem)

#--- 探索ループ
for _ in range(300):
    alg.step()

#--- 結果取得
result = alg.getMaxElement()
print("max score : {}".format(result.getScore()))

#--- テスト
model.set_weights(params_restore_shape(result.getArray(), model))
with gym.make(ENV_ID) as env:
    for i in range(5):
        reward = gym_play(env, model, is_render=True)
        print("{} reward: {}".format(i, reward))

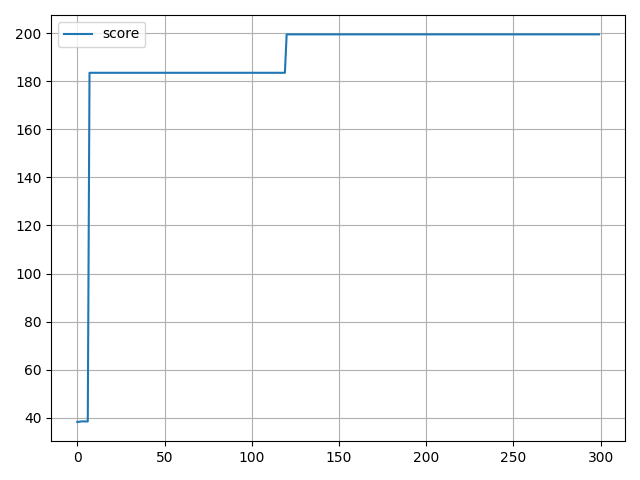
実行結果

パラメータフリーGAはエリート戦略なアルゴリズムなので、学習中に評価値が下がることはありません。

144 step, reward: 144.0
162 step, reward: 162.0
200 step, reward: 200.0
152 step, reward: 152.0
164 step, reward: 164.0

あとがき

今回は遺伝的アルゴリズムを使いましたが、他のアルゴリズムももちろん使えます。
ニューラルネットワークに対しては、進化差分を使う場合が多いようです。

ほとんどブラックボックスであるにも関わらず、ある程度学習できるのはさすがですね。