第10回今更だけど基礎から強化学習を勉強するモデルベース編(Dyna)

Last updated at 2023-11-30Posted at 2021-05-30

今まではモデルフリー強化学習を主に取り上げてきましたが、
今回からはモデルベース強化学習及びプランニングについて取り上げていきたいと思います。

また、今回は第1回と同様にテーブル型モデルの話がメインになります。
ニューラルネットワークの話はもう少し先の予定です。

第9回　遺伝的アルゴリズム編
 第10回　モンテカルロ木探索編

※ネット上の情報をかき集めて自分なりに実装しているので正確ではない可能性がある点はご注意ください

コード全体

本記事で作成したコードは以下です。

GoogleColaboratory

モデルベース強化学習

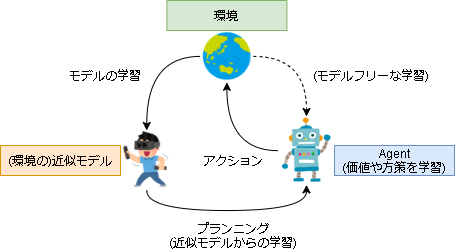
全体のイメージは以下です。

モデルベース強化学習は主に次のフェーズがあります。

モデルの学習を行う
学習したモデルから価値または方策を学習する（プランニング）

フェーズはざっくりしたものでアルゴリズムが必ずこのフェーズに従うものではありません。
例えば、囲碁などすでに既知な環境を対象としたアルゴリズムの場合はプランニングだけを扱っていたりします。

本記事では環境から学習したモデルを近似モデル(Approximate MDP)、近似モデルから経験を収集(サンプリング)し価値や方策を学習することをプランニング(Planning)、環境から直接経験を収集し学習する事を直接的な学習(Direct Reinfocement Learning)とします。

この分野は情報がほとんどないので今まで以上に間違った内容があるかもしれませんがご容赦ください。

・参考
書籍や英語の文献を記載していますが読めていません…（英語読めない…）
参考資料として紹介の意味合いが強いです。

強化学習理論の基礎4
強化学習：プランニングと学習（その１）
An Introduction to Reinforcement Learning Second edition, in progress Complete Draft
第2版のドラフトです。
Reinforcement Learning: An Introduction (Adaptive Computation and Machine Learning series) (English Edition)
第1版です。
Reinforcement Learning, second edition: An Introduction (Adaptive Computation and Machine Learning series) (English Edition)
第2版です。
強化学習
第1版（より年代的に前の内容?）の日本語訳の本です

近似モデルについて

環境のモデルは第1回で定義したマルコフ決定過程(Markov decision process:MDP)です。
※本記事の内容に合わせて少し変えています
※終了関数は実際に実装する時には必要になるので追加しています

	記号	備考
状態	$s$
行動	$a$
即時報酬	$r$
状態遷移関数	$s' \sim T(s'｜s, a)$	sにてaを選んだ後、次の状態s'へ遷移する確率(及び次の状態s')
報酬関数	$r = R(s,a)$	sにてaを選んだ後に受け取る報酬
終了関数	$d = D(s,a)$	sにてaを選んだ後に終了するかどうか

近似モデルを $M$、パラメータを $\eta$ と置いた場合、近似する関数は状態遷移関数 $T_\eta$ と報酬関数 $R_\eta$ と終了関数 $D_\eta$ になります。

\begin{align}
M_{\eta} := (T_{\eta}, R_{\eta}, D_{\eta}) \\
T_{\eta} \approx T  \\
R_{\eta} \approx R  \\
D_{\eta} \approx D  \\
\end{align}

モデルですが、状態遷移関数 $T_{\eta}$ と終了関数 $D_{\eta}$ は確率を扱うので確率分布でモデル化します。
報酬関数 $R_{\tau}$ は報酬の期待値をモデル化します。

\begin{align}
s' \sim T_{\eta}(s'|s,a) \\
r = R_{\eta}(s,a) \\
d \sim D_{\eta}(d|s,a) \\
\end{align}

近似モデルの学習

近似モデルの学習は教師あり学習となります。
報酬関数 $R_{\tau}$ は状態 $s$ と行動 $a$ から決まるので回帰問題、状態遷移関数 $T_{\eta}$ と終了関数 $D_{\eta}$ は確率を学習するので確率密度分布の推定問題として学習します。

プランニング

プランニングでやる事はモデルフリーと同じく価値関数または方策を学習することです。
ですのでモデルフリーなアルゴリズムは全てプランニングに適用できます。

またそれ以外にも近似モデルには状態遷移関数や報酬関数があるので、動的計画法による価値反復法や方策反復法(第1回を参照)、それ以外にもモデルベース特有のアルゴリズムを用いて学習することができます。

プランニングアルゴリズム

Sample-Based Planning

最も簡単なプランニング方法です。
近似モデルからランダムにサンプリングし、そのサンプルを元に学習する方法です。
サンプリングの対象が近似モデルという点以外はモデルフリーなアルゴリズムと同じです。

Simulation-Based Search

ランダムにサンプリングするのではなく、数step先を見て良い結果になるであろうアクション(Forward search)を選んでサンプリングし、学習する方法です。
イメージとしては現在の状態から探索木を構築し、葉部分が一番よさそうなアクションを選ぶイメージです。

結果が悪い部分は学習せず、良い部分のみを学習できる＝モデル全体を学習する必要がなくなる、ので効率的に学習できます。
(MDPの一部を取り扱うのでSub-MDPを学習するという事になるそうです)

Simulation-Based Search で有名な手法にモンテカルロ木探索があります。

モデルベースとモデルフリーの違い

モデルフリーとの違いを簡単に表にまとめてみました。
ソースがあるわけではなく、主観で書いたので注意してください。

	モデルフリー	モデルベース
報酬が疎な環境(チェス等)	経験から価値を推定しにくい(学習しにくい)	近似モデルから将来が(ある程度)予想できるのでまだ学習できる
経験の収集	環境に依存し、場合によっては高コスト	実際に動かすわけではないので低コスト
誤差	直接得られた経験なので誤差が小さい	推定した近似モデルを使って推定するので誤差が大きくなる
アルゴリズム	モデルフリーなアルゴリズムのみ	モデルフリーだけではなく、モデルベースなアルゴリズムも使用可能

実装における環境(テーブル型モデル)

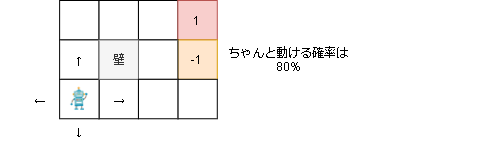
第1回と同じく以下の環境(GridEnv)を使います。

プレイヤーは上下左右に動け、右上のゴールにたどり着くと報酬1がもらえます。
しかし右真ん中のマスは報酬-1が入ってしまいます。
また、実際に動ける確率は80%で20%の確率で横方向に行ってしまいます。
(1ステップ毎に-0.04の報酬が手に入ります)

実装１，Dyna-Q

強化学習の学習には大きく２つの方法があります。

真の環境から経験を収集し、価値関数・方策を学習する(モデルフリー)
近似モデルから経験を収集し、価値関数・方策を学習する(モデルベース)

1と2両方を取り入れて学習する手法を Dyna と呼び、もっともシンプルなモデルベース強化学習の手法となります。
Dynaで価値関数・方策を学習するアルゴリズムにQ学習を用いた手法を Dyna-Q と呼び、今回実装したいと思います。

一般的な Dyna-Q は1回実環境の経験で学習した後(普通のQ学習)、N回近似モデルから得た経験で学習します。
しかし本実装では近似モデルの効果を見たいので、実環境からの学習は0回とします。

近似モデルの学習

近似モデルの学習方法ですが、テーブル型なので回数を数え上げて確率を出していきます。

\begin{align}
T_{\eta}(s'|s,a)= \frac{n_{s,a,s'}}{N_{s,a}} \\
D_{\eta}(d|s,a)= \frac{d_{s,a}}{N_{s,a}} \\
R_{\eta}(s,a)= \frac{\sum r_{s,a}}{N_{s,a}} 
\end{align}

記号の意味は以下です。
$N_{s,a}$：状態$s$でアクション$a$を訪れた回数
$n_{s,a,s'}$：状態$s$でアクション$a$を選んだ場合に次の状態$s'$を訪れた回数
$d_{s,a}$：状態$s$でアクション$a$を選んだ場合に終了した回数
$\sum r_{s,a}$：状態$s$でアクション$a$を選んだ場合に得た報酬の合計

近似モデルを表すコードは以下です。
扱いやすいようにクラス化しています。

class A_MDP():
    def __init__(self, env):

        self.env_states = env.states
        self.env_actions = env.actions

        self.trans = {}   # [state][action][next_state] = 訪れた回数
        self.reward = {}  # [state][action] = 得た報酬の合計
        self.done = {}    # [state][action] = 終了した回数
        self.count = {}   # [state][action] = 訪れた回数

        # 初期化        
        for s in env.states:
            self.reward[s] = [0.0] * len(env.actions)
            self.done[s] = [0] * len(env.actions)
            self.count[s] = [0] * len(env.actions)
            self.trans[s] = {}
            for a in env.actions:
                self.trans[s][a] = {}
                for s2 in env.states:
                    self.trans[s][a][s2] = 0
        
        # サンプリング用に実際にあった履歴を保存
        self.state_action_history = []
    
    # 全状態を返す
    @property
    def states(self):
        return self.env_states

    # 全アクションを返す
    @property
    def actions(self):
        return self.env_actions

    # 学習
    def train(self, state, action, n_state, reward, done):
        # (状態,アクション)の履歴を保存
        self.state_action_history.append([state, action])

        # 各回数をカウント
        self.count[state][action] += 1
        self.trans[state][action][n_state] += 1
        self.done[state][action] += 1 if done else 0
        self.reward[state][action] += reward

    # ランダムに履歴を返す
    def samples(self, num):
        return random.sample(self.state_action_history, num)

    # 次の状態を返す
    def sample_next_state(self, state, action):
        weights = list(self.trans[state][action].values())
        n_s_list = list(self.trans[state][action].keys())
        n_s = random.choices(n_s_list, weights=weights, k=1)[0]
        return n_s

    # 報酬を返す
    def get_reward(self, state, action):
        if self.count[state][action] == 0:
            return 0
        return self.reward[state][action] / self.count[state][action]

    # 終了状態を返す
    def sample_done(self, state, action):
        if self.count[state][action] == 0:
            return (random.random() < 0.5)
        return (random.random() < (self.done[state][action] / self.count[state][action]))
    
    # 次の状態の遷移確率を返す
    def get_next_state_probs(self, state, action):
        probs = {}
        for s2, s2_count in self.trans[state][action].items():
            probs[s2] = s2_count / self.count[state][action]
        return probs

Q学習

近似モデルを使う点以外は第1回の実装と変わりません。
コードは以下です。

class Q_learning():
    def __init__(self, env):

        self.gamma = 0.9  # 割引率
        self.lr = 0.9     # 学習率
        self.epsilon = 0.1
        
        # アクション数
        self.nb_action = len(env.actions)

        # Q関数
        self.Q = collections.defaultdict(lambda: [0] * self.nb_action)

    # 学習
    def update(self, a_mdp):

        # 近似モデルからランダムにサンプリング
        state, action = a_mdp.samples(1)[0]
        n_state = a_mdp.sample_next_state(state, action)
        reward = a_mdp.get_reward(state, action)
        done = a_mdp.sample_done(state, action)
        
        #--- Q値の計算
        if done:
            td_error = reward - self.Q[state][action]
        else:
            td_error = reward + self.gamma * max(self.Q[n_state]) - self.Q[state][action]
        self.Q[state][action] += self.lr * td_error


    def sample_action(self, state):
        # ε-greedy
        if np.random.random() < self.epsilon:
            # epsilonより低いならランダムに移動
            return np.random.randint(self.nb_action)
        elif np.sum(self.Q[state]) == 0:
            # Q値が0は全く学習していない状態なのでランダム移動
            return np.random.randint(self.nb_action)
        else:
            # Q値が最大のアクションを実行
            return np.argmax(self.Q[state])

メインフロー

env = GridEnv()

a_mdp = A_MDP(env)            # 近似モデル
q_learning = Q_learning(env)  # Q学習

# 学習ループ
for episode in range(100):  # for safety
    state = env.reset()
    done = False
    total_reward = 0

    # 1episode 最大20stepで終わりにする
    for step in range(20):

        # アクションを決定
        action = q_learning.sample_action(state)

        # 環境の1step
        n_state, reward, done, _ = env.step(action)
        total_reward += reward

        # 近似モデルの学習
        a_mdp.train(state, action, n_state, reward, done)

        # Q学習
        q_learning.update(a_mdp)

        state = n_state
        if done:
            break

学習結果

学習中の環境から取得した報酬

学習後の近似モデル(報酬)

------------------------------------------------
   -0.04   |   -0.04   |   -0.04   |    0.00   |
-0.04 -0.04|-0.04 -0.04|-0.04  0.80| 0.00  0.00|
   -0.04   |   -0.04   |   -0.04   |    0.00   |
------------------------------------------------
   -0.04   |    0.00   |   -0.11   |    0.00   |
-0.04 -0.04| 0.00  0.00|-0.04 -1.00| 0.00  0.00|
   -0.04   |    0.00   |   -0.04   |    0.00   |
------------------------------------------------
   -0.04   |   -0.04   |   -0.04   |   -0.79   |
-0.04 -0.04|-0.04 -0.04|-0.04 -0.04|-0.04 -0.17|
   -0.04   |   -0.04   |   -0.04   |   -0.04   |
------------------------------------------------

学習後の近似モデル(終了確率)

-------------------------------------------------------
      0.0%   |      0.0%   |      0.0%   |      0.0%   |
  0.0%   0.0%|  0.0%   0.0%|  0.0%  80.7%|  0.0%   0.0%|
      0.0%   |      0.0%   |      0.0%   |      0.0%   |
-------------------------------------------------------
      0.0%   |      0.0%   |      7.1%   |      0.0%   |
  0.0%   0.0%|  0.0%   0.0%|  0.0% 100.0%|  0.0%   0.0%|
      0.0%   |      0.0%   |      0.0%   |      0.0%   |
-------------------------------------------------------
      0.0%   |      0.0%   |      0.0%   |     77.8%   |
  0.0%   0.0%|  0.0%   0.0%|  0.0%   0.0%|  0.0%  13.0%|
      0.0%   |      0.0%   |      0.0%   |      0.0%   |
-------------------------------------------------------

学習後の近似モデル(遷移確率)

(0, 0):Action.UP -> (0, 0):100.0%
(0, 0):Action.DOWN -> (0, 0):4.8%
(0, 0):Action.DOWN -> (1, 0):19.0%
(0, 0):Action.DOWN -> (0, 1):76.2%
(0, 0):Action.LEFT -> (0, 0):100.0%
(0, 0):Action.RIGHT -> (0, 0):9.7%
(0, 0):Action.RIGHT -> (1, 0):80.6%
(0, 0):Action.RIGHT -> (0, 1):9.7%
(1, 0):Action.UP -> (1, 0):90.9%
(1, 0):Action.UP -> (2, 0):9.1%
(1, 0):Action.DOWN -> (0, 0):11.8%
(1, 0):Action.DOWN -> (1, 0):64.7%
(1, 0):Action.DOWN -> (2, 0):23.5%
(1, 0):Action.LEFT -> (0, 0):83.3%
(1, 0):Action.LEFT -> (1, 0):16.7%
(1, 0):Action.RIGHT -> (1, 0):22.1%
(1, 0):Action.RIGHT -> (2, 0):77.9%
(2, 0):Action.UP -> (1, 0):14.3%
(2, 0):Action.UP -> (2, 0):85.7%
(2, 0):Action.DOWN -> (2, 1):100.0%
(2, 0):Action.LEFT -> (1, 0):75.0%
(2, 0):Action.LEFT -> (2, 0):25.0%
(2, 0):Action.RIGHT -> (2, 0):8.4%
(2, 0):Action.RIGHT -> (3, 0):80.7%
(2, 0):Action.RIGHT -> (2, 1):10.8%
(0, 1):Action.UP -> (0, 0):81.3%
(0, 1):Action.UP -> (0, 1):18.7%
(0, 1):Action.DOWN -> (0, 1):25.0%
(0, 1):Action.DOWN -> (0, 2):75.0%
(0, 1):Action.LEFT -> (0, 0):13.3%
(0, 1):Action.LEFT -> (0, 1):77.8%
(0, 1):Action.LEFT -> (0, 2):8.9%
(0, 1):Action.RIGHT -> (0, 1):88.9%
(0, 1):Action.RIGHT -> (0, 2):11.1%
(2, 1):Action.UP -> (2, 0):89.3%
(2, 1):Action.UP -> (2, 1):3.6%
(2, 1):Action.UP -> (3, 1):7.1%
(2, 1):Action.DOWN -> (2, 2):100.0%
(2, 1):Action.LEFT -> (2, 1):100.0%
(2, 1):Action.RIGHT -> (3, 1):100.0%
(0, 2):Action.UP -> (0, 1):80.2%
(0, 2):Action.UP -> (0, 2):10.5%
(0, 2):Action.UP -> (1, 2):9.3%
(0, 2):Action.DOWN -> (0, 2):84.0%
(0, 2):Action.DOWN -> (1, 2):16.0%
(0, 2):Action.LEFT -> (0, 1):44.4%
(0, 2):Action.LEFT -> (0, 2):55.6%
(0, 2):Action.RIGHT -> (0, 1):4.5%
(0, 2):Action.RIGHT -> (0, 2):14.9%
(0, 2):Action.RIGHT -> (1, 2):80.6%
(1, 2):Action.UP -> (0, 2):11.1%
(1, 2):Action.UP -> (1, 2):77.8%
(1, 2):Action.UP -> (2, 2):11.1%
(1, 2):Action.DOWN -> (0, 2):4.5%
(1, 2):Action.DOWN -> (1, 2):90.9%
(1, 2):Action.DOWN -> (2, 2):4.5%
(1, 2):Action.LEFT -> (0, 2):76.7%
(1, 2):Action.LEFT -> (1, 2):23.3%
(1, 2):Action.RIGHT -> (1, 2):12.1%
(1, 2):Action.RIGHT -> (2, 2):87.9%
(2, 2):Action.UP -> (2, 1):81.8%
(2, 2):Action.UP -> (1, 2):9.1%
(2, 2):Action.UP -> (3, 2):9.1%
(2, 2):Action.DOWN -> (1, 2):4.5%
(2, 2):Action.DOWN -> (2, 2):86.4%
(2, 2):Action.DOWN -> (3, 2):9.1%
(2, 2):Action.LEFT -> (2, 1):3.6%
(2, 2):Action.LEFT -> (1, 2):89.3%
(2, 2):Action.LEFT -> (2, 2):7.1%
(2, 2):Action.RIGHT -> (2, 1):10.3%
(2, 2):Action.RIGHT -> (2, 2):3.4%
(2, 2):Action.RIGHT -> (3, 2):86.2%
(3, 2):Action.UP -> (3, 1):77.8%
(3, 2):Action.UP -> (2, 2):11.1%
(3, 2):Action.UP -> (3, 2):11.1%
(3, 2):Action.DOWN -> (3, 2):100.0%
(3, 2):Action.LEFT -> (2, 2):94.4%
(3, 2):Action.LEFT -> (3, 2):5.6%
(3, 2):Action.RIGHT -> (3, 1):13.0%
(3, 2):Action.RIGHT -> (3, 2):87.0%

学習後のQ関数

-------------------------------------------------------
     0.40    |     0.56    |     0.69    |     0.00    |
 0.47    0.57| 0.47    0.68| 0.67    0.80| 0.00    0.00|
     0.54    |     0.65    |     0.47    |     0.00    |
-------------------------------------------------------
     0.47    |     0.00    |    -0.00    |     0.00    |
 0.38    0.37| 0.00    0.00| 0.58   -1.00| 0.00    0.00|
     0.32    |     0.00    |     0.46    |     0.00    |
-------------------------------------------------------
     0.38    |     0.35    |     0.36    |    -0.79    |
 0.31    0.34| 0.30    0.42| 0.31    0.29| 0.37    0.16|
     0.30    |     0.38    |     0.44    |     0.25    |
-------------------------------------------------------

学習後のテスト結果(100回)

実装２，方策反復法

折角近似モデルを作成したのでQ学習ではなく方策反復法で学習する実装も作成してみました。
ほとんど第1回と同じですがコードを書いておきます。
また、近似モデルを学習する箇所はQ学習の場合と同じなので省略しています。

アクションですが、決定的方策なため探索用にε-greedy法を実装しています。

class PolicyIteration():
    def __init__(self, env):
        self.nb_action = len(env.actions)

        self.gamma = 0.9         # 割引率
        self.threshold = 0.0001  # 状態価値関数の計算を打ち切る閾値
        self.epsilon = 0.1

        # 方策関数、最初は均等の確率で初期化
        self.policy = {}
        for s in env.states:
            self.policy[s] = [1/len(env.actions)] * len(env.actions)


    # ポリシーにおける状態の価値を価値反復法で計算
    def estimate_by_policy(self, a_mdp):

        # 状態価値関数の初期化
        V = {s:0 for s in a_mdp.states}

        # 学習
        for i in range(100):  # for safety
            delta = 0

            # 全状態に対して
            for s in a_mdp.states:
                
                # 各アクションでの報酬期待値を計算
                expected_reward = []
                for a in a_mdp.actions:
                    
                    # 報酬期待値
                    reward = a_mdp.get_reward(s, a)

                    # ポリシーにおけるアクションの遷移確率
                    action_prob = self.policy[s][a]

                    # 割引報酬を計算
                    n_state_probs = a_mdp.get_next_state_probs(s, a)
                    r = 0
                    for s2, s2_prob in n_state_probs.items():
                        # 次の状態の価値を計算
                        r += s2_prob * (reward + self.gamma * V.get(s2, 0))
                    expected_reward.append(action_prob * r)

                # 各アクションの期待値を合計する
                value = sum(expected_reward)
                delta = max(delta, abs(V[s] - value))  # 学習打ち切り用に差分を保存
                V[s] = value

            # 更新差分が閾値以下になったら学習終了
            if delta < self.threshold:
                break
        return V

    # ポリシーの更新
    def update(self, a_mdp):

        # 現policyでの状態価値を計算
        V = self.estimate_by_policy(a_mdp)

        # 学習
        for i in range(100):  # for safety
            update_stable = True

            # 全状態をループ
            for s in a_mdp.states:

                # 各アクションでの報酬期待値を計算
                expected_reward = []
                for a in a_mdp.actions:

                    # 報酬期待値
                    reward =a_mdp.get_reward(s, a)

                    # 割引報酬を計算
                    n_state_probs = a_mdp.get_next_state_probs(s, a)
                    r = 0
                    for s2, s2_prob in n_state_probs.items():
                        # 次の状態の価値を計算
                        r += s2_prob * (reward + self.gamma * V.get(s2, 0))
                    expected_reward.append(r)

                if len(expected_reward) <= 1:
                    continue

                # 期待値が一番高いアクション
                best_action = np.argmax(expected_reward)

                # 現ポリシーで一番選ばれる確率の高いアクション
                policy_action = np.argmax(self.policy[s])

                # ベストなアクションとポリシーのアクションが違う場合は更新
                if best_action != policy_action:
                    update_stable = False

                # ポリシーを更新する
                # ベストアクションの確率を100%にし、違うアクションを0%にする
                for a in a_mdp.actions:
                    if a == best_action:
                        prob = 1
                    else:
                        prob = 0
                    self.policy[s][a] = prob

            # 更新差分がなくなったら終わり
            if update_stable:
                break


    def sample_action(self, state):
        # ε-Greedy
        if np.random.random() < self.epsilon:
            # epsilonより低いならランダムに移動
            return np.random.randint(self.nb_action)
        else:
            # ポリシー通りに実行
            targets = [i for i in range(self.nb_action)]
            weights = self.policy[state]
            return random.choices(targets, weights=weights, k=1)[0]

学習結果

学習中の環境から取得した報酬

学習後の近似モデル(報酬)

------------------------------------------------
   -0.04   |   -0.04   |   -0.04   |    0.00   |
-0.04 -0.04|-0.04 -0.04|-0.04  0.86| 0.00  0.00|
   -0.04   |   -0.04   |    0.22   |    0.00   |
------------------------------------------------
   -0.04   |    0.00   |   -0.52   |    0.00   |
-0.04 -0.04| 0.00  0.00|-0.04 -1.00| 0.00  0.00|
   -0.04   |    0.00   |   -0.13   |    0.00   |
------------------------------------------------
   -0.04   |   -0.04   |   -0.04   |   -1.00   |
-0.04 -0.04|-0.04 -0.04|-0.04 -0.04|-0.04 -0.04|
   -0.04   |   -0.04   |   -0.04   |   -0.04   |
------------------------------------------------

学習後の近似モデル(終了確率)

-------------------------------------------------------
      0.0%   |      0.0%   |      0.0%   |      0.0%   |
  0.0%   0.0%|  0.0%   0.0%|  0.0%  86.5%|  0.0%   0.0%|
      0.0%   |      0.0%   |     25.0%   |      0.0%   |
-------------------------------------------------------
      0.0%   |      0.0%   |     50.0%   |      0.0%   |
  0.0%   0.0%|  0.0%   0.0%|  0.0% 100.0%|  0.0%   0.0%|
      0.0%   |      0.0%   |      9.1%   |      0.0%   |
-------------------------------------------------------
      0.0%   |      0.0%   |      0.0%   |    100.0%   |
  0.0%   0.0%|  0.0%   0.0%|  0.0%   0.0%|  0.0%   0.0%|
      0.0%   |      0.0%   |      0.0%   |      0.0%   |
-------------------------------------------------------

学習後の近似モデル(遷移確率)

(0, 0):Action.UP -> (0, 0):88.2%
(0, 0):Action.UP -> (1, 0):11.8%
(0, 0):Action.DOWN -> (1, 0):7.1%
(0, 0):Action.DOWN -> (0, 1):92.9%
(0, 0):Action.LEFT -> (0, 0):100.0%
(0, 0):Action.RIGHT -> (0, 0):11.8%
(0, 0):Action.RIGHT -> (1, 0):80.0%
(0, 0):Action.RIGHT -> (0, 1):8.2%
(1, 0):Action.UP -> (0, 0):25.0%
(1, 0):Action.UP -> (1, 0):75.0%
(1, 0):Action.DOWN -> (1, 0):100.0%
(1, 0):Action.LEFT -> (0, 0):80.0%
(1, 0):Action.LEFT -> (1, 0):20.0%
(1, 0):Action.RIGHT -> (1, 0):17.7%
(1, 0):Action.RIGHT -> (2, 0):82.3%
(2, 0):Action.UP -> (2, 0):100.0%
(2, 0):Action.DOWN -> (3, 0):25.0%
(2, 0):Action.DOWN -> (2, 1):75.0%
(2, 0):Action.LEFT -> (1, 0):50.0%
(2, 0):Action.LEFT -> (2, 0):50.0%
(2, 0):Action.RIGHT -> (2, 0):8.3%
(2, 0):Action.RIGHT -> (3, 0):86.5%
(2, 0):Action.RIGHT -> (2, 1):5.2%
(0, 1):Action.UP -> (0, 0):74.2%
(0, 1):Action.UP -> (0, 1):25.8%
(0, 1):Action.DOWN -> (0, 1):22.2%
(0, 1):Action.DOWN -> (0, 2):77.8%
(0, 1):Action.LEFT -> (0, 1):66.7%
(0, 1):Action.LEFT -> (0, 2):33.3%
(0, 1):Action.RIGHT -> (0, 0):12.5%
(0, 1):Action.RIGHT -> (0, 1):62.5%
(0, 1):Action.RIGHT -> (0, 2):25.0%
(2, 1):Action.UP -> (2, 0):50.0%
(2, 1):Action.UP -> (3, 1):50.0%
(2, 1):Action.DOWN -> (2, 1):18.2%
(2, 1):Action.DOWN -> (3, 1):9.1%
(2, 1):Action.DOWN -> (2, 2):72.7%
(2, 1):Action.LEFT -> (2, 1):100.0%
(2, 1):Action.RIGHT -> (3, 1):100.0%
(0, 2):Action.UP -> (0, 1):80.8%
(0, 2):Action.UP -> (0, 2):10.8%
(0, 2):Action.UP -> (1, 2):8.5%
(0, 2):Action.DOWN -> (0, 2):66.7%
(0, 2):Action.DOWN -> (1, 2):33.3%
(0, 2):Action.LEFT -> (0, 2):100.0%
(0, 2):Action.RIGHT -> (0, 1):16.7%
(0, 2):Action.RIGHT -> (1, 2):83.3%
(1, 2):Action.UP -> (1, 2):100.0%
(1, 2):Action.DOWN -> (1, 2):100.0%
(1, 2):Action.LEFT -> (0, 2):77.8%
(1, 2):Action.LEFT -> (1, 2):22.2%
(1, 2):Action.RIGHT -> (1, 2):27.3%
(1, 2):Action.RIGHT -> (2, 2):72.7%
(2, 2):Action.UP -> (2, 1):60.0%
(2, 2):Action.UP -> (1, 2):20.0%
(2, 2):Action.UP -> (3, 2):20.0%
(2, 2):Action.DOWN -> (2, 2):100.0%
(2, 2):Action.LEFT -> (2, 1):30.0%
(2, 2):Action.LEFT -> (1, 2):70.0%
(2, 2):Action.RIGHT -> (2, 2):33.3%
(2, 2):Action.RIGHT -> (3, 2):66.7%
(3, 2):Action.UP -> (3, 1):100.0%
(3, 2):Action.DOWN -> (3, 2):100.0%
(3, 2):Action.LEFT -> (2, 2):100.0%
(3, 2):Action.RIGHT -> (3, 2):100.0%

学習後の方策

-----------------------------------------------------------
      0.0%    |      0.0%    |      0.0%    |    100.0%    |
  0.0%  100.0%|  0.0%  100.0%|  0.0%  100.0%|  0.0%    0.0%|
      0.0%    |      0.0%    |      0.0%    |      0.0%    |
-----------------------------------------------------------
    100.0%    |    100.0%    |      0.0%    |    100.0%    |
  0.0%    0.0%|  0.0%    0.0%|  0.0%    0.0%|  0.0%    0.0%|
      0.0%    |      0.0%    |    100.0%    |      0.0%    |
-----------------------------------------------------------
    100.0%    |      0.0%    |      0.0%    |      0.0%    |
  0.0%    0.0%|100.0%    0.0%|100.0%    0.0%|100.0%    0.0%|
      0.0%    |      0.0%    |      0.0%    |      0.0%    |
-----------------------------------------------------------

学習後の状態価値関数

 0.61    0.77    0.93    0.00   
 0.48    0.00   -0.06    0.00
 0.37    0.27    0.11    0.06

学習後のテスト結果(100回)

あとがき

まずは基礎からですね。
正直まだモデルベースの利点が見えていませんが、見えていけるようになりたいです。

次はモンテカルロ木探索を予定しています。

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

第10回 今更だけど基礎から強化学習を勉強する モデルベース編(Dyna)

コード全体

モデルベース強化学習

近似モデルについて

近似モデルの学習

プランニング

プランニングアルゴリズム

Sample-Based Planning

Simulation-Based Search

モデルベースとモデルフリーの違い

実装における環境(テーブル型モデル)

実装１，Dyna-Q

近似モデルの学習

Q学習

メインフロー

学習結果

実装２，方策反復法

学習結果

あとがき

第10回今更だけど基礎から強化学習を勉強するモデルベース編(Dyna)