モデルベース強化学習の有名な手法であるモンテカルロ木探索を見ていきたいと思います。
第10回 モデルベース基礎編
第12回 連続状態空間モデルベース編
※ネット上の情報をかき集めて自分なりに実装しているので正確ではない可能性がある点はご注意ください
コード全体
本記事で作成したコードは以下です。
追記:自作フレームワークを作成しています。そちらにも実装があります。
モンテカルロ探索(Monte-Carlo Search)
まずは木を使わない場合の探索です。
あるモデル $M_\eta$ とシミュレーション方策 $\pi$ が与えられているとします。
※$M_\eta$ は近似モデルを想定していますが、実環境でも問題ありません
※$\pi$ はシミュレーション時にアクションを選ぶ方策です
この時、ある状態 $s_t$ におけるアクションの選択方法は以下です。
q_vals = []
for action in 全アクション:
total_reward = 0
for エピソードをK回分繰り返す:
state = エピソードを開始する状態はある状態st
for 1エピソードループ:
エピソード中のアクションは方策πによって選ばれる
total_reward += 各stepの報酬
# Kエピソードの平均報酬、これが行動価値になる
reward = total_reward / K
q_vals.append(reward)
# 行動価値が一番高い行動を選択する
select_action = np.argmax(q_vals)
方策πは一般的にはランダムな方策が使われます。
その場合はモンテカルロ法で行動価値を求めていると見ることもできるので、これが名前の由来になっているのでしょう。
割引報酬に関する考察
モデルフリーなアルゴリズムでは累積報酬に関して割引率を反映していました。
G^{free}_t = r_{t+1} + \gamma G^{free}_{t+1}
しかし、モデルベースなアルゴリズムでは適用していないように見えます。
G^{base}_t = r_{t+1} + G^{base}_{t+1}
これはモデルベースでは近似モデルを採用しており、そもそも即時報酬自体が近似値なのでさらに割引して正確性を失う必要がないからではないかと思っています。
(それかモンテカルロ探索だけがそうなのかもしれません)
モンテカルロ木探索(Monte-Carlo Tree Search)
モンテカルロ探索では行動価値関数を全アクションに対して走査していましたが、最初のアクションもシミュレーション方策 $\pi$ によって決める方法がモンテカルロ木探索です。
参考
- 強化学習理論の基礎4
- 強化学習入門 Part3 - AlphaGoZeroでも重要な技術要素! モンテカルロ木探索の入門 -
- モンテカルロ木探索(Wikipedia)
- AlphaGo Zeroの動作方法と理由
モンテカルロ木探索はシミュレーション時に得た行動価値関数と訪れた(状態,アクション)の回数を保存します。
この保存した情報を元にシミュレーション方策 $\pi_{tree}$ を更新していきます。
(後述しますがモンテカルロ木探索には2つの方策があります)
シミュレーションはSelection,Expansion,Evaluation,Backupのステップがあります。
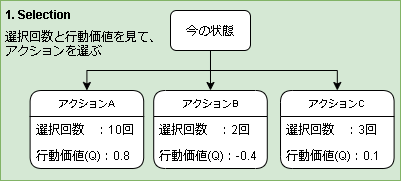
1. Selection
今いる状態からアクションを選びます。
選び方ですが、各アクションを多腕バンディット問題(Multi-armed bandit problem)として選択します。
多腕バンディット問題を簡単に言うと探索と活用のジレンマを表現した問題です。
当たる確率が分からないスロットがいくつかあります。
スロットは回せば回すほど当たる確率がわかりますが、当たらないスロットを回すと損します。
ここでスロットの本当の確率を予測する行為(探索)と今わかる確率で一番いいスロットを回す行為(活用)にトレードオフが発生し、その中で最大の報酬を得ようとする問題が多腕バンディット問題となります。
多腕バンディット問題に関しては過去に記事を書いているのでよかったらどうぞ
【強化学習】複数の探索ポリシーを実装/解説して比較してみた(多腕バンディット問題)
モンテカルロ木探索の Selection には UCB(Upper Confidence Bound)1 がよく使われ、以下の式となります。
$$
\underset{a}{argmax}
\biggl(
Q(s,a) + \sqrt{\frac{2 logN_s}{n_{s,a}}}
\biggr)
$$
$Q(s,a)$ は行動価値、$N_s$ は状態$s$を訪れた回数、$n_{s,a}$は状態$s$でアクション$a$を選んだ回数です。
state = 対象の状態
N = stateを訪れた回数
select_val_list = []
for action in 全アクション:
n = stateでactionを選んだ回数
if n == 0:
# 一度は選んでほしい
val = 9999999
else:
ucb_cost = np.sqrt(s * np.log(N)) / n
val = (state,action)の行動価値 + ucb_cost
select_val_list.append(val)
select_action = np.argmax(select_val_list)
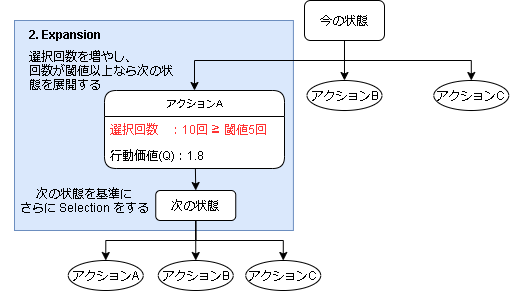
2. Expansion
Selectionで選んだアクションの回数が閾値以上なら次の状態に遷移し、その状態を基準にしてまた Selection に戻ります。
これは状態とアクションを木構造に見立てた場合、葉の要素をさらに展開する感じになります。
閾値以下の場合は Expansion はせずに Evaluation に進みます。
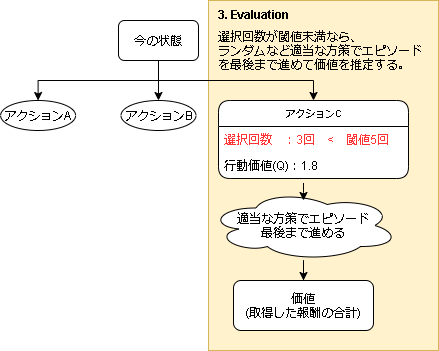
3. Evaluation
アクションの選択回数が閾値未満だった場合、その状態の価値を推定します。
評価の仕方は適当な方策 $\pi_d$ でエピソード最後までシミュレーションし、その中で得られた報酬を価値として計算します。
このエピソード最後までシミュレーションして価値を推定する事をロールアウト(Rollout)といいます。
また、モンテカルロ木探索ではシミュレーション内で2つの方策があり、Selection で使われる方策を Tree Policy ($\pi_{tree}$)といい、Evaluation で使われる方策を Default Policy ($\pi_{d}$)といいます。
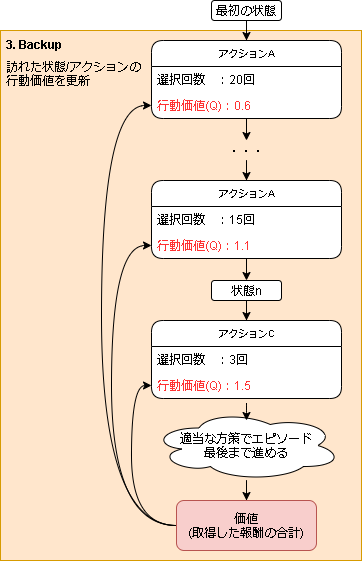
4. Backup
Expansion によって評価された値をシミュレーションで辿った(状態,アクション)の行動価値に反映させます。
反映の仕方に特に決まりはなさそうです。
今回の場合ですと、素直に考えれば累積報酬の期待値でしょうか。
G'_{t,s,a} = r_{t+1} + G'_{t+1,s,a} \\
Q(s,a) = E[G] = \frac{\sum_{i} G'_{i,s,a}}{N_{s,a}}
$G_{t,s,a}$ は$(s,a)$からエピソード最後までシミュレーションした結果得た価値、$N_{s,a}$ は$(s,a)$を訪れた回数です。
Play
最後に実際に実行するアクションを決めます。
決め方はシミュレーションの結果得た行動価値(Q値)を使えばいいのですが、他の方法もあるようです。
例えば AlphaGo では選択された回数が一番多いアクションを選択しているそうです。
(Q値より外れ値の影響を受けにくいそうです)
実装のメインフロー(共通)
アルゴリズム部分はクラス化し、メインフローはそこだけ変える形で実装しています。
env = GridEnv()
a_mdp = A_MDP(env) # 近似モデル(詳細は第10回を参照)
rl_mc = 各アルゴリズムのクラスをインスタンス化
# 学習ループ
for episode in range(100):
state = env.reset()
done = False
total_reward = 0
# 1episode 最大20stepで終わりにする
for step in range(20):
# アクションを決定
action = rl_mc.sample_action(a_mdp, state, training=True)
# 環境の1step
n_state, reward, done, _ = env.step(action)
total_reward += reward
# 近似モデルの学習
a_mdp.train(state, action, n_state, reward, done)
state = n_state
if done:
break
# 5回テストする例
for episode in range(5):
state = np.asarray(env.reset())
env.render()
done = False
total_reward = 0
# 1episode
for step in range(20):
action = rl_mc.sample_action(a_mdp, state)
n_state, reward, done, _ = env.step(action)
env.render()
state = np.asarray(n_state)
total_reward += reward
print("{} reward: {}".format(episode, total_reward))
env.close()
実装1,モンテカルロ探索
モンテカルロ探索から実装してみます。
各方策は以下で実装しました。
| 方策 | |
|---|---|
| シミュレーション方策 | ランダム |
| 実環境へのアクションの選択方法(トレーニング) | ε-Greedy法 |
| 実環境へのアクションの選択方法(テスト) | 最大のQ値 |
class MCS():
def __init__(self, env):
self.nb_action = len(env.actions) # アクション数
self.max_turn = 20 # 最大ターン数
self.epsilon = 0.1
self.simulation_times = 20
# state から近似モデル a_mdp を元に実環境へのアクションを返す
def sample_action(self, a_mdp, state, training=False):
# Q値を計算する
q_vals = self.compute_q_vals(a_mdp, state)
if training:
# トレーニング中はε-greedy
if np.random.random() < self.epsilon:
# epsilonより低いならランダムに移動
return np.random.randint(self.nb_action)
else:
# Q値が最大のアクションを実行
select_actions = []
for i, v in enumerate(q_vals):
if v == max(q_vals):
select_actions.append(i)
return random.sample(select_actions, 1)[0]
else:
return np.argmax(q_vals)
# 近似モデル a_mdp を使ってQ値を計算する
def compute_q_vals(self, a_mdp, init_state):
q_vals = []
# 全アクション
for action in a_mdp.actions:
total_reward = 0
# シミュレーション
for _ in range(self.simulation_times):
state = a_mdp.sample_next_state(init_state, action)
done = a_mdp.sample_done(init_state, action)
step = 0
# 1episode
while not done and step < self.max_turn:
step += 1
# π(ランダム)
action = np.random.randint(self.nb_action)
total_reward += a_mdp.get_reward(state, action)
done = a_mdp.sample_done(state, action)
state = a_mdp.sample_next_state(state, action)
# Kエピソードの平均報酬、これが行動価値になる
reward = total_reward / self.simulation_times
q_vals.append(reward)
return q_vals
実行結果
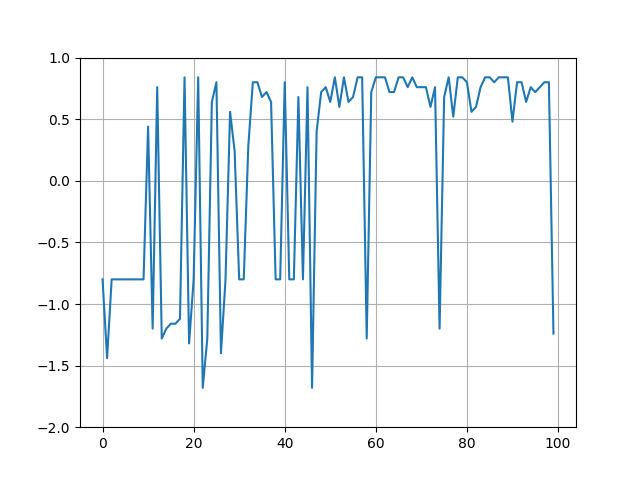
- 学習中の報酬取得の様子
- 学習後の近似モデルの報酬関数
------------------------------------------------
-0.04 | -0.04 | 0.07 | 0.00 |
-0.04 -0.04|-0.04 -0.04|-0.04 0.85| 0.00 0.00|
-0.04 | -0.04 | 0.02 | 0.00 |
------------------------------------------------
-0.04 | 0.00 | -0.13 | 0.00 |
-0.04 -0.04| 0.00 0.00|-0.04 -0.87| 0.00 0.00|
-0.04 | 0.00 | -0.18 | 0.00 |
------------------------------------------------
-0.04 | -0.04 | -0.04 | -0.76 |
-0.04 -0.04|-0.04 -0.04|-0.04 -0.04|-0.12 -0.16|
-0.04 | -0.04 | -0.04 | -0.04 |
------------------------------------------------
- 学習後の近似モデルの終了関数
-------------------------------------------------------
0.0% | 0.0% | 10.2% | 0.0% |
0.0% 0.0%| 0.0% 0.0%| 0.0% 85.5%| 0.0% 0.0%|
0.0% | 0.0% | 6.1% | 0.0% |
-------------------------------------------------------
0.0% | 0.0% | 9.1% | 0.0% |
0.0% 0.0%| 0.0% 0.0%| 0.0% 86.0%| 0.0% 0.0%|
0.0% | 0.0% | 14.3% | 0.0% |
-------------------------------------------------------
0.0% | 0.0% | 0.0% | 75.4% |
0.0% 0.0%| 0.0% 0.0%| 0.0% 0.0%| 8.3% 12.0%|
0.0% | 0.0% | 0.0% | 0.0% |
-------------------------------------------------------
- 学習後の近似モデルの遷移関数
(0, 0):Action.UP -> (0, 0):92.1%
(0, 0):Action.UP -> (1, 0):7.9%
(0, 0):Action.DOWN -> (0, 0):8.1%
(0, 0):Action.DOWN -> (1, 0):10.0%
(0, 0):Action.DOWN -> (0, 1):81.9%
(0, 0):Action.LEFT -> (0, 0):88.1%
(0, 0):Action.LEFT -> (0, 1):11.9%
(0, 0):Action.RIGHT -> (0, 0):7.4%
(0, 0):Action.RIGHT -> (1, 0):86.4%
(0, 0):Action.RIGHT -> (0, 1):6.2%
(1, 0):Action.UP -> (0, 0):11.8%
(1, 0):Action.UP -> (1, 0):83.5%
(1, 0):Action.UP -> (2, 0):4.7%
(1, 0):Action.DOWN -> (0, 0):7.5%
(1, 0):Action.DOWN -> (1, 0):85.0%
(1, 0):Action.DOWN -> (2, 0):7.5%
(1, 0):Action.LEFT -> (0, 0):78.3%
(1, 0):Action.LEFT -> (1, 0):21.7%
(1, 0):Action.RIGHT -> (1, 0):20.4%
(1, 0):Action.RIGHT -> (2, 0):79.6%
(2, 0):Action.UP -> (1, 0):8.2%
(2, 0):Action.UP -> (2, 0):81.6%
(2, 0):Action.UP -> (3, 0):10.2%
(2, 0):Action.DOWN -> (1, 0):9.1%
(2, 0):Action.DOWN -> (3, 0):6.1%
(2, 0):Action.DOWN -> (2, 1):84.8%
(2, 0):Action.LEFT -> (1, 0):79.1%
(2, 0):Action.LEFT -> (2, 0):7.0%
(2, 0):Action.LEFT -> (2, 1):14.0%
(2, 0):Action.RIGHT -> (2, 0):9.1%
(2, 0):Action.RIGHT -> (3, 0):85.5%
(2, 0):Action.RIGHT -> (2, 1):5.5%
(0, 1):Action.UP -> (0, 0):83.8%
(0, 1):Action.UP -> (0, 1):16.2%
(0, 1):Action.DOWN -> (0, 1):18.4%
(0, 1):Action.DOWN -> (0, 2):81.6%
(0, 1):Action.LEFT -> (0, 0):9.8%
(0, 1):Action.LEFT -> (0, 1):80.8%
(0, 1):Action.LEFT -> (0, 2):9.3%
(0, 1):Action.RIGHT -> (0, 0):9.8%
(0, 1):Action.RIGHT -> (0, 1):79.9%
(0, 1):Action.RIGHT -> (0, 2):10.3%
(2, 1):Action.UP -> (2, 0):78.2%
(2, 1):Action.UP -> (2, 1):12.7%
(2, 1):Action.UP -> (3, 1):9.1%
(2, 1):Action.DOWN -> (2, 1):17.9%
(2, 1):Action.DOWN -> (3, 1):14.3%
(2, 1):Action.DOWN -> (2, 2):67.9%
(2, 1):Action.LEFT -> (2, 0):5.3%
(2, 1):Action.LEFT -> (2, 1):84.2%
(2, 1):Action.LEFT -> (2, 2):10.5%
(2, 1):Action.RIGHT -> (2, 0):4.7%
(2, 1):Action.RIGHT -> (3, 1):86.0%
(2, 1):Action.RIGHT -> (2, 2):9.3%
(0, 2):Action.UP -> (0, 1):80.7%
(0, 2):Action.UP -> (0, 2):9.6%
(0, 2):Action.UP -> (1, 2):9.6%
(0, 2):Action.DOWN -> (0, 2):89.7%
(0, 2):Action.DOWN -> (1, 2):10.3%
(0, 2):Action.LEFT -> (0, 1):11.7%
(0, 2):Action.LEFT -> (0, 2):88.3%
(0, 2):Action.RIGHT -> (0, 1):8.7%
(0, 2):Action.RIGHT -> (0, 2):9.0%
(0, 2):Action.RIGHT -> (1, 2):82.3%
(1, 2):Action.UP -> (0, 2):9.0%
(1, 2):Action.UP -> (1, 2):81.4%
(1, 2):Action.UP -> (2, 2):9.6%
(1, 2):Action.DOWN -> (0, 2):8.2%
(1, 2):Action.DOWN -> (1, 2):78.9%
(1, 2):Action.DOWN -> (2, 2):12.9%
(1, 2):Action.LEFT -> (0, 2):78.0%
(1, 2):Action.LEFT -> (1, 2):22.0%
(1, 2):Action.RIGHT -> (1, 2):22.3%
(1, 2):Action.RIGHT -> (2, 2):77.7%
(2, 2):Action.UP -> (2, 1):82.1%
(2, 2):Action.UP -> (1, 2):7.1%
(2, 2):Action.UP -> (3, 2):10.7%
(2, 2):Action.DOWN -> (1, 2):5.7%
(2, 2):Action.DOWN -> (2, 2):87.1%
(2, 2):Action.DOWN -> (3, 2):7.1%
(2, 2):Action.LEFT -> (2, 1):6.8%
(2, 2):Action.LEFT -> (1, 2):84.9%
(2, 2):Action.LEFT -> (2, 2):8.2%
(2, 2):Action.RIGHT -> (2, 1):12.5%
(2, 2):Action.RIGHT -> (2, 2):8.0%
(2, 2):Action.RIGHT -> (3, 2):79.5%
(3, 2):Action.UP -> (3, 1):75.4%
(3, 2):Action.UP -> (2, 2):12.3%
(3, 2):Action.UP -> (3, 2):12.3%
(3, 2):Action.DOWN -> (2, 2):20.0%
(3, 2):Action.DOWN -> (3, 2):80.0%
(3, 2):Action.LEFT -> (3, 1):8.3%
(3, 2):Action.LEFT -> (2, 2):83.3%
(3, 2):Action.LEFT -> (3, 2):8.3%
(3, 2):Action.RIGHT -> (3, 1):12.0%
(3, 2):Action.RIGHT -> (3, 2):88.0%
- 学習後のQ値(モンテカルロ探索)
------------------------------------------------
-0.46 | -0.04 | -0.19 | -0.47 |
-0.62 -0.68|-0.28 -0.45|-0.11 -0.05|-0.50 -0.33|
-0.70 | 0.01 | -0.14 | -0.75 |
------------------------------------------------
-0.35 | -0.59 | -0.15 | -0.61 |
-0.86 -0.63|-0.38 -0.36|-0.21 -0.14|-0.45 -0.71|
-0.68 | -0.32 | -0.19 | -0.28 |
------------------------------------------------
-0.60 | -0.86 | -0.87 | -0.22 |
-1.11 -0.84|-0.82 -1.14|-0.89 -0.85|-0.17 -0.28|
-0.77 | -0.82 | -0.85 | -0.29 |
------------------------------------------------
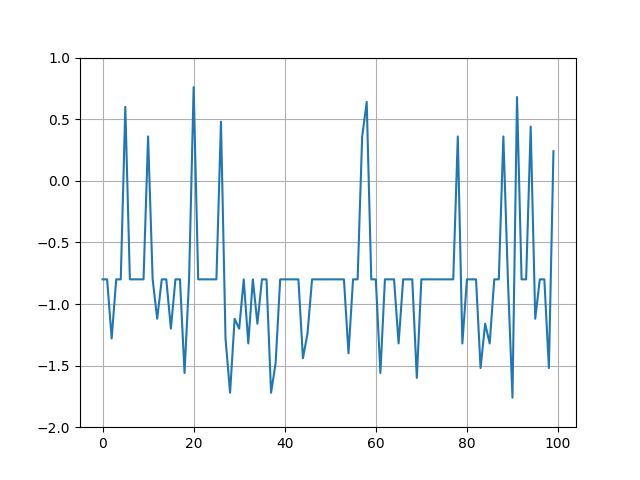
- 学習後、テスト100の結果
実装2,モンテカルロ木探索
各方策とコードは以下です。
| 方策 | |
|---|---|
| シミュレーション方策(Default Policy) | ランダム |
| シミュレーション方策(Tree Policy) | UCB1 |
| 実環境へのアクションの選択方法(トレーニング) | UCB1(Tree Policyと同じ) |
| 実環境へのアクションの選択方法(テスト) | 最大のQ値 |
class MCTS():
def __init__(self, env):
self.nb_action = len(env.actions)
self.max_turn = 20
self.nb_action = len(env.actions) # アクション数
self.max_turn = 20 # 最大ターン数
self.count_threshold = 100 # Expansionの閾値
self.simulation_times = 10 # シミュレーション回数
self.Q = collections.defaultdict(lambda: [0] * self.nb_action)
self.count = collections.defaultdict(lambda: [0] * self.nb_action)
# state から近似モデル a_mdp を元に実環境へのアクションを返す
def sample_action(self, a_mdp, state, training=False):
if training:
# 数回シミュレーションする
for _ in range(self.simulation_times):
self._simulation(a_mdp, state)
# UCBに従ってアクションを選択
return self._select_action(a_mdp, state)
else:
# テスト中はQ値が最大のアクションを選択
q = []
for action in a_mdp.actions:
if self.count[state][action] == 0:
q.append(0)
else:
q.append(self.Q[state][action] / self.count[state][action])
return np.argmax(q)
# UCBに従ってアクションを返す
def _select_action(self, a_mdp, state):
# この状態をシミュレートした回数
N = np.sum(self.count[state])
# selection
ucb_list = []
for action in a_mdp.actions:
# この(状態,アクション)をシミュレートした回数
n = self.count[state][action]
if n == 0:
# 0回は1度は選んでほしい
ucb = 99999999
else:
# UCB値を計算
cost = np.sqrt(2 * np.log(N)) / n
ucb = self.Q[state][action] / n + cost
ucb_list.append(ucb)
# UCBが最大のアクションを選ぶ(複数ある場合はその中からランダム)
select_actions = []
for i, v in enumerate(ucb_list):
if v == np.max(ucb_list):
select_actions.append(i)
return random.sample(select_actions, 1)[0]
# シミュレーションして行動価値Qと選択回数を更新する
# 再帰関数として実装し、戻り値は報酬の配列(逆順)
def _simulation(self, a_mdp, state, depth=0):
if depth >= self.max_turn:
return []
# UCBに従ってアクションを選択
action = self._select_action(a_mdp, state)
# 回数を増やす
self.count[state][action] += 1
# 報酬
reward = a_mdp.get_reward(state, action)
if self.count[state][action] < self.count_threshold:
# 閾値以下はロールアウト
reverse_reward_list = self._rollout(a_mdp, state, action)
reverse_reward_list.append(reward)
else:
done = a_mdp.sample_done(state, action)
if done:
# 終了なら展開しない
reverse_reward_list = [reward]
else:
# 展開して次の状態に
n_state = a_mdp.sample_next_state(state, action)
reverse_reward_list = self._simulation(a_mdp, n_state, depth+1)
reverse_reward_list.append(reward)
# Q値の更新
self.Q[state][action] += np.sum(reverse_reward_list)
return reverse_reward_list
# ロールアウト
def _rollout(self, a_mdp, state, action):
step = 1
done = a_mdp.sample_done(state, action)
state = a_mdp.sample_next_state(state, action)
reward_list = [a_mdp.get_reward(state, action)]
# 1episode
while not done and step < self.max_turn:
step += 1
# π(ランダム)
action = random.randint(0, len(a_mdp.actions)-1)
reward = a_mdp.get_reward(state, action)
reward_list.append(reward)
done = a_mdp.sample_done(state, action)
state = a_mdp.sample_next_state(state, action)
return list(reversed(reward_list))
実行結果
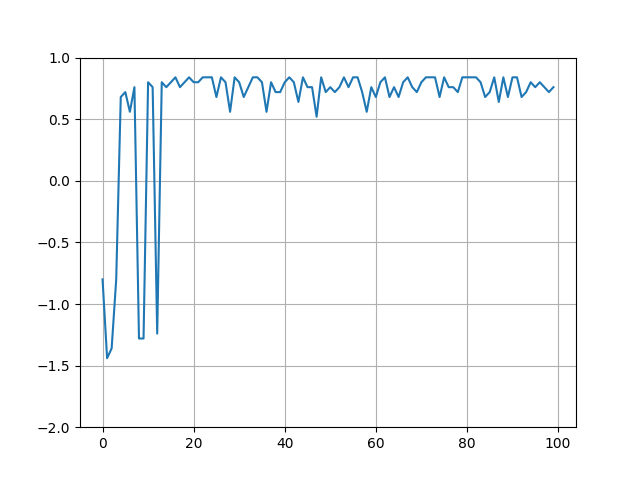
- 学習中の報酬取得の様子
- 学習後の近似モデルの報酬関数
------------------------------------------------
-0.04 | -0.04 | -0.04 | 0.00 |
0.00 -0.04| 0.00 -0.04| 0.00 0.85| 0.00 0.00|
-0.04 | 0.00 | -0.04 | 0.00 |
------------------------------------------------
-0.04 | 0.00 | -0.04 | 0.00 |
0.00 -0.04| 0.00 0.00| 0.00 -0.68| 0.00 0.00|
-0.04 | 0.00 | -0.04 | 0.00 |
------------------------------------------------
-0.04 | -0.04 | -0.04 | -0.52 |
-0.04 -0.04|-0.04 -0.04|-0.04 -0.04|-1.00 -0.04|
-0.04 | -0.04 | -0.04 | -0.04 |
------------------------------------------------
- 学習後の近似モデルの終了関数
-------------------------------------------------------
0.0% | 0.0% | 0.0% | 0.0% |
0.0% 0.0%| 0.0% 0.0%| 0.0% 85.3%| 0.0% 0.0%|
0.0% | 0.0% | 0.0% | 0.0% |
-------------------------------------------------------
0.0% | 0.0% | 0.0% | 0.0% |
0.0% 0.0%| 0.0% 0.0%| 0.0% 66.7%| 0.0% 0.0%|
0.0% | 0.0% | 0.0% | 0.0% |
-------------------------------------------------------
0.0% | 0.0% | 0.0% | 50.0% |
0.0% 0.0%| 0.0% 0.0%| 0.0% 0.0%|100.0% 0.0%|
0.0% | 0.0% | 0.0% | 0.0% |
-------------------------------------------------------
- 学習後の近似モデルの遷移関数
(0, 0):Action.UP -> (0, 0):100.0%
(0, 0):Action.DOWN -> (0, 1):100.0%
(0, 0):Action.RIGHT -> (0, 0):5.8%
(0, 0):Action.RIGHT -> (1, 0):79.3%
(0, 0):Action.RIGHT -> (0, 1):14.9%
(1, 0):Action.UP -> (1, 0):100.0%
(1, 0):Action.RIGHT -> (1, 0):20.7%
(1, 0):Action.RIGHT -> (2, 0):79.3%
(2, 0):Action.UP -> (2, 0):100.0%
(2, 0):Action.DOWN -> (2, 1):100.0%
(2, 0):Action.RIGHT -> (2, 0):3.7%
(2, 0):Action.RIGHT -> (3, 0):85.3%
(2, 0):Action.RIGHT -> (2, 1):11.0%
(0, 1):Action.UP -> (0, 0):81.0%
(0, 1):Action.UP -> (0, 1):19.0%
(0, 1):Action.DOWN -> (0, 2):100.0%
(0, 1):Action.RIGHT -> (0, 1):100.0%
(2, 1):Action.UP -> (2, 0):87.5%
(2, 1):Action.UP -> (2, 1):12.5%
(2, 1):Action.DOWN -> (2, 1):33.3%
(2, 1):Action.DOWN -> (2, 2):66.7%
(2, 1):Action.RIGHT -> (3, 1):66.7%
(2, 1):Action.RIGHT -> (2, 2):33.3%
(0, 2):Action.UP -> (0, 1):79.5%
(0, 2):Action.UP -> (0, 2):12.3%
(0, 2):Action.UP -> (1, 2):8.2%
(0, 2):Action.DOWN -> (0, 2):80.0%
(0, 2):Action.DOWN -> (1, 2):20.0%
(0, 2):Action.LEFT -> (0, 2):100.0%
(0, 2):Action.RIGHT -> (0, 1):16.7%
(0, 2):Action.RIGHT -> (1, 2):83.3%
(1, 2):Action.UP -> (0, 2):37.5%
(1, 2):Action.UP -> (1, 2):50.0%
(1, 2):Action.UP -> (2, 2):12.5%
(1, 2):Action.DOWN -> (0, 2):28.6%
(1, 2):Action.DOWN -> (1, 2):71.4%
(1, 2):Action.LEFT -> (0, 2):61.5%
(1, 2):Action.LEFT -> (1, 2):38.5%
(1, 2):Action.RIGHT -> (1, 2):16.7%
(1, 2):Action.RIGHT -> (2, 2):83.3%
(2, 2):Action.UP -> (2, 1):75.0%
(2, 2):Action.UP -> (3, 2):25.0%
(2, 2):Action.DOWN -> (2, 2):100.0%
(2, 2):Action.LEFT -> (1, 2):100.0%
(2, 2):Action.RIGHT -> (3, 2):100.0%
(3, 2):Action.UP -> (3, 1):50.0%
(3, 2):Action.UP -> (2, 2):50.0%
(3, 2):Action.DOWN -> (3, 2):100.0%
(3, 2):Action.LEFT -> (3, 1):100.0%
(3, 2):Action.RIGHT -> (3, 2):100.0%
- シミュレーション回数
-----------------------------------------------------------
66 | 5 | 22 | 9 |
4 4574| 3 5697| 17 5863| 3 590|
15 | 5 | 20 | 20 |
-----------------------------------------------------------
4002 | 0 | 252 | 2 |
4 18| 0 0| 18 33| 1 2|
15 | 0 | 18 | 2 |
-----------------------------------------------------------
1431 | 96 | 34 | 137 |
55 62| 317 76| 27 53| 90 53|
54 | 59 | 26 | 46 |
-----------------------------------------------------------
- 行動価値
----------------------------------------------------
-0.46 | -0.90 | -0.39 | -1.04 |
-1.33 0.70|-1.33 0.78|-0.48 0.83|-2.04 -0.49|
-0.66 | -0.93 | -0.40 | -0.68 |
----------------------------------------------------
0.64 | 0.00 | 0.33 | -1.02 |
-1.53 -0.72| 0.00 0.00|-0.60 -0.50|-2.00 -0.54|
-0.77 | 0.00 | -0.62 | -1.14 |
----------------------------------------------------
0.47 | -0.78 | -0.52 | -0.87 |
-0.66 -0.66| 0.12 -0.79|-0.55 -0.51|-0.88 -0.90|
-0.67 | -0.80 | -0.55 | -0.94 |
----------------------------------------------------
- コスト
----------------------------------------------------
0.06 | 0.83 | 0.19 | 0.40 |
1.03 0.00| 1.39 0.00| 0.25 0.00| 1.20 0.01|
0.27 | 0.83 | 0.21 | 0.18 |
----------------------------------------------------
0.00 | 0.00 | 0.01 | 0.99 |
1.02 0.23| 0.00 0.00| 0.19 0.10| 1.97 0.99|
0.27 | 0.00 | 0.19 | 0.99 |
----------------------------------------------------
0.00 | 0.04 | 0.09 | 0.02 |
0.07 0.06| 0.01 0.05| 0.12 0.06| 0.04 0.06|
0.07 | 0.06 | 0.12 | 0.07 |
----------------------------------------------------
- 行動価値+コスト(UCB値)
----------------------------------------------------
-0.40 | -0.07 | -0.21 | -0.65 |
-0.30 0.70| 0.05 0.78|-0.24 0.83|-0.84 -0.48|
-0.39 | -0.10 | -0.19 | -0.50 |
----------------------------------------------------
0.64 | 0.00 | 0.34 | -0.03 |
-0.51 -0.49| 0.00 0.00|-0.41 -0.40|-0.03 0.45|
-0.50 | 0.00 | -0.43 | -0.15 |
----------------------------------------------------
0.47 | -0.75 | -0.43 | -0.84 |
-0.59 -0.60| 0.13 -0.74|-0.43 -0.45|-0.84 -0.84|
-0.60 | -0.74 | -0.43 | -0.86 |
----------------------------------------------------
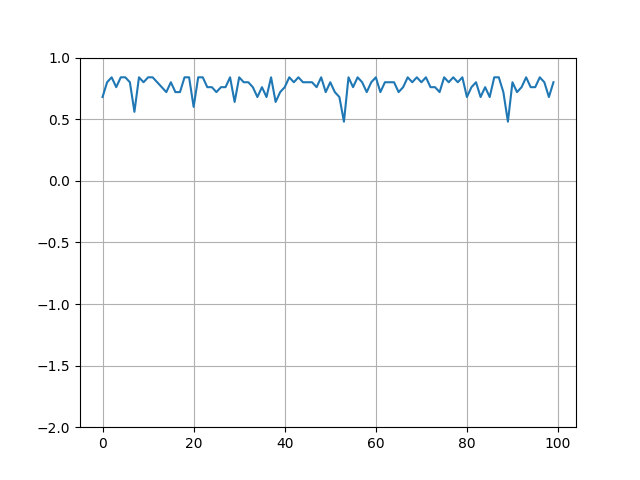
- 学習後、テスト100の結果
実行結果はかなりいい結果の場合です。
ロールアウトで-1の報酬ばかり引くとそれが伝搬して学習が失敗します。(局所解に入ります)
あとがき
乱数による影響が大きく学習はあまり安定しませんでした。
次はテーブル型ではなく関数近似したモデルを扱いたいと思います。