前回、前々回はテーブル型の状態を扱っていましたが、今回は連続空間の状態を扱います。
※ネット上の情報をかき集めて自分なりに実装しているので正確ではない可能性がある点はご注意ください
※ライブラリはTensowflow2.0(+Keras)を使っています。
コード全体
本記事で作成したコードは以下です。
はじめに
モデルベース強化学習の情報ですが論文ベースの話が多く、まだ手法の関係性についてあまり見えていません。
今までとちょっと違いますが今回の目次は以下です。
- モデルベース強化学習の分類(?)
- 近似モデルの学習(独自モデル)
- モデルベース強化学習の論文ベースの近似モデル
- PETS
モデルベース強化学習の分類(?)
下記の9pに書かれていたモデルベース強化学習の概要をそのまままとめたものです。
とりあえずモデルベース強化学習の概要をつかみたかったので…
[DL輪読会]Model-Based Reinforcement Learning via Meta-Policy Optimization
| 分類 | 概要 | 手法例 |
|---|---|---|
| Dyna-Style | 実環境から近似モデルを学習し、近似モデルのシミュレーションから方策を更新 | ME-TRPO,SLBO,MB-MPO,(モンテカルロ木探索もここだと思います) |
| Policy Search with Backpropagation through Time | 近似モデルが不正確なもの=確率的モデルとして方策を更新 | PILCO,iLQG,GPS,SVG |
| Shooting Algorithm | ある特定のアクション列を元に近似モデルから報酬を予測する手法 | RS,MB-FM,PETS-RS,RETS-CEM |
参考
-
Model-Ensemble Trust-Region Policy Optimization
ME-TRPOの論文 -
PILCO - 第一回高橋研究室モデルベース強化学習勉強会
PILCOの紹介スライド -
Learning Continuous Control Policies by Stochastic Value Gradients
強化学習のアルゴリズムの提案の中でSVGについての説明がありました。 -
モデルベース強化学習における方策ネットワーク手法の活用
モデルベース強化学習の話全般とPETSをベースにしたPOPLIN手法の提案(論文)
近似モデルの学習(独自モデル)
第10回で書いた近似モデルをそのまま表現しました。
報酬関数$R_{\eta}(s,a)$は回帰問題、状態遷移関数 $T_{\eta}$(s'|s,a) と終了関数 $D_{\eta}(d|s,a)$ は確率密度分布の推定問題として学習します。
今回の実装では以下のようにモデル化しました。
| 対象 | 入力 | 出力 | モデル化 |
|---|---|---|---|
| 状態遷移関数 | (状態,アクション) | 次の状態の正規分布 | ニューラルネットワーク |
| 報酬関数 | (状態,アクション) | 得られる報酬(の期待値) | ニューラルネットワーク |
| 終了関数 | (状態,アクション) | 終了かどうか | ランダムフォレスト |
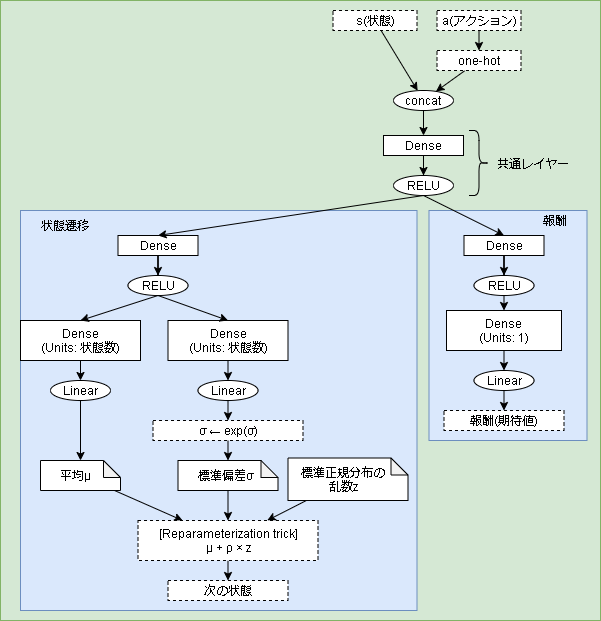
状態遷移関数と報酬関数のモデル
モデルは以下です。
報酬関数はそのまま線形です。
状態遷移関数は正規分布を出力するのでモデルとしては平均と標準偏差を出力しています。
状態遷移関数から実際に次の状態を出力する場合に乱数の処理が入るので Reparameterization trick も使用しています。(第8回を参考)
コードは以下です。
class _A_MDP_trans_reward(keras.Model):
def __init__(self, env):
super().__init__()
self.batch_size = 32
dense_units = 16
activation = "relu"
# 共通レイヤー
self.d1 = keras.layers.Dense(dense_units, activation=activation)
# rewardレイヤー
self.d2_reward = keras.layers.Dense(dense_units, activation=activation)
self.o_reward = keras.layers.Dense(1, activation="linear")
# 遷移レイヤー
self.d2_trans = keras.layers.Dense(dense_units, activation=activation)
self.o_trans_mean = keras.layers.Dense(env.observation_space.shape[0], activation="linear")
self.o_trans_stddev = keras.layers.Dense(env.observation_space.shape[0], activation="linear")
# optimizer
self.optimizer = Adam(learning_rate=0.01)
# Forward pass
def call(self, states, actions, training=False):
x = tf.concat([states, actions], axis=1)
x = self.d1(x)
#--- reward
reward = self.d2_reward(x)
reward = self.o_reward(reward)
#--- trans
t = self.d2_trans(x)
mean = self.o_trans_mean(t)
stddev = self.o_trans_stddev(t)
# σ > 0 になるように変換(指数関数)
stddev = tf.exp(stddev)
return reward, mean, stddev
# 次の状態を返す
def sample_next_state(self, mean, stddev):
# Reparameterization trick
normal_random = tf.random.normal(mean.shape, mean=0., stddev=1.)
next_states = mean + stddev * normal_random
return next_states
# モデルを更新する
def update(self, state, n_state, action, reward):
# ミニバッチ
idx = np.random.randint(0, len(state), self.batch_size)
state_batch = state[idx]
n_state_batch = n_state[idx]
action_batch = action[idx]
reward_batch = reward[idx].reshape(-1, 1)
# 勾配を計算
with tf.GradientTape() as tape:
pred_reward, mean, stddev = self(state_batch, action_batch, training=True)
pred_next_states = self.sample_next_state(mean, stddev)
# MSE
reward_loss = tf.reduce_mean(tf.square(reward_batch - pred_reward))
trans_loss = tf.reduce_mean(tf.square(n_state_batch - pred_next_states))
loss = reward_loss + trans_loss
grads = tape.gradient(loss, self.trainable_variables)
self.optimizer.apply_gradients(zip(grads, self.trainable_variables))
return trans_loss.numpy(), reward_loss.numpy()
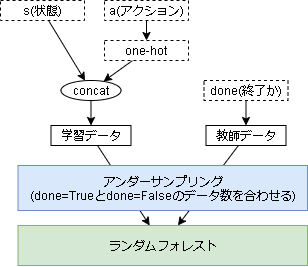
終了関数のモデル
終了関数は2値分類の学習となります。(終了するか終了しないかの学習)
ただ、そのまま学習しようとすると失敗しました。
理由は簡単で不均衡データを学習するからです。
ようするに終了するというデータに対して終了しないというデータが圧倒的に多くなります。
今回の実装では不均衡データに対してアンダーサンプリング(多いほうのデータを減らす)を適用し、ランダムフォレストで学習しています。
import sklearn.ensemble
import sklearn.metrics
import imblearn.under_sampling
class _A_MDP_done():
def __init__(self, env):
# ランダムフォレストを定義
self.model = sklearn.ensemble.RandomForestClassifier()
self.is_fit = False # 1回でもがくしゅうしていないとエラー
# Forward pass
def __call__(self, states, actions, training=False):
if not self.is_fit:
# 学習していない場合はとりあえずFalseを返す
return np.full((len(states), 1), False)
# 入力データを作成
x_all = np.append(states, actions, axis=1)
# 予測
done = self.model.predict(x_all)
return done.reshape((-1, 1))
# モデルの更新
def update(self, x_state, x_action, done):
# 入力データを作成
x_all = np.append(x_state, x_action, axis=1)
# 教師データ
y_all = done
# 終了したデータがない場合は更新をskip
if sum(y_all==True) == 0:
return 0
# アンダーサンプリング
# 終了データ 100、終了しないデータ、3000
# → 終了データ 100、終了しないデータ、100
under = imblearn.under_sampling.RandomUnderSampler(
sampling_strategy ={
0 : sum(y_all==True),
1 : sum(y_all==True)
})
x_train_under, y_train_under = under.fit_resample(x_all, y_all)
# モデルを学習
self.model.fit(x_train_under, y_train_under)
self.is_fit = True
# 評価は適合率(precision)
done_loss = sklearn.metrics.precision_score(y_all, self.model.predict(x_all))
return done_loss
ハイパーパラメータのチューニングは特にしていません。
A_MDPモデル
上記2つのモデルを管理するクラスを作成しています。
アルゴリズムには関係ないのでコードのみ載せておきます。
class A_MDP():
def __init__(self, env, buffer_size=1024):
# 終了関数モデルの更新間隔
self.done_update_interval = 50
# 各モデル
self.reward_state_model = _A_MDP_trans_reward(env)
self.done_model = _A_MDP_done(env)
# 経験キュー
self.experiences = collections.deque(maxlen=buffer_size)
# アクション情報
self.nb_actions = env.action_space.n
self.env_actions = [i for i in range(self.nb_actions)]
self.update_count = 0
# 全状態を返す
# 実際は全情報は不明なので、経験キューにある情報を返す
@property
def states(self):
return [e["state"] for e in self.experiences]
# 全アクションを返す
@property
def actions(self):
return self.env_actions
# 実環境からの経験を追加
def add(self, experience):
self.experiences.append(experience)
# 近似モデルを更新する
def update(self):
# データ整形
states = np.asarray([e["state"] for e in self.experiences])
n_states = np.asarray([e["n_state"] for e in self.experiences])
actions = np.asarray([e["action"] for e in self.experiences])
rewards = np.asarray([e["reward"] for e in self.experiences])
done_list = np.asarray([e["done"] for e in self.experiences])
# action one-hot
actions_onehot = np.identity(self.nb_actions)[actions]
# doneモデルの更新
# データにあまり変更がない状態で更新しても効果が薄いので、ある程度間隔を置いて更新する
if self.update_count % self.done_update_interval == 0:
done_loss = self.done_model.update(states, actions_onehot, done_list)
self.history_done_loss_episode.append(done_loss)
# trans,rewardモデルの更新
trans_loss, reward_loss = self.reward_state_model.update(states, n_states, actions_onehot, rewards)
self.history_train_loss_episode.append(trans_loss)
self.history_reward_loss_episode.append(reward_loss)
self.update_count += 1
# 予測した次の状態を返す
def sample_step(self, state, action):
# action one-hot
action_onehot = np.identity(self.nb_actions)[action]
rewards, mean, stddev = self.reward_state_model(states, actions)
n_states = self.reward_state_model.sample_next_state(mean, stddev)
done = self.done_model(states, actions)
return n_states, rewards, done
Q学習クラス
プランニングの手法はQ学習としています。
class Q_learning():
def __init__(self, env):
self.nb_actions = env.action_space.n
self.epsilon = 0.1
self.test_epsilon = 0.001
self.batch_size = 32 # バッチサイズ
self.gamma = 0.9 # 割引率
# Qモデル
c = input_ = keras.layers.Input(shape=env.observation_space.shape)
c = keras.layers.Dense(16, activation="relu")(c)
c = keras.layers.Dense(16, activation="relu")(c)
c = keras.layers.Dense(self.nb_actions, activation="linear")(c)
self.q_model = keras.Model(input_, c)
self.q_model.compile(optimizer=Adam(learning_rate=0.01), loss='mse')
def sample_action(self, state, training=False):
if training:
epsilon = self.epsilon
else:
epsilon = self.test_epsilon
if np.random.random() < epsilon:
# epsilonより低いならランダムに移動
return np.random.randint(self.nb_actions)
else:
# Q値が最大のアクションを実行
q = self.q_model(state.reshape(1,-1))[0].numpy()
return np.argmax(q)
# 実環境から学習
def update_from_env(self, experiences):
# ランダムに経験を取得してバッチを作成
batchs = random.sample(experiences, self.batch_size)
# データ形式を変形
states = np.asarray([e["state"] for e in batchs])
actions = np.asarray([e["action"] for e in batchs])
n_states = np.asarray([e["n_state"] for e in batchs])
rewards = np.asarray([e["reward"] for e in batchs])
done_list = np.asarray([e["done"] for e in batchs])
return self._update_model(states, actions, n_states, rewards, done_list)
# 近似モデルから学習
def update_from_a_mdp(self, a_mdp):
# ランダムに状態とアクションを取得
states = random.sample(a_mdp.states, self.batch_size)
actions = [ random.sample(a_mdp.actions, 1)[0] for _ in range(self.batch_size)]
states = np.asarray(states)
actions = np.asarray(actions)
# 予測
n_states, rewards, done_list = a_mdp.sample_step(states, actions)
return self._update_model(states, actions, n_states, rewards, done_list)
# 学習
def _update_model(self, states, actions, n_states, rewards, done_list):
# Q値をだす
q = self.q_model(states).numpy()
n_q = self.q_model(n_states).numpy()
# 各バッチでQ値を計算
for i in range(len(states)):
action = actions[i]
reward = rewards[i]
if done_list[i]:
q[i][action] = reward
else:
q[i][action] = reward + self.gamma * np.max(n_q[i])
# モデルをミニバッチ学習する
q_loss = self.q_model.train_on_batch(states, q)
メインフロー
メインフローのコードです。
env = gym.make("CartPole-v0")
buffer_size = 2048
warmup_size_a_mdp = 128
warmup_size_ql = 256
epochs = 300
# 近似モデル
a_mdp = A_MDP(env, buffer_size)
# Q学習
q_learning = Q_learning(env)
# 学習ループ
for episode in range(epochs):
state = np.asarray(env.reset())
done = False
total_reward = 0
step = 0
while not done:
action = q_learning.sample_action(state, training=True)
n_state, reward, done, _ = env.step(action)
n_state = np.asarray(n_state)
step += 1
total_reward += reward
# 経験を保存する
a_mdp.add({
"state": state,
"action": action,
"reward": reward,
"n_state": n_state,
"done": done,
})
state = n_state
# 近似モデルの学習
if len(a_mdp.experiences) == warmup_size_a_mdp-1:
print("train start A_MDP")
if len(a_mdp.experiences) >= warmup_size_a_mdp:
a_mdp.update()
# Q学習
if len(a_mdp.experiences) == warmup_size_ql-1:
print("train start Qlearning")
if len(a_mdp.experiences) >= warmup_size_ql:
#q_learning.update_from_env(a_mdp.experiences)
q_learning.update_from_a_mdp(a_mdp)
env.close()
結果
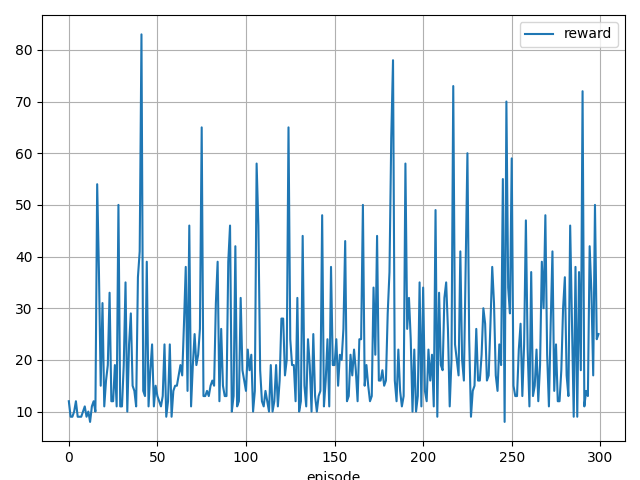
- 近似モデルを用いない場合の学習例
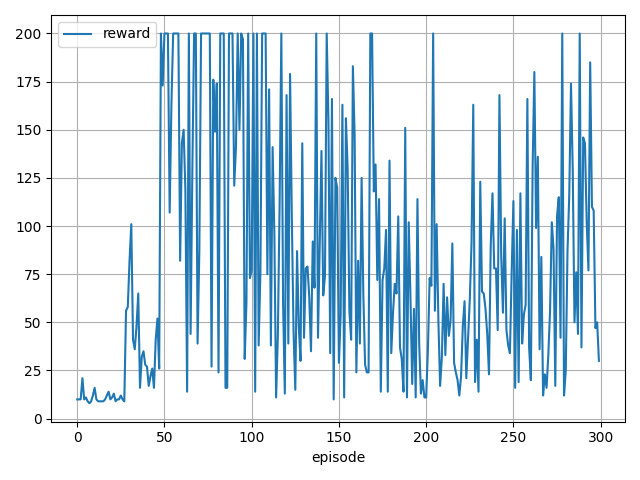
- 近似モデルのみで学習した場合
近似モデルを用いない場合と同じ学習傾向ですね。
近似モデルでも学習に問題なさそうです。
- 近似モデルのloss
状態遷移関数と報酬関数は問題なく学習できていそうです。
ただ終了関数はあまり学習できていません。(正解率10%ほど)
けどこれがないとQ学習も進まなかったので、正解率は低いですが重要な役割を持っていそうです。
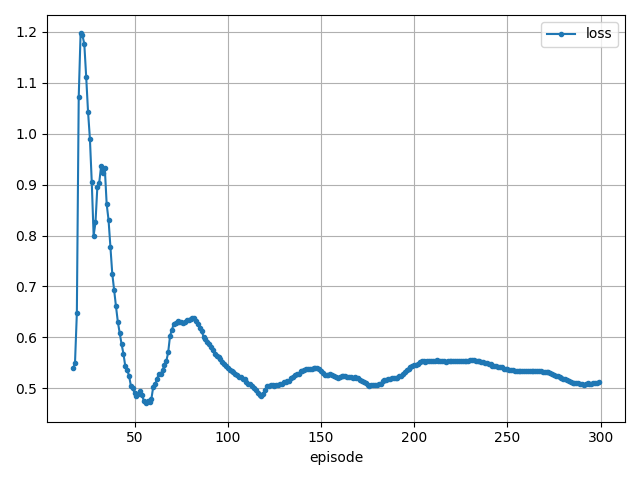
- Q学習のloss
lossから見てもちゃんと学習できていそうですね。
モデルベース強化学習の論文ベースの近似モデル
Neural Network Dynamics for Model-Based Deep Reinforcement Learning with Model-Free Fine-Tuning
上記論文のコードを参考にしています。
間違っているかも知れませんが、論文内では状態遷移関数のみが言及されているように思います。
報酬関数は環境から与えられているものとし、終了関数については特に触れられていません。
ですので、報酬関数と終了関数は自作のものを使います。
状態遷移関数モデル
モデルとしては今と次の状態の差分を学習します。
また学習時にはガウスノイズをまぜて学習させます。
また論文と違う点ですが、論文では多分バッチの学習は連続状態を想定していそうですが、実装ではランダムに取り出して学習しています。
class _A_MDP_trans(keras.Model):
def __init__(self, env):
super().__init__()
self.batch_size = 32
dense_units = 16
activation = "relu"
# 共通レイヤー
self.d1 = keras.layers.Dense(dense_units, activation=activation)
self.d2 = keras.layers.Dense(dense_units, activation=activation)
self.o = keras.layers.Dense(env.observation_space.shape[0], activation="linear")
# optimizer
self.optimizer = Adam(learning_rate=0.01)
# Forward pass
def call(self, states, actions, training=False):
x = tf.concat([states, actions], axis=1)
x = self.d1(x)
x = self.d2(x)
diff_next_state = self.o(x)
return diff_next_state
# 次の状態を返す
def sample_next_state(self, state, action):
diff_next_state = self(state, action)
next_state = state + diff_next_state
return next_state
# モデルを更新する
def update(self, state, n_state, action, reward):
# ミニバッチ
idx = np.random.randint(0, len(state), self.batch_size)
state_batch = state[idx]
n_state_batch = n_state[idx]
action_batch = action[idx]
diff_state = n_state_batch - state_batch
# ガウスノイズ
state_batch += np.random.normal(state_batch.mean(axis=0), state_batch.std(axis=0), size=state_batch.shape)
diff_state += np.random.normal(diff_state.mean(axis=0), diff_state.std(axis=0), size=diff_state.shape)
# 勾配を計算
with tf.GradientTape() as tape:
mse = 0
for i in range(len(state_batch)):
pred_diff_state = self(
state_batch[i].reshape((1, -1)),
action_batch[i].reshape((1, -1)),
training=True)
# MSE
mse += tf.reduce_mean(tf.square(diff_state[i] - pred_diff_state))
loss = mse / len(state)
grads = tape.gradient(loss, self.trainable_variables)
self.optimizer.apply_gradients(zip(grads, self.trainable_variables))
return loss.numpy()
MPC(Model Predictive Control)
モデル予測制御(MPC: Model Predictive Control)は未来をシミュレーションしながら最適な行動を予測する制御方法です。
現在の状態から近似モデルを用いて最適なアクションを選ぶ事をMPCというらしいです。
今回はMPCのアルゴリズムとして、各アクションから始めるランダムなアクション長を生成します。
それらをシミュレーションし、得た割引報酬が一番多いアクションを採用する方法を取ります。
def sample_action(a_mdp, init_satate):
nb_actions = アクション数
gamma = 0.9 # 割引率
step_length = 3 # アクション長
# 各アクションを評価
action_reward = []
for a in range(nb_actions):
# ランダムにアクション長を作成、先頭は今回のアクション
actions = [a]
actions.extend([random.randint(0, nb_actions-1) for _ in range(step_length-1)])
# そのアクションを使ってシミュレーション
step = 0
state = init_satate.reshape((1, -1))
total_reward = 0
for action in actions:
action = np.asarray([action])
# 近似モデルから次の状態を予測
reward, n_state, done = a_mdp.sample_step(state, action)
reward = reward.numpy()[0][0]
done = done[0][0]
total_reward += (gamma ** step) * reward
step += 1
if done:
break
state = n_state
action_reward.append(total_reward)
# 最大のアクションを選択
return np.argmax(action_reward)
実行結果
MPCがランダムな予測なので学習はできていません。。。
PETS
PETS(Probabilistic ensembles with trajectory sampling)は紹介のみとなります。
PETSはPEとTSで分かれています。
まずPEです。
今までの手法は状態の予測を1つのモデルで予測していました。
しかし、複数のモデルを学習させてその平均結果を用いて状態を予測する手法がPEとなります。
(アンサンブル学習)
次にTSですが、MPC部分となります。
ランダムにアクション列を決めるのではなく交差エントロピー法という手法で決める方法です。
交差エントロピー法は、確率分布を $P_r(\theta)$ とした場合、この確率分布に従って複数のアクション列を生成します。
$$ a_t = P_r(\theta_t) $$
複数のアクション列を実際にシミュレーションし、得られた報酬が一番いいアクション列で確率分布を更新する手法が交差エントロピー法です。
- Deep Reinforcement Learning in a Handful of Trials using Probabilistic Dynamics Models(論文)
- モデルベース強化学習における方策ネットワーク手法の活用
あとがき
後半少し手抜きしました。
意外にまとまった資料がないものですね。