最適化アルゴリズムを実装していくぞ（遺伝的アルゴリズム）

はじめに

最適化アルゴリズムの実装シリーズです。
まずは概要を見てください。

コードはgithubにあります。

遺伝的アルゴリズム

概要

遺伝的アルゴリズム(Genetic Algorithm: GA)は、遺伝子による進化をもとに作られたアルゴリズムです。

アルゴリズム

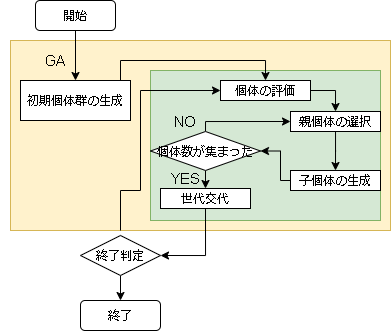
フローとしては各世代(step)で以下のことを繰り返します。

1. 親個体の選択（適応度の高い個体を優先）
2. 親個体をもとに子個体を生成
3. 子個体数が一定以上になったら親世代を子世代に変更する

子個体の生成には、交叉という親個体の特徴を受け継いだ個体を生成するのが特徴です。

• アルゴリズムのフロー

• 用語の対応

問題	遺伝的アルゴリズム
入力値の配列	個体
入力値	(個体が持っている)遺伝子
評価値	個体の環境への適応度

• コード内の変数について

変数名	意味	所感
problem	任意の問題のクラス（問題編を参照）
individual_max	個体数
mutation	突然変異の確率	大きいほどランダム探索が多くなる

親個体の選択

全個体から2つの個体を選びます。
選ぶ方法はいくつかありますが、ルーレット方式とランキング方式を実装しています。

また、実装を簡単にするために、2つの個体の重複は考慮していません。
(なので同じ個体が選ばれる可能性があります)

ルーレット方式

個体の評価値が高いものほど選ばれる確率が高くなる選択方法です。
例えば個体の評価値が
1番目：9
2番目：1
とあった場合、1番目が選ばれる確率は90%で、2番目が選ばれる確率は10%になります。

算出方法は、単純な累積和による選択方法を実装しています。

評価値が負の場合ですが、累積和では最小の値が選ばれない問題があるので、
最小の値が負の場合は0からの距離を重みとして計算しています。

コードの実装例は以下です。

import random
def selectRoulette(individuals):
    # individuals が各個体の配列を表しています。

    # 全個体の評価値を配列に入れる
    weights = [x.getScore() for x in individuals]

    w_min = min(weights)
    if w_min < 0:
        # 最小が負の場合は基準を0→w_min→に変更
        weights = [ w + (-w_min*2) for w in weights]
    
    # 重さの合計で乱数を出す
    r = random.random() * sum(weights)

    # 重さを順番に見ていき、乱数以下ならそのindexが該当
    num = 0
    for i, weights in enumerate(weights):
        num += weight
        if r <= num:
            return individuals[i]
    
    assert False, "ここには来ないはず"

ランキング方式

個体の評価値の順位をもとに選択する方法です。
例えば個体の評価値が
1番目：9（１位）
2番目：1（２位）
とあった場合、1番目が選ばれる確率は(2/3)=66.7%で、2番目が選ばれる確率は33.3%になります。

算出方法は逆関数法です。

コードの実装例は以下です。

import math
import random

# 等差数列の和
def arithmetic_sequence_sum(size, start=1, diff=1):
    return size*( 2*start + (size-1)*diff )/2

# 等差数列の和の逆関数
def arithmetic_sequence_sum_inverse(val, start=1, diff=1):
    if diff == 0:
        return val
    t = diff-2*start + math.sqrt((2*start-diff)**2 + 8*diff*val)
    return t/(2*diff)

def selectRanking(individuals):
    # 順位のためにソートする
    # 0 が最下位で len(individuals)-1 が1位
    individuals.sort(key=lambda x: x.getScore())

    # 個体の数
    size = len(individuals)

    # 全順位の合計値を出す
    num = arithmetic_sequence_sum(size)

    # 合計値から乱数を出す
    r = random.random() * num

    # 逆関数で順位を求める
    index = int(arithmetic_sequence_sum_inverse(r))

    return individuals[index]

交叉

交叉では、2つの個体(親個体)から新しい2つの個体(子個体)を生成します。
交叉にもいろいろ種類がありますが、汎用性を重視し一様交叉のみ実装します。

一様交叉は個体の遺伝子に対して、50%の確率で親の遺伝子を入れ替えるといった操作をします。

また、各遺伝子は任意の確率で突然変異(親の遺伝子情報を引き継がない)させます。

コードの実装例は以下です。

import math
import random

def cross(parent1, parent2):
    problem = 任意の問題のクラス（問題編を参照）
    mutation = 0.1  # 突然変異の確率

    genes1 = parent1.getArray()  # 親1の遺伝子情報
    genes2 = parent2.getArray()  # 親2の遺伝子情報

    # 子の遺伝子情報
    c_genes1 = []
    c_genes2 = []
    for i in range(len(genes1)):  # 各遺伝子を走査
        # 50%の確率で遺伝子を入れ替える
        if random.random() < 0.5:
            c_gene1 = genes1[i]
            c_gene2 = genes2[i]
        else:
            c_gene1 = genes2[i]
            c_gene2 = genes1[i]

        # 突然変異
        if random.random() < mutation:
            c_gene1 = problem.randomVal()  # ランダムな値にする
        if random.random() < mutation:
            c_gene2 = problem.randomVal()  # ランダムな値にする

        c_genes1.append(c_gene1)
        c_genes2.append(c_gene2)

    # 遺伝子をもとに子を生成
    childe1 = problem.create(c_genes1)
    childe2 = problem.create(c_genes2)
    return childe1, childe2

その他

エリート戦略

次世代への子の生成ですが、親世代で一番評価が高い親個体をそのまま次の世代に持ち越すことをエリート戦略といいます。
エリートを残すので交叉による最適解の低下が防げますが、エリートの遺伝子が多く残るので局所解から抜け出しにくい（多様性が失われる）可能性があります。

コード全体

import math
import random

# 等差数列の和
def arithmetic_sequence_sum(size, start=1, diff=1):
    return size*( 2*start + (size-1)*diff )/2

# 等差数列の和の逆関数
def arithmetic_sequence_sum_inverse(val, start=1, diff=1):
    if diff == 0:
        return val
    t = diff-2*start + math.sqrt((2*start-diff)**2 + 8*diff*val)
    return t/(2*diff)

class GA():
    def __init__(self, 
            individual_max,   # 個体数
            save_elite=True,  # エリートを生存させるか
            select_method="ranking",  # 選択の方式(roulette or ranking)
            mutation=0.1,     # 突然変異の確率
        ):
        self.individual_max = individual_max

        self.save_elite = save_elite
        self.select_method = select_method
        self.mutation = mutation

    def init(self, problem):
        self.problem = problem

        # 各個体を生成します。
        self.best_individual = None
        self.individuals = []
        for _ in range(self.individual_max):
            o = problem.create()
            self.individuals.append(o)

            # 最高評価の個体を保存
            if self.best_individual is None or self.best_individual.getScore() < o.getScore():
                self.best_individual = o

        # 適応度でソート
        self.individuals.sort(key=lambda x: x.getScore())


    def step(self):

        # 次世代
        next_individuals = []
        
        if self.save_elite:
            # エリートを生存させる
            next_individuals.append(self.individuals[-1].copy())
        
        for _ in range(self.individual_max):  # whileでもいいけど安全のため
            # 個数が集まるまで繰り返す
            if len(next_individuals) > self.individual_max:
                break

            # 選択する
            if self.select_method == "roulette":
                o1 = self._selectRoulette()
                o2 = self._selectRoulette()
            elif self.select_method == "ranking":
                o1 = self._selectRanking()
                o2 = self._selectRanking()
            else:
                raise ValueError()

            # 交叉する
            new_o1, new_o2 = self._cross(o1, o2)

            # 次世代に追加
            next_individuals.append(new_o1)
            next_individuals.append(new_o2)
        
        # 世代交代
        self.individuals = next_individuals

        # 適応度でソート
        self.individuals.sort(key=lambda x: x.getScore())

        # 最高評価を保存
        if self.best_individual.getScore() < self.individuals[-1].getScore():
            self.best_individual = self.individuals[-1]


    def _selectRoulette(self):
        # 全個体の評価値を配列に入れる
        weights = [x.getScore() for x in self.individuals]

        w_min = min(weights)
        if w_min < 0:
            # 最小が負の場合は基準を0→w_min→に変更
            weights = [ w + (-w_min*2) for w in weights]
        
        # 重さの合計で乱数を出す
        r = random.random() * sum(weights)

        # 重さを順番に見ていき、乱数以下ならそのindexが該当
        num = 0
        for i, weights in enumerate(weights):
            num += weight
            if r <= num:
                return self.individuals[i]
        
        raise ValueError()


    def _selectRanking(self):
        # 個体の数
        size = len(self.individuals)

        # 全順位の合計値を出す
        num = arithmetic_sequence_sum(size)

        # 合計値から乱数を出す
        r = random.random() * num

        # 逆関数で順位を求める
        index = int(arithmetic_sequence_sum_inverse(r))
        return self.individuals[index]


    def _cross(self, parent1, parent2):
        genes1 = parent1.getArray()  # 親1の遺伝子情報
        genes2 = parent2.getArray()  # 親2の遺伝子情報

        # 子の遺伝子情報
        c_genes1 = []
        c_genes2 = []
        for i in range(len(genes1)):  # 各遺伝子を走査
            # 50%の確率で遺伝子を入れ替える
            if random.random() < 0.5:
                c_gene1 = genes1[i]
                c_gene2 = genes2[i]
            else:
                c_gene1 = genes2[i]
                c_gene2 = genes1[i]

            # 突然変異
            if random.random() < self.mutation:
                c_gene1 = self.problem.randomVal()
            if random.random() < self.mutation:
                c_gene2 = self.problem.randomVal()

            c_genes1.append(c_gene1)
            c_genes2.append(c_gene2)

        # 遺伝子をもとに子を生成
        childe1 = self.problem.create(c_genes1)
        childe2 = self.problem.create(c_genes2)
        return childe1, childe2

パラメータフリーGA（PfGA）

参考サイトで見つけた、パラメータ設定を不要とするGAです。
面白そうなので実装してみました。

参考：パラメータフリーGA（PfGA）

基本的にはGAと同じなのですが、個体を集めた集団(局所集団)を用いることで個体数を限定せずにGAを行います。

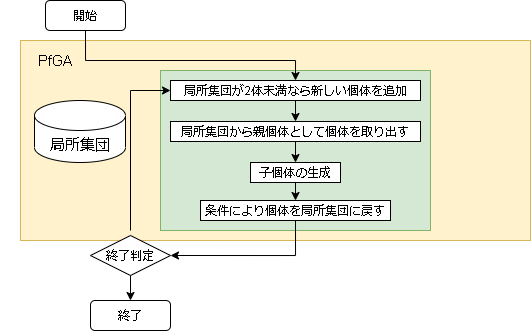
• アルゴリズムのフロー

局所集団

局所集団は最初に2体個体を入れます。
その後、局所集団からランダムに2体を取り出し、その2体で交叉して子を2体作ります。
その後4体の個体の評価値から、以下の条件で局所集団に戻します。

1. 子2個体がともに親の2個体より良かった場合は、子2個体及び適応度の良かった方の親個体計3個体が局所集団に戻り、局所集団数は1増加する。
2. 子2個体がともに親の2個体より悪かった場合は、親2個体のうち良かった方のみが局所集団に戻り、局所集団数は1減少する。
3. 親2個体のうちどちらか一方のみが子2個体より良かった場合は、親2個体のうち良かった方と子2個体のうち良かった方が局所集団に戻り、局所集団数は変化しない。
4. 子2個体のうちどちらか一方のみが親2個体より良かった場合は、子2個体のうち良かった方のみが局所集団に戻り、全探索空間からランダムに1個体選んで局所集団に追加する。局所集団数は変化しない。

コード全体

コード全体です。
ただ、パラメータフリーといいつつ突然変異の確率は設定がいるような…。

import math
import random

class PfGA():
    def __init__(self, mutation=0.1):
        self.mutation = mutation  # 突然変異の確率

    def init(self, problem):
        self.problem = problem

        # 最初に2体生成
        self.individuals = []  # 局所集団(local individuals)
        for _ in range(2):
            self.individuals.append(problem.create())


    def step(self):

        # 2未満なら追加
        if len(self.individuals) < 2:
            self.individuals.append(self.problem.create())

        # ランダムに2個取り出す
        p1 = self.individuals.pop(random.randint(0, len(self.individuals)-1))
        p2 = self.individuals.pop(random.randint(0, len(self.individuals)-1))

        # 子を作成
        c1, c2 = self._cross(p1, p2)
        
        if p1.getScore() < p2.getScore():
            p_min = p1
            p_max = p2
        else:
            p_min = p2
            p_max = p1
        if c1.getScore() < c2.getScore():
            c_min = c1
            c_max = c2
        else:
            c_min = c2
            c_max = c1

        if c_min.getScore() >= p_max.getScore():
            # 子2個体がともに親の2個体より良かった場合
            # 子2個体及び適応度の良かった方の親個体計3個体が局所集団に戻り、局所集団数は1増加する。
            self.individuals.append(c1)
            self.individuals.append(c2)
            self.individuals.append(p_max)
        elif p_min.getScore() >= c_max.getScore():
            # 子2個体がともに親の2個体より悪かった場合
            # 親2個体のうち良かった方のみが局所集団に戻り、局所集団数は1減少する。
            self.individuals.append(p_max)
        elif p_max.getScore() >= c_max.getScore() and p_min.getScore() <= c_max.getScore():
            # 親2個体のうちどちらか一方のみが子2個体より良かった場合
            # 親2個体のうち良かった方と子2個体のうち良かった方が局所集団に戻り、局所集団数は変化しない。
            self.individuals.append(c_max)
            self.individuals.append(p_max)
        elif c_max.getScore() >= p_max.getScore() and c_min.getScore() <= p_max.getScore():
            # 子2個体のうちどちらか一方のみが親2個体より良かった場合
            # 子2個体のうち良かった方のみが局所集団に戻り、全探索空間からランダムに1個体選んで局所集団に追加する。局所集団数は変化しない。
            self.individuals.append(c_max)
            self.individuals.append(self.problem.create())
        else:
            raise ValueError("not comming")


    def _cross(self, parent1, parent2):
        genes1 = parent1.getArray()  # 親1の遺伝子情報
        genes2 = parent2.getArray()  # 親2の遺伝子情報

        # 子の遺伝子情報
        c_genes1 = []
        c_genes2 = []
        for i in range(len(genes1)):  # 各遺伝子を走査
            # 50%の確率で遺伝子を入れ替える
            if random.random() < 0.5:
                c_gene1 = genes1[i]
                c_gene2 = genes2[i]
            else:
                c_gene1 = genes2[i]
                c_gene2 = genes1[i]

            # 突然変異
            if random.random() < self.mutation:
                c_gene1 = self.problem.randomVal()
            if random.random() < self.mutation:
                c_gene2 = self.problem.randomVal()

            c_genes1.append(c_gene1)
            c_genes2.append(c_gene2)

        # 遺伝子をもとに子を生成
        childe1 = self.problem.create(c_genes1)
        childe2 = self.problem.create(c_genes2)
        return childe1, childe2

ハイパーパラメータ例

各問題に対して optuna でハイパーパラメータを最適化した結果です。
最適化の1回の試行は探索時間を2秒間として結果を出しています。
これを100回実行し、最適なハイパーパラメータを optuna に探してもらいました。

• GA

問題	individual_max	mutation	save_elite	select_method
EightQueen	4	0.013873130609831266	True	roulette
function_Ackley	9	0.018218488205681442	True	ranking
function_Griewank	26	0.009297248466797036	True	ranking
function_Michalewicz	46	0.02028018029181716	False	ranking
function_Rastrigin	49	0.00831170762967785	True	ranking
function_Schwefel	11	0.015576469028724699	True	ranking
function_StyblinskiTang	37	0.01095031028776784	False	ranking
LifeGame	12	0.5516471161744092	False	ranking
OneMax	2	0.020901412496510563	True	ranking
TSP	24	0.010664979238406223	True	ranking

• PfGA

問題	mutation
EightQueen	0.03456922411806109
function_Ackley	0.011966812535822609
function_Griewank	0.023555766863728234
function_Michalewicz	0.021882782991433425
function_Rastrigin	0.011938744186117622
function_Schwefel	0.014015707940510776
function_StyblinskiTang	0.020297589468369463
LifeGame	0.7819203713430501
OneMax	0.0008382068017285835
TSP	0.012371041873054364

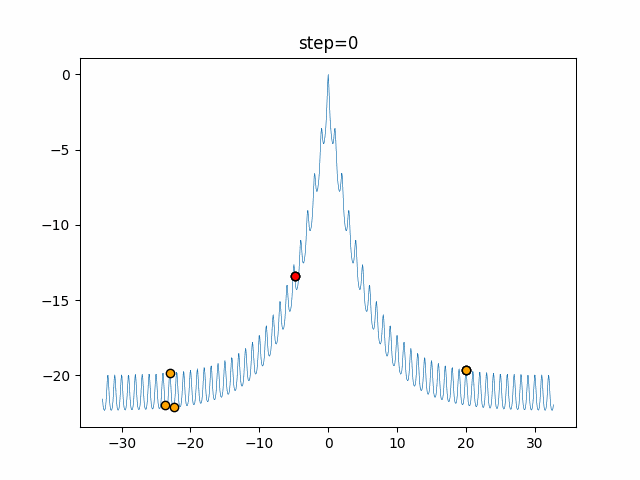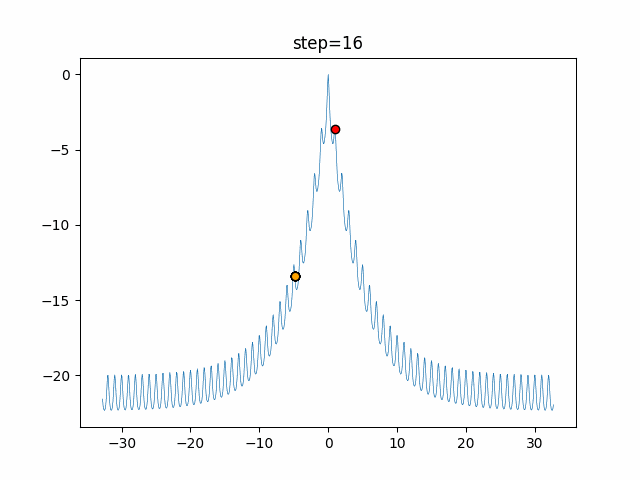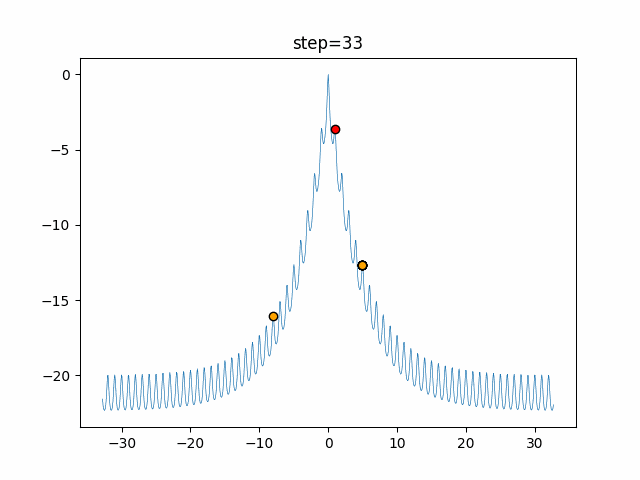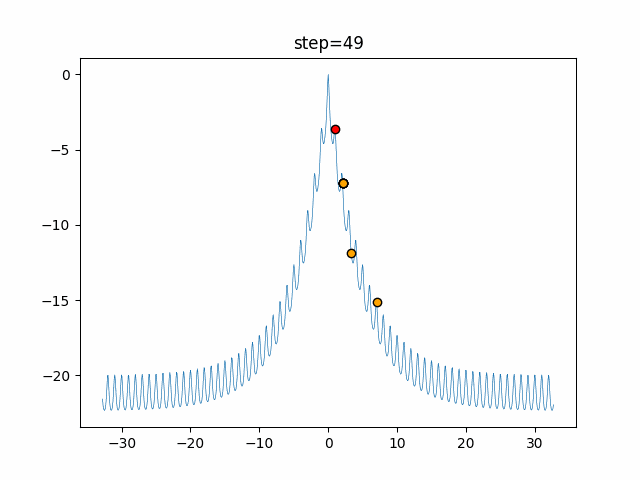
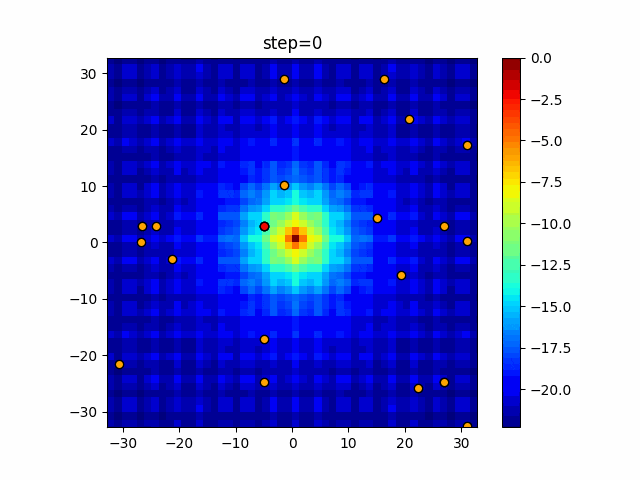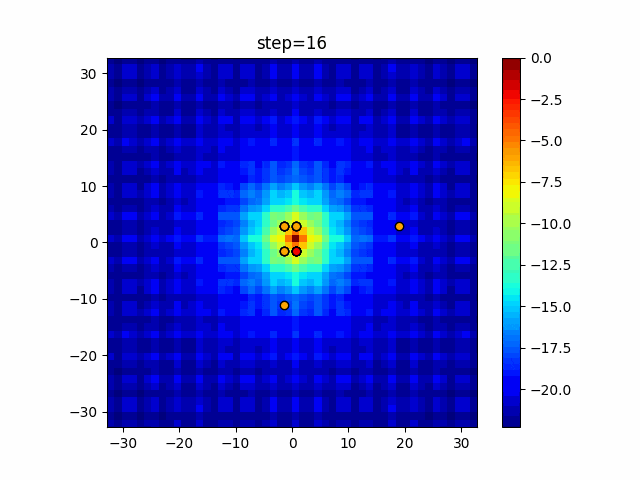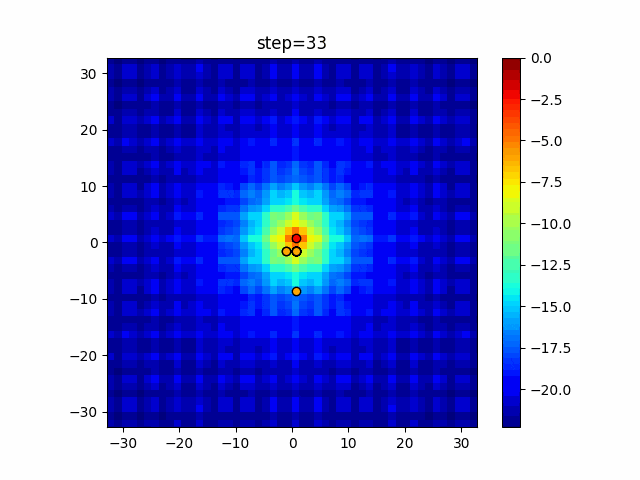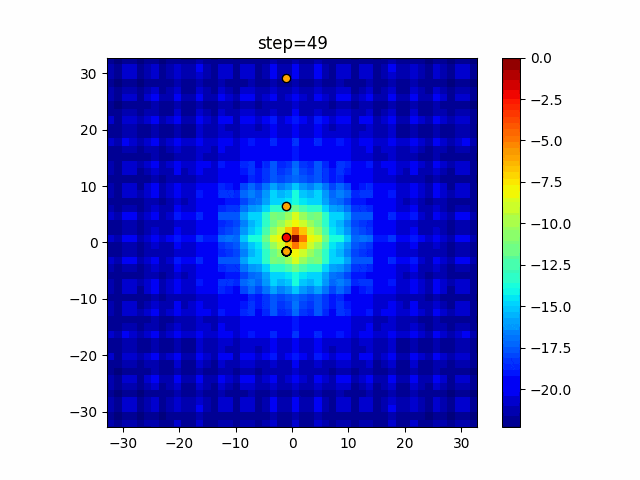
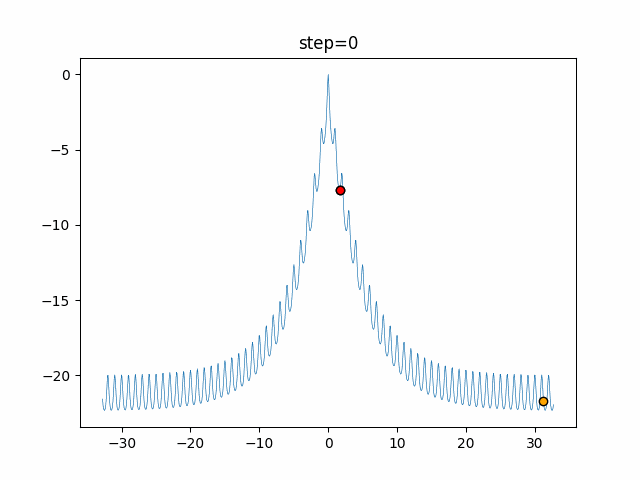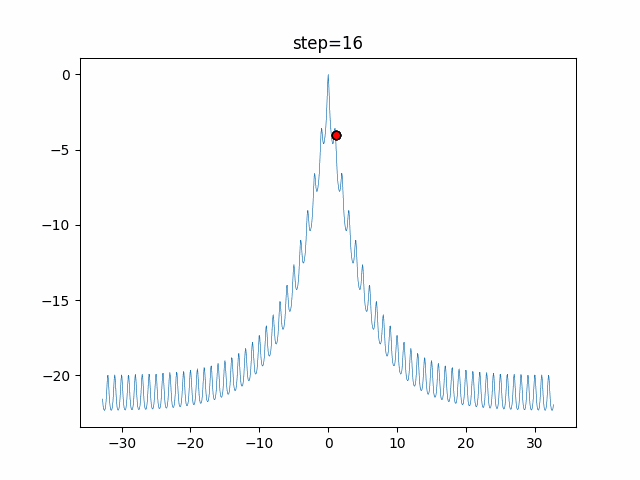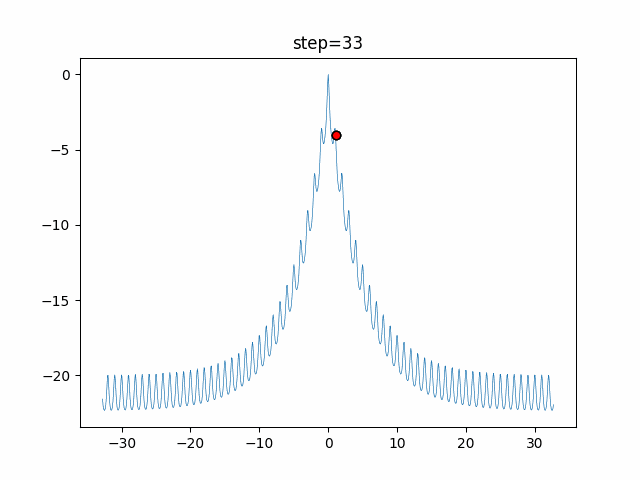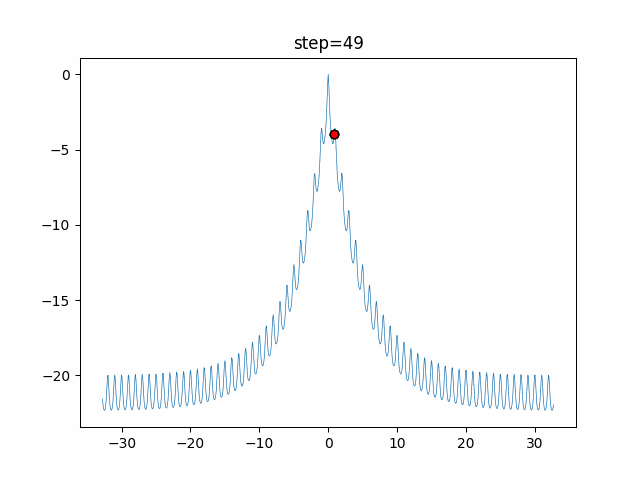
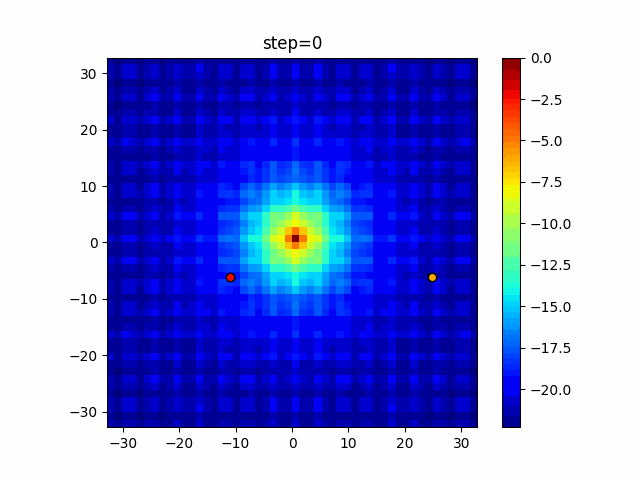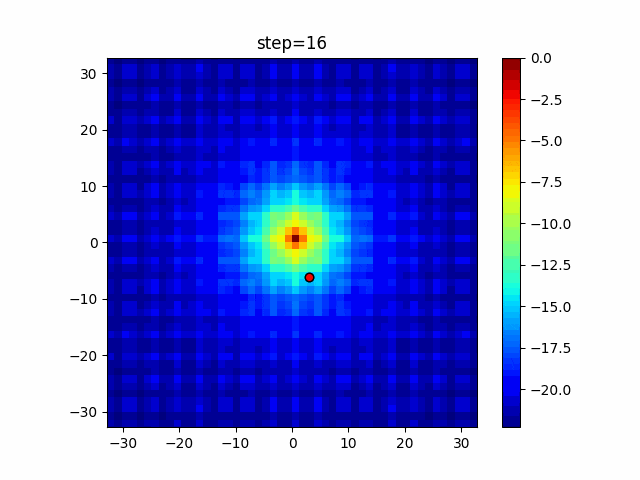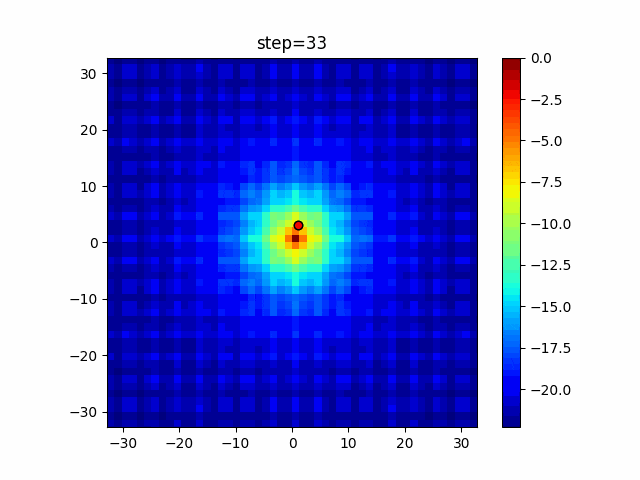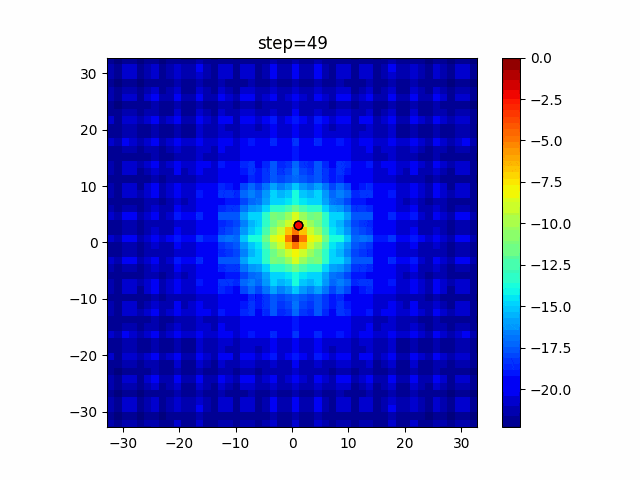
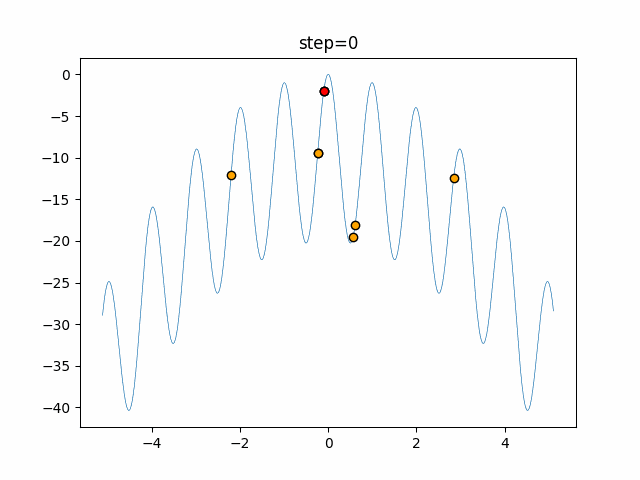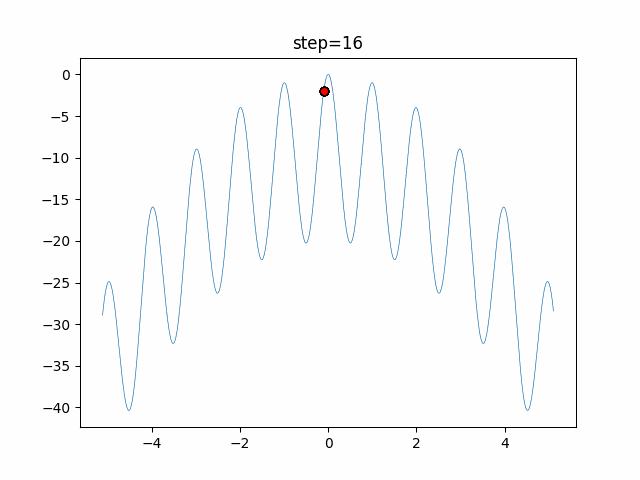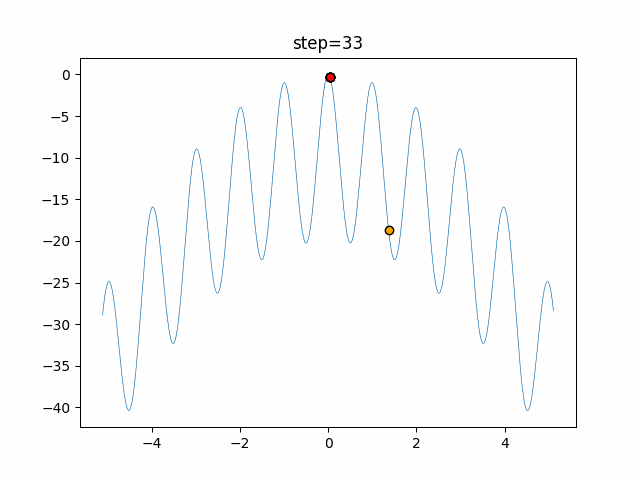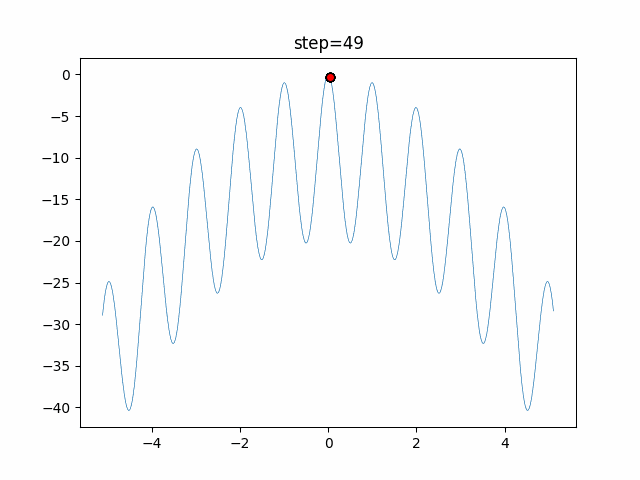
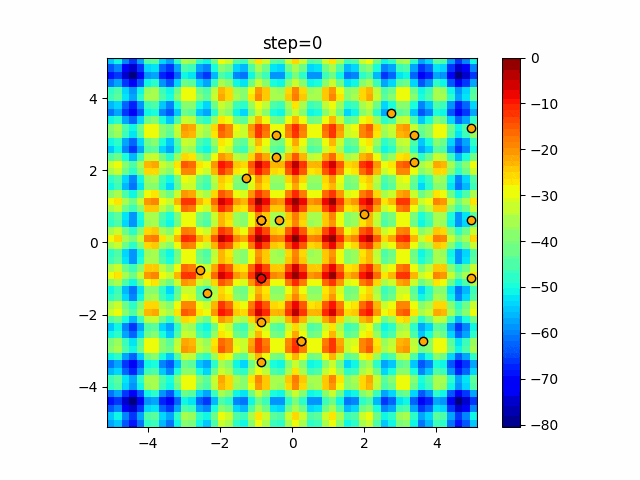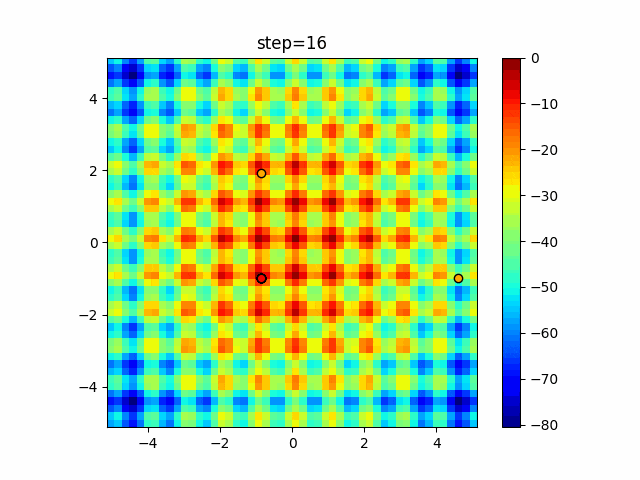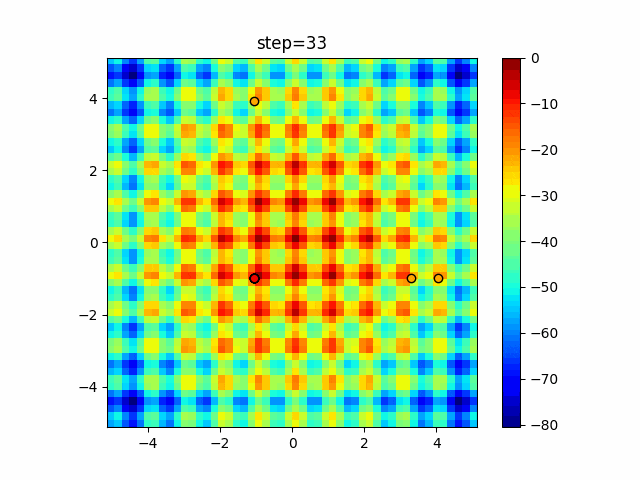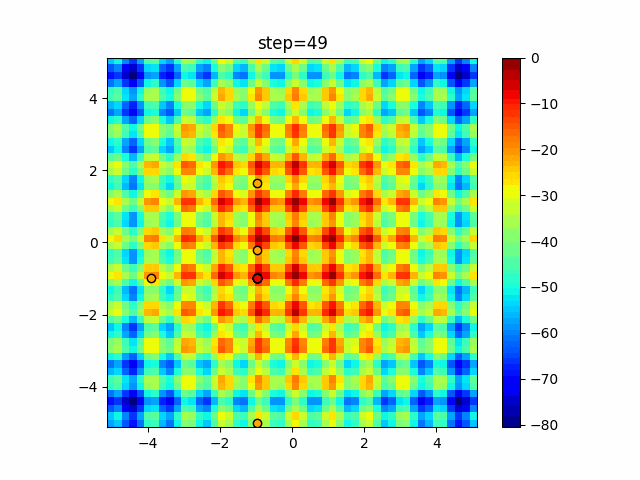
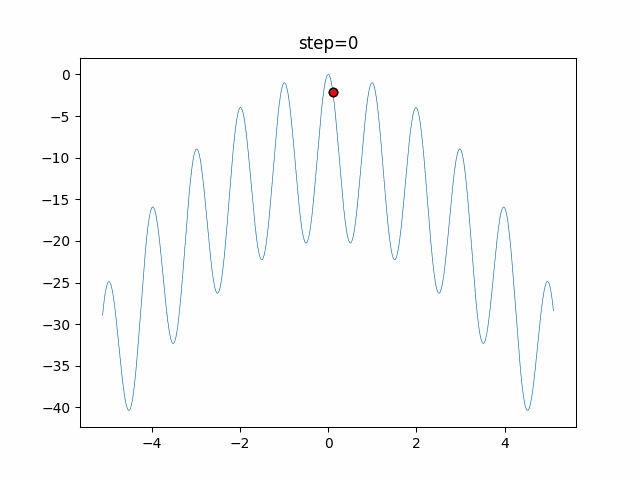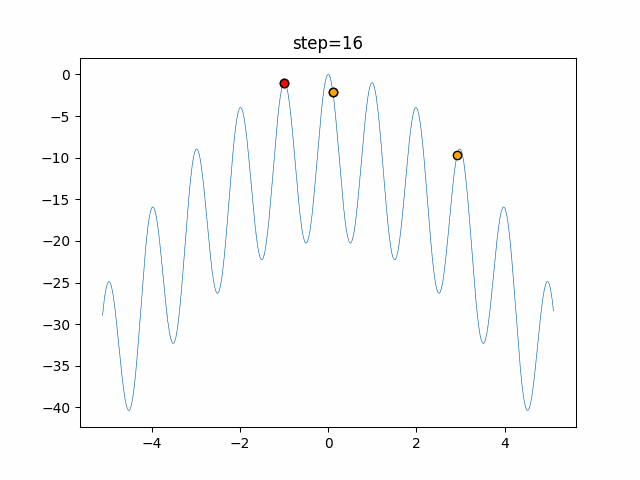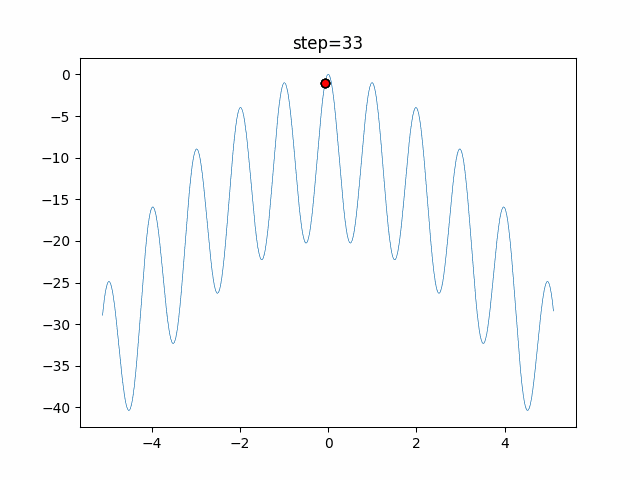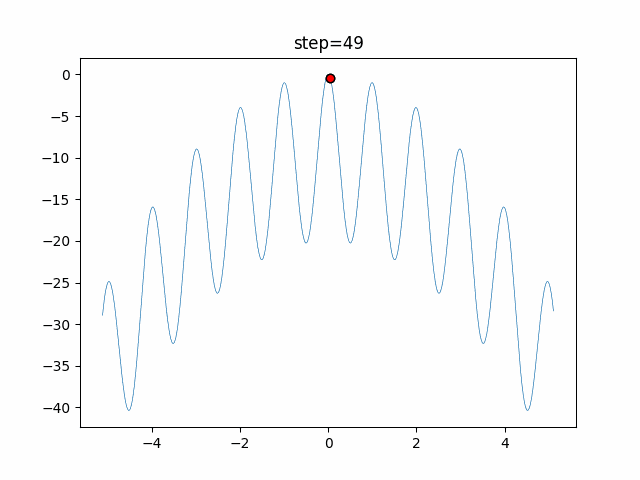
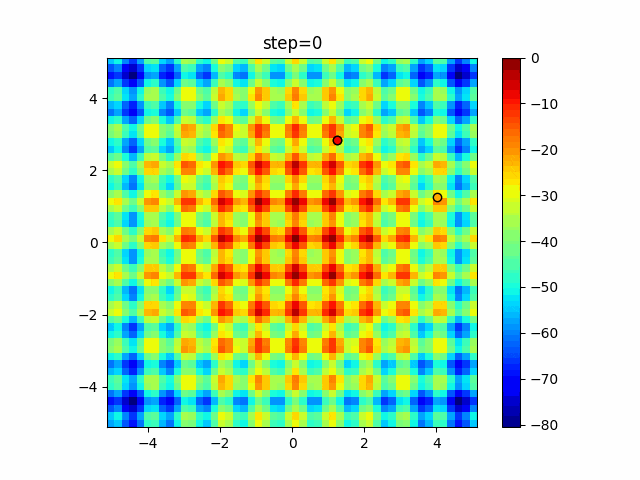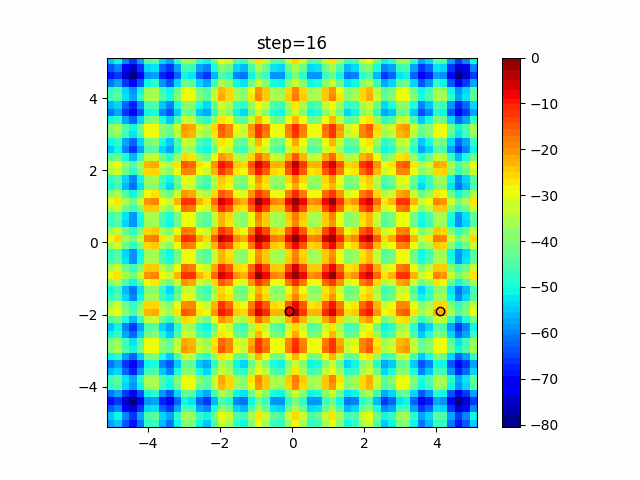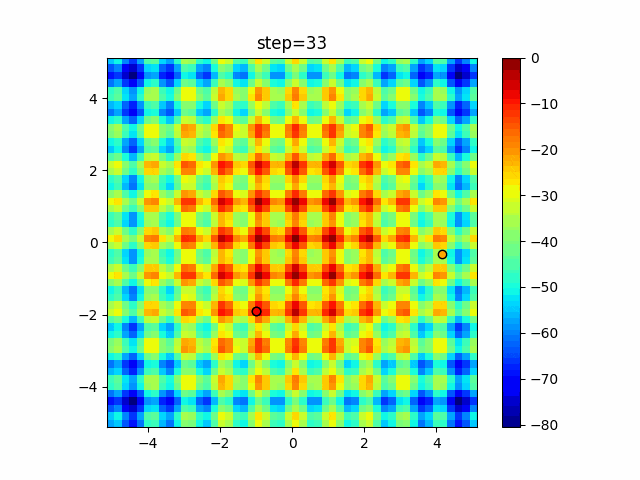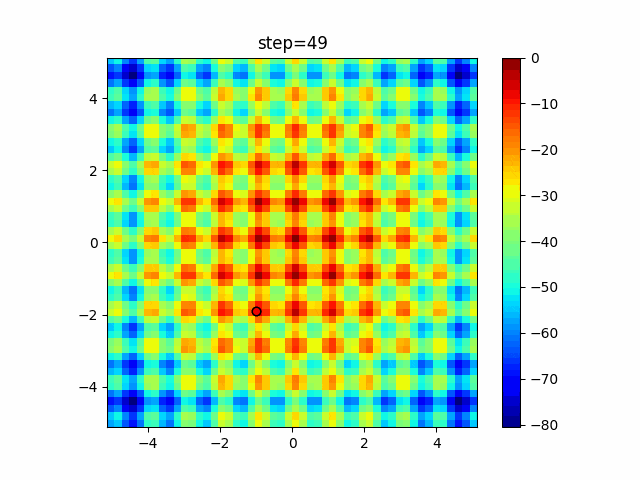
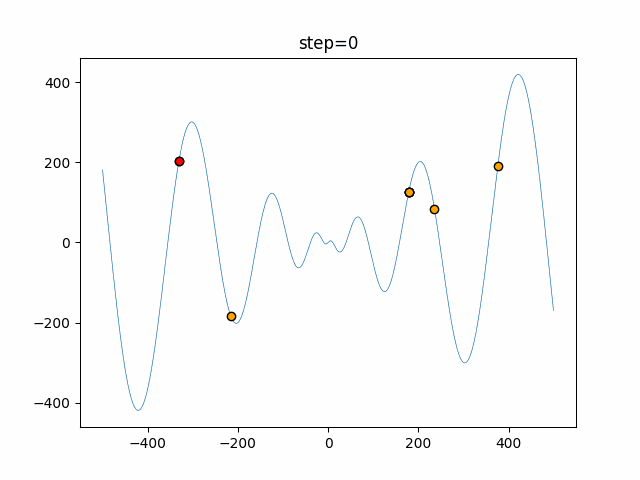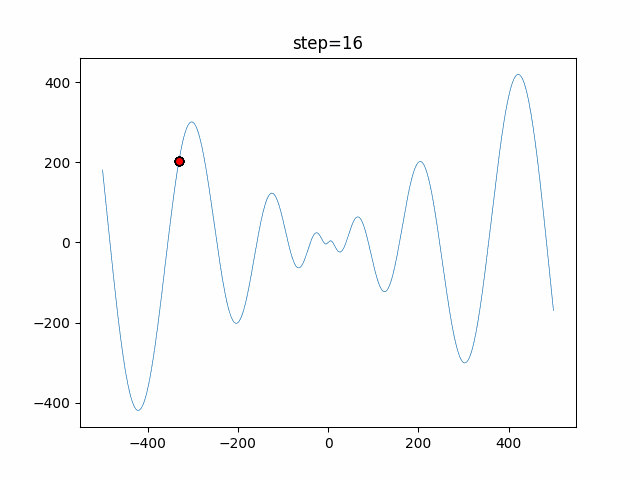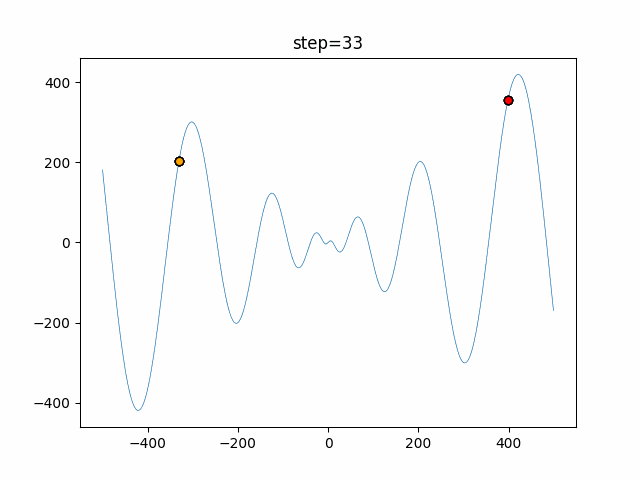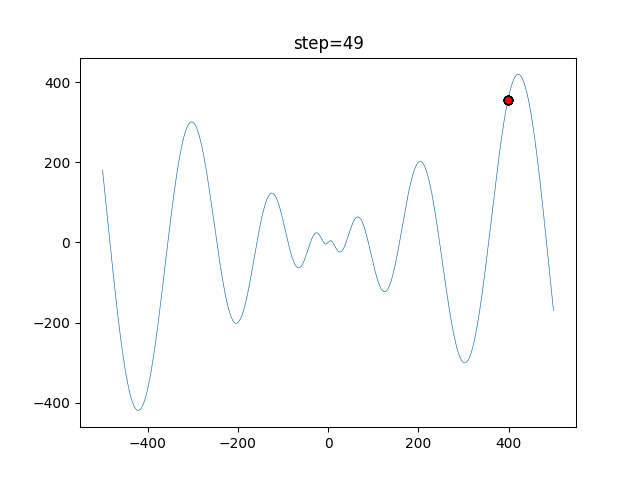
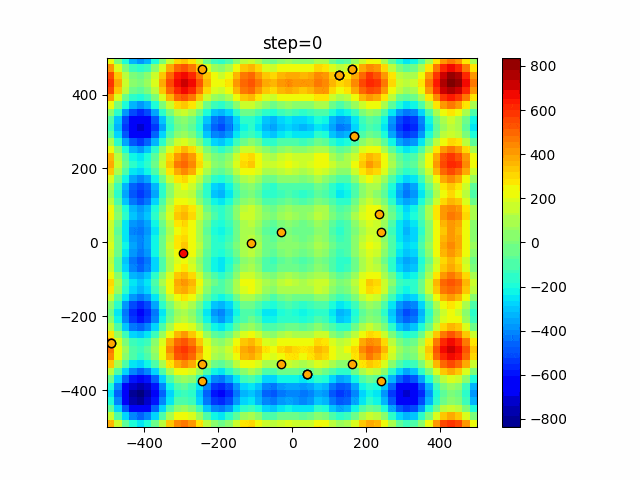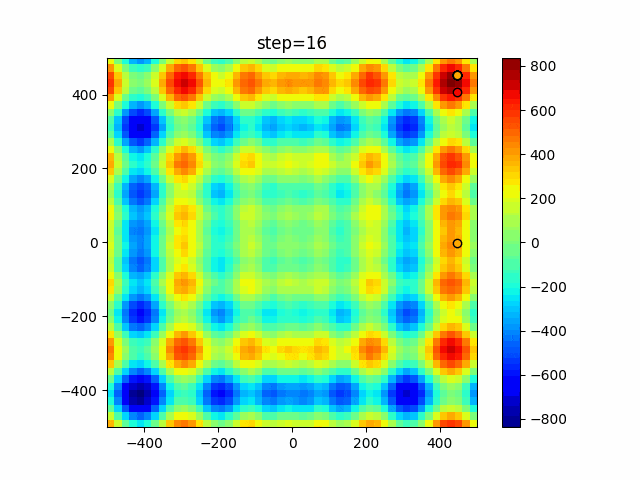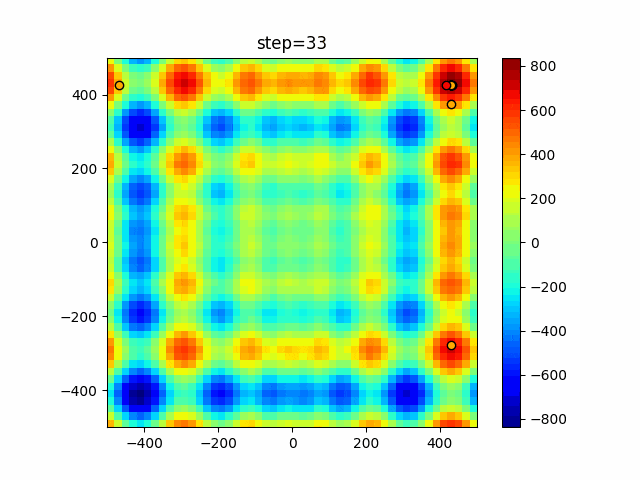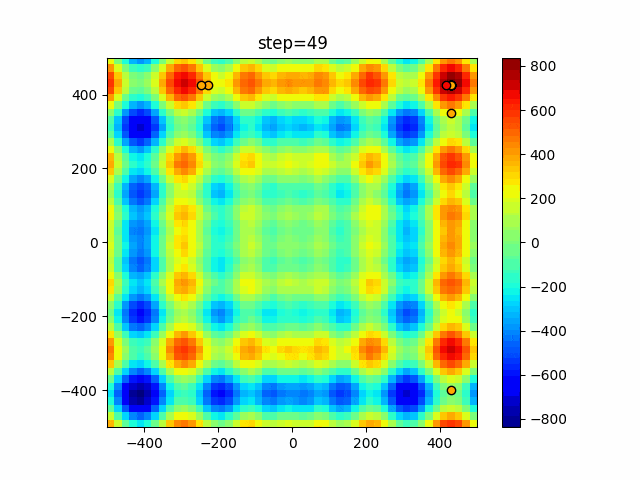
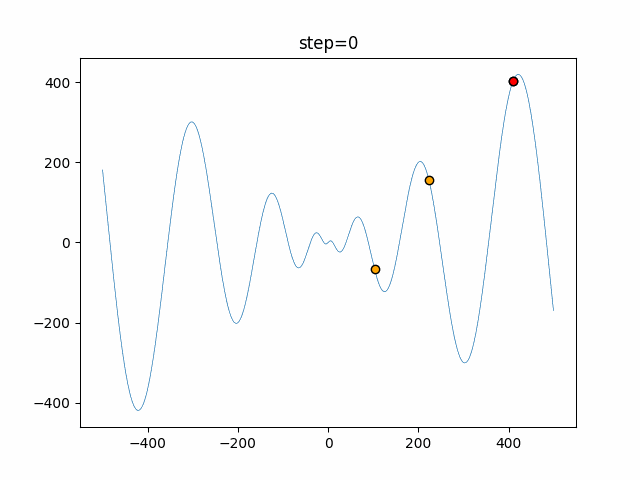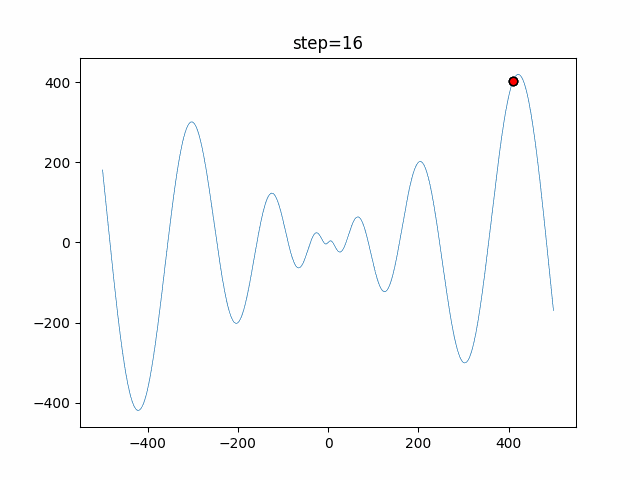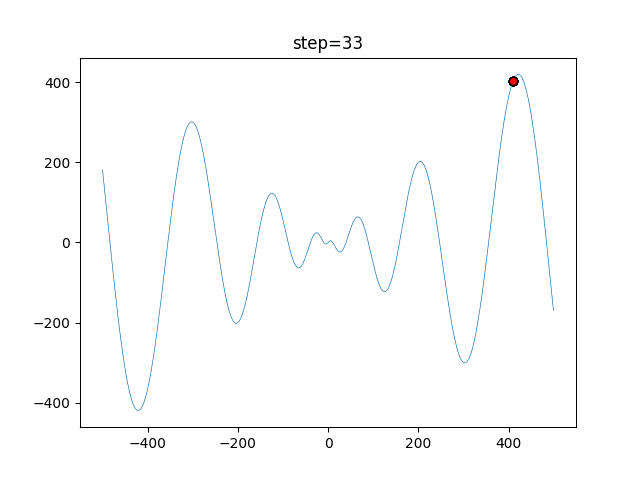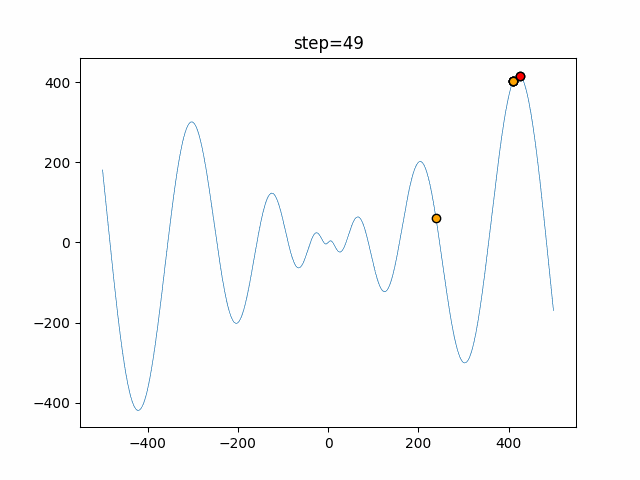
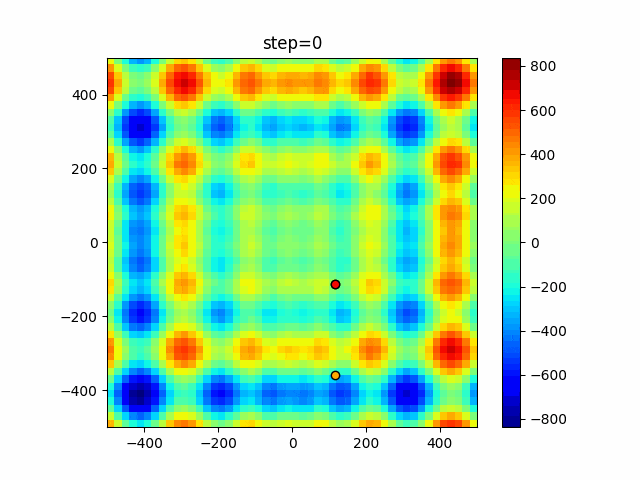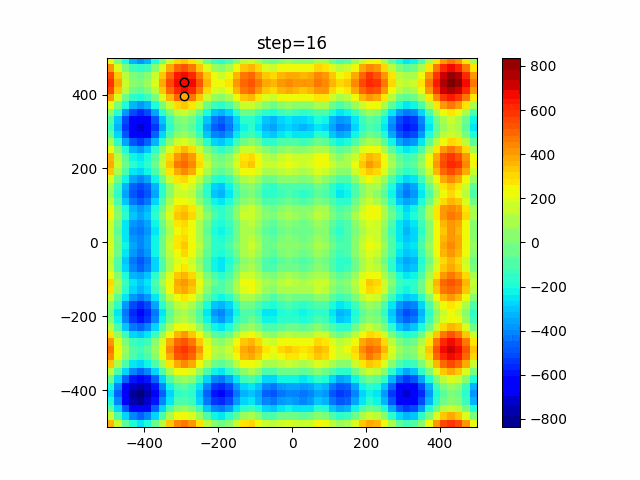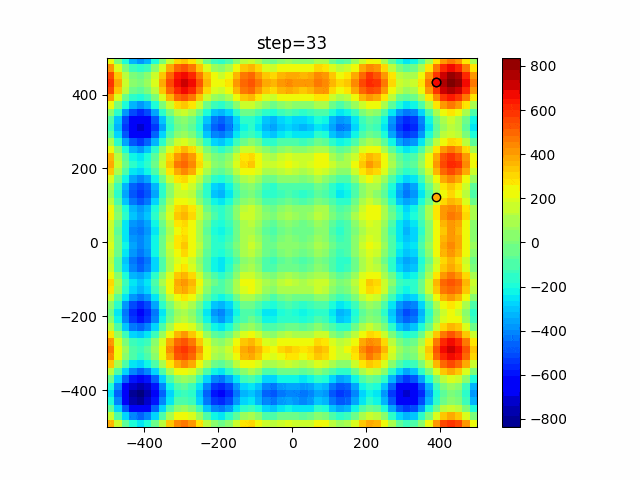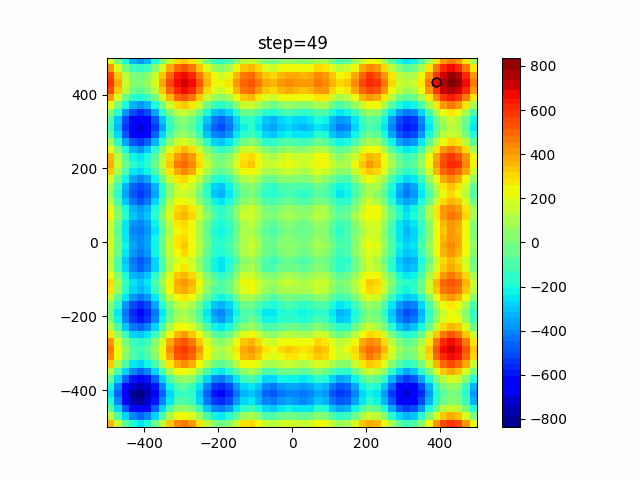
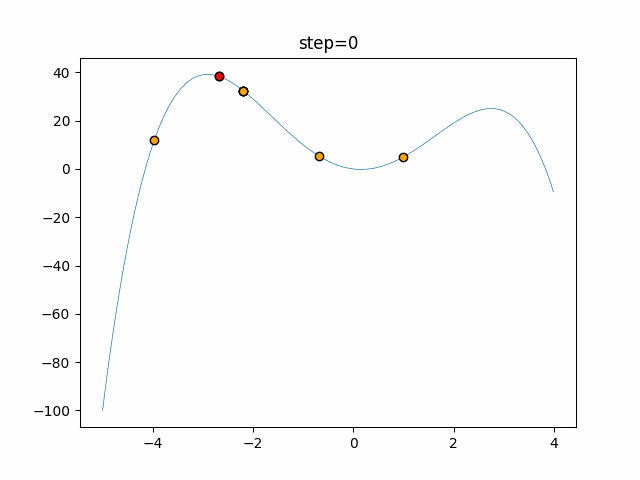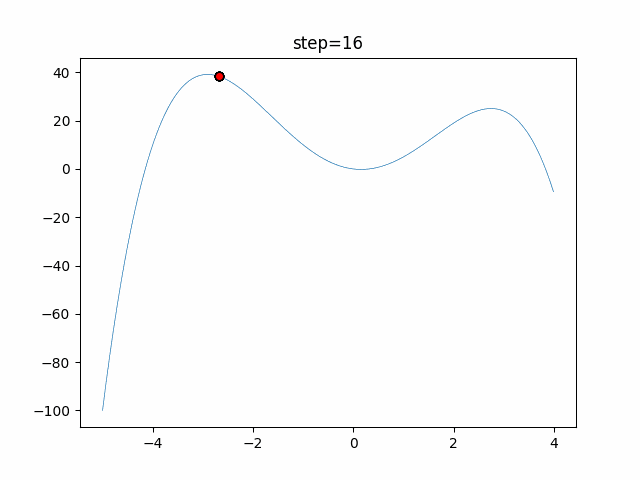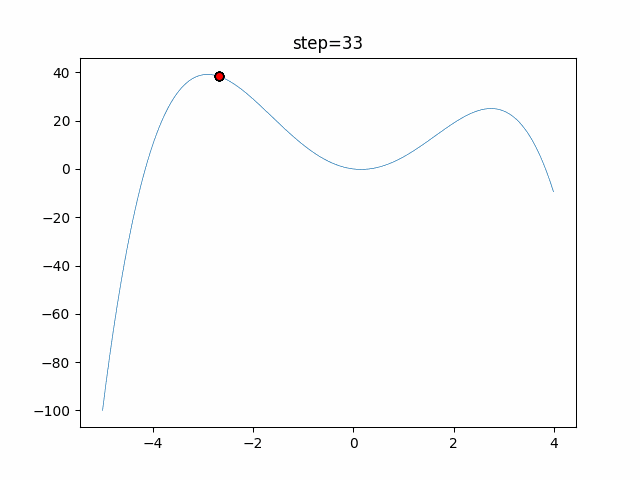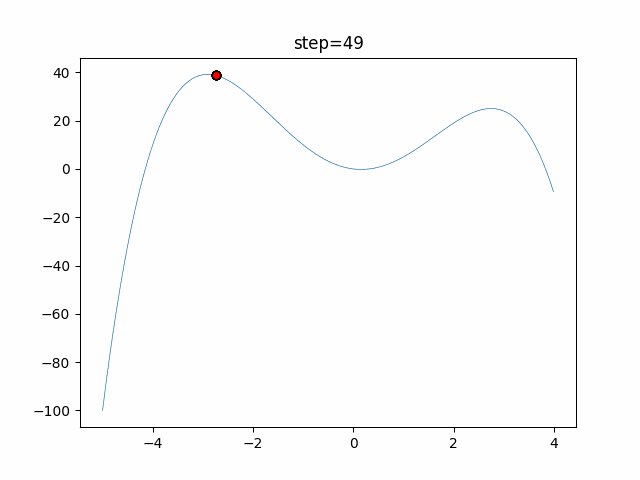
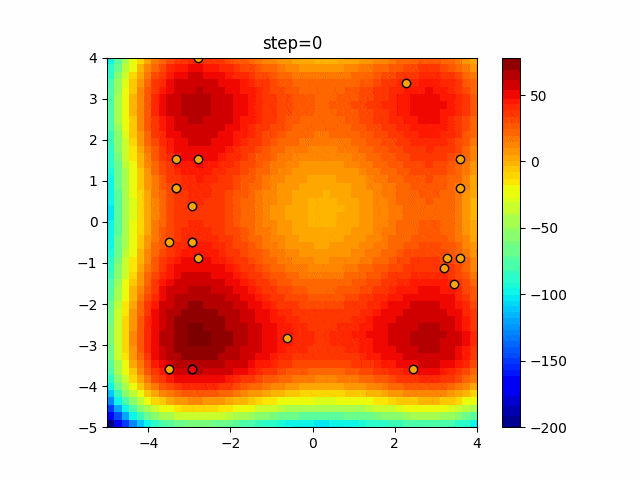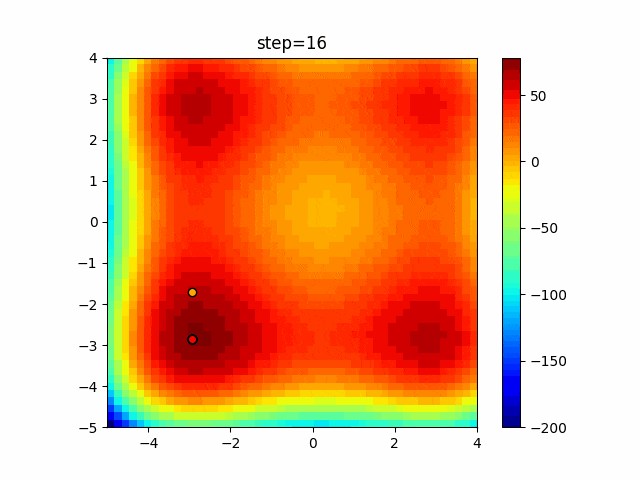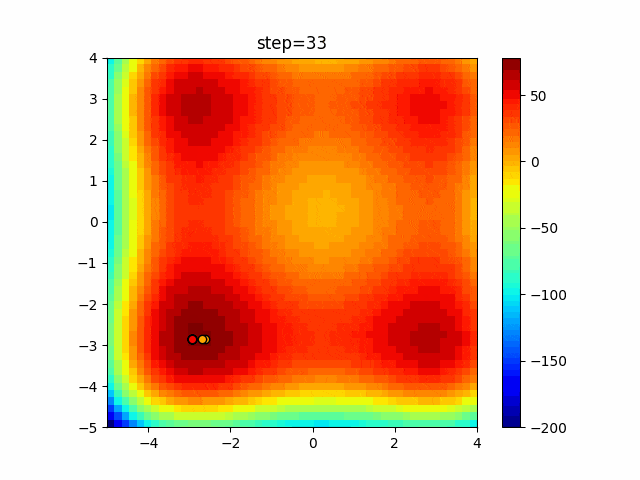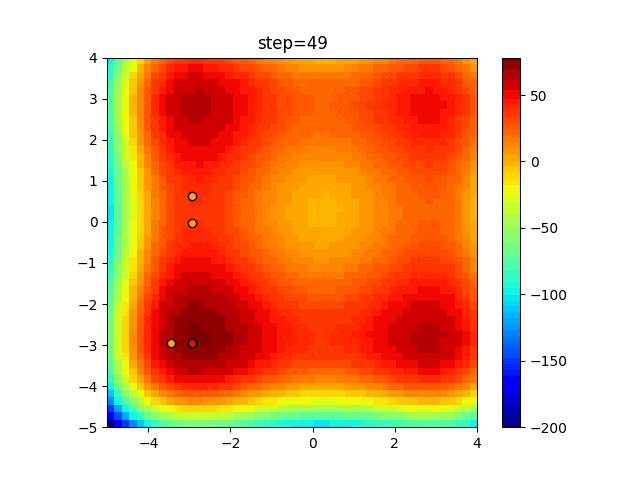
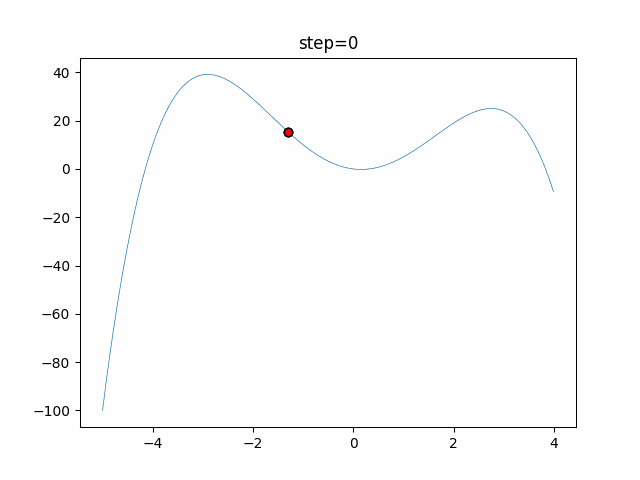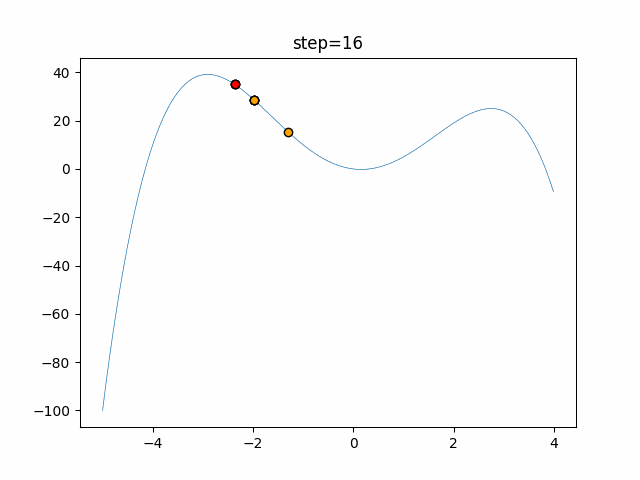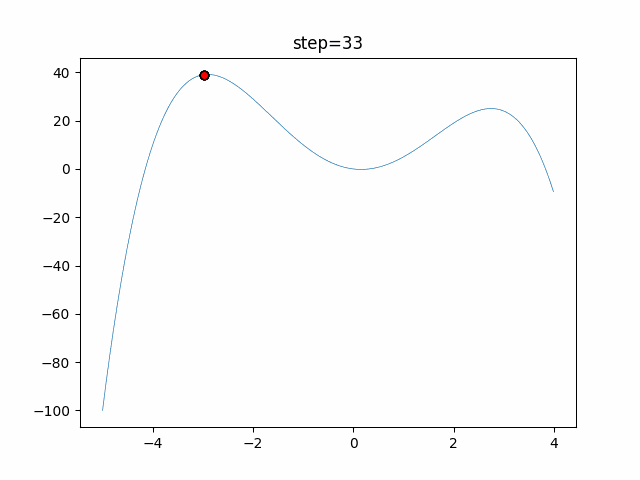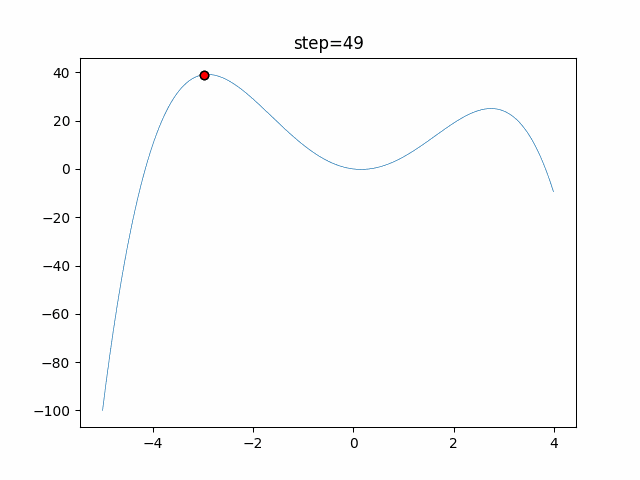
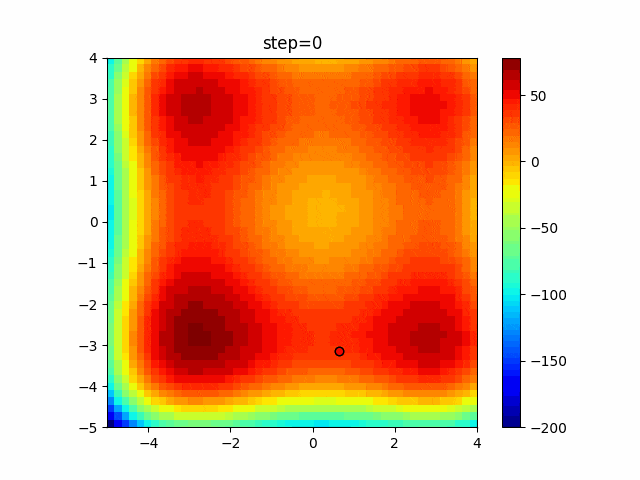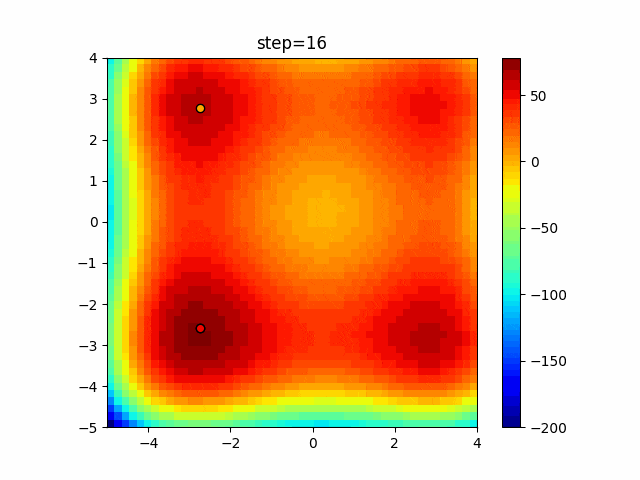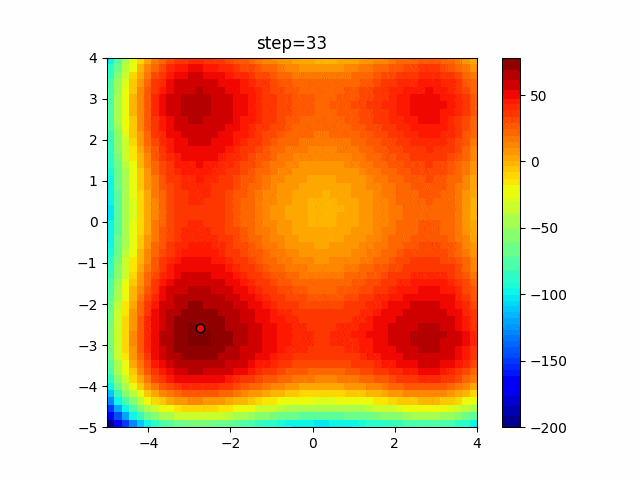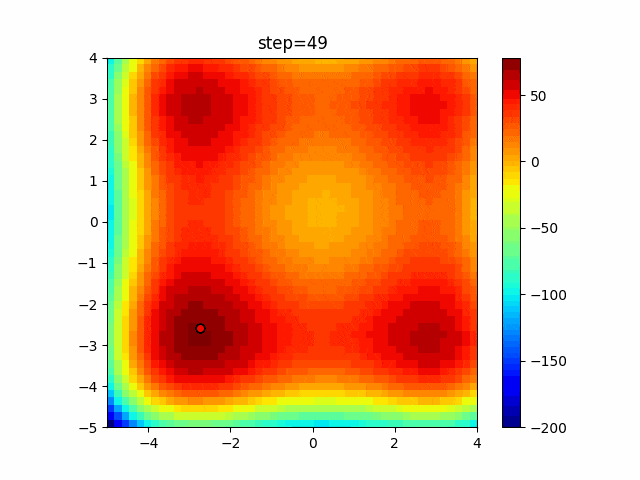
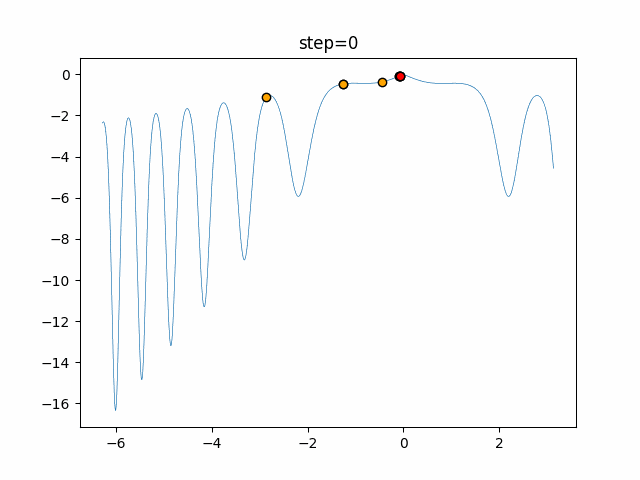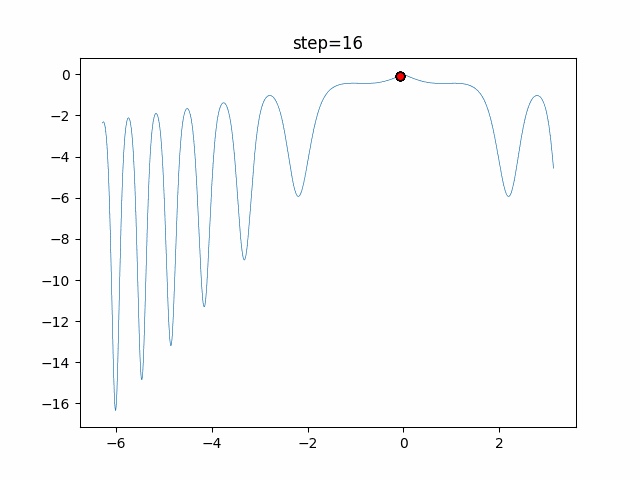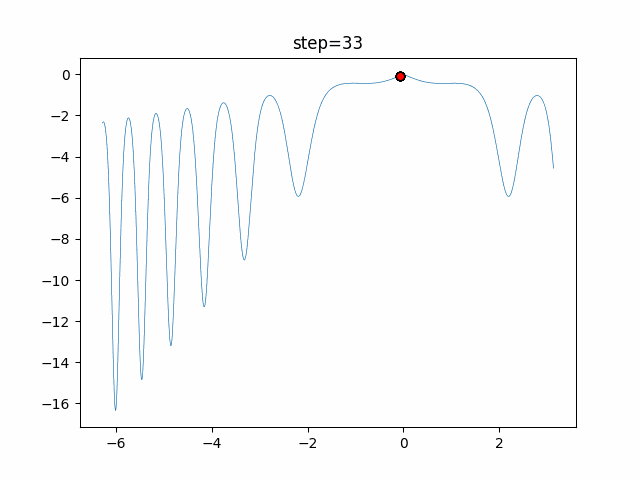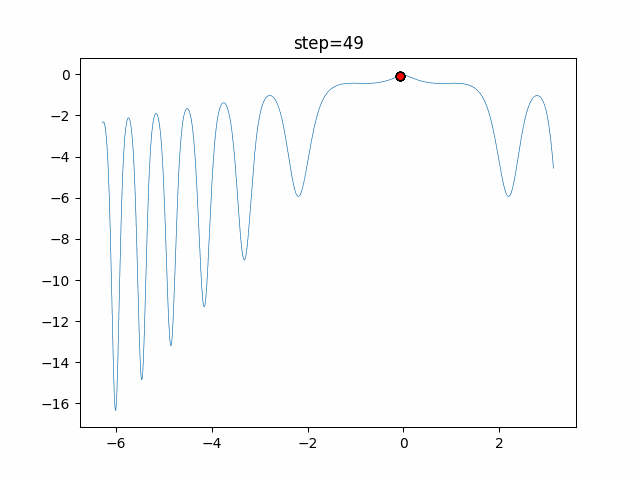
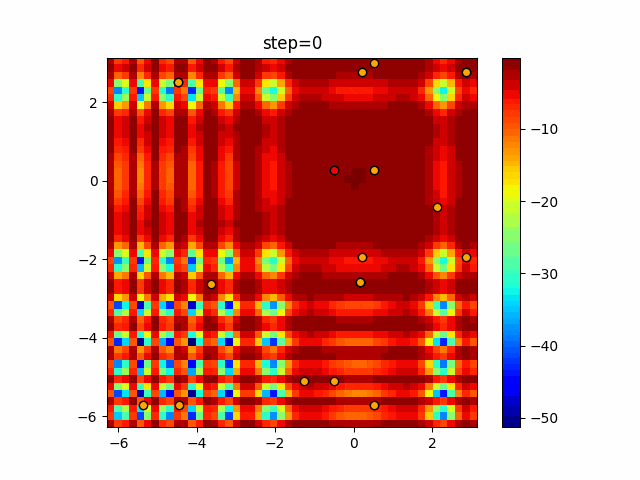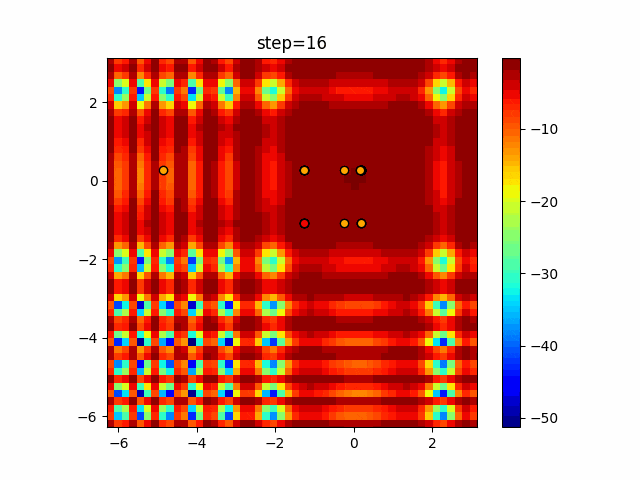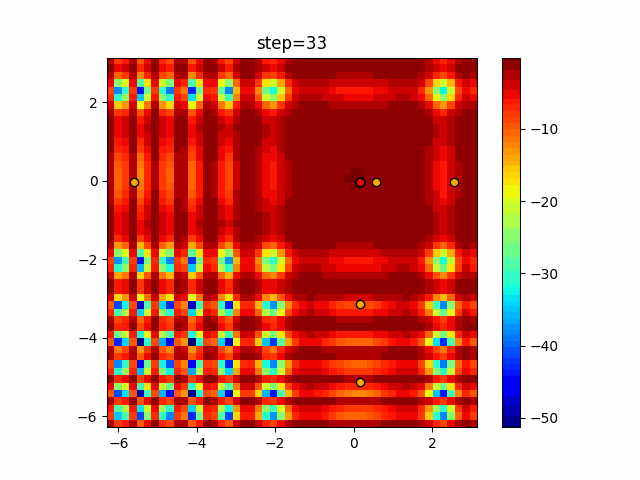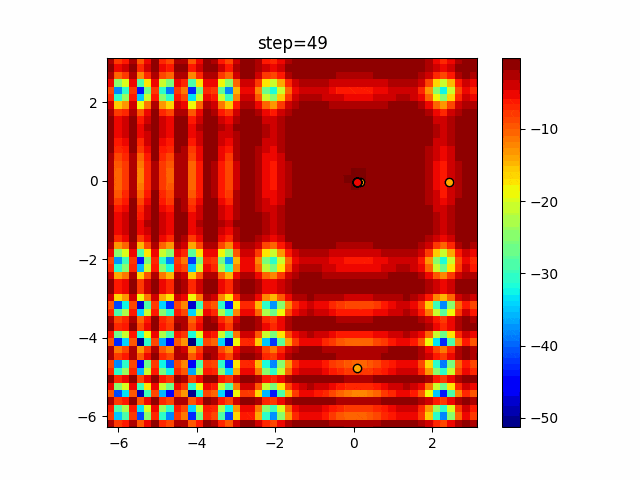
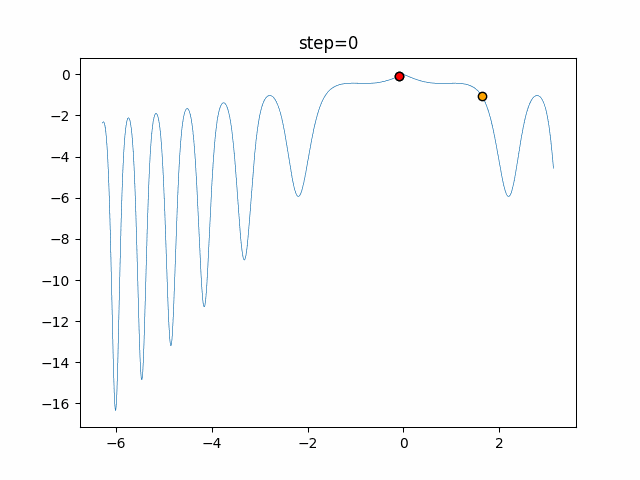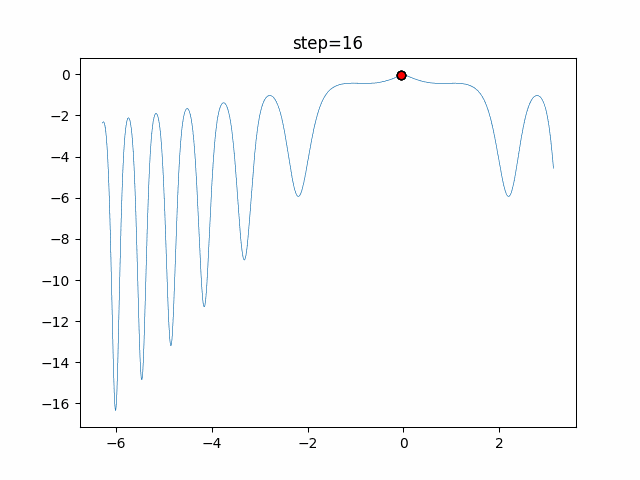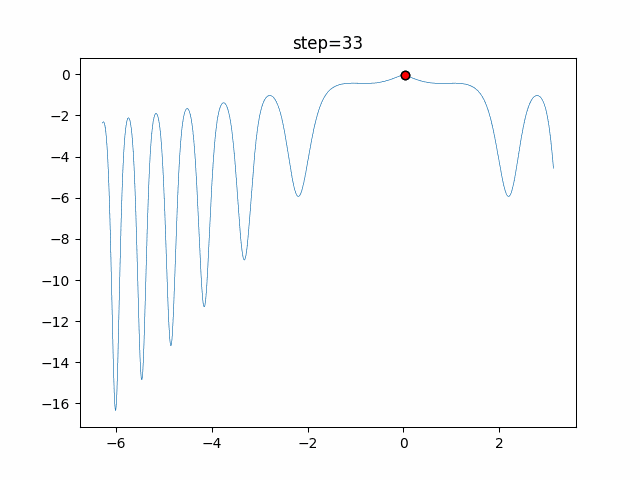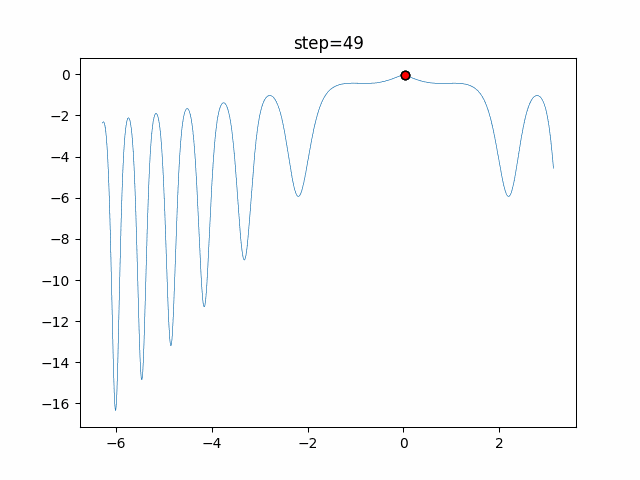
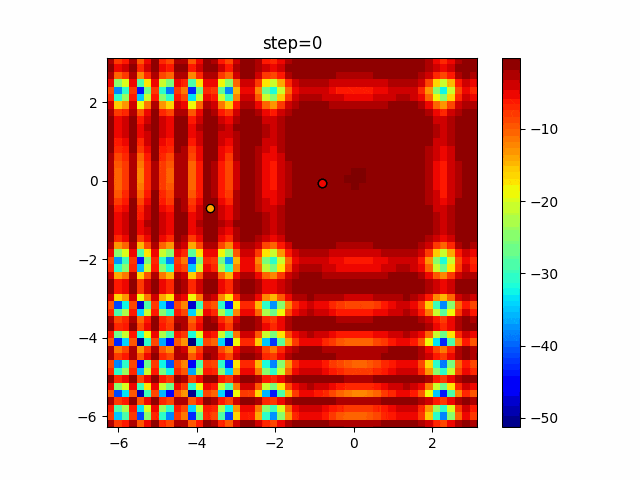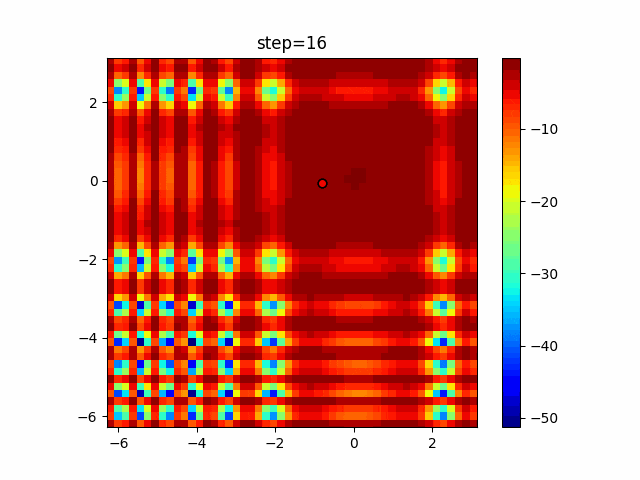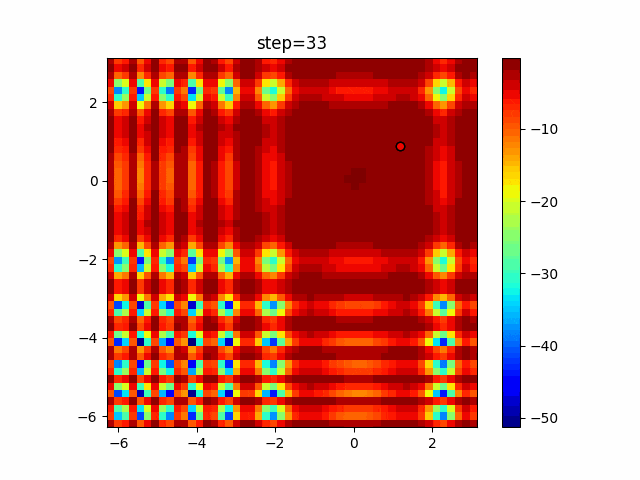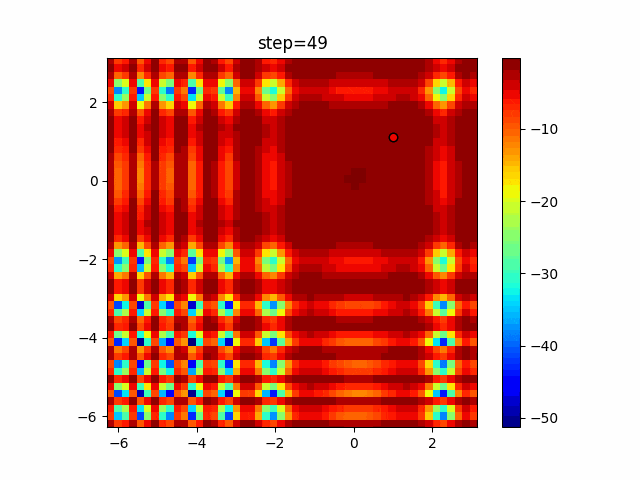
実際の動きの可視化

1次元は6個体、2次元は20個体で50step実行した結果です。
パラメータフリーGAは個体数の指定ができないのでそのままです。
赤い丸がそのstepでの最高スコアを持っている個体となります。

パラメータは以下で実行しました。

GA(N, save_elite=False, select_method="ranking", mutation=0.05)
PfGA(mutation=0.5)

function_Ackley

• GA
  • 1次元

• 2次元

• PfGA
  • 1次元

• 2次元

function_Rastrigin

• GA
  • 1次元

• 2次元

• PfGA
  • 1次元

• 2次元

function_Schwefel

• GA
  • 1次元

• 2次元

• PfGA
  • 1次元

• 2次元

function_StyblinskiTang

• GA
  • 1次元

• 2次元

• PfGA
  • 1次元

• 2次元

function_XinSheYang

• GA
  • 1次元

• 2次元

• PfGA
  • 1次元

• 2次元

あとがき

交叉が次元単位なので1次元の結果はあまり参考になりません。
（突然変異におけるランダム移動のみです）
2次元で縦と横の位置に個体が多いのが一様交叉の特徴ですね。
一様交叉ですが、これは離散値を対象にしている交叉なので実数値を対象にした交叉（BLX-α交叉やシンプレックス交叉）だと違った結果になるかもしれません。
（そのうち実装するかも？）

ちなみに突然変異の確率ですが、0%にすると最高評価の個体に収束します。