重み付き乱択アルゴリズムをまとめて計測してみた

強化学習の優先順位付き経験再生を実装しているときに、キューから優先順位に従ってランダムに要素を取り出す必要がありました。
その場合に重み付きの（偏りがある）乱数を発生させる高速な手法を調べていましたが、情報があまりない感じだったのでまとめて比較してみました。

重み付き乱択アルゴリズム

重み付きランダムサンプリングといったり重み付きランダム抽出といったり復元抽出といったり言い方は定まっていない気がします。
比較したアルゴリズムは以下です。

• シンプルな累積和
• シンプルな累積和（バイナリサーチ版）
• Numpy の choice関数（python限定）
• Numpy の multinomial関数（python限定）
• Walker's Alias法
• 二分木探索(SumTree)
• 逆関数法(※1)

※1：これだけ重みのつけ方に制限があります。

参考：
・重み付きランダムサンプリングアルゴリズム

各アルゴリズムの比較

計算量

N は重みの配列数です。
例えば N=3 なら [10%, 20%, 70%] みたいな配列を指します。

	create	choice	update
SimpleChoiceByWeight	$O(N)$ ※1	$O(N)$	-
SimpleBinaryChoiceByWeight	$O(N)$	$O(\log_N)$	-
NumpyChoiceByWeight	$O(N)$ ※2	$O(N)$?	-
NumpyMultinomialChoice	$O(N)$ ※2	$O(N)$?	-
WalkersAlias	$O(N)$	$O(1)$	-
BinaryChoiceByWeight	$O(N \log_N)$	$O(\log_N)$	$O(\log_N)$
InversionMethodSequence	$O(1)$	$O(1)$	-

※1：合計値を事前に出していれば $O(0)$
※2：重みが合計1になるように正規化していれば $O(0)$

計測結果

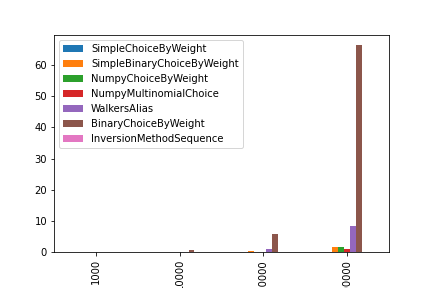
重みの初期化にかかった時間

※10回試行した場合の時間です。(単位：秒)

                             1000      10000     100000     1000000
SimpleChoiceByWeight        0.000052  0.000505  0.005860   0.058745
SimpleBinaryChoiceByWeight  0.001148  0.011905  0.165087   1.530480
NumpyChoiceByWeight         0.000950  0.009632  0.150498   1.572578
NumpyMultinomialChoice      0.000611  0.006450  0.091439   0.909843
WalkersAlias                0.007529  0.083304  0.824508   8.326392
BinaryChoiceByWeight        0.034235  0.495992  5.785159  66.483099
InversionMethodSequence     0.000013  0.000014  0.000027   0.000031

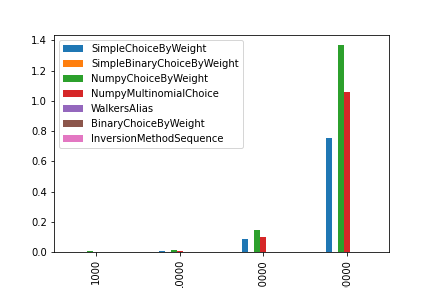
乱数の生成にかかった時間

※10回試行した場合の時間です。(単位：秒)

                             1000      10000     100000    1000000
SimpleChoiceByWeight        0.000720  0.008592  0.086020  0.752962
SimpleBinaryChoiceByWeight  0.000052  0.000078  0.000134  0.000173
NumpyChoiceByWeight         0.004678  0.015376  0.144766  1.369685
NumpyMultinomialChoice      0.002336  0.009232  0.101253  1.058034
WalkersAlias                0.000018  0.000021  0.000028  0.000051
BinaryChoiceByWeight        0.000077  0.000104  0.000155  0.000180
InversionMethodSequence     0.000032  0.000026  0.000036  0.000035

コード全体

実行結果付きです。

• GoogleColaboratory

各アルゴリズムの解説

シンプルな累積和

多分最初に思いつく方法だと思います。
合計値から乱数を生成し、順番に比較していく方法ですね。

例えば、[1,4,3,2] という重みを例に考えます。
求める乱数は 0～10 (1,4,3,2の合計値)となります。
出た値が、
0～1 なら index0
1～5 なら index1
5～8 なら index2
8～10 なら index3
になります。

計算量はまず合計値を求めるのに $O(N)$ です。

その後、乱数から指定のindexを求めますが、前方から順番に探しているので、平均N/2回かかります。(最高1回、最悪N回で求まる)
ですので、計算量は $O(N)$ です。

import random
class SimpleChoiceByWeight():
    def setWeight(self, weights):
        self.weights = weights
        self.weight_sum = sum(weights)

    def choice(self):
        r = random.random() * self.weight_sum

        num = 0
        for i, weight in enumerate(self.weights):
            num += weight
            if r <= num:
                return i
        # not comming

SimpleBinaryChoiceByWeight

SimpleChoiceByWeight の乱数の探索をバイナリサーチにすることで高速化した手法です。
バイナリサーチ用のテーブルを作成するのに $O(N)$ 、乱数からindexを探すのに $O(log_N)$ かかります。

import random
class SimpleBinaryChoiceByWeight():
    def setWeight(self, weights):
        self.weights = weights

        n = 0
        self.weight_sums = []
        for w in self.weights:
            n += w
            self.weight_sums.append(n)

    def choice(self):
        r = random.random() * self.weight_sums[-1]

        # binary search
        left, right = 0, len(self.weight_sums)
        result = -1
        while left <= right:
            mid = (left + right) // 2

            low = 0
            if mid > 0:
                low = self.weight_sums[mid-1]
            high = self.weight_sums[mid]

            if low <= r < high:
                return mid
            elif high <= r:
                left = mid + 1
            else:
                right = mid - 1

        return result

NumpyChoiceByWeight

Numpy の choice 関数で取得する方法です。
内部の実装は調べていないですが、時間的に $O(N)$ っぽい気がします。

choice関数を使うために合計1の配列に正規化する必要があり、前処理では $O(N)$ かかっています。

import numpy as np
class NumpyChoiceByWeight():
    def setWeight(self, weights):
        n = sum(weights)
        self.weights = [x/n for x in weights]
        self.target = [i for i in range(len(weights))]

    def choice(self):
        return np.random.choice(self.target, 1, p=self.weights)[0]

NumpyMultinomialChoice

Numpy の multinomial 関数は多項分布からサンプルを取得する関数です。
第2引数で与えた確率分布に従って、第1引数の回数分試行した結果を返します。

>>> np.random.multinomial(10, [0.1, 0.2, 0.7])
[1, 1, 8]   # 分布に従って10回試した結果が返ってくる

なので、これを1回だけ試してそのindexを取得すればそのまま重み付き乱択アルゴリズムになるという仕組みです。

こちらも内部の実装は調べていないですが、choice関数より少し早い結果になりました。

import numpy as np
class NumpyMultinomialChoice():
    def setWeight(self, weights):
        n = sum(weights)
        self.weights = [x/n for x in weights]

    def choice(self):
        r = np.random.multinomial(1, self.weights)
        return np.argmax(r)

Walker's Alias法

説明はいろいろな場所でされているので省きます。
テーブルの作成に $O(N)$ かかりますが、乱数の取得は $O(1)$ でできる手法です。

参考：
・重み付きランダム抽出:Walker's Alias Method
・重み付きランダム抽出:Walker's Alias Method(Python)
・Walker's Alias Methodの箱の作り方のわかりやすい説明

import random
class WalkersAlias():
    def setWeight(self, weights):
        self.n = len(weights)

        num = sum(weights)
        self.p = [ w*self.n/num for w in weights]

        self.a, hl = [0] * self.n, [0] * self.n
        low, high = 0, self.n-1
        for i in range(self.n):
            if self.p[i] < 1:
                hl[low] = i
                low += 1
            else:
                hl[high] = i
                high -= 1
        while low > 0 and high < self.n-1:
            low_i = hl[low-1]
            high_i = hl[high+1]
            self.a[low_i] = high_i
            self.p[high_i] -= 1 - self.p[low_i]
            if self.p[high_i] < 1:
                hl[low-1] = high_i
                high += 1
            else:
                low -= 1

    def choice(self):
        r = random.random() * self.n
        n = int(r)
        if r-n < self.p[n]:
            return n
        else:
            return self.a[n]

二分木探索(SumTree)

優先順位付き経験再生のpriorityで使われているアルゴリズムです。
この手法の特徴は値を更新できる点です。(他の手法は値を更新しようとするとテーブルを作り直さないといけません)

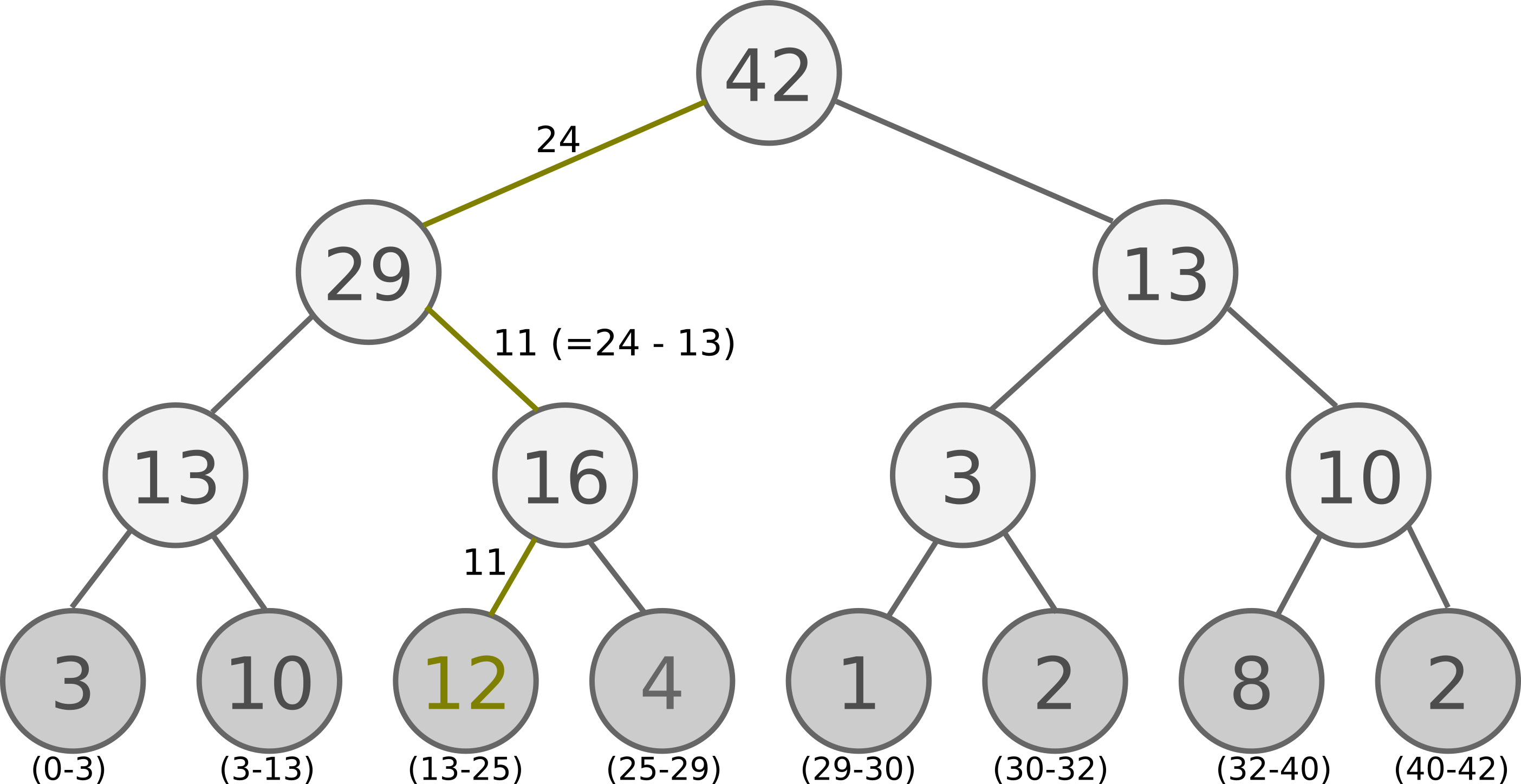
アルゴリズムですが、以下の図のような二分木を作ります。

この二分木は一番下の段に配列の重みが並んでおり、1段上の要素は下の2要素を足した数字になっています。
ですので、最上位の数字は全重みの合計です。

この二分木からサンプリングする方法ですが、まずは0～最上位(ここでは42)の間で乱数を出します。
乱数が左の子の要素と比べて小さければ左に移動し、そうじゃなければ左の値を引いて右に移動します。
これを繰り返して最下段まで行った時の要素が対象のインデックスになります。

テーブルの作成には $O(N \log_N)$ (追加に $O(\log_N)$ × 要素N分) かかってしまいますが、
一度作れば取得は $O(\log_N)$、更新も $O(\log_N)$ でできるかなり高速な手法です。

参考：
・二分木探索
・Let’s make a DQN: Double Learning and Prioritized Experience Replay

import random
class BinaryChoiceByWeight():
    def setWeight(self, weights):
        self.capacity = 1
        while self.capacity < len(weights):
            self.capacity *= 2
        self.write = 0
        self.tree = [0] * (self.capacity*2-1)

        for w in weights:
            self._add(w)

    def _add(self, w):
        self.update(self.write, w)
        self.write += 1

    def _propagate(self, idx, change):
        parent = (idx - 1) // 2

        self.tree[parent] += change

        if parent != 0:
            self._propagate(parent, change)

    def _retrieve(self, idx, s):
        left = 2 * idx + 1
        right = left + 1

        if left >= len(self.tree):
            return idx

        if s <= self.tree[left]:
            return self._retrieve(left, s)
        else:
            return self._retrieve(right, s-self.tree[left])

    def update(self, idx, p):
        tree_idx = idx + self.capacity - 1
        change = p - self.tree[tree_idx]

        self.tree[tree_idx] = p
        self._propagate(tree_idx, change)


    def choice(self):
        r = random.random() * self.tree[0]
        treeIdx = self._retrieve(0, r)
        dataIdx = treeIdx - self.capacity + 1
        return dataIdx

逆関数法

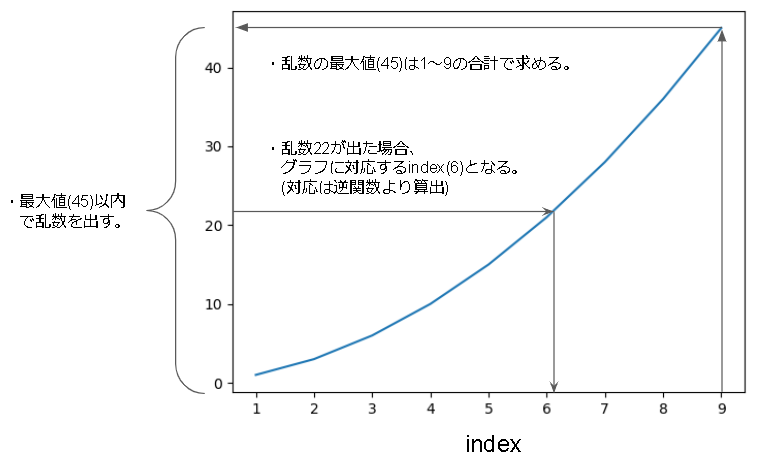
重みが数式で表せる場合に使える手法です。
仕組みとしては累積分布関数の逆関数を用いることで、確率分布からindexの分布に変換するという手法です。

テスト用のコードは、重みが等差数列に従う場合を実装しています。
等差数列に従う場合の例としては、順位に従って出る確率を高くしたい場合(１位ほどでやすく、ビリになるほど出にくい)等で使えると思います。

全て数式で計算するだけなので、合計値の計算は $O(1)$、乱数取得も $O(1)$ と超高速です。

import random
import math
class InversionMethodSequence():
    def setWeight(self, start, diff, size):
        self.start = start
        self.diff = diff
        self.total = self.rank_sum(start, diff, size)

    def choice(self):
        r = random.random() * self.total
        index = self.rank_sum_inverse(self.start, self.diff, r)
        return int(index)

    def rank_sum(self, start, diff, size):
        return size*( 2*start + (size-1)*diff )/2

    def rank_sum_inverse(self, start, diff, val):
        if diff == 0:
            return val
        t = diff-2*start + math.sqrt((2*start-diff)**2 + 8*diff*val)
        return t/(2*diff)

あとがき

重み付き乱択アルゴリズムを使う状況は、多腕バンディット問題でのアーム選択や、遺伝的アルゴリズムでの遺伝選択、ゲームのガチャ実装時などがあると思います。
テーブル作成も含めてもうちょっと早いアルゴリズムがありそうでしたが見つからなかったのが残念でした。