重み付きランダム抽出:Walker's Alias Method

#なにこの記事
重み付きランダム復元抽出アルゴリズムである、Walker's Alias Methodについて

#重み付きランダム復元抽出
要素ごとに抽選される確率が異なり、(重み付き)
選んだ要素を都度母集団に戻す抽出方法(復元抽出)
のこと。
素直に実装すると
重みをつけてランダムに何か出したいや
重み付きランダム
のようになります。
線形探索で実装すれば、計算量は抽選1回毎にO(n)
バイナリサーチなら準備にO(n)、抽選1回毎にO(log n)

#Walker's Alias Method
準備にO(n)で、抽選1回毎になんとO(1)というアルゴリズム。
同じ大きい集団に対して何度も抽選しないといけない用途向け。
(GAとか粒子フィルタとか。)
ググればわかりやすい説明が出てきます。

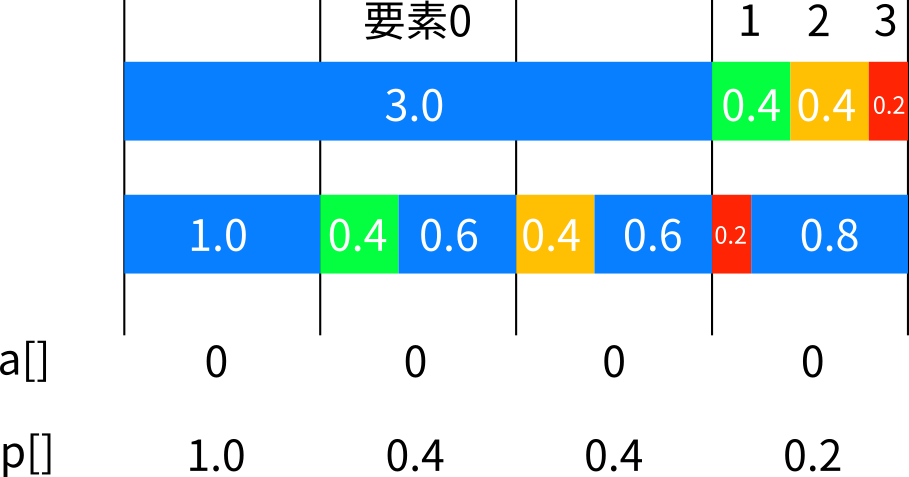
図の上のような重みリストでは、
乱数が3~4の時にどの要素を抽出するかを最高で2回判定する必要があります。
これを下のようなリストに並べ替えたとする(閾値リストと別名リストを生成する)と、
乱数の整数部分と小数部分を使い、一回の比較だけで抽出できるようになります。
例えば下のリストで
1.1を引いた場合、整数部が1なので閾値リストの要素1:p[1]をみて、
小数部分0.1はp[1]を超えていないので、要素1を選択します。
2.5を引いた場合、整数部が2なので閾値リストの要素1:p[2]をみて、
小数部分0.5はこれを超えるので、別名リストa[2]の中身である、要素0を選択します。

#適当な実装(C#)

public class WalkersAliasMethod
{
    private double[] probList;
    private int[] aliasList;
    private double[] weightList;
    private Random rnd;

    public WalkersAliasMethod()
    {
        rnd = new Random();
    }

    public WalkersAliasMethod(int seed)
    {
        rnd = new Random(seed);
    }

    //準備
    public void UpdateList(double[] weightList)
    {
        probList = new double[weightList.Length];
        aliasList = new int[weightList.Length];
        this.weightList = weightList;
        int size = weightList.Length;
        double[] norWeightList = new double[size];
        weightList.CopyTo(norWeightList, 0);
        double sum = weightList.Sum();
        double[] v = new double[size];//0~要素数で正規化された確率リスト
        for (int i = 0; i < size; i++)
        {
            norWeightList[i] /= sum;
            v[i] = norWeightList[i] * size;
        }

        List<int> small = new List<int>();
        List<int> large = new List<int>();

        for (int i = 0; i < size; i++)
        {

            if (v[i] < 1)
                small.Add(i);
            else
                large.Add(i);
        }

        int g, l;
        while (small.Count > 0 && large.Count > 0)
        {
            l = small[0];
            g = large[0];
            small.RemoveAt(0);
            large.RemoveAt(0);

            probList[l] = v[l];
            aliasList[l] = g;
            v[g] += -1.0 + v[l];
            if (v[g] < 1)
                small.Add(g);
            else
                large.Add(g);
        }
        while (large.Count > 0)
        {
            g = large[0];
            large.RemoveAt(0);
            probList[g] = 1;
        }
        while (small.Count > 0)
        {
            l = small[0];
            small.RemoveAt(0);
            probList[l] = 1;
        }
    }

    //重みを元にランダムに復元抽出してインデックスを返す
    public int Resampling()
    {
        double v = rnd.NextDouble() * (double)weightList.Length;
        int k = (int)v;
        double u = 1 + k - v;
        if (u < probList[k])
        {
            return k;
        }
        return aliasList[k];
    }
}