Walker's Alias Methodの箱の作り方のわかりやすい説明

はじめに

指定された重みに従って離散的な値を確率的に選択したい、ということがよくある。例えば[1,4,5]という配列が与えられた時、確率10%で0、40%で1、50%で2というインデックスを返すような関数が欲しい。

普通に考えると部分和をとって乱数を一度振り、どの場所が選択されたか二分探索で調べる、というアルゴリズムが思いつくが、これは要素数Nに対して$O(\log(N))$の手間がかかる。logの手間というのは無視できることが多いが、この関数呼び出しが頻繁にある場合には無視できないコストになる。

さて、こんな用途のためにWalker's Alias Methodというアルゴリズムがある。この手法は一度$O(N)$の手間で配列を作ってしまえば、後は$O(1)$でインデックスを選ぶことができる。

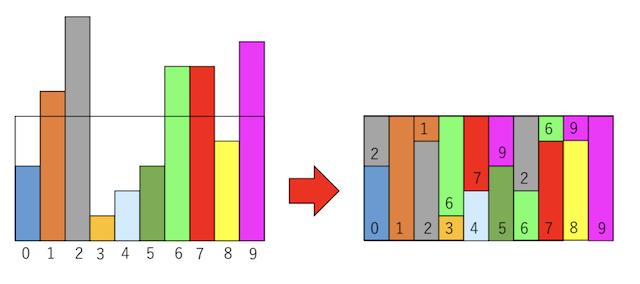
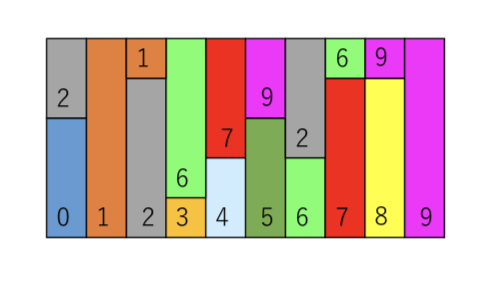
例えば重みとして[3, 6, 9, 1, 2, 3, 7, 7, 4, 8]という10個の要素を持つ配列を考えよう。この重みに比例して確率的に配列のインデックスを返す関数が作りたい。Walker法は、まず10個の「容器」を用意し、その箱に重みに比例する形で箱を詰めていく。ただしこの時、各容器に、箱がたかだか二個までしか入らないようにする。

先程の例では、要素数が10個、合計が50であるので、サイズ5の容器を10個用意できる。この容器に「たかだか2個までしか箱を入れない」という制約で箱をうまく切って詰めると、例えばこんな感じになる。

下側は数字が順番になっており、上側はバラバラになっていることがわかるかと思う。また、もとの色の面積も保存している。この箱ができてしまうと、以下のアルゴリズムで重みに比例するインデックスを返すことができる。

1. 1から10の整数の一様乱数をふり、その数に従って容器を選ぶ。例えば3が出たら、左から3番目の容器を選ぶ
2. 選ばれた容器は、たかだか2個までの箱があるので、また乱数を振ってそのどちらかを選ぶ。左から三番目の容器なら、確率4/5で2を、1/5で1を返せば良い。

以上の手続きでは、インデックスを一つ選ぶのに乱数を2度しか呼ばないため、$O(1)$の方法となっていることがわかる。

しかし、問題は「どうやってこの図の右の箱を作るか」である。これについてウェブ上にあまりわかりやすい解説が見つからない。そこで、(あくまで私基準で)わかりやすい解説を試みる。

箱の作り方

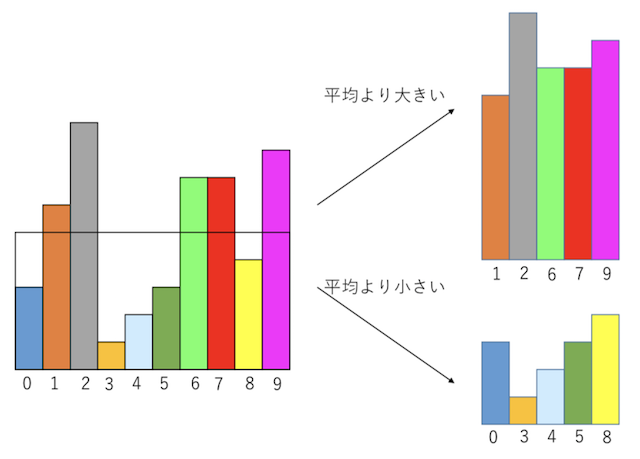
重み配列として[3, 6, 9, 1, 2, 3, 7, 7, 4, 8]を考える。要素数10、合計50なので、この重みを切り貼りすれば、サイズ5の容器10個に入れることができる。そのために、まず「平均値より大きいグループ」と「小さいグループ」にわける。平均値とぴったり同じ場合はどちらに入れても良いが、後で行う手続きと矛盾がないようにしておこう。ここでは「平均値以下」を小さいグループに入れることと約束する。

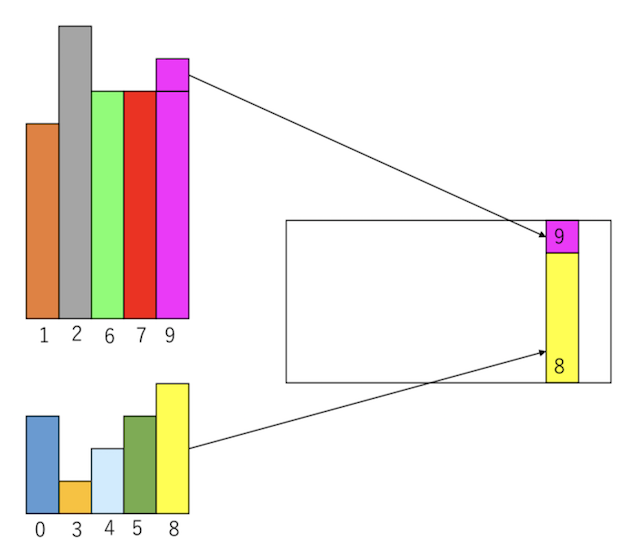
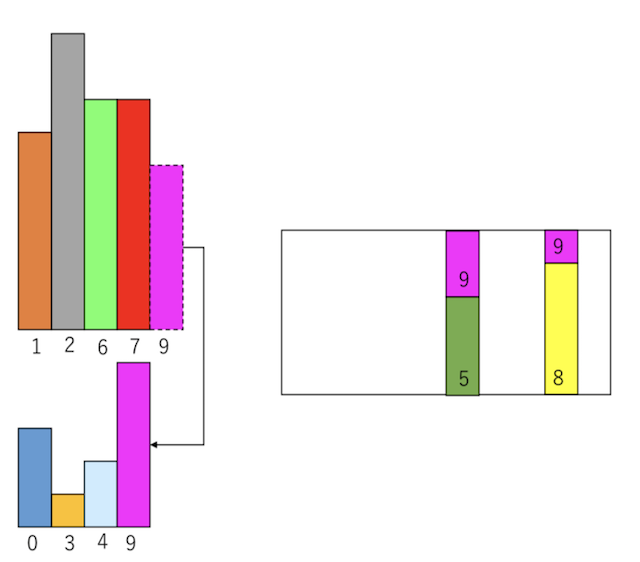
さて、平均より小さいグループと、大きいグループの右端を見る。ここでは、小さいグループのインデックスが8でサイズが4、大きいグループのインデックスが9でサイズが8である。

この時、小さいグループのインデックスに対応する場所にまず小さい箱をそのまま入れる。インデックス8はサイズ4なので、あと1たりない。そこでインデックス9のデータを1だけもらう。小さいグループからインデックス8のデータは取り除かれる。

次に、小さいグループの右端を見ると、インデックスが5で、サイズは3である。そこでインデックス9から2だけもらってくる。

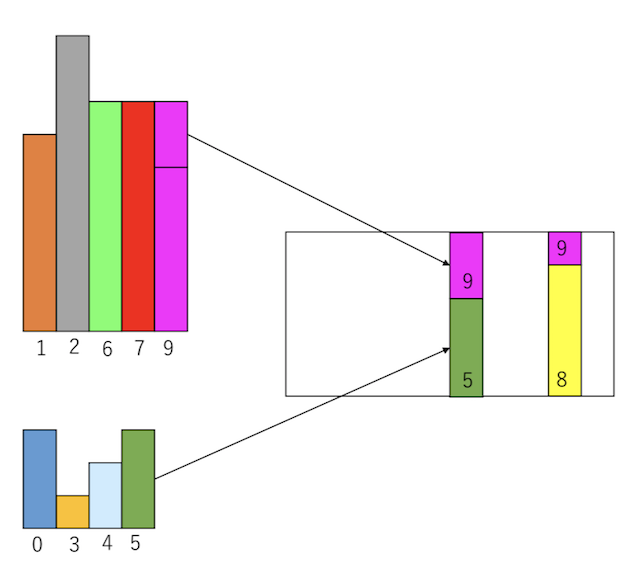
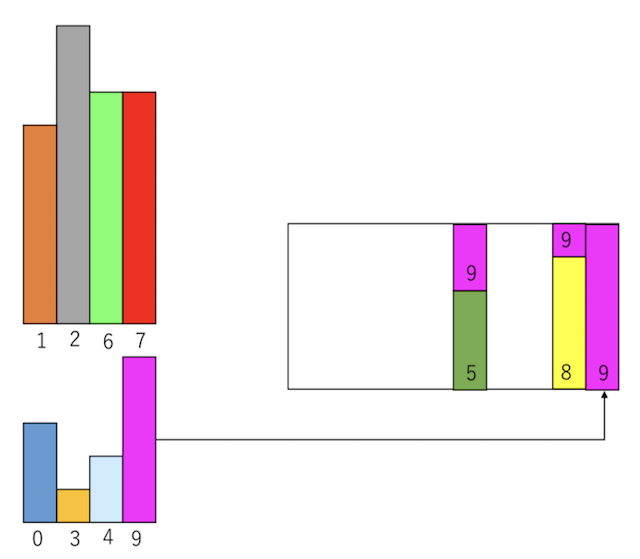
さて、インデックス9のデータは、最初8だったのだが、1が引かれ、次いで2が引かれたため、サイズ5になった。「平均値以下」は小さいグループに入れる約束だったため、インデックス9のデータを「小さいグループ」に移動する。

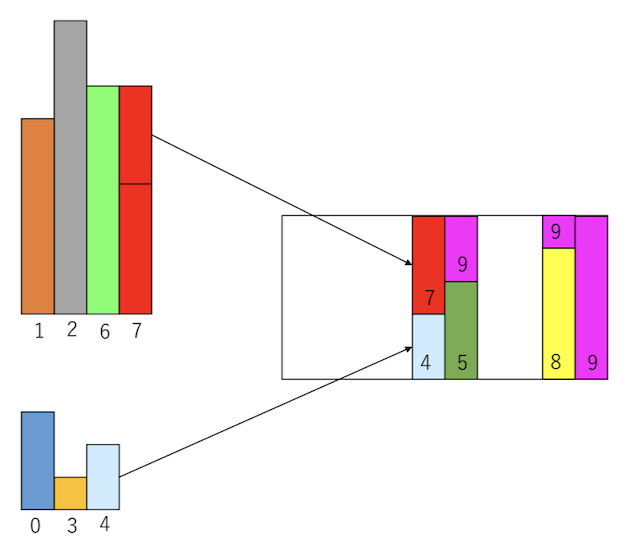
次に「小さいグループ」の右端を見ると、先程追加したインデックス9である。これはサイズ5なので、そのまま容器に詰める。この時、「大きいグループ」の右端のインデックスが7であることを覚えておいて欲しい。アルゴリズム的には「インデックス7からサイズ0」をもらっていることになる。

次の「小さいグループ」の右端はインデックス4であり、サイズ2である。「大きいグループ」の右端のインデックス7からサイズ3だけもらって容器に詰める。するとインデックス7は平均値以下になるため、「小さいグループ」に移動する。

以上の手続きを繰り返すと、最初に示した容器が出来上がる。

それぞれの容器に箱が1個ないし2個詰めてあり、かつ下側の箱が順番どおりになっていることがわかるかと思う。

箱の作成サンプルスクリプト

以上の手続きをRubyで書いてみる。一般には実数を使うが、わかりやすさのため、整数で容器を作ろう。

waker_i.rb

a = [3, 6, 9, 1, 2, 3, 7, 7, 4, 8]

ave = a.inject(0) { |sum, n| sum + n } / a.size

large = []
small = []

a.size.times do |i|
  if a[i] < ave
    small.push i
  else
    large.push i
  end
end

index = Array.new(a.size) { |i| i }

while !small.empty? and !large.empty?
  j = small.pop
  k = large[-1]
  index[j] = k
  a[k] = a[k] - (ave - a[j])
  if a[k] <= ave
    small << k
    large.pop
  end
end

puts "index"
p index
puts "threshold"
p a

実行するとこうなる。

$ ruby waker_i.rb
index
[2, 1, 1, 6, 7, 9, 2, 6, 9, 7]
threshold
[3, 5, 4, 1, 2, 3, 2, 4, 4, 5]

さっきの容器と比べてみよう。indexは「上側のインデックス」であり、thresholdは「上と下の境目の場所」を意味する。ただし、「ぴったり平均値」の値があると、「上の段のインデックス」は意味を持たない。例えば一番右の容器はインデックス9の箱が一つだけ置いてあるが、indexには7が指定されている。これは先程のアルゴリズムで「インデックス7からサイズ0だけもらった」ことを意味するもので、この容器でインデックス7は選ばれないので問題ない。

乱数生成サンプルスクリプト

この「箱」ができてしまえば、重みに従ってインデックスを返す関数を作るのは簡単だと思う。平均値を1に規格化しておけば、「上側のインデックス」をindex、「上下の箱の境目」をthとすると、

def get_index(index, th)
  r = rand(index.size)
  if th[r] > rand
    return r
  else
    return index[r]
  end
end

という関数を呼べば、重みに比例したインデックスを返すことがわかる。

コード全体はこんな感じ。

walker.rb

def make_table(a)
  ave = a.inject(0.0) { |r, i| r += i } / a.size
  a.map! { |v| v / ave }
  small = []
  large = []
  a.size.times do |i|
    if a[i] <= 1.0
      small << i
    else
      large << i
    end
  end

  index = Array.new(a.size) { |i| i }
  while !small.empty? and !large.empty?
    j = small.pop
    k = large[-1]
    index[j] = k
    a[k] = a[k] - (1 - a[j])
    if a[k] <= 1.0
      small << k
      large.pop
    end
  end
  return index, a
end

def get_index(index, th)
  r = rand(index.size)
  if th[r] > rand
    return r
  else
    return index[r]
  end
end

srand(1)
a = [3, 6, 9, 1, 2, 3, 7, 7, 4, 8]
index, th = make_table(a)

result = Array.new(index.size) { 0.0 }
TRIAL = 1000000
tinv = 1.0 / TRIAL.to_f

TRIAL.times do
  i = get_index(index, th)
  result[i] += tinv
end

result.each_with_index do |v, i|
  puts "#{i} #{v * 50}"
end

実行結果はこんな感じ。

$ ruby walker.rb
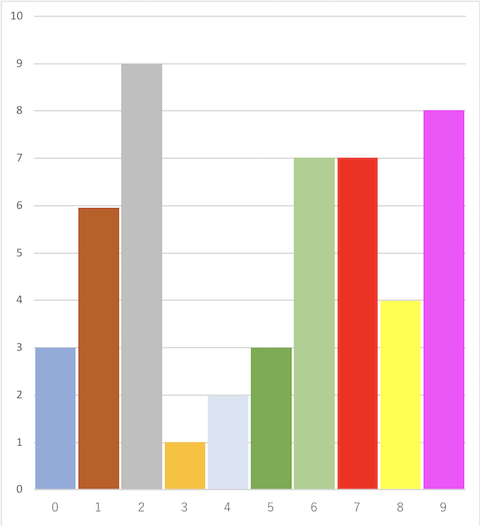
0 2.9956500000019632
1 6.00255000000497
2 9.012450000007979
3 0.9983999999999658
4 2.0149000000009822
5 2.9853000000019527
6 6.985600000005952
7 6.990100000005957
8 3.9948000000029618
9 8.020250000006987

ちゃんと重みに比例してインデックスが選ばれていますね。

まとめ

Walker's Alias Methodの「箱の作り方」の説明をしてみた。原理がわかってからWikipediaなり疑似コードなりを見てみると「なるほど」と思うんだけれど、いきなり疑似コードから動作原理を理解するのは(僕には)難しかった。この記事が誰かの役に立てば幸いである。

参考文献

• Alias method Wikipediaの記述
• New fast method for generating discrete random numbers with arbitrary frequency distributions Walkerによる原著論文
• D. E. Knuth, Art of Computer Programming, Volume 2: Seminumerical Algorithms (3rd Edition) (Addison- Wesley Professional, 1997).

Walker's Alias Methodをモンテカルロ法に適用した応用例として以下のようなものがある。

• Hidemaro Suwa and Synge Todo, "Markov Chain Monte Carlo Method without Detailed Balance", Phys. Rev. Lett. 105, 120603 (2010): 詳細釣り合い条件を満たさない遷移を許すことで、棄却率を下げる
• Kouki Fukui and Synge Todo, "Order-N cluster Monte Carlo method for spin systems with long-range interactions", J. Comput. Phys. 228, 2629
  7 (2009).: 長距離相互作用系においてモンテカルロステップを$O(N)$で実行する。