はじめに
最適化アルゴリズムにおけるメタヒューリスティクスアルゴリズムを主に実装していきます。
メタヒューリスティクスは、問題に依存しないで解を得られることが最大の利点ですが、
実際の問題に対してどうアプローチしていいかがいまいち分かりにくかったのでまとめてみました。
やりたいことは、
- できる限りわかりやすく一般化して、問題に対する共通のインターフェースをつくる
- 各アルゴリズムを比較
です。
また、各アルゴリズムについては別記事にして少しずつ上げていく予定です。
(記事を上げたらリンクをつけていきます)
コードはgithubにあります。
対象アルゴリズム
- 遺伝的アルゴリズム(Genetic Algorithm: GA)
- 実数型遺伝的アルゴリズム
- 人口蜂コロニーアルゴリズム(Artificial Bee Colony: ABC)
- 粒子群最適化(Particle Swarm Optimization: PSO)
- ホタルアルゴリズム(Firefly Algorithm)
- コウモリアルゴリズム(Bat Algorithm)
- カッコウ探索(Cucko Search)
- ハーモニーサーチ(Harmony Search)
- くじらさんアルゴリズム(The Whale Optimization Algorithm: WOA)
- 差分進化(Differential Evolution: DE)
- タブーサーチ(Tabu Search)
※気になるアルゴリズムがあれば追加するかもしれません
対象の問題
問題の詳細は問題編にまとめてあります。
実装した問題は以下です。
- OneMax問題
- 巡回セールスマン問題(Traveling Salesman Problem: TSP)
- エイト・クイーン(Eight Queens)
- ライフゲーム
- 2048
- 最適化アルゴリズムを評価するベンチマーク関数まとめよりいくつか抜粋
比較結果
ニューラルネットワークの学習
利用例の1つとして、ニューラルネットワークのパラメータ調整に最適化アルゴリズムを使った記事を書いたのでリンクを張っておきます。
第9回 今更だけど基礎から強化学習を勉強する 遺伝的アルゴリズム編(閑話)
問題について
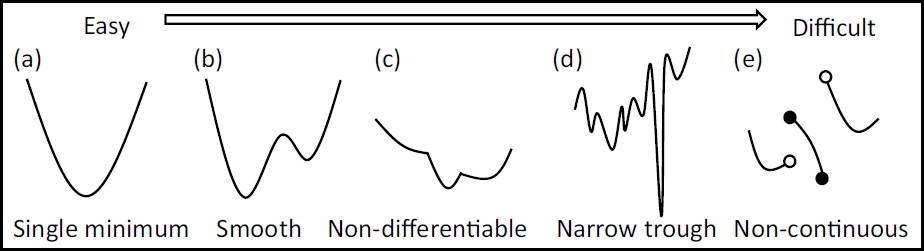
組み合わせ最適化問題とは、ある目的関数(問題)が与えられたとき目的関数の結果が最大(または最小)となる関数への入力(組み合わせ)を見つける事が目的となります。
本記事で想定する目的関数は、一番難しい不連続なもの(図でいうと(e))を想定しています。
(図は最適化アルゴリズムを評価するベンチマーク関数まとめより引用)
(e)のような関数を解く手法の1つにメタヒューリスティクスアルゴリズムがあります。
問題の一般化
一般化の目的は、ある問題を今回紹介するアルゴリズムに適用したい場合、問題側はどういうインターフェース(入力形式だったり出力形式だったり)を用意すればいいかを表現することです。
そしてアルゴリズム側の責務は、そのインターフェースのみを使って結果を出すことになります。
(もちろん各アルゴリズムの特性を理解してそれに合ったチューニングをしたほうが性能は上がります)
本記事では問題側の入力と出力を以下のように定義しました。
| 問題への入力のサイズ | $N$ | |
| 問題への入力 | $\vec{x}=(x_1,x_2,...,x_N)$ | |
| 問題への入力の1要素(入力値) | $x_i (i=1...N)$ | |
| 1要素の範囲 | $Prob_{min}\leqq x_i \leqq Prob_{max}$ | |
| 入力値の配列を問題へ渡した結果(評価値) | $Score = Prob(\vec{x})$ |
$Prob$ は問題毎に変化する要素です。
入力はn次元の配列 $(x_1,x_2,...,x_N)$ で各$x$は問題側で指定した範囲の値を持ちます。
問題側はこの配列を受け取ったら評価し、評価値を返します。
この評価値を最大にすることがアルゴリズム側の責務です。
※入力値は汎用性を持たせるために実数値としています。ので、問題によっては評価するときに離散値にする必要があります。
※最大値を対象にしています。最小にしたい場合は問題側でマイナスする事としています。
プログラムコードでのインターフェースの表現
問題を表すクラスと入力を表すクラスを分離しています。
- 問題クラス
問題を表すクラスの責務は入力の作成及び、入力を受け取ったときの評価です。
各問題で共通に実装しなければいけない内容のみ記載しています。
import random
class Problem():
def __init__(self, size):
self.size = size # 目的関数への入力サイズ(N)
self.MIN_VAL = 0 # 要素の最低値(問題毎に指定)(Prob_min)
self.MAX_VAL = 1 # 要素の最大値(問題毎に指定)(Prob_max)
def create(self, arr=None):
"""
入力の値を生成します。
引数が None の場合はランダムな入力を作成し、
値が指定されている場合はその値で入力を作成します。
ProblemDataについては後述
"""
o = ProblemData(self, self.size)
if arr is None:
arr = [ self.randomVal() for _ in self.size]
o.setArray(arr)
return o
def randomVal(self):
"""
1要素のランダムな値を返す関数です
"""
return self.MIN_VAL + random.random() * (self.MAX_VAL - self.domain.MIN_VAL)
def init(self):
"""
問題の初期化、任意で作成
"""
raise NotImplementedError()
def eval(self, arr):
"""
入力に対して評価をし、結果を返します
ここが目的関数部分に相当します
"""
raise NotImplementedError()
- 問題への入力クラス
入力クラスの責務は入力の操作及び、評価値をキャッシュして返すことです。
問題によっては評価値を出すことが一番時間がかかるので、入力クラス側でキャッシュさせます。
これにより問題クラス側でキャッシュを考える必要がなくなるようにしています。
class ProblemData():
def __init__(self, domain, size):
self.domain = domain # 問題クラスです
self.size = size # 目的関数への入力サイズ
self.arr = [ 0 for _ in range(self.size)] # 入力値
self.score = None # 評価値(キャッシュ用)
def copy(self):
"""
自身のcopyを返します
"""
o = ProblemData(self.domain, self.size)
o.arr = [ x for x in self.arr] # deepcopy
o.score = self.score
return o
def getArray(self):
"""
入力値を返します。
安全のため、複製して返します。
"""
return [ x for x in self.arr]
def setArray(self, arr):
"""
入力値を設定します。
"""
# 下限と上限でまるめます
for i in range(len(arr)):
if arr[i] < self.domain.MIN_VAL:
arr[i] = self.domain.MIN_VAL
if arr[i] > self.domain.MAX_VAL:
arr[i] = self.domain.MAX_VAL
self.arr = arr
self.score = None # キャッシュクリア
def getScore(self):
"""
評価値を返します
"""
if self.score is not None:
return self.score
self.score = self.domain.eval(self.arr)
return self.score
アルゴリズムの一般化
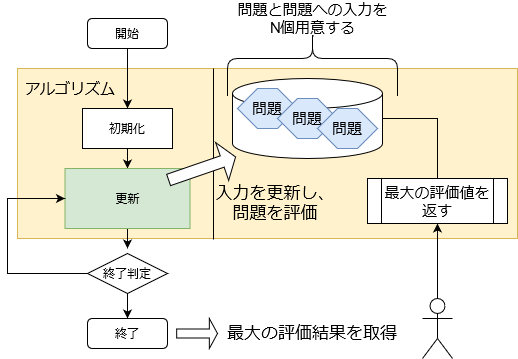
アルゴリズムでは問題を $M$ 個持ちます。
(必ず持つ必要はないのですが、複数問題を持つアルゴリズムしか今のところありません)
各問題への入力を更新することで、評価値が最大となる問題を探すことが目的となります。
※実装では評価値を最大にする場合のみを想定しています。
- アルゴリズムクラス
class IAlgorithm():
def init(self, problem):
"""
初期化関数です
引数で問題を関連付けし、アルゴリズム側の初期化も行います
"""
raise NotImplementedError()
def step(self):
"""
アルゴリズム側の1回の更新です
"""
raise NotImplementedError()
def getMaxElement(self):
"""
アルゴリズム内の最大評価値の問題を返します
"""
raise NotImplementedError()
def getElements(self):
"""
アルゴリズム内で使っている全問題を返します
"""
raise NotImplementedError()
def getScores(self):
"""
アルゴリズム内で使っている全問題の評価値を返します
"""
return [x.getScore() for x in self.getElements()]
def getMaxScore(self):
"""
アルゴリズム内の最大評価値を返します
"""
return self.getMaxElement().getScore()
main関数
上記の問題クラスとアルゴリズムクラスは、以下のように動かすことを想定しています。
prob = Problem(N) # N次元の入力をもった問題を作成
alg = IAlgorithm() # アルゴリズムを指定
# 初期化
prob.init()
alg.init(prob) # アルゴリズムと問題を紐づけ
# 任意の回数loop
for i in range(100):
alg.step()
# 結果
result = alg.getMaxElement()
print("max score : {}".format(result.getScore()))
print("max values: {}".format(result.getArray()))