はじめに
最適化アルゴリズムの実装シリーズです。
まずは概要を見てください。
コードはgithubにあります。
粒子群最適化
概要
粒子群最適化(Particle Swarm Optimization:PSO)とは、スズメやイワシといった小さい個体が大きな群れを作って効率よく餌を探す行動に着目して作られたアルゴリズムです。
群れに属する個体は以下のような行動モデルに基づいているといわれています。
- 近くにいる個体に影響されて行動する
- 他の個体の近くにとどまろうとするが、一定以上は近づかない
- 他の個体の速度に合わせて移動する
参考
・粒子群最適化法(PSO)を救いたい
・進化計算アルゴリズム入門 生物の行動科学から導く最適解(amazonリンク)
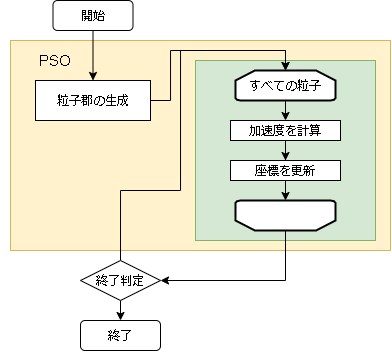
アルゴリズム
各個体を粒子と呼びます。
全粒子の中で今までに一番良かった位置をグローバルベスト、自分自身がこれまでに見つけた位置の中で一番良かった位置をパーソナルベストとして覚えておきます。
これら2つの情報を元に次の自分の位置を更新していく探索が粒子群最適化となります。
- アルゴリズムのフロー
- 問題との対応
| 問題 | 粒子群最適化 |
|---|---|
| 入力値の配列 | 粒子 |
| 入力値 | 粒子の座標 |
| 評価値 | 粒子の評価値 |
- コード内で使う変数の意味
| 変数名 | 数式 | 意味 | 所感 |
|---|---|---|---|
| problem | 任意の問題のクラス(問題編を参照) | ||
| particle_max | 粒子の数 | ||
| inertia | $I$ | 慣性係数 | 加速度の減少率 |
| global_acceleration | $A_g$ | 加速係数(グローバルベスト) | グローバルベストに近づく割合 |
| personal_acceleration | $A_p$ | 加速係数(パーソナルベスト) | パーソナルベストに近づく割合 |
| particles | 粒子の配列 | ||
| particles[i]["personal"] | i番目の粒子のパーソナルベスト | ||
| particles[i]["v"] | i番目の粒子の速度 |
粒子の位置と加速度の更新
加速度と座標の初期値は空間内の範囲でランダムに初期化します。
位置を求めるにあたりまずは加速度が更新されます。
時刻(t)から時刻(t+1)への速度はグローバルベストとパーソナルベストを用いて以下の式となります。
\begin{align}
\vec{v_i}(t+1) =& \quad I \vec{v_i}(t) \\
&+ A_g ( \vec{g}(t) - \vec{x_i}(t) ) \times rand[0,1] \\
&+ A_p ( \vec{p}(t) - \vec{x_i}(t) ) \times rand[0,1] \\
\end{align}
$I$ は慣性係数、$A_g$と$A_p$は加速係数で3つとも1より小さい値を指定します。
また、$\vec{g}$はグローバルベストの位置を表し、$\vec{p}$はその粒子が持っているパーソナルベストの位置を表します。
$rand[0,1]$ は0~1の乱数です。
コード全体
コード全体です。
import math
import random
import numpy as np
class PSO():
def __init__(self,
particle_max,
inertia=0.9,
global_acceleration=0.9,
personal_acceleration=0.9,
):
self.particle_max = particle_max
self.inertia = inertia
self.global_acceleration = global_acceleration
self.personal_acceleration = personal_acceleration
def init(self, problem):
self.problem = problem
# 初期粒子群を生成
self.global_best = None
self.particles = []
for _ in range(self.particle_max):
o = problem.create() # ランダムな位置に粒子を作成
# 初期加速度
v = [(problem.MAX_VAL - problem.MIN_VAL) * random.uniform(-1, 1) for _ in range(problem.size)]
# パーソナルベストと速度の情報を付与する
d = {
"particle": o,
"personal": None,
"v": np.asarray(v),
}
self.particles.append(d)
# パーソナルベストとグローバルベストの更新
self._updateBest(d)
def step(self):
# 各粒子に対して
for particle in self.particles:
# 各座標を出力(numpy化してベクトル計算をしやすくしています)
pos = np.asarray(particle["particle"].getArray())
g_pos = np.asarray(self.global_best.getArray())
p_pos = np.asarray(particle["personal"].getArray())
# 加速度を計算
v = particle["v"]
v = self.inertia * v
v += self.global_acceleration * (g_pos - pos) * random.random()
v += self.personal_acceleration * (p_pos - pos) * random.random()
particle["v"] = v
# 座標を更新
particle["particle"].setArray(pos + v)
# パーソナルベストとグローバルベストの更新
self._updateBest(particle)
def _updateBest(self, particle):
# パーソナルベストの更新
if particle["personal"] is None or particle["personal"]["particle"].getScore() < particle["particle"].getScore():
# パーソナルベストとしてコピーして保存する
particle["personal"] = particle["particle"].copy()
# グローバルベストの更新
if self.global_best is None or self.global_best.getScore() < particle["particle"].getScore():
# グローバルベストとしてコピーして保存する
self.global_best = particle["particle"].copy()
ハイパーパラメータ例
各問題に対して optuna でハイパーパラメータを最適化した結果です。
最適化の1回の試行は、探索時間を2秒間として結果を出しています。
これを100回実行し、最適なハイパーパラメータを optuna に探してもらいました。
| 問題 | global_acceleration | inertia | particle_max | personal_acceleration |
|---|---|---|---|---|
| EightQueen | 0.7839287773369192 | 0.8235075101639827 | 28 | 0.9467161852490191 |
| function_Ackley | 0.11778673996028691 | 0.062427889313103786 | 47 | 0.6739352477292235 |
| function_Griewank | 0.1939265329859151 | 0.9886894890970368 | 21 | 0.9870275206300417 |
| function_Michalewicz | 0.5004800811479669 | 0.7828732926170527 | 23 | 0.5089894615381799 |
| function_Rastrigin | 0.7067489271622391 | 0.8580154745241855 | 31 | 0.2988574441297245 |
| function_Schwefel | 0.6251927739536115 | 0.9030347446658787 | 42 | 0.2540225969044799 |
| function_StyblinskiTang | 0.970834173658411 | 0.9365843106326938 | 31 | 0.9298455482443944 |
| LifeGame | 0.539526858214075 | 0.08845815509172461 | 14 | 0.4249882950339423 |
| OneMax | 0.5056801912085691 | 0.6273453999411102 | 42 | 0.29656995228071314 |
| TSP | 0.7018381808726923 | 0.888427895281042 | 48 | 0.6464768696714887 |
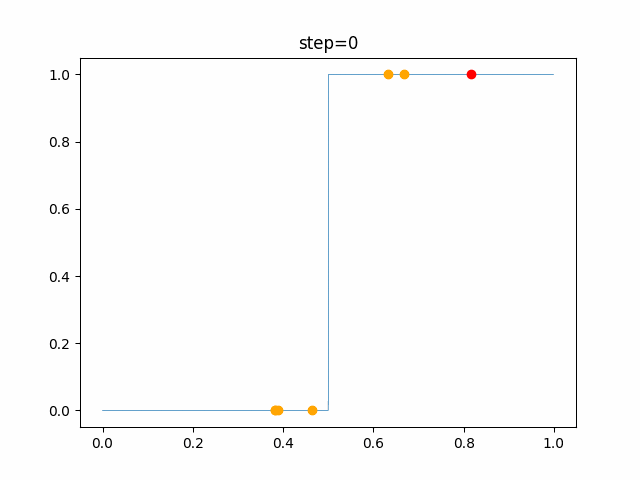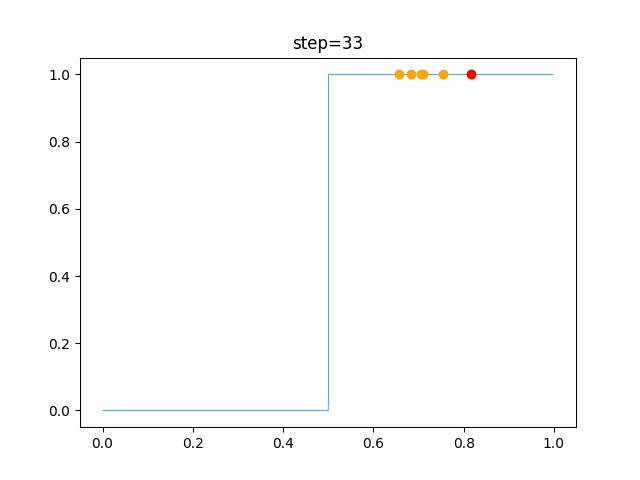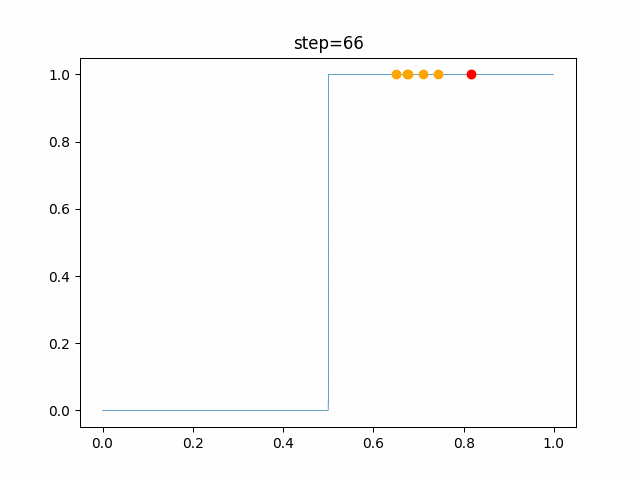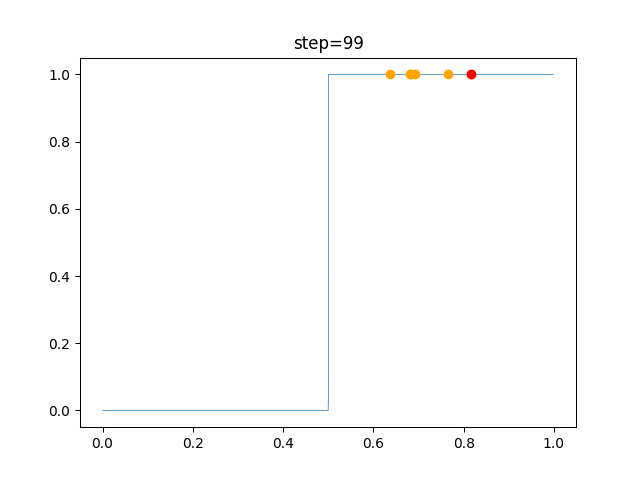
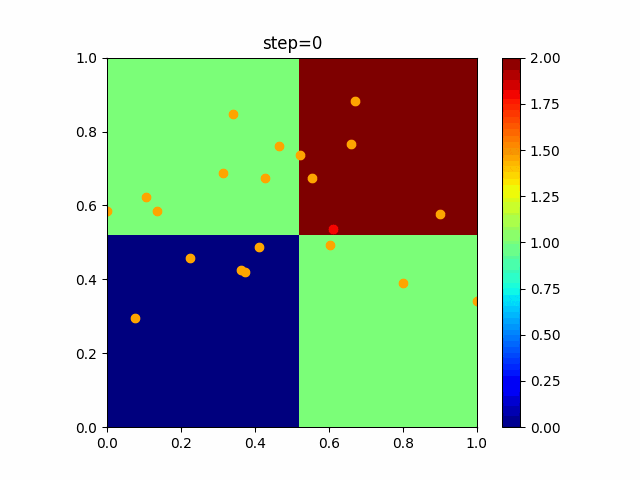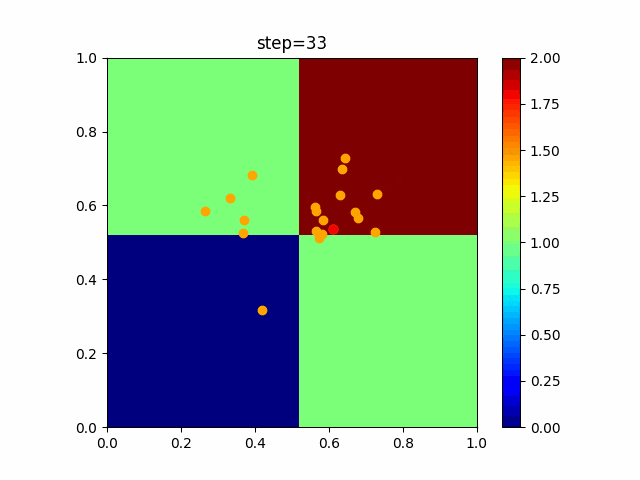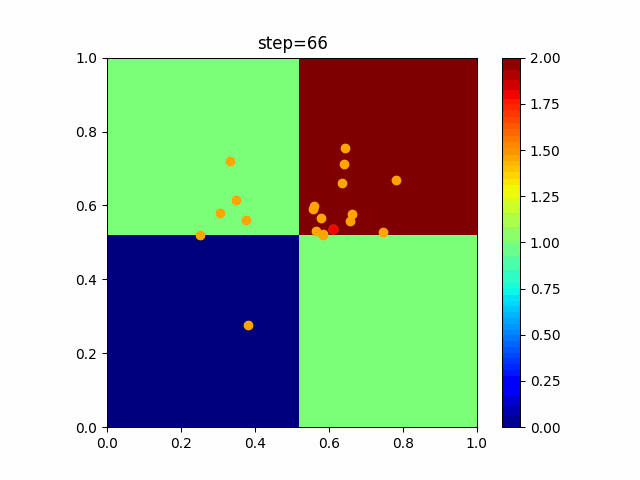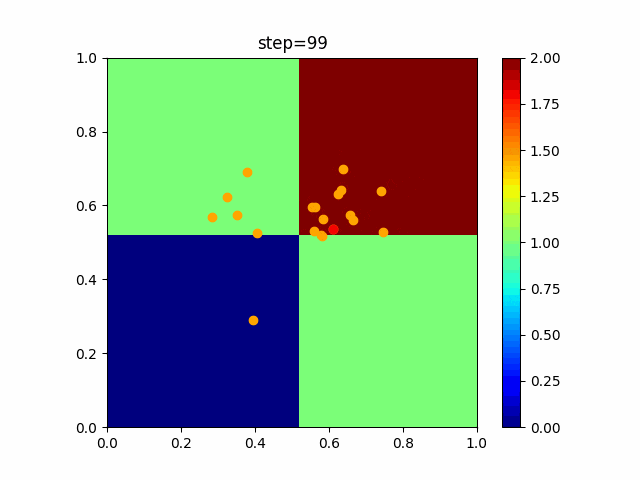
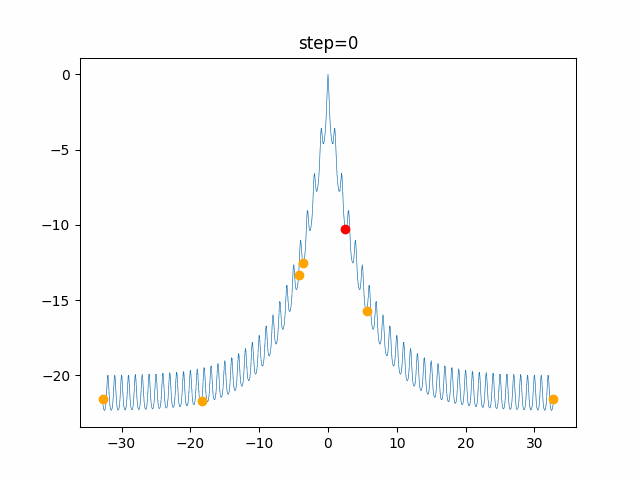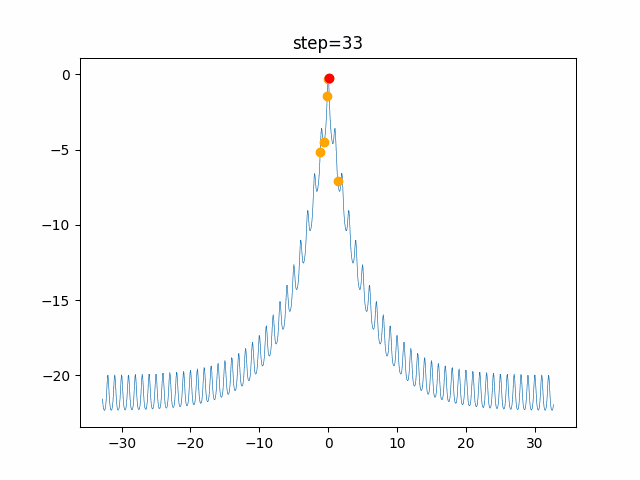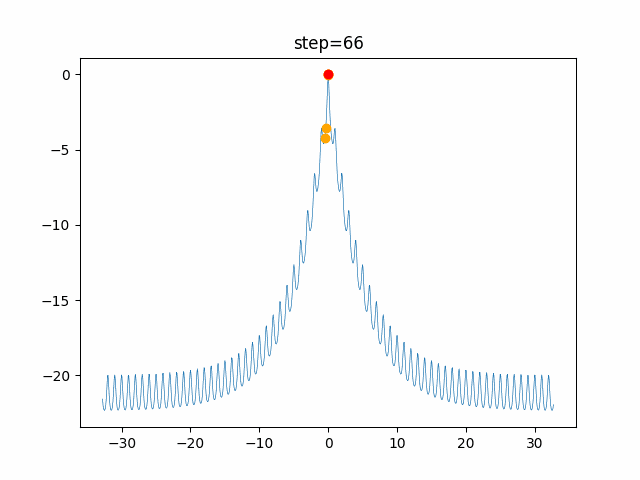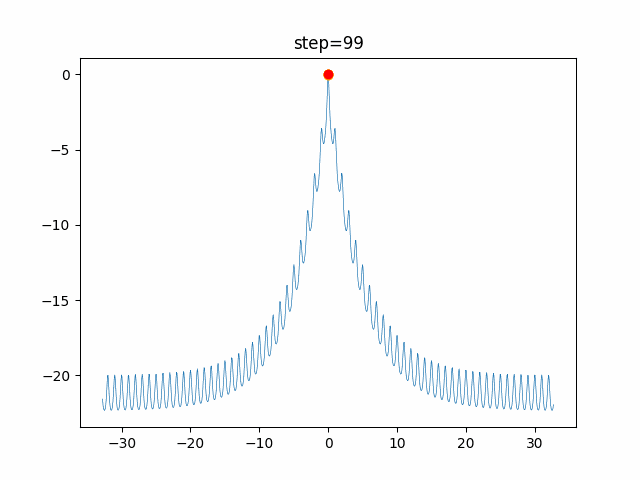
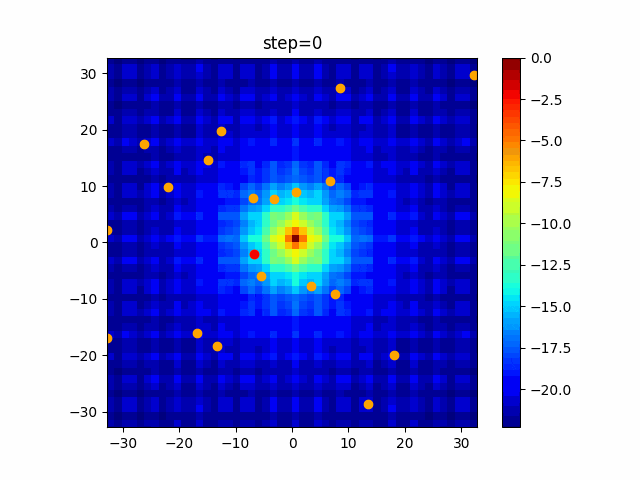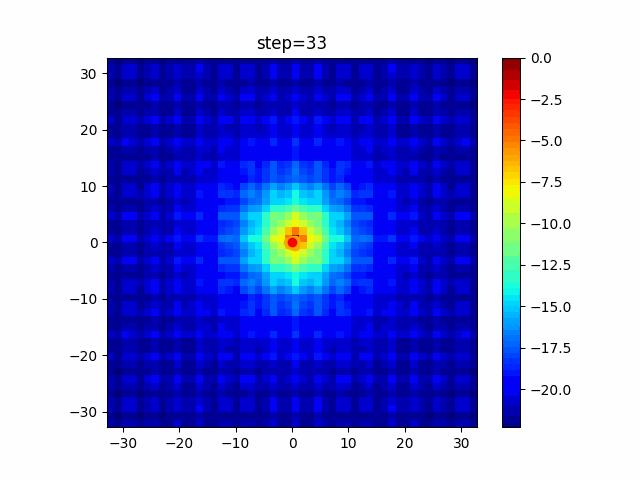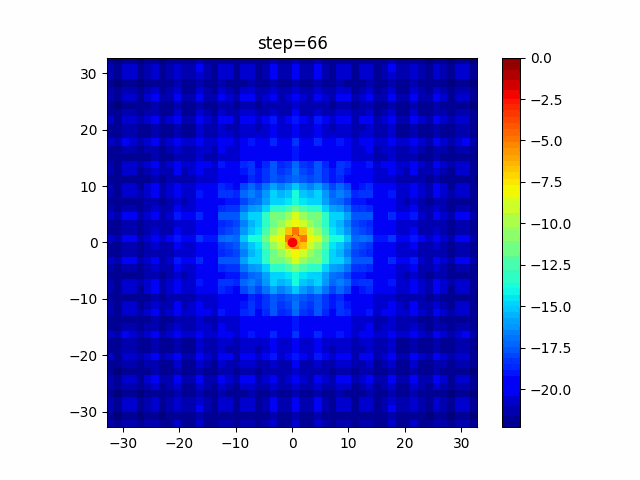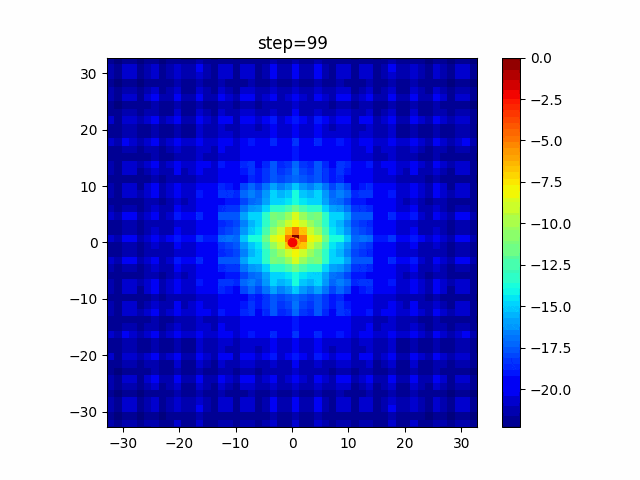
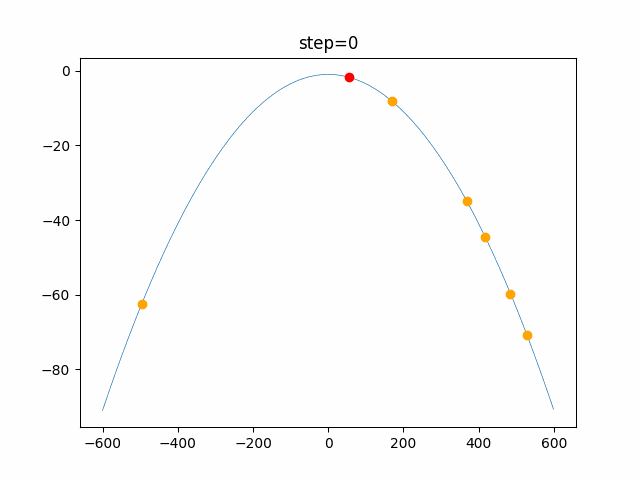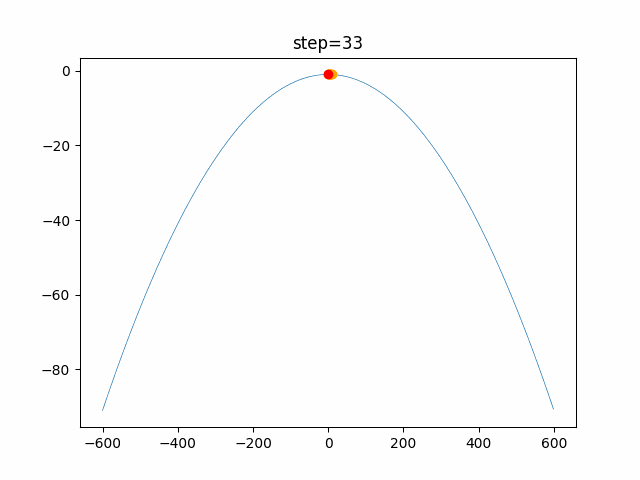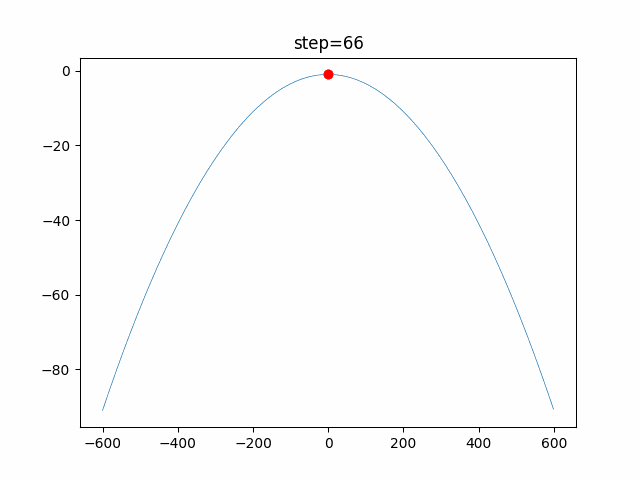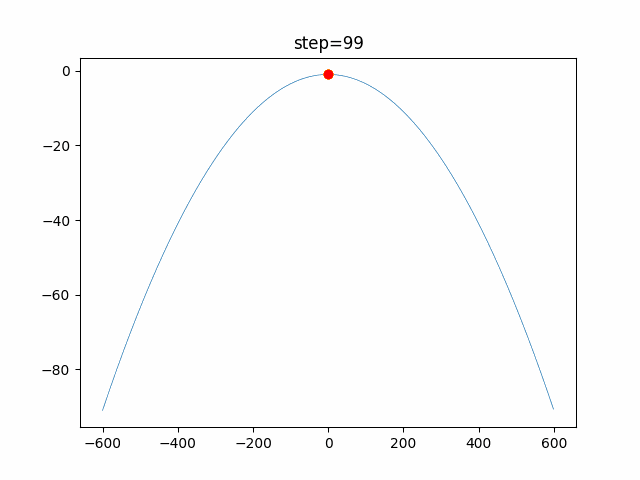
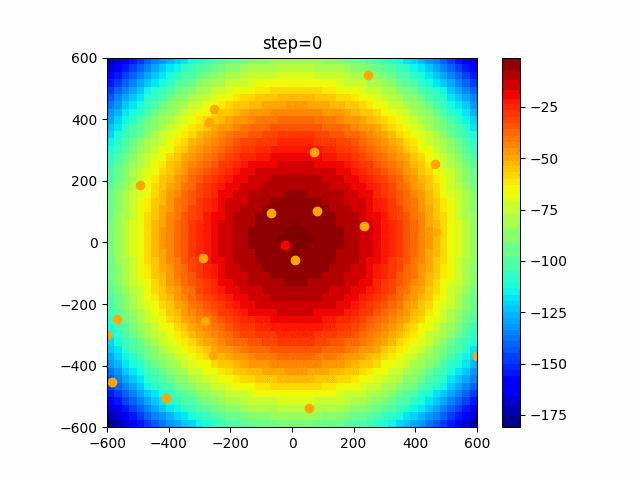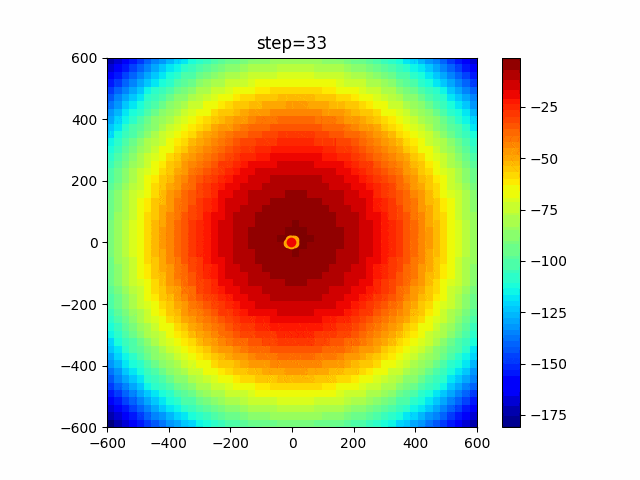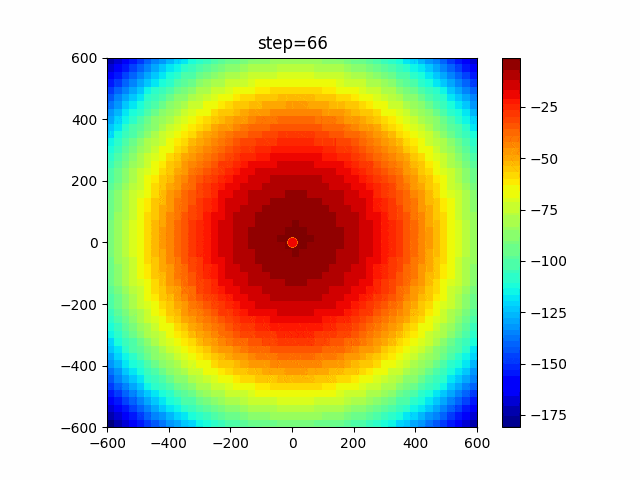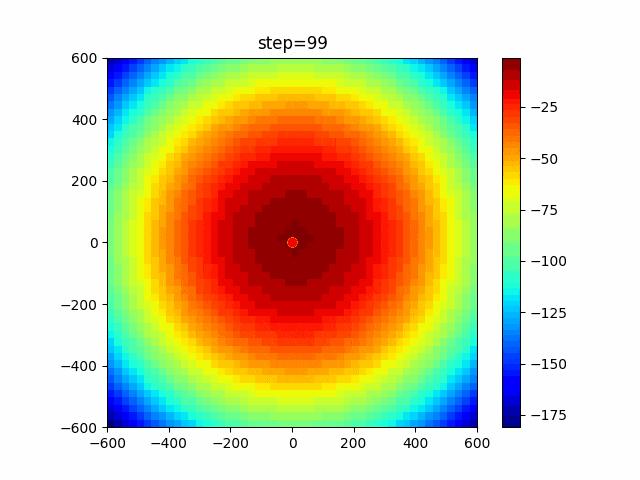
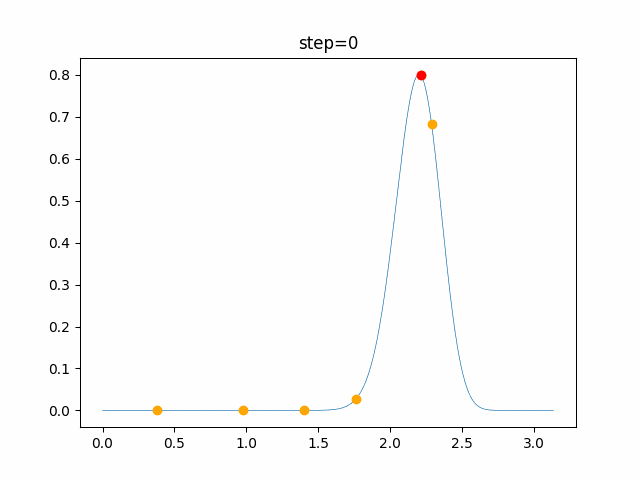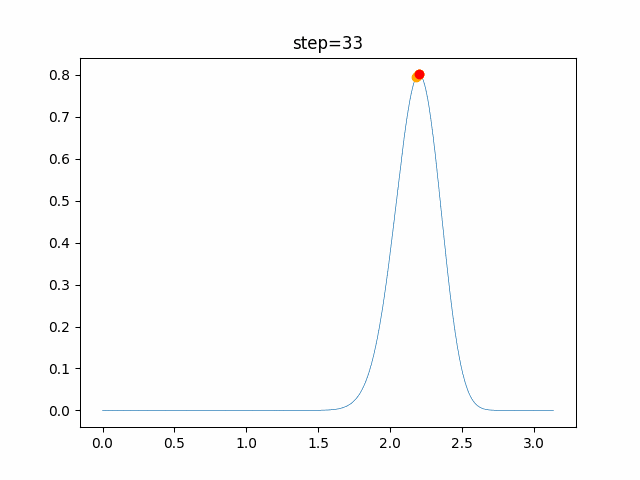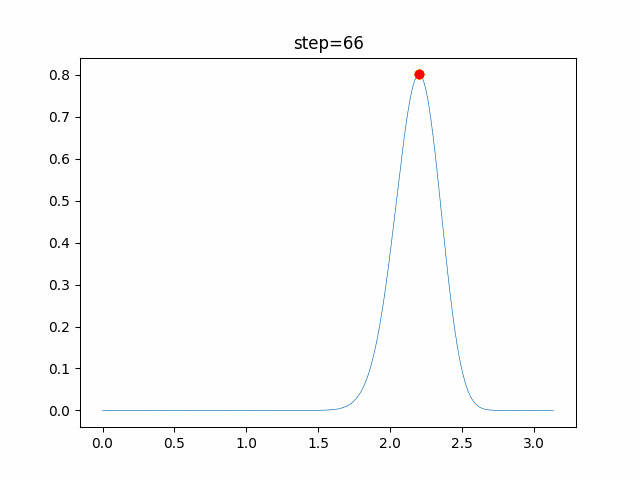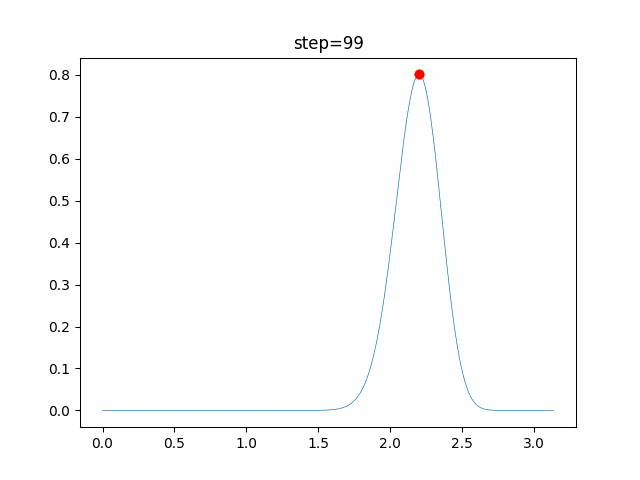
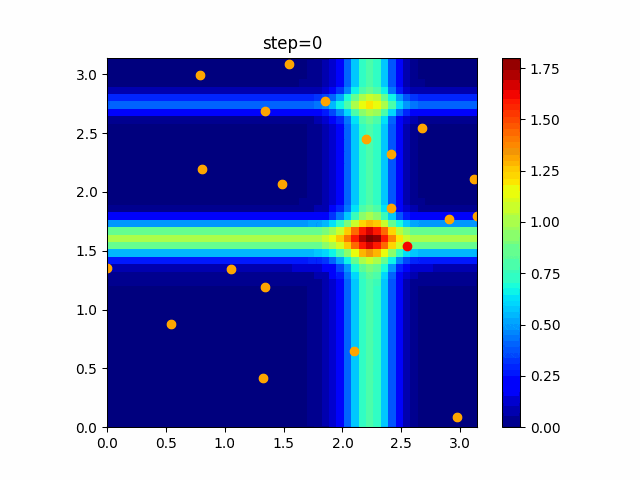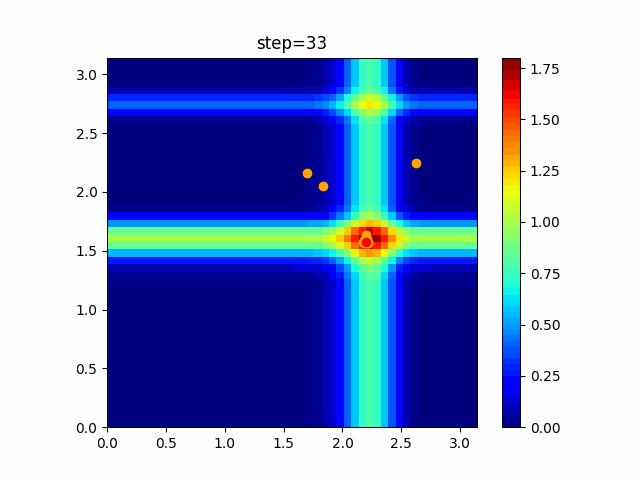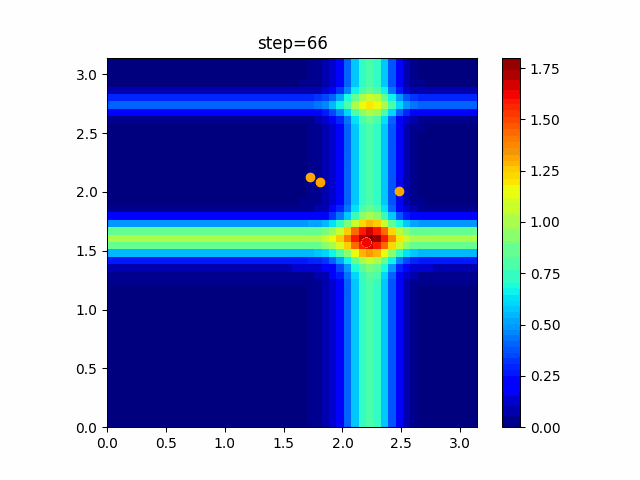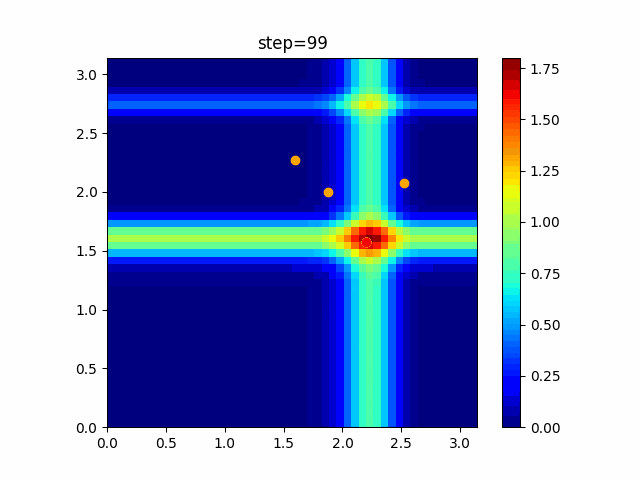
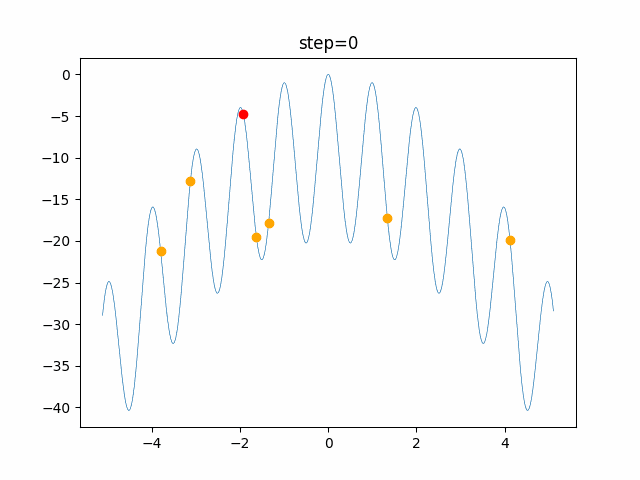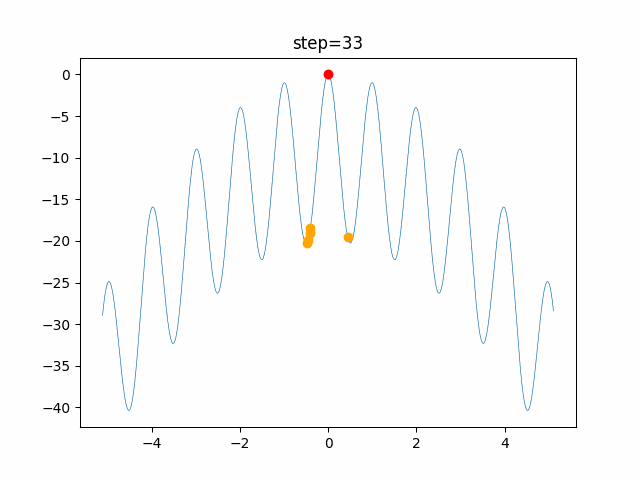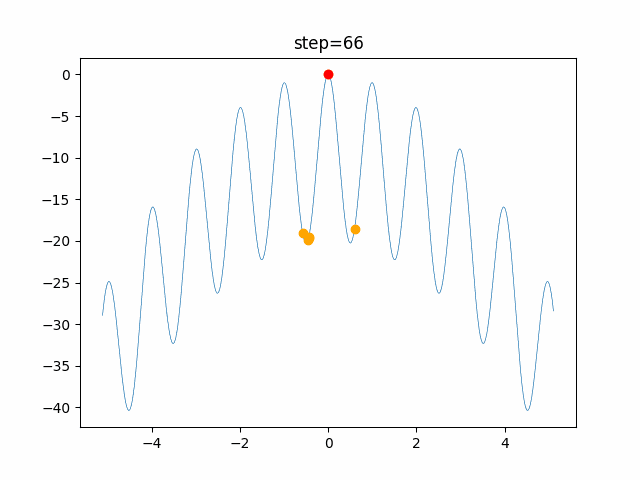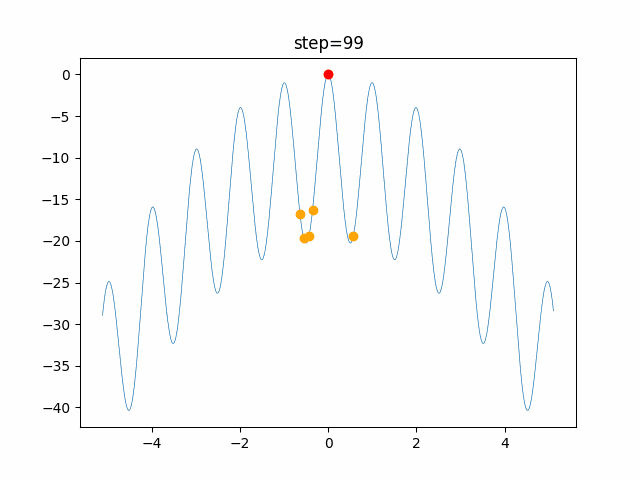
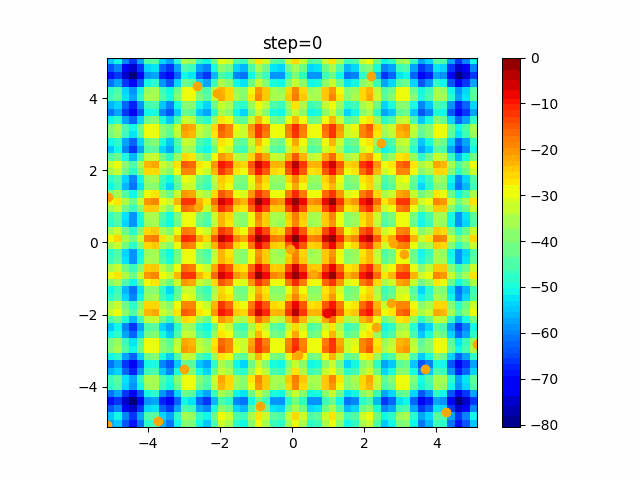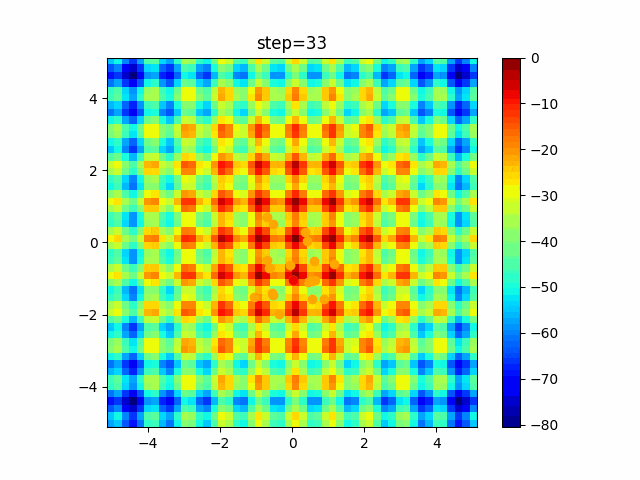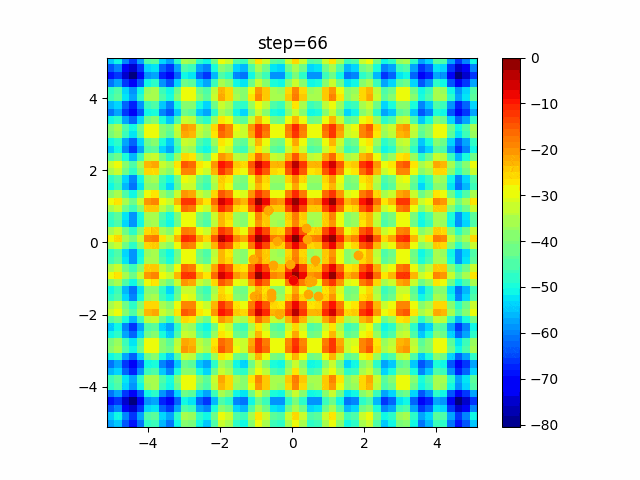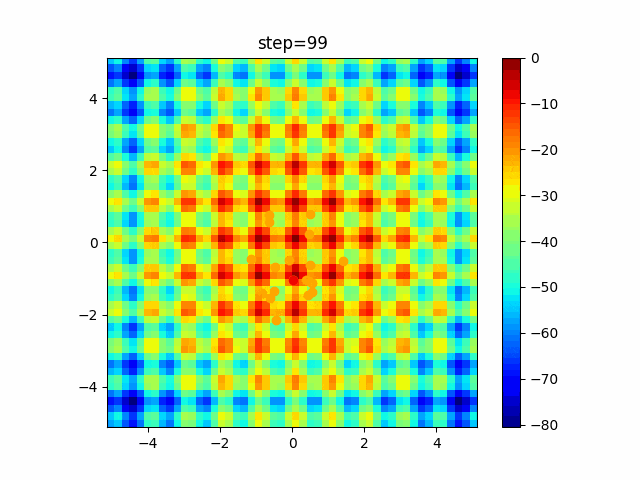
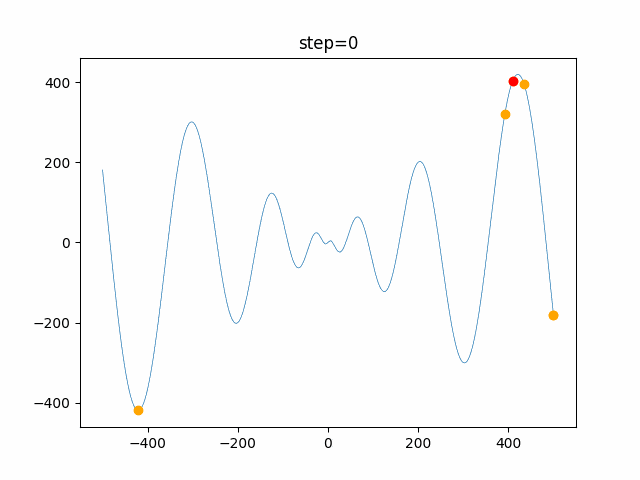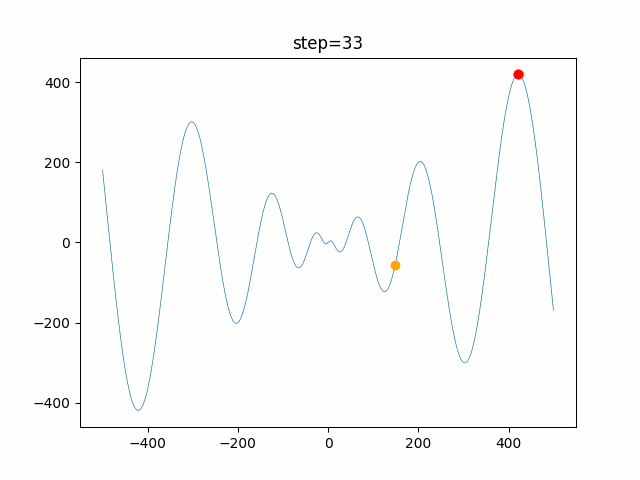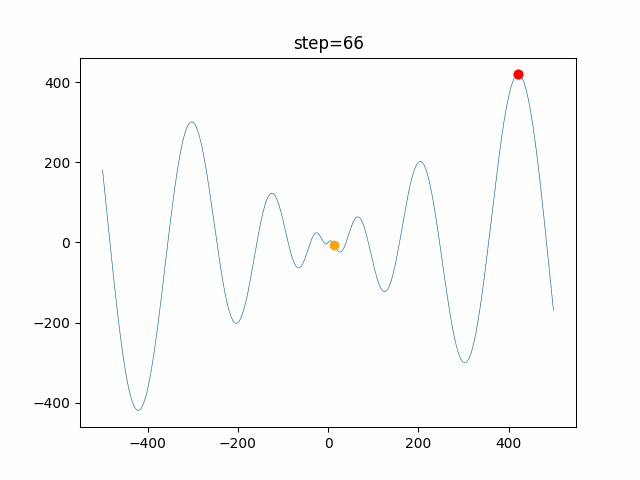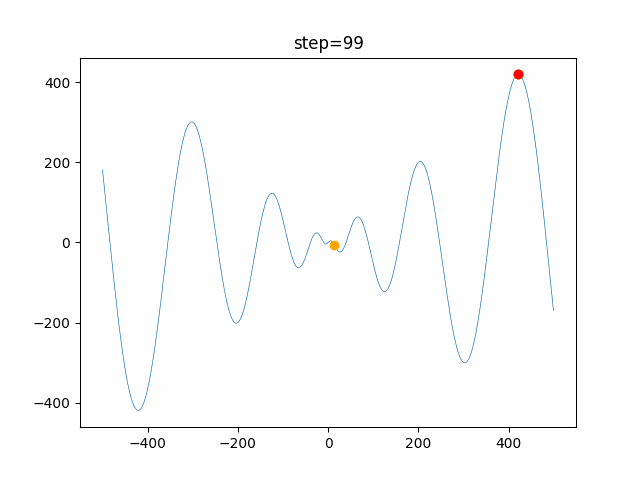
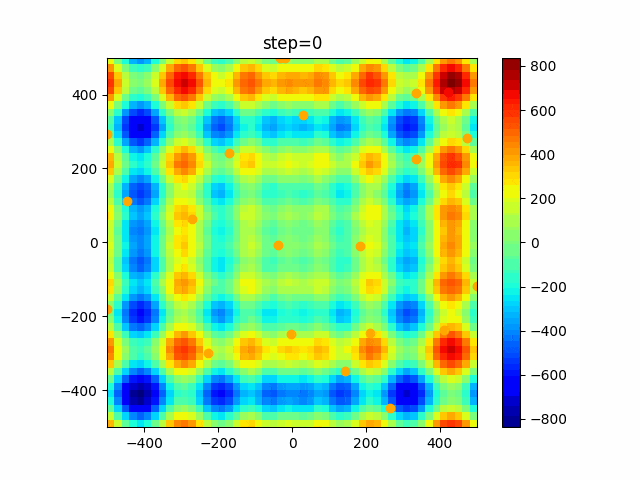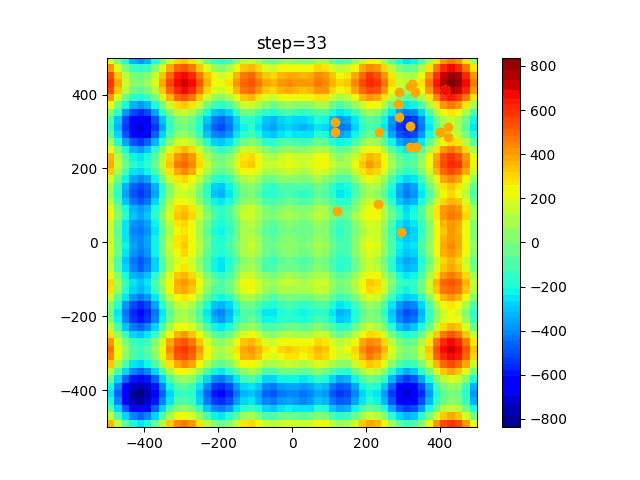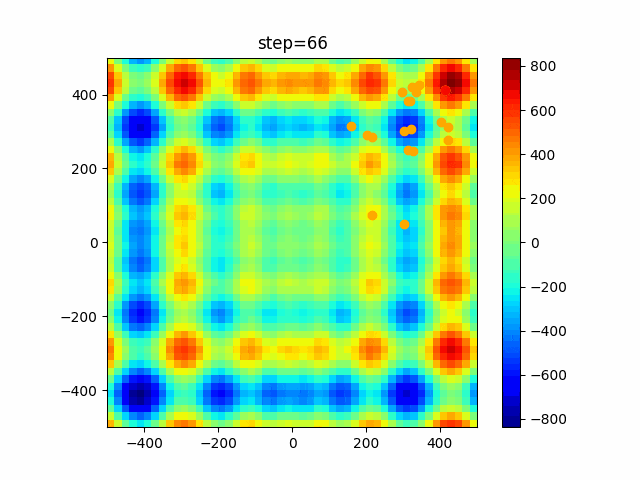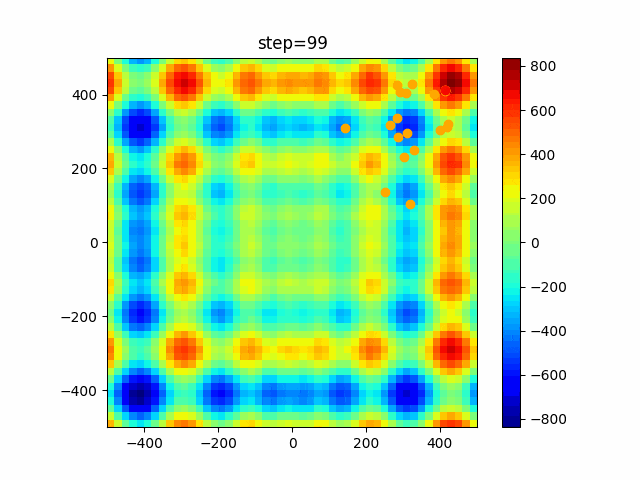
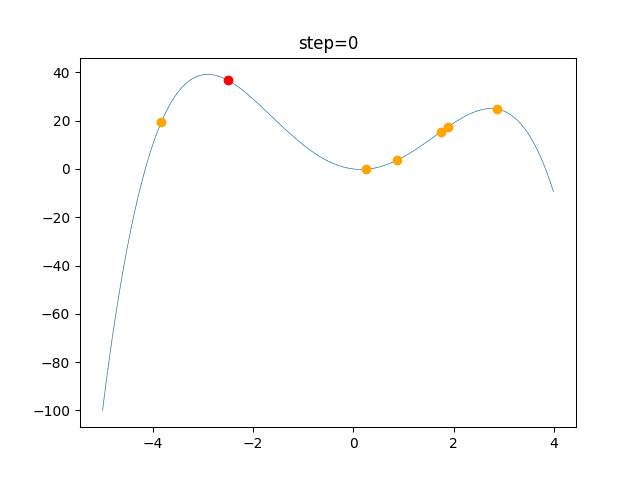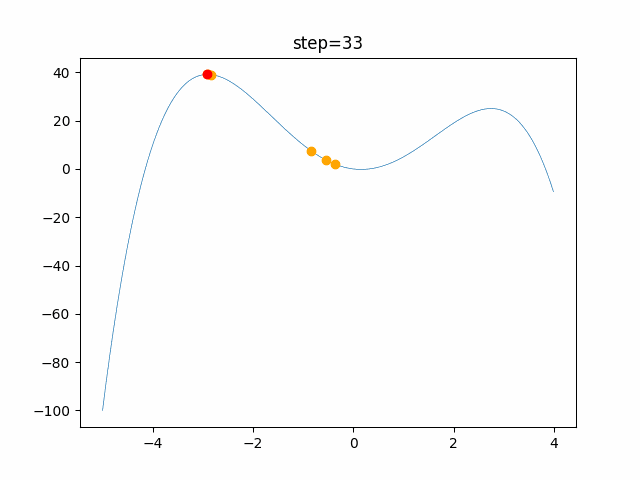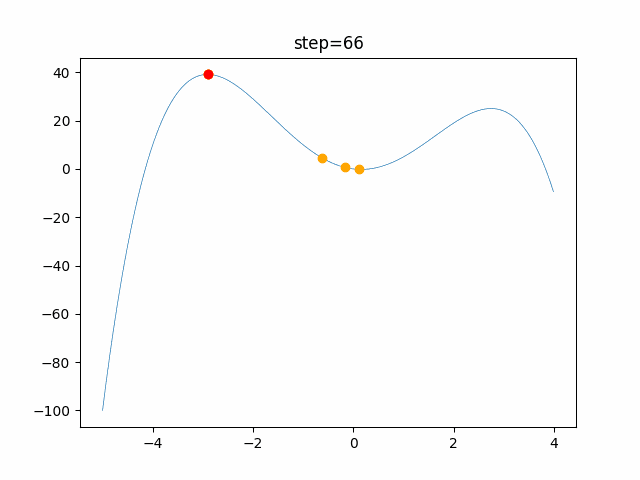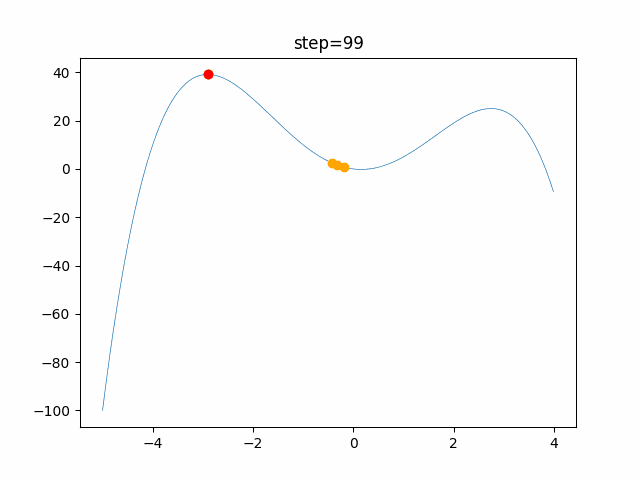
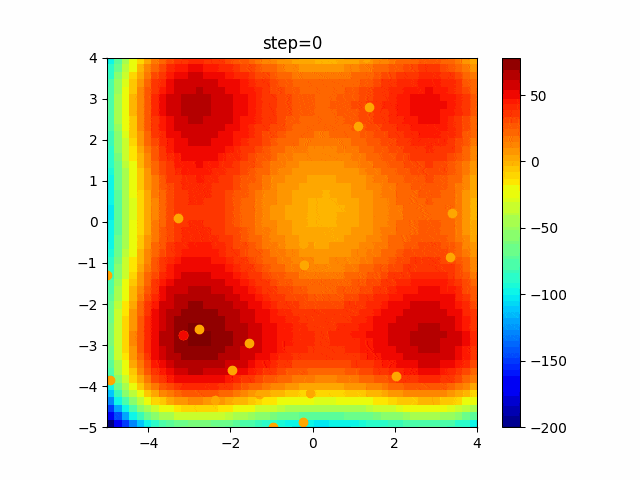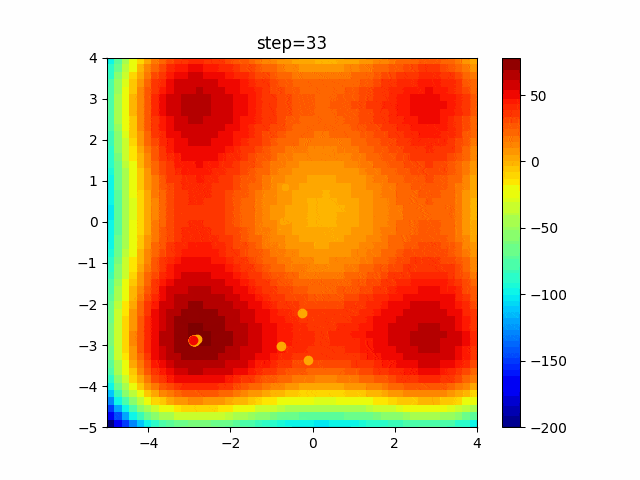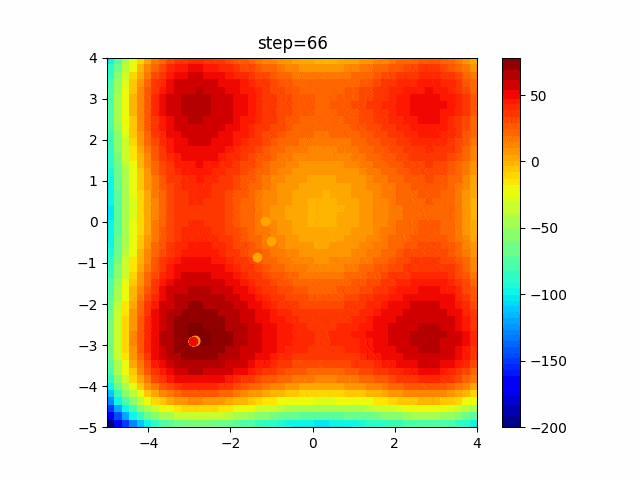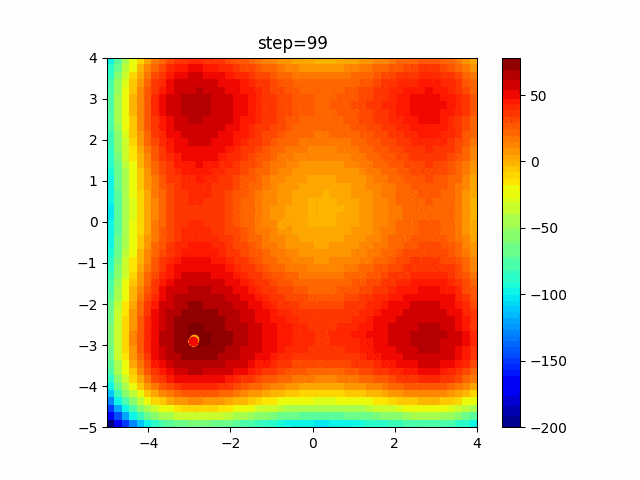
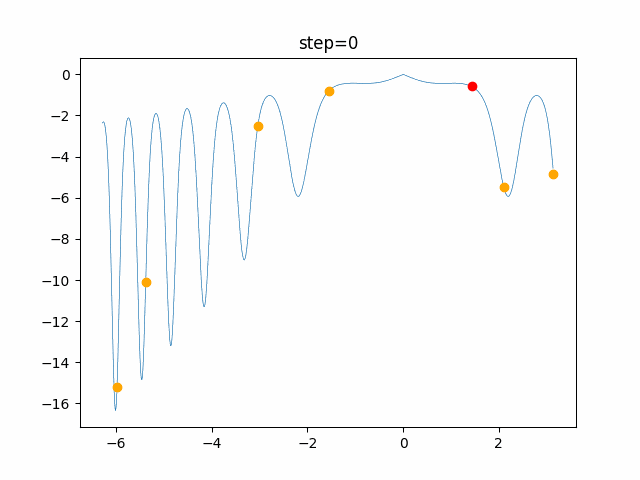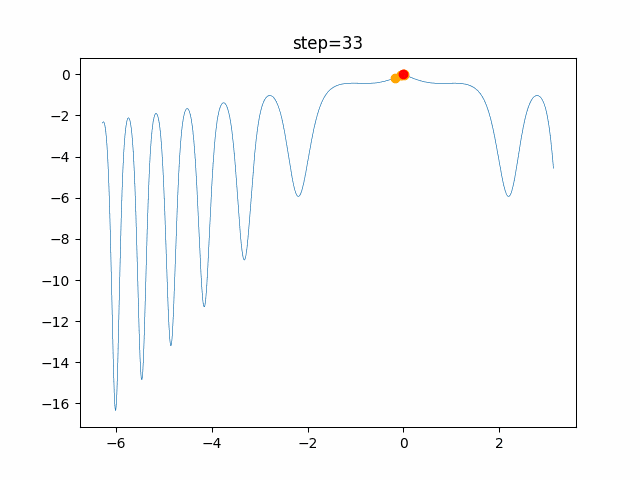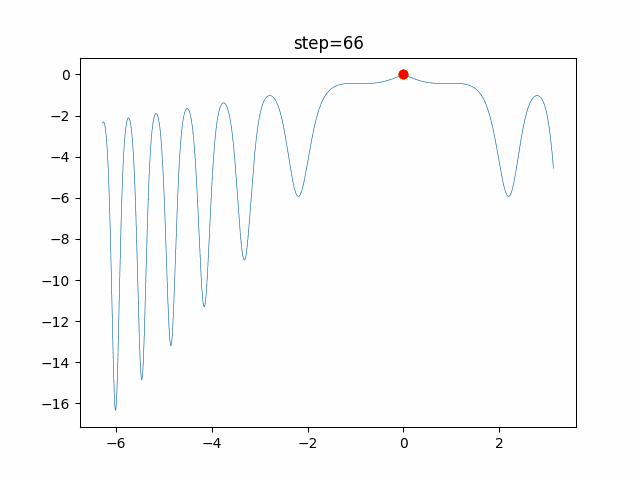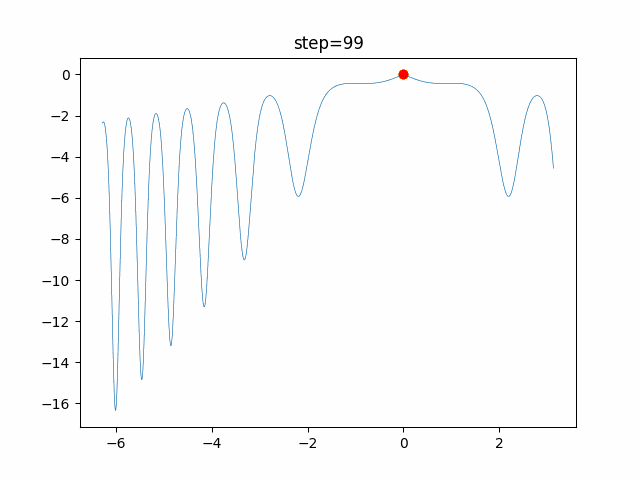
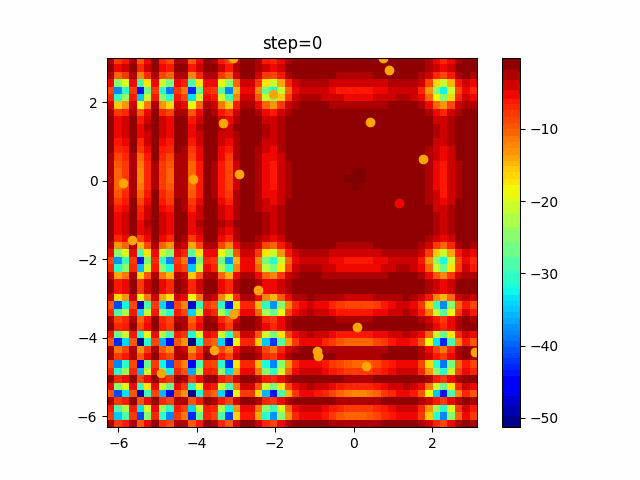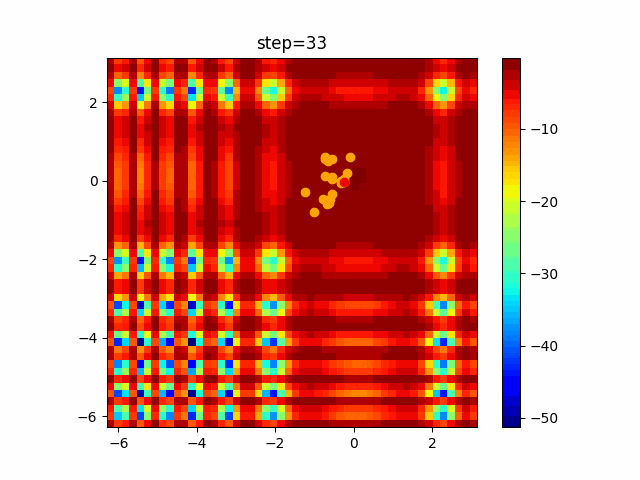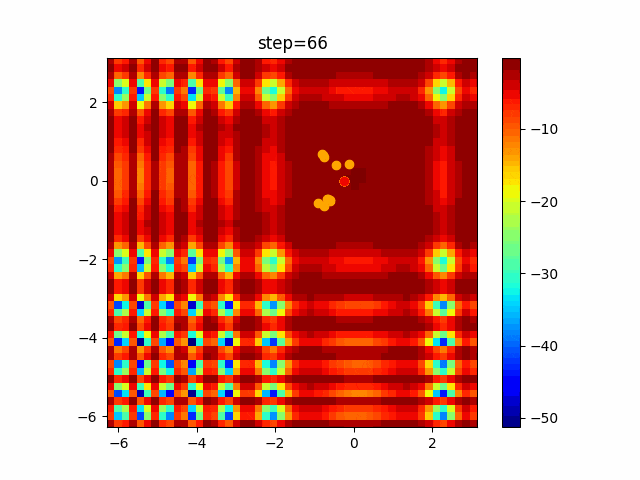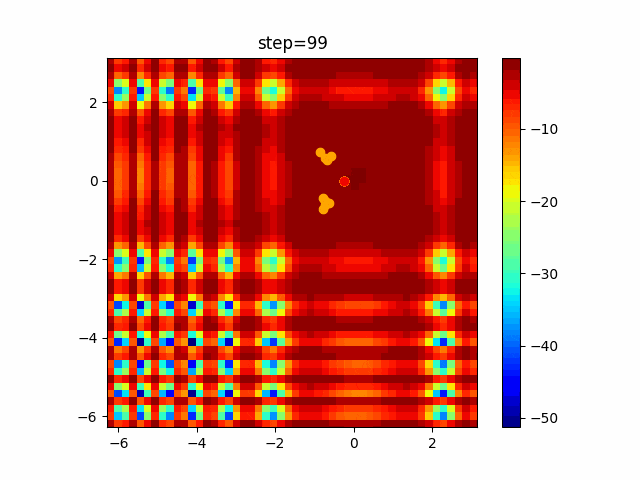
実際の動きの可視化
1次元は6個体、2次元は20個体で100step実行した結果です。
赤い丸がそのstepでの最高スコアを持っている個体です。
パラメータは以下で実行しました。
PSO(N, inertia=0.2, global_acceleration=0.2, personal_acceleration=0.2)
OneMax
- 1次元
- 2次元
function_Ackley
- 1次元
- 2次元
function_Griewank
- 1次元
- 2次元
function_Michalewicz
- 1次元
- 2次元
function_Rastrigin
function_Schwefel
- 1次元
- 2次元
function_StyblinskiTang
- 1次元
- 2次元
function_XinSheYang
- 1次元
- 2次元
あとがき
現状の最適解にみんなが集まってくる様子が粒子群っぽくていいですね。
アルゴリズム的には、一度局所解に入ってしまうとみんなそこに集まってしまうので抜け出せなさそうなイメージです。
また現状の最適解周辺でうろうろしている個体はパーソナルベストとグローバルベストの両方に引っ張られて釣り合っている個体ですね。
今回実装した内容は一番シンプルなPSOなので、改良されたPSOならこれらの問題点が解決されているかもしれません。