-1. 私は誰?
秋田で
- 群知能(おそらくメイン)
- 競技プログラミング(趣味)
- DeepLearning(来年からやりそう)
を主に研究している学生のガナリヤです。
環境構築・プログラミング言語の理解を苦手としています。
0. はじめに
群知能という最適化分野は、海外だとメジャーですが、日本ではかなり影が薄い分野です(工学系の方が多いので数理最適化などが多いのかもしれません)。
このままだと寂しいので、今回は、群知能のメジャーなフレームワークPSOについてまとめようと思います。
僕はまだまだ群知能に関しても、Pythonに関してもプログラミングに関しても技術が未熟です。
ぜひ、わからない点や、ソースコードに変なところがありましたら、コメントをいただけるとありがたいです!
1. 粒子群最適化(PSO)とは?
粒子群最適化とは、Particle Swarm Optimizationの略称であり、
現実の鳥の群れや魚の群れの動きから着想を得た最適化アルゴリズム・フレームワークです。
現実の鳥の動きをプログラム上に落とし込み、連続的目的関数の上でたくさんの鳥を模した粒子を動かすことで、もっとも目的関数を最小化する解の位置を探します。
2. 現実の鳥の群れの特徴は?
PSOは、現実の鳥の群れの特徴からヒントを得ています。
それでは、現実の鳥の群れにはどのような特徴があるのでしょうか?
なぜならば、この現実の鳥の群れに、最適化の観点からメリットがなければ、そもそも最適化フレームワークとして取り出す必要もないからです。
2-1. 現実の鳥は集団で飛ぶらしい
現実の鳥は、群れになって集団で飛行を行います。
単体に飛ぶ強い鳥(タカ)などもいますが、都会にいるスズメやカラスなどは集団でいることの方が多いですね。
田舎にいるハトなどは、精米所の周辺で交互に顔を見上げながら米粒を食べています。
最近はいませんが...
2-2. 現実の鳥が集団でいるとメリットが大きいらしい
弱い鳥たちは集団でいますが、これは多くのメリットがあるから集団で行動をしています。
例えば、「視野が広がる」といったメリットがあります。
もともと鳥は周囲$300$度くらい見渡せるなど、多くの視野を持ちます。
それでも、空中を飛ぶ際は上下左右・背後などあらゆる方向から危険が迫ってきます。
しかし、鳥たちが集団でいれば、視野の広さは大きく広がり、外敵を素早く発見できる可能性が高まります。
うれしいですね。
また、「自分が食べられる危険性は減らせる」といったメリットがあります。
弱い鳥たちは集団でいると、当然外敵からもより目につきやすくはなります。
しかし、外敵に攻撃されても集団で反抗したり、集団で散らばることで、自分が食べられる可能性は大きく減ります。
集団でいるとメリットが大きいのは、人間も鳥も同じようです。
3. 現実の鳥の集団はどうしてぶつからないの?
現実の鳥の集団が、それぞれの鳥にとって大きなメリットをもたらすという事がわかりました。
しかし、理由がわかっても、現在集団で行動できる理由がわかっていません。
例えば、人間が$100$人集められてお互いに意思表示を禁止された状態で、好き勝手に動けと言われると、多くの頻度で衝突してしまう・肩がぶつかってしまう、ということは用意に想像できます。
しかし、鳥たちはお互いに意思表示をしなくても、空中で互いに衝突することなく、群れとしての行動を全うすることができます。
どうして、集団でお互いに意思交換を行わずとも互いにぶつからないのでしょうか?
3-1. 実は鳥は対して周囲が見えてないらしい
実は鳥は周囲全体を見ることができていません。
$100$匹の鳥の群れがあったとき、その中央にいる鳥が見える周囲の鳥はたかだか$6, 7$匹であると言われています。
遠くのほうの鳥の動きなどは理解しておらず、周囲にいる鳥の動きを真似て行動しています。
よって、中央にいる鳥ほど、どこにいくかもおおよそわからないまま、周囲に合わせてついていっているというイメージになります。
人間も、スクランブル交差点を渡る際は、$50$メートル先の人間のことは考えず前を歩いている人間を追いかけるので、根っこは同じかもしれませんね。
3-2. 鳥は3つのルールで動いているらしい
現実の鳥の動きを物理モデルシミュレーション化したものにboidsモデルがあります。
boidsモデルのわかりやすい記事はこの記事などが非常に良いです!(ビットがきれい、好き)
シミュレーション化したboidsモデルでは
- 分離
- 整列
- 結合
のシンプルなルールの下、自分の周りの鳥の位置と照らし合わせて
互いに位置を情報共有しながら飛行を行います。
3-3. boidsモデルから最適化モデルPSOへ
boidsモデルの自分の周り・最近傍の鳥のみと互いに位置を情報共有するという発想を、組合せ最適化問題に言い換えたのがPSOというアルゴリズムになります。
よって、boidsモデルとPSOモデルの中身のソースコード自体は大きく違いますが、
自分の周りのみと情報共有する、という基本アイデアは同じになっています。
4. PSOの着想イメージ
いよいよPSOの内容に入っていきますが(長くなりました)、そもそもPSOはどのような問題に適用できて、どのような効果があるのでしょうか?
そのためには、まずPSOがどのようなイメージで誕生し、どのようなイメージで動いているのか?を理解する必要があります。
4-1. 連続的目的関数
PSOは、もともと連続的目的関数の最小値(最大値)となるような解の位置を発見することを目的としています。
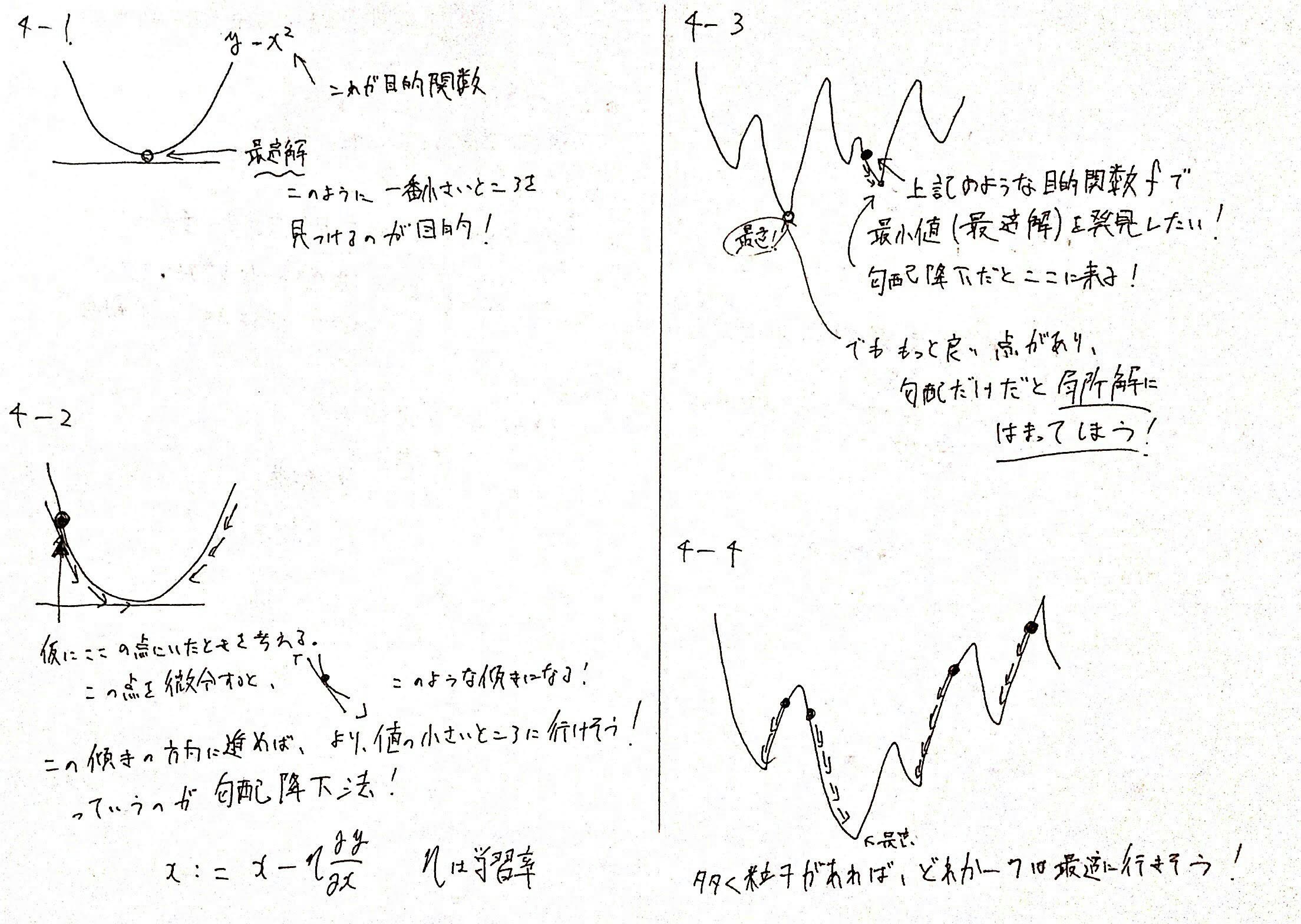
例えば、$f(x) = x^2$という連続的目的関数を考えます。
この関数$f$の最小値$y$を求める解の位置$x$はどこでしょうか?
これは簡単ですね、$x=0$です(それはそう)。
これは人間が視認すれば、一発で最小の位置がわかります。
しかし、コンピュータ上でプログラムで最小の目的関数の値を取る$x$の位置を求めることは難しいです。(人間みたいにグラフを書いて、目で見て判断できないので)
どうすれば最小の目的関数の値を取る$x$の位置を求められるのでしょうか?
4-2. 勾配降下法
このような、目的関数$f$の最小値$y$を満たす解$x$の位置を求める手法として勾配降下法というものがあります。
最近機械学習・DeepLearningが非常に話題になっていますが、あれの基本もこの勾配降下法です。
勾配降下法のイメージは以下のとおりです。
ただ、勾配降下法でわかりやすいリンクがあるのでこれを見ると良いと思います。
4-3. 難しい連続的目的関数
勾配降下法は
その場で一番目的関数の値を減らせそうな方向に進むというGreedy法の上に成り立っています。
そのため、そもそも現在の位置から、最も目的関数を減らせそうな方向に進んだとしても、その先が局所解だとすると、最も良い最適解を見つけることができません。
勾配降下法だと、複雑な目的関数の上では、局所解に陥るリスクが非常に高いです。
どうすればよいのでしょうか?
4-4. 目的関数上で動く粒子を増やしてみる
目的関数上で動く、点のことを、後々のPSOのために粒子と呼ぶことにします。
先程までは、一個の粒子のみで計算をしていました。
このままだと、粒子が局所解に陥ってしまいます。
そこで、粒子を$N$個に増やすことにしてみましょう。
$i$番目の粒子の位置を$x_i$と表すことにします。
すると、以下のようになります。
どれかの粒子は、スタート時点で、そこから移動していけば、最適解にたどり着くような位置にいるかもしれません。
こうすれば、局所解に陥る危険性はある程度減らせそうです。
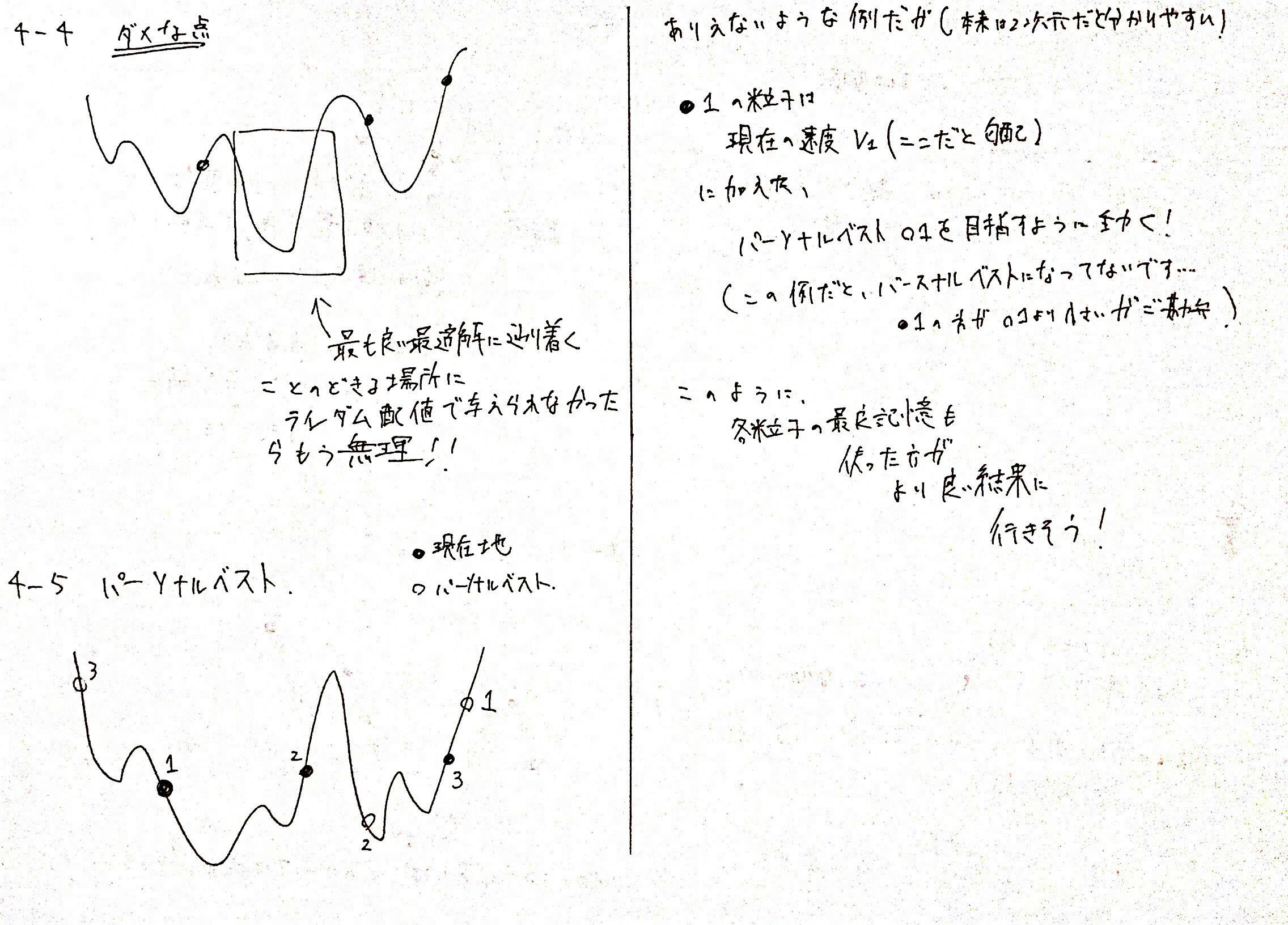
しかし、まだ、ランダムに配置しても最適解にたどり着くような位置に粒子がない場合も考えられます。
どうすればよいのでしょうか?
4-5. 各粒子に、今までで一番良かった位置を記憶させる
粒子を$N$個に増やしても、局所解に陥る理由は
その場限りの勾配を利用して、後先考えずに進むという場当たりな行動をずっとしてしまっているからです。
そこで、各粒子$i$ごとに、これまでで一番目的関数の値が小さくなった位置$p_i$を記憶することにします。
これを$i$番目の粒子のパーソナルベストと呼びます。
そして、目的関数の値が小さくなる方向と、現在の位置$x_i$から、一番値が小さくなって嬉しかった位置$p_i$に進む方向のベクトルの和の方向に進むことにします。
こうすれば、各個体ごとに現在の勾配は利用するけれども、これまでの記憶を利用して最も良い位置にも移動しようとすることで、より最適解を見つけやすくなりそうです。
4-6. さらにすべての粒子の中で最も一番良かった位置を記憶する
4-5で行ったことは、各粒子$i$のうち、もっともこれまでで良かった位置$p_i$を記憶させることです。
しかし、この方法のみでは、例えば$3$番目の粒子が現在位置$x_3$, これまでの良い位置$p_3$ともにひどい局所解で全く動かないみたいな状況が考えられます。
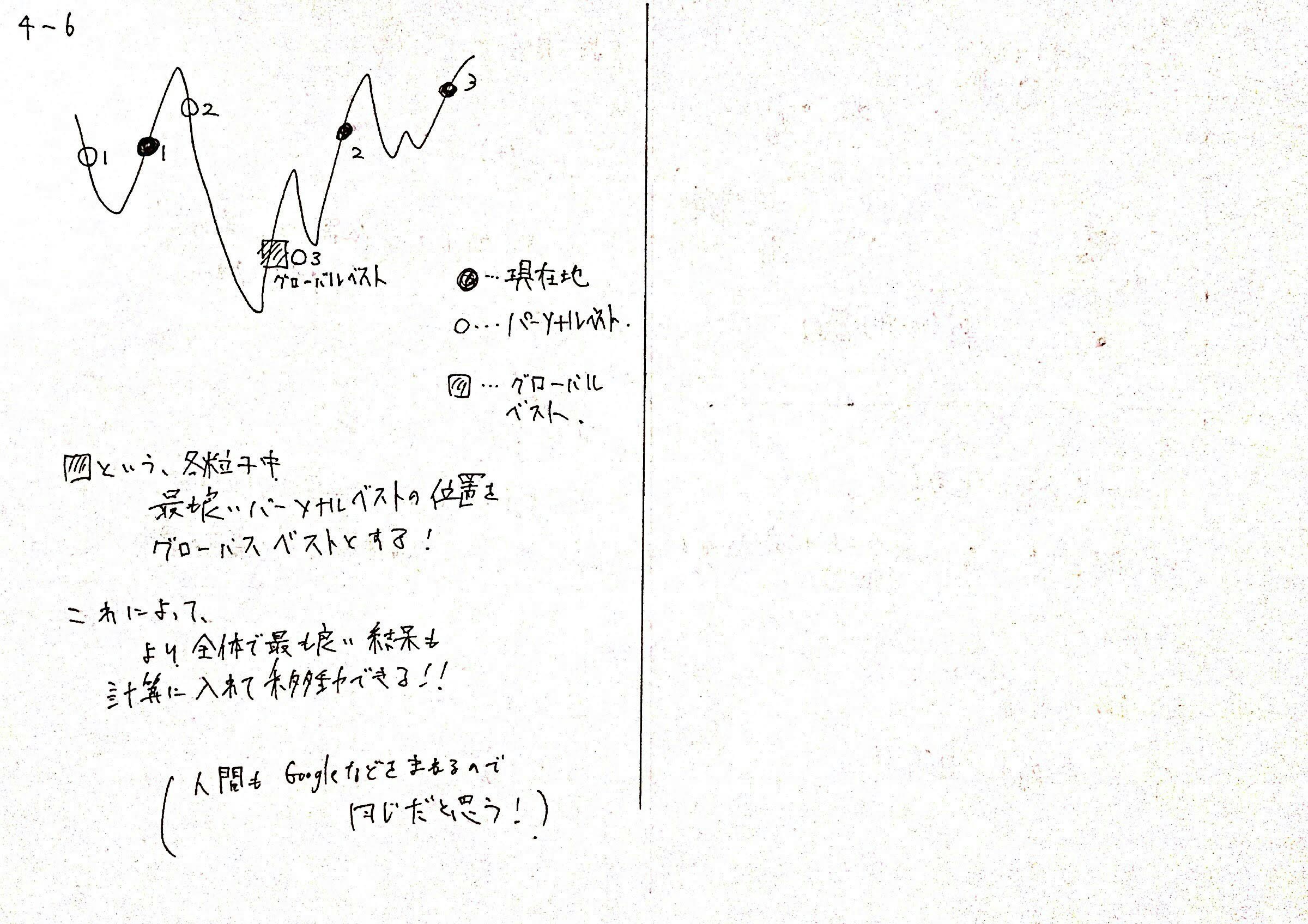
そこで、$N$個のこれまでのパーソナルベスト$p_i$のうち、最も目的関数を小さくする位置$p_i$を、$g$とし、グローバルベストと呼ぶことにします。
各粒子は毎回移動する際は
- 現在の勾配方向
- これまでのパーソナルベスト位置$p_i$に向かう方向
- これまでの、$N$個全体のグローバルベスト位置$g$に向かう方向
すべてを足し合わせたベクトル方向に移動します。
これによって、より局所解を避けて、$N$個の粒子が協力しあって最適解を探すことができます。
5. PSOの式
PSOのイメージは持ってもらえたでしょうか。
PSOは、このようにもともと連続関数の最小値を求める位置を発見するアルゴリズムとして開発されています。
ここで、修正点でしたが、
4の内容までは「勾配」を利用していましたが
PSOでは、「勾配」ではなく「前回の移動スピード$v_i$の慣性」を利用します。
これも式を見ながら理解していきます。
また、PSOはシミュレーションモデルであるため、$t$というサイクル変数が出てくることに注意してください。
これはプログラム上だと、for文の変数$t$に値します。
5-1. PSOの変数
5-1-0. サイクル
サイクルは$t$と表されます。
次の実行サイクルのタイミングは$t+1$のように実行されます。
つまり
$0$秒(サイクル)なら$t=0$
$1$秒(サイクル)なら$t=1$
$2$秒(サイクル)なら$t=2$
のように表します。
5-1-1. 粒子の数
粒子の数は$N$と表されます。
5-1-2. 目的関数
最小化したい目的関数は$f$と表します。
例えば、$D = 2$次元の入力が与えられて値を返すなら
$f(x^1, x^2)$のように表されます。
この目的関数の次元$D$は非常に大事なので覚えておいてください。
この目的関数に、後述の各粒子の位置ベクトル$x_i$を入れると
その目的関数の値$f(x_i)$が帰ってきます。
この値の最小化を行うような位置$x$を見つけることが目的となります。
5-1-3. 各粒子の位置
$i$番目の粒子の位置は、位置ベクトル$x_i$と表されます。
ベクトルと表されるのは、目的関数の次元は$1$次元に限らないからです。
例えば、$y=x^2$なら、目的関数の次元は$1$次元です。これは$x=1$のみで決まるからです。
しかし、$y=x^{(1)} + x^{(2)} $ならば、目的関数の次元は$D = 2$次元です。
ここで、$x^{(i)}$は、解空間$R^D$におけるベクトル$x$の$i$番目の要素を表します。
よって、$D=5$次元の$3$番目の粒子の位置ベクトルは$x_3$と表し、
さらに$D=5$次元の$3$番目の粒子の$2$次元目の要素は$x_3^{(2)}$と表されます。
また、ここにサイクルはいつか?という変数が入ってきます。(多いですね...)
$i$番目の粒子のサイクル$t$の位置ベクトルは、$x_i(t)$と表されます。
よって、以下にまとめを行います。
- $x_i(t)$
- $i$番目の粒子のサイクル$t$における次元$D$の位置ベクトル
- $x_i^{j}(t)$
- $i$番目の粒子のサイクル$t$における次元$D$の位置ベクトルの、$j$次元目の要素
5-1-4. 各粒子の速度
各粒子$i$は、位置$x_i$から速度ベクトルを足して、次の位置に移動します。
この速度ベクトルは$v_i$と表します。
これは、位置と同様の表し方をします。
- $v_i(t)$
- $i$番目の粒子のサイクル$t$における次元$D$の速度ベクトル
- $v_i^{j}(t)$
- $i$番目の粒子のサイクル$t$における次元$D$の速度ベクトルの、$j$次元目の要素
位置、速度ともに
$x_i, v_i{\in}R^D, \ \ x_i^{j}, v_i^{j}{\in}R$
を満たします。
5-1-5. パーソナルベスト
パーソナルベスト$p_i$は、粒子$i$がサイクル$0$からサイクル$t$まで解空間を移動してきた中で
もっとも目的関数の値が小さくなった、良さげな位置ベクトル$x_i$を保存しています。
- $p_i(t)$
- $i$番目の粒子の、サイクル$0$からサイクル$t$までで、最も良い位置ベクトル$x_i$
- $p_i^{j}(t)$
- $i$番目の粒子の、サイクル$0$からサイクル$t$までで、最も良い位置ベクトル$x_i$の$j$次元目の要素
5-1-6. グローバルベスト
グローバルベスト$g$は、$N$個の粒子がサイクル$0$からサイクル$t$まで移動してきた中で、
もっとも目的関数の値が小さくなった、良さげな位置ベクトル$p_i$を保存しています。
- $g(t)$
- $N$個の粒子のうち、サイクル$0$からサイクル$t$までで、最も良い位置ベクトル$p_i$
- $g^{j}(t)$
- $N$個の粒子のうち、サイクル$0$からサイクル$t$までで、最も良い位置ベクトル$p_i$の$j$次元目の要素
5-2. 式の更新
PSOでは、サイクルごとに
- 速度
- 位置
- パーソナルベスト
- グローバルベスト
を更新していきます。
では、どのように更新していくのでしょうか?
5-2-1. 速度の更新式
各次元の成分$j$ごと
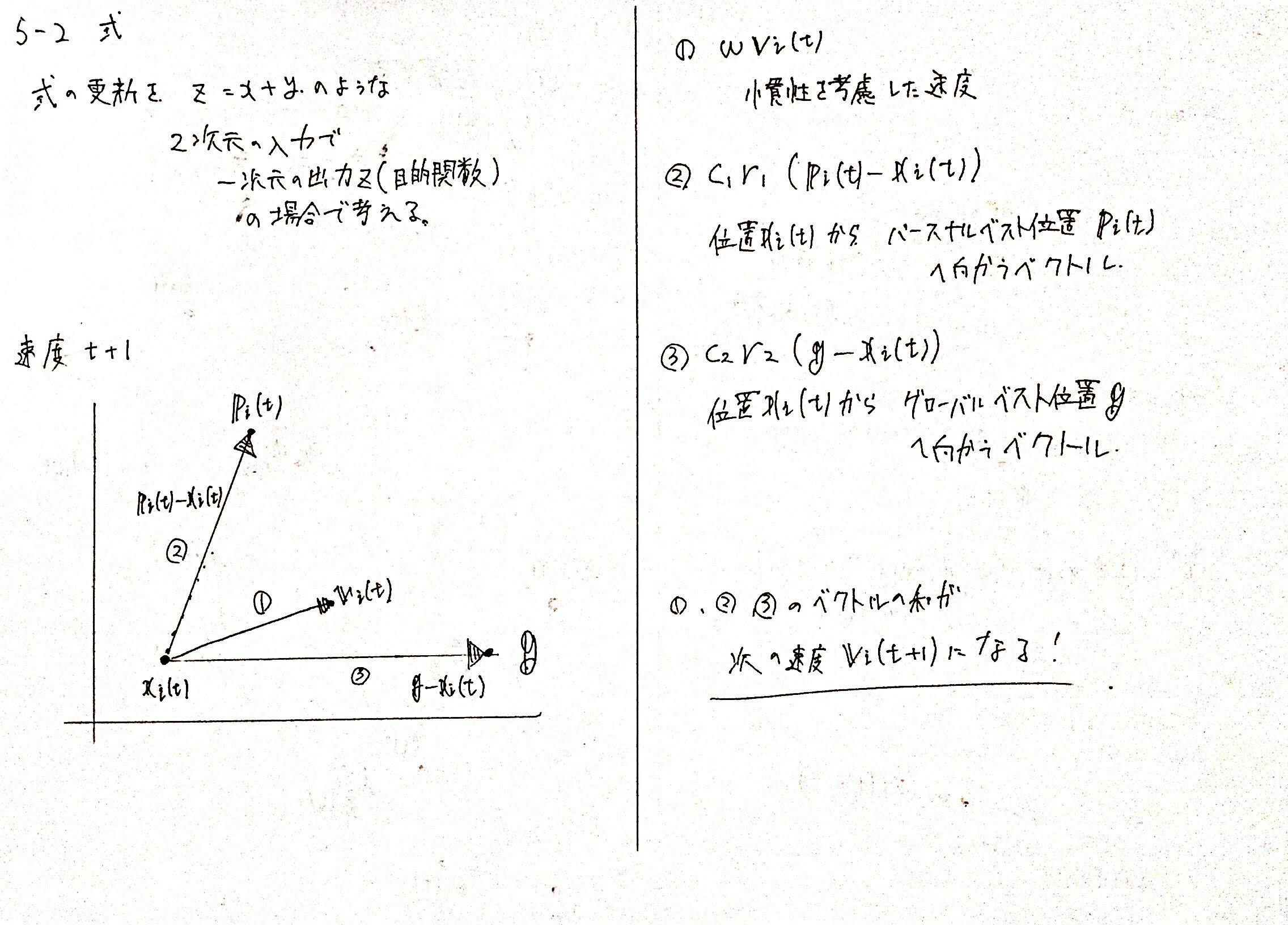
$v_i^{(j)}(t+1) = wv_i^{(j)}(t) + c_1r_1(p_i^{(j)}(t) - x_i^{(j)}(t)) + c_2r_2(g^{(j)}(t) - x_i^{(j)}(t))$
ベクトルとして計算
$v_i(t+1) = wv_i(t) + c_1r_1(p_i(t) - x_i(t)) + c_2r_2(g(t) - x_i(t))$
当然ですが、ベクトルとして計算したほうがきれいですね。
ここで、新しく$w, c_1, r_1, c_2, r_2$が出てきています。
これはパラメータであり、人間がプログラム実行前にソースコードに定数として設定する必要があります。
これの詳細は後の節で記載します。
5-2-2. 位置の更新式
各次元の成分$j$ごと
$x_i^{(j)}(t+1) = x_i^{(j)}(t) + v_i^{(j)}(t+1)$
ベクトルとして計算
$x_i(t+1) = x_i(t) + v_i(t+1)$
サイクル$t+1$、つまり次の粒子の位置$x_i(t+1)$は、現在の粒子の位置に速度を足すだけで求めることができます。
計算式はなんと上記の速度・更新に関してのみです。
簡単ですね。
5-3. 速度の更新式の意味
PSOで難しいのは、この
$v_i(t+1) = wv_i(t) + c_1r_1(p_i(t) - x_i(t)) + c_2r_2(g(t) - x_i(t))$
の公式の意味の理解だと思います。
しかし、部分部分で分解すれば非常に簡単な概念なので、見ていきたいと思います。
ここで頭にいれるべきなのは「やっていることは高校で習ったベクトルの和にすぎない」ということです。
5-3-1. 第1項 慣性
第$1$項は、$wv_i(t)$の部分を指します。
$v_i(t)$は、$i$番目の粒子のサイクル$t$での速度を指し、慣性と呼ばれます。
例えば、高速道路で走っている車が急ブレーキをしたとしても、$0.0001$秒で一気に止まることはありません。早ければ早いほど慣性で動き続けます。
よって、この第$1$項は、これまでの速度を、次のサイクルの速度として、保存する!という効果があります。
この慣性の項によって、サイクル$t$の速度がもし最適解に向かっている速度ベクトルだったとき、その速度をある程度活かしながら次の速度を計算することができます。
$w$は慣性重みと呼ばれており、どれくらいこの慣性を重要視するか?を表します。
プログラムに人間が記載する定数になっています。
5-3-2. 第2項 認知(パーソナルベスト)
第$2$項は、$c_1r_1(p_i(t) - x_i(t))$の部分です。
これは$i$番目の粒子が、現在サイクル$t$において、$x_i(t)$の位置にいる粒子が、$i$番目の粒子がこれまでに経験した最も良い位置$p_i(t)$にどれくらい引き寄せられるか?の、ある意味引力による速度を表します。
各粒子は、慣性のみで行動するともちろん、貪欲に現在向かっている方向に永遠に進み続けます。
しかし、それでは局所解に陥ってしまう可能性があります。
そこで、現在の速度の慣性に加えて、$i$番目の粒子がこれまでに経験した最も良い位置$p_i$に向かうことで、より良い位置が発見できるだろう! というアイディアに基づいたのがこの第$2$項です。
この第$2$項は、認知(cognitive part)と呼ばれ、各個体がこれまでに認知した良い位置を目指したい、という意味を指します。
$r_1$は乱数で一様乱数で決定します。つまり、ランダム要素です。
$c_1$は、個としての経験パラメータであり、この$c_1$をソースコード上で大きく設定すればするほど、その個体の経験を信じて行動します。
この値を0にすれば、慣性のみや、次の項の社会性パートで移動します。
5-3-3. 第3項 社会性(グローバルベスト)
第$3$項は、$c_2r_2(g(t) - x_i(t))$の部分です。
基本的なアイディアは、第$2$項と同じです。
つまり、$N$個全体の粒子のうちでこれまでに経験した最も良い位置$g = argmax(f(p_i(t)))$の方向に向かうような引力の速度を表します。
慣性に加えて、認知パートで各個体はこれまでに経験した最も良い位置にも向かおうとします。
しかし、このままでは、$i$番目の粒子がこれまでに経験した位置が非常にショボかったら、この粒子は局所解に収まってしまいます。
よって、他の粒子全体で最も良い位置にも向かうことで、局所解を避けて、より良い経験をした位置に向かう、といった効果を出します。
これは、人間社会にも言えて、Googleなどの大手企業がAIなどで成功すれば、そのグローバルに最も良い経験を自分たちも得たいと、Googleのマネをしだす中小企業が出てくる道理に少し似ていますね。
このようにPSOでは、それぞれの位置をお互いに情報共有して、グローバルベストに基づいて移動することで、最適解をより見つけやすくできます。
(変数$c_2, r_2$は同様です。)
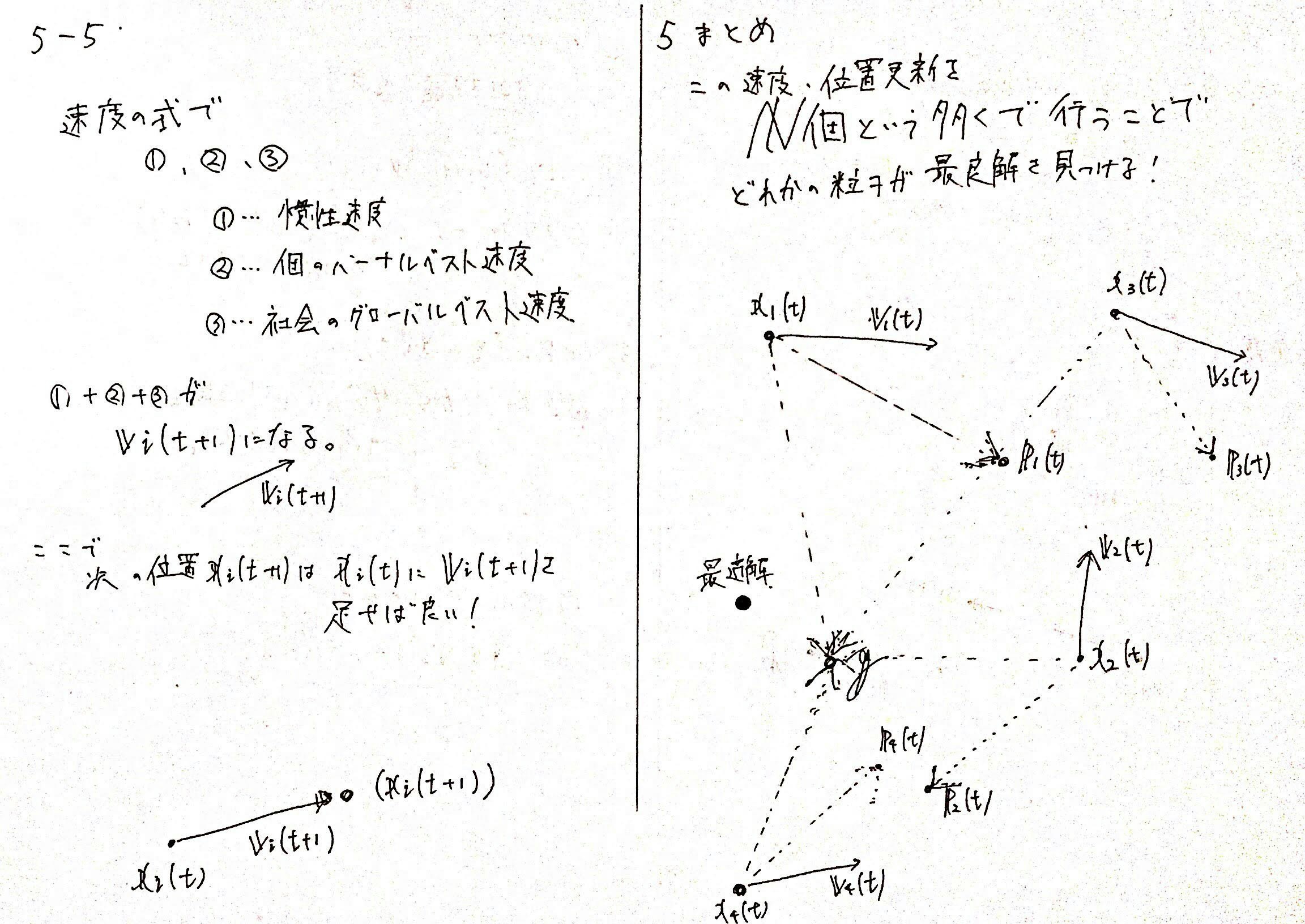
5-4. 速度式の図式化
これらの速度式を、$2$次元座標上で見てみましょう。
5-5. 位置の更新式の意味
これは簡単です。
速度式を求めたあと、現在の位置にその速度を足して、次の位置を求めています。
6. ソースコード(python)
ソースコードは以下のようになります。
まずは、コード全体を見てみましょう。
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import random
# 目的関数
# def objective_function(position):
# return np.sum(position * position)
def objective_function(position):
t1 = 20
t2 = -20 * np.exp(-0.2 * np.sqrt(1.0 / len(position) * np.sum(position ** 2, axis=0)))
t3 = np.e
t4 = -np.exp(1.0 / len(position) * np.sum(np.cos(2 * np.pi * position), axis=0))
return t1 + t2 + t3 + t4
# 描画のための初期化
def init_plot(xy_min, xy_max):
matplot_x = np.arange(xy_min, xy_max, 1.0)
matplot_y = np.arange(xy_min, xy_max, 1.0)
matplot_mesh_X, matplot_mesh_Y = np.meshgrid(matplot_x, matplot_y)
Z = []
for i in range(len(matplot_mesh_X)):
z = []
for j in range(len(matplot_mesh_X[0])):
result = objective_function(np.array([matplot_mesh_X[i][j], matplot_mesh_Y[i][j]]))
z.append(result)
Z.append(z)
Z = np.array(Z)
plt.ion()
plt.title("PSO")
fig = plt.figure()
axes = Axes3D(fig)
axes.set_xlabel('x')
axes.set_ylabel('y')
axes.set_zlabel('f(x, y)')
mesh_XYZ = {
"X": matplot_mesh_X,
"Y": matplot_mesh_Y,
"Z": Z
}
return axes, mesh_XYZ
# 描画
def play_plot(axes, mesh_XYZ, positions, personal_best_positions, personal_best_scores, global_best_particle_position, velocities):
axes.plot_wireframe(mesh_XYZ['X'], mesh_XYZ['Y'], mesh_XYZ['Z'], alpha=0.3)
axes.scatter(positions[:, 0], positions[:, 1], np.apply_along_axis(objective_function, 1, positions), marker='^',
c="red", linewidths=5)
axes.scatter(personal_best_positions[:, 0], personal_best_positions[:, 1], personal_best_scores, linewidths=5,
marker='x', c='blue')
axes.scatter(global_best_particle_position[0], global_best_particle_position[1],
objective_function(global_best_particle_position), linewidths=8, marker='o', c='green')
axes.quiver(positions[:,0], positions[:,1], np.apply_along_axis(objective_function, 1, positions), velocities[:, 0], velocities[:, 1], np.zeros(len(velocities)), color='gray')
plt.draw()
plt.pause(1)
plt.cla()
# 各粒子の位置更新
def update_positions(positions, velocities):
positions += velocities
return positions
# 各粒子の速度更新
def update_velocities(positions, velocities, personal_best_positions, global_best_particle_position, w=0.5,
ro_max=0.14):
rc1 = random.uniform(0, ro_max)
rc2 = random.uniform(0, ro_max)
velocities = velocities * w + rc1 * (personal_best_positions - positions) + rc2 * (
global_best_particle_position - positions)
return velocities
def main():
print("Particles: ")
number_of_particles = int(input())
print("Dimensions: ")
dimensions = int(input())
print("LimitTimes: ")
limit_times = int(input())
xy_min, xy_max = -32, 32
# グラフの初期化
axes, mesh_XYZ = init_plot(xy_min, xy_max)
# 各粒子の位置
positions = np.array(
[[random.uniform(xy_min, xy_max) for _ in range(dimensions)] for _ in range(number_of_particles)])
# 各粒子の速度
velocities = np.zeros(positions.shape)
# 各粒子ごとのパーソナルベスト位置
personal_best_positions = np.copy(positions)
# 各粒子ごとのパーソナルベストの値
personal_best_scores = np.apply_along_axis(objective_function, 1, personal_best_positions)
# グローバルベストの粒子ID
global_best_particle_id = np.argmin(personal_best_scores)
# グローバルベスト位置
global_best_particle_position = personal_best_positions[global_best_particle_id]
# 規定回数
for T in range(limit_times):
# 速度更新
velocities = update_velocities(positions, velocities, personal_best_positions,
global_best_particle_position)
# 位置更新
positions = update_positions(positions, velocities)
# パーソナルベストの更新
for i in range(number_of_particles):
score = objective_function(positions[i])
if score < personal_best_scores[i]:
personal_best_scores[i] = score
personal_best_positions[i] = positions[i]
# グローバルベストの更新
global_best_particle_id = np.argmin(personal_best_scores)
global_best_particle_position = personal_best_positions[global_best_particle_id]
# グラフ描画
play_plot(axes, mesh_XYZ, positions, personal_best_positions, personal_best_scores,
global_best_particle_position, velocities)
if __name__ == '__main__':
main()
6-0. 変数
重要な変数はmainに入っています。
number_of_particiesは、文字通り粒子の個数です。
dimensionsは、この解空間の次元数$D$です。$f(x^1, x^2, x^3)$という目的関数なら$3$を設定します。
ただし、今回は$3$次元のプロットを行い、$Z = f(x, y)$ のように$Z$軸に目的関数の値を描画したいため、$2$と設定してください。
limit_timesは何回サイクルを行うかです。
positionsは、$N$個の粒子の$D$次元分の位置を表します。
最初はxy_min, xy_maxの範囲にランダムに各次元分設定します。
velocitiesは、$N$個の粒子の$D$次元分の速度です。
personal_best_positionsは、$N$個の粒子それぞれの最も良かったパーソナルベスト位置を表します。
personal_best_scoresは、personal_best_positionsを目的関数に代入することで得られるスコアです。
グローバルベストを持つ粒子のIDと、その値を求めるために使用される変数です。
global_best_particle_idは、personal_best_positionsのうち、最も目的関数の値が良いパーソナルベスト位置をもつ粒子のidを知る必要があるので、np.argminでそのIDを求めます。
global_best_particle_positonは、実際の最も良かったglobal_best_particle_id番目の粒子のパーソナルベストの位置を、グローバルベストとして持っておきます。
axes, mesh_XYZは描画用なのでPSOとは関係ない変数です。
6-1. import文
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import random
まず、今回使用するコードをimportしています。
numpyは、Pythonで科学計算によく用いられる配列などのパッケージです。
このパッケージのおかげで、PythonのDeepLearningの流れができたと言っても過言でないような気もします。
matplitlibは、Pythonのグラフパッケージです。
わかりやすい図などを作成できます。
mpl_toolkits.mplot3dは、matplitlibの付属パッケージで、Alex3DはMatplitlibで3Dグラフを作る用のクラスになっていまっす。
6-2. objective_function
def objective_function(position):
t1 = 20
t2 = -20 * np.exp(-0.2 * np.sqrt(1.0 / len(position) * np.sum(position ** 2, axis=0)))
t3 = np.e
t4 = -np.exp(1.0 / len(position) * np.sum(np.cos(2 * np.pi * position), axis=0))
return t1 + t2 + t3 + t4
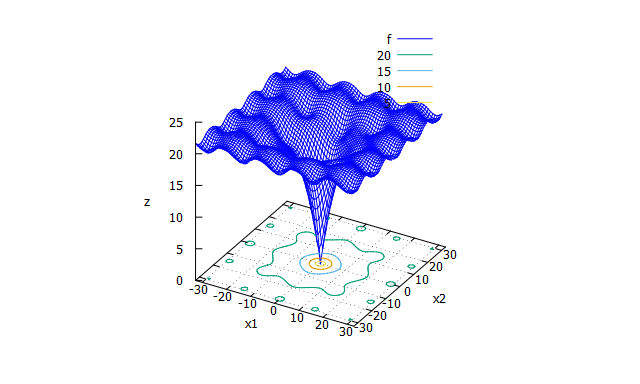
目的関数の式です。
この式は
最適化アルゴリズムを評価するベンチマーク関数まとめ
ならびに
python: ベンチマーク関数お試しコード
を参考にさせていただいた、Ackley functionという関数です。
以上の画像は、python: ベンチマーク関数お試しコードからお借りしています。ありがとうございます。
6-3. init_plot
# 描画のための初期化
def init_plot(xy_min, xy_max):
matplot_x = np.arange(xy_min, xy_max, 1.0)
matplot_y = np.arange(xy_min, xy_max, 1.0)
matplot_mesh_X, matplot_mesh_Y = np.meshgrid(matplot_x, matplot_y)
Z = []
for i in range(len(matplot_mesh_X)):
z = []
for j in range(len(matplot_mesh_X[0])):
result = objective_function(np.array([matplot_mesh_X[i][j], matplot_mesh_Y[i][j]]))
z.append(result)
Z.append(z)
Z = np.array(Z)
plt.ion()
plt.title("PSO")
fig = plt.figure()
axes = Axes3D(fig)
axes.set_xlabel('x')
axes.set_ylabel('y')
axes.set_zlabel('f(x, y)')
mesh_XYZ = {
"X": matplot_mesh_X,
"Y": matplot_mesh_Y,
"Z": Z
}
return axes, mesh_XYZ
mapplitlibで描画するための初期化関数です。
matplot_x, yは今回の$x$の取りうる範囲
$-32$から$32$までを$0.1$ずつ区切ったndarrayになっています。
それをnp.meshgridで二次元配列にして、この目的関数の形自体をプロットできるように準備しています。
plt.ion()は、maplotlibで描画されたグラフにインタラクティブモード(クリックなどを可能とする)ように設定します。
また、plt.figure()はグラフの図全体のインスタンスへの参照を取得します。
そして、axes = Axes3D(fig)は、グラフ図全体の軸などの要素を操作しやすい用にラップしてくれます。
axesに要素を追加することで、3D図を作成することができます。
6-4. update_velocities
# 各粒子の速度更新
def update_velocities(positions, velocities, personal_best_positions, global_best_particle_position, w=0.5,
ro_max=0.14):
rc1 = random.uniform(0, ro_max)
rc2 = random.uniform(0, ro_max)
velocities = velocities * w + rc1 * (personal_best_positions - positions) + rc2 * (
global_best_particle_position - positions)
return velocities
速度更新を行う関数です。
rc1は$r_1c_1$に当たるものであり、今回は簡単化のために完全な乱数にしています。
そして、その下の
velocities = velocities * w + rc1 * (personal_best_positions - positions) + rc2 * (
global_best_particle_position - positions)
return velocities
は、速度更新式の計算を行っています。
6-5. update_positons
# 各粒子の位置更新
def update_positions(positions, velocities):
positions += velocities
return positions
位置を更新する関数です。
numpyを使えば、更新し終わった速度配列をそのまま足し込むことで
位置を更新できます。
嬉しいですね。
6-6. main分の用意部分
def main():
print("Particles: ")
number_of_particles = int(input())
print("Dimensions: ")
dimensions = int(input())
print("LimitTimes: ")
limit_times = int(input())
xy_min, xy_max = -32, 32
# グラフの初期化
axes, mesh_XYZ = init_plot(xy_min, xy_max)
# 各粒子の位置
positions = np.array(
[[random.uniform(xy_min, xy_max) for _ in range(dimensions)] for _ in range(number_of_particles)])
# 各粒子の速度
velocities = np.zeros(positions.shape)
# 各粒子ごとのパーソナルベスト位置
personal_best_positions = np.copy(positions)
# 各粒子ごとのパーソナルベストの値
personal_best_scores = np.apply_along_axis(objective_function, 1, personal_best_positions)
# グローバルベストの粒子ID
global_best_particle_id = np.argmin(personal_best_scores)
# グローバルベスト位置
global_best_particle_position = personal_best_positions[global_best_particle_id]
ここは、PSOサイクルを行うための用意を行っています。
ソースコードが汚いかもしれません。(なにぶん、Pythonは初心者で、競技プログラミングぐらいでしか触っていません。)
ぜひ、アドバイスいただければ幸いです!
6-7. PSOサイクル
# 規定回数
for T in range(limit_times):
# 速度更新
velocities = update_velocities(positions, velocities, personal_best_positions,
global_best_particle_position)
# 位置更新
positions = update_positions(positions, velocities)
# パーソナルベストの更新
for i in range(number_of_particles):
score = objective_function(positions[i])
if score < personal_best_scores[i]:
personal_best_scores[i] = score
personal_best_positions[i] = positions[i]
# グローバルベストの更新
global_best_particle_id = np.argmin(personal_best_scores)
global_best_particle_position = personal_best_positions[global_best_particle_id]
# グラフ描画
play_plot(axes, mesh_XYZ, positions, personal_best_positions, personal_best_scores,
global_best_particle_position, velocities)
ここがメインになります。
まず、limit_times回だけ
- $N$個各粒子の位置・速度
- $N$個すべてのパーソナルベストの更新
- $N$個のうち、最も良いパーソナルベストをグローバルベストとして更新
- グラフの描画
を行っていることに注意してください。
まず、速度を更新して$v_i(t + 1)$を求めます。
そして、その速度を用いて$x_i(t+1)$に位置を更新します。
その後はパーソナルベストを更新する必要があるため
各粒子$i$ごとに現在位置のスコアを求めて、$i$のこれまでのパーソナルベストと比較します。
もし、現在位置のほうがよいなら、更新します。
そして、パーソナルベストを用いて、グローバルベストを更新します。
最後に、プロットを行います。
意外と、ソースコード内のPSO自体が綺麗に収まるのが嬉しい限りです。
7. PSOのメリット・デメリット
PSOをつらつらと見てきました。
このようにPSOは連続関数の最適解を満たす$x$の位置を発見することができます。
しかし、PSO以外にも多くのメタヒューリスティック解法があります。
例えば、群知能ならば
- ACO(蟻)
- ABC(ハチ)
- Cat Swarm Optimization(ネコ)
など、多くあります。
また、群知能以外にも
- 数理最適化
- 焼き鈍し法
- 最近傍法(Greedyみたいなやつ)
- 遺伝的アルゴリズム
など多くの手法があります。
これらと比べてPSOのメリット・デメリットとは何なのでしょうか?
7-1. PSOのメリット
7-1-1. シンプル
PSOは非常にシンプルなヒューリスティック解法になっています。
具体的には、
- 更新式が$2$つしかない
- 速度
- 位置
- 目的関数さえわかれば良い
- パラメータもそこまで多くはない
などによります。
つまり、他の群知能やメタヒューリスティック解法と比べて、更新式の実装も非常にシンプルであり、応用しやすいというメリットがあります。
7-1-2. 目的関数が非連続でもよい
目的関数$f$についてですが、ときたま非連続であったり、微分不可能であったりします。
すると、勾配降下法などでは微分ができないため変な実行結果になったりしてしまいます。
しかし、PSOでは位置$x$を目的関数に代入することによって最適解を求めます。
また、パーソナルベストへ向かうベクトルや、速度のベクトルなどを用いるため、そもそも非連続でも扱える形になっています。
よって、目的関数の形がわからないとき、非連続かもしれないですが、PSOは扱うことができます。
7-1-3. 拡張性にすぐれている
PSOはシンプルな構造であるため、色々とアルゴリズムが変更させやすい利点があります。
また、ある程度$N$を大きくすれば実行結果は変わらず良い結果を求めます。
そのため、あまり計算量が問題スケールによって変化しないというメリットがあります。
7-1-4. 動的性
数理最適化などはどちらかというと静的なアルゴリズム、というか数学的解析手法と言ったほうが正しいかもしれません。
よって、与えられた静的な問題を解析はできますが、動的に問題が変化していくと毎回計算し直しになってしまいます。
しかし、PSOでは、実行をずっと続ければ最適解を探し続けるため、動的に問題がスケール・変更しても対応することができます。
7-2. PSOのデメリット
7-2-1. パラメータ調整
当然ですが、メタヒューリスティック手法においてはこのパラメータ調整が性能を左右します。
適切なパラメータを選択しない限り変な実行結果や、的外れな答えが出てしまいます。
このようにすればよい!というパラメータをある程度研究されていますが、結局は問題によりけりです。
そのため、パラメータ調整に時間がかかる、というのはデメリットになっています。
7-2-2. 確率性
PSOは、確率で左右します。
具体的には、最初の$N$個の粒子の配置はランダムになっています。
そのため、数理最適化とは異なり、毎回の実行で異なる計算結果・最適解が出てきます。
解析的でなく、実行しないとわからないシミュレーション解法特有のデメリットになります。
8. PSOのさらなる拡張
今回記載したPSOは一番シンプルなPSOらしいです。
最近のPSO論文ではより効率的かつ、最適解を求めやすい手法になっているため、これらをまとめようと思います。
そのうち、これらの拡張を取り入れたソースコード + Classにモジュール化したものを記事にまとめたいです。
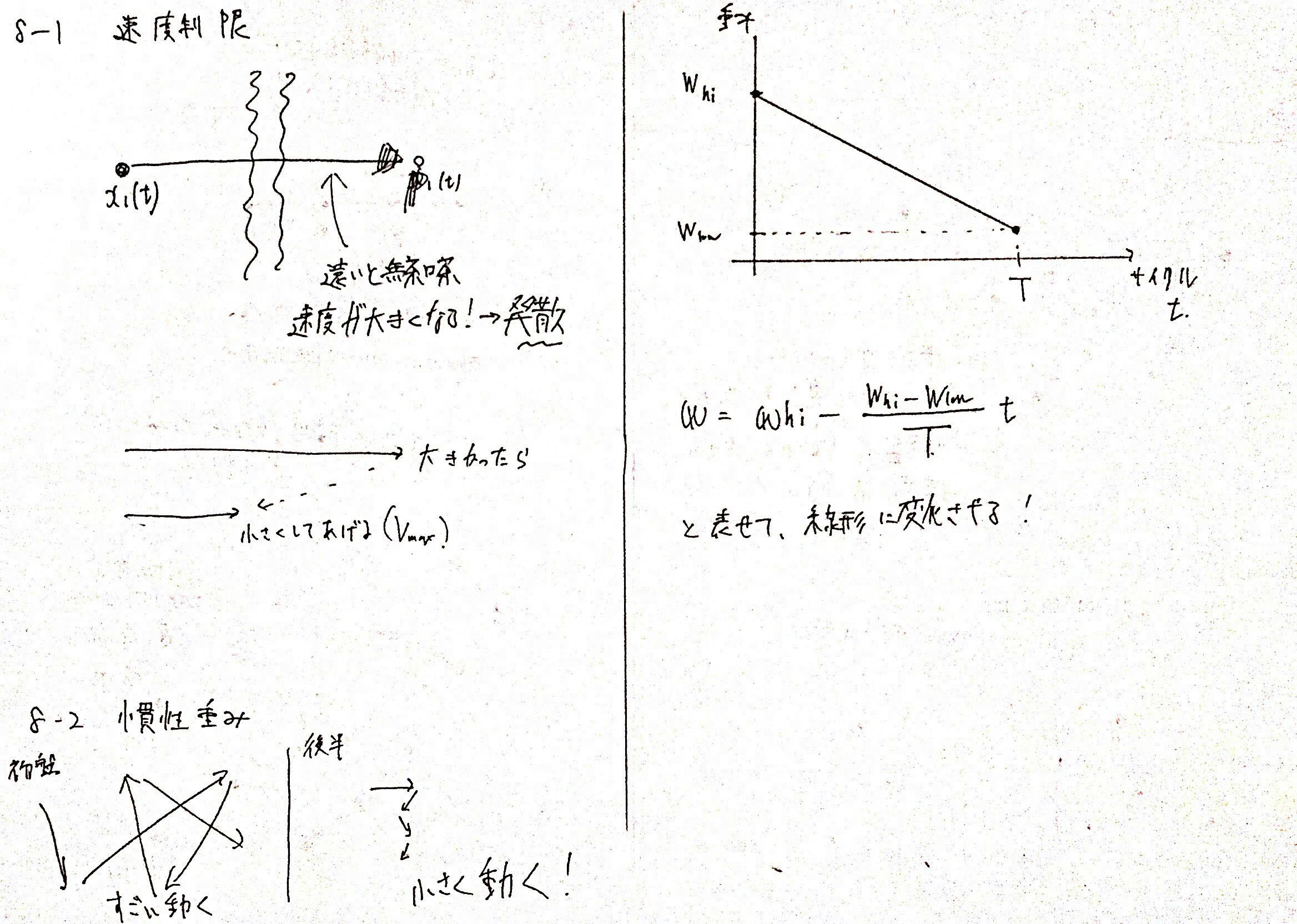
8-1. 速度制限
速度式で、著しく現在の位置とパーソナルベストの位置が異なると、このパーソナルベストに向かう速度が発散してしまいます。
$v_i(t+1) = wv_i(t) + c_1r_1(p_i(t) - x_i(t)) + c_2r_2(g(t) - x_i(t))$
上記の速度式では、
$c_1r_1(p_i(t) - x_i(t))$の部分であり、
$p_i(t) >> x_i(t)$の場合や、$p_i(t)<< x_i(t)$の場合、著しくパーソナルベストに向かう速度が発散することがあります。
グローバルベストも同様です。
これは探索空間が大きい場合に発生することがあります。
当然発散してしまうと正しい解は求められず、関数の定義外に出ることもあります。
そこで、最大速度・最小速度の閾値$v_{max}, v_{min}$を定めると良いです。
もし、速度の更新結果$v_i(t+1)$がこの最大速度・最小速度を超えていたら丸めてあげます。
これによって、速度制限を行って正しい結果を求めることができます。
デメリットとしては、設定すべきパラメータの量が増えることです。
しかし、Abidoさんの論文で
$v_{max} = {\frac{x_{max}^{(d)} - x_{min}^{(d)}}{K}}$
とすると良いという結果がでています。
$x_{max}^{(d)}$は、$N$個の$x_i$すべてのうち、$d$次元目の要素の最大の$x$です。
同様に$x_{min}^{(d)}$も定義します。
$K$はユーザー定義パラメータで、どれぐらい速度を制限するか?を決めます。
8-2. 慣性重み
速度式$v_i(t+1) = wv_i(t) + c_1r_1(p_i(t) - x_i(t)) + c_2r_2(g(t) - x_i(t))$
の$v_i(t+1) = wv_i(t)$の$w$を時間経過とともに減少させていくことを慣性重みの工夫とします。
PSOでは、できる限り最初のうちは大きくグローバル的に解の位置を探したいです。
そして、後半は大幅に絞り込まれたうち、よりよい局所的な良い位置を探すべきです。
よって、$w$を時間経過とともに減らすことで、最初は大胆に速度を慣性として保存して移動し、後半は速度を落とすことで局所的な探索を行います。
$w$の変化設定方法ですが、
最大の実行回数を$T$とすると(これはユーザが決める粒子たちの移動回数)
$w(t) = w_{hi} - (w_{hi} - w_{low}){\frac{t}{T}}$
とするとよいです。
$w_{hi}$は最初のスタート時点でも慣性重みで、
$w_{low}$は、最後に移動し終わったときに残っていて欲しい慣性重みです。
$w_{low}$を0にしない理由は、最後まったく慣性がないのはそれはそれで問題だからです。
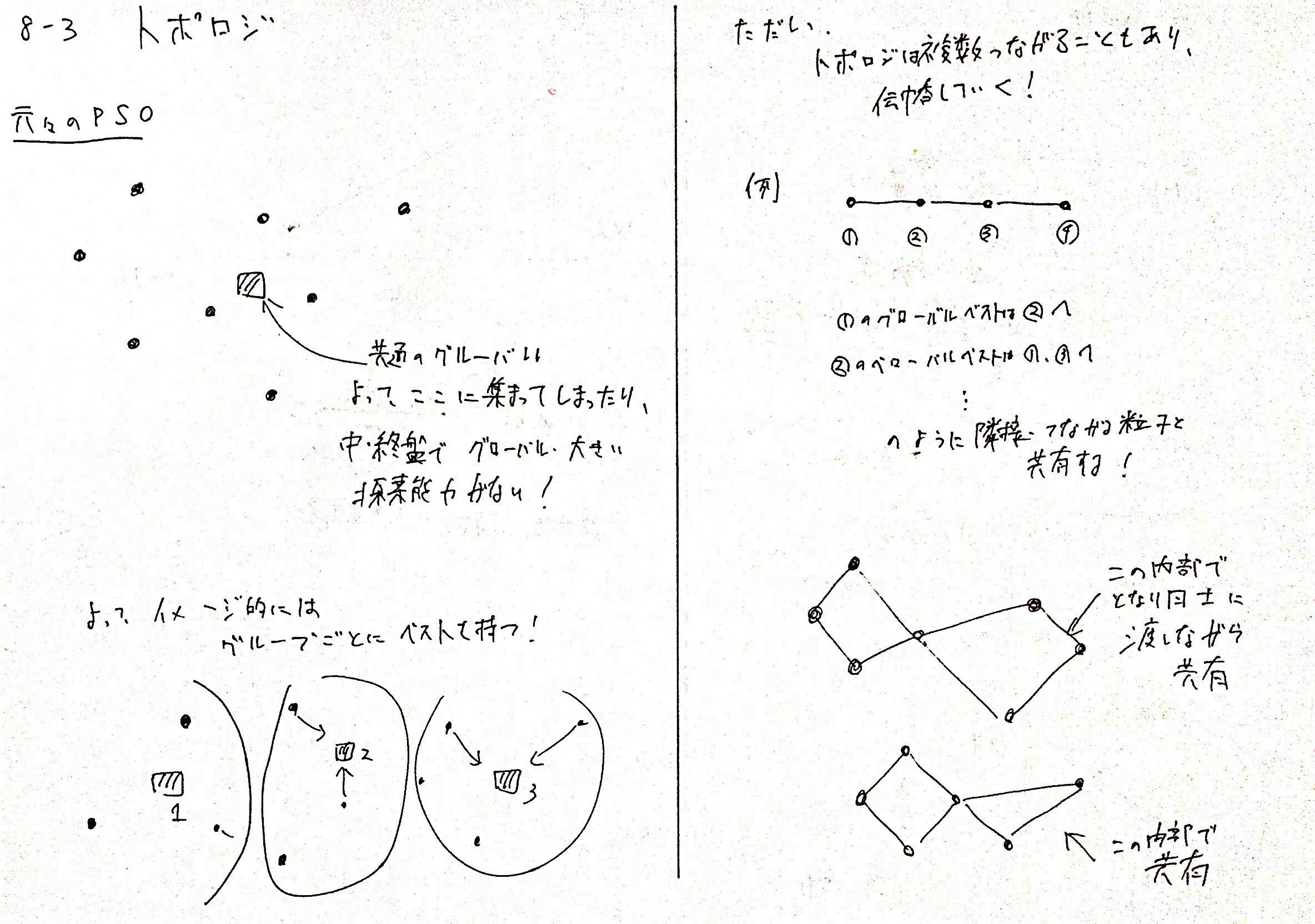
8-3. トポロジ
現状のPSOのグローバルベストは$N$個の粒子の最も良いパーソナルベスト位置が担っています。
しかし、このままでは、一度8-2の$w$、つまり慣性重みが探索中盤から小さくなってくると、大きい探索能力は消えて、局所のみになってしまいます。
また、一つのグローバルベストしかないため、すべての粒子が、パーソナルベストや慣性はあるものの、グローバルベストに引っ張られるため、移動が偏ってしまう問題も発生します。
そこで、本来の鳥の群れの習性である、近くの鳥しか見ていないという発想から、PSOでも近くの鳥のみとしかグローバルベストを共有しないようにしよう!というのがトポロジという工夫です。
トポロジを構成し、グローバルベストを繋がっている鳥たちを介して少しずつ共有することで、最良解をそれぞれ共有しながらもある意味グループ化してゆっくりと伝えることで、より広範囲の探索を可能にできます。
この繋がっている集団を近傍と呼びます。
近傍ですが、
- ランダムなインデックスでつなげる
- 実際の粒子間の距離
- 前もってトポロジ構造をユーザが定義してつなげる
という方法などで定義します。
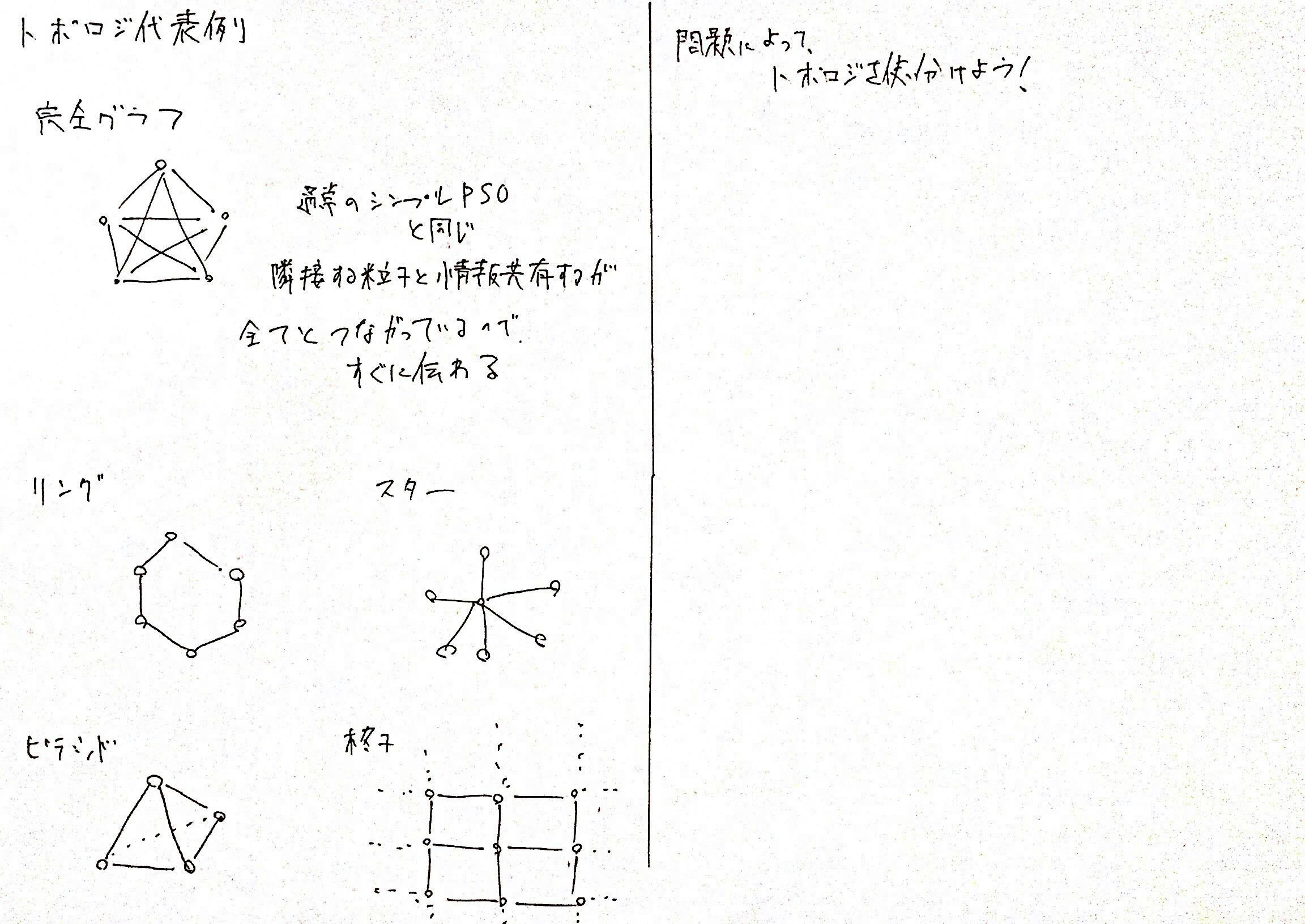
実際のトポロジは以下のようなものが多く利用されます。
もとのPSOは、完全グラフでグローバルベストが完全に一回の更新で共有されます。
統計としては
接続数が少ないトポロジほど、汎用的に多くの問題を解くことができます。
また、接続数が多い高密度トポロジは、単峰性に優れ、収束が早い
という特徴があります。
トポロジの設定も問題の性質や、ユーザの趣味によって変わります。
メタヒューリスティックのパラメータの難しい部分であると思います。
∞. 最後に
PSOは、群知能ではACOと肩を並べるほど有名なアルゴリズムです。
多くの適用事例や、応用が考えられています。
近年、DeepLearningや強化学習の話題で持ちっきりですが
群知能という生物の力を借りたアルゴリズムも非常に面白く、未来があります。
(日本だと知名度は低いです・・・)
もっと僕も理解していきたいと思います。