- 更新履歴
- 最適解と探索範囲を追記しました。
- 2016/11/29 @fimbulさん 編集リクエストありがとうございました。修正しました。
- 2017/7/10 @tomochiiiさん 編集リクエストありがとうございました。Easom functionを引用元の数式に修正、Schaffer function N. 2とN. 4の数式の修正
- 2018/5/9 @applicative62045 さん 編集リクエストありがとうございました(編集リクエストの確認遅くなりました。2019/12/31記載) Griek functionを修正
- 2019/12/31 @okamoto6496 さん 指摘ありがとうございました。Five-well potential functionの数式を修正。
- 2020/01/20 @higedura さん 指摘ありがとうございます。Bukin function N.6の数式を修正
- 2020/02/20 @nabenabe0928 さん 指摘ありがとうございます。k-tabletの数式を修正
この投稿はアルゴリズム Advent Calendar 2015 9日目になります。
はじめまして!とみっと(@tomit3)といいます。普段は地図屋でSEをやっています。趣味で.NETで使える最適化アルゴリズムライブラリ「LibOptimization」というものを作っています。
テーマがアルゴリズムなのでNature-Inspireな最適化アルゴリズムの解説を、、、と思ったのですが、ベンチマーク関数について触れられる投稿を見かけないので最適化の話を踏まえて簡単ですがまとめてみました。参考程度に。
最適化って何?
最適化っていったい何?という方に定義を下記に示します[1]。
与えられた制約条件のもとで関数の値を最大または最小にする変数の値を求めることを最適化と呼ぶ。
簡単にいうと何かしらの関数の一番小さい/大きい値になる変数を見つけることを最適化といいます。ここで何かしらの関数は評価関数とか目的関数とかエネルギー関数と呼ばれています。
ちなみに、数式では下記のような表現になります。$f(x)$が評価関数になります。
- 最小化
\min_{\substack{x}} f(x)
- 最大化
\max_{\substack{x}} f(x)
最適化の利用シーン
普段の生活で周長が一定である直方体で面積を最大にする形を作らなければならないという問題に遭遇したとします(秒速1cm/sで動く点Pみたいなもんです)。この時、評価関数を面積にし、変数を辺の長さとなるように評価関数を設計します。この評価関数を最大化する最適化問題を解くことで周長の面積が最大になる形を求めることが出来ます。
最適化するためには何か目的があって、その目的に応じ評価関数を設計する必要があります。
もう少し身近な製品をもとに利用シーンを下記に示します。
- カメラレンズ
- 新幹線の先端形状
- 経路探索
何を最小/最大化するか(評価関数の設計)は下記のようになります。
- カメラレンズ ⇒ 収差やレンズ枚数を評価関数にし、最小化する。
- 新幹線の先端形状 ⇒ 空気抵抗を評価関数にし、最小化する。
- 経路探索 ⇒ 経路長/移動費用を評価関数にし、最小化する。
最近ホットな話題である機械学習も最適化の問題といえます。学習用データと構築するモデルの誤差を評価関数の形に表し、誤差を最小化させる(学習データを再現できるモデルが出来る)ことで分類/回帰を行います。
最適化の難しさ
最適化アルゴリズムは最適化を行う過程で勾配(評価関数の微分)を用いるか用いないかで2種類に分けることが出来ます。
勾配を用いる最適化アルゴリズムの代表例が最急降下法です。
最急降下法は評価関数の1階微分を用いて最適解を探索します。評価関数の1階微分は評価関数の一番小さい/大きい値(最適解)の方向になるので得られた値を随時を更新していくことでいずれ最適解が見つかります。
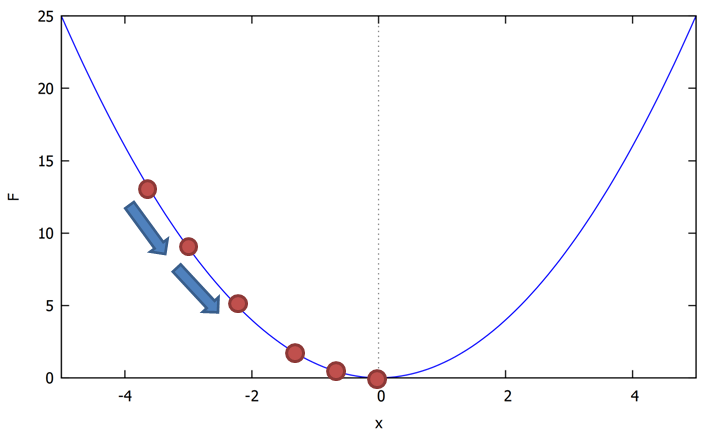
$f(x)=x^2$(最小値は、$x=0$の位置で$f(0)=0$)の例を示します。
最急降下法を用いて最適解を探索するイメージが下記になります(勾配はボールを転がる方向に相当)。
しかし、評価関数の勾配を使えば常に一番小さい値/大きい値が見つかるわけではありません。
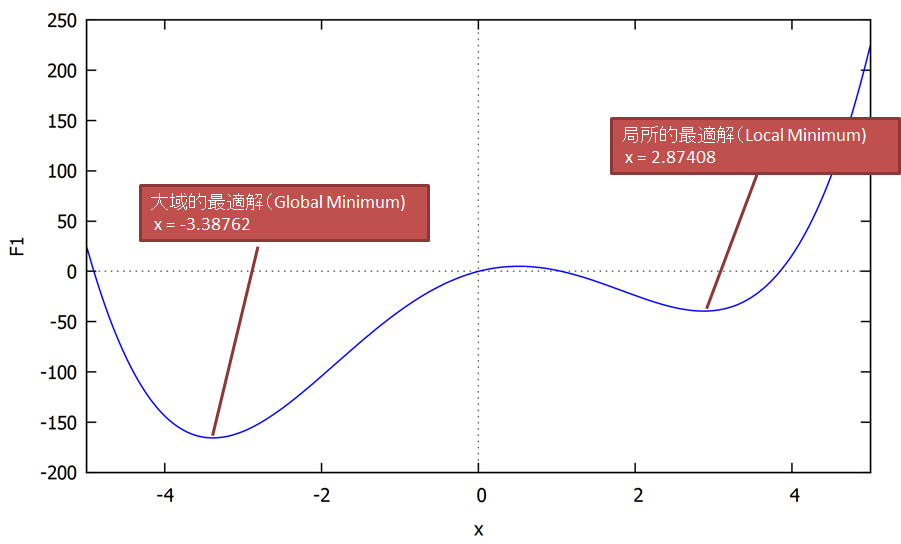
$f(x)=x^4-20x^2+20x$の例を示します。
先ほどの関数$f(x)=x^2$はたまたま一つの谷しか存在しませんでしたが、今回の例では谷が2つあります。
最急降下法を行う初期値(ボールを転がす最初の位置)によっては一番小さい/大きい値を得ることが出来ません。
※一番小さい/大きい時の最適解を大域的最適解(Global minimum/maximum)、それ以外の最適解を局所的最適解(Local minimum/maximum)と呼びます。
最急降下法は勾配を求めて最適解を探索します。しかし、評価関数によっては勾配を求めることが出来ない場合があります。この場合、勾配を用いない最適化アルゴリズムを用いることで最適解(近似解)を求めることが可能です。勾配を用いない最適化アルゴリズムは多数提案されています。代表的なアルゴリズムは遺伝的アルゴリズムです。勾配を用いない最適化アルゴリズムは評価関数上に多数の点を配置し探索(多点探索)を行います。点の配置方法、更新に各種アルゴリズムの特徴があります(説明は割愛します)。
最適化の難しさの分類
最適化の難しさについて保木さんの論文にわかりやすい図があったので引用します[2](この論文は、コンピュータ将棋の評価関数の最適化技法のものです)。図の左にあるものほど最適化が簡単で、右に行くほど難しくなることを表しています。
図の(a)~(e)はそれぞれ評価関数の形状を表しそれぞれ、
- **(a)**は関数の形状が単峰性
- **(b)、(d)**は関数の形状が多峰性
- **(c)、(e)**は関数が不連続(微分不可)
を表しています。
**(b)、(d)はそれぞれ谷が複数ある状態で初期値(ボールを転がす最初の位置)によって大域的最適解が求められないためやや困難です。特に(d)**の場合、最急降下法を用いるときはよほど都合よい位置から始めなければ最適解に辿りつきません。
**(c)、(e)**の場合は不連続の部分で勾配を求めることができないため、勾配を用いる最適化アルゴリズムは使うことができません。
最適化が難しい具体的な実例
データからデータを説明する数式(回帰式)を求め値を予測する(単/重)回帰分析という技法があります。
回帰分析は、目的変数と回帰式から求めた推測値の残差平方和の評価関数を最小化する最小二乗法を用いることで回帰式を求めることが出来ます。
- (通常の)回帰分析の評価関数
Q=||y-\hat y||^2
※具体的には評価関数と回帰係数の微分を0として連立方程式を解くことになります($\frac{\partial Q}{\partial w}=0$ 微分が必須!)。
回帰分析の技法の中でLasso回帰というものがあります。回帰係数を0(疎:スパース)にする事で変数選択と同じような効果が選られる回帰分析技法のひとつです。Lasso回帰の評価関数には残差平方和と正則化項である回帰係数のL1ノルム(絶対値の和。$|w|$に相当)が含まれています。
- Lasso回帰の評価関数
Q=||y-\hat y||^2 - \alpha|w|
このL1ノルムが絶対値のため先と同じ最小二乗法で求めるのが難しく、別の解法を用いる必要があります。
最適化アルゴリズムとベンチマーク関数
下記に最適化アルゴリズムの一例を列挙しました。最近ですが自然界をアイデアにした勾配を使用しない最適化アルゴリズムが多数提案されています。
- PatternSearch法
- Nelder-Mead法
- 遺伝的アルゴリズム
- 粒子群最適化
- 差分進化法
- カッコーサーチ
- ホタルアルゴリズム など
これら最適化アルゴリズムの性能の良し悪しを決めるために用いるのがベンチマーク関数(テスト関数とも呼ばれます)です。ベンチマーク関数は先に説明した、単峰性/多峰性、関数の不連続などを特徴に持ち、探索の範囲が設定され、最小値/最大値が既に分かっている関数です。最適化アルゴリズムの評価はこれらベンチマーク関数を評価関数として最適解を探させることで性能の良し悪しを比較しています。
ベンチマーク関数まとめ
ここからが本題です。ベンチマーク関数の特徴、数式、探索範囲と最適解、出典(2次、3次の引用になっているのはご了承ください)をまとめました。下記に列挙したベンチマーク関数は制約条件が無いものをピックアップしています。
形状はMaximaで作りました。Maximaファイルはgithubにあげています。
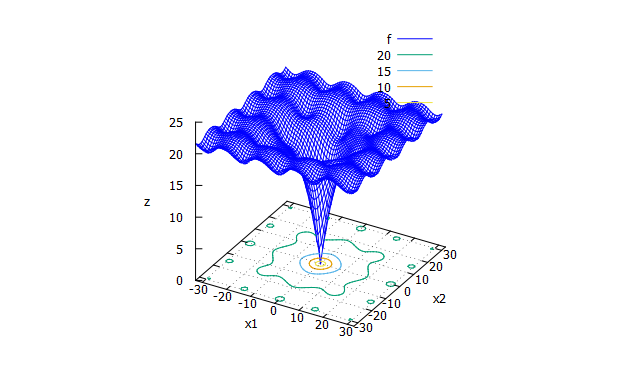
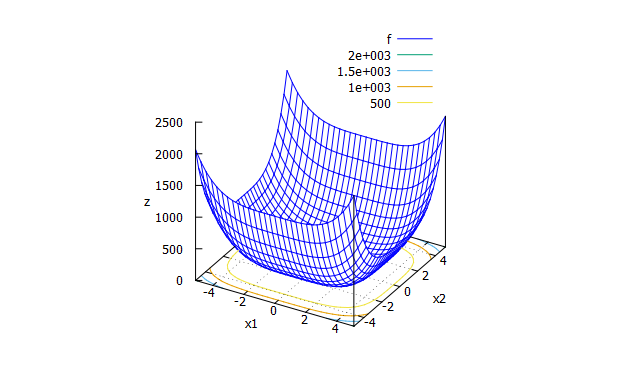
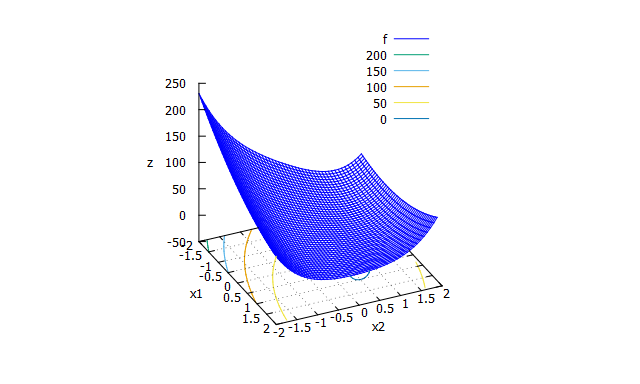
Ackley function
-
特徴
多峰性関数。大域的最適解の周辺に多数の局所解をもつ。 -
数式
f(x_{1} \cdots x_{n})=20-20\exp \biggl( -0.2\sqrt{\frac{1}{n}\sum_{i=1}^{n}x_{i}^2} \biggr) +e-\exp \biggl(\frac{1}{n}\sum_{i=1}^{n}\cos(2\pi x_{i}) \biggr)
- 探索範囲と最適解
-32.768 \leqq x_{i} \leqq 32.768 \\
f_{min}(0, \cdots , 0)=0
- 出典
- Test functions for optimization(en:Wikipedia)
- Xin-She Yang, "Test Problems in Optimization", arXiv(http://arxiv.org/abs/1008.0549)
- ※探索範囲
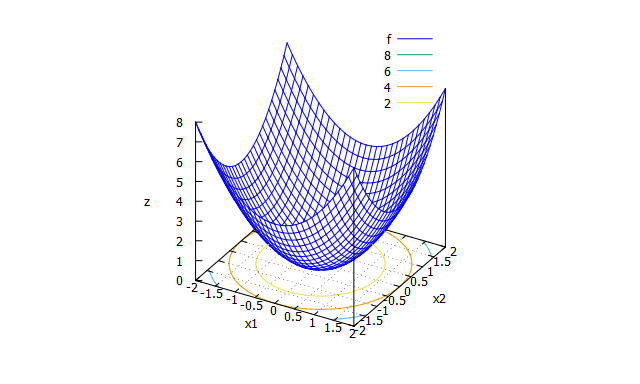
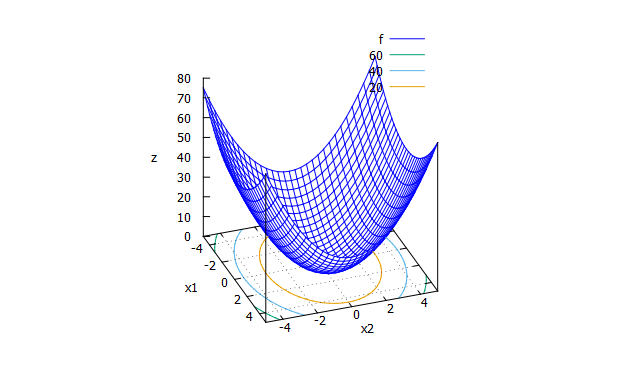
Sphere function
-
特徴
基本的な関数。 -
数式
f(x_{1} \cdots x_{n})=\sum_{i=1}^{n}x_{i}^2
- 探索範囲と最適解
\infty \leqq x_{i} \infty \\
f_{min}(0, \cdots , 0)=0
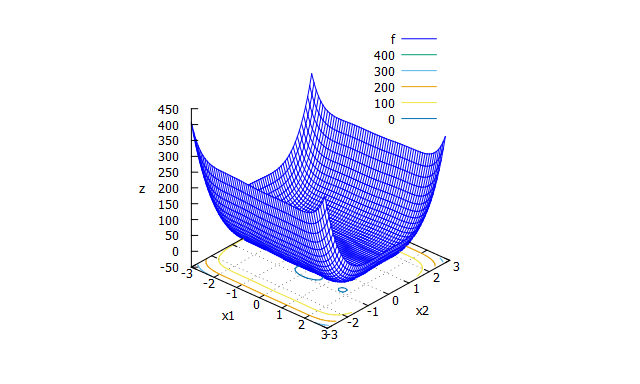
Rosenbrock function
-
特徴
単峰性関数。ベンチマーク関数の代表。別名バナナ関数。 -
数式
f(x_{1} \cdots x_{n-1})=\sum_{i=1}^{n}(100(x_{i+1}-x_{i}^2)^2+(x_{i}-1)^2)
- 探索範囲と最適解
-5 \leqq x_{i} \leqq 5 \\
f_{min}(1, \cdots , 1)=0
- 出典
- Test functions for optimization(en:Wikipedia)
- Xin-She Yang, "Test Problems in Optimization", arXiv(http://arxiv.org/abs/1008.0549)
- ※探索範囲
Beale function
-
特徴
多峰性関数。 -
数式
f(x_{1},x_{2})=(1.5-x_{1}+x_{1}x_{2})^2+(2.25-x_{1}+x_{1}x_{2}^2)^2+(2.625-x_{1}+x_{1}x_{2}^3)^2
- 探索範囲と最適解
-4.5 \leqq x_{1} , x_{2} \leqq 4.5 \\
f_{min}(3,0.5)=0
Goldstein-Price function
-
特徴
多峰性関数。 -
数式
\begin{split}
f(x_{1},x_{2})= & \Bigl(1+(x_{1}+x_{2}+1)^2(19-14x_{1}+3x_{1}^2-14x_{2}+6x_{1}x_{2}+3x_{2}^2)\Bigr) \\
& \Bigl(30+(2x_{1}-3x_{2})^2(18-32x_{1}+12x_{1}^2+48x_{2}-36x_{1}x_{2}+27x_{2}^2)\Bigr)
\end{split}
- 探索範囲と最適解
-2 \leqq x_{1} , x_{2} \leqq 2 \\
f_{min}(0,-1)=3
Booth function
-
特徴
単峰性関数。 -
数式
f(x_{1},x_{2})=(x_{1}+2x_{2}-7)^2 + (2x_{1}+x_{2}-5)^2
- 探索範囲と最適解
-10 \leqq x_{1} , x_{2} \leqq 10 \\
f_{min}(1,-3)=0
Bukin function N.6
-
特徴
多峰性関数。谷に多くの局所解をもつ。 -
数式
f(x_{1},x_{2})=100*\sqrt{|x_{2}-0.01x_{1}^2|}+0.01|x_{1}+10|
- 探索範囲と最適解
-15 \leqq x_{1} \leqq -5 \\
-3 \leqq x_{2} \leqq 3 \\
f_{min}(-10,1)=0
Matyas function
-
特徴
単峰性関数。 -
数式
f(x_{1},x_{2})=0.26(x_{1}^2+x_{2}^2)-0.48x_{1}x_{2}
- 探索範囲と最適解
-10 \leqq x_{1} , x_{2} \leqq 10 \\
f_{min}(0,0)=0
Levi function N.13
-
特徴
多峰性関数。 -
数式
f(x_{1},x_{2})=\sin^2(3\pi x_{1})+(x_{1}-1)^2\bigl(1+\sin^2(3\pi x_{2})\bigr)+(x_{2}-1)^2\bigl(1+\sin^2(2\pi x_{2})\bigr)
- 探索範囲と最適解
-10 \leqq x_{1} , x_{2} \leqq 10 \\
f_{min}(1,1)=0
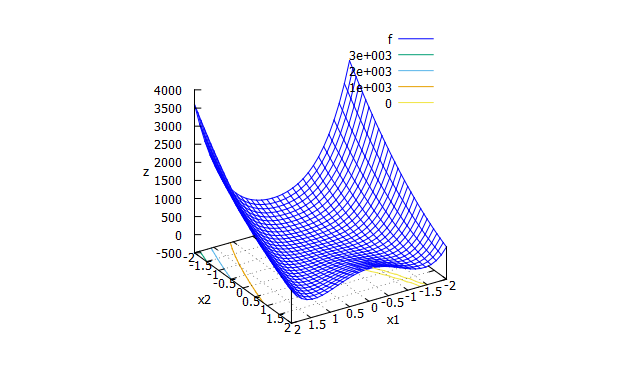
Three-hump camel function
拡大
-
特徴
多峰性関数。 -
数式
f(x_{1},x_{2}) = 2x_{1}^2-1.05x_{1}^4+\frac{x_{1}^6}{6}+x_{1}x_{2}+x_{2}^2
- 探索範囲と最適解
-5 \leqq x_{1} , x_{2} \leqq 5 \\
f_{min}(0,0)=0
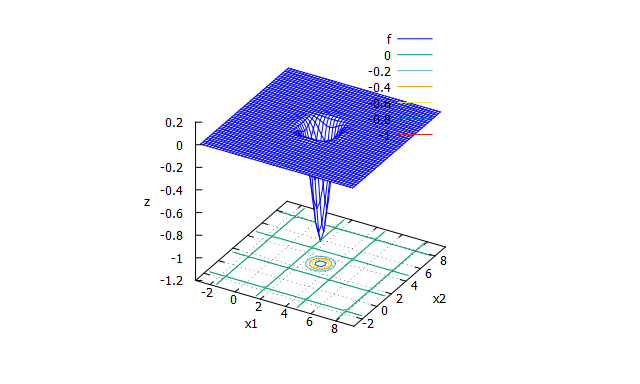
Easom function
-
特徴
多峰性関数。大域的最適解は限られた範囲の位置から探索する必要がある -
数式
f(x_{1},x_{2}) = -\cos(x_{1})\cos(x_{2})\exp(-((x_{1}-\pi)^2+(x_{2}-\pi)^2))
- 探索範囲と最適解
-100 \leqq x_{1} , x_{2} \leqq 100 \\
f_{min}(\pi,\pi)=-1
Eggholder function
-
特徴
多峰性関数。 -
数式
f(x_{1},x_{2})=-(x_{2}+47)\sin\bigl(\sqrt{|x_{2}+\frac{x_{1}}{2}+47|}\bigr)-x_{1}\sin\bigl(\sqrt{|x_{1}-(x_{2}+47)|}\bigr)
- 探索範囲と最適解
-512 \leqq x_{1} , x_{2} \leqq 512 \\
f_{min}(512,404.2319)=-959.6407
McCormick function
-
特徴
多峰性関数。 -
数式
f(x_{1},x_{2})=\sin(x_{1}+x_{2})+(x_{1}-x_{2})^2-1.5x_{1}+2.5x_{2}+1
- 探索範囲と最適解
-1.5 \leqq x_{1} \leqq 4 \\
-3 \leqq x_{2} \leqq 4 \\
f_{min}(-0.54719,-1.54719)=-1.9133
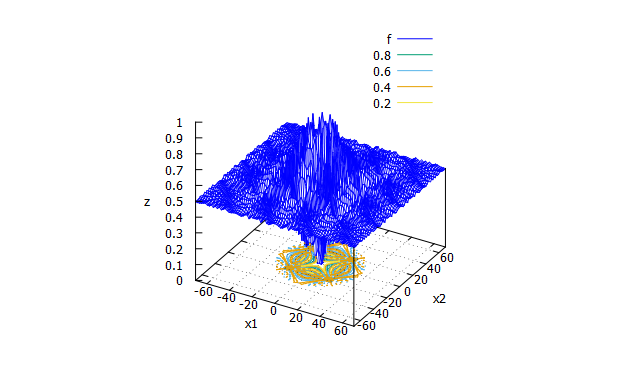
Schaffer function N. 2
-
特徴
多峰性関数。大域的最適解の周辺に多数の局所解をもつ。 -
数式
f(x_{1},x_{2})=0.5+\frac{\sin^2(x_{1}^2-x_{2}^2)-0.5}{\bigl(1+0.001(x_{1}^2+x_{2}^2)\bigr)^2}
-100 \leqq x_{1} , x_{2} \leqq 100 \\
f(0,0)=0
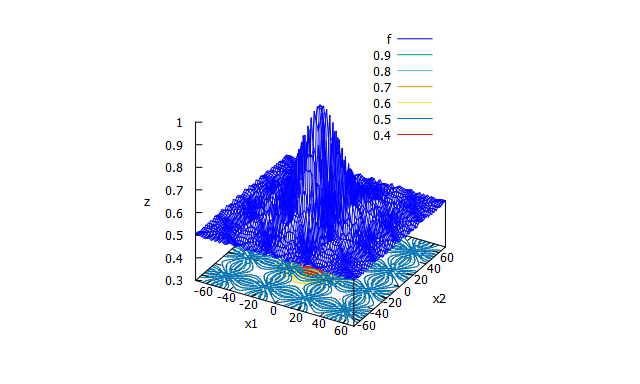
Schaffer function N. 4
-
特徴
多峰性関数。大域的最適解の周辺に多数の局所解をもつ。 -
数式
f(x_{1},x_{2})=0.5+\frac{\cos^2\bigl(\sin(|x_{1}^2-x_{2}^2|)\bigr)-0.5}{\bigl(1+0.001(x_{1}^2+x_{2}^2)\bigr)^2}
- 探索範囲と最適解
-100 \leqq x_{1} , x_{2} \leqq 100 \\
f_{min}(0,1.25313)=0
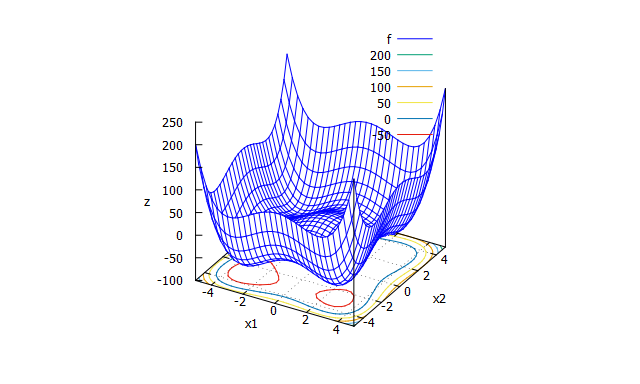
Styblinski-Tang function
-
特徴
多峰性関数。 -
数式
f(x_{1} \cdots x_{n})=\frac{\sum_{i=1}^{n}x_{i}^4-16x_{i}^2+5x_{i}}{2}
- 探索範囲と最適解
-5 \leqq x_{1} \leqq 4 \\
-3 \leqq x_{2} \leqq 4 \\
-39.16617n \leq f(-2.903534, \cdots , -2.903534) \leq -39.16616n \\
f_{min}(-2.903534, \cdots , -2.903534) \approx -39.166165n
De Jong’s function F1
-
特徴
Sphere functionと同じ -
数式
Sphere functionと同じ -
探索範囲と最適解
Sphere functionと同じ -
出典
- Kenneth Alan De Jong, "Analysis of the behavior of a class of genetic adaptive system", August 1975, Technical Report No.185
- Test functions for optimization(en:Wikipedia)
De Jong’s function F2
-
特徴
Rosenblock functionと同じ -
数式
Rosenblock functionと同じ -
探索範囲と最適解
Rosenblock functionと同じ -
出典
- Kenneth Alan De Jong, "Analysis of the behavior of a class of genetic adaptive system", August 1975, Technical Report No.185
- Test functions for optimization(en:Wikipedia)
- Xin-She Yang, "Test Problems in Optimization"
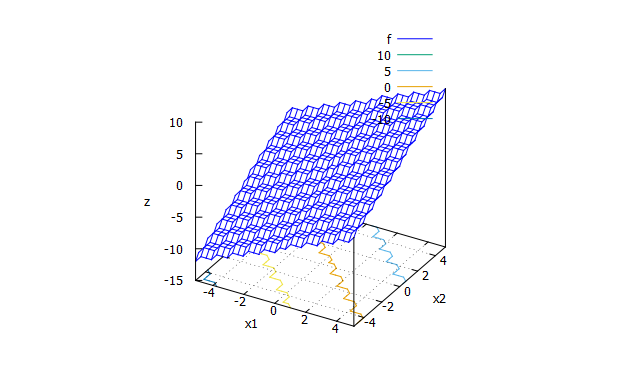
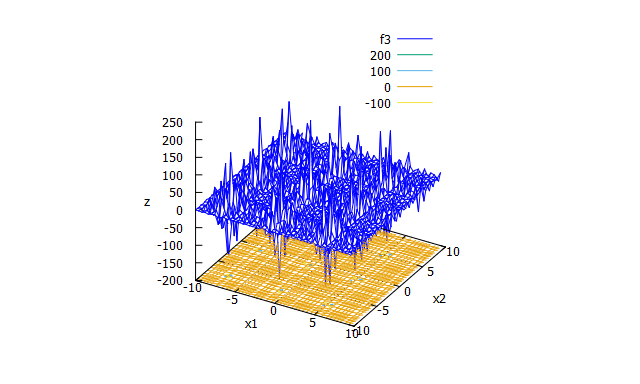
De Jong’s function F3
-
特徴
単峰性関数。整数に切り捨てる処理のため階段状になるのが特徴。 -
数式
f(x_{1} \cdots x_{5})=\sum_{i=1}^{5}[x_{i}] \\
[]は浮動小数点を切り捨て、整数にする記号
- 探索範囲と最適解
-5.12 \leqq x_{1} \leqq 5.12 \\
-5.12 \leqq x_{2} \leqq 5.12 \\
f_{min}(-5.12 \sim -5, \cdots , -5.12 \sim -5)=0
- 出典
- Kenneth Alan De Jong, "Analysis of the behavior of a class of genetic adaptive system", August 1975, Technical Report No.185
De Jong’s function F4
-
特徴
Sphere関数の重みづけ+正規分布乱数を付与。 -
数式
単峰性関数。
f(x_{1} \cdots x_{30})=\sum_{i=1}^{30}ix_{i}^4+Gauss(0,1) \\
Gauss(0,1)は平均0の標準偏差1の正規分布の乱数
- 探索範囲と最適解
-1.28 \leqq x_{1} \leqq 1.28 \\
-1.28 \leqq x_{2} \leqq 1.28 \\
f_{min}(0, \cdots , 0)=0+Gauss(0,1)
- 出典
- Kenneth Alan De Jong, "Analysis of the behavior of a class of genetic adaptive system", August 1975, Technical Report No.185
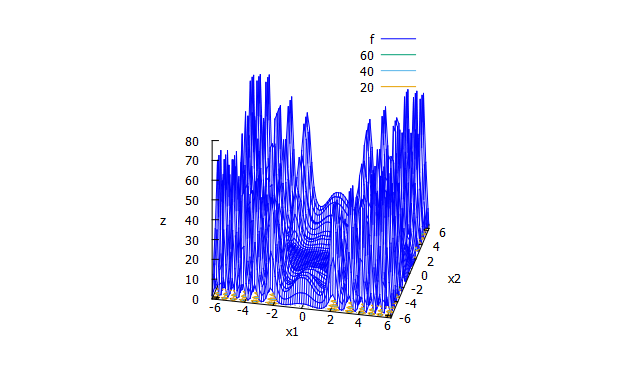
De Jong’s function F5
※De Jong’s function F5はExcelから作りました
-
特徴
多峰性関数。25個の局所解をもつ。 -
数式
\frac{1}{f(x_{1} \cdots x_{25})}=\frac{1}{500}+\sum_{j=1}^{25}\frac{1}{j+\sum_{i=1}^{2}(x_{i}-a_{ij})^6} \\
\begin{align*}
& a= \left(
\begin{array}{cccccc}
-32 & -16 & 0 & 16 & 32 & -32 & -16 & 0 & 16 & 32 \\
-32 & -32 & -32 & -32 & -32 & -16 & -16 & -16 & -16 & -16
\end{array}
\right. \\
& \left.
\begin{array}{cccccc}
\qquad\quad -32 & -16 & 0 & 16 & 32 & -32 & -16 & 0 & 16 & 32 & -32 & -16 & 0 & 16 & 32 \\
\qquad\quad 0 & 0 & 0 & 0 & 0 & 16 & 16 & 16 & 16 & 16 & 32 & 32 & 32 & 32 & 32
\end{array}
\right)
\end{align*}
- 探索範囲と最適解
-65.536 \leqq x_{1} \leqq 65.536 \\
-65.536 \leqq x_{2} \leqq 65.536 \\
f_{min}(-32 , 32) \approx 1
- 出典
- Kenneth Alan De Jong, "Analysis of the behavior of a class of genetic adaptive system", August 1975, Technical Report No.185
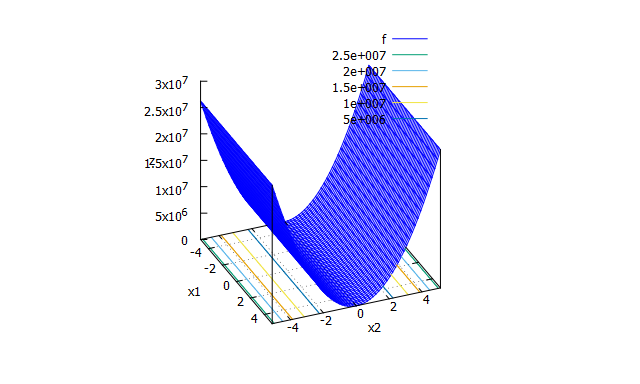
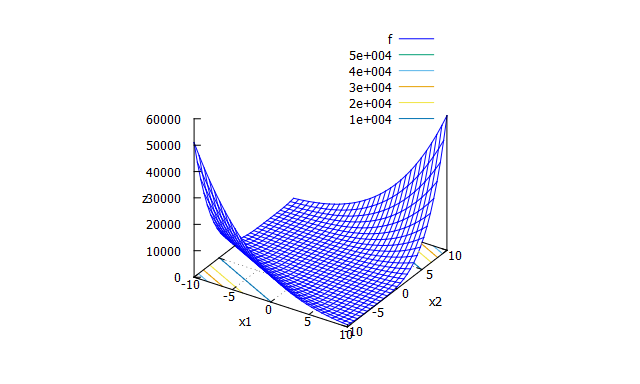
Ellipsoid function
-
特徴
-
数式
f(x_{1} \cdots x_{n}) = \sum_{i=1}^{n}(1000^\frac{i-1}{n-1}x_{i})^2
- 探索範囲と最適解
-5.12 \leqq x_{i} \leqq 5.12 \\
f_{min}(0, \cdots , 0)=0
- 出典
- 小林重信, "実数値GAのフロンティア",人工知能学会誌 Vol. 24, No. 1, pp.147-162 (2009)
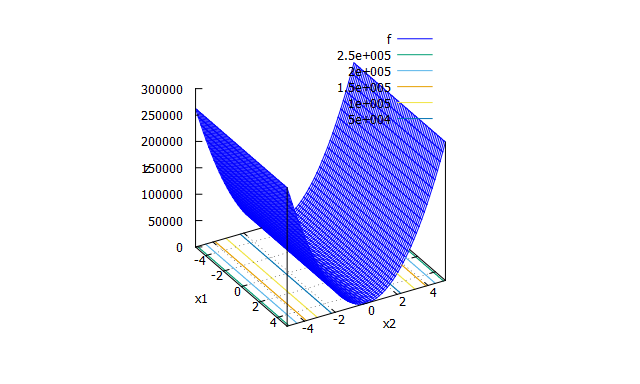
k-tablet function
-
特徴
単峰性関数。k-tablet構造という悪スケール性※を持つ(※方向によってスケーリングが異なる性質を悪スケール性という)。 -
数式
f(x_{1} \cdots x_{n}) = \sum_{i=1}^{k}x_{i}^2 + \sum_{i=k+1}^{n}(100x_{i})^2 \\
k=n/4
- 探索範囲と最適解
-5.12 \leqq x_{i} \leqq 5.12 \\
f_{min}(0, \cdots , 0)=0
- 出典
*小林重信, "実数値GAのフロンティア",人工知能学会誌 Vol. 24, No. 1, pp.147-162 (2009)
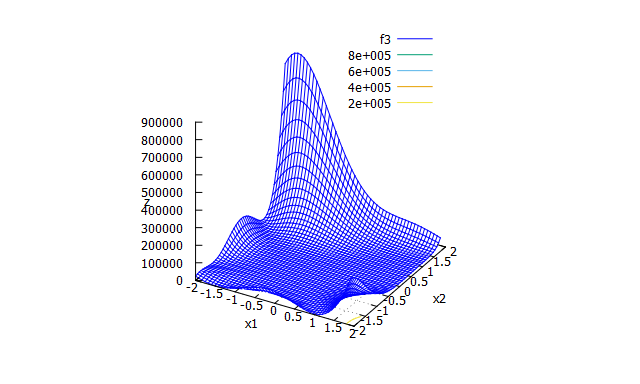
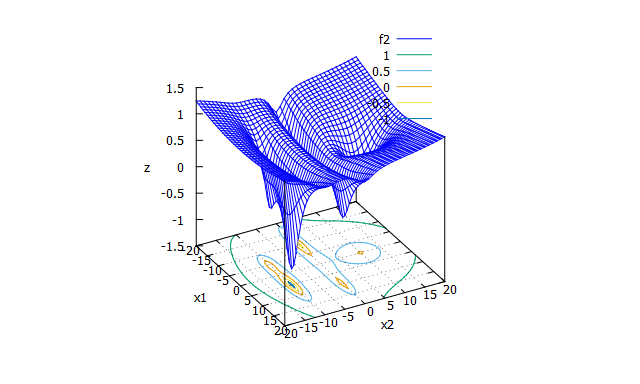
Five-well potential function
-
特徴
多峰性関数。5個の局所解がある。 -
数式
\begin{split}
f(x_{1} , x_{2})= & \Biggl(1-\frac{1}{1+0.05\bigl(x_{1}^2+(x_{2}-10)^2\bigr)} \\
& \quad -\frac{1}{1+0.05\bigl((x_{1}-10)^2+x_{2}^2\bigr)} \\
& \quad -\frac{1.5}{1+0.03\bigl((x_{1}+10)^2+x_{2}^2\bigr)} \\
& \quad -\frac{2}{1+0.05\bigl((x_{1}-5)^2+(x_{2}+10)^2\bigr)} \\
& \quad -\frac{1}{1+0.1\bigl((x_{1}+5)^2+(x_{2}+10)^2\bigr)} \Biggr) \Biggl(1+0.0001(x_{1}^2+x_{2}^2)^{1.2}\Biggr)
\end{split}
- 探索範囲と最適解
-20 \leqq x_{1} \leqq 20 \\
-20 \leqq x_{2} \leqq 20 \\
f(4.92 , -9:89)=-1.4616
- 出典
- Ilya Pavlyukevich, "Levy flights, non-local search and simulated annealing", Journal of Computational Physics 226 (2007) 1830-1844
Weighted Sphere function or hyper ellipsodic function
-
特徴
単峰性関数。Sphere関数に重みづけしたベンチマーク関数。 -
数式
f_{min}(x_{1} \cdots x_{n})=\sum_{i=1}^{n}ix_{i}^2
- 探索範囲と最適解
-5.12 \leqq x_{i} \leqq 5.12 \\
f_{min}(0, \cdots , 0)=0
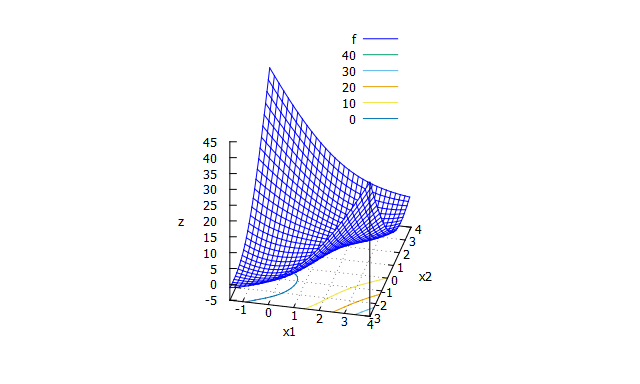
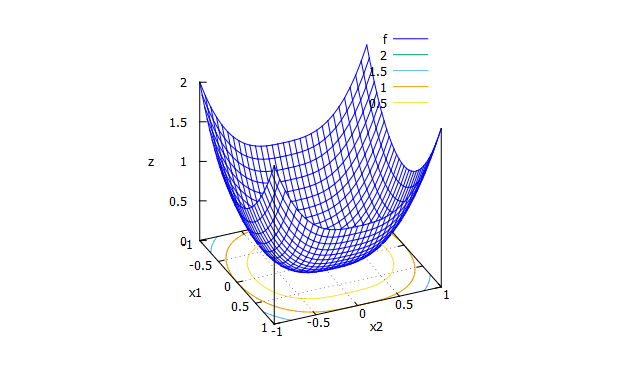
Sum of different power function
-
特徴
単峰性関数。絶対値がある。 -
数式
f(x_{1} \cdots x_{n})=\sum_{i=1}^{n}|x_{i}|^{i+1}
- 探索範囲と最適解
-1 \leqq x_{i} \leqq 1 \\
f_{min}(0, \cdots , 0)=0
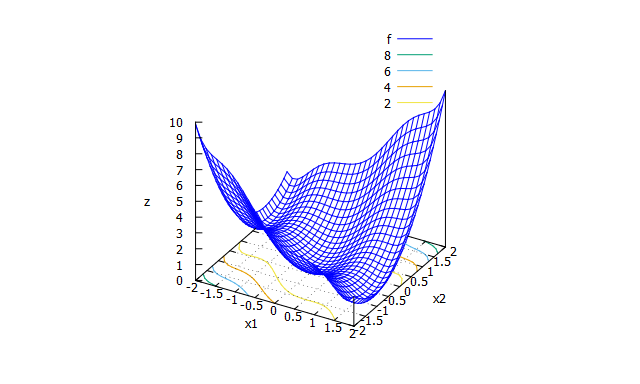
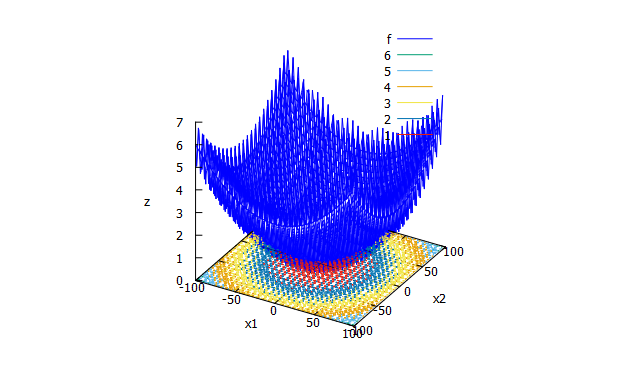
Griewank function
-
特徴
多峰性関数。非常に多くの局所解をもつ。 -
数式
f(x_{1} \cdots x_{n})=1+\frac{1}{4000}\sum_{i=1}^{n}x_{i}^2-\prod_{i=1}^{n}\cos\Bigl(\frac{x_{i}}{\sqrt{i}}\Bigr)
- 探索範囲と最適解
-600 \leqq x_{i} \leqq 600 \\
f_{min}(0, \cdots , 0)=0
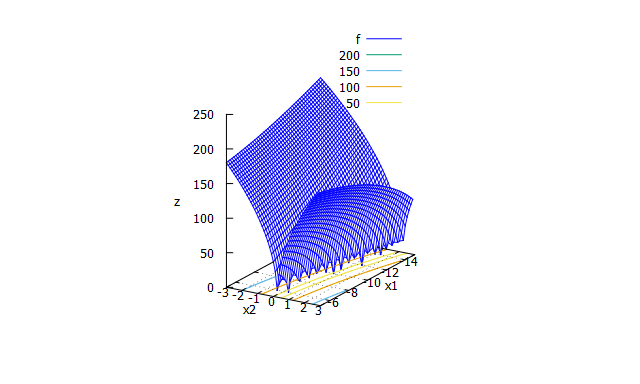
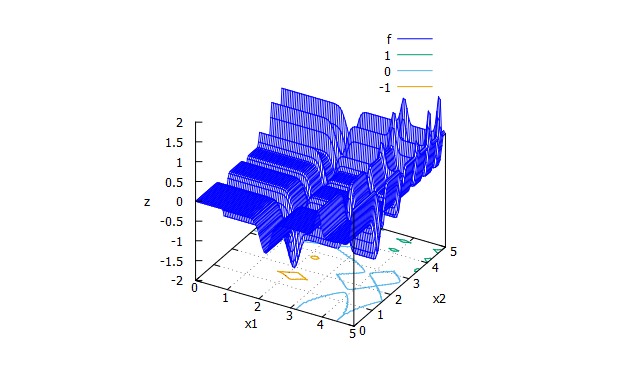
Michalewicz function
-
特徴
多峰性関数。次元数によって大域的最適解が異なる。 -
数式
f(x_{1} \cdots x_{n})=-\sum_{i=1}^{n}\sin(x_{i})\sin^{2m}(\frac{ix_{i}^2}{\pi}) \\
m=10
- 探索範囲と最適解
0 \leqq x_{i} \leqq \pi \\
n=2の場合\\
f_{min}(2.20319,1.57049) \approx -1.8013
Perm function
-
特徴
単峰性関数。 -
数式
f(x_{1} \cdots x_{n})=\sum_{j=1}^{n} \Biggl(\sum_{i=1}^{n}(i+\beta)\biggl(x_{i}^j- \bigl( \frac{1}{i} \bigr)^j \biggr) \Biggr)^2 \\
\beta > 0
- 探索範囲と最適解
-1 \leqq x_{i} \leqq 1 \\
f_{min}(1, \frac{1}{2} , \cdots , \frac{1}{n}) = 0
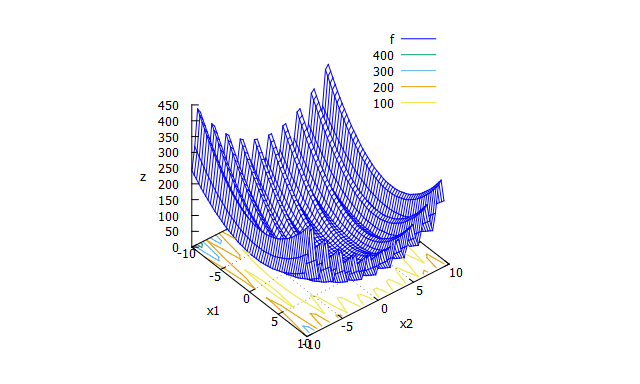
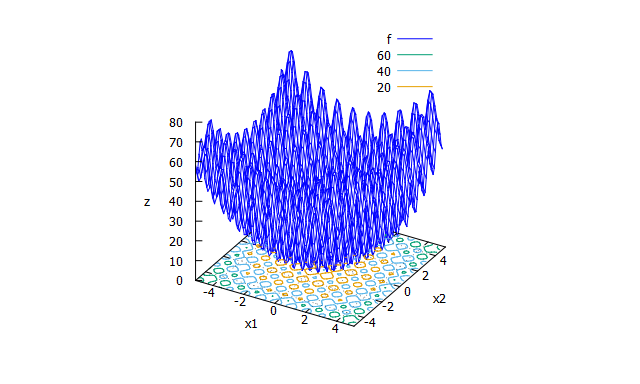
Rastrigin function
-
特徴
多峰性関数。非常に多くの局所解をもつ。 -
数式
f(x_{1} \cdots x_{n})=10n+\sum_{i=1}^{n}(x_{i}^2-10\cos(2 \pi x_{i}))
- 探索範囲と最適解
-5.12 \leqq x_{i} \leqq 5.12 \\
f_{min}(0, \cdots , 0) = 0
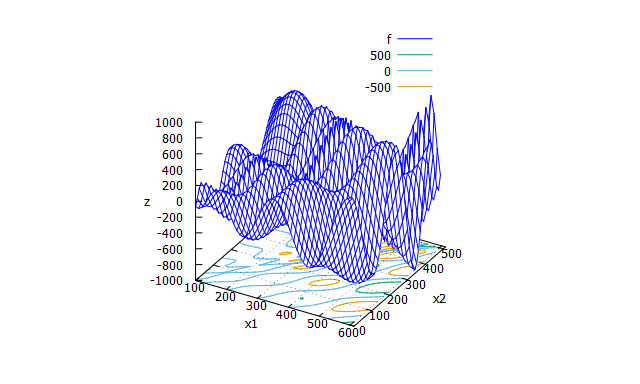
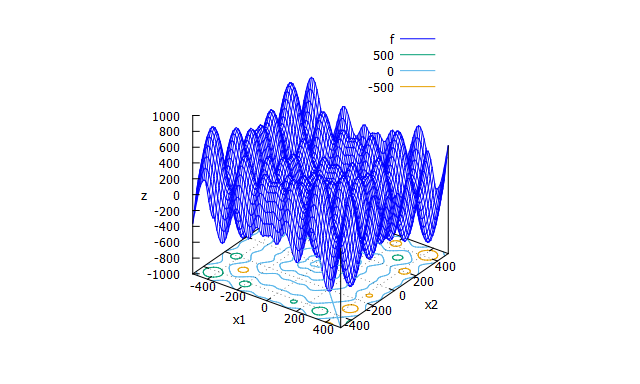
Schwefel function
-
特徴
多峰性関数。 -
数式
f(x_{1} \cdots x_{n})=-\sum_{i=1}^{n}x_{i}\sin\bigl(\sqrt{|x_{i}|}\bigr)
- 探索範囲と最適解
-500 \leqq x_{i} \leqq 500 \\
f_{min}(420.9687, \cdots , 420.9687) \approx -418.9829n
Six-hump camel function
-
特徴
多峰性関数。 -
数式
f(x_{1},x_{2}) = (4-2.1x_{1}^2+\frac{1}{3}x_{1}^4)x_{1}^2+x_{1}x_{2}+4(x_{2}^2-1)x_{2}^2
- 探索範囲と最適解
-3 \leqq x_{1} \leqq 3 \\
-2 \leqq x_{2} \leqq 2 \\
f_{min}(0.0898,-0.7126) = f_{min}(-0.0898,0.7126) \approx -1.0316
Shuberts function
-
特徴
多峰性関数。大域的最適解が18個ある。 -
数式
f(x_{1},x_{2}) = \bigl( \sum_{i=1}^{n}i\cos(i+(i+1)x_{1}) \bigr) \bigl( \sum_{i=1}^{n}i\cos(i+(i+1)x_{2}) \bigr) \\
n = 5
- 探索範囲と最適解
※n=5の場合の探索範囲 \\
-10 \leqq x_{1}\\
x_{2} \leqq 10\\
f_{min}=-186.7309
Xin-She Yang function
-
特徴
多峰性関数。 -
数式
f(x_{1} \cdots x_{n})=\bigl(\sum_{i=1}^{n}|x_{i}| \bigr) \exp \bigl(-\sum_{i=1}^{n}\sin(x_{i}^2) \bigr)
- 探索範囲と最適解
-2 \pi \leqq x_{i} \leqq 2 \pi \\
f_{min}(0, \cdots , 0) = 0
Zakharov function
-
特徴
単峰性関数。 -
数式
f(x_{1} \cdots x_{n})=\sum_{i=1}^{n}x_{i}+\bigl(\frac{1}{2}\sum_{i=1}^{n}ix_{i} \bigr)^2+\bigl(\frac{1}{2}\sum_{i=1}^{n}ix_{i} \bigr)^4
- 探索範囲と最適解
探索範囲無し。 \\
f_{min}(0, \cdots , 0) = 0
参考文献
- 金谷 健一, "これなら分かる最適化数学―基礎原理から計算手法まで", 共立出版株式会社, 2007年, 初版第7刷
- K. Hoki and T. Kaneko, "Large-Scale Optimization for Evaluation Functions with Minimax Search", Journal of Artificial Intelligence Research (JAIR), 2014, Volume 49, pages 527-568
- Test functions for optimization(en:Wikipedia)
- Kenneth Alan De Jong, "Analysis of the behavior of a class of genetic adaptive system", August 1975, Technical Report No.185
- Xin-She Yang, "Test Problems in Optimization", arXiv(http://arxiv.org/abs/1008.0549)
- 佐久間 淳, 小林 重信, "高次元k-tablet構造を考慮した実数値GA 隠れ変数上の交叉LUNDX-mの提案と評価", 人工知能学会論文誌Vol. 19 (2004) No. 1 P 28-37
- Ilya Pavlyukevich, "Levy flights, non-local search and simulated annealing", Journal of Computational Physics 226 (2007) 1830-1844
下記Qiita投稿について参考にしました。
LibOptimization
少し宣伝。趣味で.NET Frameworkで使える最適化アルゴリズムライブラリを作っています。ご興味ある方はぜひ。
実装している最適化アルゴリズム
- 最急降下法
- ニュートン法
- (HookeJeeves)PatternSearch
- Nelder-Mead法
- 実数値遺伝的アルゴリズム(RGA)
- BLX-α
- UNDX
- SPX
- PCX
- 粒子群最適化(PSO)
- LDIW
- AIW
- ChaoticIW
- 差分進化法(DE)
- DE/rand/1/bin, DE/rand/2/bin, DE/best/1/bin, DE/best/2/bin
- カッコーサーチ
- ホタルアルゴリズム
- 焼きなまし法