基本は全て「最適化アルゴリズムを評価するベンチマーク関数まとめ」より抜粋.図や式の引用は全てこちらからした.今回引用したのは $n$ 次元空間においても利用できるものだけ.単純にベンチマーク関数を使用したいだけなのに,ベンチマーク関数はやたらと書くのがめんどくさい,さっさと使いたいという人向け.
コード利用のためだけのページなので説明は省略.上の参考ページをみていただければと思います.
なお,全てのクラスにおいて,
import numpy as np
をしている.
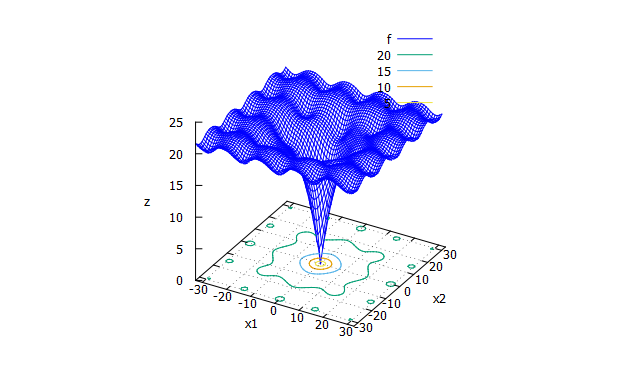
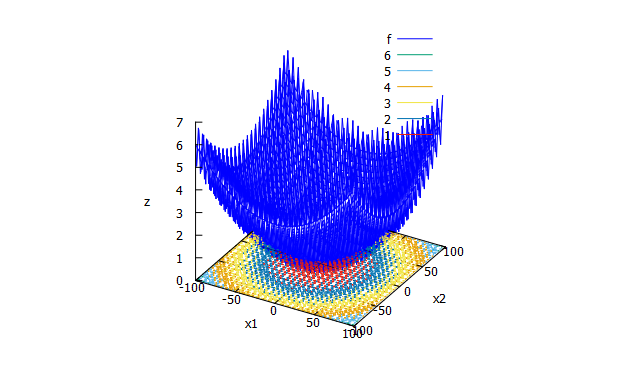
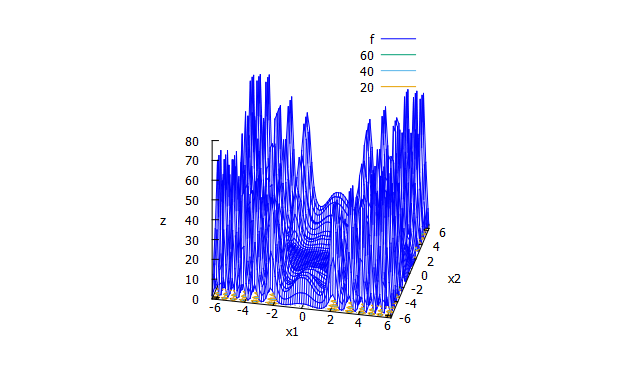
Ackley function
- 数式
f(x_{1} \cdots x_{n})=20-20\exp \biggl( -0.2\sqrt{\frac{1}{n}\sum_{i=1}^{n}x_{i}^2} \biggr) +e-\exp \biggl(\frac{1}{n}\sum_{i=1}^{n}\cos(2\pi x_{i}) \biggr)
- 探索範囲と最適解
-32.768 \leqq x_{i} \leqq 32.768 \\
f_{min}(0, \cdots , 0)=0
- コード
class ackley():
def __init__(self):
print("this is Ackley function.")
self.boundaries = np.array([-32.768, 32.768])
print("boundary is {}".format(self.boundaries))
print("minimum is {}".format(0))
def f(self, x):
t1 = 20
t2 = - 20 * np.exp(- 0.2 * np.sqrt(1.0 / len(x) * np.sum(x ** 2)))
t3 = np.e
t4 = - np.exp(1.0 / len(x) * np.sum(np.cos(2 * np.pi * x)))
return t1 + t2 + t3 + t4
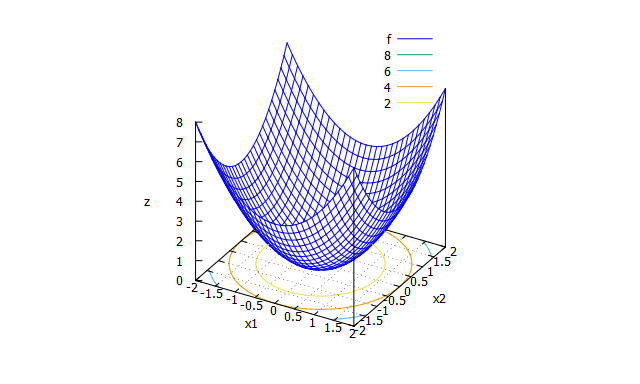
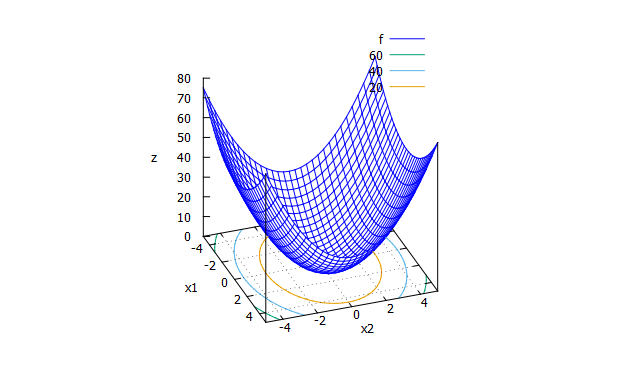
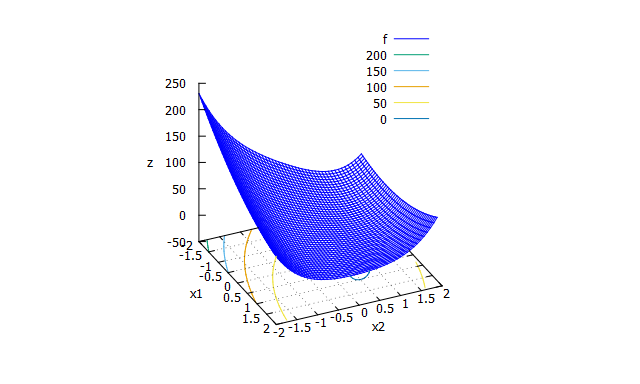
Sphere function
- 数式
f(x_{1} \cdots x_{n})=\sum_{i=1}^{n}x_{i}^2
- 探索範囲と最適解
\infty < x_{i} < \infty \\
f_{min}(0, \cdots , 0)=0
- コード
class sphere():
def __init__(self):
print("this is Sphere function.")
self.boundaries = np.array([-100, 100])
print("boundary is {}".format(self.boundaries))
print("minimum is {}".format(0))
def f(self, x):
return np.sum(x ** 2)
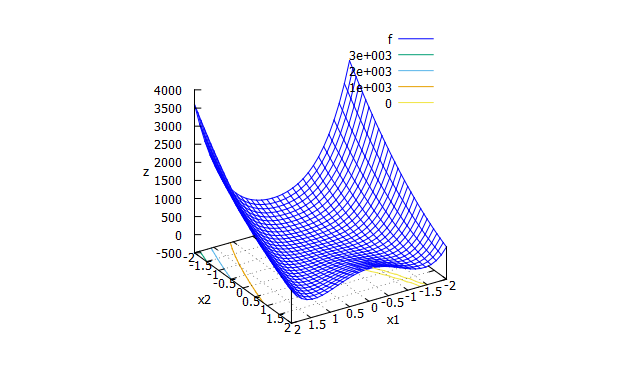
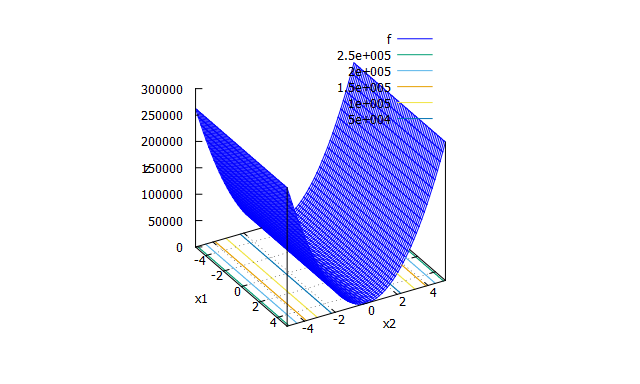
Rosenbrock function
- 数式
f(x_{1} \cdots x_{n})=\sum_{i=1}^{n-1}(100(x_{i+1}-x_{i}^2)^2+(x_{i}-1)^2)
- 探索範囲と最適解
-5 \leqq x_{i} \leqq 5 \\
f_{min}(1, \cdots , 1)=0
- コード
class rosenbrock():
def __init__(self):
print("this is Rosenbrock function.")
self.boundaries = np.array([-5, 5])
print("boundary is {}".format(self.boundaries))
print("minimum is {}".format(0))
def f(self, x):
val = 0
for i in range(0, len(x) - 1):
t1 = 100 * (x[i + 1] - x[i] ** 2) ** 2
t2 = (x[i] - 1) ** 2
val += t1 + t2
return val
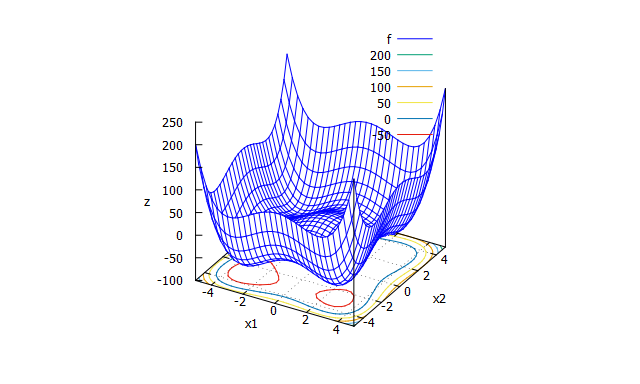
Styblinski-Tang function
- 数式
f(x_{1} \cdots x_{n})=\frac{\sum_{i=1}^{n} (x_{i}^4-16x_{i}^2+5x_{i})}{2}
- 探索範囲と最適解
-5 \leqq x_{i} \leqq 5 \\
-39.16617n \leq f(-2.903534, \cdots , -2.903534) \leq -39.16616n \\
f_{min}(-2.903534, \cdots , -2.903534) \approx -39.166165n
- コード
class styblinski():
def __init__(self):
print("this is Styblinski-Tang function.")
self.boundaries = np.array([-5, 4])
print("boundary is {}".format(self.boundaries))
print("minimum is {} times n_dim".format(-39.166165))
def f(self, x):
t1 = np.sum(x ** 4)
t2 = - 16 * np.sum(x ** 2)
t3 = 5 * np.sum(x)
return 0.5 * (t1 + t2 + t3)
k-tablet function
- 数式
f(x_{1} \cdots x_{n}) = \sum_{i=1}^{k}x_{i}^2 + \sum_{i=k+1}^{n}(100x_{i})^2 \\
k=n/4
- 探索範囲と最適解
-5.12 \leqq x_{i} \leqq 5.12 \\
f_{min}(0, \cdots , 0)=0
- コード
class k_tablet():
def __init__(self):
print("this is k-tablet function.")
self.boundaries = np.array([-5.12, 5.12])
print("boundary is {}".format(self.boundaries))
print("minimum is {}".format(0))
def f(self, x):
k = int(np.ceil(len(x) / 4.0))
t1 = np.sum(x[:k] ** 2)
t2 = 100 ** 2 * np.sum(x[k:] ** 2)
return t1 + t2
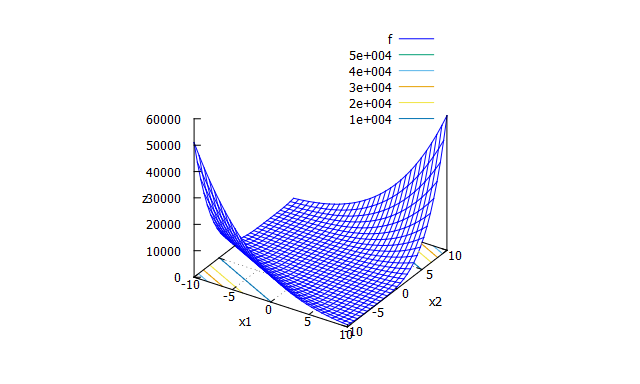
Weighted Sphere function or hyper ellipsodic function
- 数式
f_{min}(x_{1} \cdots x_{n})=\sum_{i=1}^{n}ix_{i}^2
- 探索範囲と最適解
-5.12 \leqq x_{i} \leqq 5.12 \\
f_{min}(0, \cdots , 0)=0
- コード
class weighted_sphere():
def __init__(self):
print("this is Weighted Sphere function or hyper ellipsodic function.")
self.boundaries = np.array([-5.12, 5.12])
print("boundary is {}".format(self.boundaries))
print("minimum is {}".format(0))
def f(self, x):
val = np.array([ (i + 1) * xi ** 2 for i, xi in enumerate(x)])
return np.sum(val)
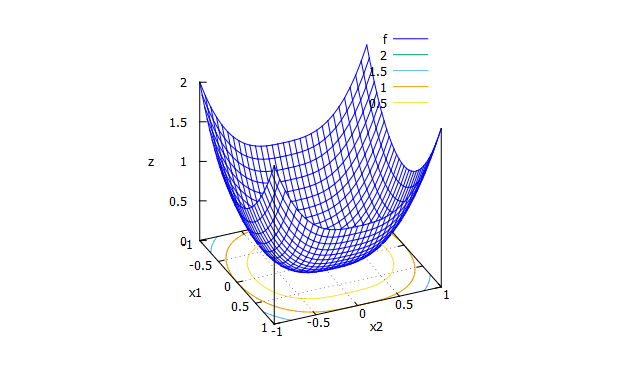
Sum of different power function
- 数式
f(x_{1} \cdots x_{n})=\sum_{i=1}^{n}|x_{i}|^{i+1}
- 探索範囲と最適解
-1 \leqq x_{i} \leqq 1 \\
f_{min}(0, \cdots , 0)=0
- コード
class different_power():
def __init__(self):
print("this is Sum of different power function.")
self.boundaries = np.array([-1, 1])
print("boundary is {}".format(self.boundaries))
print("minimum is {}".format(0))
def f(self, x):
val = 0
for i, v in enumerate(x):
val += np.abs(v) ** (i + 2)
return val
Griewank function
- 数式
f(x_{1} \cdots x_{n})=1+\frac{1}{4000}\sum_{i=1}^{n}x_{i}^2-\prod_{i=1}^{n}\cos\Bigl(\frac{x_{i}}{\sqrt{i}}\Bigr)
- 探索範囲と最適解
-600 \leqq x_{i} \leqq 600 \\
f_{min}(0, \cdots , 0)=0
- コード
class griewank():
def __init__(self):
print("this is Griewank function.")
self.boundaries = np.array([-600, 600])
print("boundary is {}".format(self.boundaries))
print("minimum is {}".format(0))
def f(self, x):
w = np.array([1.0 / np.sqrt(i + 1) for i in range(len(x))])
t1 = 1
t2 = 1.0 / 4000.0 * np.sum(x ** 2)
t3 = - np.prod(np.cos(x * w))
return t1 + t2 + t3
Perm function
- 数式
f(x_{1} \cdots x_{n})=\sum_{j=1}^{n} \Biggl(\sum_{i=1}^{n}(i+\beta)\biggl(x_{i}^j- \Biggl( \frac{1}{i} \Biggr)^j \Biggr) \Biggr)^2 \\
\beta > 0
- 探索範囲と最適解
-1 \leqq x_{i} \leqq 1 \\
f_{min}\Bigl(1, \frac{1}{2} , \cdots , \frac{1}{n}\Bigl) = 0
- コード
class perm():
def __init__(self):
print("this is Perm function.")
self.boundaries = np.array([-1, 1])
print("boundary is {}".format(self.boundaries))
print("minimum is {}".format(0))
def f(self, x):
val = 0
for j in range(len(x)):
v = 0
for i in range(len(x)):
v += (i + 2) * (x[i] ** (j + 1) - ( ( 1 / (i + 1) ) ** (j + 1) ) )
val += v ** 2
return val
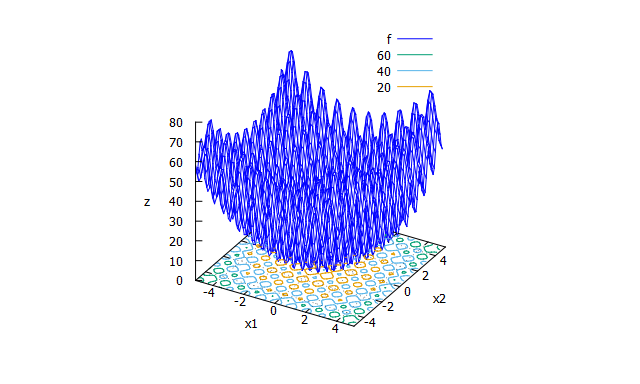
Rastrigin function
- 数式
f(x_{1} \cdots x_{n})=10n+\sum_{i=1}^{n}(x_{i}^2-10\cos(2 \pi x_{i}))
- 探索範囲と最適解
-5.12 \leqq x_{i} \leqq 5.12 \\
f_{min}(0, \cdots , 0) = 0
- コード
class rastrigin():
def __init__(self):
print("this is Rastrigin function")
self.boundaries = np.array([-5.12, 5.12])
print("boundary is {}".format(self.boundaries))
print("minimum is {}".format(0))
def f(self, x):
t1 = 10 * len(x)
t2 = np.sum(x ** 2)
t3 = - 10 * np.sum(np.cos(2 * np.pi * x))
return t1 + t2 + t3
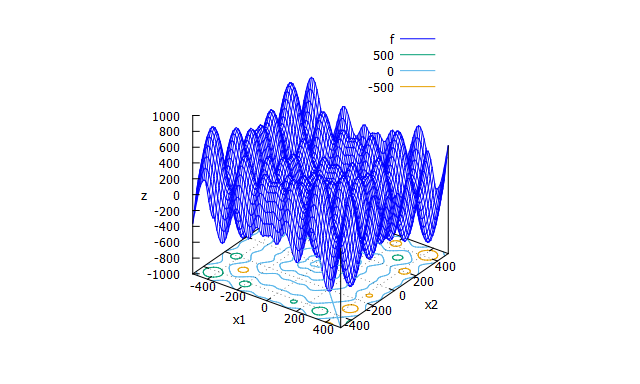
Schwefel function
- 数式
f(x_{1} \cdots x_{n})=-\sum_{i=1}^{n}x_{i}\sin\bigl(\sqrt{|x_{i}|}\bigr)
- 探索範囲と最適解
-500 \leqq x_{i} \leqq 500 \\
f_{min}(420.9687, \cdots , 420.9687) \approx -418.9829n
- コード
class schwefel():
def __init__(self):
print("this is Schwefel function")
self.boundaries = np.array([-500, 500])
print("boundary is {}".format(self.boundaries))
print("minimum is {} times n_dim".format(-418.9829))
def f(self, x):
return - np.sum(x * np.sin( np.sqrt( np.abs(x) ) ) )
Xin-She Yang function
- 数式
f(x_{1} \cdots x_{n})=\Bigl(\sum_{j=1}^{n}|x_{j}| \Bigr) \exp \Bigl(-\sum_{i=1}^{n}\sin(x_{i}^2) \Bigr)
- 探索範囲と最適解
-2 \pi \leqq x_{i} \leqq 2 \pi \\
f_{min}(0, \cdots , 0) = 0
- コード
class xin_she():
def __init__(self):
print("this is Xin-She Yang function.")
self.boundaries = np.array([-2 * np.pi, 2 * np.pi])
print("boundary is {}".format(self.boundaries))
print("minimum is {}".format(0))
def f(self, x):
t1 = np.sum( np.abs(x) )
e1 = - np.sum( np.sin(x ** 2) )
t2 = np.exp(e1)
return t1 * t2
Zakharov function
- 数式
f(x_{1} \cdots x_{n})=\sum_{i=1}^{n}x_{i}+\Biggl(\frac{1}{2}\sum_{i=1}^{n}ix_{i} \Biggr)^2+\Biggl(\frac{1}{2}\sum_{i=1}^{n}ix_{i} \Biggr)^4
- 探索範囲と最適解
探索範囲無し。 \\
f_{min}(0, \cdots , 0) = 0
- コード
class zakharov():
def __init__(self):
print("this is Zakharov function.")
self.boundaries = np.array([-100, 100])
print("boundary is {}".format(self.boundaries))
print("minimum is {}".format(0))
def f(self, x):
t1 = np.sum(x)
w = np.array([ i + 1 for i in range(len(x))])
wx = np.dot(w, x)
t2 = 0.5 ** 2 * wx ** 2
t3 = 0.5 ** 4 * wx ** 4
return t1 + t2 + t3
他のベンチマーク関数
以下のサイトに先に紹介した関数とは別のベンチマーク関数があったので,そちらも合わせて載せます.$n$ 次元に一般化可能であり,煩雑なパラメータ設定不要で大域解の判明しているものを選定しました.
Virtual Library of Simulation Experiments
以下,断りがない限り上記ページからの引用となります.
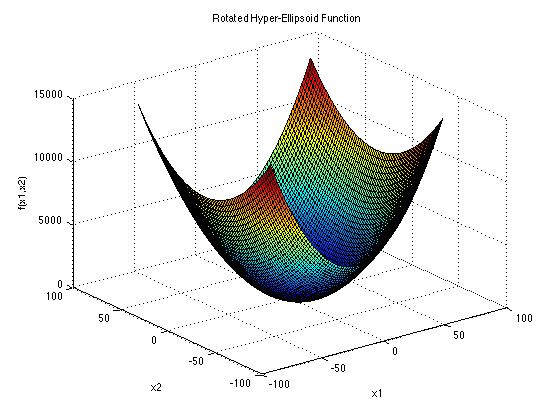
Rotated Hyper-Ellipsoid function
- 数式
f(x_{1} \cdots x_{n})=\sum_{i=1}^{n}\sum_{j=1}^{j}x_{i}^2
- 探索範囲と最適解
-65.536 < x_{i} < 65.536 \\
f_{min}(0, \cdots , 0)=0
- コード
class rotated_hyper_ellipsoid():
def __init__(self):
print("this is rotated hyper ellipsoid function.")
self.boundaries = np.array([-65.536, 65.536])
print("boundary is {}".format(self.boundaries))
print("minimum is {}".format(0))
def f(self, x):
val = 0
for i in range(len(x)):
val += np.sum(x[:i + 1] ** 2)
return val
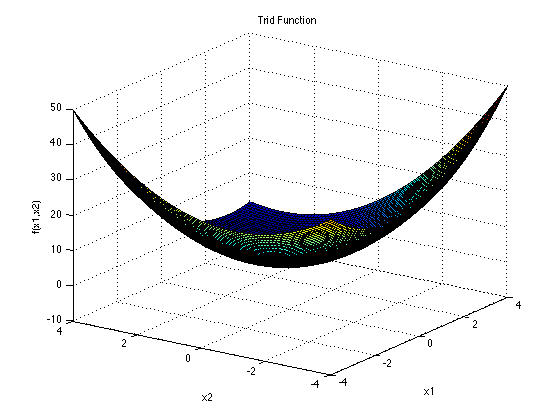
Trid function
- 数式
f(x_{1} \cdots x_{n})=\sum_{i=1}^{n}(x_i - 1)^2 - \sum_{i=2}^{n}x_{i}x_{i-1}
- 探索範囲と最適解
-n^2 < x_{i} < n^2 \\
f_{min}(n + 1 - 1, \cdots ,i (n + 1 - i), \cdots, n (n + 1 - n))=0
- コード
class trid():
def __init__(self, n_dim = 10):
print("this is rotated trid function.")
print("boundary is {}".format(self.boundaries))
print("minimum is {}".format(0))
def f(self, x):
n_dim = len(x)
self.boundaries = np.array([- n_dim ** 2, n_dim ** 2])
t1 = np.sum( (x - 1) ** 2 )
t2 = - np.sum( x[1:n_dim] * x[0:n_dim - 1] )
return t1 + t2
Powell function
- 数式
f(x_{1} \cdots x_{n})=\sum_{i=1}^{\frac{n}{4}}\bigl[
(x_{4i-3} - 10x_{4i-2})^2 +
5(x_{4i-1} - x_{4i})^2 +
(x_{4i-2} - 2x_{4i-1})^4 +
10(x_{4i-3} - x_{4i})^4
\bigl]
- 探索範囲と最適解
-4 < x_{i} < 5 \\
f_{min}(0, \cdots ,0)=0
- コード
not available now
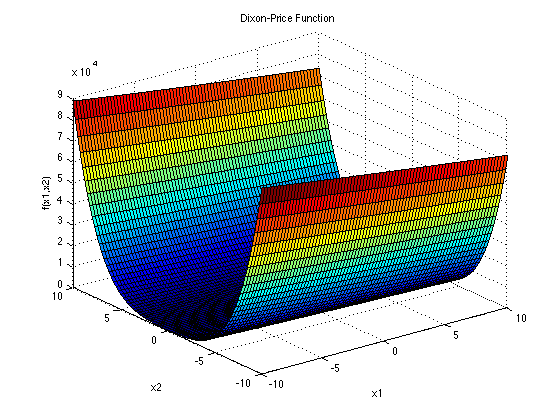
Dixon-Price function
- 数式
f(x_{1} \cdots x_{n})=(x_1 - 1)^2 + \sum_{i=2}^{n}i(2x_i^2 - x_{i - 1})^2
- 探索範囲と最適解
-10 < x_{i} < 10 \\
f_{min}(2^{-\frac{2^1-2}{2^1}}, \cdots , 2^{-\frac{2^n-2}{2^n}})=0
- コード
class dixon_price():
def __init__(self):
print("this is rotated dixon price function.")
self.boundaries = np.array([- 10, 10])
print("boundary is {}".format(self.boundaries))
print("minimum is {}".format(0))
def f(self, x):
n_dim = len(x)
c = np.array([i + 2 for i in range(n_dim - 1)])
t1 = (x[0] - 1) ** 2
t2 = np.sum( c * (2 * x[1:n_dim] ** 2 - x[0:n_dim - 1] ) ** 2 )
return t1 + t2
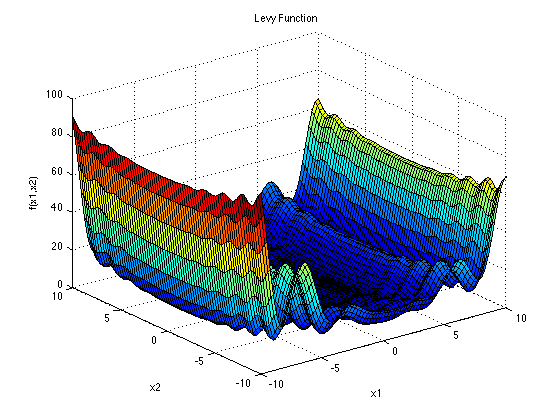
Levy function
- 数式
f(x_{1} \cdots x_{n})=
sin^2(\pi w_1) +
\sum_{i=1}^{n - 1}(w_i - 1)^2
\bigl[
1 + 10sin^2(\pi w_i + 1)
\bigl] +
(w_n - 1)^2 \bigl[
1 + sin^2(2\pi w_n)
\bigl]
ただし,w_i\ の値は \
w_i = 1 + \frac{x_i - 1}{4} \ によって,定義される.
- 探索範囲と最適解
-10 < x_{i} < 10 \\
f_{min}(1, \cdots , 1)=0
- コード
class levy():
def __init__(self):
print("this is levy price function.")
self.boundaries = np.array([- 10, 10])
print("boundary is {}".format(self.boundaries))
print("minimum is {}".format(0))
def f(self, x):
w = np.array(1. + (x - 1) / 4.)
t1 = np.sin(np.pi * w[0]) ** 2
t2 = (w[-1] - 1) ** 2 * (1 + np.sin(2 * np.pi * w[-1]) ** 2)
t3 = np.sum( (w[:-1] - 1) ** 2 * (1 + 10 * np.sin(np.pi * w[:-1] + 1) ** 2) )
return t1 + t2 + t3