最適化アルゴリズムを実装していくぞ（実数型遺伝的アルゴリズム）

はじめに

最適化アルゴリズムの実装シリーズです。
まずは概要を見てください。

コードはgithubにあります。

遺伝的アルゴリズム

概要

遺伝的アルゴリズム(Genetic Algorithm: GA)については遺伝的アルゴリズム編を見てください。
前の記事では潜在的に離散値を対象としていましたが、連続値(実数)を対象に拡張されたGAがあるので実装してみました。

参考：実数型GAに於ける交叉法の改良

実数値への拡張

変更箇所は交叉の仕方です。
GAの一様交叉では親の情報をそのまま引き継ぎます。
しかし実数を考えた場合、細かい調整ができないことがわかると思います。

例えば親の遺伝子が1と2で最適解が1.5の場合、普通のGAでは子はどう頑張っても1と2の値しかとりません(突然変異を除く)
実数を考慮して交叉する手法を紹介します。

BLX-α交叉

簡単に言うと親個体からα倍大きくなった範囲内でランダムに子を生成する方法です。

親個体の各座標成分を$x1_i$、$x2_i$とした場合、

$$ x_{min} = min(x1_i, x2_i) $$
$$ x_{max} = max(x1_i, x2_i) $$
$$ d = |x1_i - x2_i| $$

$min(a,b)$ は小さいほう、$max(a,b)$ は大きいほうの値をとります。

$$ r_{min} = x_{min} - \alpha d $$
$$ r_{max} = x_{max} + \alpha d $$
$$ newx_i = rand[r_{min}, r_{max}] $$

$\alpha$ はハイパーパラメータです。
子のi座標成分は $r_{min}$ から $r_{max}$ の範囲のランダムな値で出します。

コードは以下です。

genes1 = parent1.getArray()  # 親1の遺伝子情報
genes2 = parent2.getArray()  # 親2の遺伝子情報

# 子の遺伝子情報
c_genes1 = []
c_genes2 = []
for i in range(len(genes1)):  # 各遺伝子

    if genes1[i] < genes2[i]:
        x_min = genes1[i]
        x_max = genes2[i]
    else:
        x_min = genes2[i]
        x_max = genes1[i]
    dx = abs(genes1[i] - genes2[i])
    r_min = x_min - blx_a * dx
    r_max = x_max + blx_a * dx

    # r_min～r_maxの間で乱数をだす
    c_gene1 = (r_max - r_min) * random.random() + r_min
    c_gene2 = (r_max - r_min) * random.random() + r_min

    # 結果を追加
    c_genes1.append(c_gene1)
    c_genes2.append(c_gene2)

コード(BLX-α交叉)

GAと同じ部分は省略しています。

class GA_BLXa():
    def __init__(self, 
            individual_max,
            save_elite=True,
            select_method="ranking",
            mutation=0.1,
            blx_a=0.3,
        ):
        self.individual_max = individual_max

        self.save_elite = save_elite
        self.select_method = select_method
        self.mutation = mutation
        self.blx_a = blx_a

    # GAと比べて交叉のみ変わります。
    def _cross(self, parent1, parent2):
        genes1 = parent1.getArray()  # 親1の遺伝子情報
        genes2 = parent2.getArray()  # 親2の遺伝子情報

        # 子の遺伝子情報
        c_genes1 = []
        c_genes2 = []
        for i in range(len(genes1)):  # 各遺伝子を走査

            if genes1[i] < genes2[i]:
                min_x = genes1[i]
                max_x = genes2[i]
            else:
                min_x = genes2[i]
                max_x = genes1[i]
            dx = abs(genes1[i] - genes2[i])
            min_cx = min_x - self.blx_a * dx
            max_cx = max_x + self.blx_a * dx

            c_gene1 = (max_cx - min_cx) * random.random() + min_cx
            c_gene2 = (max_cx - min_cx) * random.random() + min_cx

            # 突然変異
            if random.random() < self.mutation:
                c_gene1 = self.problem.randomVal()
            if random.random() < self.mutation:
                c_gene2 = self.problem.randomVal()

            c_genes1.append(c_gene1)
            c_genes2.append(c_gene2)

        # 遺伝子をもとに子を生成
        childe1 = self.problem.create(c_genes1)
        childe2 = self.problem.create(c_genes2)
        return childe1, childe2

SPX(シンプレックス交叉)

n次元において、n+1個の頂点からなる図研(シンプレックス)をもとに子を生成する手法です。
話を簡単にして、2次元3個体から子を生成する方法を説明します。

まずは3個体の重心を出します。

$$ \vec{g} = \frac{(\vec{x_1} + \vec{x_2} + \vec{x_3})}{3} $$

次に親個体と同じ数だけ以下のベクトルを求めます。

$$ \vec{y_1} = \vec{g} + \epsilon(\vec{x_1} - \vec{g}) $$

$$ \vec{y_2} = \vec{g} + \epsilon(\vec{x_2} - \vec{g}) $$

$$ \vec{y_3} = \vec{g} + \epsilon(\vec{x_3} - \vec{g}) $$

$\epsilon$ は拡張率と呼ばれる1より大きい定数で、$\sqrt{n+2}$ 等の値が用いられるそうです。
今回だと $\epsilon = \sqrt{2+2}$ ですね。

次に子個体($\vec{c_1},\vec{c_2},\vec{c_3}$)を以下で求めます。

$$ \vec{c_1} = \vec{y_1} $$
$$ \vec{c_2} = \vec{y_2} + r_1(\vec{y_1} - \vec{y_2}) $$
$$ \vec{c_3} = \vec{y_3} + r_2(\vec{y_2} - \vec{y_3} + r_1(\vec{y_1} - \vec{y_2})) $$

$r$は0～1の乱数です。
一般式で書くと以下です。

\vec{c_i} = \left\{
  \begin{array}{l}
    \vec{x_i} \quad (i=1)\\
    \vec{x_i} + r_{i}( \vec{c_{i-1}} - \vec{x_i} ) \quad (i=2,3,...,n)
  \end{array}
\right.

制約に関して

アルゴリズムを見てわかる通り、次元数+1の個体が必要です。
これは高次元の問題と非常に相性が悪いです。（本記事だとOneMaxの問題は10000次元で比較しています）
個体数を10001体にすると多分有限時間では終わらないと思うのでこのアルゴリズムは本記事では紹介のみとしています。（ほかのアルゴリズムと比較していません）

コード全体(SPX)

GAと同じ部分は省略しています。

class GA_SPX():
    def __init__(self, 
            individual_max,   # 個体数
            save_elite=True,  # エリートを生存させるか
            select_method="ranking",  # 選択の方式(roulette or ranking)
            mutation=0.1,     # 突然変異の確率
        ):
        （省略）

    def init(self, problem):
        self.problem = problem

        # εを計算
        self.spx_e = math.sqrt(problem.size+2)

        （省略）


    def step(self):

        # 次世代
        next_individuals = []

        if self.save_elite:
            # エリートを生存させる
            next_individuals.append(self.individuals[-1].copy())

        for _ in range(self.individual_max):  # whileでもいいけど安全のため
            # 個数が集まるまで繰り返す
            if len(next_individuals) > self.individual_max:
                break

            # 選択する
            v_list = []
            for _ in range(self.problem.size+1):
                # ベクトルにして追加
                v_list.append(np.asarray(self._select().getArray()))

            # 交叉する
            children = self._cross(v_list)
            for c in children:
                next_individuals.append(c)

        （省略）


    def _cross(self, v_list):
        # 重心
        g_vec = None
        for v in v_list:
            if g_vec is None:
                g_vec = v.copy()
            else:
                g_vec += v
        g_vec /= len(v_list)

        # 外側ベクトルを計算
        s_vec = []
        for v in v_list:
            sx = g_vec + self.spx_e * (v - g_vec)
            s_vec.append(sx)

        # 子を生成
        cx = None
        children = []
        for i, sx in enumerate(s_vec):
            if i == 0:
                cx = sx.copy()
            else:
                cx = sx + random.random() * (cx - sx)

            children.append(self.problem.create(cx))

        return children

ハイパーパラメータ例

各問題に対して optuna でハイパーパラメータを最適化した結果です。
最適化の1回の試行は、探索時間を2秒間として結果を出しています。
これを100回実行し、最適なハイパーパラメータを optuna に探してもらいました。

結果はBLX-α交叉のみです。

問題	blx_a	individual_max	mutation	save_elite	select_method
EightQueen	0.4980715968226679	6	0.03109945311374338	True	ranking
function_Ackley	0.22974874981713062	32	0.0038431194747462387	False	ranking
function_Griewank	0.7188255812223371	5	0.001555508499828215	True	ranking
function_Michalewicz	0.5302073671586125	5	0.0026309573609158005	True	ranking
function_Rastrigin	0.31432864624578105	5	0.002290664353905646	True	ranking
function_Schwefel	0.21010977945084422	28	0.00272501749604866	True	ranking
function_StyblinskiTang	0.4903425376568267	8	0.005198104262758373	True	ranking
function_XinSheYang	0.6270227379180398	2	0.0019297924933880002	True	ranking
g2048	0.6221833031768063	36	0.5171118613222166	False	ranking
LifeGame	0.6820864714532836	31	0.3738909249467709	True	ranking
OneMax	0.613852005264575	3	0.05645959934246039	True	ranking
TSP	0.6539815570680515	3	0.005874777798067224	True	ranking

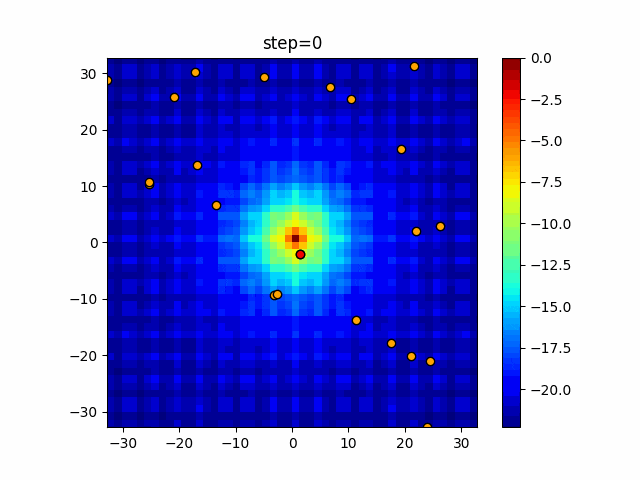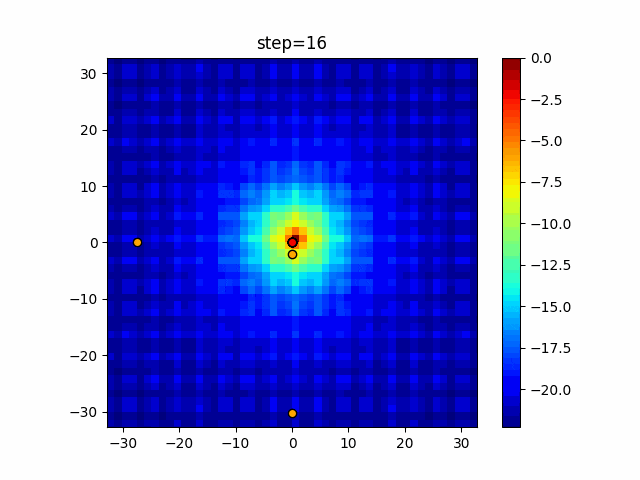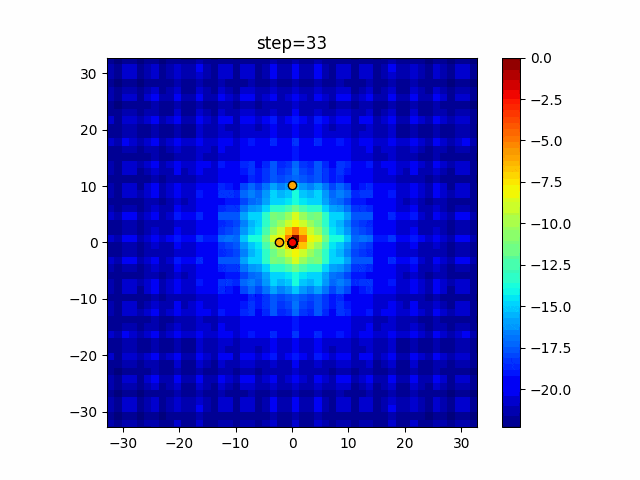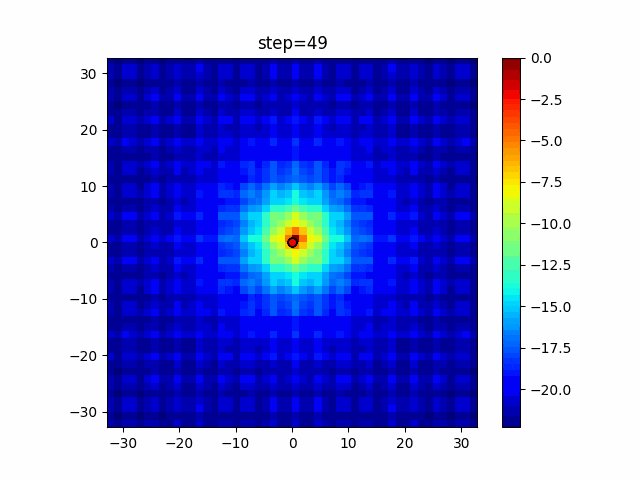
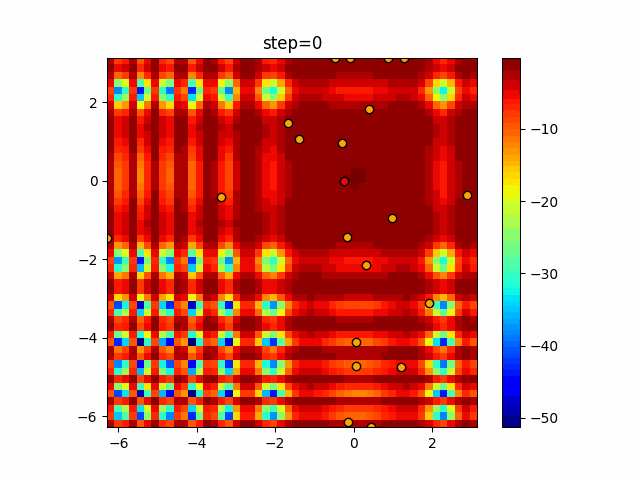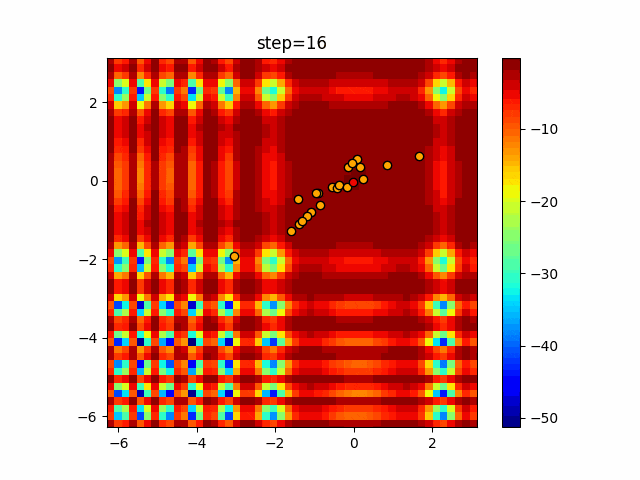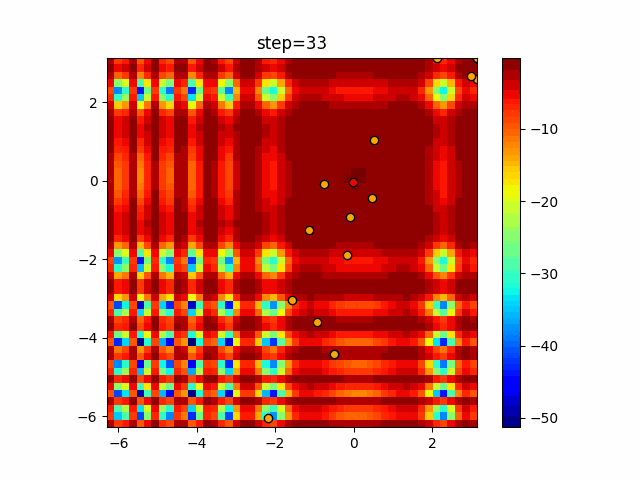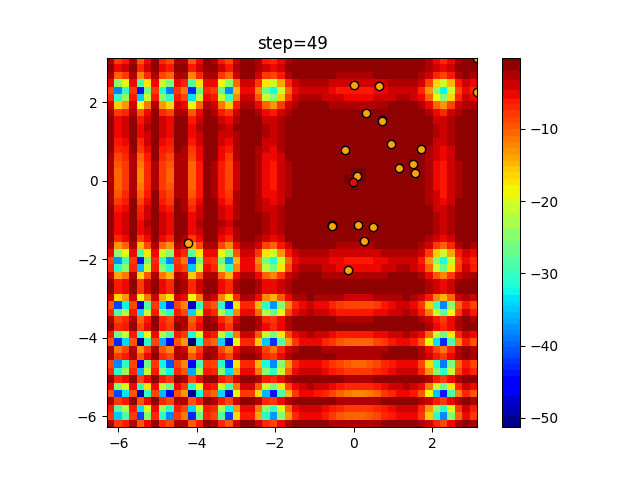
実際の動きの可視化

1次元は6個体、2次元は20個体で100step実行した結果です。
パラメータフリーGAは個体数の指定ができないのでそのままです。
赤い丸がそのstepでの最高スコアを持っている個体となります。

パラメータは以下で実行しました。

GA_BLXa(N, save_elite=False, select_method="ranking", mutation=0.05, blx_a=0.1)
GA_SPX(N, save_elite=False, select_method="ranking", mutation=0.05)

function_Ackley

• GA_BLXa
  • 1次元

• 2次元

• GA_SPX
  • 1次元

• 2次元

function_Rastrigin

• GA_BLXa
  • 1次元

• 2次元

• GA_SPX
  • 1次元

• 2次元

function_Schwefel

• GA_BLXa
  • 1次元

• 2次元

• GA_SPX
  • 1次元

• 2次元

function_StyblinskiTang

• GA_BLXa
  • 1次元

• 2次元

• GA_SPX
  • 1次元

• 2次元

function_XinSheYang

• GA_BLXa
  • 1次元

• 2次元

• GA_SPX
  • 1次元

• 2次元

あとがき

なかなか面白い動きをしますね。
局所解に入ると脱出するのは突然変異しかなくなります。

SPXが３次元で斜めに移動しているのは重複を許可しているからですね。