はじめに
最適化アルゴリズムの実装シリーズです。
まずは概要を見てください。
コードはgithubにあります。
ハーモニーサーチ
概要
ハーモニーサーチ(Harmony Search)は音楽家が即興演奏する際の思考に着目して作られたアルゴリズムです。
音楽家は以下の考えの元フレーズを決めていると考えます。
- 使用頻度の高いフレーズをそのまま奏でる
- 使用頻度の高いフレーズを調整して奏でる
- 新しいフレーズを作成して奏でる
参考
・進化計算アルゴリズム入門 生物の行動科学から導く最適解
アルゴリズム
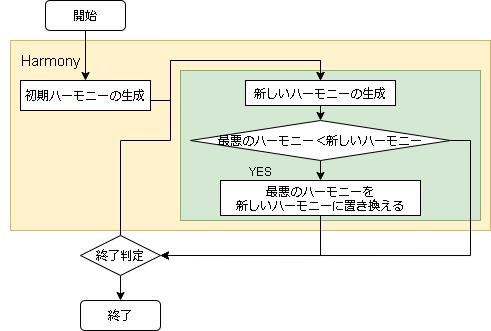
- アルゴリズムのフロー
- 用語の対応
| 問題 | ハーモニーサーチ |
|---|---|
| 入力の1要素 | 和音(フレーズ) |
| 問題への入力 | ハーモニー |
| 評価値 | ハーモニーの評価値 |
- ハイパーパラメータに関して
| 変数名 | 意味 | 備考 |
|---|---|---|
| bandwidth | バンド幅 | 和音を調整する際の調整率 |
| select_rate | 新しい和音を生成する確率 | |
| change_rate | 和音を調整する確率 |
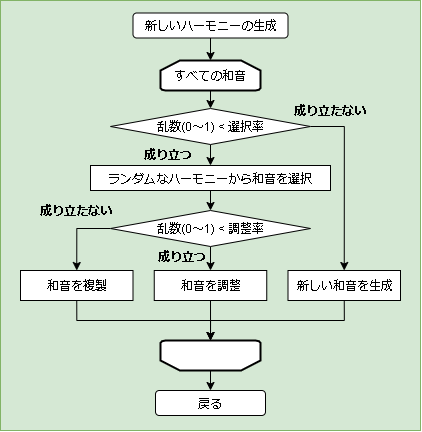
和音の複製
そのまま対象の和音を使います。
x^{new}_i = x^r_i
和音を調整して使用
以下の式で調整します。
$$ x^{new}_i = x^r_i + B \times rand[-1,1]$$
$B$ はバンド幅で、ユーザが指定する変数です。
バンド幅の改良
本記事オリジナルです。
上記式ですが、$B$ の値は問題の1要素の下限上限値にかなり依存しています。
そこで $B$ を直接使用するのではなく、割合で指定する方法をとりました。
$$ B' = B * (Prob_{max} - Prob_{min})$$
コード全体
import math
import random
class Harmony():
def __init__(self,
harmony_max,
bandwidth=0.1,
enable_bandwidth_rate=False, # bandwidthを割合にするか、値にするか
select_rate=0.8,
change_rate=0.3,
):
self.harmony_max = harmony_max
self.bandwidth = bandwidth
self.enable_bandwidth_rate = enable_bandwidth_rate
self.select_rate = select_rate
self.change_rate = change_rate
def init(self, problem):
self.problem = problem
self.harmonys = []
for _ in range(self.harmony_max):
self.harmonys.append(problem.create())
def step(self):
# 新しいharmonyを作成
arr = []
for i in range(self.problem.size):
if random.random() < self.select_rate:
# 新しく和音を生成
arr.append(self.problem.randomVal())
continue
# harmonyを1つ選択
h_arr = self.harmonys[random.randint(0, self.harmony_max-1)].getArray()
if random.random() < self.change_rate:
# 和音を変更
if self.enable_bandwidth_rate:
# 割合で bandwidth を指定
bandwidth = self.bandwidth * (self.problem.MAX_VAL - self.problem.MIN_VAL)
else:
bandwidth = self.bandwidth
n = h_arr[i] + bandwidth * (random.random()*2-1)
arr.append(n)
else:
# 和音を複製
arr.append(h_arr[i])
harmony = self.problem.create(arr)
# 新しいharmonyが最悪のharmonyより評価が高ければ置き換え
self.harmonys.sort(key=lambda x: x.getScore())
if self.harmonys[0].getScore() < harmony.getScore():
self.harmonys[0] = harmony
ハイパーパラメータ例
各問題に対して optuna でハイパーパラメータを最適化した結果です。
最適化の1回の試行は、探索時間を5秒間として結果を出しています。
これを100回実行し、最適なハイパーパラメータを optuna に探してもらいました。
| 問題 | bandwidth | change_rate | enable_bandwidth_rate | harmony_max | select_rate |
|---|---|---|---|---|---|
| EightQueen | 0.199731235367978 | 0.007945406417271816 | False | 8 | 0.05285166540946163 |
| function_Ackley | 0.6478593586012942 | 0.37819472248801433 | False | 24 | 0.0045960067336094125 |
| function_Griewank | 0.957845478793464 | 0.6531645473958932 | False | 19 | 0.0065542485084037 |
| function_Michalewicz | 0.3020087834816175 | 0.0063312721531867296 | False | 8 | 0.009704544614251957 |
| function_Rastrigin | 0.9244843154507476 | 0.003091269983721383 | False | 19 | 0.005363972453695971 |
| function_Schwefel | 0.6525179901987925 | 0.6847228820427808 | False | 24 | 0.017390991518258108 |
| function_StyblinskiTang | 0.012259017079907453 | 0.005592287367206683 | True | 5 | 0.010574637751612243 |
| function_XinSheYang | 0.021452540527582796 | 0.5116052912533812 | False | 43 | 0.000560227904147548 |
| g2048 | 0.5208515497767559 | 0.9192443470308422 | False | 6 | 0.025020522147974456 |
| LifeGame | 0.12412374231584394 | 0.3047344866221531 | True | 15 | 0.3351269586087304 |
| OneMax | 0.6404754184189828 | 0.11674742823674397 | True | 3 | 0.21323358379499358 |
| TSP | 0.9991577906059103 | 0.026545669987045384 | False | 35 | 0.026355483052867487 |
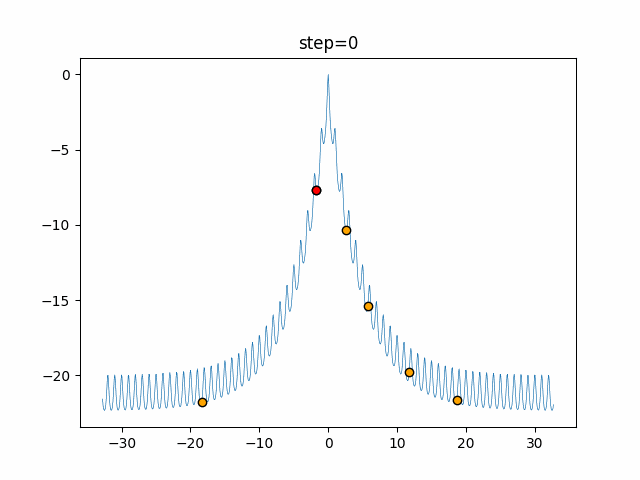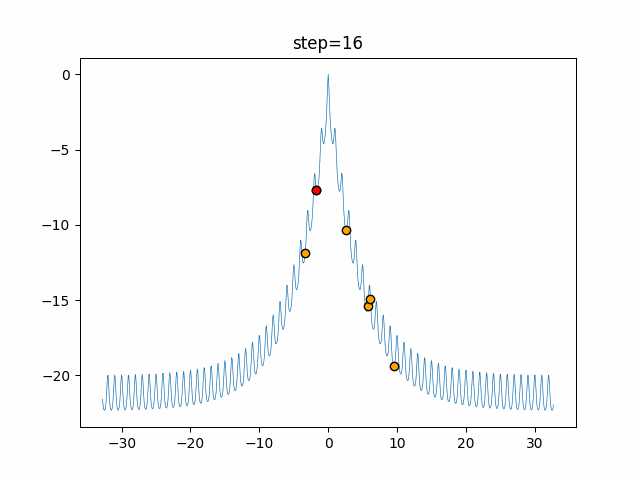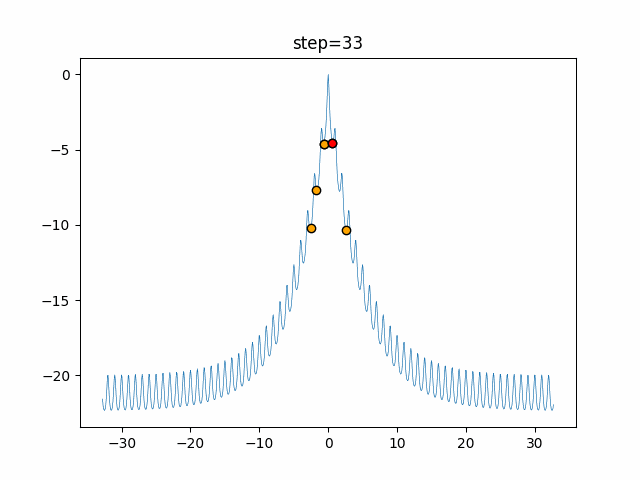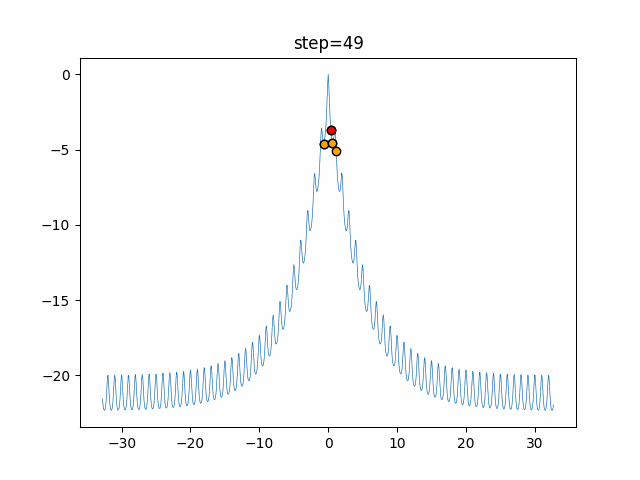
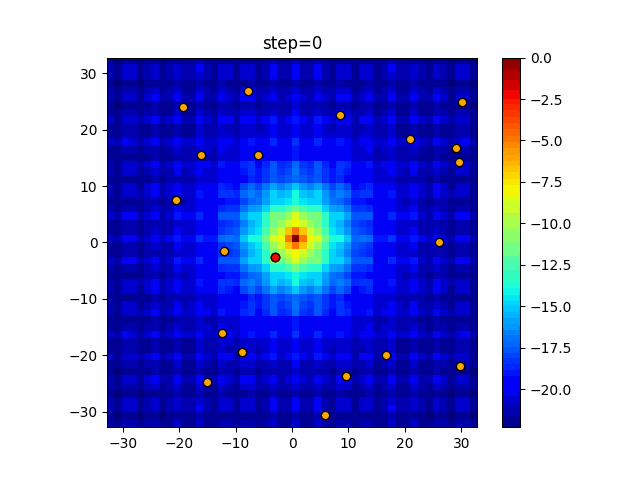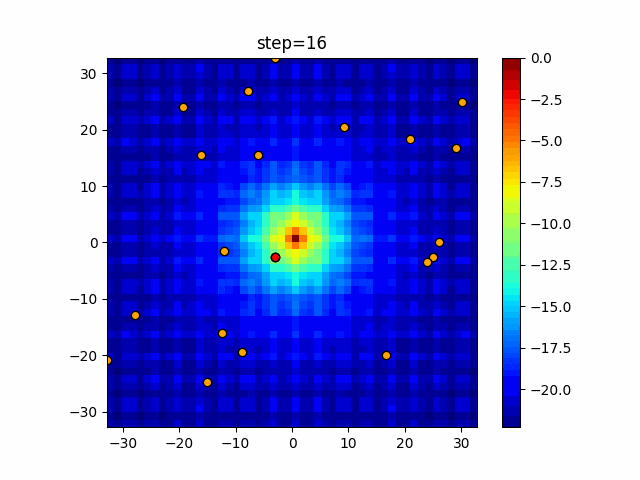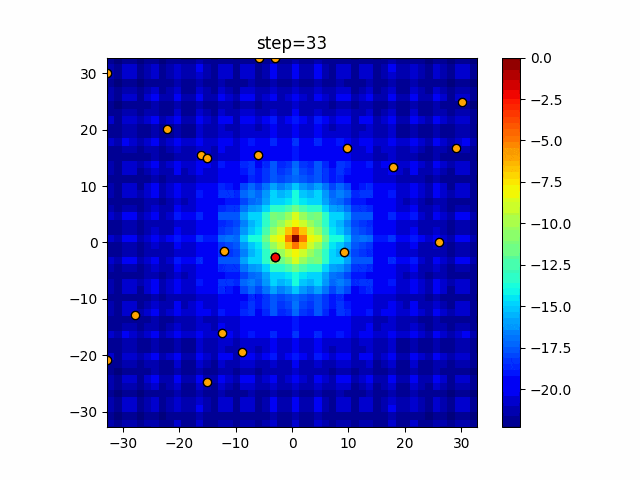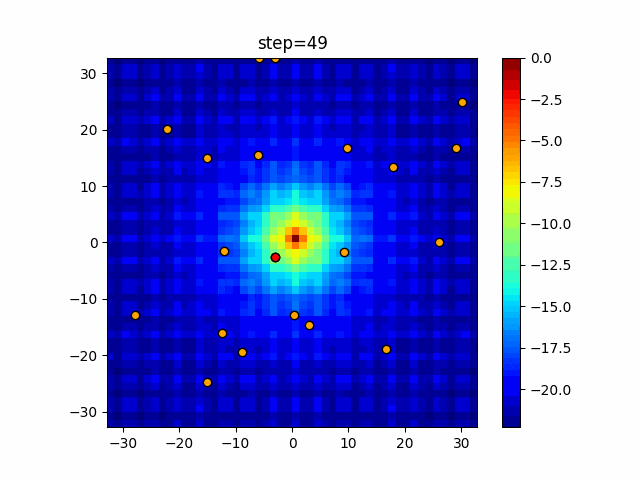
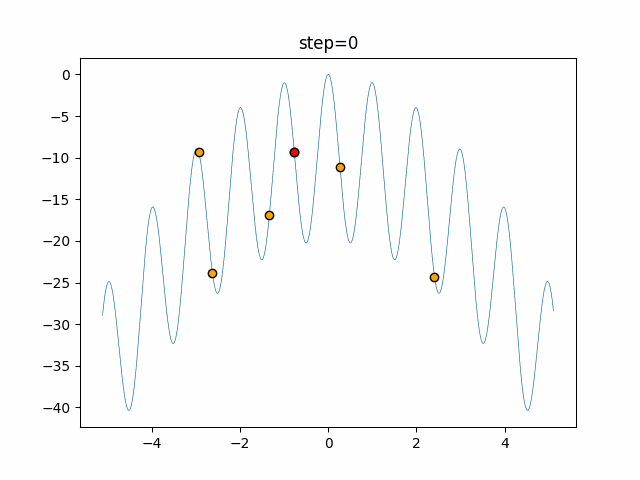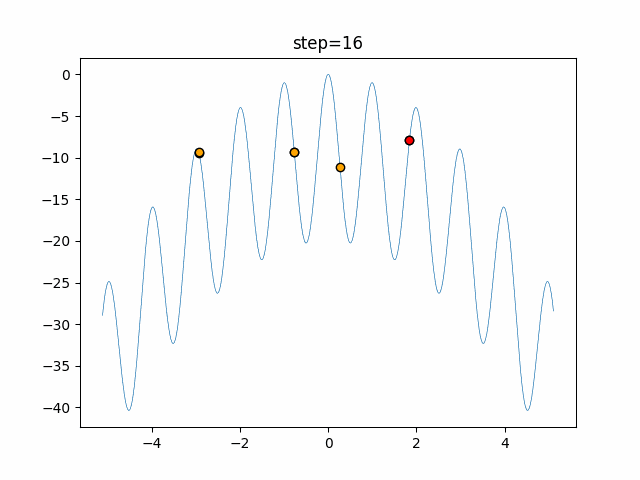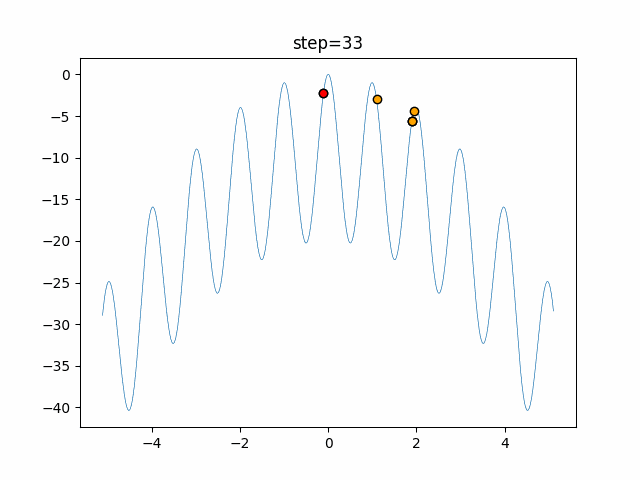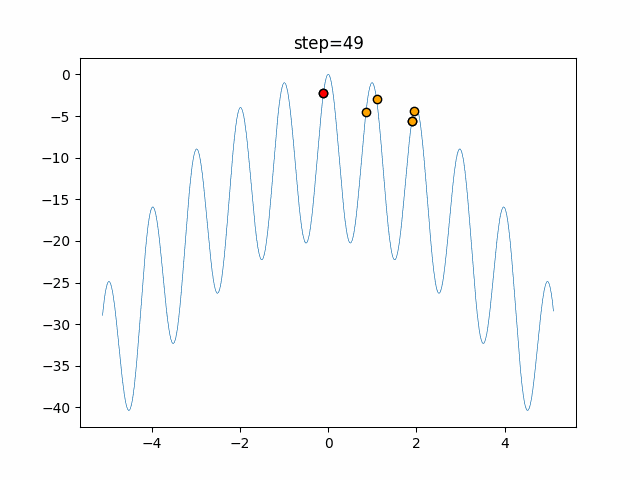
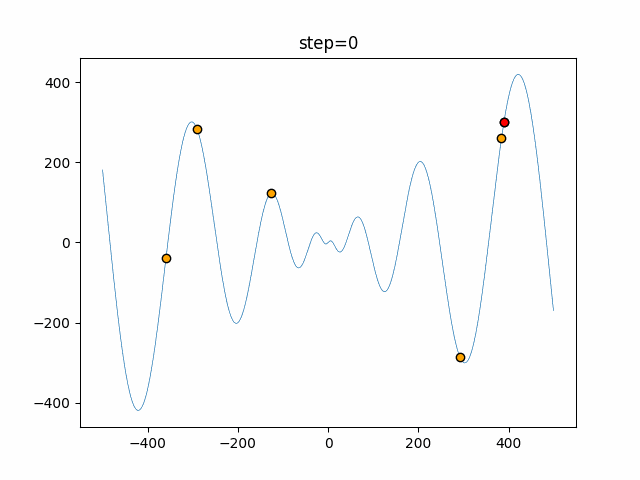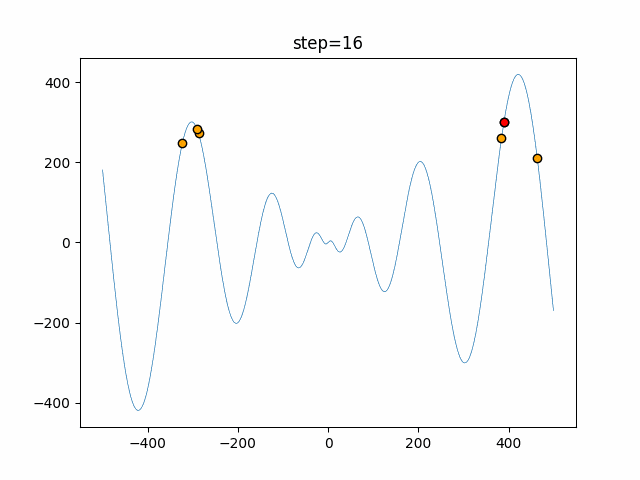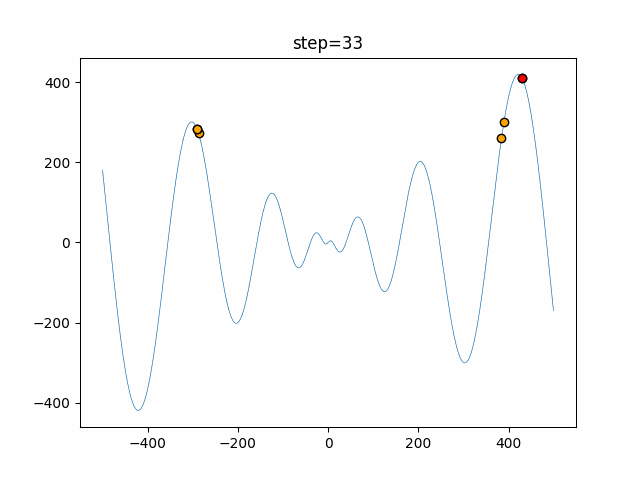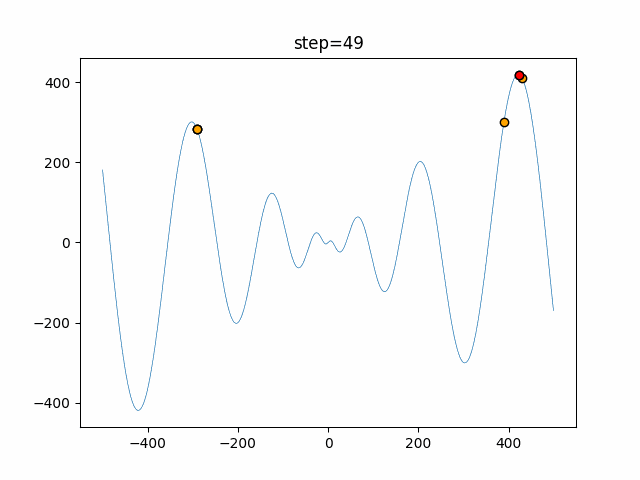
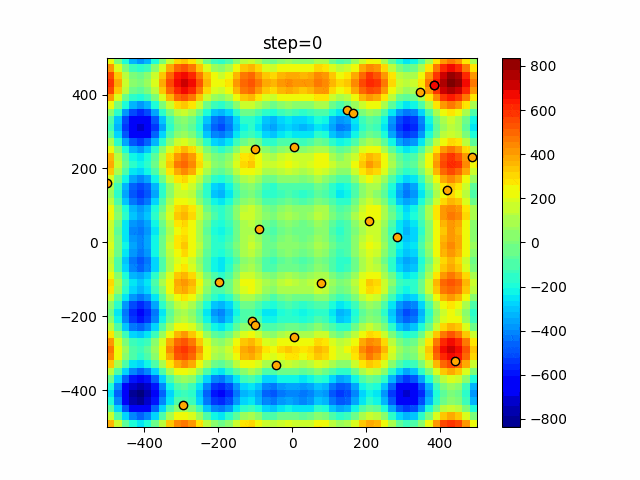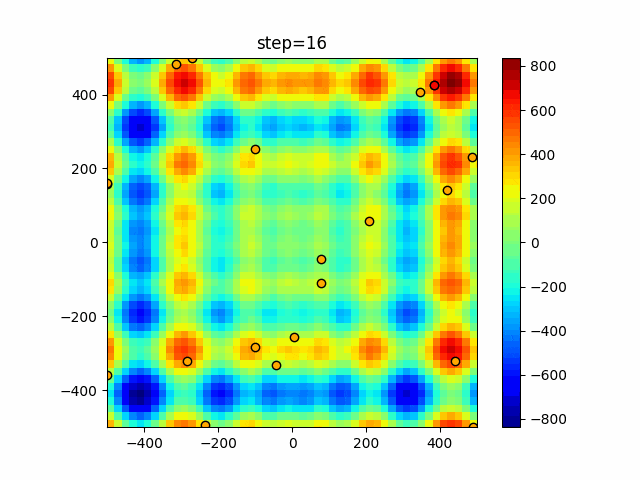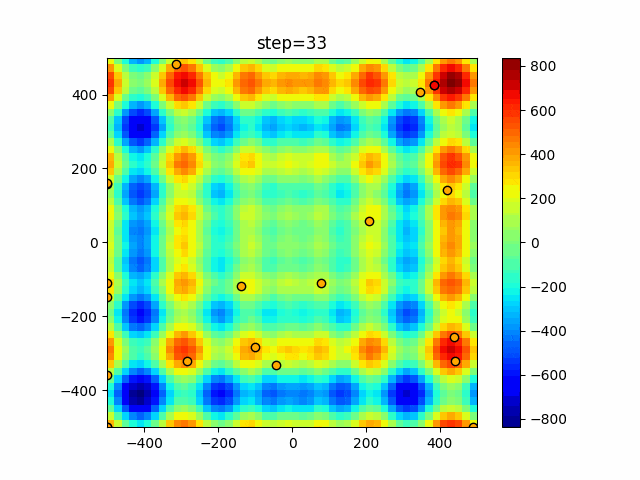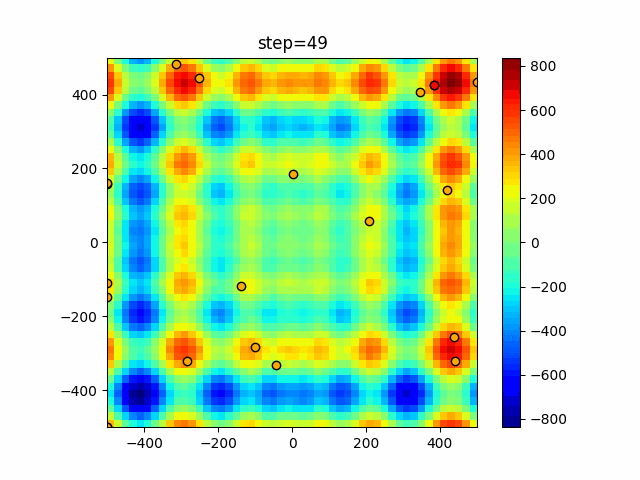
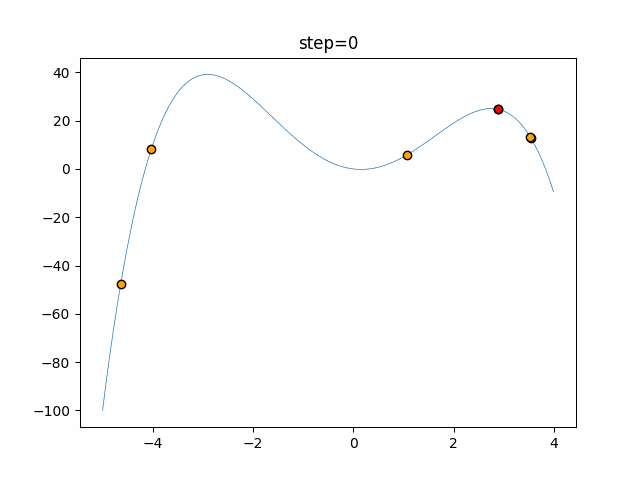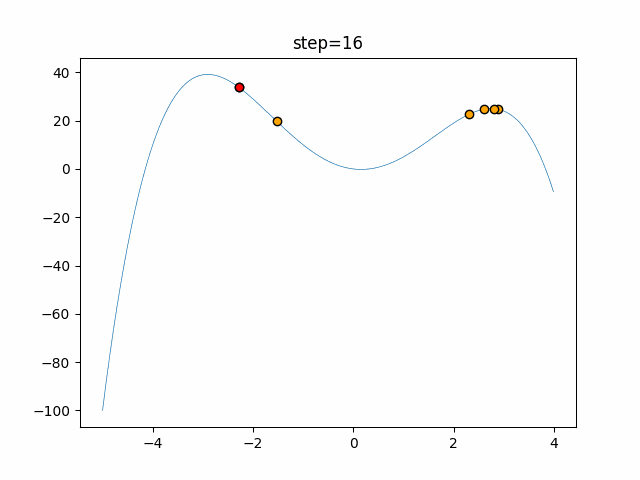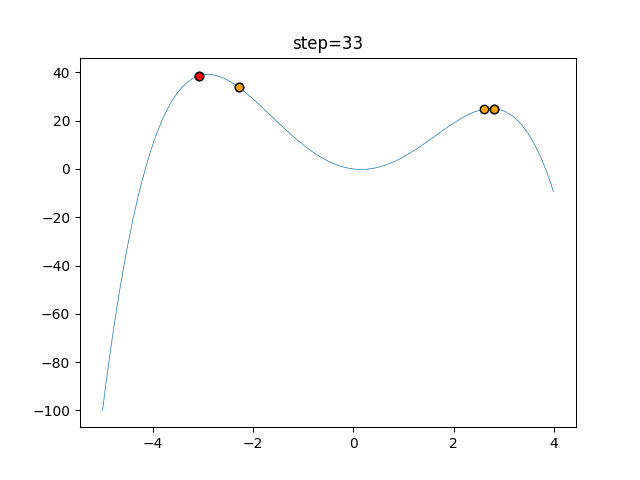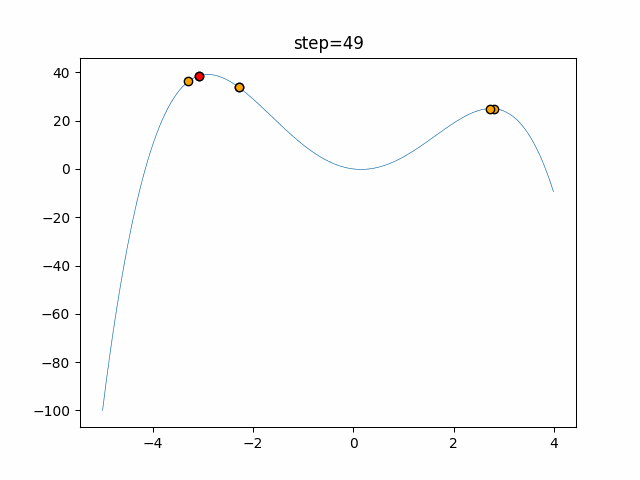
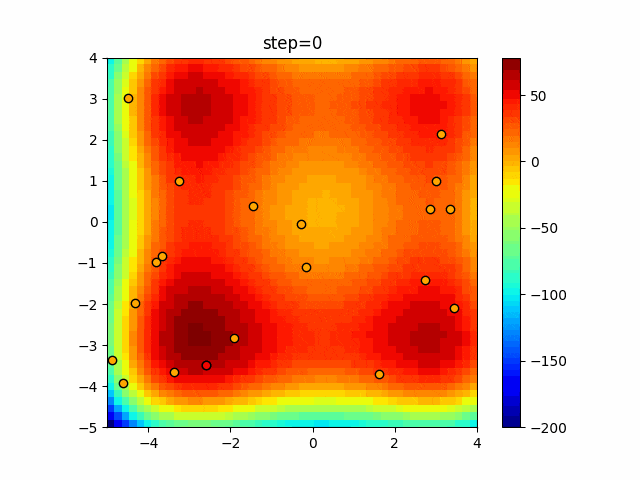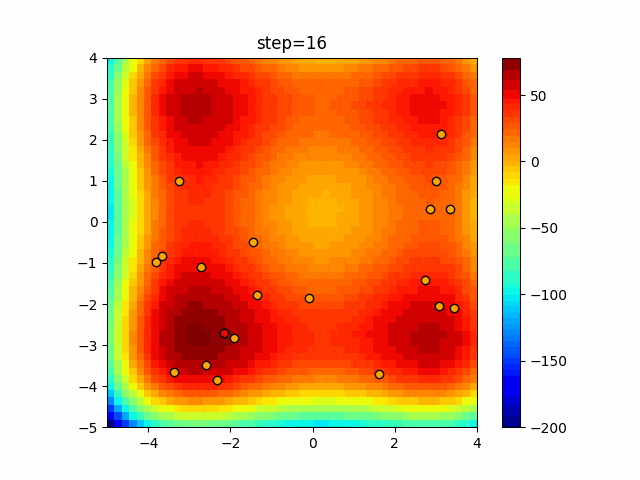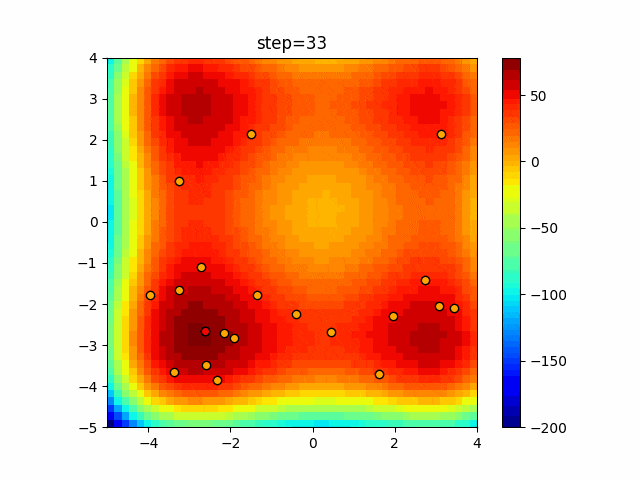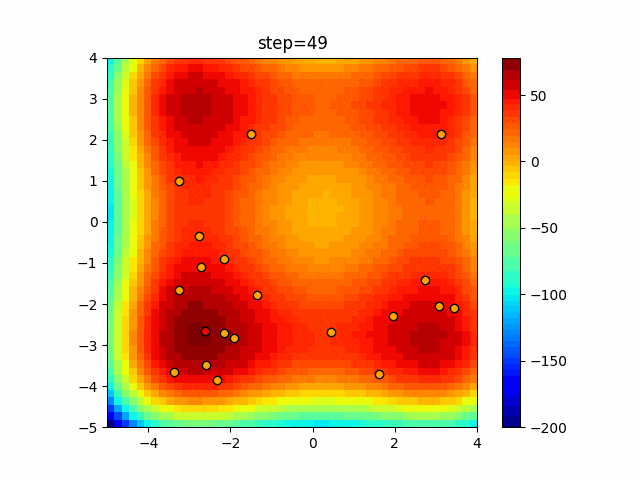
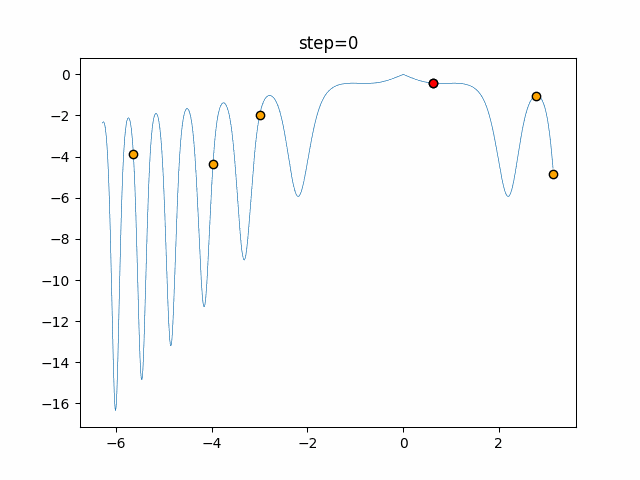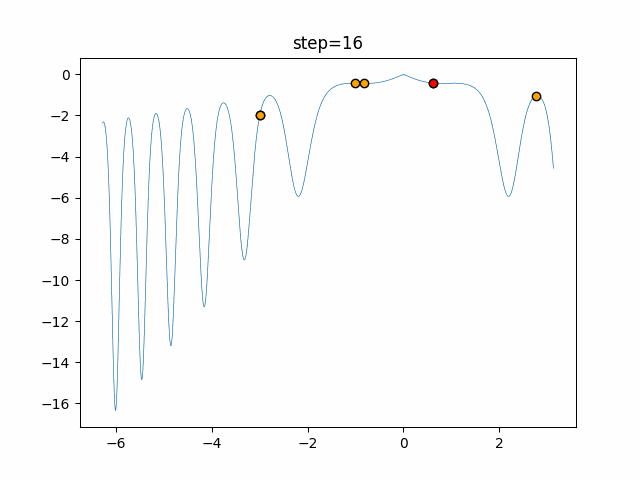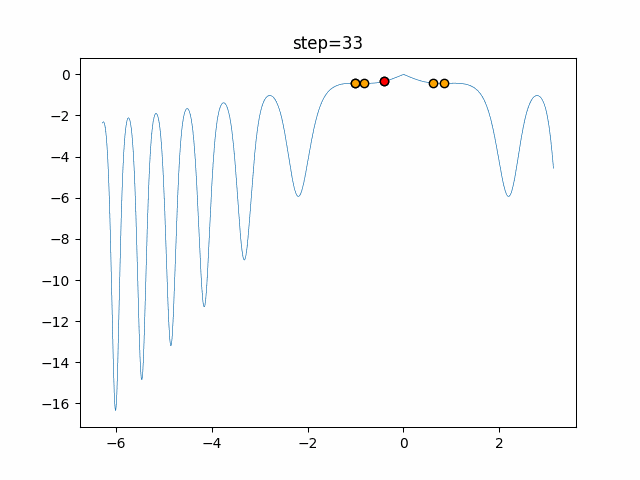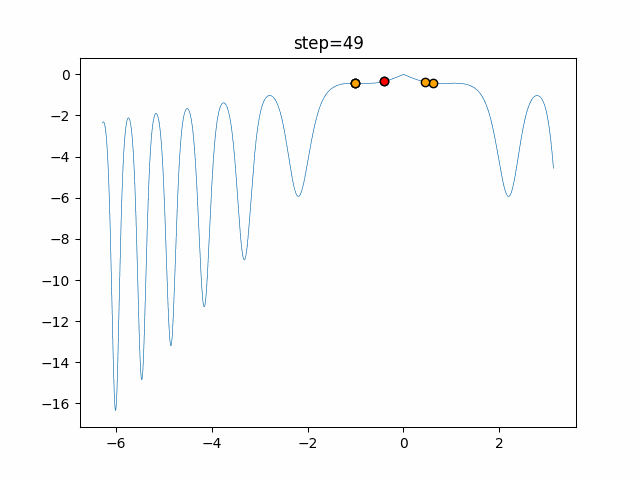
実際の動きの可視化
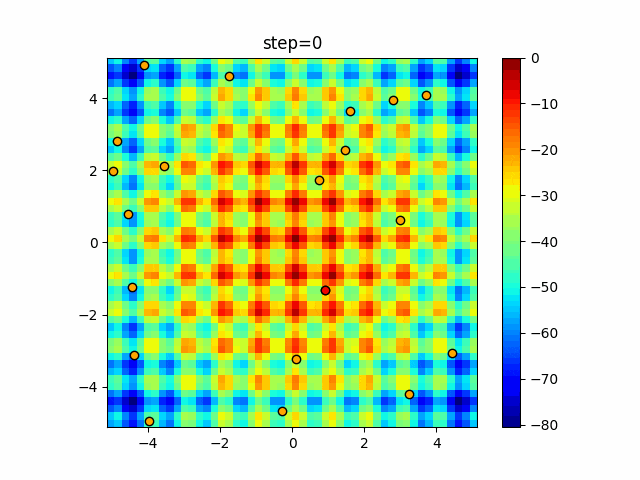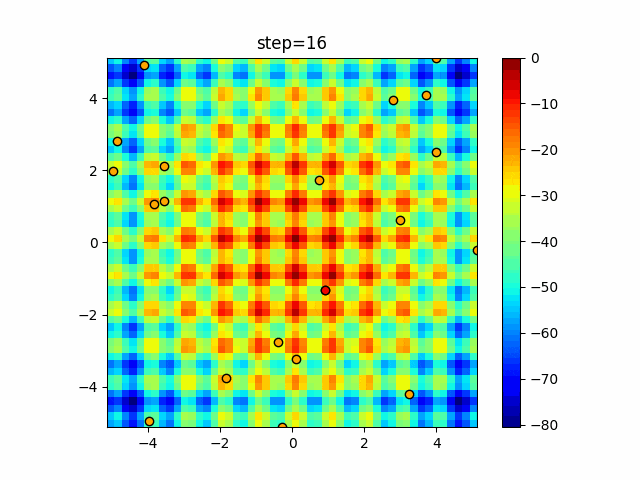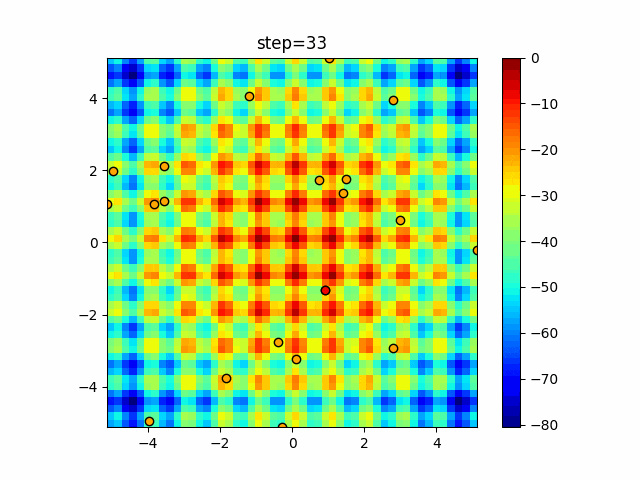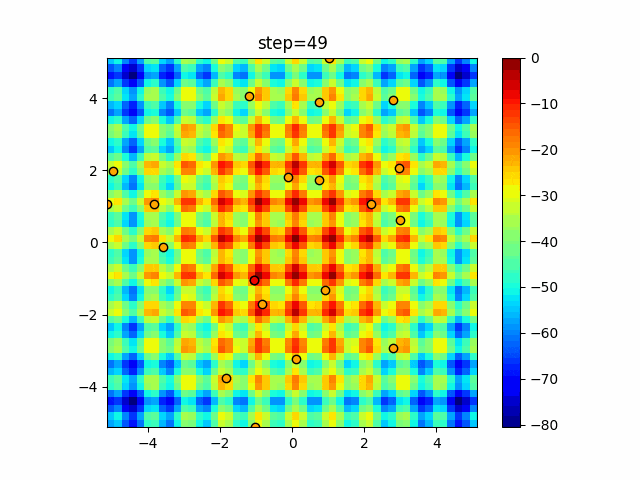
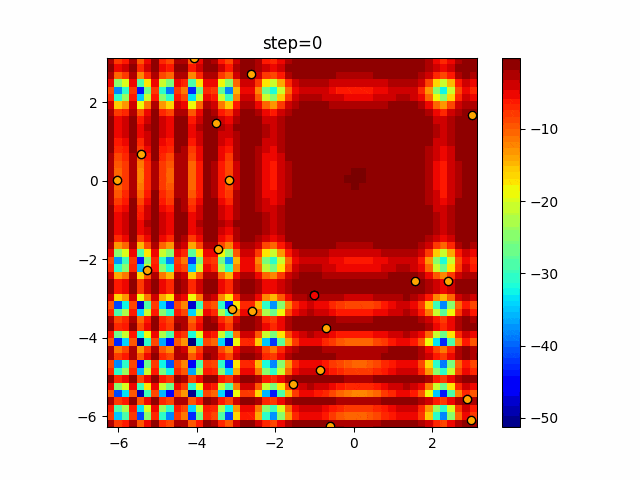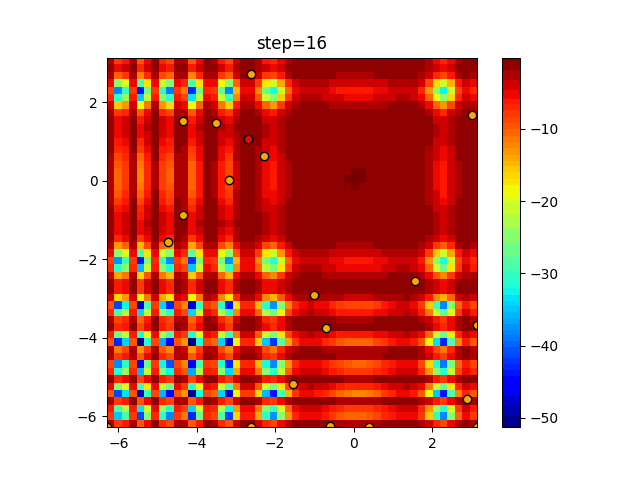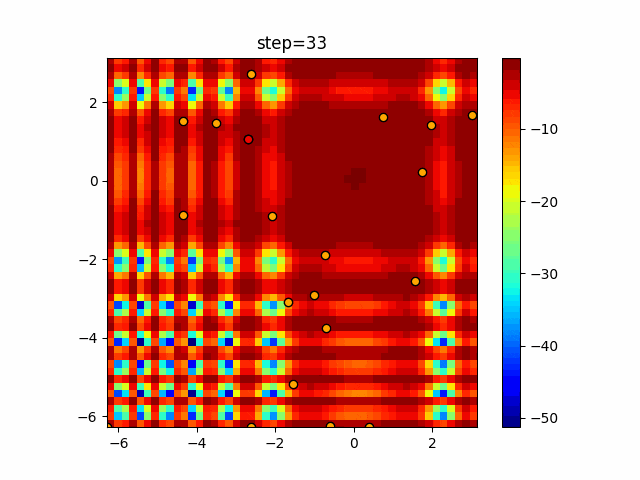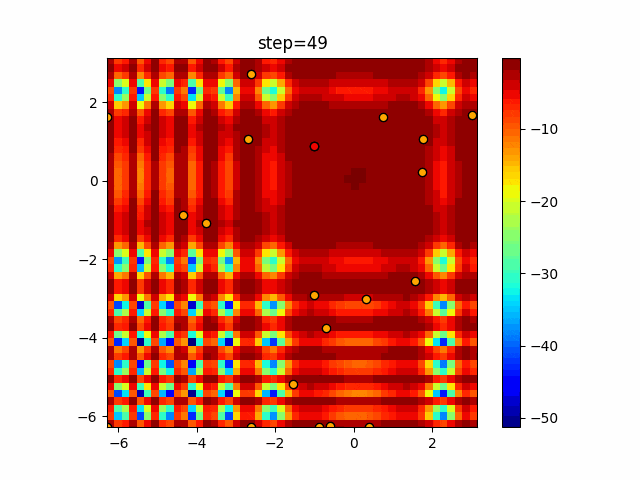
1次元は6個体、2次元は20個体で50step実行した結果です。
赤い丸がそのstepでの最高スコアを持っている個体となります。
パラメータは以下で実行しました。
Harmony(N, bandwidth=1.0, enable_bandwidth_rate=True, select_rate=0.4, change_rate=0.9)
function_Ackley
- 1次元
- 2次元
function_Rastrigin
- 1次元
- 2次元
function_Schwefel
- 1次元
- 2次元
function_StyblinskiTang
- 1次元
- 2次元
function_XinSheYang
- 1次元
- 2次元
あとがき
評価値が一番低い個体を置き換えるというのは他のアルゴリズムにない特徴です。
画像で学習が遅く見えるのは1stepで1個体しか評価していないからですね。
(カッコウ探索も似ており、1step≒1個体評価です)