最適化アルゴリズムを実装していくぞ（くじらさんアルゴリズム）

はじめに

最適化アルゴリズムの実装シリーズです。
まずは概要を見てください。

コードはgithubにあります。

くじらさんアルゴリズム

概要

くじらさんアルゴリズム(The Whale Optimization Algorithm; WOA)はクジラの捕食行動に着目して作られたアルゴリズムです。
クジラはバブルネットという群行動によって獲物を捕食します。
バブルネットは図のように円を描きながら獲物を追い詰めて捕食する行動のようです。

参考
・くじらさんアルゴリズム
・Whale Optimization Algorithm

アルゴリズム

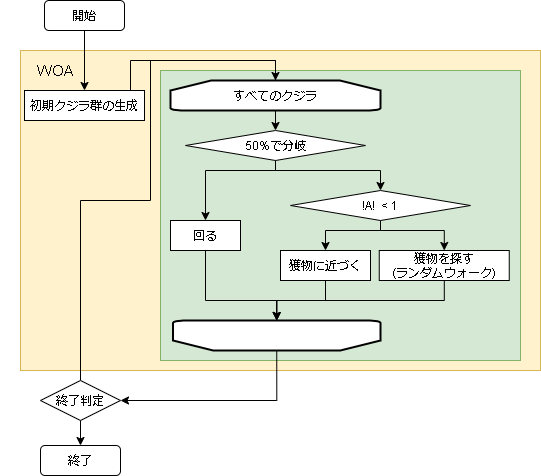
獲物に近づく、獲物を探す、円を描くの３つの行動のどれかを選んで獲物を見つけます。

• アルゴリズムのフロー

• 用語の対応

問題	くじらさんアルゴリズム
問題への入力	クジラの位置≒獲物の位置
評価値	クジラの位置における評価値

• ハイパーパラメータに関して

変数名	意味	備考
a_decrease	aの減少値	最初はランダムに移動し、後半は獲物に近づく。aはその移行速度
logarithmic_spiral	対数螺旋の係数	大きいほど回るときに大きく動く

獲物に近づく

獲物に近づくと書いていますが実際に獲物がどこにいるかは分からないので、現状で最も評価が高いクジラを獲物と扱い、そこに近づきます。

まずは $\vec{A}$ と $\vec{C}$ を出します。

$$ \vec{A} = 2a\vec{r_1} - a$$

$$ \vec{C} = 2\vec{r_2}$$

$\vec{r_1}$ と $\vec{r_2}$ は座標と同じ次元の 0～1 の乱数です。
$a$ は初期値2から毎step減少していく変数です。($2 \geqq a \geqq 0$)

ここで $\vec{A}$ のノルム（$|\vec{A}|$）が1以下なら獲物に近づく行動をし、
違う場合は獲物を探す行動をします。

獲物に近づく場合の数式は以下です。

$$ \vec{D} = |\vec{C} \vec{X_{best}}(t) - \vec{X}(t)| $$
$$ \vec{X}(t+1) = \vec{X_{best}}(t) - \vec{A}\vec{D} $$

$\vec{X}$ が自分の座標を表し、$\vec{X_{best}}$ が最も評価の高いクジラです。
コードだと以下になります。

import numpy as np

a = 2  # 毎step減少する

r1 = np.random.rand(problem.size)  # 0-1の乱数を生成
r2 = np.random.rand(problem.size)  # 0-1の乱数を生成

A = (2.0 * np.multiply(a, r1)) - a
C = 2.0 * r2

i = 対象のクジラのindex

if np.linalg.norm(A) < 1:
    pos = np.asarray(whales[i].getArray())  # 対象クジラの座標
    best_pos = np.asarray(best_whale.getArray())  # 最良クジラの座標

    D = np.linalg.norm(np.multiply(C, best_pos) - pos)
    pos = best_pos - np.multiply(A, D)

獲物を探す

獲物に近づくで説明した $|A|$ が1以上の場合は獲物に近づきます。
近づき方は"獲物に近づく"場合と同じで、対象のクジラが最も評価の高いクジラからランダムなクジラに変わっただけです。

$$ \vec{D} = |\vec{C} \vec{X_p}(t) - \vec{X}(t)| $$
$$ \vec{X}(t+1) = \vec{X_p}(t) - \vec{A}\vec{D} $$

$\vec{X_p}$ はランダムなクジラの座標となります。

import numpy as np

i = 対象のクジラのindex

if np.linalg.norm(A) >= 1:
    pos = np.asarray(whales[i].getArray())  # 対象クジラの座標
    p_pos = np.asarray(whales[random.randint(0, len(whales)-1)].getArray())  # ランダムなクジラの座標

    D = np.linalg.norm(np.multiply(C, p_pos) - pos)
    pos = p_pos - np.multiply(A, D)

円を描く

円は獲物（評価値最大のクジラ）を基準に以下の式で描きます。

$$ \vec{D'} = |\vec{X_{best}}(t) - \vec{X}(t)| $$
$$ \vec{X}(t+1) = \vec{D'} e^{bL} \cos(2 \pi L) + \vec{X_{best}}(t) $$

$b$ は対数螺旋の係数(はlogarithmic_spiral)、$L$ は[-1, 1]のランダムな値です。

import numpy as np

i = 対象のクジラのindex

pos = np.asarray(whales[i].getArray())  # 対象クジラの座標
best_pos = np.asarray(best_whale.getArray())  # 最良クジラの座標

# 回る
D = np.linalg.norm(best_pos - pos)
L = np.random.uniform(-1, 1, problem.size)  # [-1,1]の乱数
_b = logarithmic_spiral
pos = np.multiply(np.multiply(D, np.exp(_b*r)), np.cos(2.0*np.pi*r)) + best_pos

スパイラルのグラフ

円を描くがどういう移動をしているかを見てみました。

グラフのx軸が-1から1の乱数($L$）で、y軸が移動距離です。
数式だと以下の部分だけをグラフ化しています。

$$ spiral = \vec{D'} e^{bL} \cos(2 \pi L) $$

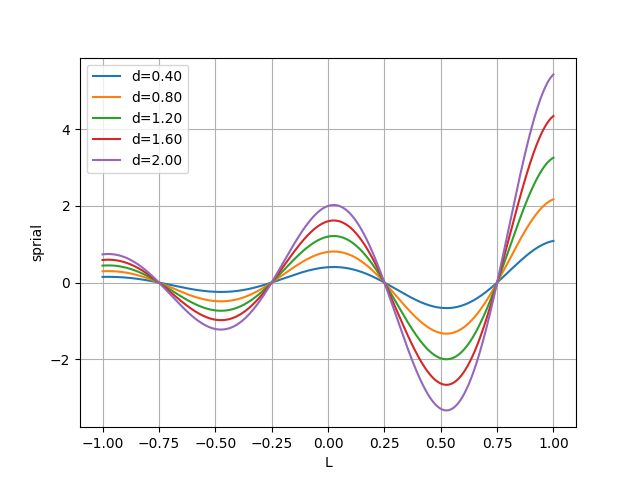
• ユークリッド距離による変化

$b$(logarithmic_spiral) を1に固定して、$\vec{D'}$のみを変化させた場合のグラフです。
$\vec{D'}$ は自分と獲物(最良クジラ)とのユークリッド距離を表しているので、獲物との距離による移動の変化を表しているといえます。

離れているほど大きく移動する可能性が高い事がわかりますね。

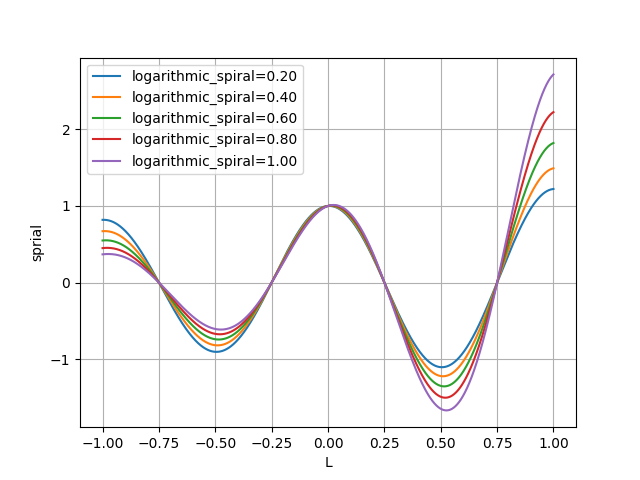
• 対数螺旋係数による変化

今度は$b$(logarithmic_spiral)を変化させた場合です。
$D'$ は 1 に固定しています。

$D'$ の場合と同じように $b$ が大きくなれば変化が大きいようです。

コード全体

コード全体です。
コードを作成するにあたりここのコードを参考にしています。

import math
import random

import numpy as np

class WOA():
    def __init__(self, 
        whale_max,         # クジラの数
        a_decrease=0.001,  # 変数aの減少値
        logarithmic_spiral=1,  # 対数螺旋の係数
    ):
        self.whale_max = whale_max
        self.a_decrease = a_decrease
        self.logarithmic_spiral = logarithmic_spiral

    def init(self, problem):
        self.problem = problem

        self.best_whale = None
        self.whales = []
        for _ in range(self.whale_max):
            o = problem.create()
            self.whales.append(o)

            if self.best_whale is None or self.best_whale.getScore() < o.getScore():
                self.best_whale = o.copy()
        self._a = 2


    def step(self):

        for whale in self.whales:
            pos = np.asarray(whale.getArray())

            if random.random() < 0.5:
                r1 = np.random.rand(self.problem.size)  # 0-1の乱数
                r2 = np.random.rand(self.problem.size)  # 0-1の乱数

                A = (2.0 * np.multiply(self._a, r1)) - self._a
                C = 2.0 * r2

                if np.linalg.norm(A) < 1:
                    # 獲物に近づく
                    new_pos = self.best_whale.getArray()
                else:
                    # 獲物を探す
                    new_pos = self.whales[random.randint(0, len(self.whales)-1)].getArray()
                new_pos = np.asarray(new_pos)

                D = np.linalg.norm(np.multiply(C, new_pos) - pos)
                pos = new_pos - np.multiply(A, D)

            else:
                # 回る
                best_pos = np.asarray(self.best_whale.getArray())

                D = np.linalg.norm(best_pos - pos)
                L = np.random.uniform(-1, 1, self.problem.size)  # [-1,1]の乱数
                
                _b = self.logarithmic_spiral
                pos = np.multiply(np.multiply(D, np.exp(_b*L)), np.cos(2.0*np.pi*L)) + best_pos

            whale.setArray(pos)
            if self.best_whale.getScore() < whale.getScore():
                self.best_whale = whale.copy()

        self._a -= self.a_decrease
        if self._a < 0:
            self._a = 0

ハイパーパラメータ例

各問題に対して optuna でハイパーパラメータを最適化した結果です。
最適化の1回の試行は、探索時間を5秒間として結果を出しています。
これを100回実行し、最適なハイパーパラメータを optuna に探してもらいました。

問題	a_decrease	logarithmic_spiral	whale_max
EightQueen	0.020366541568838378	1.5723091675627572	45
function_Ackley	0.012846425355295324	1.817054209171554	49
function_Griewank	0.014055305155620233	1.5507180701447845	48
function_Michalewicz	0.019651164901908023	1.7671279692872293	46
function_Rastrigin	0.0173318428180831	0.7578390758302801	46
function_Schwefel	0.007491644624065206	1.6917050129680944	9
function_StyblinskiTang	0.024426401837372255	1.9474471085818506	50
function_XinSheYang	0.005722874915111857	0.4779624408790928	24
g2048	0.043666294831303784	1.09050483219953	37
LifeGame	0.0054058667884643585	0.06834119701477159	50
OneMax	0.014922301994610046	0.8650190784964947	27
TSP	0.0287871077043457	1.3855183848189636	45

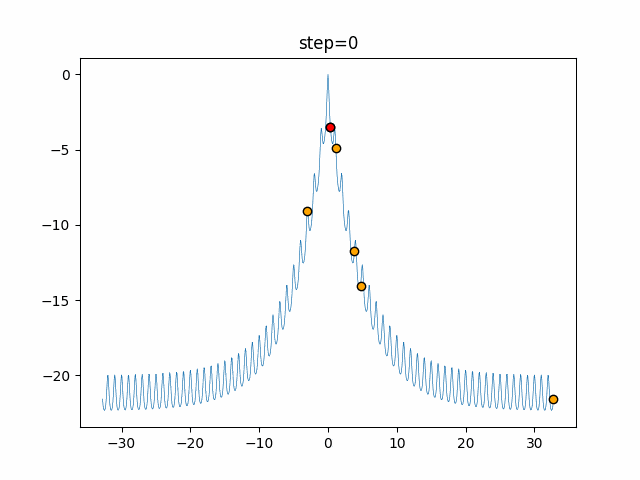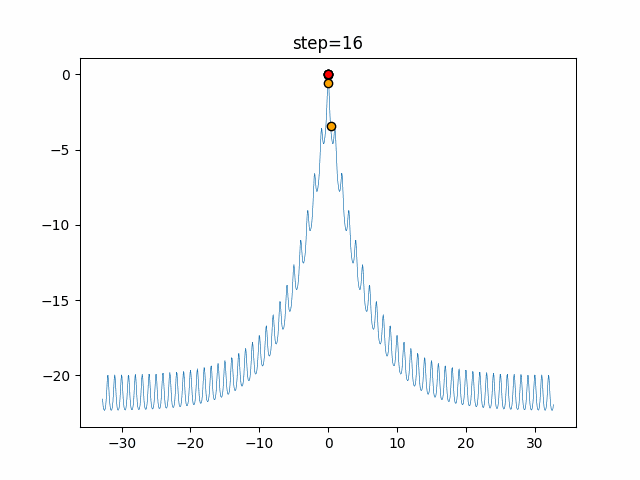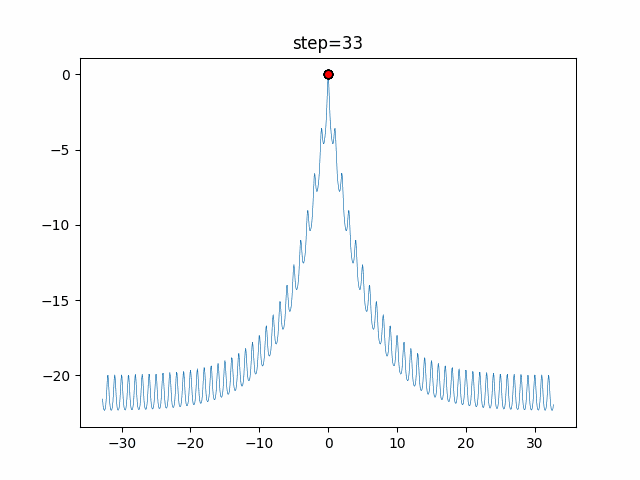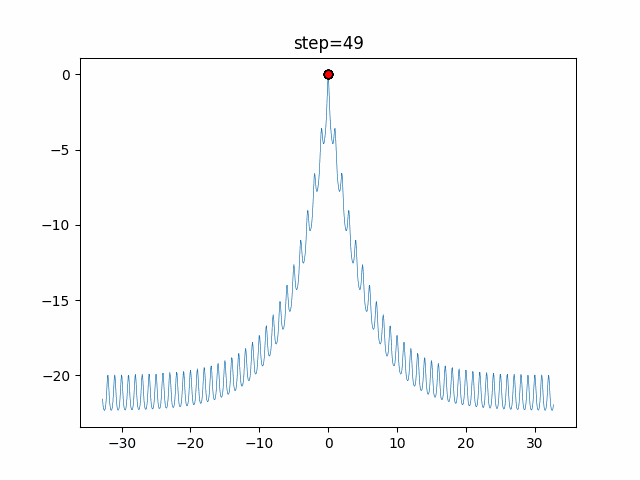
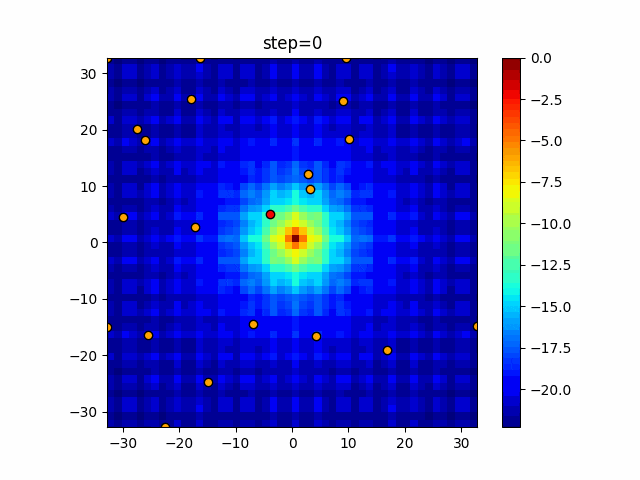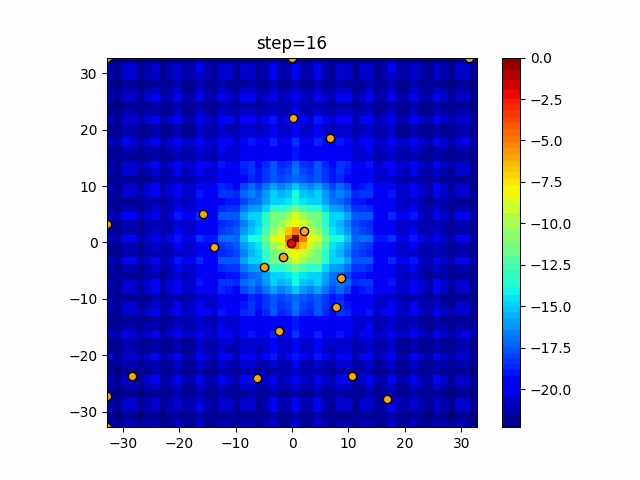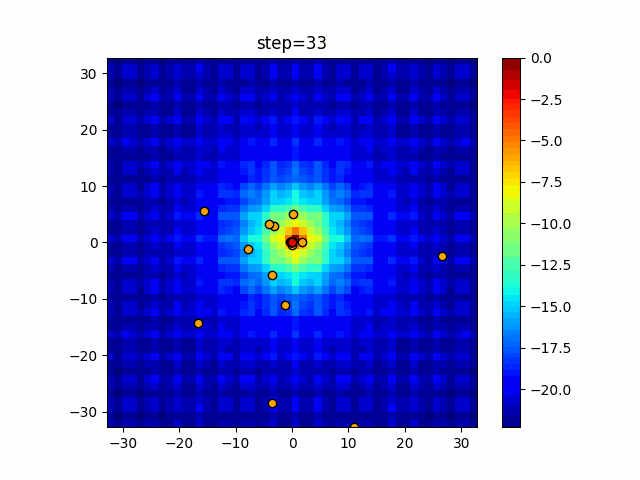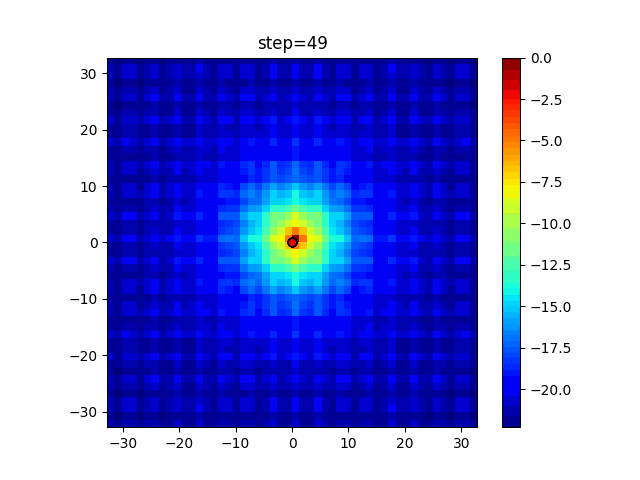
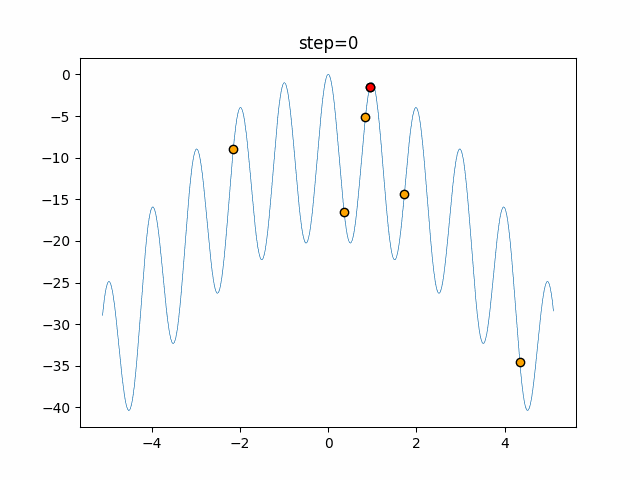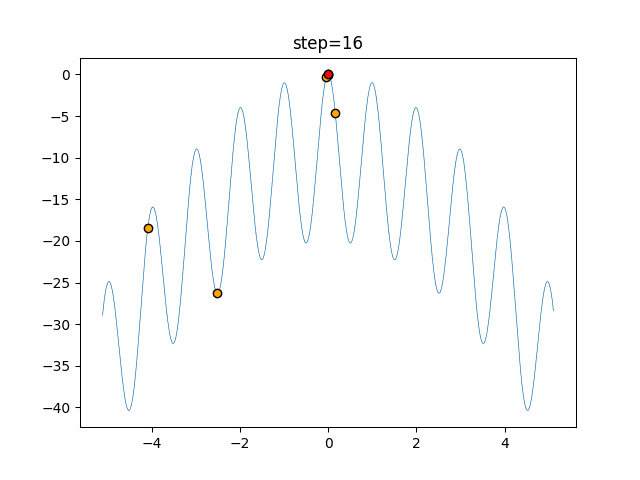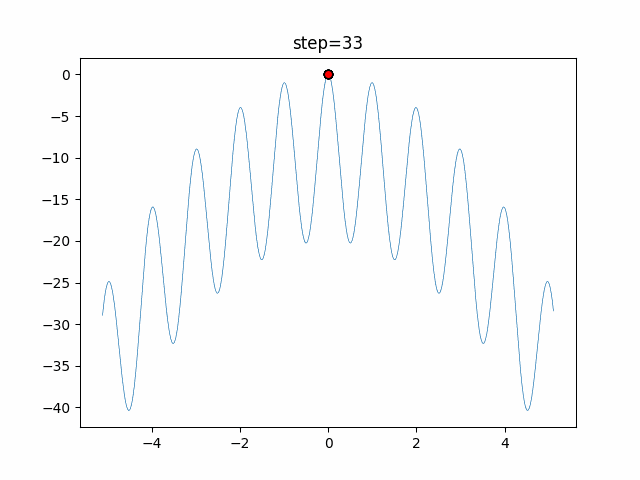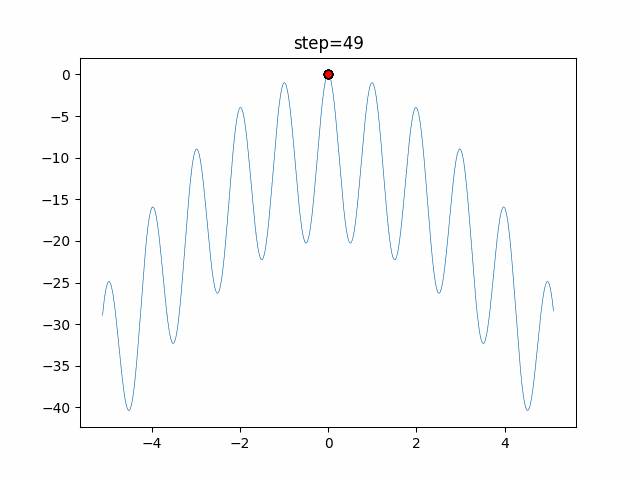
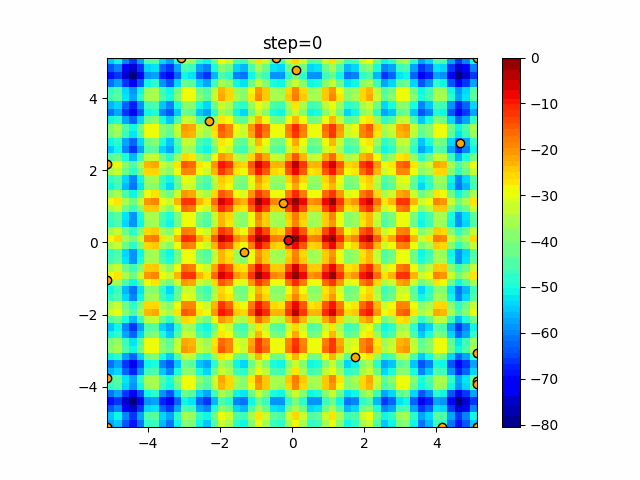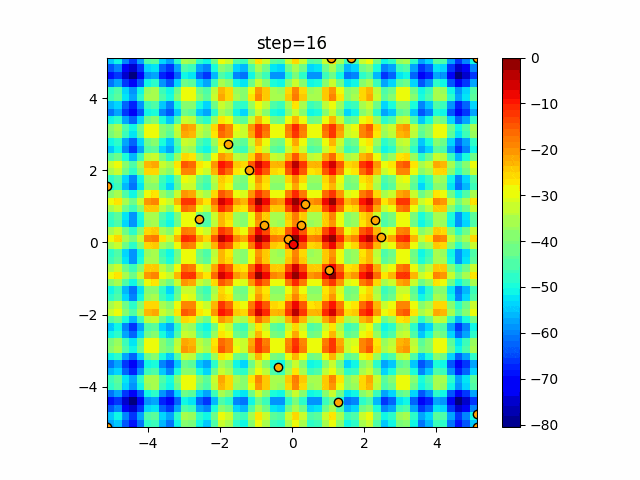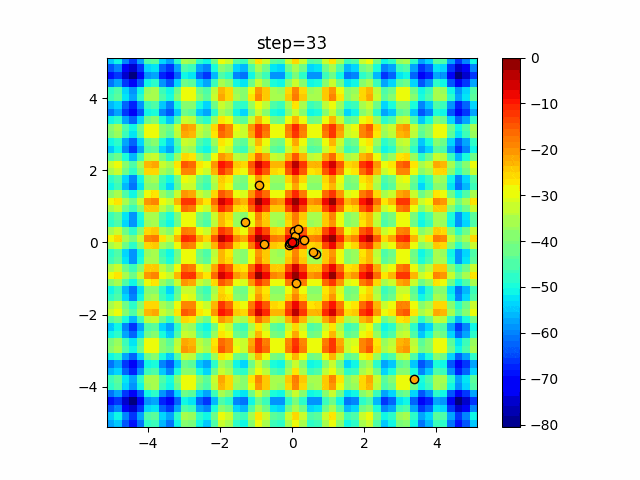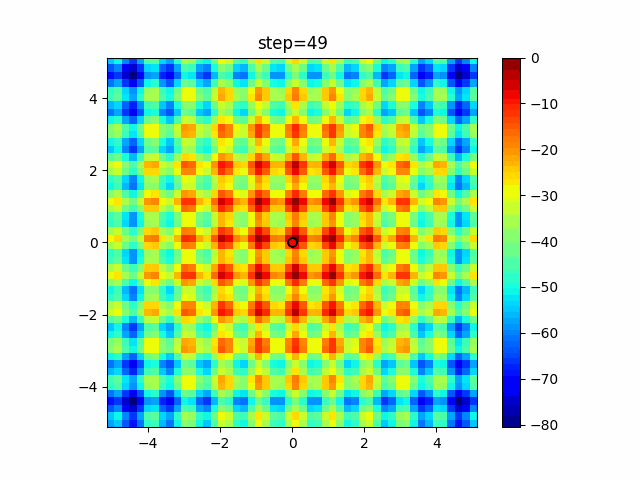
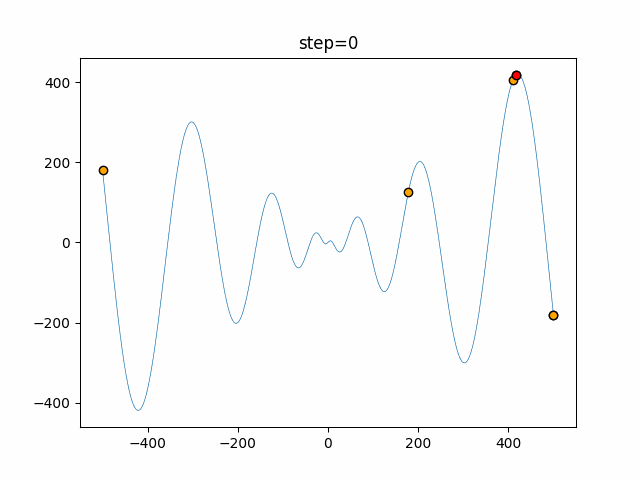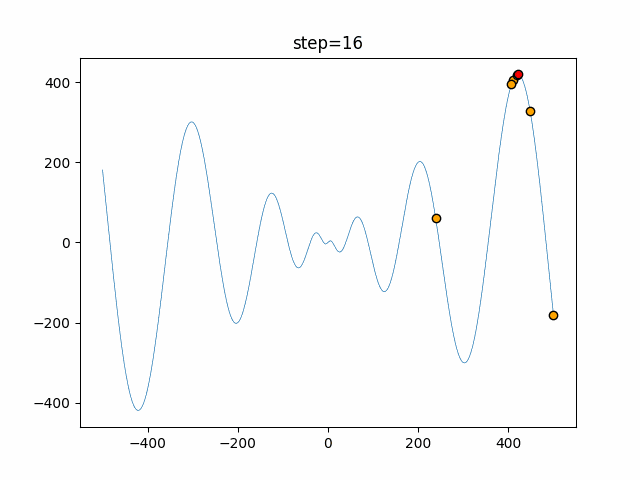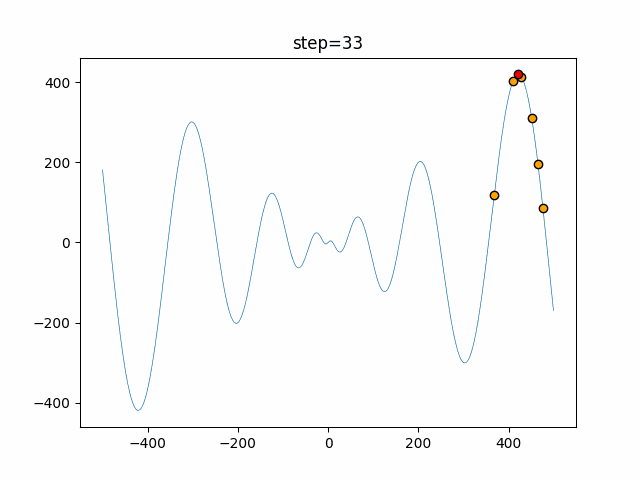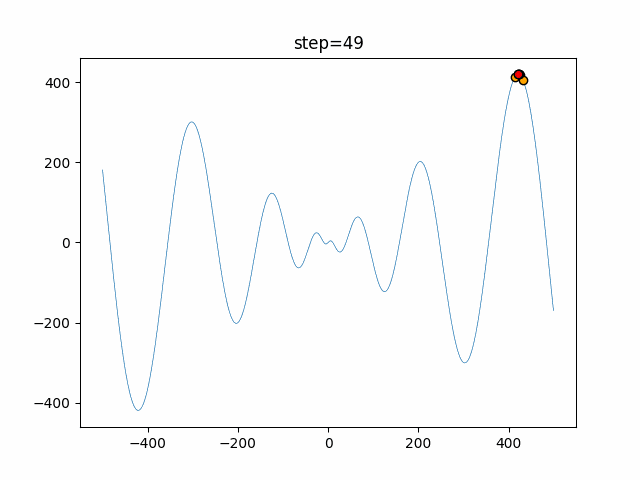
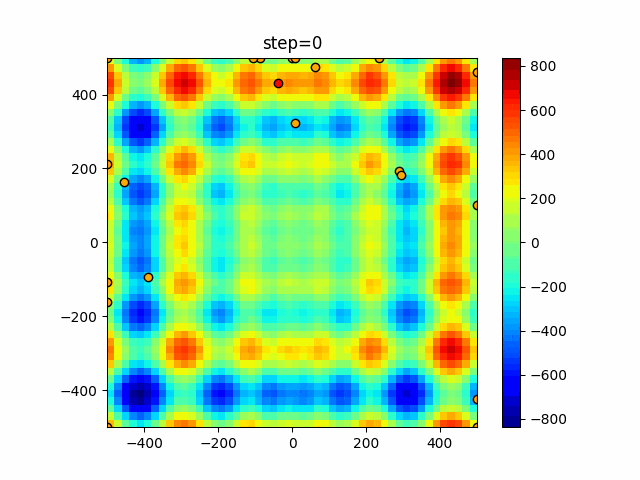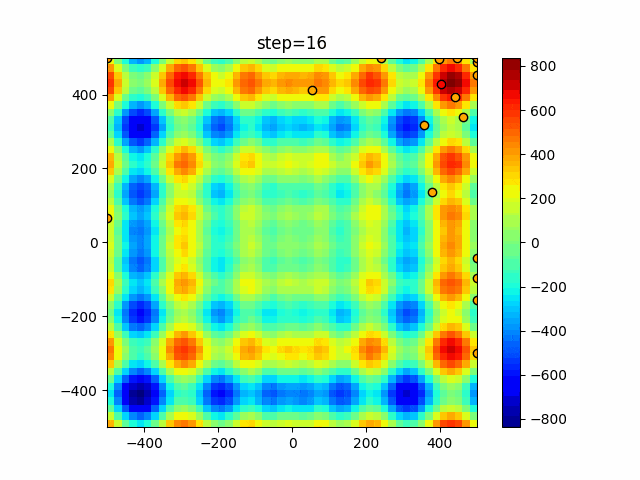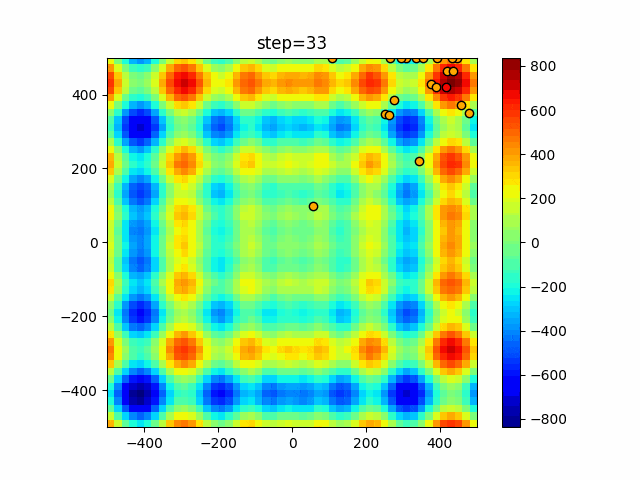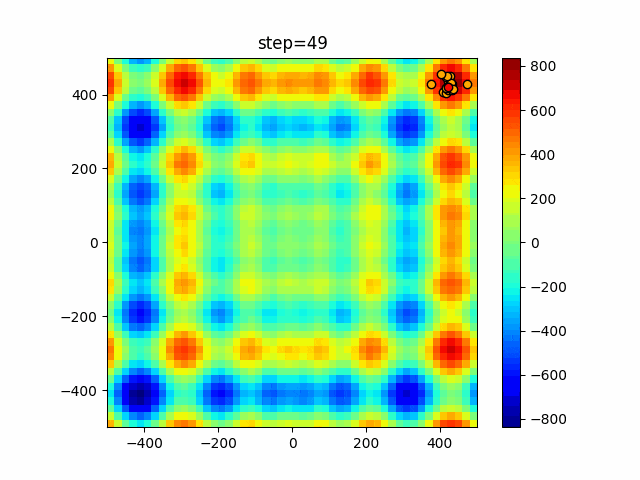
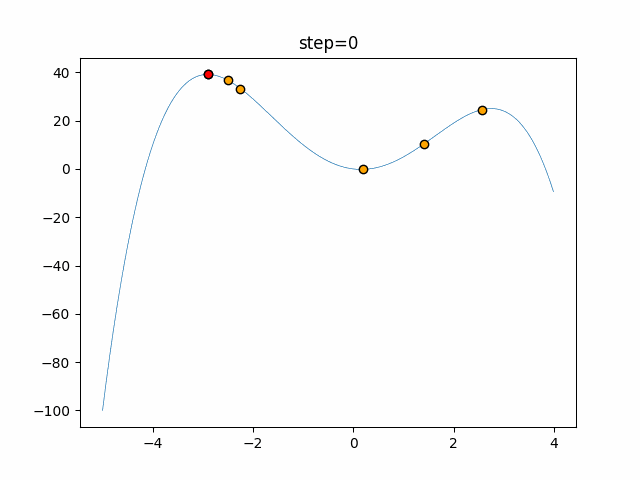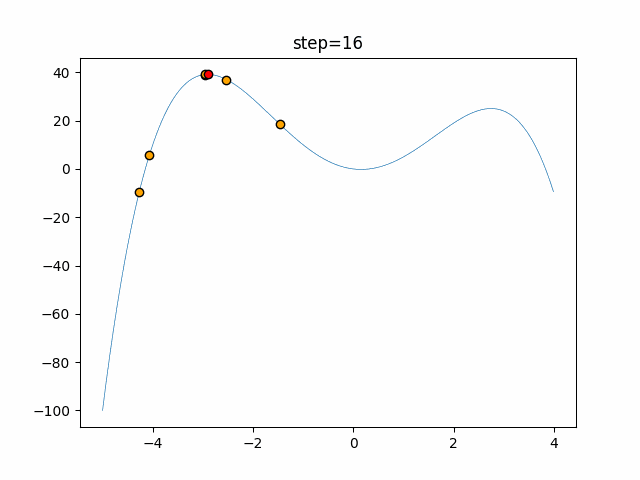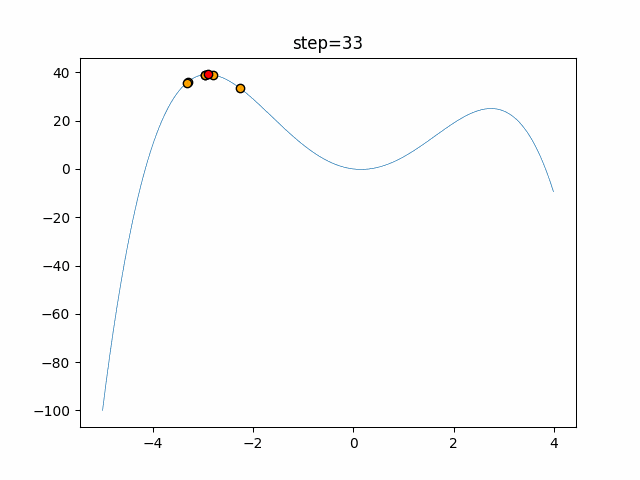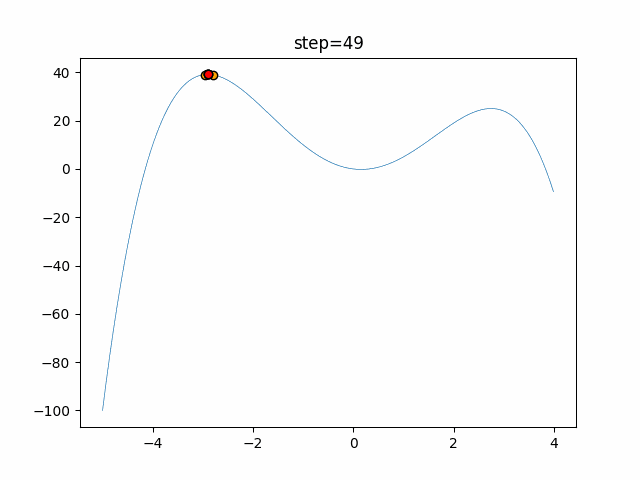
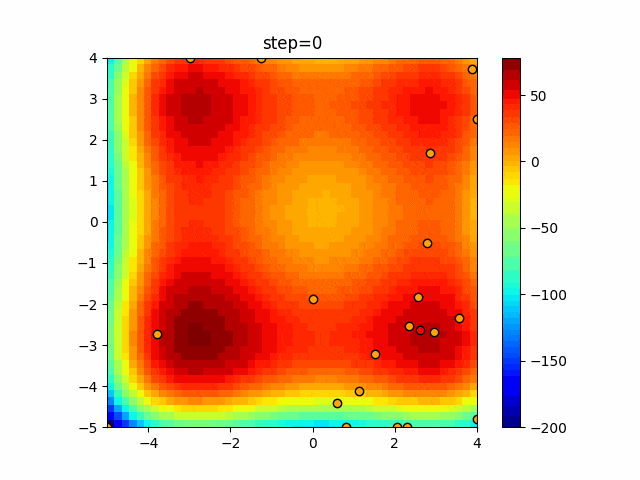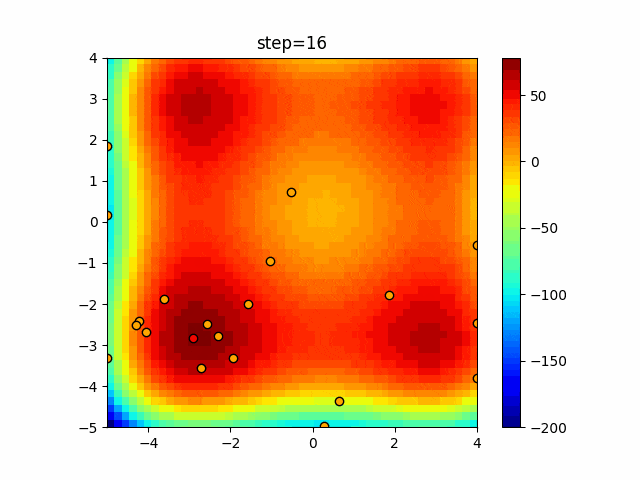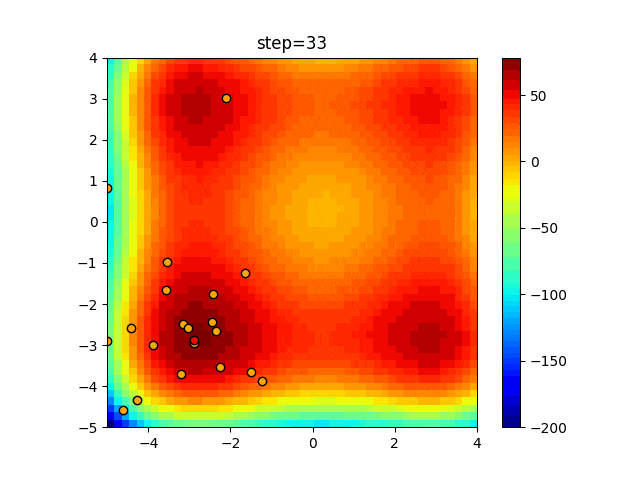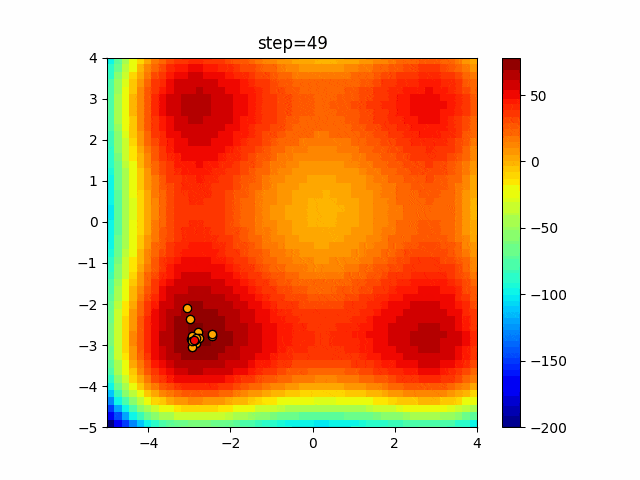
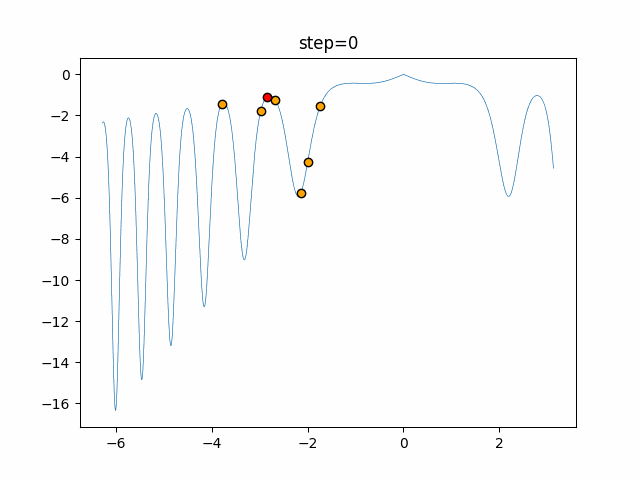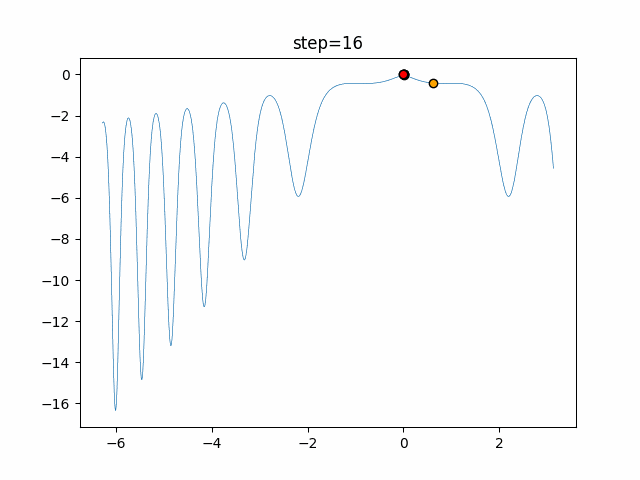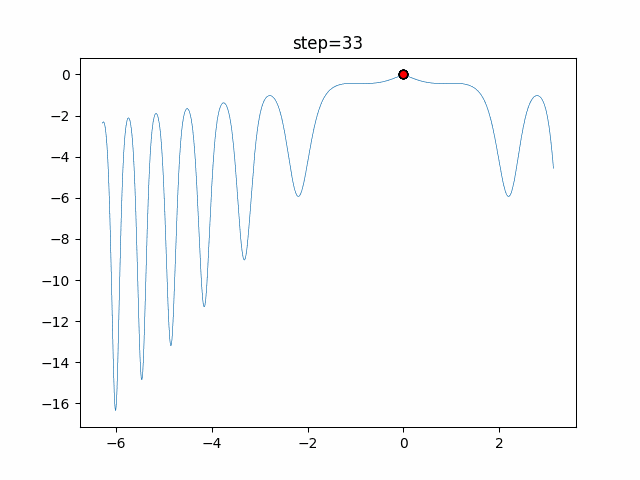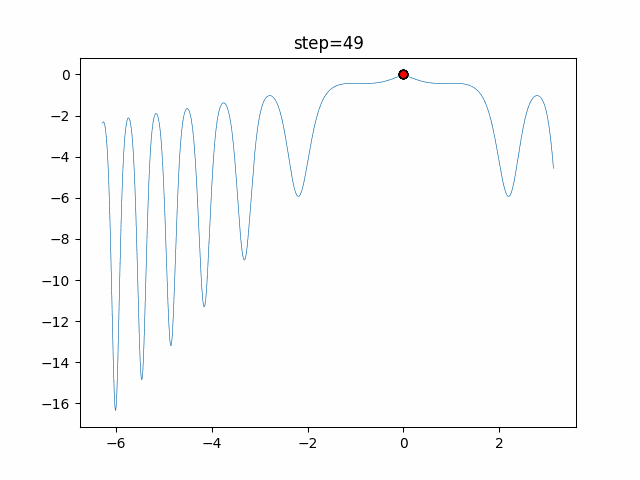
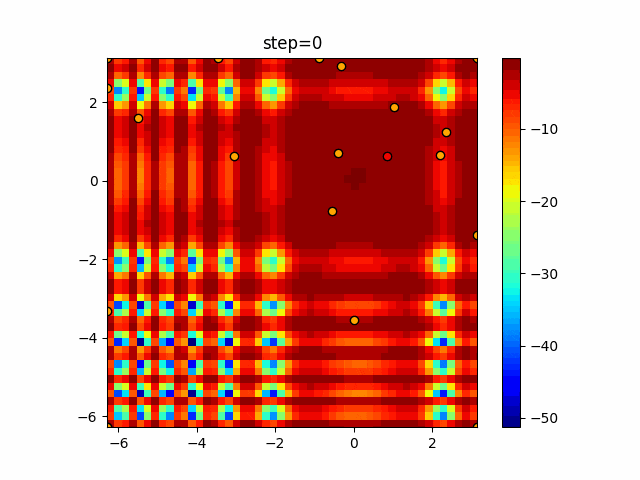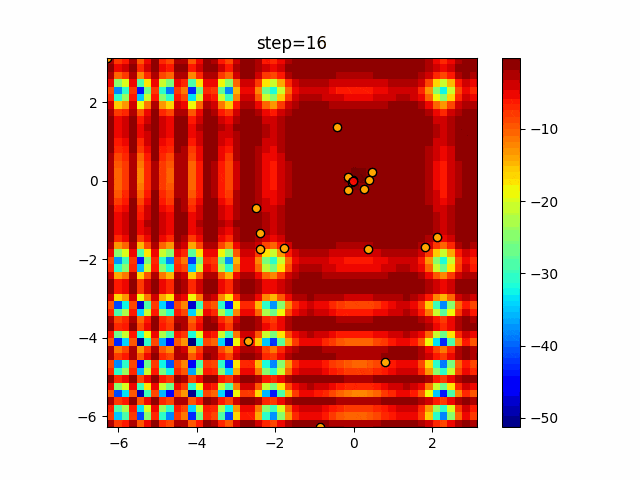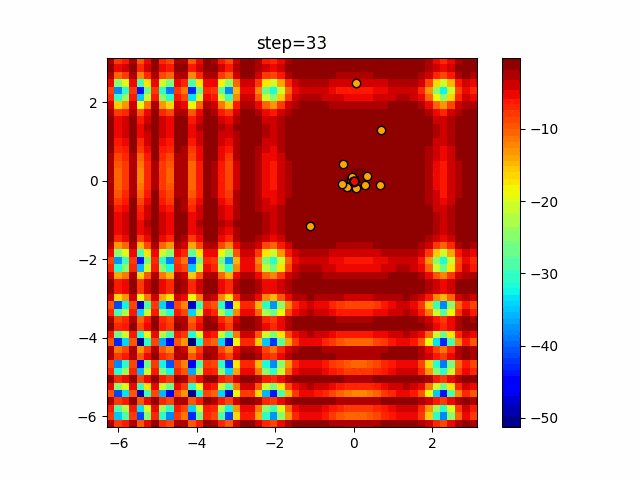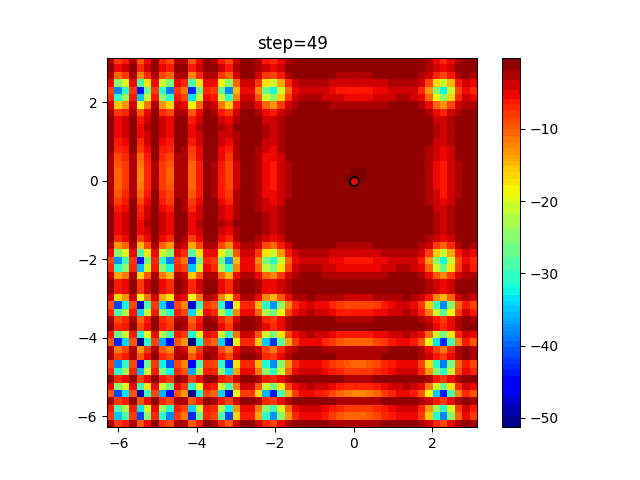
実際の動きの可視化

1次元は6個体、2次元は20個体で50step実行した結果です。
赤い丸がそのstepでの最高スコアを持っている個体となります。

パラメータは以下で実行しました。

WOA(N, a_decrease=2/50, logarithmic_spiral=1)

function_Ackley

• 1次元

• 2次元

function_Rastrigin

• 1次元

• 2次元

function_Schwefel

• 1次元

• 2次元

function_StyblinskiTang

• 1次元

• 2次元

function_XinSheYang

• 1次元

• 2次元

あとがき

ぐるぐる渦巻きながらいい感じに集まっていきますね。
ただ、一度収束してしまうとそこから脱出することはないので a の値をどう制御するかが重要そうです。