雑談

Genetic ProgrammingのAdvent Calendarを作ろうと思ったけど，自分以外の投稿がないことが容易に想像できたので，「群知能と最適化」のAdvent Calendarに来ました．

本記事にいいねした人は来年，Genetic ProgrammingのAdvent Calendarに記事投稿してください．

はじめに

今回紹介するのはThe Whale Optimization Algorithm(WOA)¹です．2016年に発表された手法ですが，2019年11月の時点では日本語の記事はありません．

僕も最近知ったので，解説のついでに理解を深めたいと思います．

くじらさんアルゴリズム(The Whale Optimization Algorithm; WOA)

Inspiration

皆さんはクジラについてどれだけ知っていますか？

Whales are fancy creatures. They are considered as the biggest mammals in the world. An adult whale can grow up to 30 m long and 180 t weight. There are 7 different main species of this giant mammal such killer, Minke, Sei, humpback, right, finback, and blue. Whales are mostly considered as predators. They never sleep because they have to breathe from the surface of oceans. In fact, half of the brain only sleeps. The interesting thing about the whales is that they are considered as highly intelligent animals with emotion.

ちなみにこの引用は，原著から抜いてきました．なんとこの論文を読むと，新しいアルゴリズムを知れるだけでなく，クジラについても詳しくなれるのです．みんなも読もう．

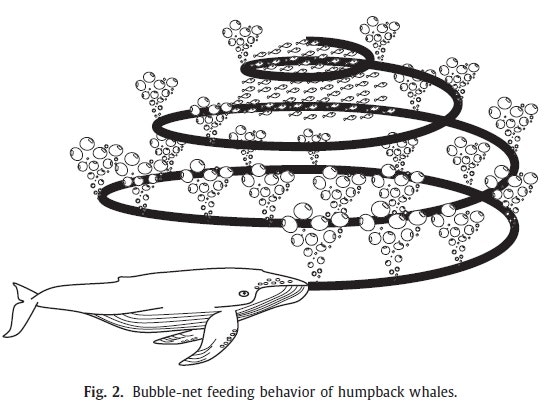
なぜ，クジラアルゴリズムという名前なのかというと，クジラの捕食行動をモデルにしているからです．
ザトウクジラは，バブルネットという群行動によって獲物を捕食します．この様に円を描きながら，獲物(Optima)にたどり着くのがWOAです．

Algortihm

獲物を取り囲むモデル

実際には，最適化において獲物(Optima)は未知です．
そこで，WOAでは現時点での最良の解候補を，中心の獲物として扱い，それに向かって他のエージェントの位置更新を行います．

このときの位置更新式は

\vec{D} = |\vec{C} \cdot\vec{X^*}(t) - \vec{X}(t)|
\\
\vec{X}(t+1) = \vec{X^*}(t) - \vec{A} \cdot \vec{D}

となります．
ここで　$\vec{X^*}(t)$は現時点での最良解候補の位置を，$\vec{X}(t)$は各エージェントの位置を表しています．
また，$\vec{A}$および，$\vec{C}$はランダム係数ベクトルです．

簡単に言うと，最良解候補へと，各エージェントが進むだけです．

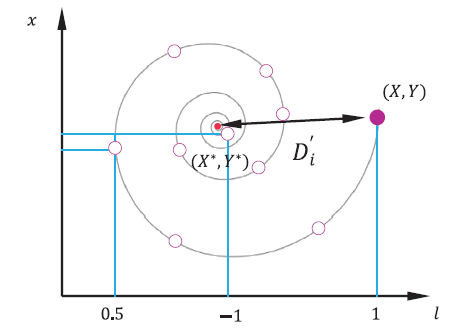
円を描くモデル

さらに，ザトウクジラは円を描きながら獲物へ向かうため，これも取り入れます．

\vec{X}(t+1)=\vec{D'} \cdot e^{bl} \cdot \cos{(2\pi l)} + \vec{X^*}(t)

深く考えなくても大丈夫です．回転するだけなので．

この二つの行動を確率に行うため，エージェントの位置更新式は次のようになります．

\vec{X}(t+1)=\left\{
\begin{array}{ll}
\vec{X^*}(t) - \vec{A} \cdot \vec{D} & (p \lt 0.5) \\
\vec{D'} \cdot e^{bl} \cdot \cos{(2\pi l)} + \vec{X^*}(t) & (p \geq 0.5)
\end{array}
\right.

(図・式は原著より抜粋)

獲物の探索

バブルネット式の移動に加えてザトウクジラはランダムに獲物を探します．

\vec{D} = |\vec{C} \cdot\vec{X_{rand}} - \vec{X}|
\\
\vec{X}(t+1) = \vec{X_{rand}} - \vec{A} \cdot \vec{D}

$\vec{X_{rand}}$は群の中のランダムなクジラを表します．まぁ実質ランダムウォークでしょう．

つまり，クジラの行動は，3パターンあります

獲物に近づく
回る
獲物を探す

全体のアルゴリズム

疑似コードは次のようになります．Wikiversityより

Input data, Number of maxiter and Population etc 
Initialize the whales population  Xi (i = 1, 2, ..., n) 
Initialize a, A, C, l and p
Calculate the fitness of each search agent
X*= the best search agent
while (it < Maxiter)
      for each search agent
             if (p < 0.5)  
                      if (|A| < 1)
                                獲物に近づく
                      else if (|A| ≥ 1)
                                獲物を探す
                      end 
             else if (p ≥ 0.5) 
                   回る 
             end 
      end
Calculate the fitness of each search agent
Update X* if there is a better solution 
it=it+1
Update a, A, C, l and p
end while

return X*

10分で実装できそうな簡単なアルゴリズムですね
卒論や修論の比較手法としてどうぞ

実験結果

原著ではいろんな実験をしていますが，ベンチマーク問題の実験だけ抜粋します．

2016年時点での強いアルゴリズムとの比較を行っており，けっこういい成績です．

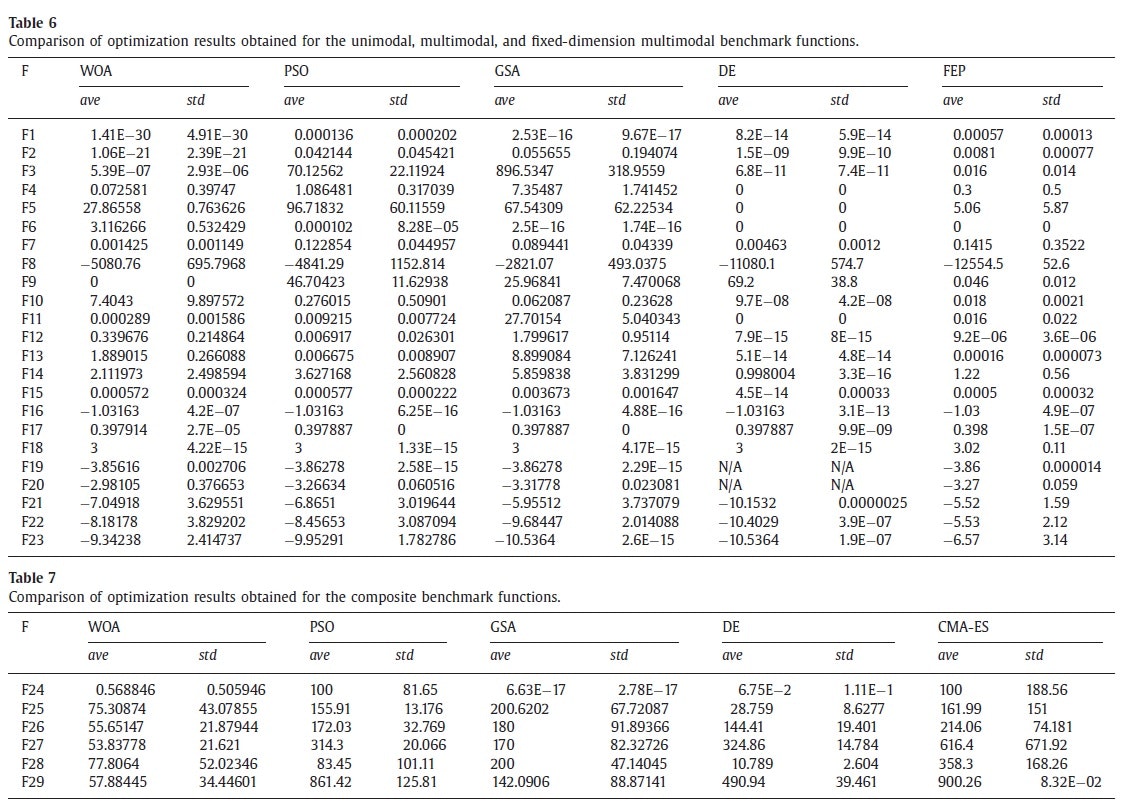
おそらく，回るというランダムウォークでもないし，探索行動でもない動作が，local optimaを脱出するのに効くのだと思います(超個人的な意見)．

ほかにも，いろんな実問題とか，多種多様なアルゴリズムと比較しているので原著見るだけで，最適化に詳しくなります．

暇な人は見るといいでしょう．

おわりに

今回はクジラサンアルゴリズムについて解説しました．
~~よく考えたら，現状の最良解候補を獲物(中心)として扱うのは...共食いでは？~~
この論文のタイトルとInspirationを読んだときは，ネタ度高いなと思いましたが，以降の章はまじめでした．やっぱりネタ度高めるには，いい結果でてないとダメだなと思いました．

Mirjalili, Seyedali, and Andrew Lewis. "The Whale Optimization Algorithm." Advances in engineering software 95 (2016): 51-67. ↩