最適化アルゴリズムを実装していくぞ（コウモリアルゴリズム）

はじめに

最適化アルゴリズムの実装シリーズです。
まずは概要を見てください。

コードはgithubにあります。

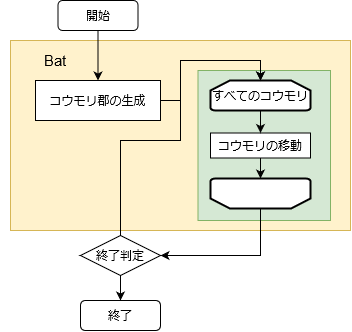
コウモリアルゴリズム

コウモリアルゴリズム(Bat Algorithm)はコウモリが超音波により獲物や障害物の位置を特定する反響定位行動に着目したアルゴリズムです。

コウモリは、速度、周波数、パルス率、音量の4つの要素を踏まえ行動を決めます。

・進化計算アルゴリズム入門 生物の行動科学から導く最適解

• アルゴリズムのフロー

• 用語の対応

問題	コウモリアルゴリズム
入力値の配列	コウモリの位置
入力値	コウモリ
評価値	コウモリの位置における評価値

• コード内で使う変数の意味

変数名	意味	所感
problem	任意の問題のクラス（問題編を参照）
bat_max	コウモリの数
frequency_min	周波数の最低値	最良コウモリへの移動割合の下限値
frequency_max	周波数の最大値	最良コウモリへの移動割合の上限値
good_bat_rate	良いコウモリの割合
volume_init	音量の初期値	音量が大きいほど乱数性が強くなり広域を探索
volume_update_rate	音量の減少率	音量は時間が進むほど小さくなる
pulse_convergence_value	パルス率の収束値	パルス率は良いコウモリの近くへ移動するかの確率、収束値が1だと最終的に移動しなくなる
pulse_convergence_speed	パルス率の収束の速さ	0.5だと10回、0.2だと20回ぐらいで収束する

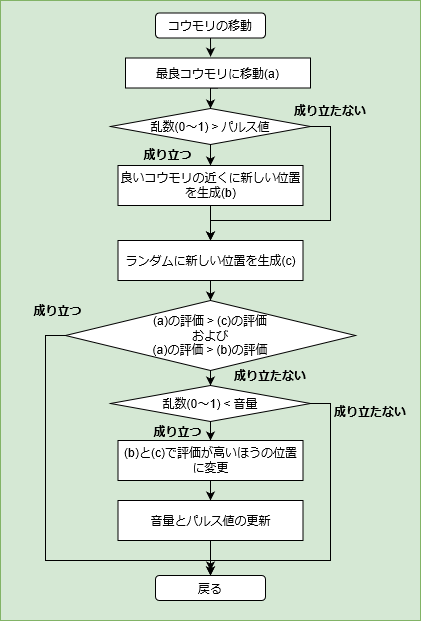
最良コウモリに向かって近づく

最良コウモリへの移動は、最良コウモリの位置と自分の位置の差分と周波数を元に速度を更新し、その速度を使って移動します。

$$
\vec{v_i}(t+1) = \vec{v_i}(t) + f_{req} \bigl( \vec{g}(t) - \vec{x_i}(t) \bigr)
$$

$$
\vec{x_i}(t+1) = \vec{x_i}(t) + \vec{v_i}(t+1)
$$

$\vec{v_i}$ が速度、$\vec{x_i}$が位置、$\vec{g}$ が最良コウモリの位置になります。

また、周波数は下限($f_{min}$)～上限($f_{max}$)の間における乱数となります。

$$
f_{req} = f_{min} + (f_{max} - f_{min}) \times rand[0,1]
$$

import random
import numpy as np

# 周波数
frequency = frequency_min + (frequency_max - frequency_min) * random.random()

pos_best = np.asarray(best_bat.getArray())
pos = np.asarray(bat["bat"].getArray())

# 速度を計算
bat["v"] = bat["v"] + frequency * (pos_best - pos)

# 位置を更新し、新しい位置のコウモリを作成
new_bat1 = problem.create(pos + bat["v"])

良いコウモリの近傍に移動する

良いコウモリへの移動ですが、まずパルス率と乱数を比較し、乱数値以上なら移動をしません。

移動する場合は、まず良いコウモリを選びます。
良いコウモリは全コウモリの内、上位数%のコウモリの中からランダムに選択します。

そして、良いコウモリの近くに移動します。

$$
\vec{x_i}(t+1) = \vec{b}(t) + \bar{A} \vec{\epsilon}
$$

ここで $\bar{A}$ は全コウモリの平均音量、$\vec{\epsilon}$ は-1～1の乱数ベクトルになります。

import random
import numpy as np

new_bat2 = None

# 乱数で良いコウモリの近くに移動
if bat["pulse"] < random.random():

    # ソートする
    bats.sort(key=lambda x: x["bat"].getScore())

    # いいコウモリをランダムに選ぶ
    r = random.randint(1, good_bat_num)
    pos_good = np.asarray(bats[-r]["bat"].getArray())

    # 全コウモリの平均音量
    volume = np.average([x["volume"] for x in self.bats])

    rn = np.random.uniform(-1, 1, len(pos_good))  # -1,1の乱数
    new_pos2 = pos_good + volume * rn
    new_bat2 = problem.create(new_pos2)

更新

パルス率($r_i$)の更新式は以下です。

$$
r_i(t+1) = R_0(1 - \epsilon^{-\gamma t} )
$$

$R_0$ はパルス率の収束値(定数)、$\gamma$ はパルス率の収束の速さ(定数)です。

また、音量($A_i$)の更新式は以下です。

$$
A_i(t+1) = \alpha A_i(t)
$$

$\alpha$ は音量を減少させる割合(定数)です。

更新はアルゴリズムのフロー図通りに更新していきます。

import random

volume_update_rate = 0.9
pulse_convergence_value = 0.5
pulse_convergence_speed = 0.9

def _calcPulse(count):
    return pulse_convergence_value * (1-math.exp(-pulse_convergence_speed*count))

# ランダムに新しい位置を生成
new_bat3 = problem.create()

score1 = new_bat1.getScore()
score2 = None if new_bat2 is None else new_bat2.getScore()
score3 = new_bat3.getScore()

if (score2 is None or score1 > score2) and score1 > score3 :
    # 音量の乱数
    if random.random() < bat["volume"]:
        if score2 is None or score2 <= score3:
            # ランダムな位置で更新
            bat["bat"] = new_bat3
        else:
            # 良いコウモリ付近の位置で更新
            bat["bat"] = new_bat3

        # パルス率の更新
        bat["pulse"] = _calcPulse(step_count)

        # 音量の更新
        bat["volume"] = volume_update_rate * bat["volume"]

    else:
        # 最良コウモリへの位置で更新
        bat["bat"] = new_bat1
else:
    # 最良コウモリへの位置で更新
    bat["bat"] = new_bat1

# ステップカウント+1
step_count += 1

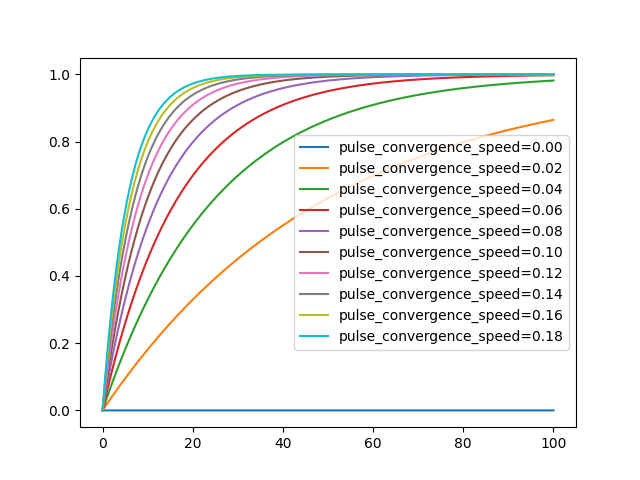
パルス率について

パルス率ですが、収束スピードによって以下のように変化します。(pulse_convergence_value=1の場合)
0.2でも２０回ぐらいで収束と、結構収束するのが早いので小さい値がいいかもしれません。

コード全体

import math
import random

import numpy as np

class Bat():
    def __init__(self,
        bat_max,
        frequency_min=0,
        frequency_max=1,

        good_bat_rate=0.2,
        volume_init=1.0,
        volume_update_rate=0.9,
        pulse_convergence_value=0.5,
        pulse_convergence_speed=0.9,
    ):
        self.bat_max = bat_max
        self.frequency_min = frequency_min
        self.frequency_max = frequency_max

        self.good_bat_num = int(bat_max * good_bat_rate + 0.5)
        if self.good_bat_num > bat_max:
            self.good_bat_num = bat_max
        if self.good_bat_num < 1:
            self.good_bat_num = 1
        self.volume_init = volume_init
        self.volume_update_rate = volume_update_rate
        self.pulse_convergence_value = pulse_convergence_value
        self.pulse_convergence_speed = pulse_convergence_speed


    def init(self, problem):
        self.problem = problem
        self.count = 0

        self.step_count = 0
        self.best_bat = None
        self.bats = []
        for _ in range(self.bat_max):
            o = problem.create()

            d = {
                "bat": o,
                "pulse": self._calcPulse(0),
                "volume": self.volume_init,
                "v": np.zeros(problem.size)
            }
            self.bats.append(d)

            if self.best_bat is None or self.best_bat.getScore() < o.getScore():
                self.best_bat = o

    def _calcPulse(self, count):
        return self.pulse_convergence_value*(1-math.exp(-self.pulse_convergence_speed*count))

    def step(self):
        self.bats.sort(key=lambda x: x["bat"].getScore())

        for bat in self.bats:

            # 周波数
            frequency = self.frequency_min + (self.frequency_max - self.frequency_min) * random.random()

            # 最良のコウモリに近づく
            pos_best = self.best_bat.getArray()
            pos = bat["bat"].getArray()
            bat["v"] = bat["v"] + frequency * (pos_best - pos)
            new_bat1 = self.problem.create(pos + bat["v"])

            # 音量判定
            if random.random() >= bat["volume"]:
                # 新しい位置で更新
                bat["bat"] = new_bat1

                # 最良コウモリチェック
                if self.best_bat.getScore() < bat["bat"].getScore():
                    self.best_bat = bat["bat"]
                continue

            # 乱数で良いコウモリの近くに移動
            new_bat2 = None
            if bat["pulse"] < random.random():

                # 全コウモリの平均音量
                volume = np.average([x["volume"] for x in self.bats])

                # いいコウモリを選ぶ
                r = random.randint(1, self.good_bat_num)
                pos_good = self.bats[-r]["bat"].getArray()

                rn = np.random.uniform(-1, 1, len(pos_good))  # -1,1の乱数
                new_bat2 = self.problem.create(pos_good + volume * rn)

            # ランダムに生成
            new_bat3 = self.problem.create()

            # 新しい位置の比較
            score1 = new_bat1.getScore()
            score2 = None if new_bat2 is None else new_bat2.getScore()
            score3 = new_bat3.getScore()
            if (score2 is None or score1 > score2) and score1 > score3 :
                if score2 is None or score2 <= score3:
                    bat["bat"] = new_bat3
                else:
                    bat["bat"] = new_bat2

                # パルス率の更新
                bat["pulse"] = self._calcPulse(self.step_count)

                # 音量の更新
                bat["volume"] = self.volume_update_rate * bat["volume"]
            else:
                bat["bat"] = new_bat1

            # 最良コウモリチェック
            if self.best_bat.getScore() < bat["bat"].getScore():
                self.best_bat = bat["bat"]

        self.step_count += 1

ハイパーパラメータ例

各問題に対して optuna でハイパーパラメータを最適化した結果です。
最適化の1回の試行は、探索時間を2秒間として結果を出しています。
これを100回実行し、最適なハイパーパラメータを optuna に探してもらいました。
※frequency_minは0で固定しています

問題	bat_max	frequency_max	frequency_min	good_bat_rate	pulse_convergence_speed	pulse_convergence_value	volume_init	volume_update_rate
EightQueen	21	0.16056311709148877	0.0	0.18895324827898902	0.7743073337572011	0.015299647553258189	0.37862199762341764	0.5219340167573981
function_Ackley	6	0.5807409179883148	0.0	0.8431315762963505	0.6168807797723693	0.41730375451852453	0.41343060460565206	0.15049946819845028
function_Griewank	8	0.9452402185165402	0.0	0.7201234515965615	0.7260546767194784	0.130926854366477	0.013897440965911972	0.018889941226347226
function_Michalewicz	49	0.4179217659403093	0.0	0.6361175345153247	0.5018316263776195	0.42459903007426236	0.4968382725357193	0.1065841508592828
function_Rastrigin	4	0.6140740614258697	0.0	0.08321822782531468	0.37791620723418984	0.5942334579901081	0.2272362640804505	0.6090017290739149
function_Schwefel	5	0.9974629382587714	0.0	0.48057178703432885	0.017850539098788976	0.8624933090356682	0.008382588455720222	0.9676085790533966
function_StyblinskiTang	9	0.9919883606063762	0.0	0.3096861786862085	0.6695497098867679	0.8832509763124465	1.3802416508441109	0.24307207412221196
LifeGame	17	0.17520950919099773	0.0	0.5512117484751708	0.3239752160390367	0.5877290654832432	0.6901442886406529	0.7052284742486757
OneMax	47	0.4118670851332011	0.0	0.4420165018547974	0.1217770472809899	0.8862495030963856	1.0185236105175342	0.5188797824478796
TSP	8	0.44386885244368085	0.0	0.19840772635097428	0.24715859136402973	0.3995313116893353	0.40899114232584255	0.00012730831532623

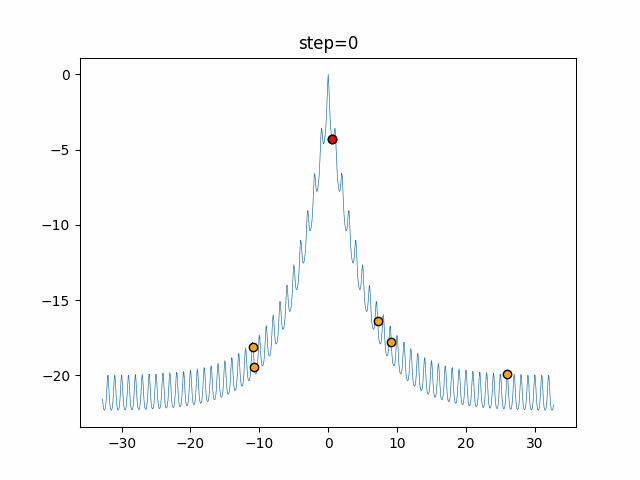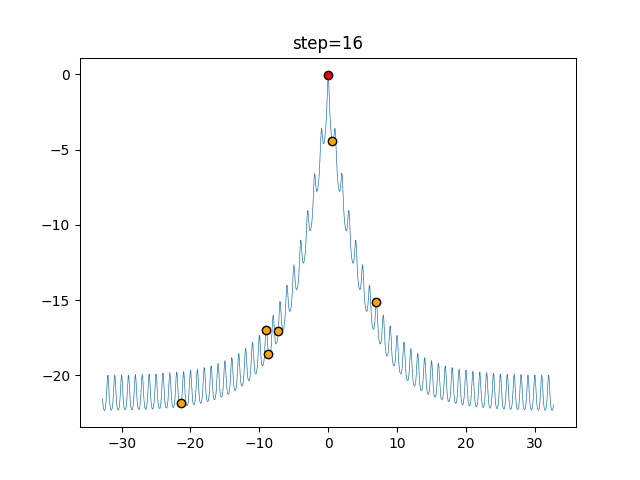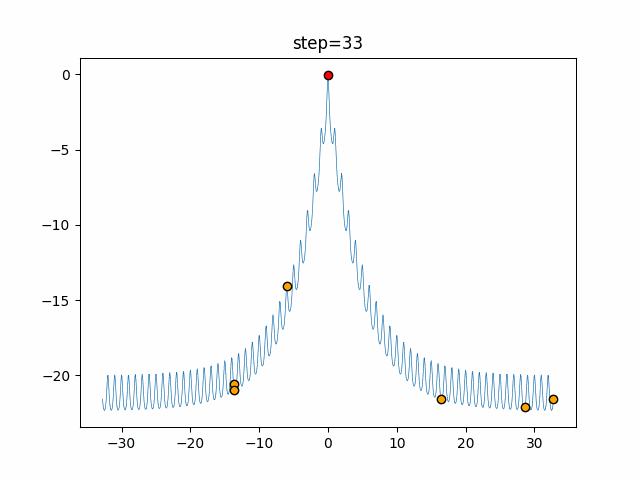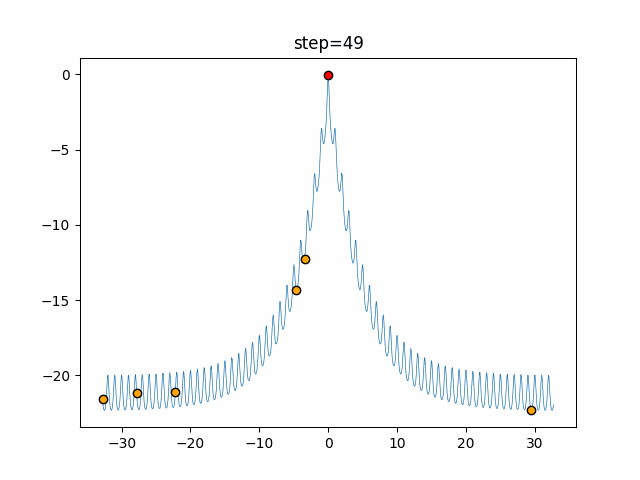
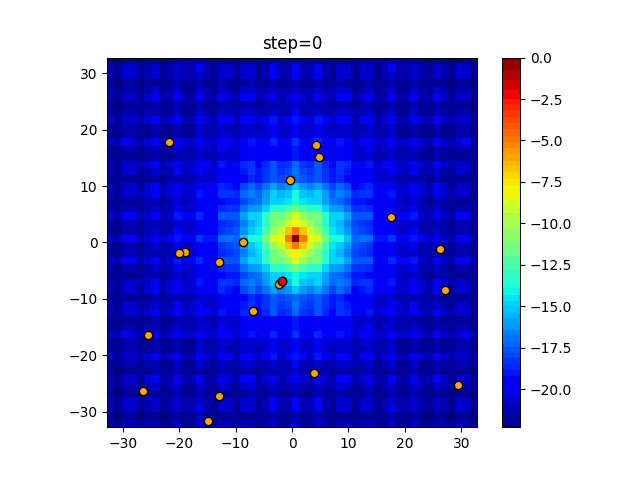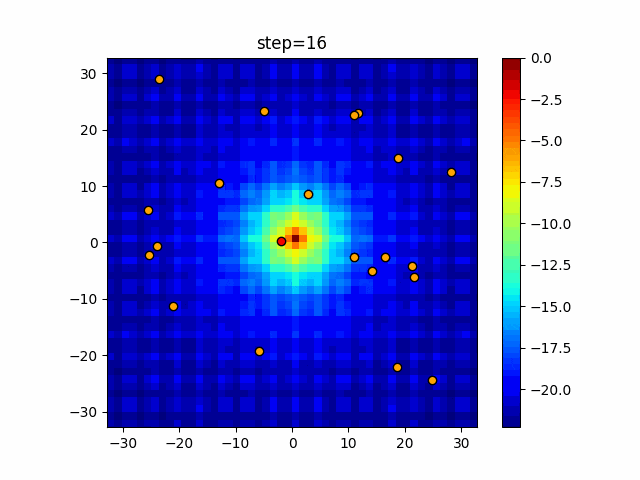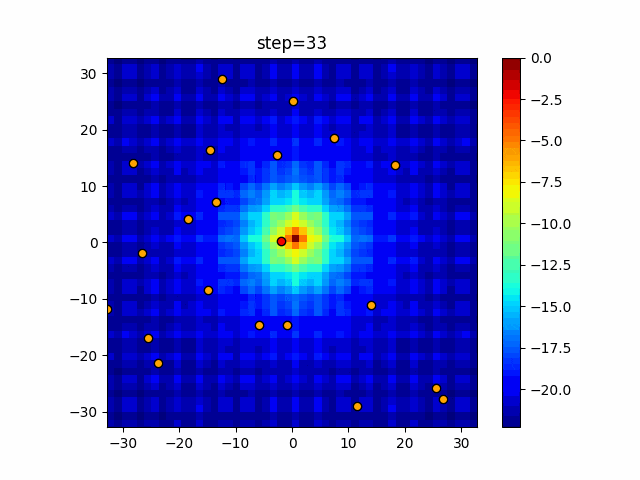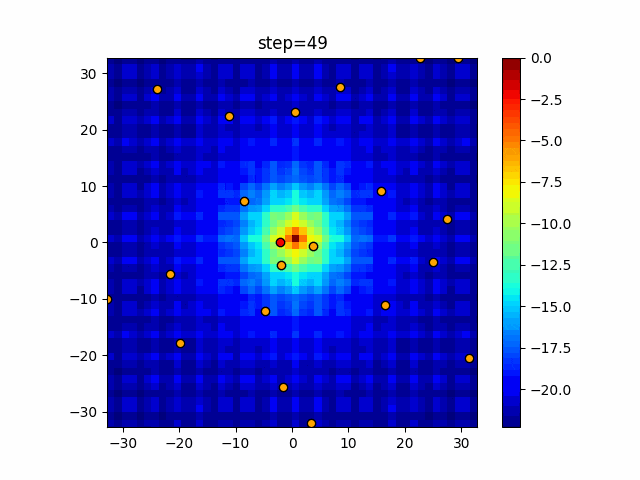
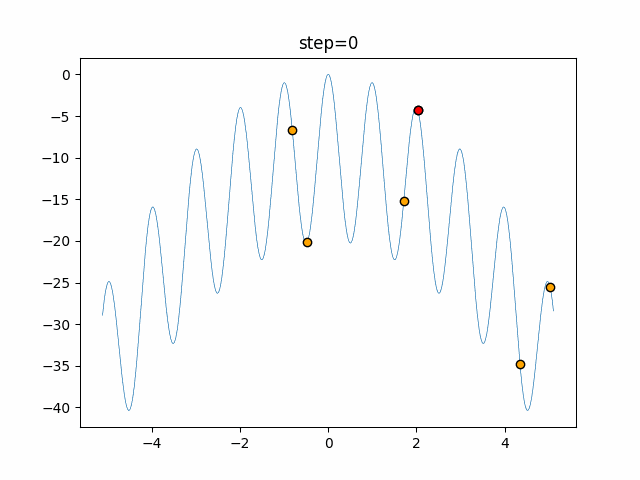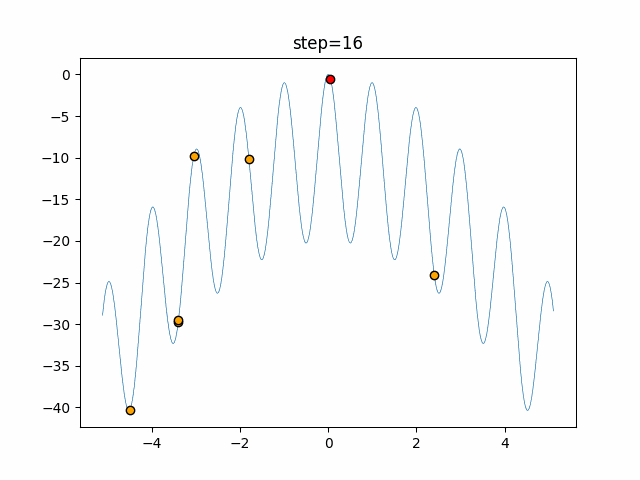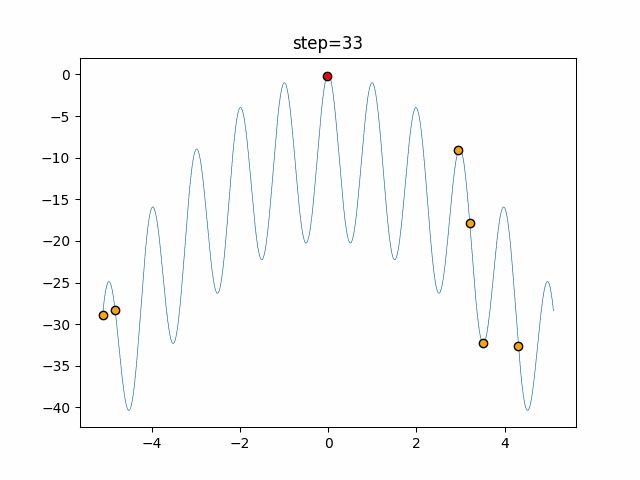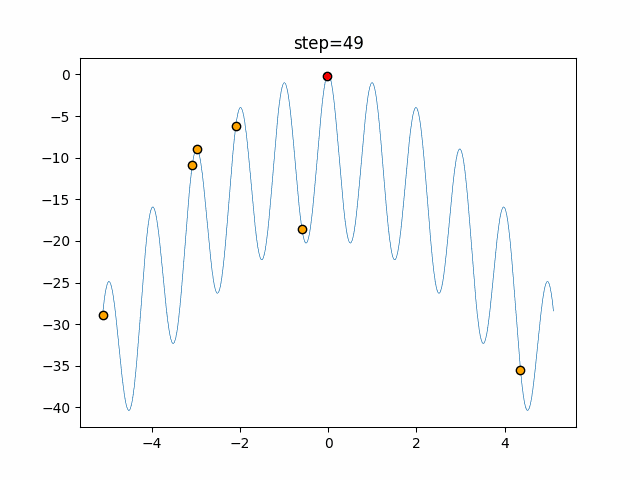
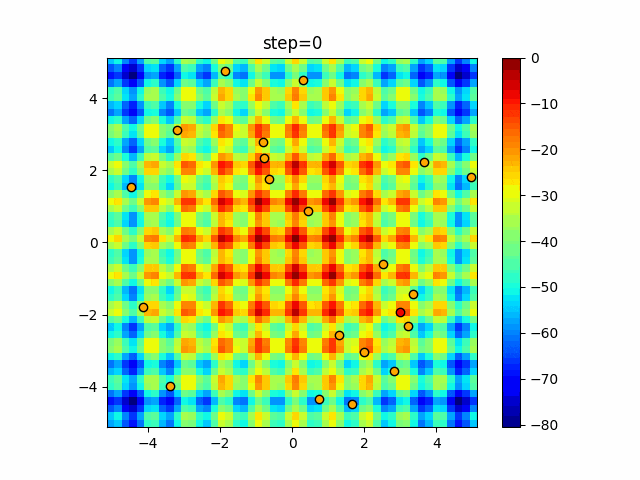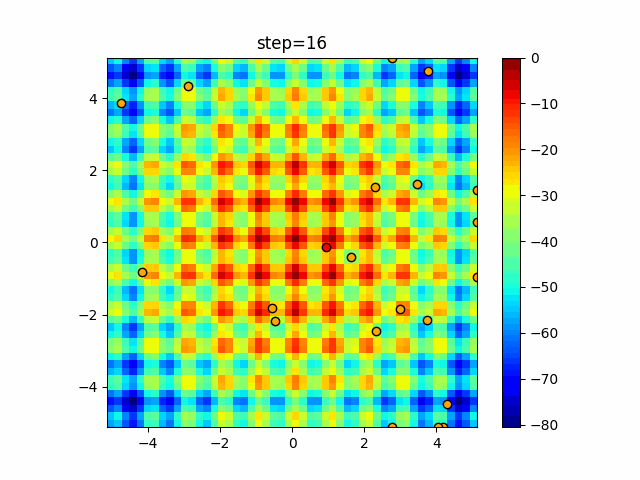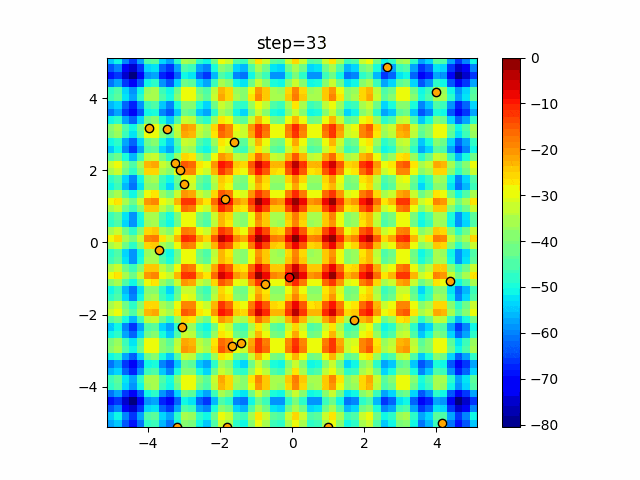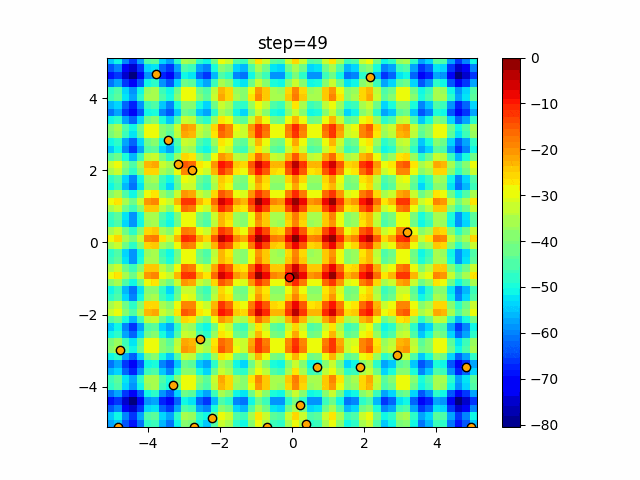
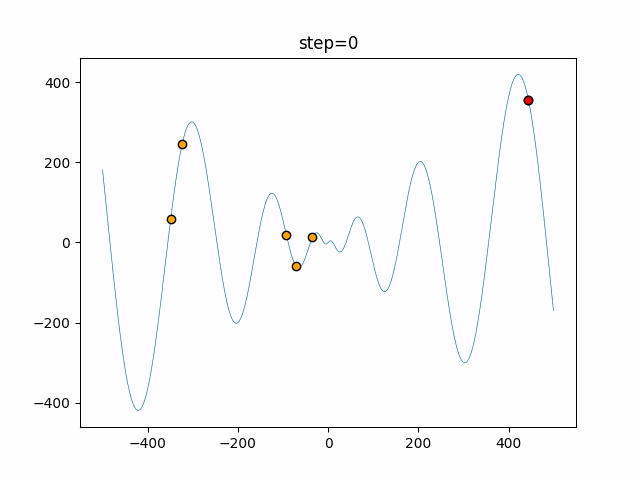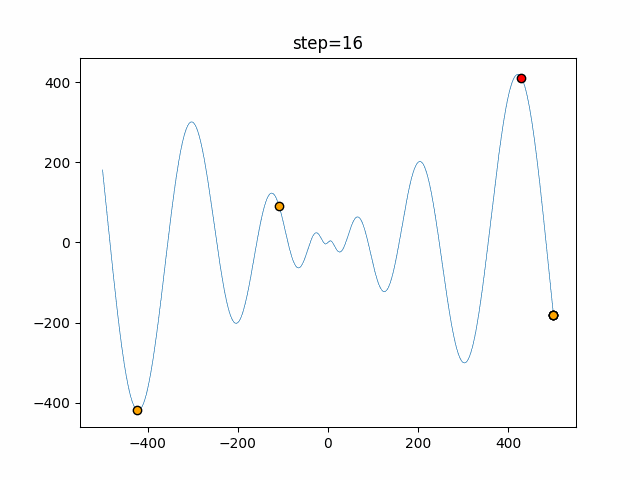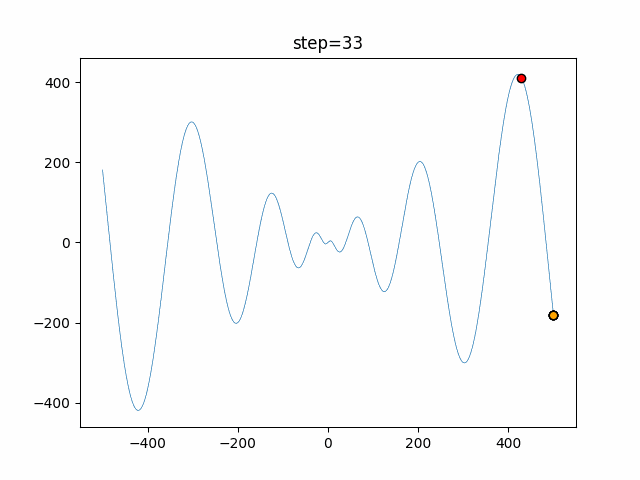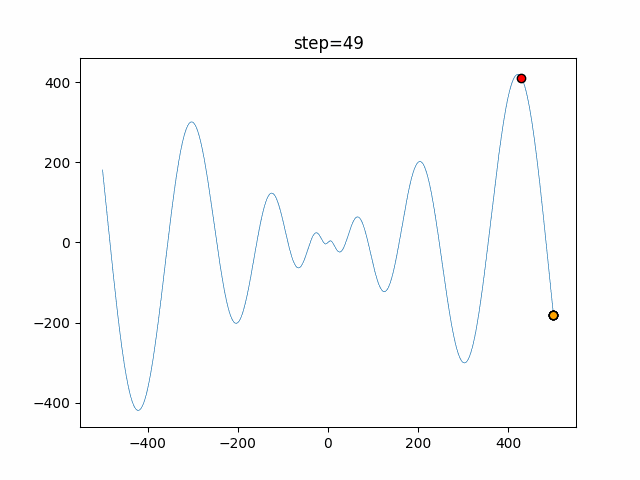
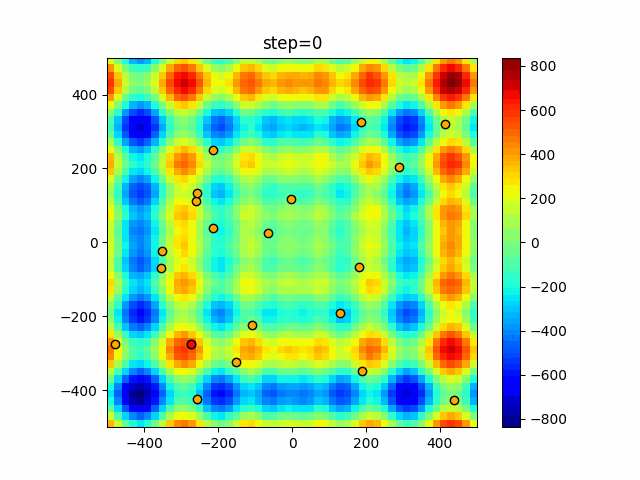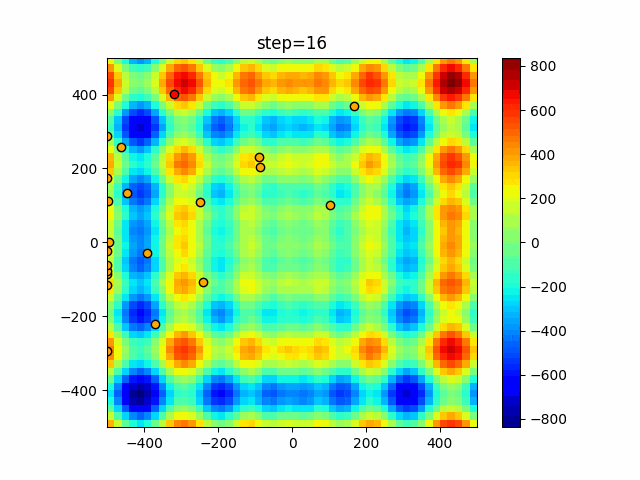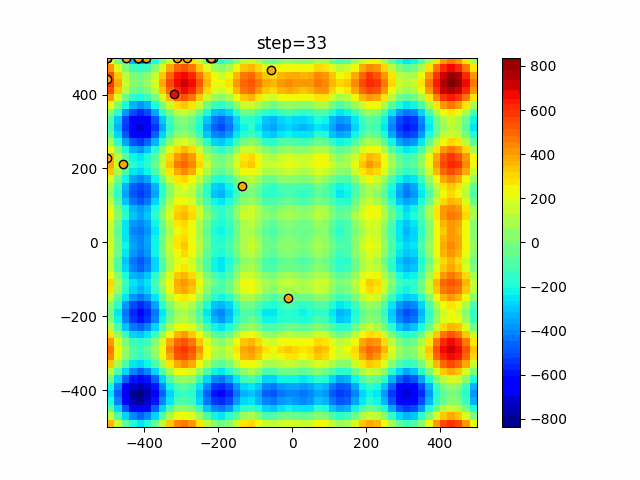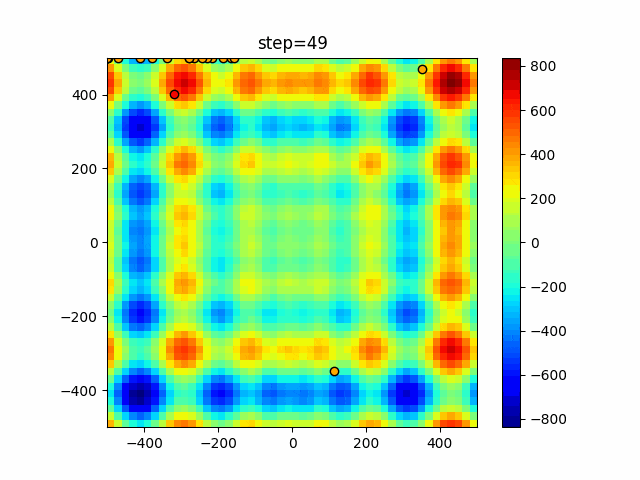
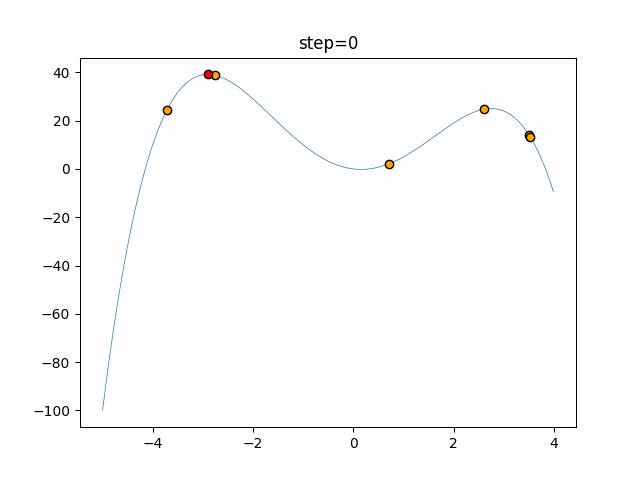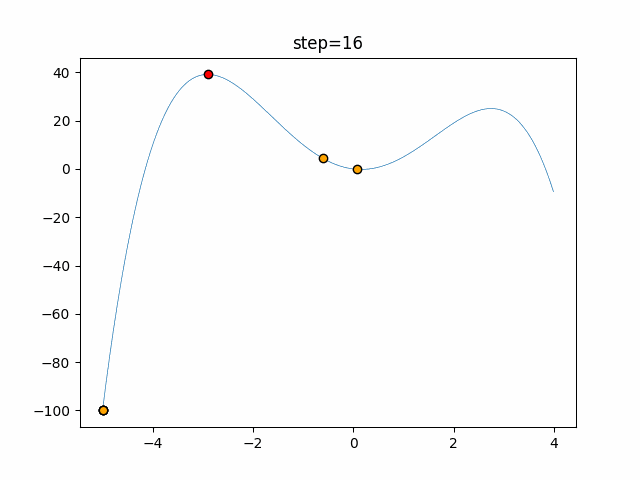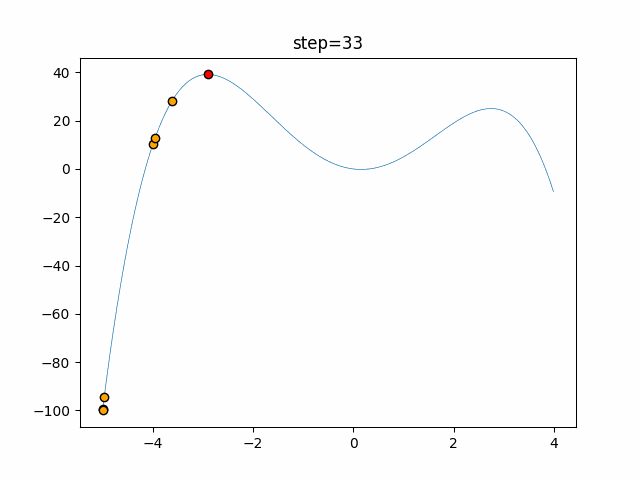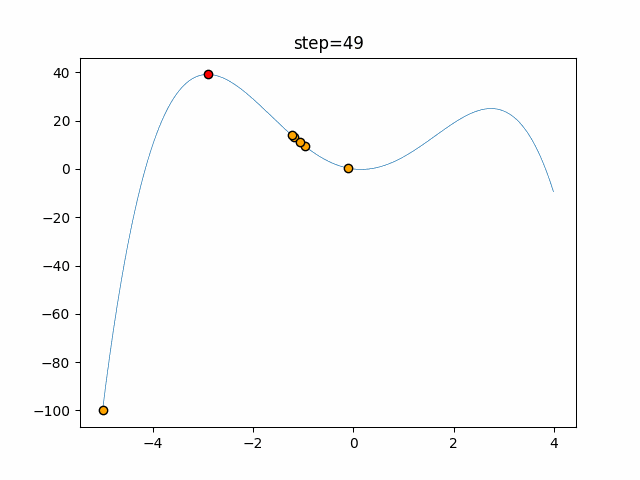
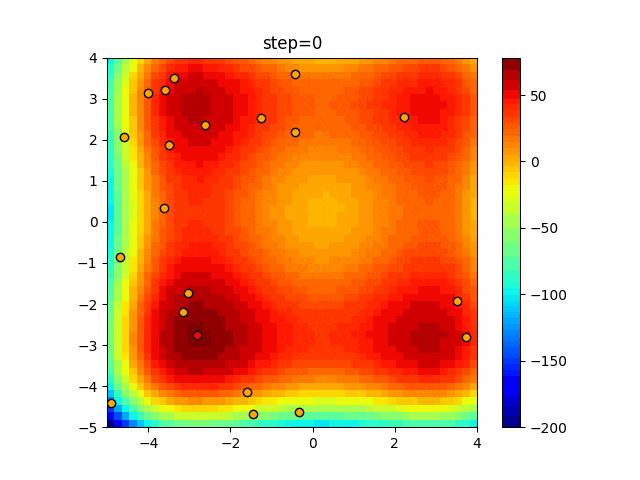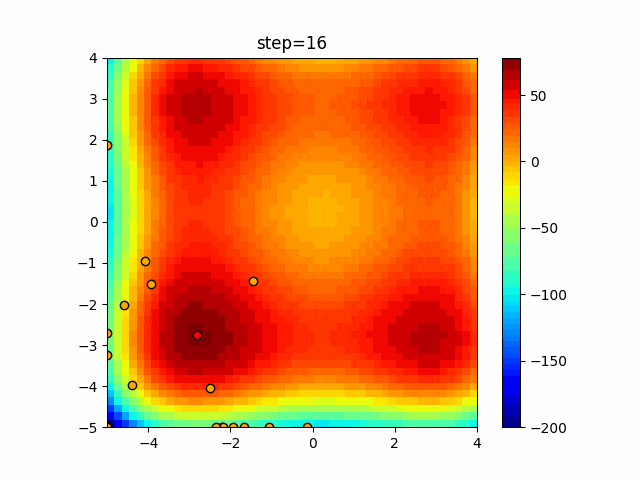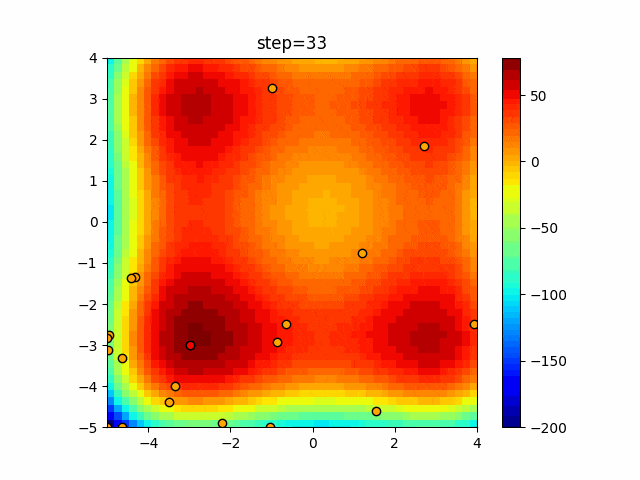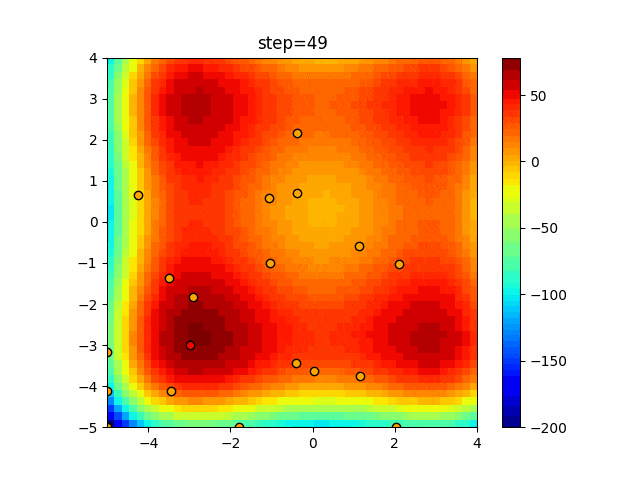
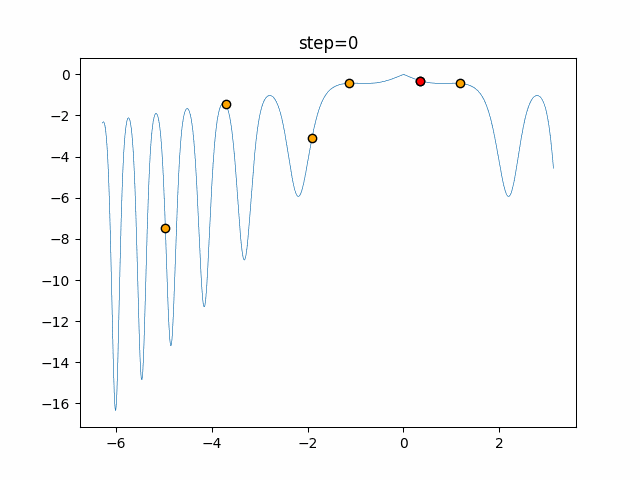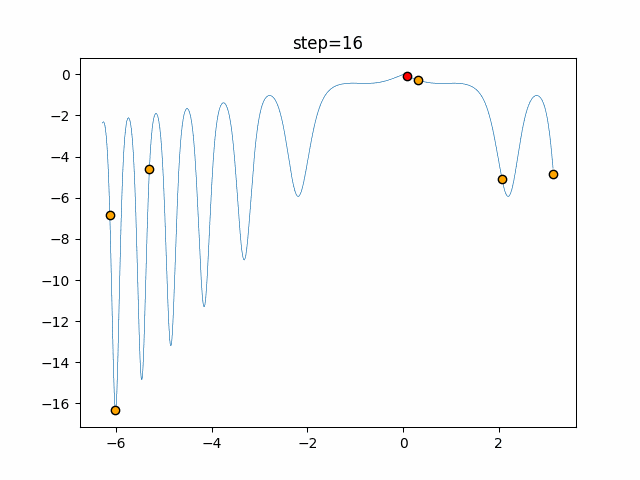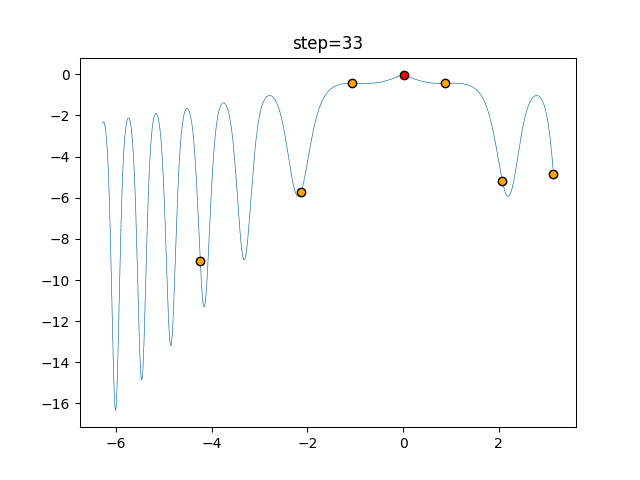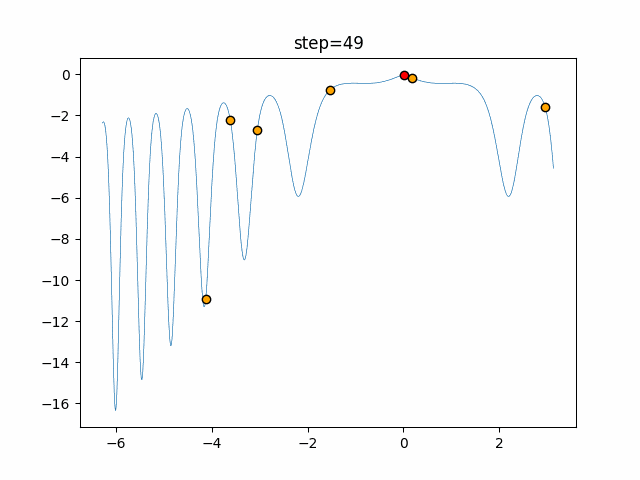
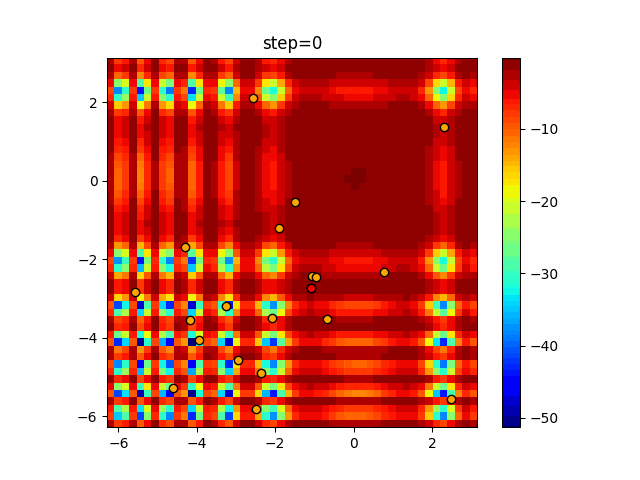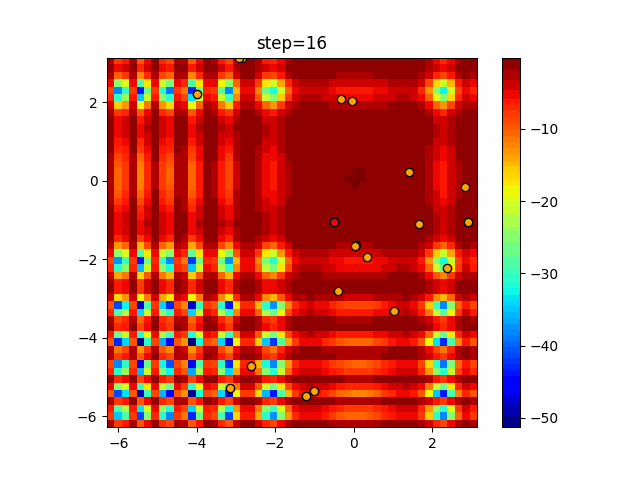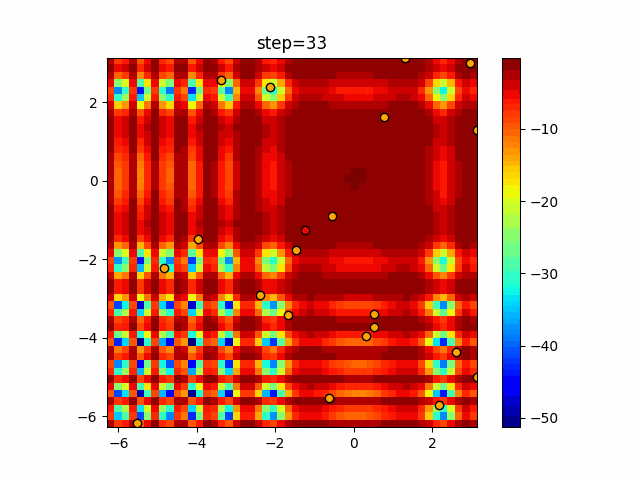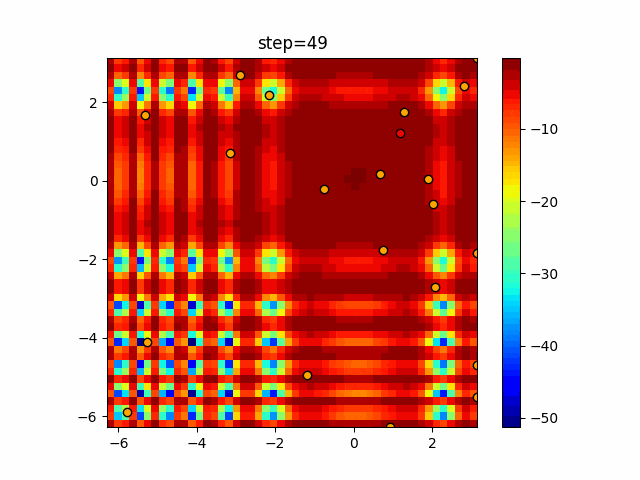
実際の動きの可視化

1次元は6個体、2次元は20個体で50step実行した結果です。
赤い丸がそのstepでの最高スコアを持っている個体となります。

パラメータは以下で実行しました。

Bat(N, frequency_min=0, frequency_max=0.05, good_bat_rate=0.1, volume_init=0.5, pulse_convergence_value=0.9, pulse_convergence_speed=0.1)  

function_Ackley

• 1次元

• 2次元

function_Rastrigin

• 1次元

• 2次元

function_Schwefel

• 1次元

• 2次元

function_StyblinskiTang

• 1次元

• 2次元

function_XinSheYang

• 1次元

• 2次元

あとがき

近傍に移動した後に速度が残ったままになるので、それで広域を探索している感じがします。
また、速度が基本残ったままになるので後半ほど移動がすごいおおざっぱになるような…。
ハイパーパラメータの調整が結構シビアかもしれません。