最適化アルゴリズムを実装していくぞ（タブーサーチ）

はじめに

最適化アルゴリズムの実装シリーズです。
まずは概要を見てください。

コードはgithubにあります。

タブーサーチ

概要

タブーサーチ(Tabu Search)は人工知能の概念に基づいた局所探索法を一般化した手法らしいです。

参考
・タブーサーチ
・タブー探索法
・入門タブー探索法

アルゴリズム

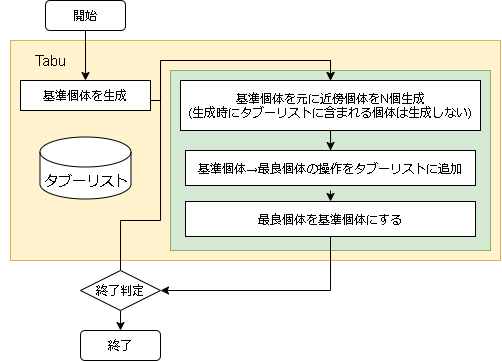
• アルゴリズムのフロー

• 用語の対応

問題	タブーサーチ
問題への入力	個体の座標
評価値	個体の評価値

• ハイパーパラメータに関して

変数名	意味	備考
individual_max	生成する近傍の数
epsilon	近傍を生成する際の各成分の変更確率
tabu_list_size	タブーリストのサイズ
tabu_range_rate	タブーとする範囲の割合(問題が取りうる値を基準)

タブーリスト

タブーリストは基準個体の遷移が局所解でループしないように設定するリストです。
このリストにある遷移を一定時間しない(リストから消えるまで)ことで局所解のループから脱出する事を目的としています。

タブーリストの記載方法は解自体を記述する方法と、遷移を記述する方法があるようですが、遷移を記述する方法を実装しています。
また、遷移で判断する値は実数値となるので、以下のように問題が取りうる値の割合($R$, tabu_range_rate)で指定できるようにしました。

$$ X_{range} = R (Prob_{max} - Prob_{min})$$

tabu_range = tabu_range_rate * (problem.MAX_VAL - problem.MIN_VAL)

# 判定する場合
if tabu_val - tabu_range < val and val < tabu_val + tabu_range:
    タブーリストに該当
else:
    タブーリストに該当しない

近傍の生成

近傍の生成に決まった方法はなく、問題に依存するところが大きいようです。

本記事では各成分をε-greedy法でランダムに変更する方法にしました。
また、1要素は必ず変更するようにしています。

pos = individual.getArray()  # 基準個体の座標
ri = random.randint(0, len(pos))  # 1成分は必ず変更
for i in range(len(pos)):
    if i == ri or random.random() < epsilon:
        # ランダムな値に変更
        pos[i] = problem.randomVal()

コード全体

import math
import random

class Tabu():
    def __init__(self, 
        individual_max,
            epsilon=0.1,
            tabu_list_size=100,
            tabu_range_rate=0.1,
        ):
        self.individual_max = individual_max

        self.epsilon = epsilon
        self.tabu_list_size = tabu_list_size
        self.tabu_range_rate = tabu_range_rate


    def init(self, problem):
        self.problem = problem

        # タブー判定の範囲
        self.tabu_range = (problem.MAX_VAL - problem.MIN_VAL) * self.tabu_range_rate

        # タブーリスト
        self.tabu_list = []

        # 初期個体の生成
        self.best_individual = problem.create()
        self.individuals = [self.best_individual]


    def step(self):

        # 基準となる個体(前stepの最良個体)
        individual = self.individuals[-1]

        # 個体数が集まるまで近傍を生成
        next_individuals = []
        for _ in range(self.individual_max*99):  # for safety
            if len(next_individuals) >= self.individual_max:
                break
            
            # 近傍の座標を生成
            pos = individual.getArray()
            ri = random.randint(0, len(pos))  # 1成分は必ず変更
            trans = []  # タブーリスト用
            for i in range(len(pos)):
                if i == ri or random.random() < self.epsilon:
                    # ランダムな値に変更
                    val = self.problem.randomVal()
                    trans.append((i, pos[i]-val))  # 変更内容を保存
                    pos[i] = val
            
            # タブーリストにある遷移は作らない
            if self._isInTabuList(trans):
                continue
            
            # 近傍を生成
            o = self.problem.create(pos)
            # ソートしたいので個体と変更内容を保存
            next_individuals.append((o, trans))

        # 近傍が0なら新しく生成する
        if len(next_individuals) == 0:
            o = self.problem.create()
            if self.best_individual.getScore() < o.getScore():
                self.best_individual = o
            self.individuals = [o]
            return

        # sort
        next_individuals.sort(key=lambda x: x[0].getScore())

        # 次のstep用に保存
        self.individuals = [x[0] for x in next_individuals]

        # このstepでの最良個体
        step_best = next_individuals[-1][0]
        if self.best_individual.getScore() < step_best.getScore():
            self.best_individual = step_best
        
        # タブーリストに追加
        step_best_trans = next_individuals[-1][1]
        self.tabu_list.append(step_best_trans)
        if len(self.tabu_list) > self.tabu_list_size:
            self.tabu_list.pop(0)


    def _isInTabuList(self, trans):
        for tabu in self.tabu_list:
            # 個数が違えば違う
            if len(tabu) != len(trans):
                continue
            
            f = True
            for i in range(len(trans)):
                # 対象要素が違えば違う
                if tabu[i][0] != trans[i][0]:
                    f = False
                    break
                # 範囲内じゃないなら非該当
                tabu_val = tabu[i][1]
                val = trans[i][1]
                if not(tabu_val - self.tabu_range < val and val < tabu_val + self.tabu_range):
                    f = False
                    break

            # 該当するものがある
            if f:
                return True

        return False

ハイパーパラメータ例

各問題に対して optuna でハイパーパラメータを最適化した結果です。
最適化の1回の試行は、探索時間を5秒間として結果を出しています。
これを100回実行し、最適なハイパーパラメータを optuna に探してもらいました。

問題	epsilon	individual_max	tabu_list_size	tabu_range_rate
EightQueen	0.011151919824816751	24	33	0.003497750329001216
function_Ackley	0.000110909916091936	18	146	0.0032544838729771236
function_Griewank	0.0012284413321756848	48	6	0.8866006526200017
function_Michalewicz	0.0005626187277017018	42	300	0.7351059491323495
function_Rastrigin	0.00022273162093360693	29	15	0.03345590467119916
function_Schwefel	0.00010033345050305172	49	10	0.4450495107614175
function_StyblinskiTang	0.0019068533760369163	50	16	0.5646323547501031
function_XinSheYang	0.0005997343899621366	47	295	0.001967269783955519
g2048	0.9996213921785719	12	22	0.014073734875355126
LifeGame	0.0066786013632043895	25	259	0.6435199139608611
OneMax	0.00046850780076445296	19	60	0.9692455801618902
TSP	0.0006803511143661416	31	20	0.5199790701315284

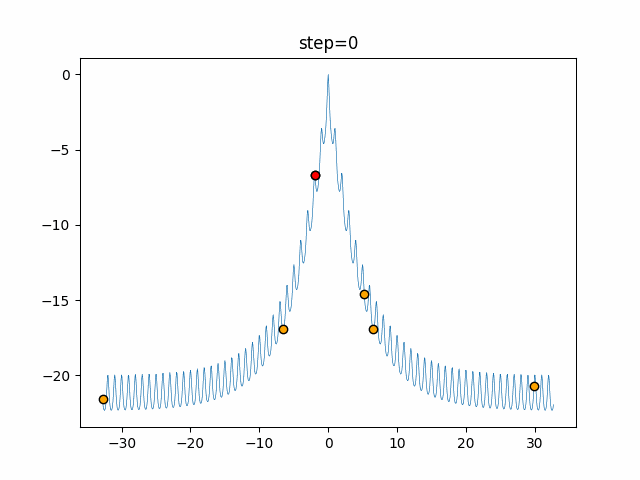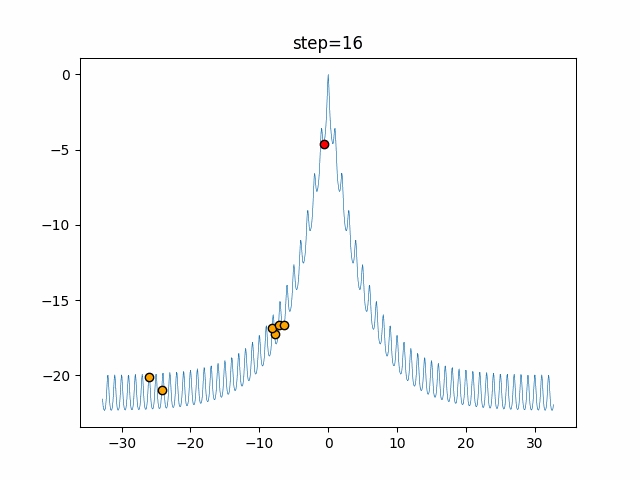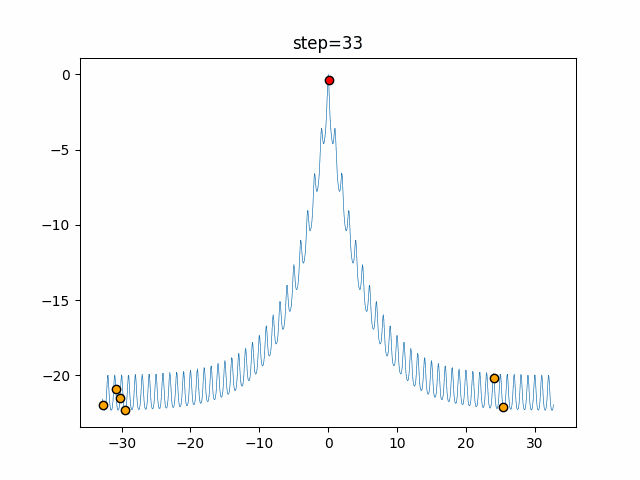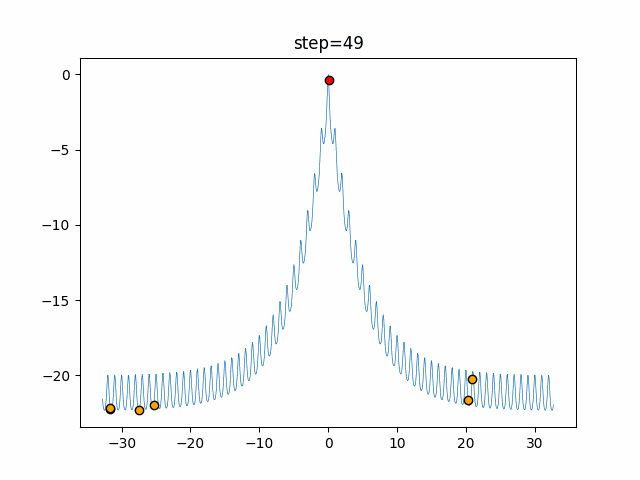
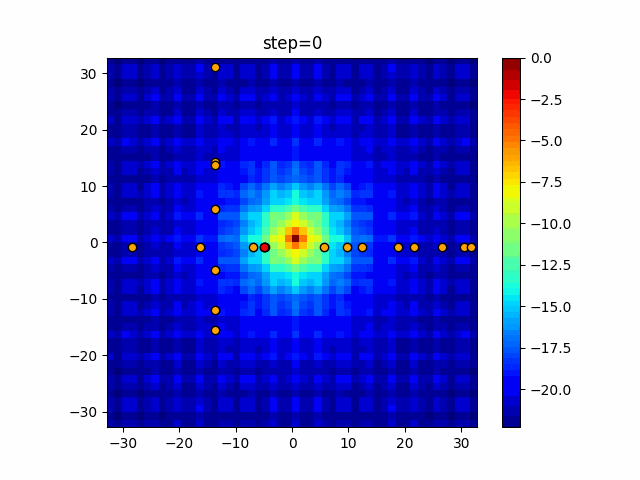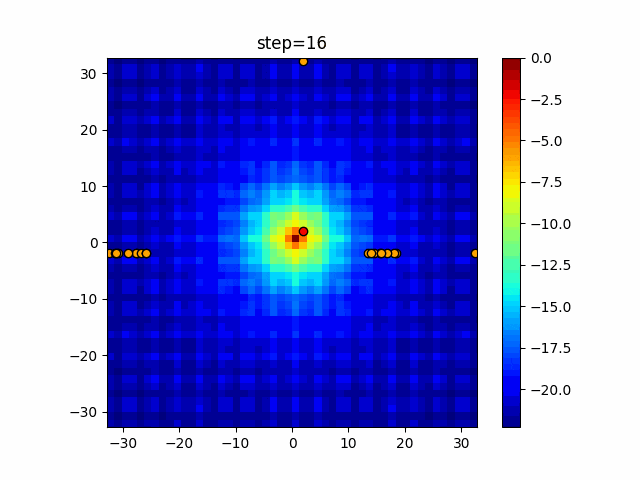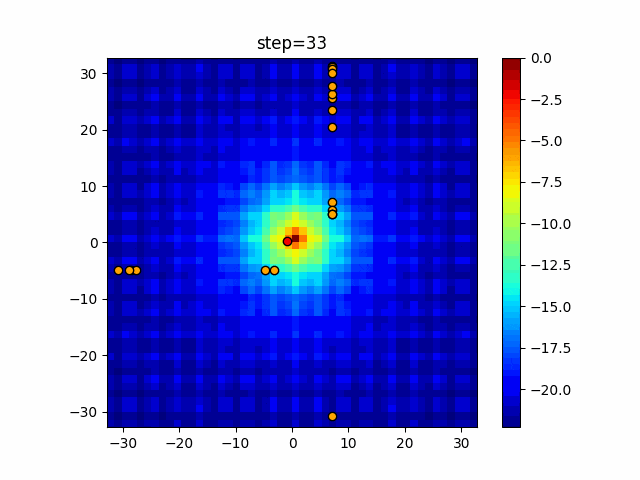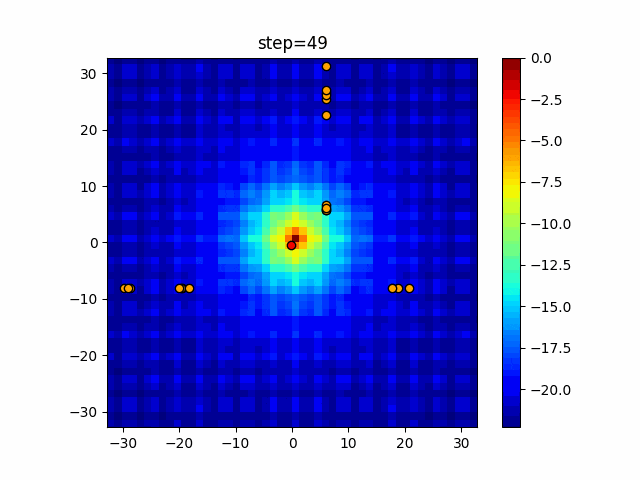
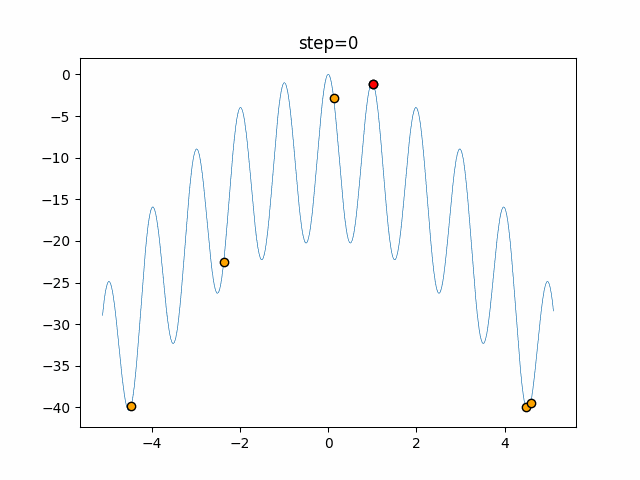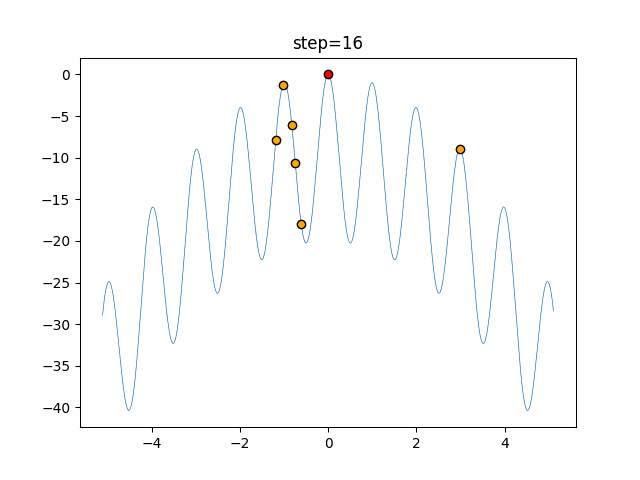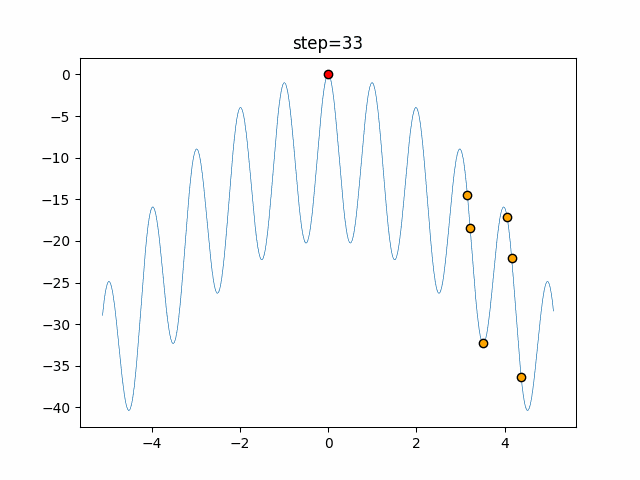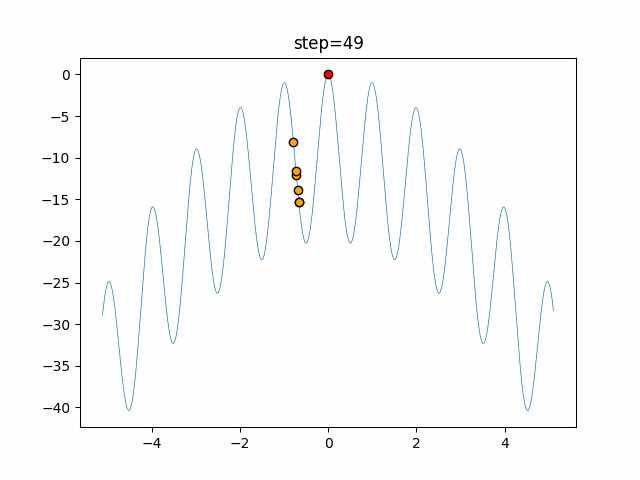
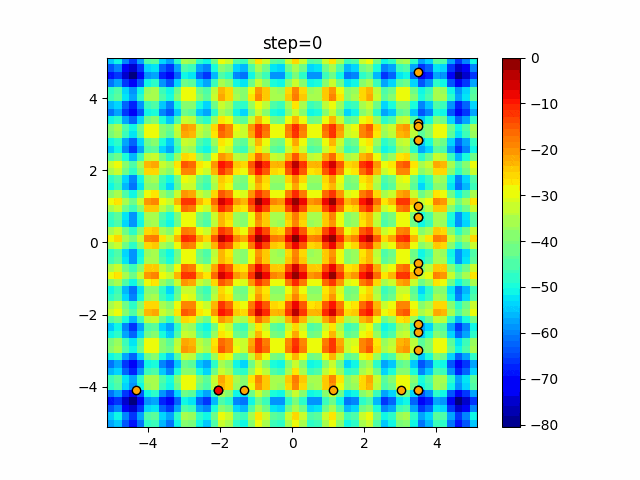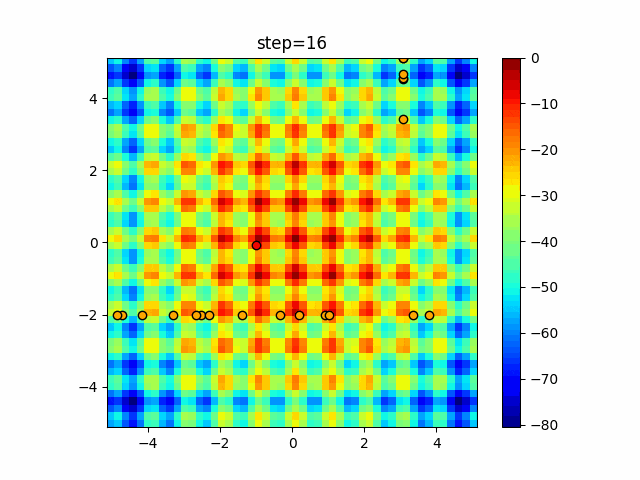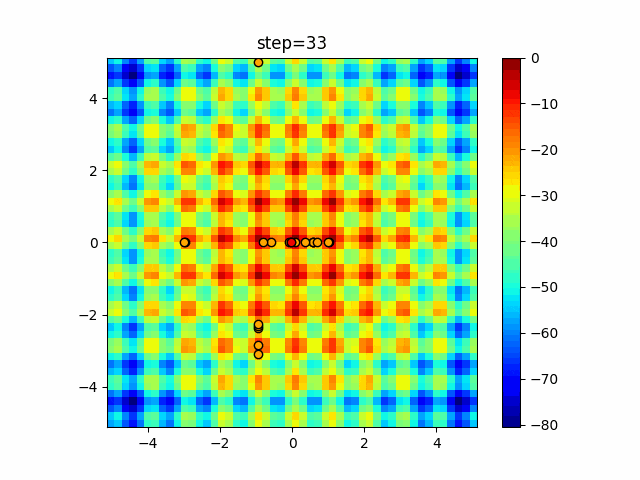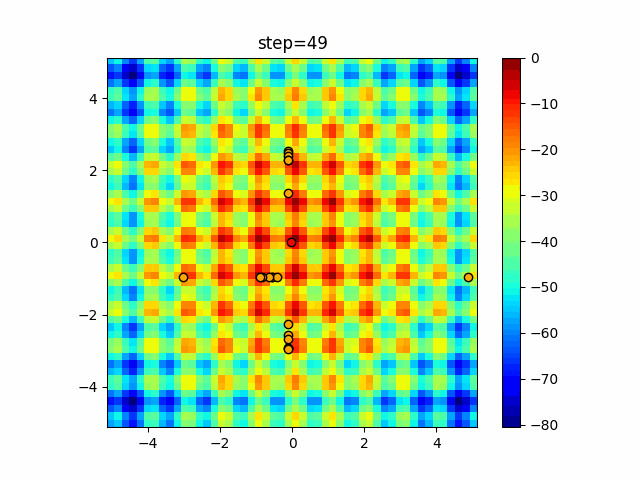
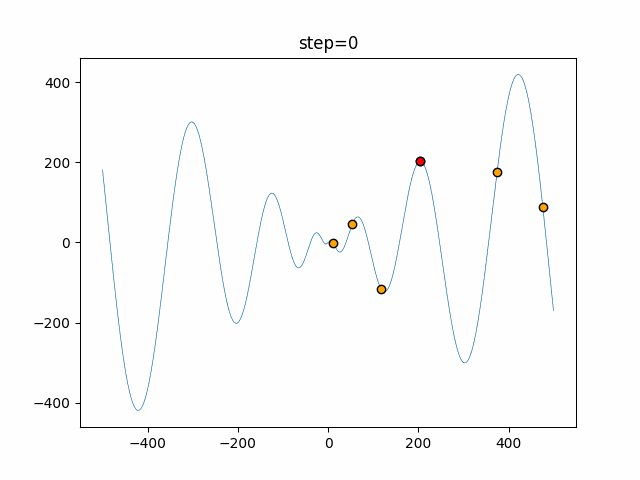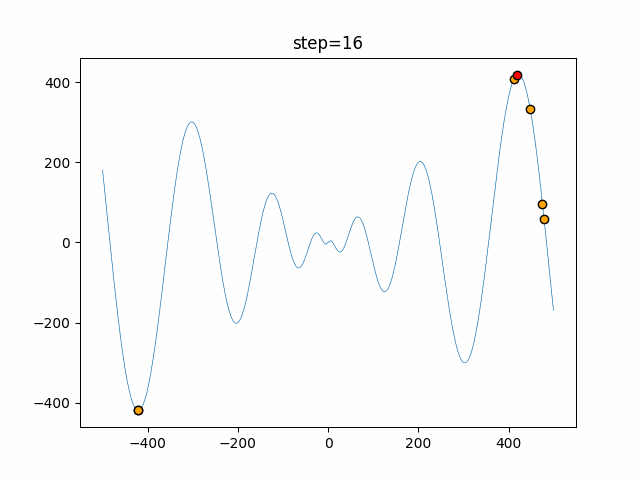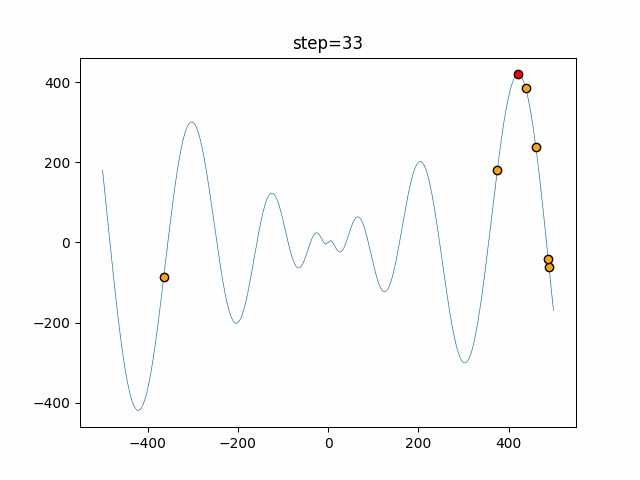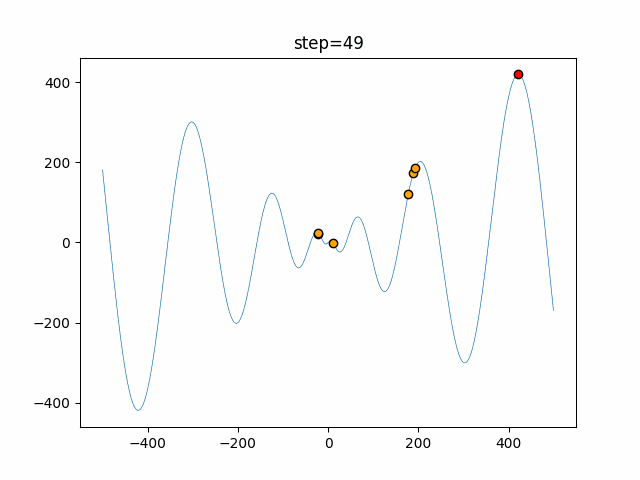
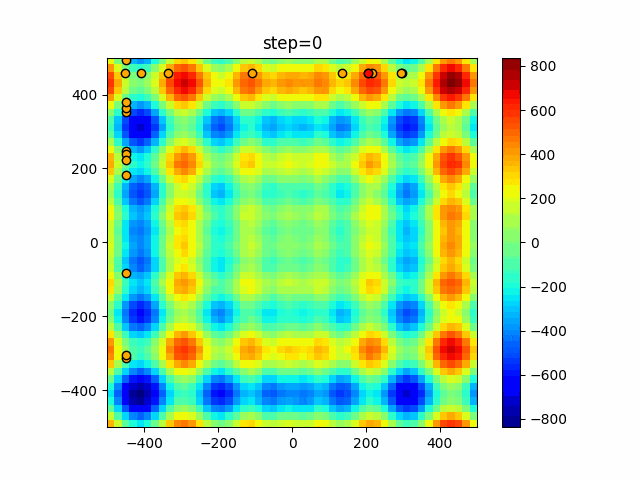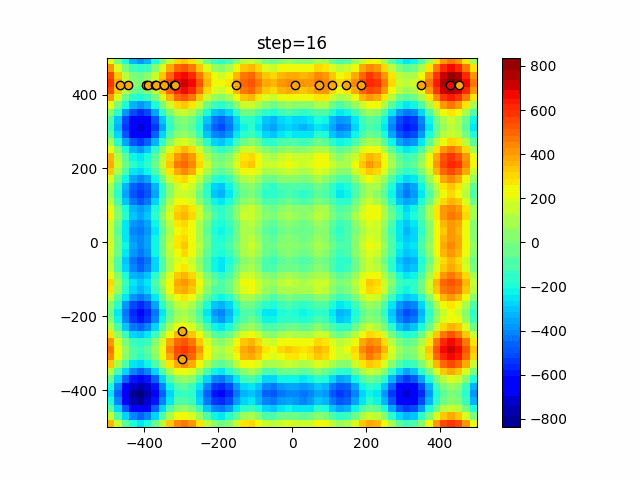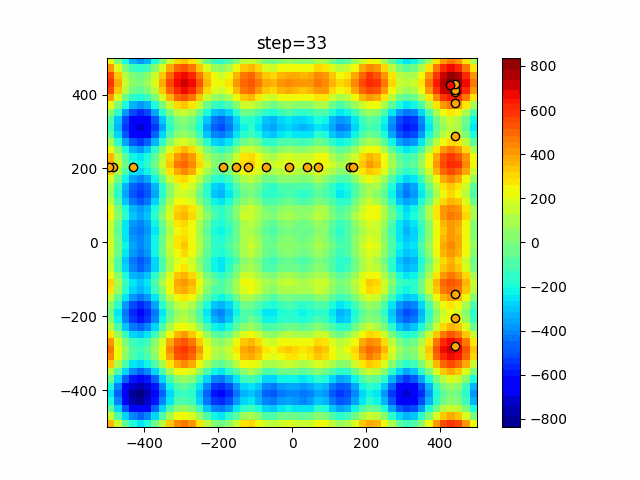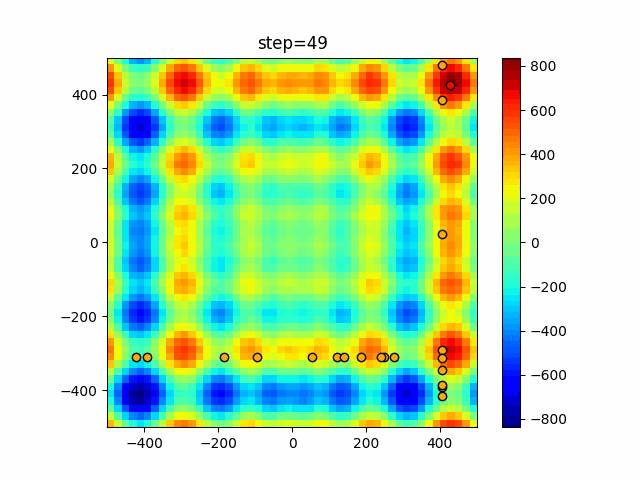
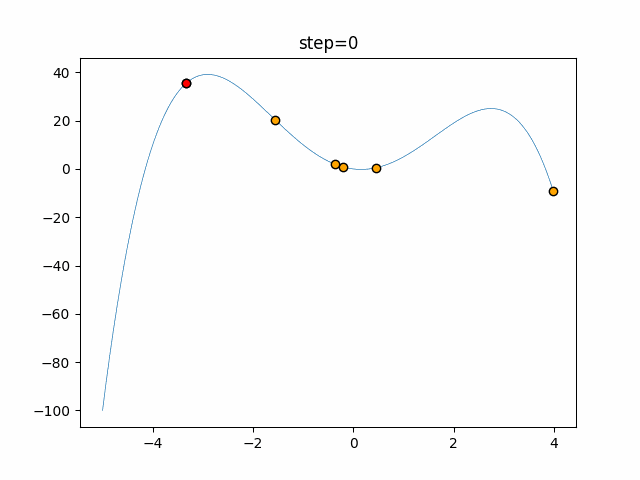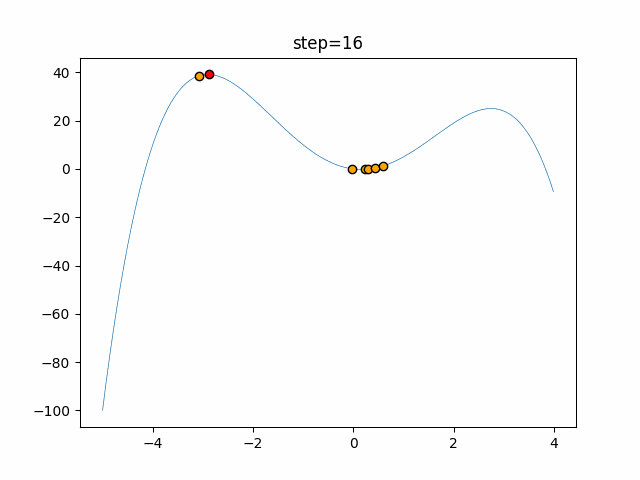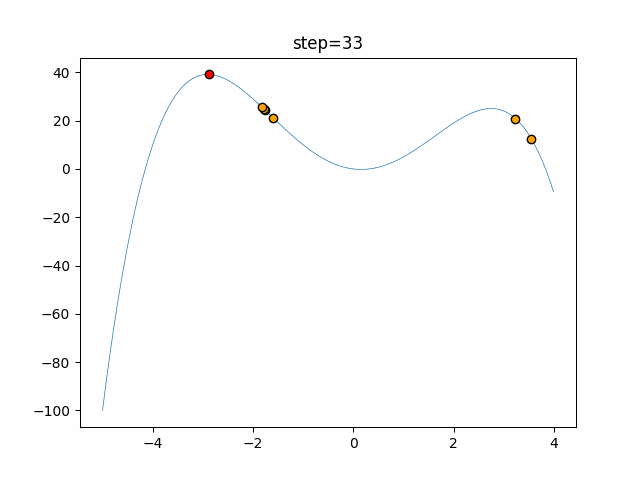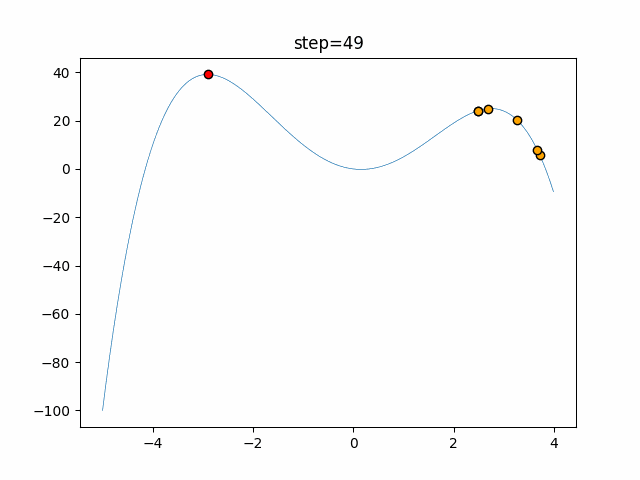
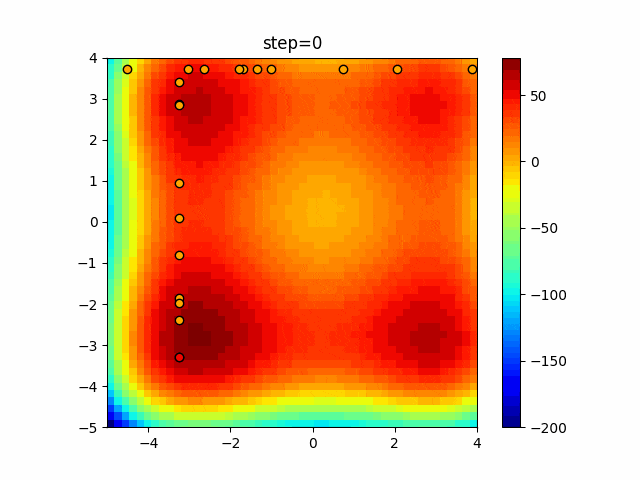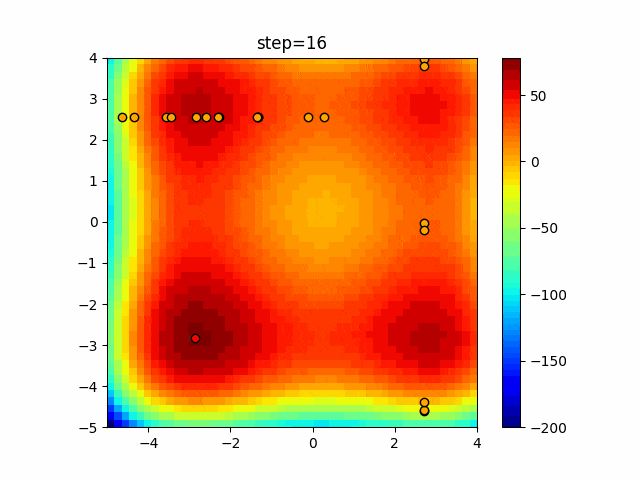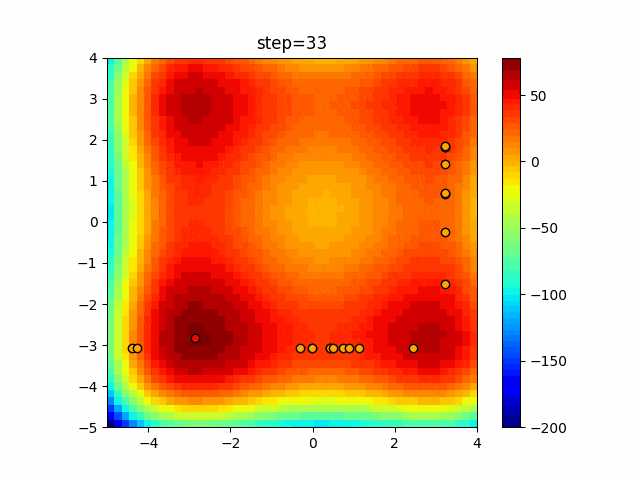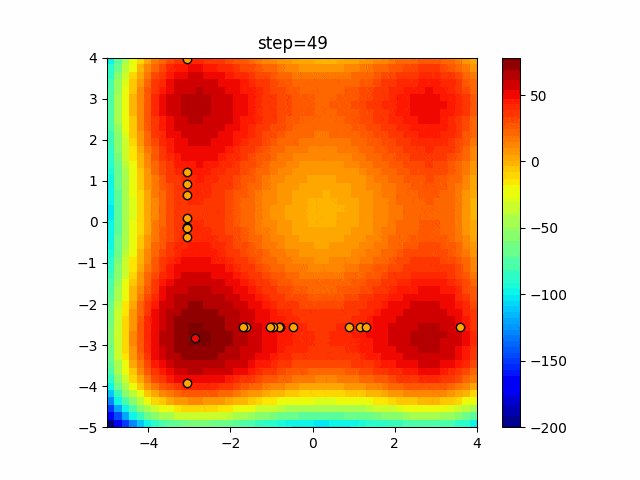
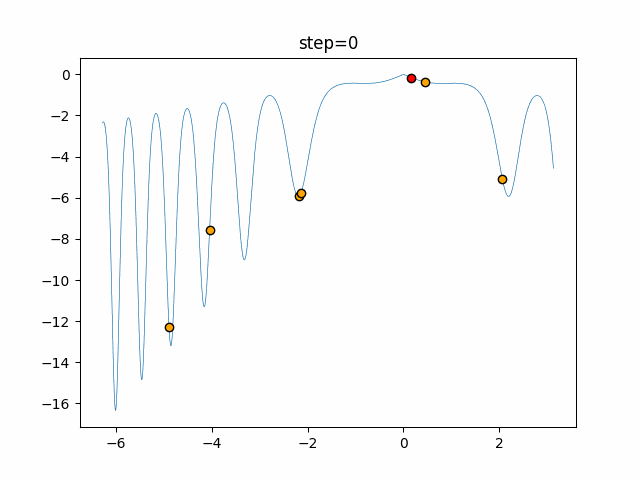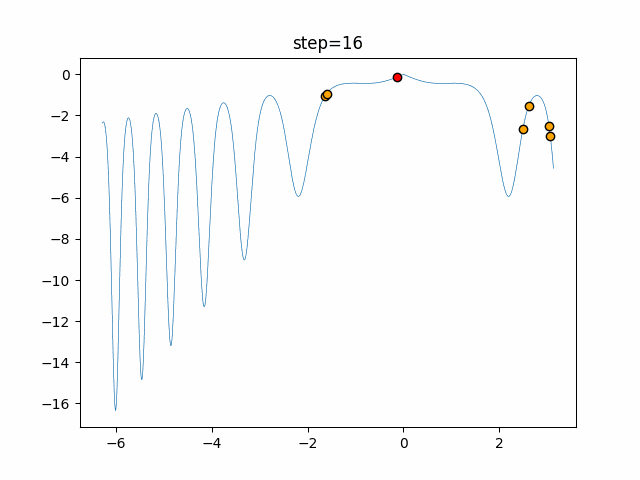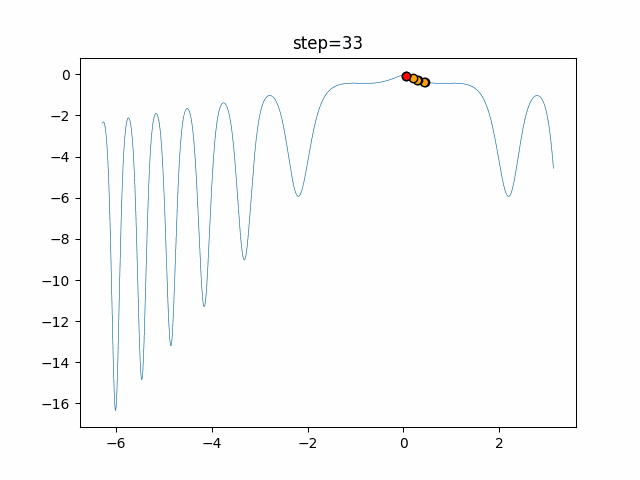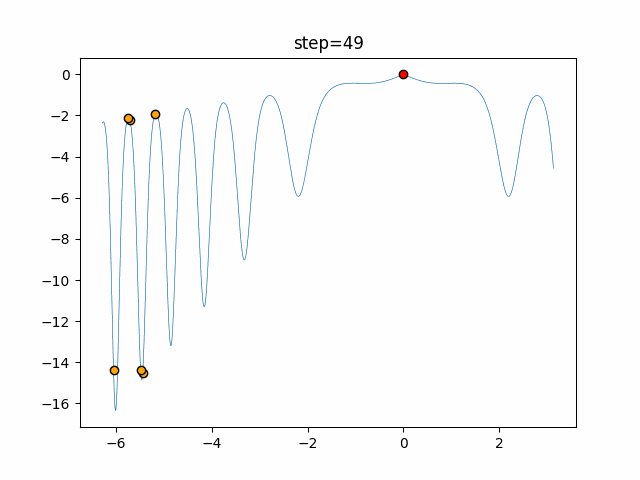
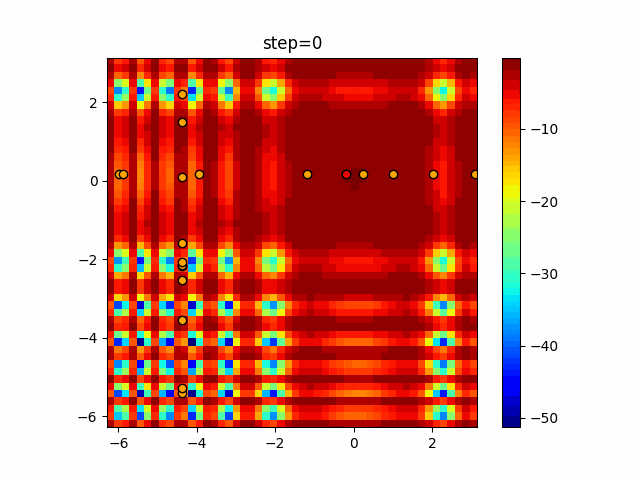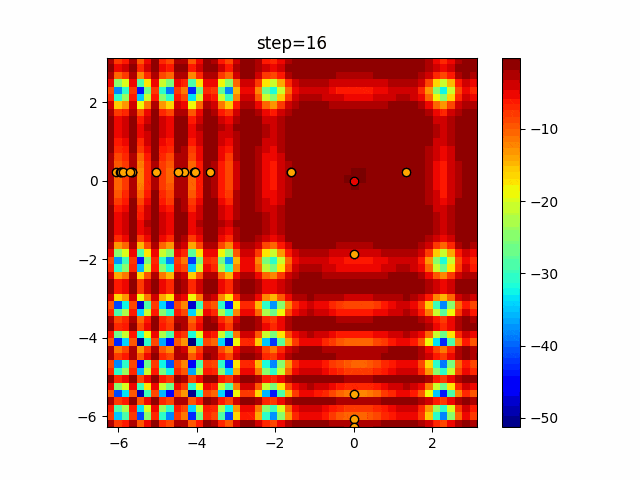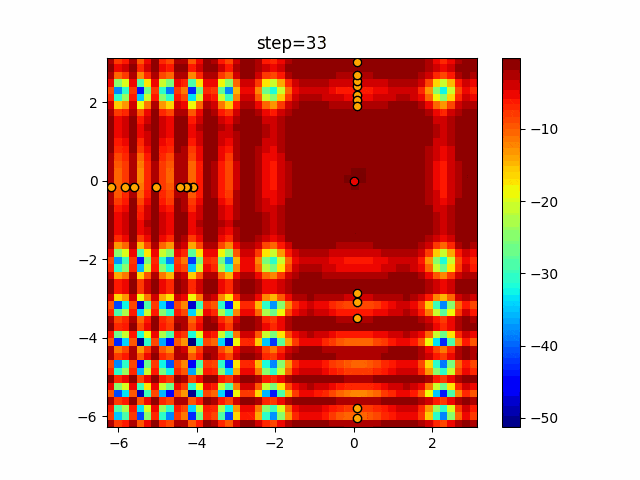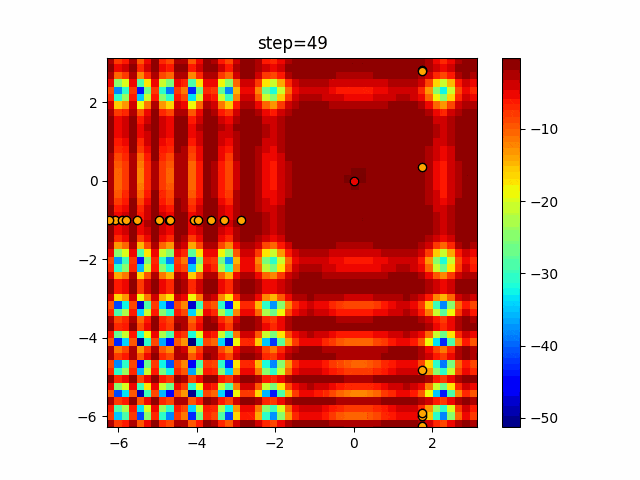
実際の動きの可視化

1次元は6個体、2次元は20個体で50step実行した結果です。
赤い丸がそのstepでの最高スコアを持っている個体となります。

パラメータは以下で実行しました。

Tabu(N, epsilon=0, tabu_list_size=10, tabu_range_rate=0.1)

function_Ackley

• 1次元

• 2次元

function_Rastrigin

• 1次元

• 2次元

function_Schwefel

• 1次元

• 2次元

function_StyblinskiTang

• 1次元

• 2次元

function_XinSheYang

• 1次元

• 2次元

あとがき

タブーリストのサイズが10なので、10stepまで空白が目立ったエリアが10stepからは埋まっていきまた20stepから埋められている感じですね。
2次元で上下に動いているのはεを0にしているので必ず1次元のみ遷移するからです。(もう１次元は元の位置を使用する)