はじめに
最適化アルゴリズムの実装シリーズです。
まずは概要を見てください。
コードはgithubにあります。
差分進化
差分進化(Differential evolution:DE)は、生物の進化をもとに考案された遺伝的アルゴリズムと似ている手法です。
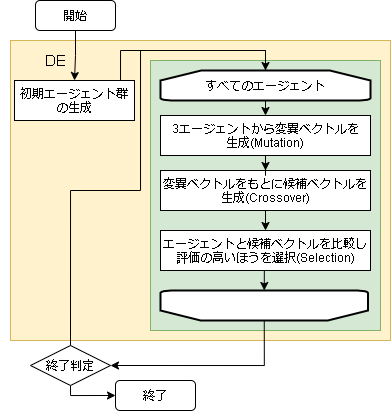
大きく、Mutation(突然変異)、Crossover(交叉)、Selection(生存選択)の3つのフェーズがあります。
遺伝的アルゴリズムみたいにフェーズ毎にアルゴリズムがいろいろあるようですが、本記事では一番簡単なアルゴリズムで実装しています。
参考
・差分進化法でハイパーパラメータチューニング
・差分進化(Wikipedia)
- アルゴリズムのフロー
- 用語の対応
| 問題 | 差分進化 |
|---|---|
| 入力値の配列 | エージェントの位置 |
| 入力値 | エージェント |
| 評価値 | エージェントの評価値 |
- ハイパーパラメータに関して
| 変数名 | 意味 | 所感 |
|---|---|---|
| crossover_rate | 交叉する確率 | 変異ベクトルになる確率 |
| scaling | 変異ベクトルのスケール率(長さ) | 大きいほど移動範囲が大きい |
Mutation(突然変異)
ランダムに選んだ3人のエージェントから変異ベクトルを作成します。
import random
i = 自分を表すindex
# i番目を除いた3エージェントをランダムに選択
r1, r2, r3 = random.sample([ j for j in range(len(agents)) if j != i ], 3)
pos1 = agents[r1].getArray()
pos2 = agents[r2].getArray()
pos3 = agents[r3].getArray()
変異ベクトルは以下の式で出します。
$$ \vec{v} = \vec{x_1} + F (\vec{x_2} - \vec{x_3}) $$
$F$ は変異差分の適用率(スケール因子:scaling factor)を表す0~2の実数です。
pythonコードだと以下になります。
# ベクトル計算しやすいようにnumpy化
import numpy as np
pos1 = np.asarray(pos1)
pos2 = np.asarray(pos2)
pos3 = np.asarray(pos3)
m_pos = pos1 + scaling * (pos2 - pos3)
Crossover(交叉)
一様交叉(binary crossover)で交叉します。
ある確率(crossover_rate)で成分を入れ替える交叉となります。
また交叉は、変異ベクトル側の要素を1成分だけ必ず取り入れます。
import random
# 変異ベクトルで交叉させる(一様交叉)
pos = agent.getArray()
ri = random.randint(0, len(pos)) # 1成分は必ず変異ベクトル
for j in range(len(pos)):
if ri == j or random.random() < self.crossover_rate:
pos[j] = m_pos[j]
else:
pass # 更新しない
# 新しい位置のエージェントを作成
new_agent = problem.create(pos)
生存選択
交叉でできた新しいエージェントと今のエージェントを比べ、更新されていれば置き換えます。
# 優れている個体なら置き換える
if agents[i].getScore() < new_agent.getScore():
agents[i] = new_agent
コード全体
コード全体です。
クラス化しているので上記コードと少し違います。
import math
import random
import numpy as np
class DE():
def __init__(self,
agent_max, # エージェント数
crossover_rate=0.5, # 交叉率
scaling=0.5, # 差分の適用率
):
self.agent_max = agent_max
self.crossover_rate = crossover_rate
self.scaling = scaling
def init(self, problem):
self.problem = problem
# 初期位置の生成
self.agents = []
for _ in range(self.agent_max):
self.agents.append(problem.create())
def step(self):
for i, agent in enumerate(self.agents):
# iを含まない3個体をランダムに選択
r1, r2, r3 = random.sample([ j for j in range(len(self.agents)) if j != i ], 3)
pos1 = self.agents[r1].getArray()
pos2 = self.agents[r2].getArray()
pos3 = self.agents[r3].getArray()
# 3個体から変異ベクトルをだす
pos1 = np.asarray(pos1)
pos2 = np.asarray(pos2)
pos3 = np.asarray(pos3)
m_pos = pos1 + self.scaling * (pos2 - pos3)
# 変異ベクトルで交叉させる(一様交叉)
pos = agent.getArray()
ri = random.randint(0, len(pos)) # 1成分は必ず変異ベクトル
for j in range(len(pos)):
if ri == j or random.random() < self.crossover_rate:
pos[j] = m_pos[j]
else:
pass # 更新しない
# 優れている個体なら置き換える
new_agent = self.problem.create(pos)
self.count += 1
if agent.getScore() < new_agent.getScore():
self.agents[i] = new_agent
ハイパーパラメータ例
各問題に対して optuna でハイパーパラメータを最適化した結果です。
最適化の1回の試行は、探索時間を2秒間として結果を出しています。
これを100回実行し、最適なハイパーパラメータを optuna に探してもらいました。
| 問題 | agent_max | crossover_rate | scaling |
|---|---|---|---|
| EightQueen | 5 | 0.008405098138137779 | 1.7482804860765253 |
| function_Ackley | 36 | 0.4076390525351224 | 0.2908895854800526 |
| function_Griewank | 14 | 0.27752386128521395 | 0.4629100940098222 |
| function_Michalewicz | 12 | 0.1532879607238835 | 0.0742830755371933 |
| function_Rastrigin | 28 | 0.33513859646880306 | 0.0754225020709786 |
| function_Schwefel | 13 | 0.00032331965923372563 | 0.13153649005308807 |
| function_StyblinskiTang | 39 | 0.21247741932099348 | 0.08732185323441227 |
| function_XinSheYang | 33 | 0.0955103914325307 | 0.008270969294347359 |
| LifeGame | 39 | 0.6612227467897149 | 1.136453380180552 |
| OneMax | 4 | 0.1190487045395953 | 1.1581036102901494 |
| TSP | 23 | 0.41212989299137665 | 0.014644735558753091 |
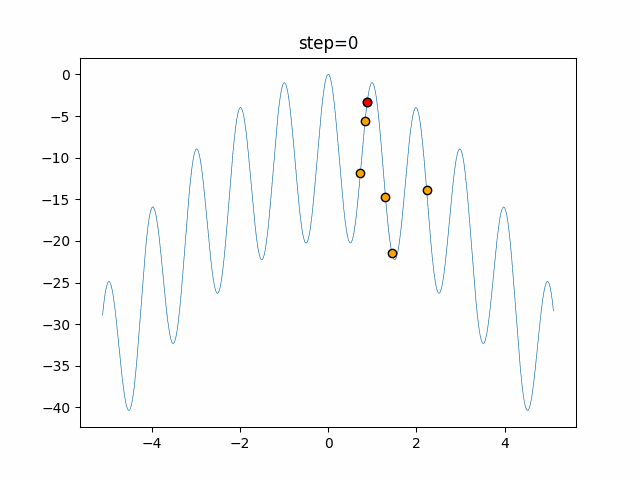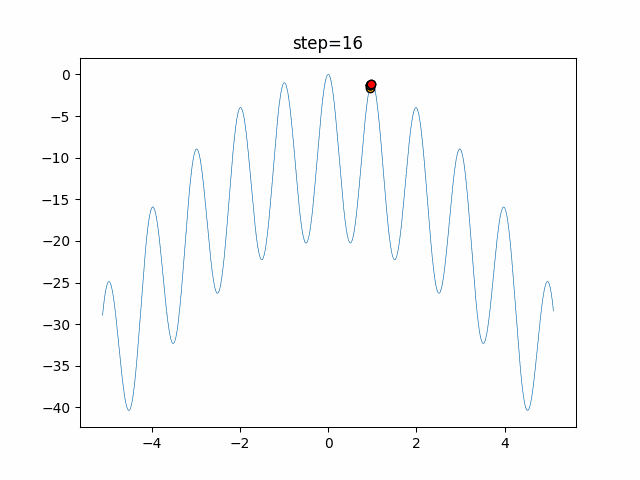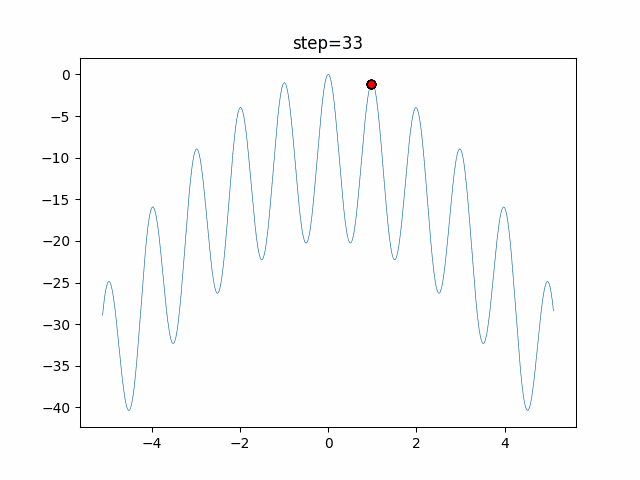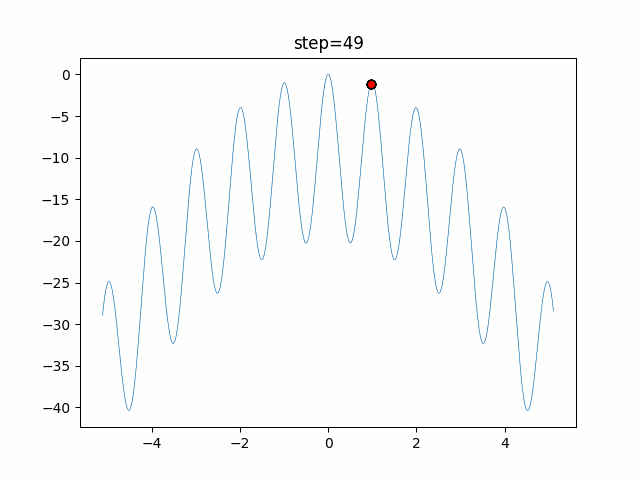
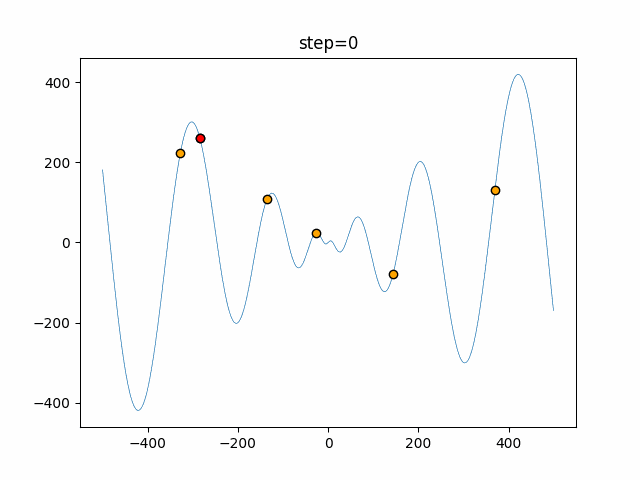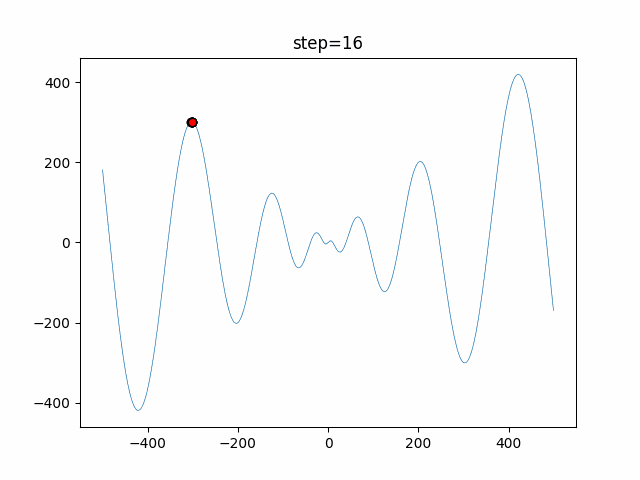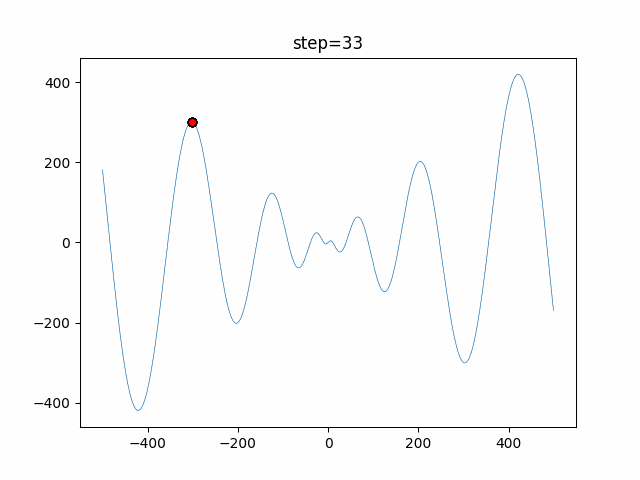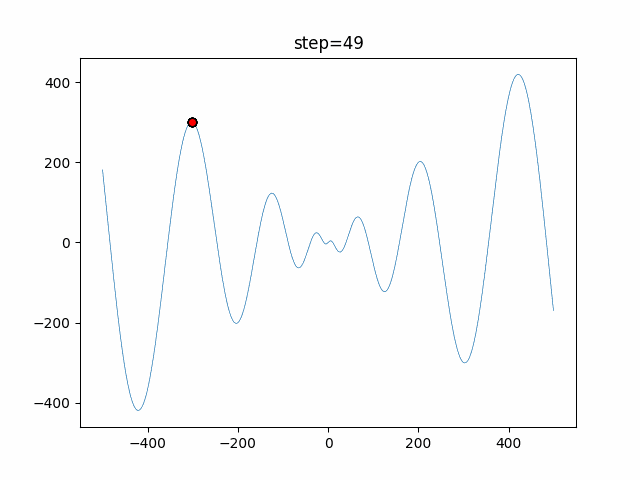
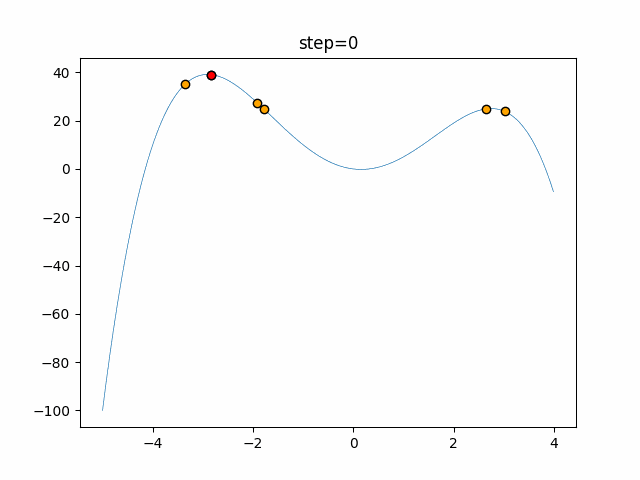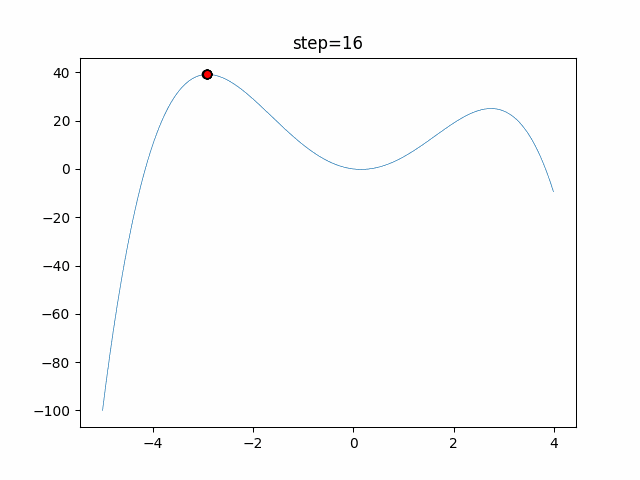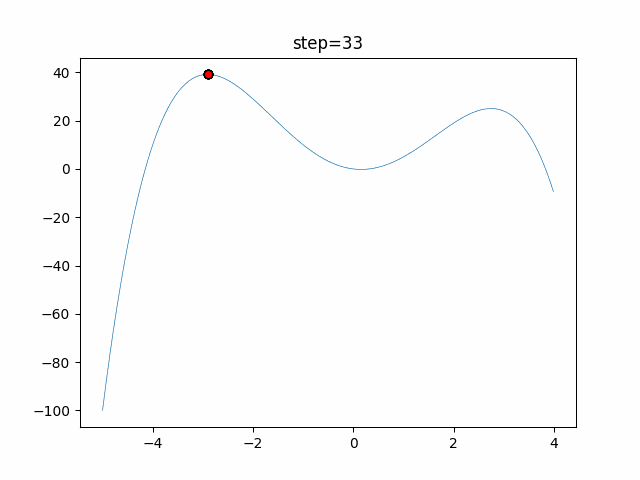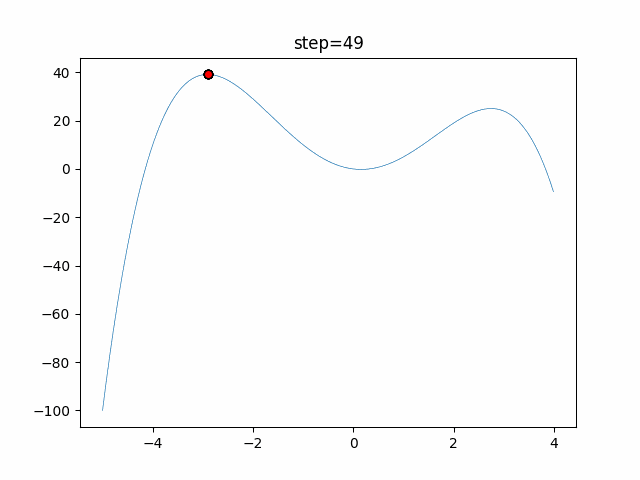
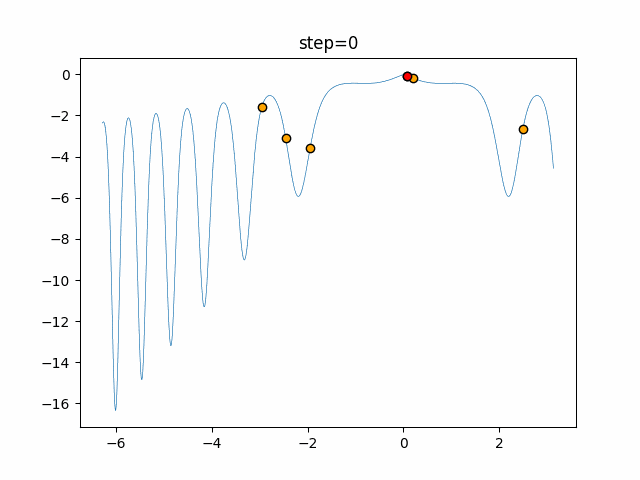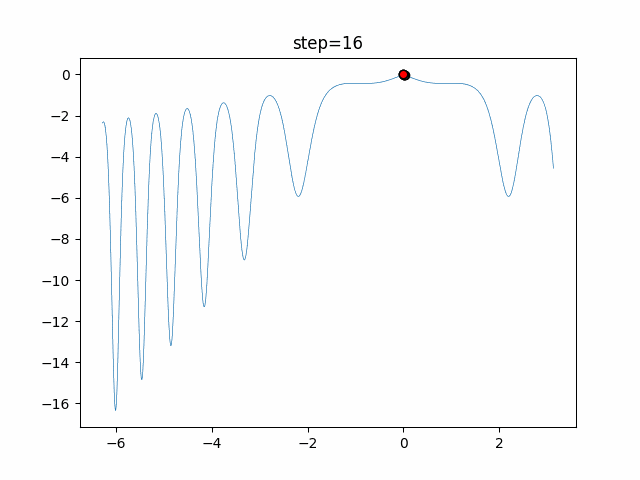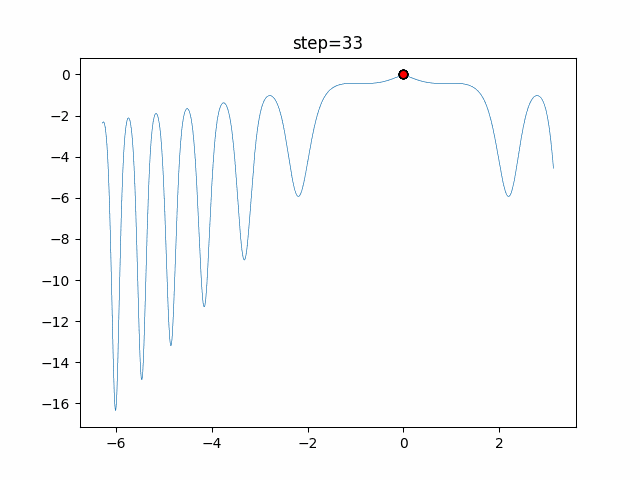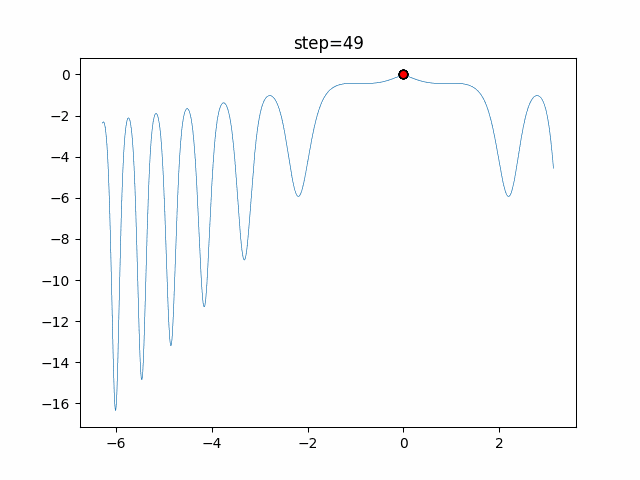
実際の動きの可視化
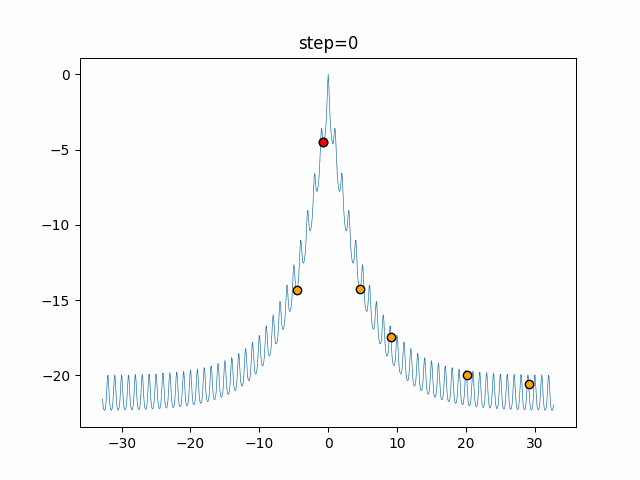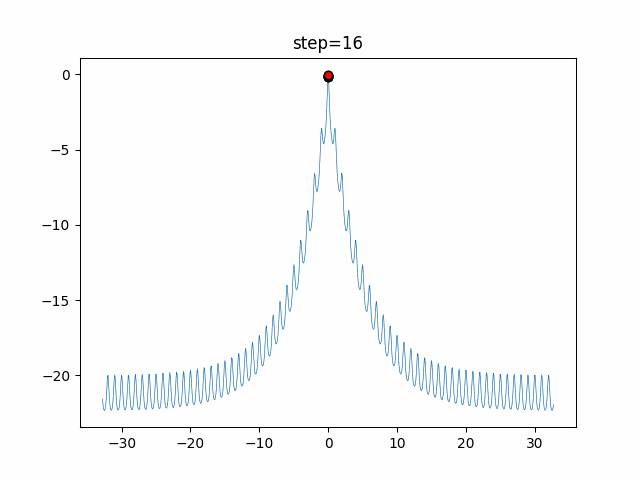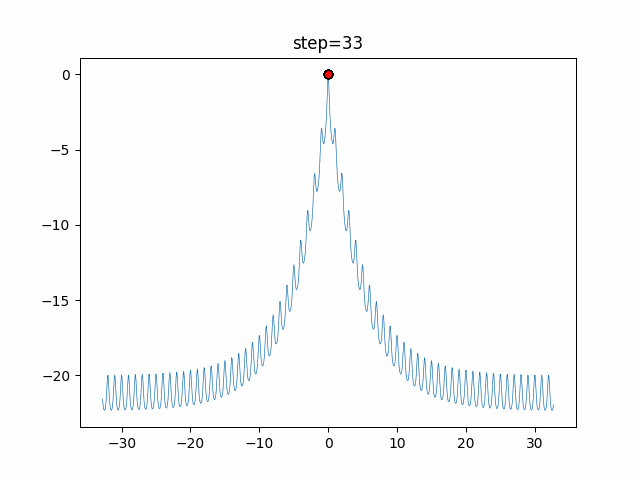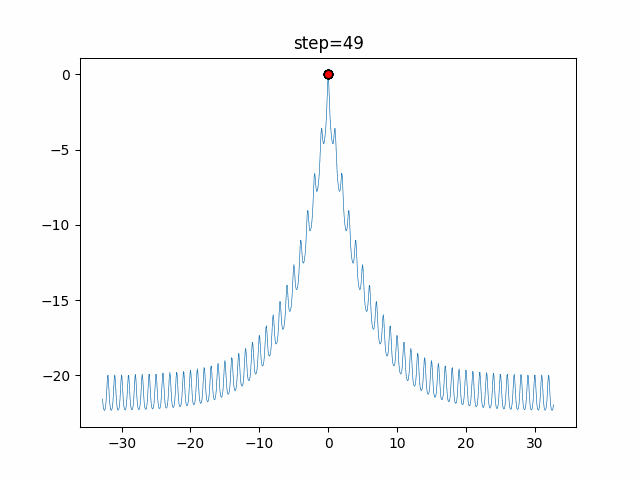
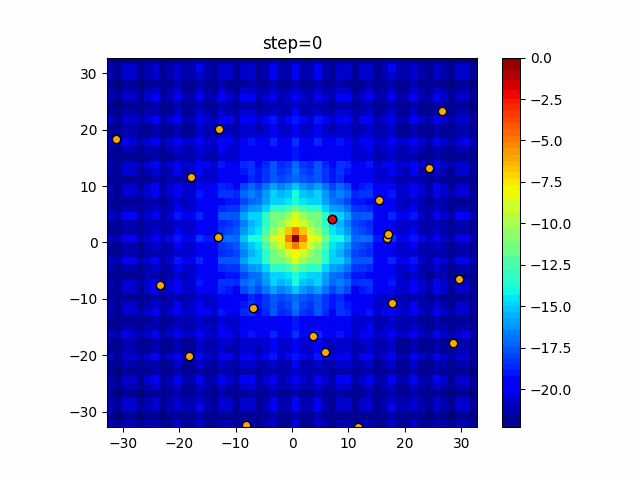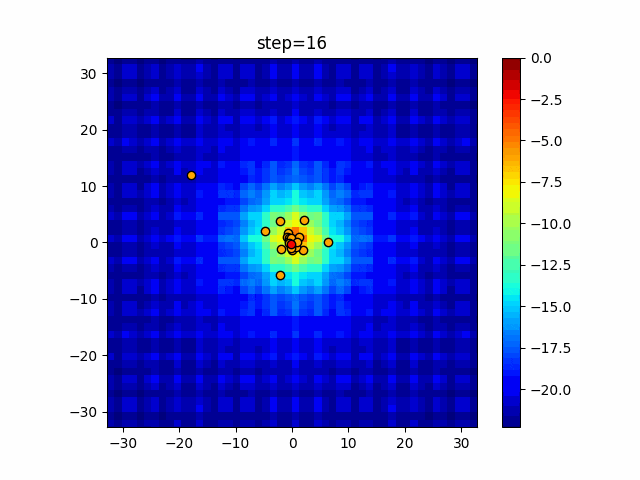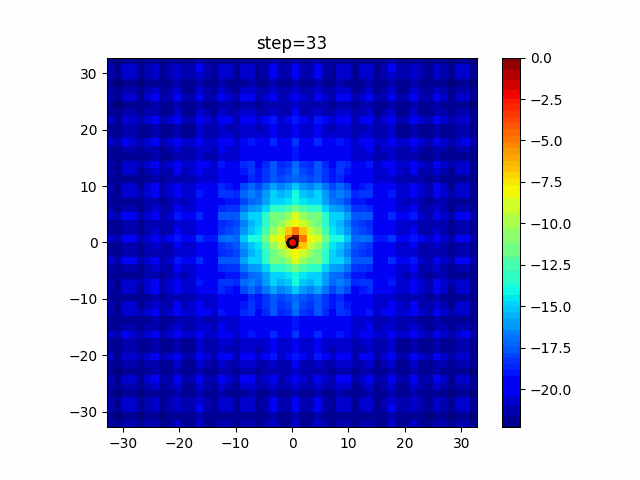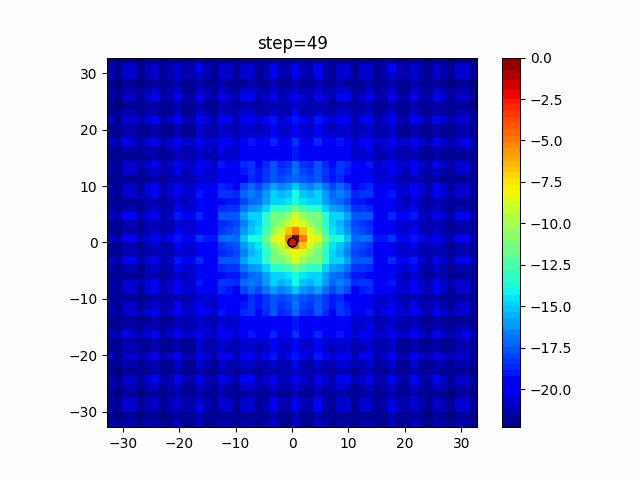
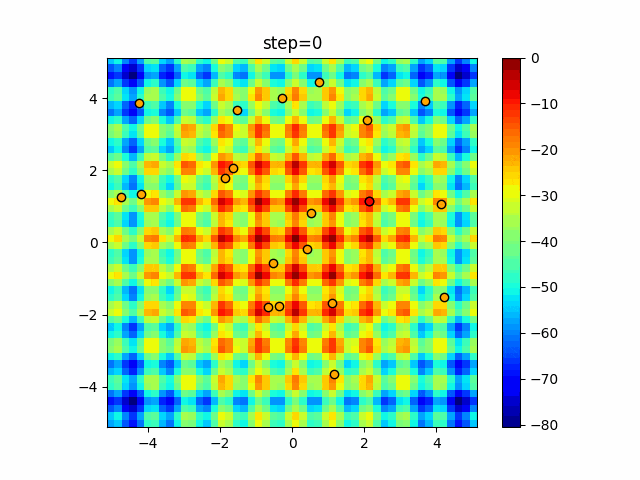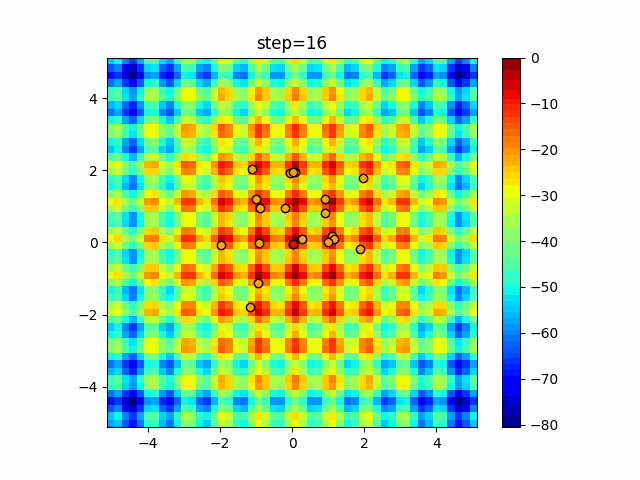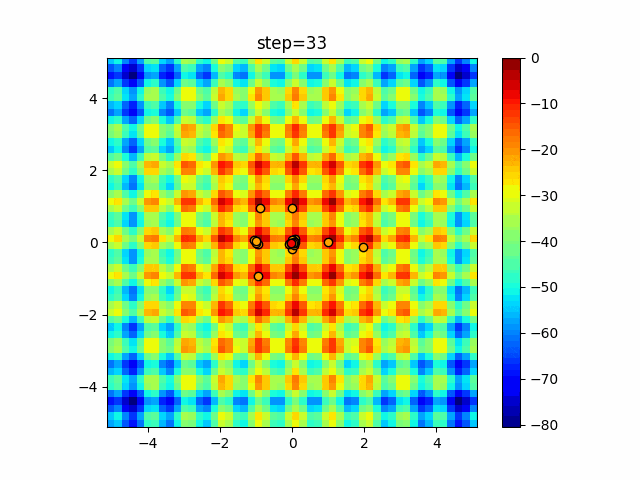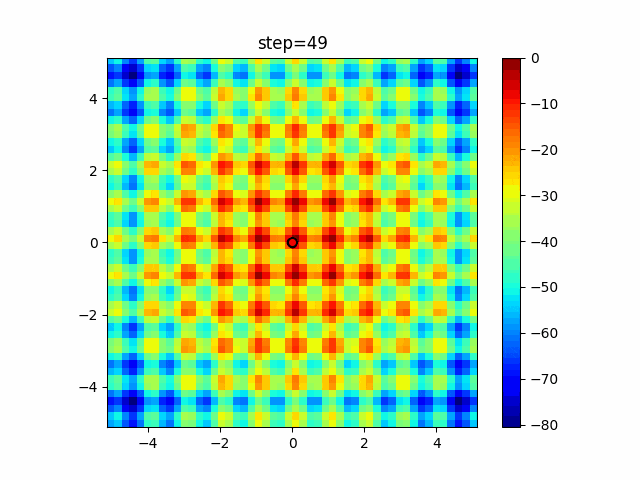
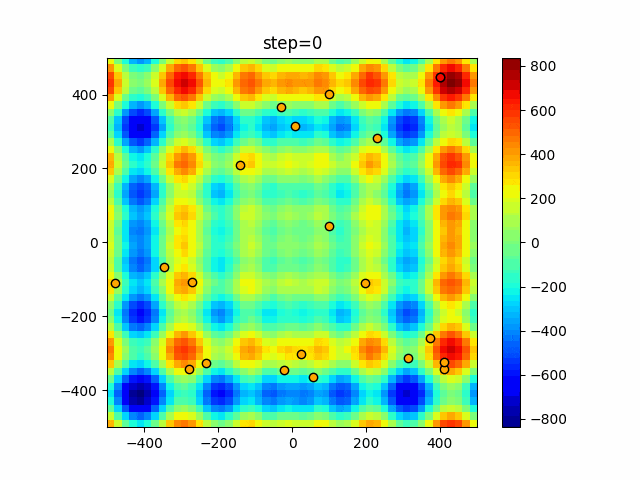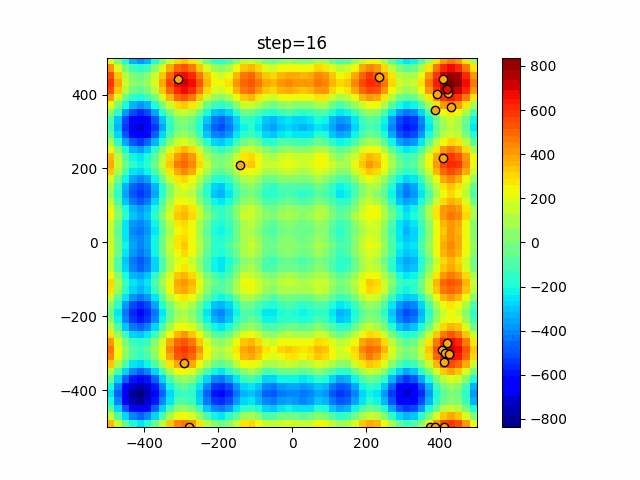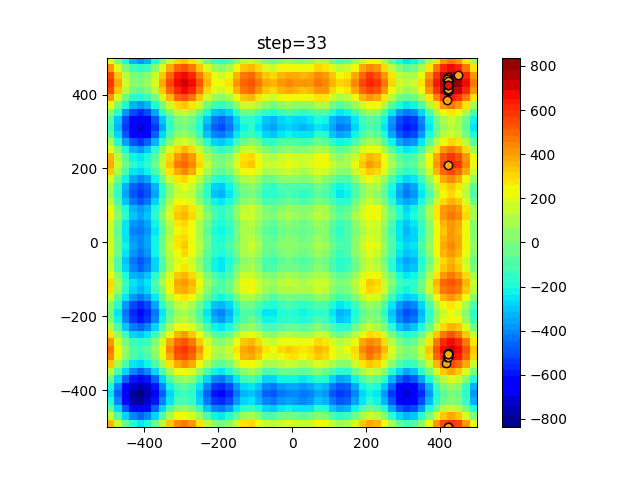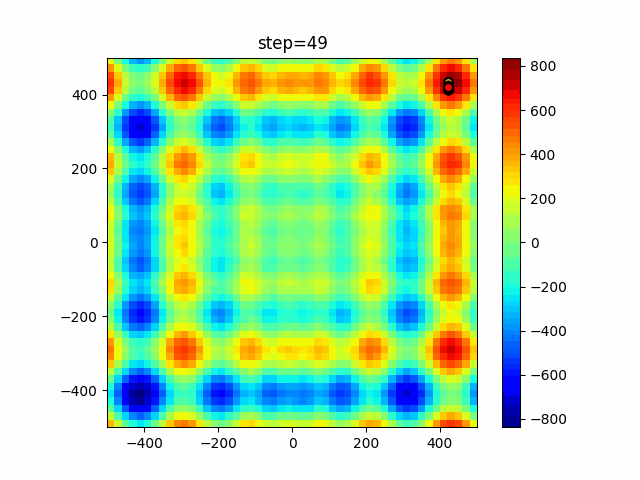
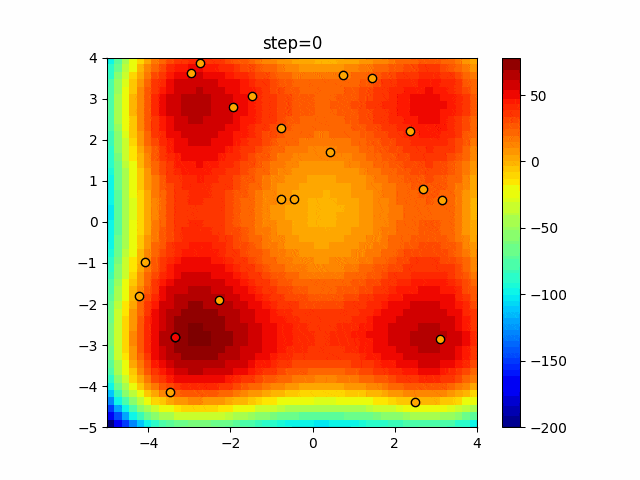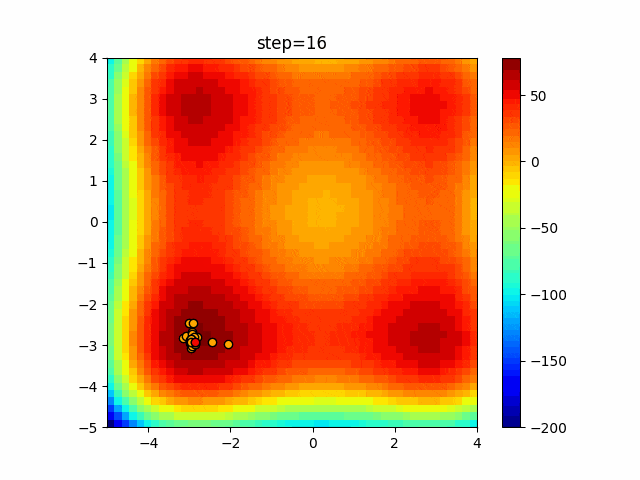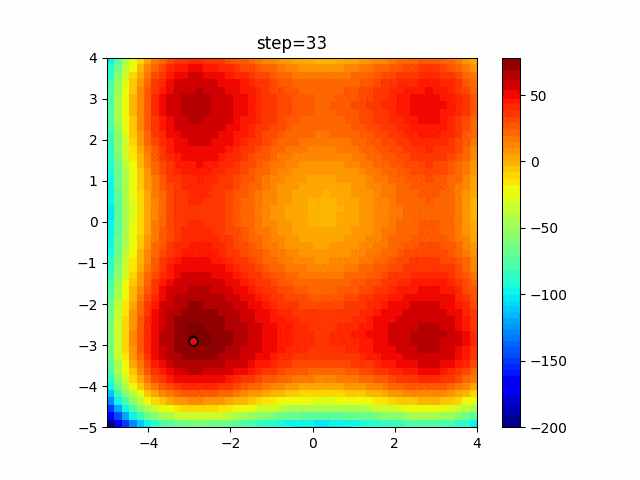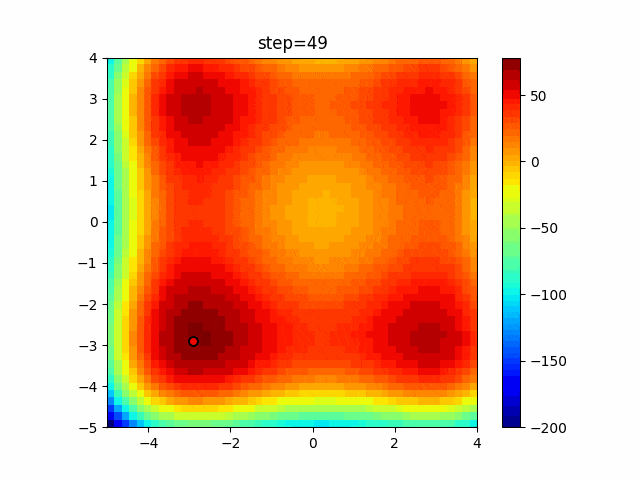
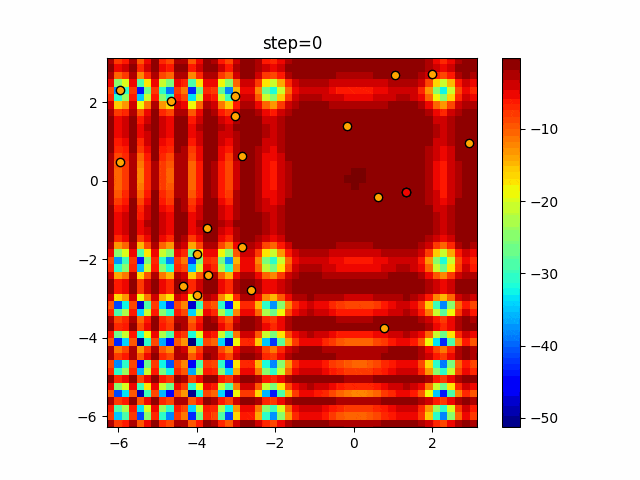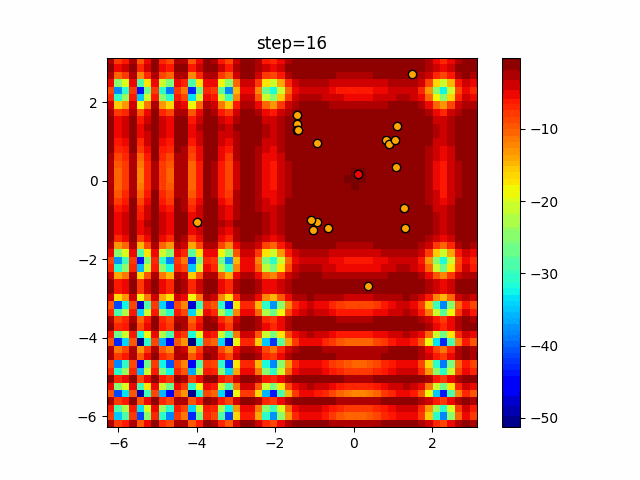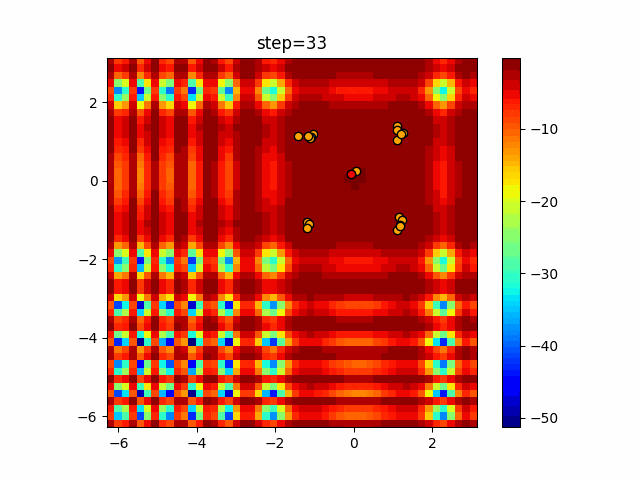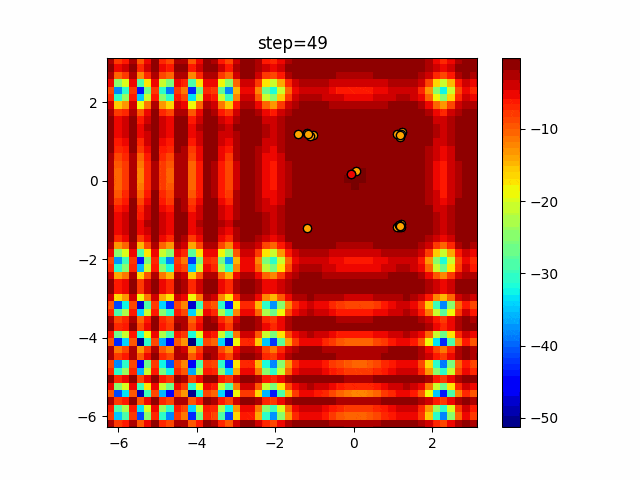
1次元は6個体、2次元は20個体で50step実行した結果です。
赤い丸がそのstepでの最高スコアを持っている個体となります。
パラメータは以下で実行しました。
DE(N, crossover_rate=0, scaling=0.4)
function_Ackley
- 1次元
- 2次元
function_Rastrigin
- 1次元
- 2次元
function_Schwefel
- 1次元
- 2次元
function_StyblinskiTang
- 1次元
- 2次元
function_XinSheYang
- 1次元
- 2次元
あとがき
いい感じに収束していきますね。
ただランダム移動がないので局所解に陥りやすい気はします。