はじめに

毎年、アドベントカレンダーのネタをどうしようかと考えて、ニューラルガスなりSonnetなりニューラルネット関連の斜め上ばかりに手を出していましたが、またニューラルネットに手を出すとどこかで被りそうなので、今年は初心に立ち返ってテーマを「最適化」にします。
最適化と一口に言っても、ターゲットにする問題や目的によって様々なので、「多点探索手法による連続変数最適化」に的を絞り、今回は差分進化法に注目します。
手法自体は1995年に最初の論文[1]が出ているかなりレガシーな手法ですが、連続変数最適化手法として強力な手法として知られています。

で、ただ最適化アルゴリズムの紹介をしても面白くないので、最近巷で話題のハイパーパラメータチューニングに応用してみました。
ハイパーパラメータチューニングといえば、最近Preferred NetworksからOPTUNAというハイパーパラメータ最適化のフレームワークがリリースされました。また、Pythonで使えるハイパーパラメータ最適化フレームワークといえば、Hyperoptがメジャーどころです。

本稿では別にOPTUNAやHyperoptに張り合いたい訳ではなく、ただ差分進化法の応用先にこんなものがあります、という紹介程度のものです（そもそも３日程度で作ったコードで勝てるわけ。。）。

多点探索による連続変数最適化

多点探索手法

多点探索手法とは、文字通り複数の探索点によって最適解を探す手法です。
一般的な（よくNN学習で使う）最適化では、勾配降下法をベースとした単点探索法が主流ですが、多点探索では探索点を複数ばら撒き、互いに情報交換等のやりとりをしながら更新して最適解を探します。
多点探索手法の利点としては、複数の探索点それぞれが独立して探索を行うことで1つの局所解に陥りにくくなる、探索範囲全体を効率よく探索できる、といったことが挙げられます。さらに、探索点それぞれが独立して探索を行うので、アルゴリズムによっては容易に並列計算に持ち込むことができます。

多点探索手法の例をあげると、

遺伝的アルゴリズム (GA)
- 生物の進化過程を模倣
Particle Swarm Optimization (PSO)
- 鳥の群が餌を探す行動を模倣
アントコロニー最適化 (ACO)
- 蟻や蜂などの社会性昆虫の習性を模倣
差分進化法 (DE)
- Nelder-Mead法[2]に進化的アルゴリズム(EA)を応用

といったところがメジャーです。ほとんどが自然界の現象を参考に考案された手法ですね。

で、今回取り上げるのは、「差分進化法」です。

差分進化法

差分進化法（Differential Evolution: DE）は、連続変数最適化手法の一つで、進化的アルゴリズムを基に探索点の更新を行う手法です。
最初にも述べましたが、原著論文は1995年に発表されており、手法としては古いですが、最適化手法の中でも強力な手法として知られており、今尚研究が続いているようです。

根幹のアイディアとしては、複数の探索点の中から、自身以外の点をいくつか選んで新たな探索点を作成し、自身とその探索点を評価して更新する、といった感じです。
新しく探索点を作成する際に、2つ以上の探索点から作成した差分ベクトルを使うことから、差分進化法と呼ばれています。

アルゴリズム

ざっくりとしたアルゴリズムは以下の通りです。

探索点の初期化 (Initialize)
各探索点について変異ベクトルを生成 (Mutation)
交叉演算で各探索点の候補ベクトルを作成 (Crossover)
各探索点とその候補ベクトルについて、評価値の良い探索点をそれぞれ選択 (Selection)
2. ~ 4.を一定回数繰り返す

Mutation

Mutationフェーズでは、探索点集合の中から変異ベクトル(mutant vector)と呼ばれる更新候補点の基を生成します。遺伝的アルゴリズムで言うところの「突然変異」にあたる操作です。

変異ベクトルの生成方法はいくつか種類がありますが、ここではもっとも基本的な生成方法(rand/1)[1]について言及します。

$N$個の探索点からなる探索点集合(={$x_n|n=1, \dots, N$})のうち、$i$番目の探索点に注目しているとします。
rand/1では、$N$個の探索点から$i$番目以外の3つの探索点をランダムに選択します。選んだ探索点のインデックスをそれぞれ$r_1$, $r_2$, $r_3$としておきます。このとき、$r_1$, $r_2$, $r_3$は互いに被らないように選択します。つまり、$r_1 \neq r_2 \neq r_3 \neq i$。
選ばれた探索点を使って、以下の式で変異ベクトル$v^i$を生成します。

$$v^i = x^{r_1} + F(x^{r_2} - x^{r_3})$$

$F \in [0, 1]$はスケーリングファクタと呼ばれる定数です。rand/1の「1」は、変異ベクトルを生成するときの差分ベクトルの数を表しています。

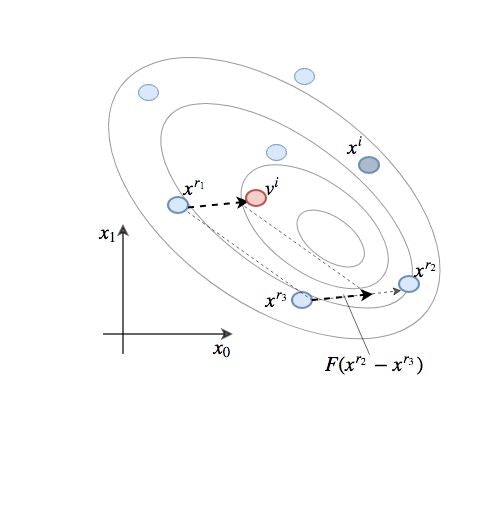
数式だけだとわかりづらいので、絵を描くとこんな感じです。

わかりやすいように、ひとまず探索空間は2次元とします。
楕円は最適化したい関数の等高線を表しており、一番内側の楕円の中心が最小点、つまり最適解を表しています。
$x^i$以外の探索点から$x^{r_1}$, $x^{r_2}$, $x^{r_3}$の3点を選び、$x^{r_2}$と$x^{r_3}$を使って差分ベクトル$F(x^{r_2} - x^{r_3})$　を作成します。この差分ベクトルを$x^{r_1}$に足すことで、変異ベクトル$v^i$を生成します。

Crossover

Crossoverフェーズでは、注目している探索点$x^i$と変異ベクトル$v^i$を使って、候補ベクトル(trial vector)を生成します。遺伝的アルゴリズムで言うところの「交叉演算」にあたる操作です。

交叉演算にもいくつか種類がありますが、ここでは一様交叉(Binomial Crossover)について言及します。

$x^i$と$v^i$のそれぞれの成分について、候補ベクトル$u^i$の各成分を以下のように決定します。

u^i_j = \begin{cases} v^i_j & (rand_j(0, 1) \leq C_r \cup j=j_{rand}) \\
                       x^i_j & (\rm{otherwise}) \end{cases}

ここで、$j_{rand}$は探索空間の次元数$D$を最大とした自然数からランダムに選択したインデックス、$C_r \in [0, 1]$は交叉率と呼ばれる、各成分の選択確率です。
$j_{rand}$で選択される成分は、必ず変異ベクトルの成分が選択されるため、少なくとも1成分は変異ベクトルの成分が受け継がれることが保証されます。
一様交叉では、各成分ごとに乱数を振って変異ベクトル/探索点のどちらの成分を受け継ぐかを決定します。
文献[2]のこの絵がわかりやすいかもです。

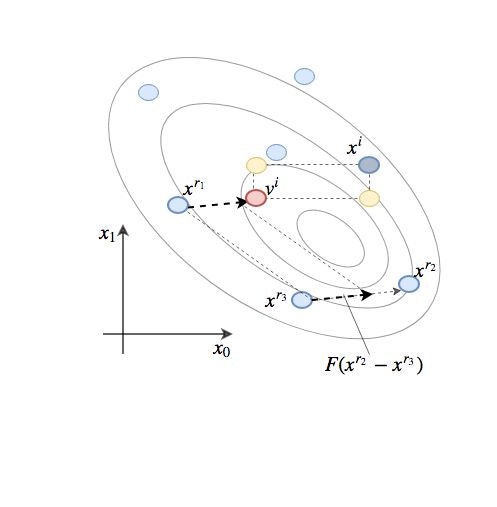
絵で描くとこんな感じです。

黄色い2点が、交叉演算で生成されうる候補ベクトルです。
2次元空間の場合、生成されうる候補ベクトルは

[v^i_0, v^i_1], [v^i_0, x^i_1], [x^i_0, v^i_1]

の３通りとなります。つまり赤い点$v^i$自身と、黄色い2点。

同様に3次元空間の場合は、$v^i$と$x^i$が対角線になるような直方体の端点8点のうち、$x^i$を除いた7点が生成されうる候補ベクトルとなります。

このように、交叉演算では$v^i$と$x^i$が対角線に位置するような超矩形の端点のうち、$x^i$以外の点を確率的に生成する操作となります。要するに$v^i$と$x^i$の間に位置するような適当なベクトルを成分の組み合わせだけで1個作る、ということです。

Selection

Selectionフェーズでは、最適化したい関数の値を使って、次の世代に残す探索点を決定します。こちらも遺伝的アルゴリズムで例えると、「生存選択」にあたる操作です。
バリエーションとしては遺伝的アルゴリズムと同じようにいくつか選択の方法があるのですが、ここではもっともシンプルな選択方法を説明します。

現在の世代数（ステップ数）を$t$としたとき、次の世代の探索点$x^i(t+1)$は以下のように決定します。

x^i(t+1) = \begin{cases}
             u^i(t) & (f(u^i(t)) < f(x^i(t))) \\
             x^i(t) & (\rm{otherwise})
\end{cases}

$f(x)$は最小化したい関数です。やってることはすごくシンプルで、関数値が小さい方を即採用、というだけです。
上の図では、仮に交叉演算で左上の黄色の点が$u^i$として生成されたとすると、$x^i$と比較して$u^i$の方が関数値が小さくなっているので、次の$x^i$として$u^i$が選ばれます。

上記で紹介したアルゴリズムは、DE/rand/1/binと表記されるもっともシンプルなDEのアルゴリズムです。他にも、変異ベクトルのベースを探索点集合中の最良点とするbest/1や、差分ベクトルの数を増やしたrand/2, best/2、各成分の交叉確率が指数的に変化するようにしたrand/1/expなど、バリエーションは様々です。

最近では、スケーリングファクタ$F$と交叉率$C_r$を適応的に決定するJADE[3]やSHADE[4]という手法が提案されているそうです。

応用：ハイパーパラメータチューニング

応用編です。DEをハイパーパラメータチューニングに適用してみます。
なぜハイパーパラメータチューニングにDEを使おうと思ったかというと、DEの大きな利点として

勾配計算を必要としない
並列化が容易

の二つがある（と勝手に思っている）からです。
DEに限らず、PSOやACOなどのいわゆる「メタヒューリスティクス」と呼ばれる手法には、勾配計算を必要としないという大きな利点があります。なので、微分不可能点を含む目的関数でも何不自由なく適用することができます。

ハイパーパラメータチューニングで最適化するパラメータには、連続値だけではなく整数値を含むことがよくあります（例: ランダムフォレストにおける決定木の数、学習回数、SVMにおけるカーネルの種類、など）。
これらのパラメータは、無理やり連続値変換しても、微分不可能な点が存在してしまうため、一般的な勾配降下法では解くことができません。

また、ハイパーパラメータチューニングにおける目的関数は、あるパラメータにおけるモデルの精度となります。とすると、1回評価するためにモデルの学習を行う必要があり、単点探索では最適化にかなりの時間を要してしまい、とても非効率です。
一方で多点探索手法では、各探索点が独立しているので、それぞれにプロセスを割り当てるなりして並列化することで、効率的に探索できます。

ちなみに、詳細は省きますが、HyperoptやOPTUNAではTree-structured Parzen Estimatorというベイズ最適化の一種を使っているそうです。
こちらの記事に、アルゴリズムの解説が載っています。

一応、ハイパーパラメータチューニングにDEを使っている例があるか調べたところ、ちらっと検索しただけで結構ありました。
そのうちの一つ[5]は、LSTMのパラメータチューニングにDEを使ったそうです。

変数を変換

上で書いたように、ハイパーパラメータチューニングでは、連続変数以外の変数を扱う必要があります。扱う変数は以下の通りです。

連続変数（実数値：線形スケール）
- 例：SVMのペナルティ係数$C$、ニューラルネットのDropout率
連続変数（実数値：対数スケール）
- 例：ニューラルネットの学習率、正規化係数
離散変数（整数値）
- 例：ニューラルネットの学習回数、ランダムフォレストの決定木数、最大深さ、K-meansのクラスタ数
カテゴリ変数
- 例：SVMのカーネル種類、ニューラルネットの活性化関数の種類

連続変数については、線形スケールと対数スケールであえて分けて書きました。
一方で、DEは連続変数最適化のための最適化手法であるため、連続変数以外の変数は全て連続変数に変換する必要があります。

そこで、それぞれ以下のように変換して一様に線形スケールの連続変数$x_n$に変換します。

対数スケールの連続変数

x_n =  \log_{10}x_{log, n}\\
x_{log, n} = 10^{x_n}

離散変数

x_n = x_{disc, n} \\
x_{disc, n} = \lfloor x_n \rfloor

カテゴリ変数

x_n = index(x_{cat, n}; c)\\
x_{cat, n} = c_j, j = \lfloor x_n \rfloor

$c$はカテゴリ変数の集合を一列に並べたリスト、$index(x; c)$は、リスト$c$の中の$x$に対応するインデックスを返す関数です。

数式で書くとこんな感じですが、要するに

対数スケールは対数化してリスケーリング
離散変数とカテゴリ変数は整数に丸める

っていうだけです。

実装

長々と説明しましたが、ここまでの話をPythonで実装しました。
https://github.com/s-naoto/de_tuner
（README全然書いてないです。。すみません。。）

まずDEの実装です。
https://github.com/s-naoto/de_tuner/blob/master/differential_evolution.py
使い方はこんな感じです。

import numpy as np
from differential_evolution import DE

def f(x):
    # 最適化する関数（最小化）
    # 例：　Ackley関数 (2次元)
    f = 20. - 20. * np.exp(-0.2 * np.sqrt(1. / 2 * np.sum(x ** 2))) \
            + np.e - np.exp(1. / 2 * np.sum(np.cos(2. * np.pi * x)))
    return f

lower_limit = np.array([-32.768 for _ in range(2)])
upper_limit = np.array([32.768 for _ in range(2)])

de = DE(objective_function=f, ndim=2, lower_limit=lower_limit, upper_limit=upper_limit, minimize=True)
# シングルプロセス
x_best = de.optimize(k_max=500, population=20, mutant='rand', num=1, cross='bin', sf=0.7, cr=0.3)

# マルチプロセス
x_best = de.optimize_mp(k_max=500, population=20, mutant='rand', num=1, cross='bin', sf=0.7, cr=0.3, proc=None)

最適化を実行する関数はシングルプロセスとマルチプロセスの両方を用意しました。
変異ベクトルの作り方mutantは

rand
best
current-to-rand
current-to-best

から選べます。それぞれの詳細は参考文献[6]を見てください。
差分ベクトルの数はnumで指定します。一応、1以上の自然数ならば通りますが、1か2にするのが無難です。
また、交叉方法crossは

bin
exp

から選べます。指数交叉expについては、参考文献[2]を見てください。

続いて、DEを使ってハイパーパラメータチューニングを行うモジュールです。
https://github.com/s-naoto/de_tuner/blob/master/tuner.py

使い方はこんな感じです。
例として、手書き文字認識の10クラス分類問題をランダムフォレストで学習します。

from sklearn.datasets import load_digits
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score

# 探索範囲
search_space = {
    'n_estimators': {'scale': 'category', 'range': [10, 50, 100, 200, 250, 300]},
    'max_depth': {'scale': 'integer', 'range': [1, 8]},
    'min_samples_split': {'scale': 'log', 'range': [-3, 0]},
    'min_samples_leaf': {'scale': 'linear', 'range': [0, 0.5]},
    'min_weight_fraction_leaf': {'scale': 'linear', 'range': [0, 0.5]},
    'max_features': {'scale': 'category', 'range': ['auto', 'sqrt', 'log2', None]}
}

# 手書き文字認識データセット
dataset = load_digits()

tuner = HyperTuner(model=RandomForestClassifier(), space=search_space, k_fold=5, sf=0.7)
best_param = tuner.tuning(eval_function=accuracy_score, x=dataset.data, t=dataset.target, minimize=False)

利用できるモデルは、scikit-learnの学習モデルとしています。なので、学習/推論がscikit-learn likeなI/FのインスタンスならOKです。（学習をfit, 推論をpredictで実行）
また、評価関数もscikit-learn.metricsとしています。こちらも、同じI/Fの関数であればOKです。（引数にy_pred, y_true）

探索範囲は上で示したように指定します。例えば、線形スケールで最小値1、最大値10であれば

'パラメータ名': {'scale': 'linear', 'range': [1, 10]}

対数スケールで最小値$10^{-3}$、最大値$10^2$であれば

'パラメータ名': {'scale': 'log', 'range': [-3, 2]}

カテゴリ変数で['a', 'b', 'c']から選ぶなら

'パラメータ名': {'scale': 'category', 'range': ['a', 'b', 'c']}

といった感じです。
1つの探索点の評価では、学習データに対してK-fold法による交差検定で評価を行い、その平均値を返しています。
モジュール内部ではマルチプロセス実行のDEが呼ばれており、実行すると並列DEによって最適化を実行します。
DEのパラメータは、HyperTunerインスタンスのコンストラクタで指定できます。デフォルトは

k_max = 100
population = 10
mutant = best
num = 1
cross = bin
sf = 0.7
cr = 0.4

です。

ちなみに、上記のランダムフォレストを実行したところ、最適解は

'n_estimators' = 250
'max_depth' = 8
'min_samples_split' = 0.002429223837440966
'min_samples_leaf' = 0.000989397206099375
'min_weight_fraction_leaf' = 0.0008311199268419173
'max_features' ='log2'

だそうです。この時の学習データのaccuracyは0.972となっています。
max_depth、随分深いな。。

最後に

今回はノリと勢いでDEを実装してパラメータチューニングに突っ込んでみました。話の軸をDEに持っていったので、パラメータチューニングの精度検証や比較等は一切していません。。（時間がなk）
ほんとはOPTUNA使ってみたかったですが。

余裕があれば、この辺りの比較や、JADE、SHADEを実装して比較してみようと思います。

参考文献

[1] Storn, R. and Price, K., Differential Evolution - a simple and efficient adaptive scheme for global optimization over continuous spaces, Technical Report TR-95-012, ICSI

[2] K. V. Price, R. N. Storn, and J. A. Lampinen. Differential Evolution: A Practical Approach to Global Optimization. Natural Computing Series. Springer, 2005.

[3] J. Zhang and A. C. Sanderson. JADE: Adaptive Differential Evolution With Optional External Archive. IEEE Tran. Evol. Comput., 13(5):945–958, 2009.

[4] R. Tanabe and A. Fukunaga. Success-History Based Parameter Adaptation for Differential Evolution. In IEEE CEC, pages 71–78, 2013.

[5] Nakisa, Bahareh & Rastgoo, Naim & Rakotonirainy, A & Maire, Frederic & Chandran, V. (2018). Long Short Term Memory Hyperparameter Optimization for a Neural Network Based Emotion Recognition Framework. IEEE Access. PP. 1-1. 10.1109/ACCESS.2018.2868361.

[6] 田邊遼司, 福永Alex: 自動チューナーを用いた異なる最大評価回数におけるDifferential Evolutionアルゴリズムのパラメータ設定の調査, 進化計算学会論文誌, vol. 6, no. 2, pp. 67-81

差分進化法でハイパーパラメータチューニング