hyperoptのロジック、使い方、検証結果についてまとめる

はじめに

機械学習でモデルを作成する際、hyper-parameterのチューニングが必要になります。

gridサーチで徹底的に調べることができればいいのですが、DNNのようにパラメータ数が多くなると、計算量がとんでもないことになります。

ランダムサーチでパラメータの探索を行えば、計算量を少なくすることは可能ですが、最適なパラメータを見つける確率は低くなります。

そこで、効率よく、良さげなパラメータを探索していく方法に、Sequential Model-based Global Optimization（SMBO）というものがあります。

pythonには、SMBOを利用するためのライブラリであるhyperoptというものがあります（kagglerがよく利用しているらしい・・・）。

hyperoptで検索すると、使い方を説明した記事は見つかるのですが、内部のロジックや検証まで説明している記事はあまりありませんでした・・・。

そこで、本記事では、hyperoptの使い方だけでなく、内部のロジック、検証結果についてもまとめます。
とにかく使えればいいやという方は、前半部分は読み飛ばしてください。

hyperoptのロジック

hyperoptとは

hyperoptとは、機械学習のモデルのパラメータ探索を効率よく行ってくれるpythonのライブラリです。

hyperoptには、SMBOの中でも、Tree-structured Parzen Estimator Approach（TPE）というロジックが実装されています。

そこで本章ではSMBOの大枠について説明したのちに、TPEの計算方法をざっくりと説明します。

参考にした記事は、以下の２つです。

特に、後者は英語の記事ですが、SMBO -> gaussian process -> TPEのくだりを図とともにわかりやすく説明してくれているので、おすすめです。

Sequential Model-based Global Optimization（SMBO）

SMBOは、モデルのパラメータの探索を効率よく行うための枠組みの一つです。

SMBOのAlgorithmのフローは以下のようになります。

Algorithm: SMBO

Algorithms for Hyper-Parameter Optimizationより

記号の説明

$x$: パラメータ
$f(x)$: パラメータ$x$を使用した際の損失
$H$: パラメータ$x$とそのパラメータを使用した際のモデルの損失$f(x)$の集合
$T$: 繰り返し試行回数
$M$: パラメータ$x$を入力とし、そのパラメータを使用した際の損失$f(x)$を予測する関数
$S$: あるパラメータ$x$を使用した際に、どれくらい損失が減りそうか期待値を計算する関数

SMBOのポイントは、関数$M$と関数$S$にあります。

関数$M$はあるパラメータ$x$を使用した際に、どれくらいの損失になりそうか予測します。
この関数$M$を使用することで、わざわざ$x$を使用してモデルを推定しなくても、どのくらいの損失になりそうか、予測することができます。
$M$は例えば、線形回帰のようなモデルでもいいのですが、よく使われるのはgaussian processであり、hyperoptでは、TPEが用いられます。

関数$S$は、パラメータ$x$を使用した際に、どのくらい損失が減りそうか、期待値を計算します。

例えば、あるパラメータ$x$を使用した場合、関数$M$を用いて精度を予測したところ、50%の確率で損失0.3、50%の確率で損失0.1になるという結果が出たとしましょう。
この場合、関数$S$では、パラメータ$x$を使用した場合、損失の期待値は$0.3*0.5+0.1*0.5=0.2$であると計算します。

関数$S$を使用することで、一番損失が減りそうなパラメータ$x$を求めることができます。

あとは、推定したパラメータ$x$を用いて、モデルを計算し、実際にどれくらいの損失になったか記録します。
さらに、このパラメータ$x$と損失$f(x)$を元に、損失を予測する関数$M$を更新します。

この計算を$T$回繰り返し、一番損失が低かったパラメータ$x$とその損失を返すのがSMBOの概要です。

Tree-structured Parzen Estimator Approach（TPE）

TPEはhyperoptの元論文の新規性であり、前節で説明した関数$M$と$S$を計算する手法です。

TPEではまず、パラメータ$x$の値を元に、損失が$y$になる確率を求める関数$M$を以下のように計算します。

p(x|y) = \left\{
\begin{array}{ll}
l(x) & (y \lt y^*) \\
g(x) & (y \geq y^*)
\end{array}
\right.

$y^*$は閾値であり、ある損失より小さくなるパラメータ$x$の分布$l(x)$、ある損失より大きくなるパラメータの分布$g(x)$を計算します。

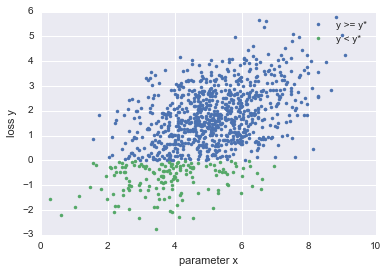
関数$M$のイメージを説明すると以下の図のような感じ

パラメータ$x$と損失$y$のプロット	$l(x)$と$g(x)$のプロット

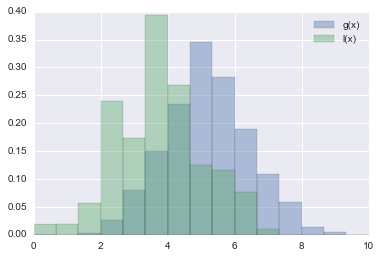このように関数$M$を定義することで、損失が$y^*$より小さくなる時のパラメータ$x$の分布、$y^*$より大きくなる時のパラメータ$x$の分布を計算することができます。

TPEでは、$l(x)$、$g(x)$を元に、パラメータ$x$を選んだ際の期待損失を計算する関数$S$を以下のように定義しています。

EI_{y^*}(x) = (\gamma + \frac{g(x)}{l(x)}(1 - \gamma))^{-1}

ただし、$\gamma$は何割のデータを閾値$y^*$とするか決定するパラメータです。

この値が大きくするためには、$g(x)$をできるだけ小さく、$l(x)$をできるだけ大きくすれば良い。
つまり、閾値$y^*$よりも損失が小さくなる確率の高いパラメータ$x$を選ぶのが関数$S$となります。

TPEでは、このようにして次に損失を計算するパラメータ$x$の探索を行います。

注釈

この章では、だいぶ簡略化してhyperoptのロジックについて説明しました。
なので、少し誤解を与える部分もあります。
例えば、TPEとは正確には$l(x)$、$g(x)$を計算する手法をさしています。
正確なロジックを知りたい場合は、ぜひ元論文を読んでみてください。

hyperoptの使い方

本章では、pythonでhyperoptを使用する方法を説明します。
参考にしたのは、公式のチュートリアルです。

まずhyperoptからhp, tpe, Trials, fminの4つのモジュールをインポートしてください。

from hyperopt import hp, tpe, Trials, fmin

各モジュールの説明を以下にまとめます。

hp: パラメータをどの分布からサンプルするか決定するために使用
tpe: randomサーチするか、tpeのロジックを使用するか決定するために使用
Trials: hyperoptの計算の過程を記録するインスタンスを作成
fmin: hyperoptの計算を実際に行う関数

hyperoptを使用するためには、

どのパラメータを探索するか
どの値を最小化するか

を事前に定義する必要があります。

具体例を元に説明するために、今回はSVMを使用する場合を仮定します。

探索するパラメータの定義

SVMで、チューニングしたいパラメータが、例えば、$C$, $gamma$, $kernel$であった場合、まず以下のように探索するパラメータを辞書型、もしくはリスト型で定義します。

hyperopt_parameters = {
    'C': hp.uniform('C', 0, 2),
    'gamma': hp.loguniform('gamma', -8, 2),
    'kernel': hp.choice('kernel', ['rbf', 'poly', 'sigmoid'])
}

hp.uniformは、パラメータを一様分布からサンプルするための関数で、パラメータ名, min, maxを指定します。

hp.loguniformはパラメータを$exp(min)$から$exp(max)$までの範囲で、パラメータの探索を行います。したがって、SVMの$C$や$gamma$などのように、$10^{-5}$から$10^{2}$程度の範囲で探索するのが適しているパラメータの場合は、hp.loguniformを使用するのが適しています（のちの章で検証します）。

hp.choiceはカテゴリをサンプルすることができます。SVMのkernelを選択する場合は、この関数を使用するのが適しています。

ここで示した分布以外も指定することができます。
詳しくは、公式のチュートリアルを参照してください。

最小化する値の定義

hyperoptでは、何を最小化するか、関数として定義する必要があります。

関数の定義はSVMの場合、以下のように行います。

def objective(args):
    # モデルのインスタンス化
    classifier = SVC(**args)
    # trainデータを使ってモデルの学習
    classifier.fit(x_train, y_train)
    # validationデータを使用して、ラベルの予測
    predicts = classifier.predict(x_test)
    # 予測ラベルと正解ラベルを使用してmicro f1を計算
    f1 = f1_score(y_test, predicts, average='micro')
    # 今回はmicro f1を最大化したいので、-1をかけて最小化に合わせる
    return -1*f1

引数のargsには、前節で定義したhyperopt_parametersが入ります。

この例の場合、まず定義したパラメータをセットして、SVMのインスタンスを作成しています。

次に、trainデータを使用してモデルの学習を行います。

学習したモデルを利用して、validationデータのラベルを予測します。

今回はmicro f1を最大化するパラメータを求めることを目的とし、validationデータのmicro f1を計算

最後に計算したmicro f1を返すのですが、注意点として、hyperoptは最小化にしか対応していません。
そこで、今回のように値を最大化するパラメータを求める場合は-1をかけて返します。

hyperoptの計算

事前に定義したhyperopt_parameters、def objectiveを用いて、パラメータの探索を行います。

以下のようにすることで、パラメータの探索を行います。

# iterationする回数
max_evals = 200
# 試行の過程を記録するインスタンス
trials = Trials()

best = fmin(
    # 最小化する値を定義した関数
    objective,
    # 探索するパラメータのdictもしくはlist
    hyperopt_parameters,
    # どのロジックを利用するか、基本的にはtpe.suggestでok
    algo=tpe.suggest,
    max_evals=max_evals,
    trials=trials,
    # 試行の過程を出力
    verbose=1
)

関数fminにhyperopt_parameters、def objectiveを渡すことで、パラメータの探索を行ってくれるのですが、それ以外にも計算結果を記録するためのインスタンスtrials、何回探索するか指定するmax_evalsも指定しています。

このように計算することで、obejctiveを一番最小化するパラメータを計算してくれます。

以上の例では、bestの中身は以下のようになります。

$ best
>> {'C': 1.61749553623185, 'gamma': 0.23056607283675354, 'kernel': 0}

また、実際に計算したmicro f1の値や、試したパラメータの値を確認する場合は、trialsを使用します。

$ trials.best_trial['result']
>> {'loss': -0.9698492462311558, 'status': 'ok'}

$ trials.losses()
>> [-0.6700167504187605, -0.9095477386934674, -0.949748743718593, ...]

$ trials.vals['C']
>> [2.085990722493943, 0.00269991295234128, 0.046611673333310344, ...]

hyperoptの精度検証

今回検証した内容は主に以下の2つです。

hp.loguniformとhp.uniformのどちらを使用する方が良いのか
hyperoptはランダムサーチと比較して精度が良いのか

使用したデータセットはsklearnにあるdigits（64次元の手書き数字のデータ）です。
1200個をtrainデータとして利用し、残りをvalidationデータとしました。

分類器には、sklearnのSVCを利用しました。
探索したパラメータは、前章で具体例に出した、$C$, $gamma$, $kernel$の3つです。

検証に利用したコードは
https://github.com/kenchin110100/machine_learning/blob/master/sampleHyperOpt.ipynb
にあります。

LogUniform vs Uniform

前章で、SVCの場合は、hp.loguniformを利用した方が良いと書きましたが、本当にそうなのか検証しました。

検証方法として、LogUniform、Uniform、それぞれ、50iterationの探索を100回ずつ行い、推定されたベストなmicro f1値の分布で比較しました。

それぞれの`hyperopt_parametersは以下のように設定しました。

hyperopt_parameters_loguniform = {
    'C': hp.loguniform('C', -8, 2),
    'gamma': hp.loguniform('gamma', -8, 2),
    'kernel': hp.choice('kernel', ['rbf', 'poly', 'sigmoid'])
    }

hyperopt_parameters_uniform = {
    'C': hp.uniform('C', 0, 10),
    'gamma': hp.uniform('gamma', 0, 10),
    'kernel': hp.choice('kernel', ['rbf', 'poly', 'sigmoid'])
    }

比較した結果を以下の図にまとめます。

LogUniform vs Uniform

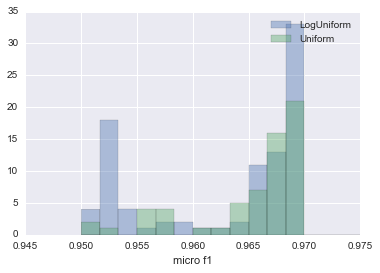LogUnifromの結果のhistgramが青、Uniformの結果のhistgramが緑です。
LogUniformの方が低いmicro f1を推定する確率が高いものの、今回最大のmicro f1家であった0.96985を記録した回数が倍近くあります。

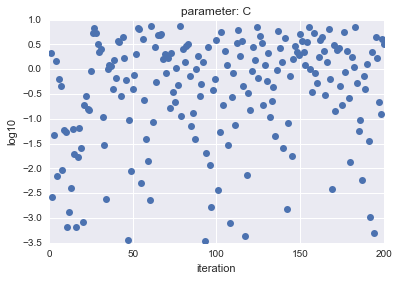
LogUniformの場合、Uniformの場合で、サンプルしたパラメータ$C$、$gamma$をプロットしたところ以下のようになりました。

LogUniformの場合

parameter $C$	parameter $gamma$

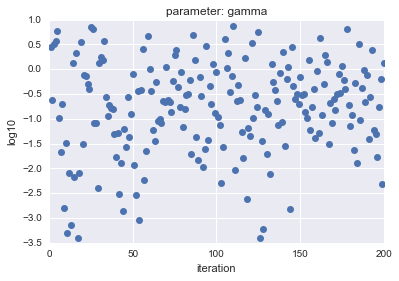Uniformの場合

parameter $C$	parameter $gamma$

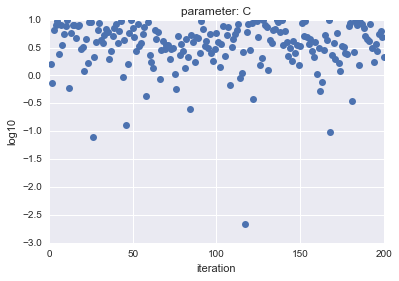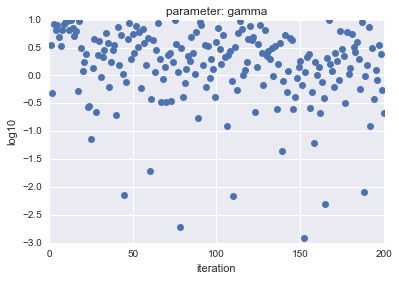横軸はiteration、縦軸は対数表示した$C$, $gamma$の値を示しています。

見ての通り、LogUniformの方が、全体から満遍なくサンプルができていることがわかります。
全体から満遍なくサンプルできることで、精度が高くなるパラメータを探索できる可能性が高くなると言えます（逆に低くなる可能性も上がりますが・・・）

HyperOpt vs RandomSearch

次にHyperOptを使用した場合と、RandomSearchでパラメータを推定した場合で、どちらの方が精度の高いパラメータを推定できる可能性が高いのか検証しました。

使用したデータセットや、実験条件は前節のものと同様です。
HyperOpt、RandomSearchでそれぞれ100回推定を行い、得られたベストなmicro f1値の頻度を比較しました。

比較した結果を以下の図にまとめます。

HyperOpt vs RansomSearch

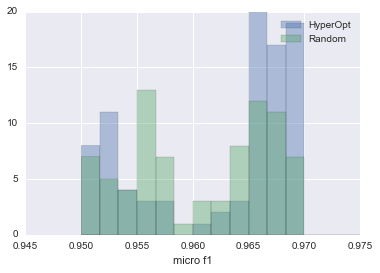青の方がHyperOpt、緑の方がRandomSearchです。
見ての通り、HyperOptの方がmicro f1値0.965以上をだすパラメータを推定できる確率が2倍以上になります。

このことからRandomSearchよりも、HyperOptを使った方が良いということがわかります。

追加実験

RandomSearchよりもHyperOptの方が精度がいいといっても、計算時間が長くなるんじゃないの？という疑問を検証するために、計算時間の比較を行いました。
それぞれ200iteration回し、かかった時間を計測しました。

# HyperOptの計算時間
%timeit hyperopt_search(200)
>> 1 loop, best of 3: 32.1 s per loop

# RandomSearchの計算時間
%timeit random_search(200)
>> 1 loop, best of 3: 46 s per loop

あれ、、、むしろhyperoptの方が早い・・・
RandomSearchは自前実装したので、私のコーディングに問題があるかもしれませんが、実はhyperoptは自動で分散処理してくれるようにコーディングされているそうです。
なので、hyperoptを使っても、random searchと同等か、それ以上の速さで計算ができるようです。

まとめ

今回は、pythonのhyperoptについて、ロジック、使い方、精度の検証を行いました。

やはりRandom Searchでパラメータをチューニングするより、hyperoptを使った方が良さそうです。

TPE最強みたいな書き方をしてしまいましたが、TPEに課題は存在するようです（変数間の依存関係を無視しているなど）。

それでもhyperoptはsklearnやxgboostと一緒に使えるというメリットがあるので、これから多用していこうと思います。

hyperoptって何してんの？