はじめに
最適化アルゴリズムの実装シリーズです。
まずは概要を見てください。
コードはgithubにあります。
比較について
比較はアルゴリズムの優劣をつける事ではなく、アルゴリズム毎の解きやすい問題・解きにくい問題の傾向を把握するために実施しています。
最適化アルゴリズムにはノーフリーランチ定理という考えがあり、汎用的ではありますが決して万能ではありません。
ですのでこの比較はあくまで参考程度に見てください。
結果
各問題の詳細に関しては問題編を見てください。
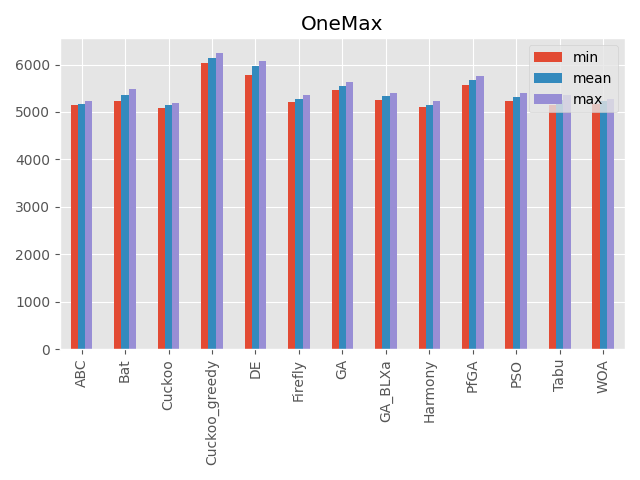
OneMax
| パラメータ | 最大評価値 | 難しさ |
|---|---|---|
| 10000次元 | 10000 | ☆ |
局所解はなく、最適解も広い範囲であります。
なので次元数を大きく設定しました。
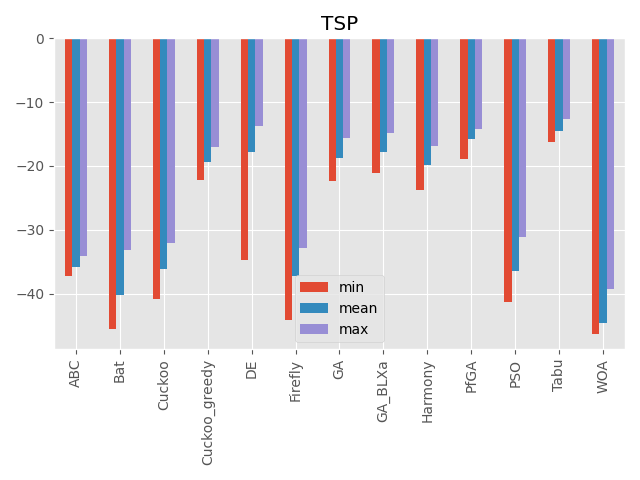
巡回セールスマン問題
| パラメータ | 最大評価値 | 難しさ |
|---|---|---|
| 80次元(80都市) | 0に近い値 | ☆☆☆ |
各入力が都市を回る順番を表しています。
1つの入力の値を変えただけで全部の入力値に影響があるのが特徴です。
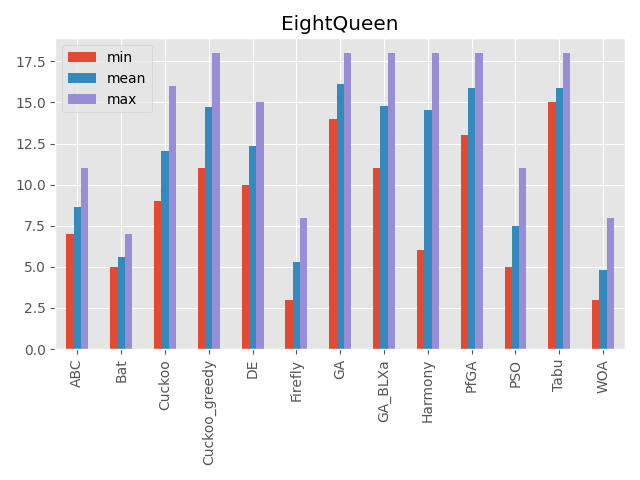
エイト・クイーン
| パラメータ | 最大評価値 | 難しさ |
|---|---|---|
| 20次元(20クイーン) | 20 | ☆☆☆ |
2次元のクイーンの座標を入力としています。
入力の次元により意味が変わる事が特徴です。
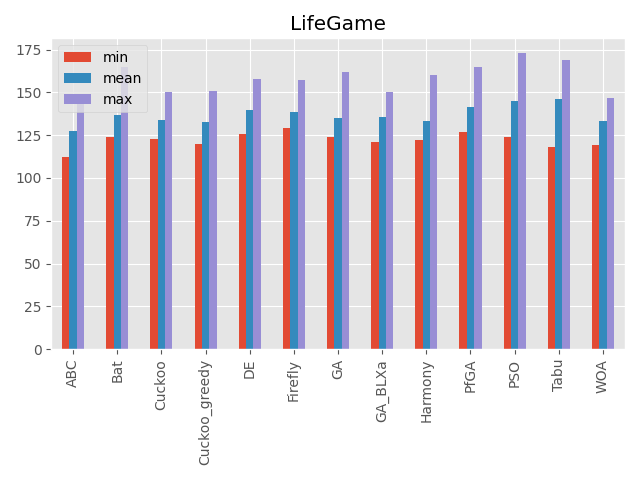
ライフゲーム
| パラメータ | 最大評価値 | 難しさ |
|---|---|---|
| 400次元(20×20)、5ターン | 400に近い値 | ☆☆☆ |
入力と結果の関係が特殊なルールで決まります。
入力値の良し悪しがすぐに判断できません。
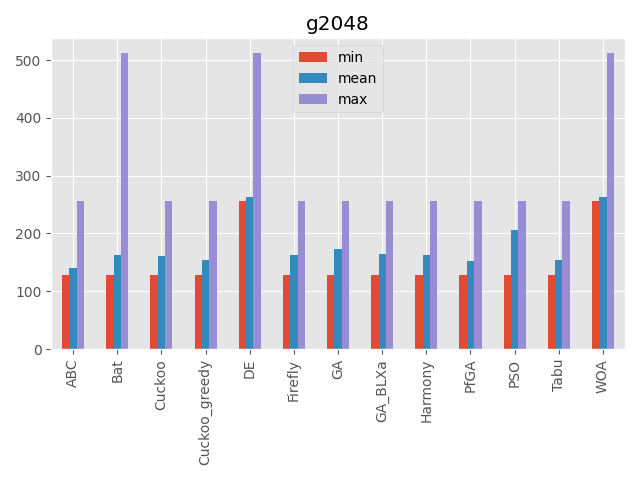
2048
| パラメータ | 最大評価値 | 難しさ |
|---|---|---|
| 350次元(350ターン) | 不明 | ☆☆☆ |
入力が時系列を表しています。
ある入力値を変えるとそれ以降の入力値の意味が変わるのが特徴です。
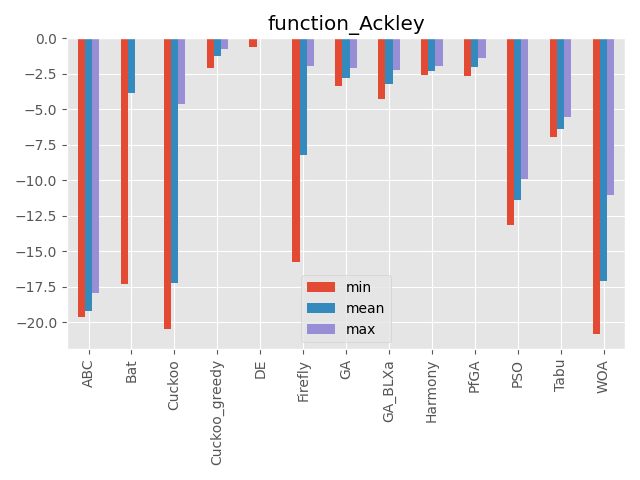
Ackley function
| パラメータ | 最大評価値 | 難しさ |
|---|---|---|
| 50次元 | 0 | ☆☆ |
多数の局所解はありますが、局所解の深さはそこまで深くありません。
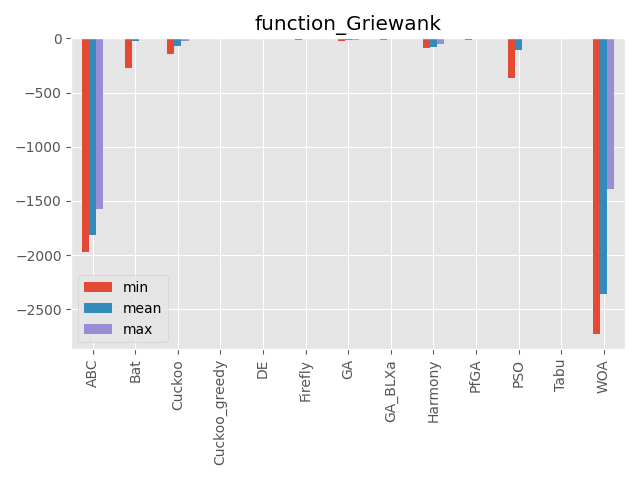
Griewank function
| パラメータ | 最大評価値 | 難しさ |
|---|---|---|
| 100次元 | 0 | ☆? |
単峰性関数に見える…。
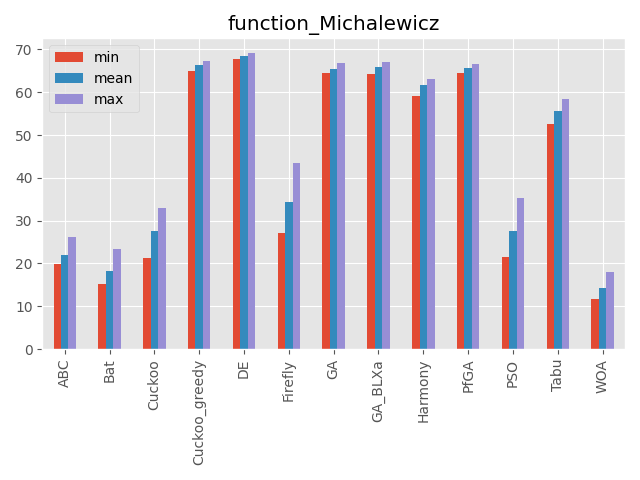
Michalewicz function
| パラメータ | 最大評価値 | 難しさ |
|---|---|---|
| 70次元 | 不明 | ☆☆ |
次元数だけ局所解が増える関数。
最適解が中心にないのも特徴です。
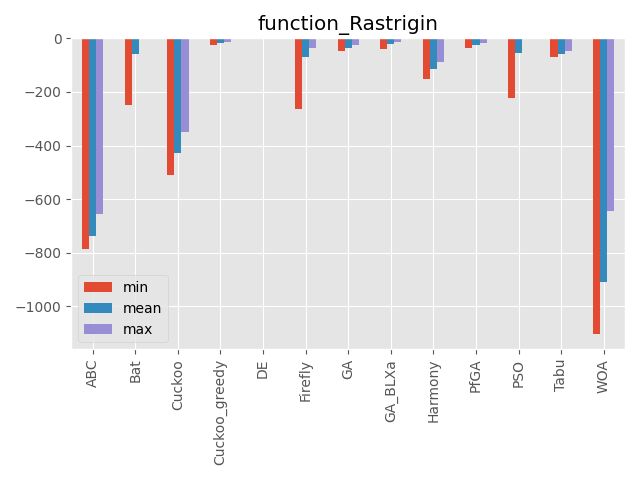
Rastrigin function
| パラメータ | 最大評価値 | 難しさ |
|---|---|---|
| 70次元 | 0 | ☆☆ |
局所解が多数あります。
その局所解も深いものが多いです。
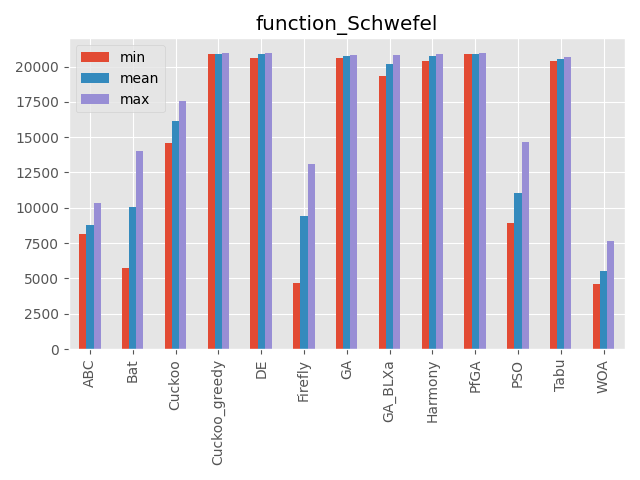
Schwefel function
| パラメータ | 最大評価値 | 難しさ |
|---|---|---|
| 50次元 | 20,949.145 | ☆☆ |
深い局所解と最適解が離れているのが特徴です。
また最適解が中心にありません。
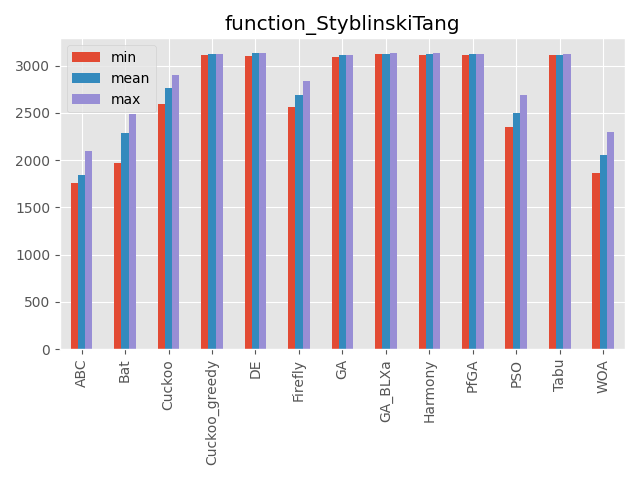
StyblinskiTang function
| パラメータ | 最大評価値 | 難しさ |
|---|---|---|
| 80次元 | 3,133.2932 | ☆☆ |
最適解と局所解が広い範囲で広がっています。
また最適解が中心にありません。
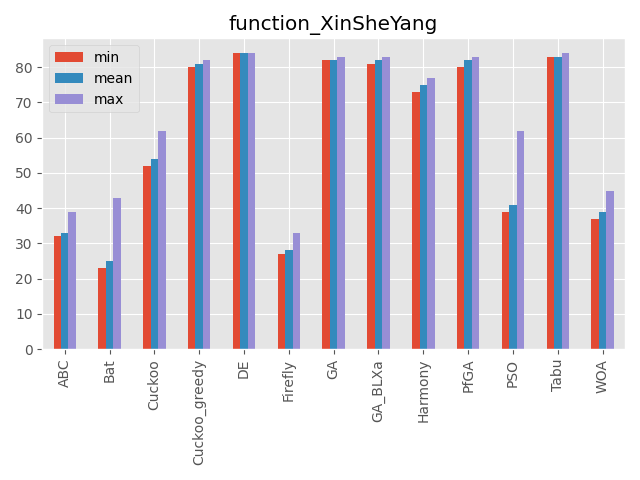
XinSheYang function
| パラメータ | 最大評価値 | 難しさ |
|---|---|---|
| 200次元 | 0 | ☆☆ |
かなり面白い形をしている関数です。
最適解が中心にありません。
評価値がものすごく小さい値なので小数の桁数で比較しています。(指数表記時の指数部を使っています)
比較まとめ
こうしてみると、カッコウ探索(ε-greedy版)、差分進化、遺伝的アルゴリズムとパラメータフリーGA、ハーモニーサーチ、タブーサーチあたりが全体的にいい感じですね。
コウモリアルゴリズムは安定はしていないですが、一部の問題でいい評価を出しています。
またくじらさんアルゴリズムは2048ではいい結果を出していますね。
GA_BLXaは遺伝的アルゴリズムの実数値版ですが、シンプルな遺伝的アルゴリズムとあまり結果が変わらないように見えます(一部は悪くなっている)
比較方法
比較方法ですが、2段階に分けています。
1段階目はハイパーパラメータを探索するフェーズ、
2段階目は実際に測定するフェーズです。
どちらの段階でも実際に探索させる動作は同じものを使っており、コードは以下です。
def run(problem, algorithm, timeout):
# 問題の初期化、乱数は固定する
random.seed(1)
problem.init()
random.seed()
# アルゴリズムの初期化
algorithm.init(problem)
# timeout になるまで loop
t0 = time.time()
while time.time() - t0 < timeout:
algorithm.step()
# 最大スコアを返す
return algorithm.getMaxScore()
問題の初期化は同じ問題になるように乱数を固定しています。
また試行回数ですが、アルゴリズム毎で1stepでの探索回数に差がでるので時間で回数を決めています。
- ハイパーパラメータの探索
ハイパーパラメータの探索では optuna を使用して値を求めています。
各アルゴリズムの探索時間は5秒とし、これを100回繰り返してハイパーパラメータを求めています。
OneMaxを遺伝的アルゴリズムで学習する例は以下です。
import optuna
# optuna用の関数を作成
def objective_degree(prob_cls, alg_cls, timeout):
def objective(trial):
if alg_cls.__name__ == GA.__name__:
# optunaの探索範囲を指定
algorithm = GA(
trial.suggest_int('individual_max', 2, 50),
trial.suggest_categorical('save_elite', [False, True]),
trial.suggest_categorical('select_method', ["ranking", "roulette"]),
trial.suggest_uniform('mutation', 0.0, 1.0),
)
(略)
if prob_cls.__name__ == OneMax.__name__:
problem = OneMax(10000)
(略)
score = run(problem, algorithm, timeout)
return score
return objective
# 学習する対象を指定
prob_cls = OneMax
alg_cls = GA
# optunaによる探索
study = optuna.create_study(direction="maximize")
study.optimize(objective_degree(prob_cls, alg_cls, timeout=5), n_trials=100)
# optunaの結果を取得
print(study.best_params)
print(study.best_value)
- 実際の測定
optunaで学習したハイパーパラメータを用いて実際に結果を計測しています。
計測方法は同じく5秒間探索してその間の最高評価値を結果としています。
これを100回繰り返して集計した結果をもとにグラフ化しています。
# optunaで探索したハイパーパラメータでアルゴリズムを作成
algorithm = alg_cls(**study.best_params)
# 問題を作成
if prob_cls.__name__ == OneMax.__name__:
problem = OneMax(10000)
(略)
# 100回探索して結果を集計
results = []
for _ in range(100):
score = run(problem, algorithm, timeout=5)
results.append(score)
# 結果の表示
print("min : {}".format(min(results)))
print("max : {}".format(max(results)))
実際の表示はグラフ化するためにもう少しいろいろ書いています。
詳しく見たい人はgithubにコードが置いてあります。