最適化アルゴリズムを実装していくぞ（問題編）

はじめに

最適化アルゴリズムの実装シリーズです。
まずは概要を見てください。

全体コードはgithubにあります。

問題

実装した問題は以下です。

• OneMax問題
• 巡回セールスマン問題(Traveling Salesman Problem: TSP)
• エイト・クイーン(Eight Queens)
• ライフゲーム
• 2048
• 最適化アルゴリズムを評価するベンチマーク関数まとめよりいくつか抜粋

OneMax問題

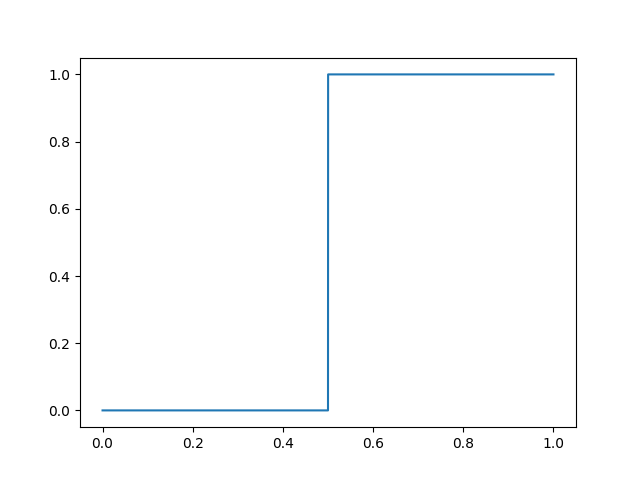
値が0か1のN次元の配列において、合計が最大となるようにする問題です。
最高値はすべてが1の場合です。

４次元の場合の例：[0, 1, 1, 0] → 2

	範囲
入力のサイズ	$N \geqq 1$
入力値の範囲	$0 \leqq x_i \leqq 1$
評価値	入力値を四捨五入した値の合計
評価値の最大値(最適解)	$Prob(1 , \cdots , 1)=N$

• 入力が1次元の場合のグラフ

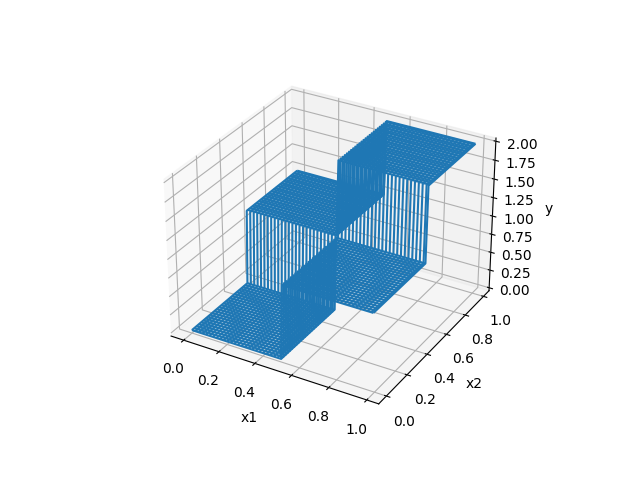
• 入力が2次元の場合のグラフ

プログラムコード

class OneMax():
    def __init__(self, size):
        self.size = size
        self.MIN_VAL = 0
        self.MAX_VAL = 1
        self.SCORE_MIN = 0
        self.SCORE_MAX = size

    def init(self):
        pass

    def eval(self, arr):
        t = [int(x+0.5) for x in arr]  # 四捨五入
        return sum(t)

巡回セールスマン問題

複数の都市を巡回する場合、どの順番でまわれば一番移動距離が少なるなるかという問題です。

本記事では以下のように定義しました。

	範囲
都市の場所	２次元(x,y)の座標で、0～1の間に乱数で配置
入力のサイズ	$N \geqq 2$
入力値の範囲	$0 \leqq x_i \leqq 1$
評価値	移動した距離のマイナス値（最小値を求めたいので符号を反転）
評価値の最大値(最適解)	不明(0に近いほうが良い)

※最初のスタート地点は(0,0)からとしています

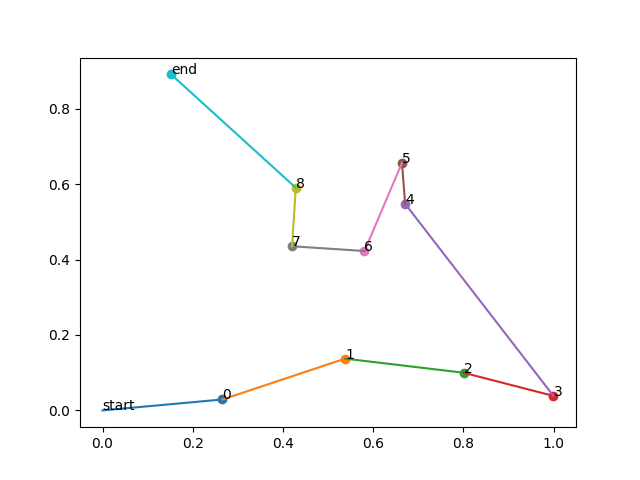
入力ですが、配列のindexと都市のindexが対応しており、入力値が小さい都市から順番に回るようにしています。
例えば都市が３つ(A,B,C)で入力が[0.3, 0.1, 0.2]の場合、回る順番は (0,0)→B→C→A となります。

• 描画例

プログラムコード

import math
class TSP():
    def __init__(self, size):
        self.size = size
        self.MIN_VAL = 0
        self.MAX_VAL = 1
        self.SCORE_MIN = -(math.sqrt(1+1) * size)
        self.SCORE_MAX = 0

    def init(self):
        # 都市の位置をランダムに作成
        self.towns = [
            {
                "x": random.random(),
                "y": random.random()
            } for _ in range(self.size)
        ]

    def eval(self, arr):
        score = 0

        # 入力値にソートした入力のindexを取得
        tmp = [(i, x) for i, x in enumerate(arr)]
        tmp = sorted(tmp, key=lambda x: x[1])

        for i in range(len(tmp)):
            if i == 0:
                # 最初は 0,0 から始める
                town = {"x":0, "y":0}
            else:
                town = self.towns[tmp[i-1][0]]
            next_town = self.towns[tmp[i][0]]

            # 移動距離がスコア
            d = abs(town["x"] - next_town["x"])
            d += abs(town["y"] - next_town["y"])
            score += d

        # 最小を求めたいので符号反転させる
        return -score

エイト・クイーン

8×8のチェス盤に8個のクイーンを置く問題です。
ただし、クイーン同士は縦横斜めでかぶってはいけません。
8としていますがN個の場合に拡張できます。

4クイーンの場合の解は以下です。

□□■□
■□□□
□□□■
□■□□

	範囲
盤のサイズ	$M \geqq 4$
入力のサイズ	$N=M×2$（(x,y)の2次元配列を1次元に並べる）
入力値の範囲	$0 \leqq x_i \leqq M$ （マス内の座標）
評価値	他と被らないクイーンの数
評価値の最大値(最適解)	M

入力ですが、各クイーンのxとy座標を並べた１次元配列としています。
たとえば[0, 0, 1, 2, 2, 1] とあった場合、(0,0)(1,2)(2,1) に3個のクイーンが置かれていることになります。

プログラムコード

class EightQueen():
    def __init__(self, size):
        self.size = size
        self.MIN_VAL = 0
        self.MAX_VAL = size
        self.SCORE_MIN = 0
        self.SCORE_MAX = size

    def init(self):
        pass

    def eval(self, arr):
        arr = [int(x+0.5) for x in arr]  # 四捨五入

        # 座標に変換
        koma_list = []
        for i in range(0, len(arr), 2):
            koma_list.append((arr[i], arr[i+1]))
        
        score = 0
        for i in range(len(koma_list)):
            f = True
            for j in range(len(koma_list)):
                if i==j:
                    continue
                # x
                if koma_list[i][0] == koma_list[j][0]:
                    f = False
                    break
                # y
                if koma_list[i][1] == koma_list[j][1]:
                    f = False
                    break
                # 斜め
                ax = abs(koma_list[i][0] - koma_list[j][0])
                ay = abs(koma_list[i][1] - koma_list[j][1])
                if ax == ay:
                    f = False
                    break
            if f:
                score += 1

        return score

ライフゲーム

ライフゲームです。細胞の生き死にを模倣したゲームですね。

ルールはN×Nの盤があり、それぞれのマス(セル)は1（生）、0（死）の状態を持っています。
これらのセルは時間が進むごとに以下条件で生死を繰り返します。

1. 誕生：死んでいるセルに隣接する生きたセルがちょうど3つあれば、次の世代が誕生する。
2. 生存：生きているセルに隣接する生きたセルが2つか3つならば、次の世代でも生存する。
3. 過疎：生きているセルに隣接する生きたセルが1つ以下ならば、過疎により死滅する。
4. 過密：生きているセルに隣接する生きたセルが4つ以上ならば、過密により死滅する。

	範囲
盤のサイズ	$M \geqq 2$
入力のサイズ	$N=M×M$（2次元の盤のマスを1次元に並べる）
入力値の範囲	$0 \leqq x_i \leqq 1$
評価値	生存しているセルの合計
評価値の最大値(最適解)	不明（M×Mに近い値）

評価ではXターン(max_turn)経過した後、生存しているセルの数を評価値としています。

プログラムコード

class LifeGame():
    def __init__(self, size, max_turn):
        self.field_size = size
        self.max_turn = max_turn
        self.MIN_VAL = 0
        self.MAX_VAL = 1
        self.SCORE_MIN = 0
        self.SCORE_MAX = size*size

    def init(self):
        pass

    def eval(self, arr):
        arr = [int(x+0.5) for x in arr]  # 四捨五入

        # 1次元→2次元に
        cells = []
        for y in range(self.field_size):
            d = []
            for x in range(self.field_size):
                d.append(arr[y*self.field_size + x])
            cells.append(d)

        # 更新
        for _ in range(self.max_turn):
            cells = self._step(cells)

        # 合計を出す
        n = 0
        for y in range(self.field_size):
            for x in range(self.field_size):
                n += cells[y][x]
        return n

    def _step(self, cells):
        # 0でいったん初期化
        next_cells = [[ 0 for _ in range(field_size)] for _ in range(self.field_size)]

        for y in range(self.field_size):
            for x in range(self.field_size):
                n = 0
                n += self._get(cells, x-1, y-1)
                n += self._get(cells, x  , y-1)
                n += self._get(cells, x+1, y-1)
                n += self._get(cells, x+1, y)
                n += self._get(cells, x-1, y)
                n += self._get(cells, x-1, y+1)
                n += self._get(cells, x  , y+1)
                n += self._get(cells, x+1, y+1)
                if self._get(cells, x, y) == 0:
                    if n == 3:
                        next_cells[y][x] = 1
                else:
                    if n == 2 or n == 3:
                        next_cells[y][x] = 1
                    else:
                        next_cells[y][x] = 0
        
        return next_cells

    def _get(self, cells, x, y):
        if x < 0:
            return 0
        if y < 0:
            return 0
        if x >= self.field_size:
            return 0
        if y >= self.field_size:
            return 0
        return cells[y][x]
    

2048

イタリア人のガブリエレ・チルリさんによって作られたオープンソースのゲームです。

参考：https://ja.wikipedia.org/wiki/2048_(%E3%82%B2%E3%83%BC%E3%83%A0)

4×4のマスに数字がランダムに置かれ、上下右左のいずれかですべてのマスを同時にスライドすることができます。
スライドしたときに同じ数字が重なった場合、数字が足されていきます。
ゴールは2048のタイルを作ることです。

	範囲
入力のサイズ	$N$（ターン数）
入力値の範囲	$0 \leqq x_i \leqq 3$（ターンでのコマンド）
評価値	最大のマスの数字
評価値の最大値(最適解)	不明

入力サイズをターン数にし、そのターンで行う行動を入力値としています。
行動は以下のように決めました。
0：上にスライド
1：右にスライド
2：下にスライド
3：左にスライド

プログラムコード

class g2048():
    def __init__(self, max_turn):
        self.MIN_VAL = 0
        self.MAX_VAL = 3
        self.SCORE_MIN = 0
        self.SCORE_MAX = float('inf')

        self.max_turn = max_turn

    def init(self):
        # 初期フィールド
        self.fields = [[0 for _ in range(4)] for _ in range(4)]
        for _ in range(2):
            self.fields[random.randint(0, 3)][random.randint(0, 3)] = 2

        # 生成する乱数はinitで固定する
        self.create_pos = []
        for _ in range(self.max_turn):
            self.create_pos.append((random.randint(0, 3), random.randint(0, 3)))


    def eval(self, arr):
        arr = [int(x+0.5) for x in arr]  # 四捨五入

        # 初期フィールドをコピー
        fields = [ x[:] for x in self.fields]

        # turn分実行
        for i in range(self.max_turn):

            # 更新
            for y in range(4):
                for x in range(4):
                    self._move(fields, arr[i], x, y)
            
            # 新しく2を設置、すでにあれば次のセルを見る
            pos = self.create_pos[i]
            x = pos[0]
            y = pos[1]
            for _ in range(4*4):
                if fields[y][x] == 0:
                    fields[y][x] = 2
                    break
                x += 1
                if x >= 4:
                    x = 0
                    y += 1
                if y >= 4:
                    y = 0

        # 最後の盤面で最大値がスコア
        score = 0
        for y in range(4):
            for x in range(4):
                if score < fields[y][x]:
                    score = fields[y][x]
        
        return score

    def _move(self, fields, cmd, x, y):
        if fields[y][x] == 0:
            return
        
        if cmd == 0:  # up
            if y == 0:
                return
            tx = x
            ty = y-1
        elif cmd == 1:  # right
            if x == 3:
                return
            tx = x+1
            ty = y
        elif cmd == 2:  # down
            if y == 3:
                return
            tx = x
            ty = y+1
        elif cmd == 3:  # left
            if x == 0:
                return
            tx = x-1
            ty = y
        else:
            raise ValueError()

        if fields[ty][tx] == 0:
            # 対象がが開いているので移動
            fields[ty][tx] = fields[y][x]
            fields[y][x] = 0
            self._move(fields, cmd, tx, ty)
        elif fields[ty][tx] == fields[y][x]:
            # 同じ数字なので合成
            fields[ty][tx] += fields[y][x]
            fields[y][x] = 0
    

ベンチマーク関数

数式に関しては最適化アルゴリズムを評価するベンチマーク関数まとめを見てください。
グラフとコードのみ紹介します。

※最大値にするために数式には-1を掛けています。

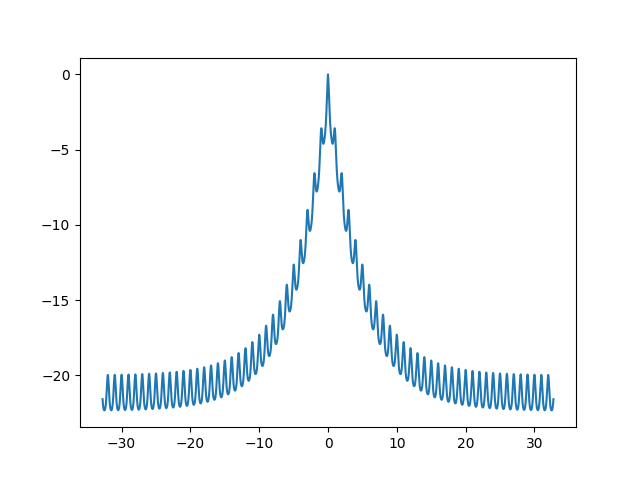
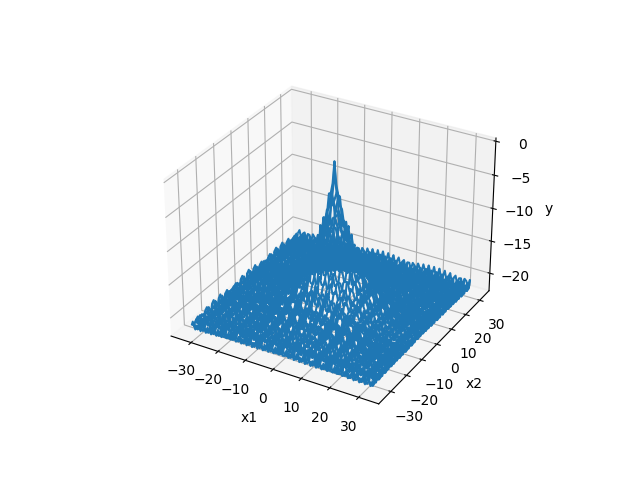
Ackley function

• 1次元のグラフ

• 2次元のグラフ

• プログラムコード

import math
class function_Ackley():
    def __init__(self, size):
        self.size = size
        self.MIN_VAL = -32.768
        self.MAX_VAL = 32.768
        self.SCORE_MIN = -float('inf')
        self.SCORE_MAX = 0

    def init(self):
        pass

    def eval(self, arr):
        sum1 = sum([x**2 for x in arr])
        sum2 = sum([math.cos(2*math.pi*x) for x in arr])
        n = len(arr)

        score = 20 - 20 * math.exp(-0.2 * math.sqrt(sum1/n)) + math.e - math.exp(sum2/n)
        return -score
    

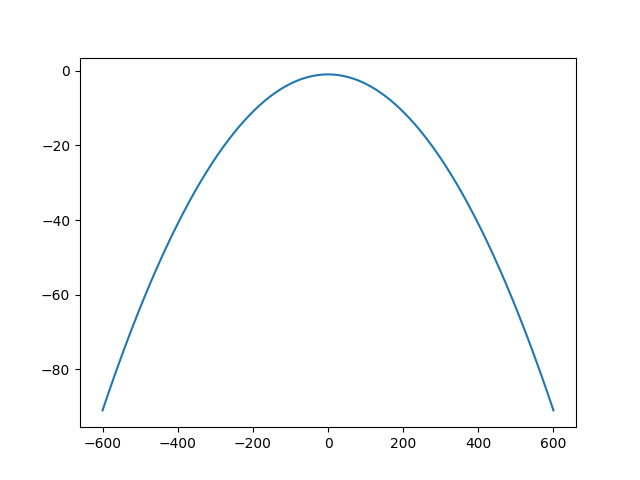
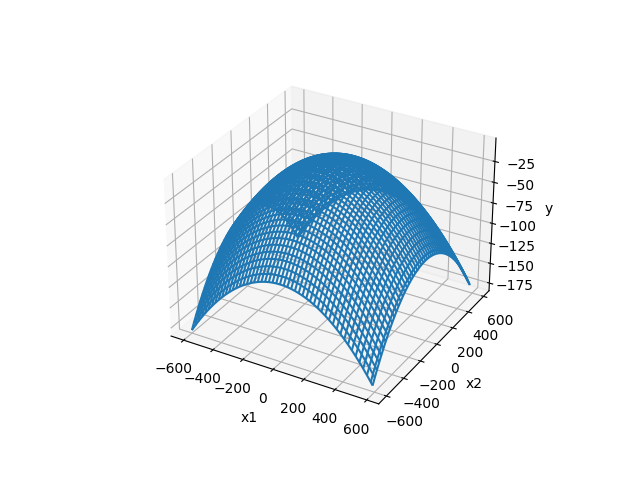
Griewank function

• 1次元のグラフ

• 2次元のグラフ

• プログラムコード

import math
class function_Griewank():
    def __init__(self, size):
        self.size = size
        self.MIN_VAL = -600
        self.MAX_VAL = 600
        self.SCORE_MIN = -float('inf')
        self.SCORE_MAX = 0

    def init(self):
        pass

    def eval(self, arr):
        sum1 = sum([x**2 for x in np_arr])
        prod = 1
        for i, x in enumerate(np_arr):
            prod *= math.cos( x / math.sqrt(i+1) )
        n = 1 + (sum1 - prod) / 4000
        return -n

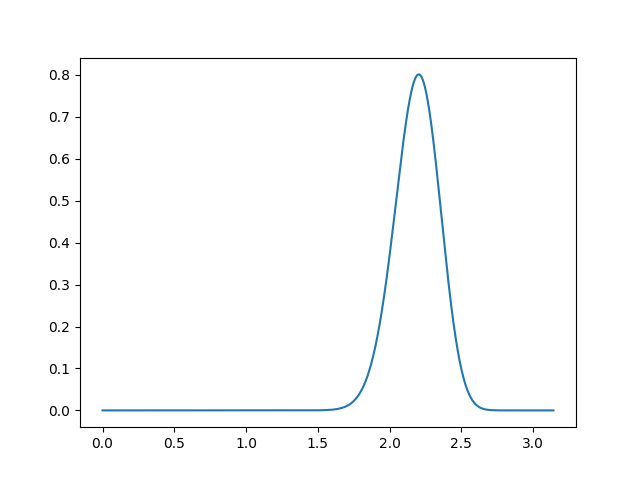
Michalewicz function

• 1次元のグラフ

• 2次元のグラフ

• プログラムコード

import math
class function_Michalewicz():
    def __init__(self, size):
        self.size = size
        self.MIN_VAL = 0
        self.MAX_VAL = math.pi
        self.SCORE_MIN = -float('inf')
        self.SCORE_MAX = 0

    def init(self):
        pass

    def eval(self, arr):
        n = -sum([math.sin(x) * math.sin((i+1)*(x**2)/math.pi)**(2*10) for i,x in enumerate(np_arr)])
        return -n

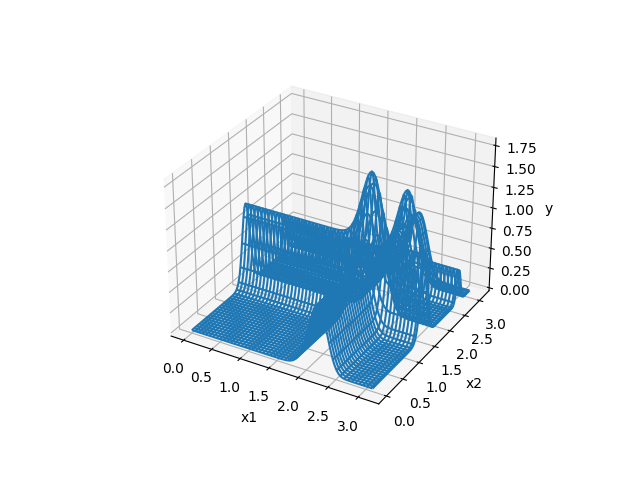
Rastrigin function

• 1次元のグラフ

• 2次元のグラフ

• プログラムコード

import math
class function_Rastrigin():
    def __init__(self, size):
        self.size = size
        self.MIN_VAL = -5.12
        self.MAX_VAL = 5.12
        self.SCORE_MIN = -float('inf')
        self.SCORE_MAX = 0

    def init(self):
        pass

    def eval(self, arr):
        n = sum([x**2 - 10 * math.cos(2*math.pi*x) for x in np_arr])
        return -( 10*self.size + n)

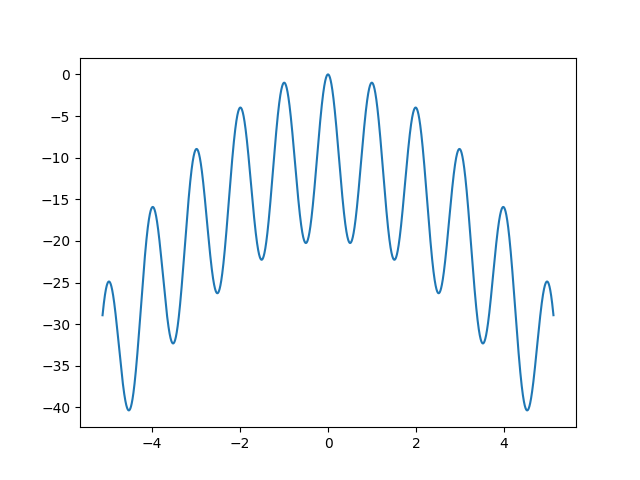
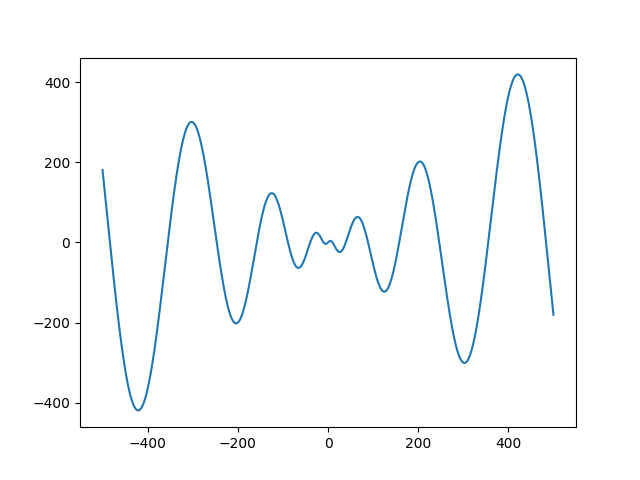
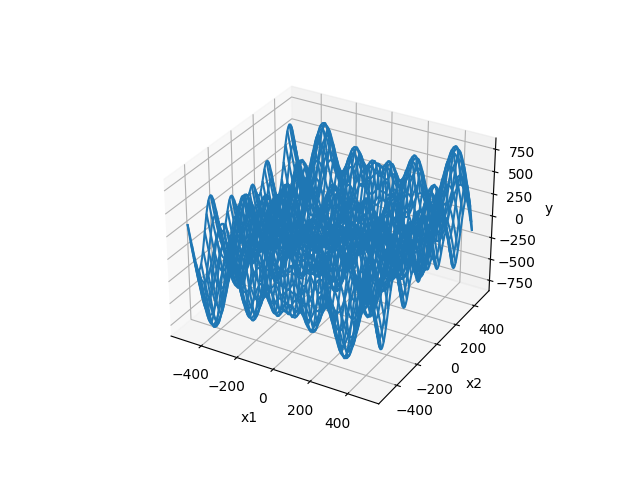
Schwefel function

• 1次元のグラフ

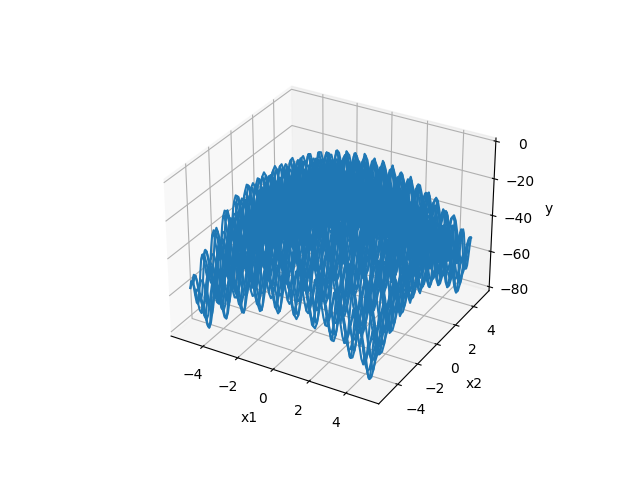
• 2次元のグラフ

• プログラムコード

import math
class function_Schwefel():
    def __init__(self, size):
        self.size = size
        self.MIN_VAL = -500
        self.MAX_VAL = 500
        self.SCORE_MIN = -float('inf')
        self.SCORE_MAX = 0

    def init(self):
        pass

    def eval(self, arr):
        n = sum([x * math.sin(math.sqrt(abs(x))) for x in np_arr])
        return n

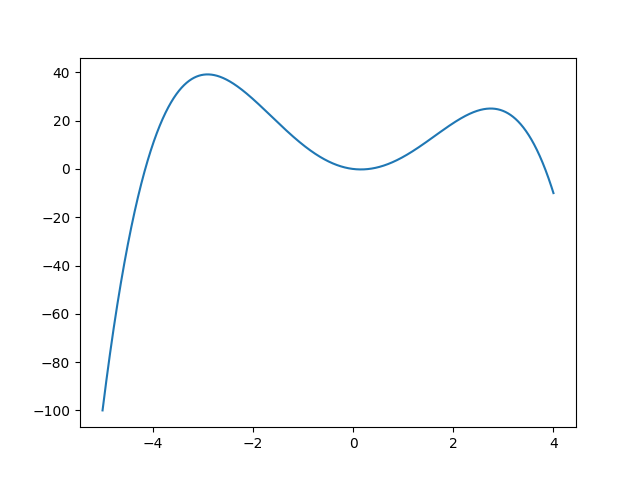
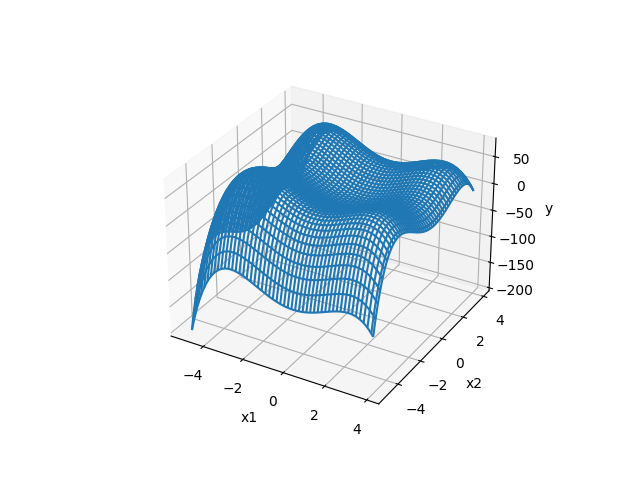
StyblinskiTang function

• 1次元のグラフ

• 2次元のグラフ

• プログラムコード

import math
class function_StyblinskiTang():
    def __init__(self, size):
        self.size = size
        self.MIN_VAL = -5
        self.MAX_VAL = 4
        self.SCORE_MIN = -float('inf')
        self.SCORE_MAX = 0

    def init(self):
        pass

    def eval(self, arr):
        n = sum([x ** 4 - 16*(x**2) + 5*x for x in np_arr])
        return -n/2

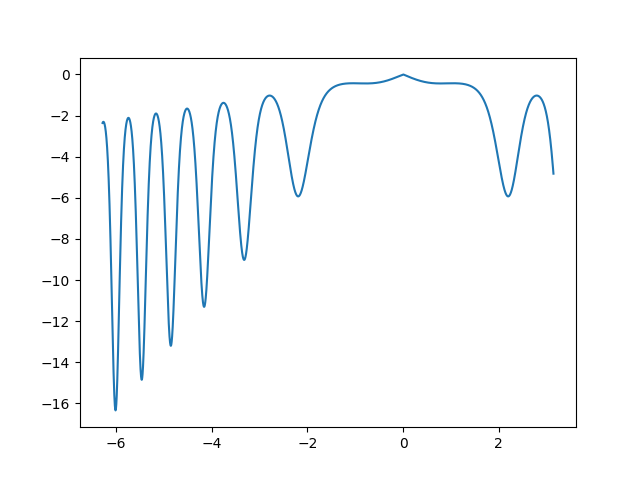
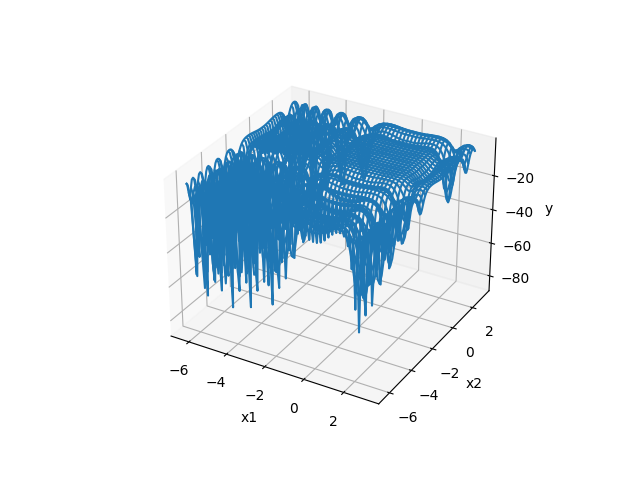
XinSheYang function

• 1次元のグラフ

• 2次元のグラフ

• プログラムコード

import math
class function_XinSheYang():
    def __init__(self, size):
        self.size = size
        self.MIN_VAL = -2*math.pi
        self.MAX_VAL = math.pi
        self.SCORE_MIN = -float('inf')
        self.SCORE_MAX = 0

    def init(self):
        pass

    def eval(self, arr):
        sum1 = sum([abs(x) for x in np_arr])
        sum2 = sum([math.sin(x**2) for x in np_arr])
        n = sum1 * math.exp(-sum2)
        return -n