最適化アルゴリズムを実装していくぞ（カッコウ探索）

はじめに

最適化アルゴリズムの実装シリーズです。
まずは概要を見てください。

コードはgithubにあります。

カッコウ探索

概要

カッコウ探索(Cucko Search)は、カッコウの托卵という行動をもとに作られたアルゴリズムです。
托卵は他の種類の鳥の巣に卵を産み、その巣の親に育成を頼む行為です。

また、カッコウを含めた野生動物は獲物を探すときにレヴィフライトというレヴィ分布と呼ばれる分布に従って移動することが知られています。

参考
・Cuckoo search
・進化計算アルゴリズム入門 生物の行動科学から導く最適解

アルゴリズム

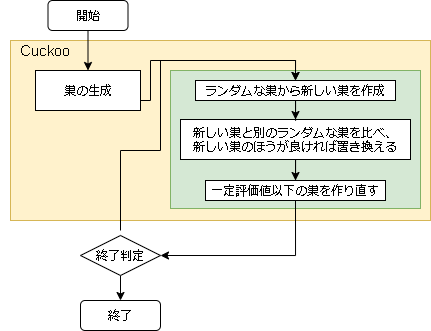
ランダムな巣を元に卵を作成し、別の巣を作ります。
この時に作成される卵は、レヴィ分布に従って生成されます。

作成された巣はさらに別のランダムな巣と比較し、良ければ置き換えられます。

最後に評価値の悪い巣は破棄され、新しい巣に置き換えられます。

• アルゴリズムのフロー

• 用語の対応

問題	カッコウ探索
入力値の配列	巣
入力値	卵
評価値	巣の評価値

• ハイパーパラメータに関して

変数名	意味	所感
scaling_rate	レヴィ分布の尺度	大きいほど遠くに移動しやすくなる
levy_rate	レヴィフライトの反映率	大きいほどレヴィフライトによる移動が大きい
bad_nest_rate	悪い巣の割合	高いほど巣の入れ替え（探索範囲）が多くなる

巣の作成

ランダムに選んだ巣からレヴィ分布に従って新しい巣を作成します。

$$ x^{new}_i = x^{r}_i + \alpha s $$

$s$ はレヴィ分布に従った乱数（レヴィフライト）で、$\alpha$ はレヴィフライトの反映率となります。
この巣の生成がカッコウ探索のすべてですが、レヴィフライトがちょっと厄介です。

レヴィ分布は以下です。

$$ f(x; \mu, c) = \sqrt{ \frac{c}{2 \pi} } \frac{ \exp^{\frac{-c}{2(x - \mu)}} }{ (x - \mu)^{\frac{2}{3}}} $$

import math
def levy(x, u=0, c=1):
    if x == 0:
        return 0
    t = math.exp((-c/(2 * (x-u))))
    t /= (x-u) ** (3/2)
    return math.sqrt(c/(2*math.pi)) * t

このレヴィ分布に従った乱数を生成する必要があります。
レヴィ分布に従った乱数は Mantegna アルゴリズムで求めます。

$$ s = \frac{u}{|v|^{\frac{1}{\beta}}} $$

ここで $\beta$ はスケーリング指数で0～2の実数をとります。
$u$ は平均0,分散 $\sigma^2$の正規分布に従う乱数、
$v$ は標準正規分布に従う乱数です。

$\sigma$ は以下の式で求まります。

$$ \sigma = \Biggl( \frac{ \Gamma(1+\beta) \sin(\frac{\pi \beta}{2}) }{ \Gamma(\frac{1+\beta}{2}) \beta 2^{\frac{(\beta-1)}{2}} } \Biggr)^{\frac{1}{\beta}} $$

$\Gamma$ はガンマ関数を表します。

$$ \Gamma(x) = \int_{0}^{\infty} t^{x-1}e^{-t} dt $$

• 正規分布の乱数

正規分布の乱数ですが、pythonのnumpyライブラリを使うと以下で簡単に出せます。

import numpy as np
np.random.randn()  # 標準正規分布の一様乱数を生成
np.random.normal(0, sigma)  # 平均0、分散sigma^2の正規分布に従う乱数

が、他の言語(主にluaとか)での実装も考えているのでライブラリを使わない方法も書いておきます。

標準正規分布の乱数はボックス＝ミュラー法で出すことができます。

$$ z = \sqrt{-2 \log{X}} \cos{2\pi Y} $$

ここで X と Y は互いに独立した一様乱数になります。
pythonだと以下です。

import math
def random_normal():
    r1 = random.random()
    r2 = random.random()
    return math.sqrt(-2.0 * math.log(r1)) * math.cos(2*math.pi*r2)

• ガンマ関数

ガンマ関数も math を使うと簡単に出せます。

import math
math.gamma(x)

使わない場合はここのサイトのコードを使わせてもらいました。
（コードは全体コードに記載しています）

レヴィ分布に関して

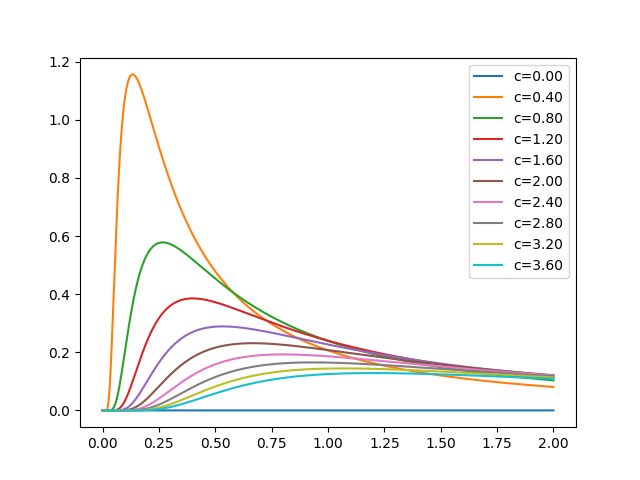
レヴィ分布のグラフです。

レヴィ分布ですが見てわかるように範囲が 0～∞ です。
これは卵を生成する場合に少しネックになります。

例えばOneMaxの問題だと範囲が0～1しかとりません。
この問題に対してレヴィ分布で生成された1以上の値をどうするかは決まっていません。
ここで、例えば1以上の値は1にするとした場合、生成された乱数がレヴィ分布に従わなくなります。
(1の生成確率だけ高くなってしまう)

これはどうなんでしょうかね。
解決方法もよくわからないので今のところは放置しています。

コード全体

import math
import random

import numpy as np


############################################
# Γ（ｘ）の計算（ガンマ関数，近似式）
#      ier : =0 : normal
#            =-1 : x=-n (n=0,1,2,･･･)
#      return : 結果
#      coded by Y.Suganuma
# https://www.sist.ac.jp/~suganuma/programming/9-sho/prob/gamma/gamma.htm
############################################
def gamma(x):
    if x <= 0:
        raise ValueError("math domain error")

    ier = 0

    if x > 5.0 :
        v = 1.0 / x
        s = ((((((-0.000592166437354 * v + 0.0000697281375837) * v + 0.00078403922172) * v - 0.000229472093621) * v - 0.00268132716049) * v + 0.00347222222222) * v + 0.0833333333333) * v + 1.0
        g = 2.506628274631001 * math.exp(-x) * pow(x,x-0.5) * s

    else:

        err = 1.0e-20
        w   = x
        t   = 1.0

        if x < 1.5 :

            if x < err :
                k = int(x)
                y = float(k) - x
                if abs(y) < err or abs(1.0-y) < err :
                    ier = -1

            if ier == 0 :
                while w < 1.5 :
                    t /= w
                    w += 1.0

        else :
            if w > 2.5 :
                while w > 2.5 :
                    w -= 1.0
                    t *= w

        w -= 2.0
        g  = (((((((0.0021385778 * w - 0.0034961289) * w + 0.0122995771) * w - 0.00012513767) * w + 0.0740648982) * w + 0.0815652323) * w + 0.411849671) * w + 0.422784604) * w + 0.999999926
        g *= t

    return g


def random_normal():
    """
    正規分布の乱数
    ボックス＝ミュラー法
    """
    r1 = random.random()
    r2 = random.random()
    return math.sqrt(-2.0 * math.log(r1)) * math.cos(2*math.pi*r2)


def mantegna(beta):
    """
    mantegna アルゴリズム
    """
    #beta:  0.0 - 2.0
    if beta < 0.005:
        # 低すぎると OverflowError: (34, 'Result too large')
        beta = 0.005
    # siguma
    t = gamma(1+beta) * math.sin(math.pi*beta/2)
    t = t/( gamma((1+beta)/2) * beta * 2**((beta-1)/2) )
    siguma = t**(1/beta)

    u = random_normal()*siguma  # 平均0 分散siguma^2 の正規分布に従う乱数
    v = random_normal()  # 標準正規分布に従う乱数

    s = (abs(v)**(1/beta))
    if s < 0.0001:
        # 低すぎると ValueError: supplied range of [-inf, inf] is not finite
        s = 0.0001
    s = u / s
    return s


class Cuckoo():
    def __init__(self, 
        nest_max,
        scaling_rate=1.0,
        levy_rate=1.0,
        bad_nest_rate=0.1
    ):
        self.nest_max = nest_max
        self.scaling_rate = scaling_rate
        self.levy_rate = levy_rate

        # 悪い巣の割合から悪い巣の個数を算出
        self.bad_nest_num = int(nest_max * bad_nest_rate + 0.5)
        if self.bad_nest_num > nest_max-1:
            self.bad_nest_num = nest_max-1
        if self.bad_nest_num < 0:
            self.bad_nest_num = 0

    def init(self, problem):
        self.problem = problem

        self.nests = []
        for _ in range(self.nest_max):
            self.nests.append(problem.create())

    def step(self):
        # ランダムに巣を選択
        r = random.randint(0, self.nest_max-1)  # a<=x<=b

        # 新しい巣を作成
        arr = self.nests[r].getArray()

        for i in range(len(arr)):

            # レヴィフライで卵を作る
            arr[i] = arr[i] + self.levy_rate * mantegna(self.scaling_rate)

        new_nest = self.problem.create(arr)

        # ランダムな巣と比べてよければ変える
        r = random.randint(0, self.nest_max-1)  # a<=x<=b
        if self.nests[r].getScore() < new_nest.getScore():
            self.nests[r] = new_nest

        # 悪い巣を消して新しく作る
        self.nests.sort(key=lambda x:x.getScore())
        for i in range(self.bad_nest_num):
            self.nests[i] = self.problem.create()

カッコウ探索(ε-greedy)

これは本記事オリジナルです。（探せばあるかも？）
カッコウ探索はとてもシンプルなアルゴリズムですが、レヴィフライトの実装がすごく厄介です。

そこでレヴィフライトをε-greedyに置き換えてみました。
ε-greedyに置き換えることで実装がすごい簡単になりましたね。

ε-greedyでもそこそこの精度がでるような気がします。

コード全体

import math
import random

class Cuckoo_greedy():
    def __init__(self, 
        nest_max,
        epsilon=0.1, 
        bad_nest_rate=0.1
    ):
        self.nest_max = nest_max
        self.epsilon = epsilon

        # 悪い巣の割合から悪い巣の個数を算出
        self.bad_nest_num = int(nest_max * bad_nest_rate + 0.5)
        if self.bad_nest_num > nest_max-1:
            self.bad_nest_num = nest_max-1
        if self.bad_nest_num < 0:
            self.bad_nest_num = 0

    def init(self, problem):
        self.problem = problem

        self.nests = []
        for _ in range(self.nest_max):
            self.nests.append(problem.create())

    def step(self):
        # ランダムに巣を選択
        r = random.randint(0, self.nest_max-1)  # a<=x<=b

        # 新しい巣を作成
        arr = self.nests[r].getArray()

        for i in range(len(arr)):

            # ε-greedy で卵を新しく作成する
            if random.random() < self.epsilon:
                arr[i] = self.problem.randomVal()

        new_nest = self.problem.create(arr)

        # ランダムな巣と比べてよければ変える
        r = random.randint(0, self.nest_max-1)  # a<=x<=b
        if self.nests[r].getScore() < new_nest.getScore():
            self.nests[r] = new_nest

        # 悪い巣を消して新しく作る
        self.nests.sort(key=lambda x:x.getScore())
        for i in range(self.bad_nest_num):
            self.nests[i] = self.problem.create()

ハイパーパラメータ例

各問題に対して optuna でハイパーパラメータを最適化した結果です。
最適化の1回の試行は、探索時間を2秒間として結果を出しています。
これを100回実行し、最適なハイパーパラメータを optuna に探してもらいました。

• カッコウ探索

問題	bad_nest_rate	levy_rate	nest_max	scaling_rate
EightQueen	0.09501642206708413	0.9797131483689493	14	1.9939515457735189
function_Ackley	0.0006558326608885681	0.3538825414958845	4	0.9448539685962172
function_Griewank	0.23551408245457767	0.30150681160121073	2	0.9029863706820189
function_Michalewicz	0.00438839398648697	0.0004796264527609298	2	1.5288609934193742
function_Rastrigin	0.13347040982335695	0.031401149135082206	7	1.6949622109706082
function_Schwefel	0.0003926596935418525	0.02640034426449156	4	0.5809451877075759
function_StyblinskiTang	0.08462936367613791	0.0633939067767827	5	1.7236388666366773
LifeGame	0.8819375718376719	0.015175414454036936	33	1.3899842408715666
OneMax	0.89872646833605	0.1261650035421213	17	0.04906594355889626
TSP	0.024559598255857823	0.008225444982304852	4	1.8452535160497248

• カッコウ探索(ε-greedy)

問題	bad_nest_rate	epsilon	nest_max
EightQueen	0.004374125594794304	0.03687227169502155	7
function_Ackley	0.5782260075661492	0.031195954391595435	2
function_Griewank	0.23314007403872794	0.05206930732996057	2
function_Michalewicz	0.11845570554906226	0.02242832420874199	3
function_Rastrigin	0.009725819291390304	0.025727770986639094	3
function_Schwefel	0.22978641596753258	0.048159183280607774	2
function_StyblinskiTang	0.14184473157004032	0.01965829867603547	2
LifeGame	0.7358005558643367	0.9115290938258255	39
OneMax	0.0016700608620328905	0.006003869128710593	2
TSP	0.00023997215188062415	0.030790166824531992	29

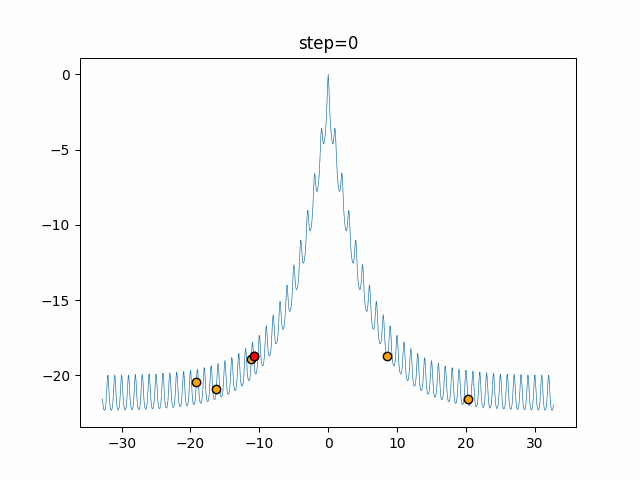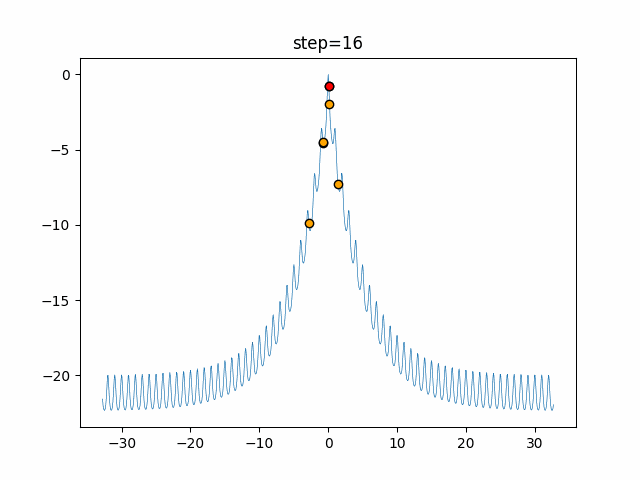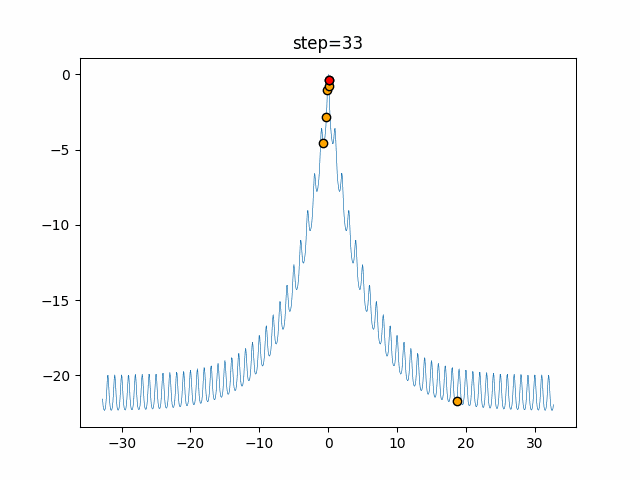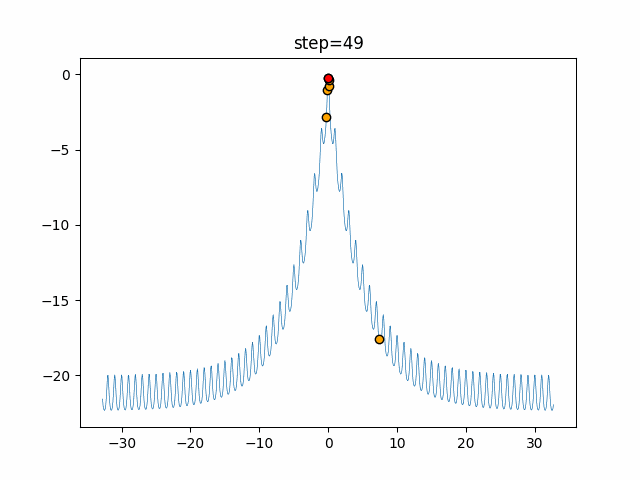
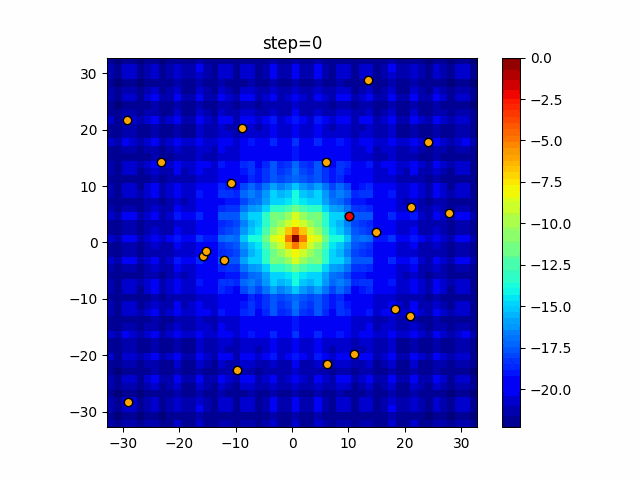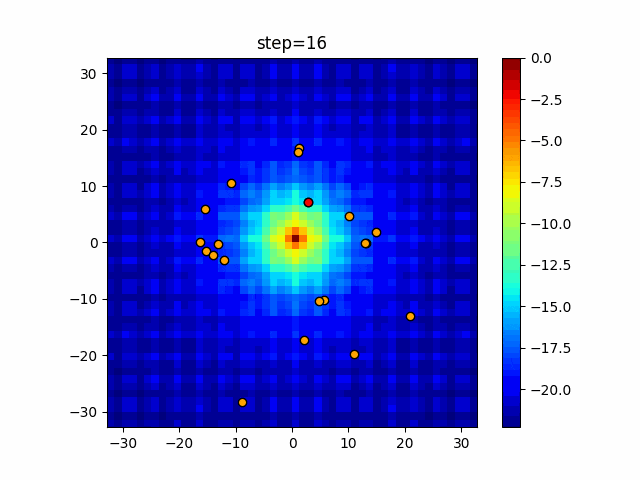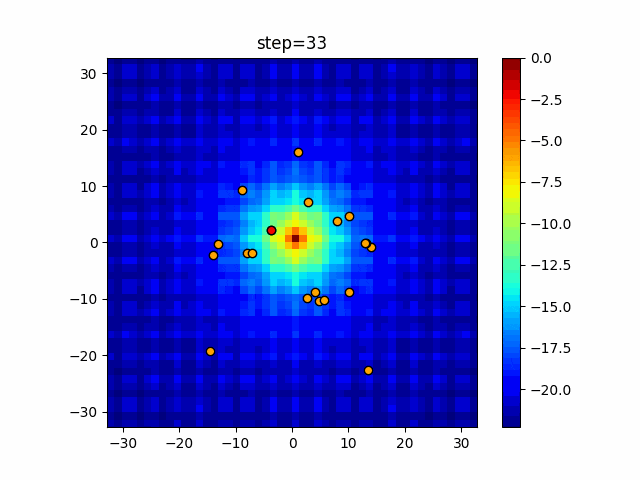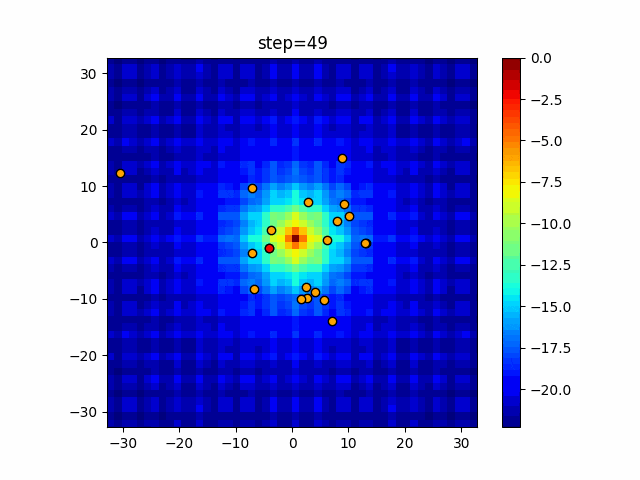
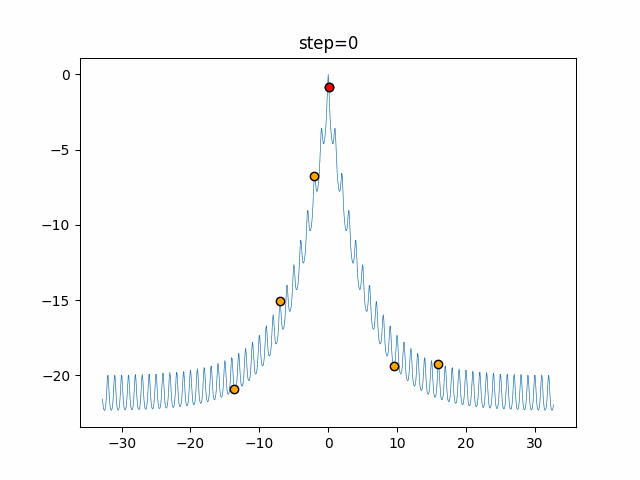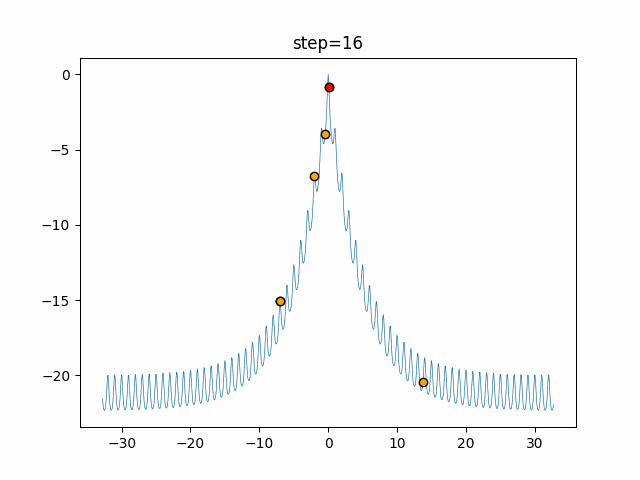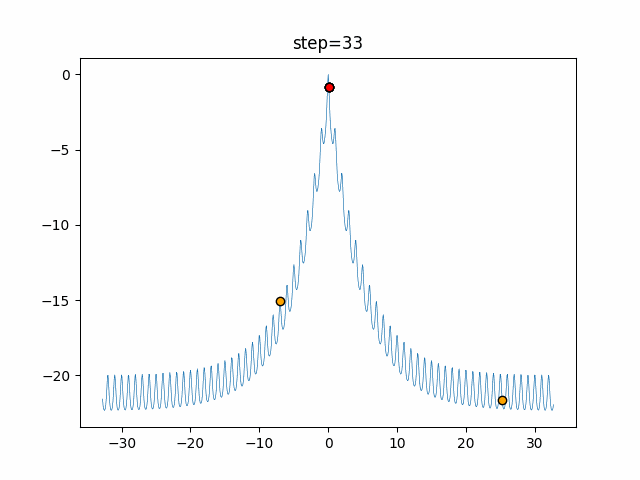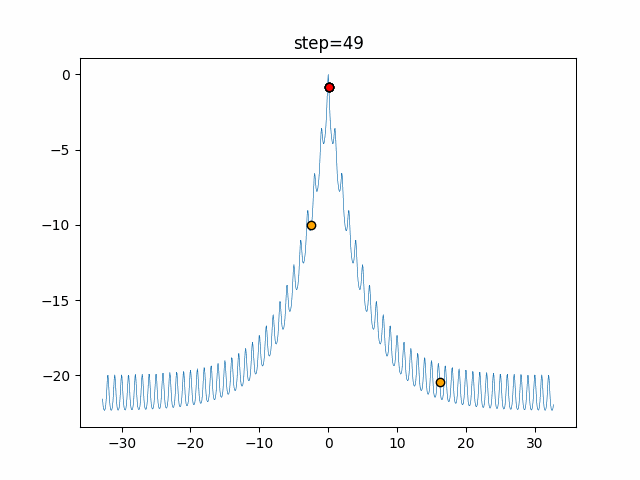
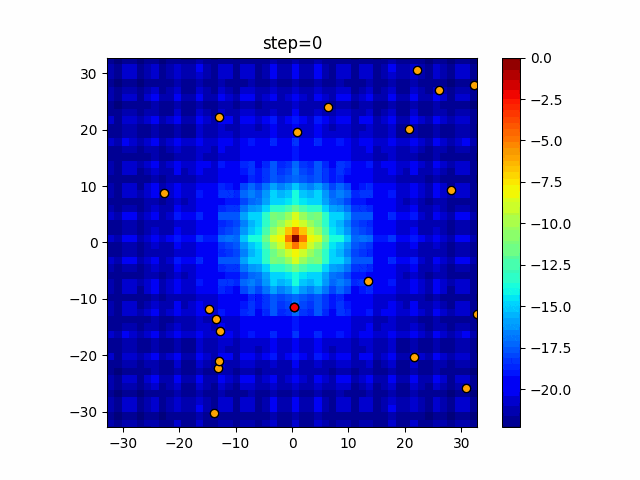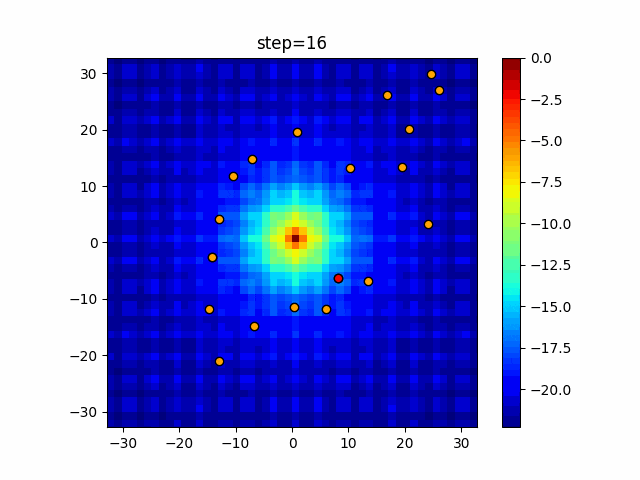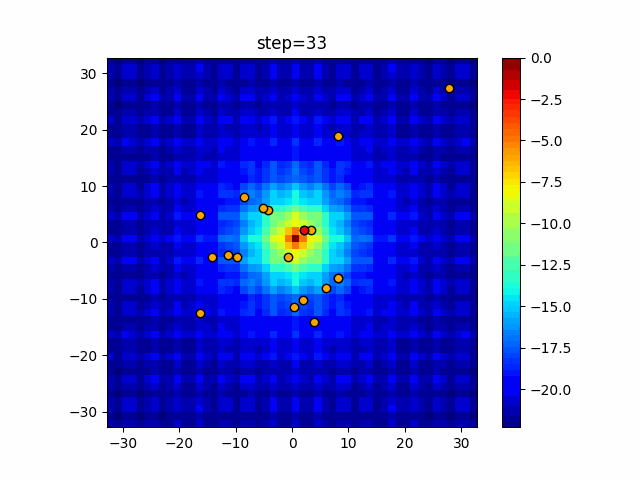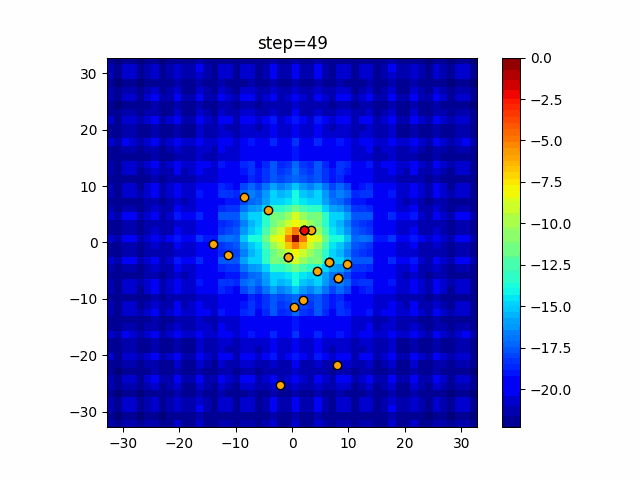
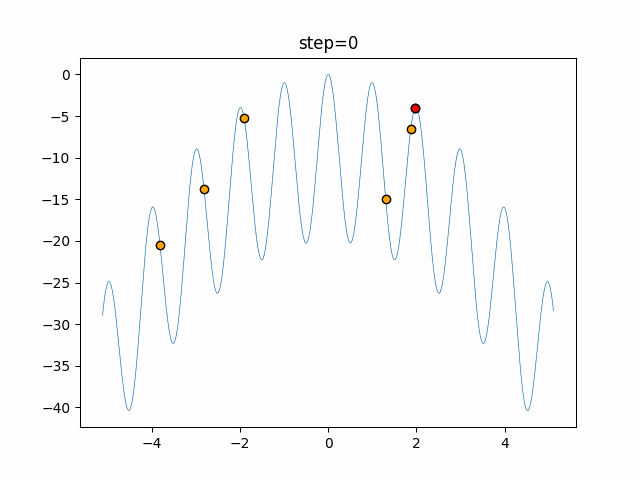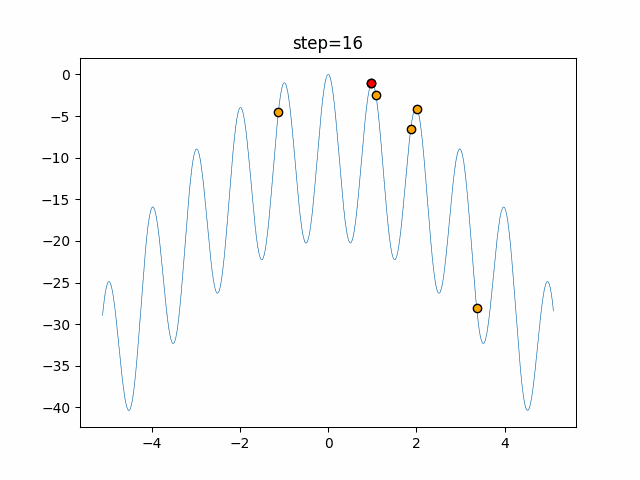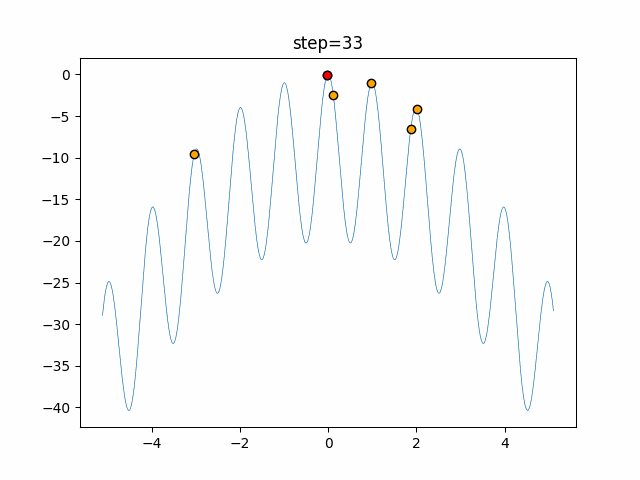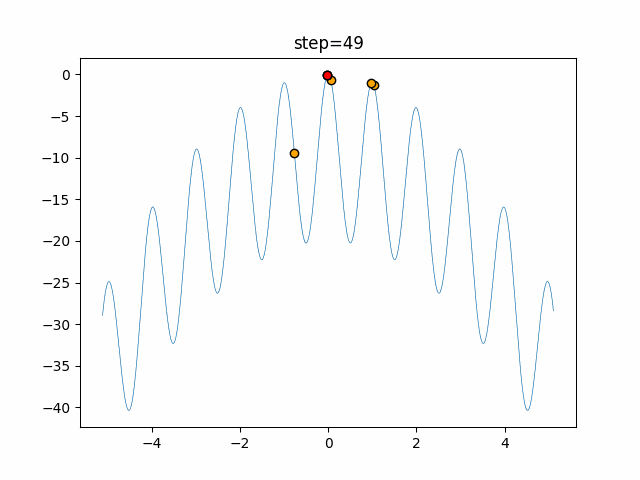
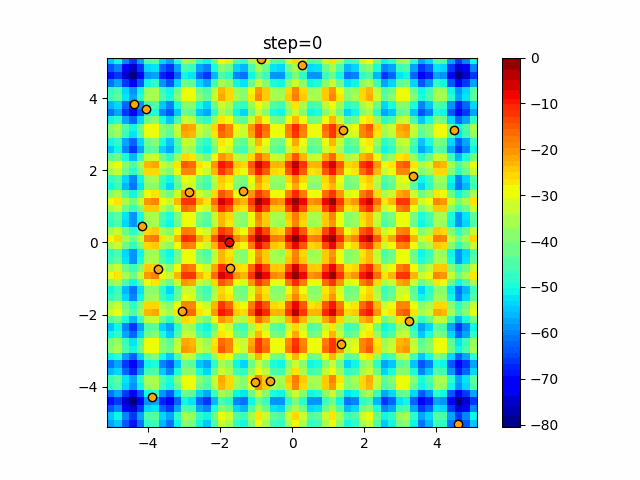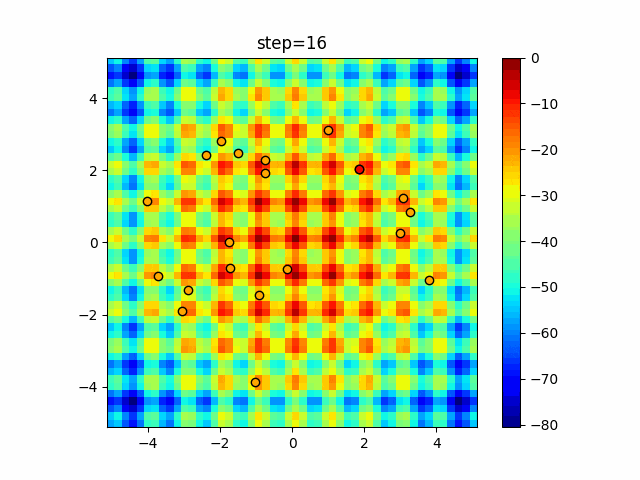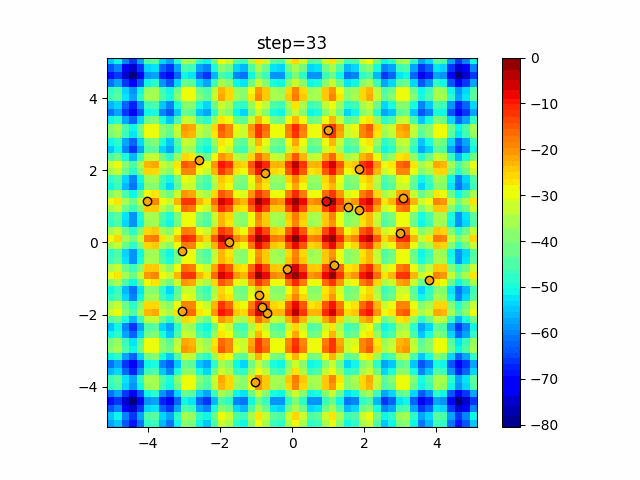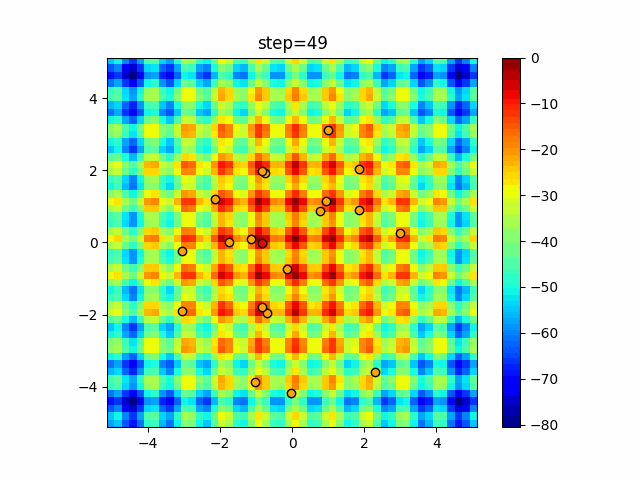
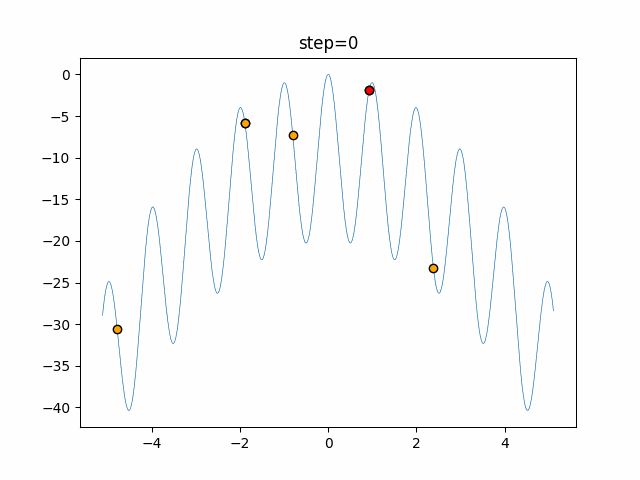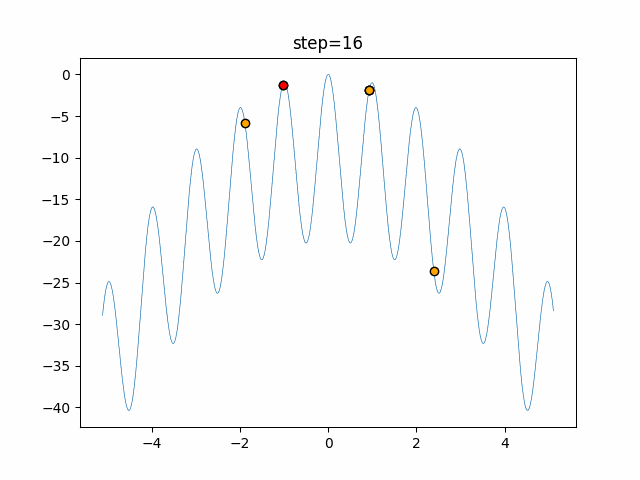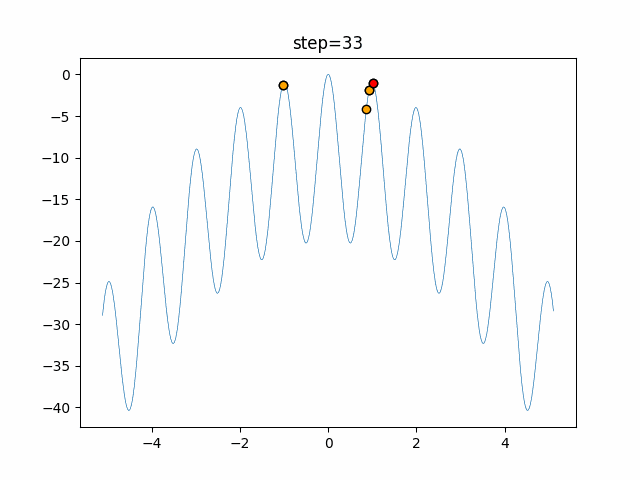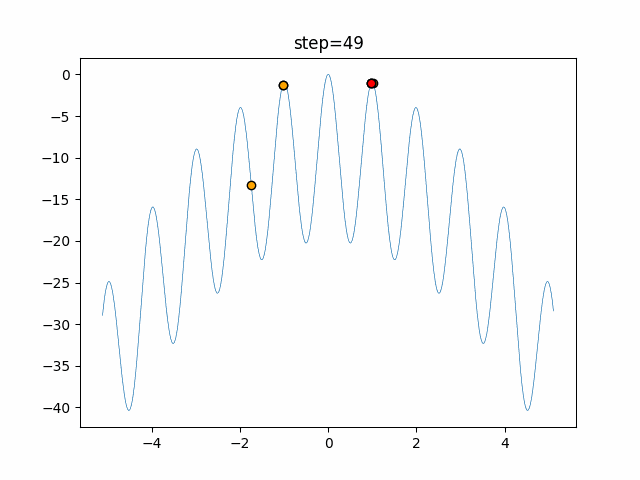
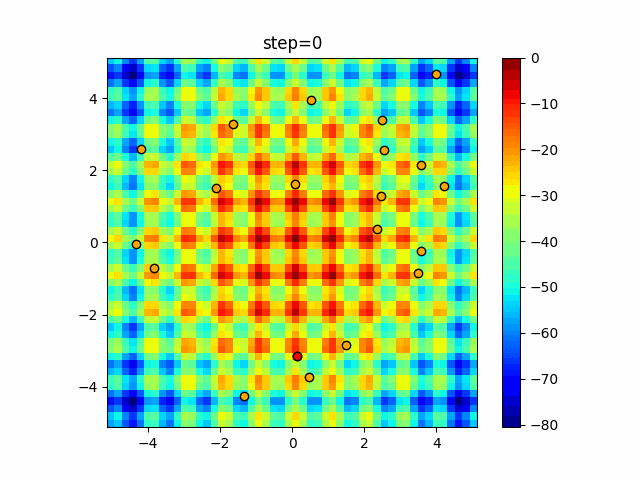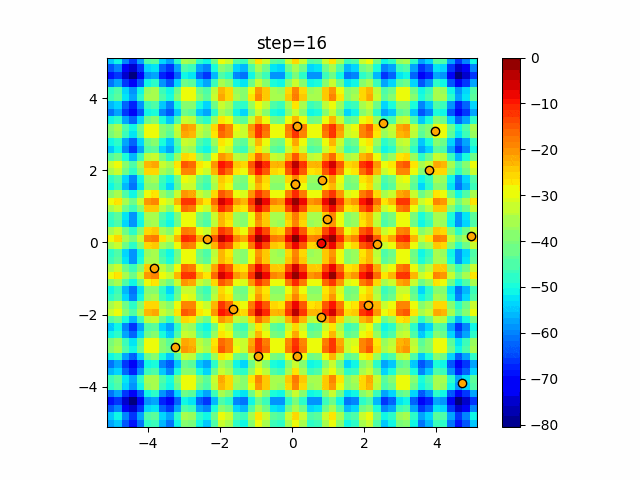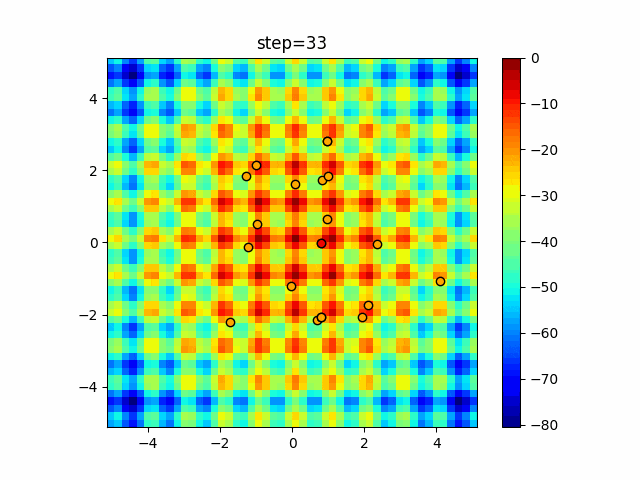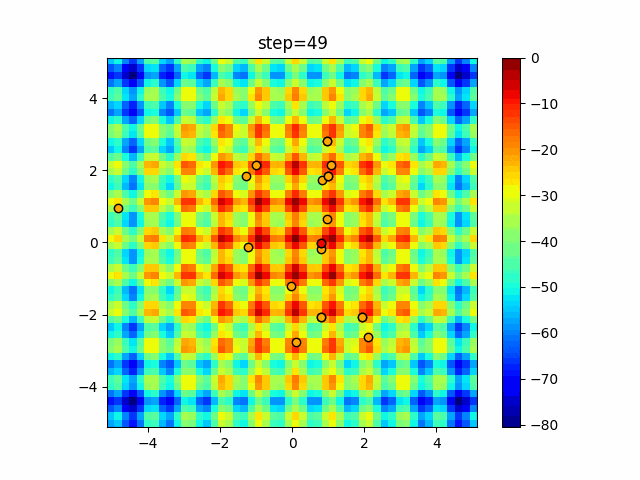
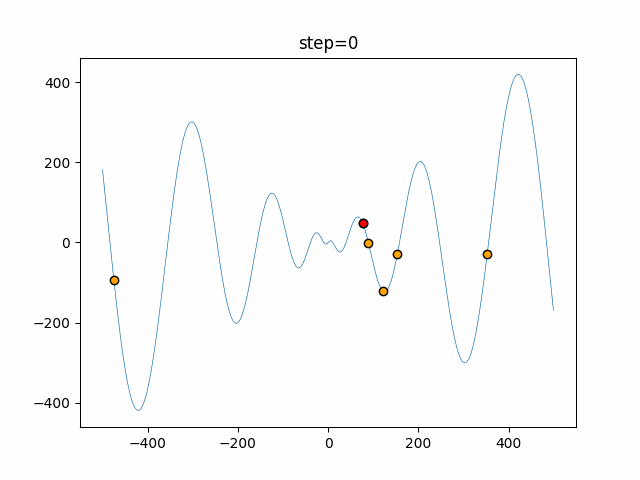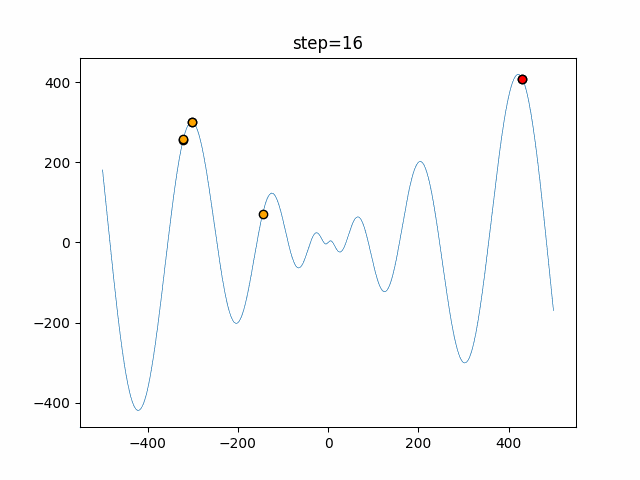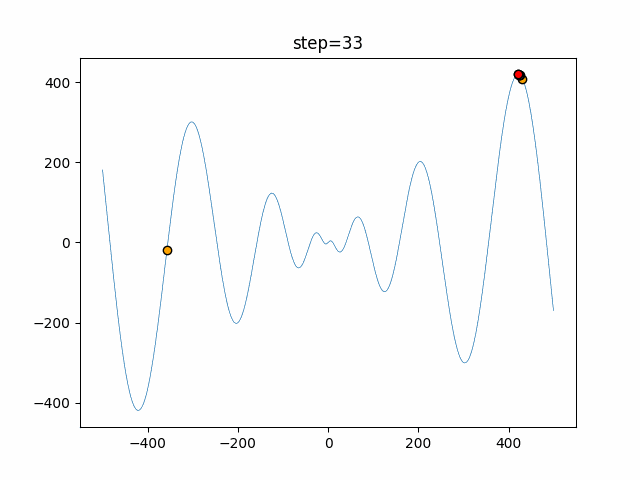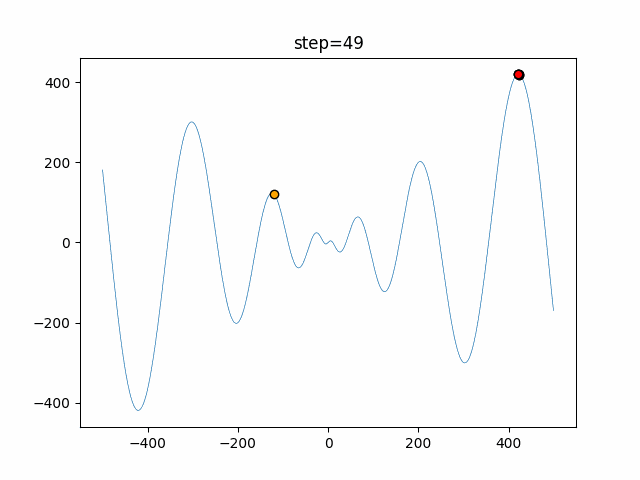
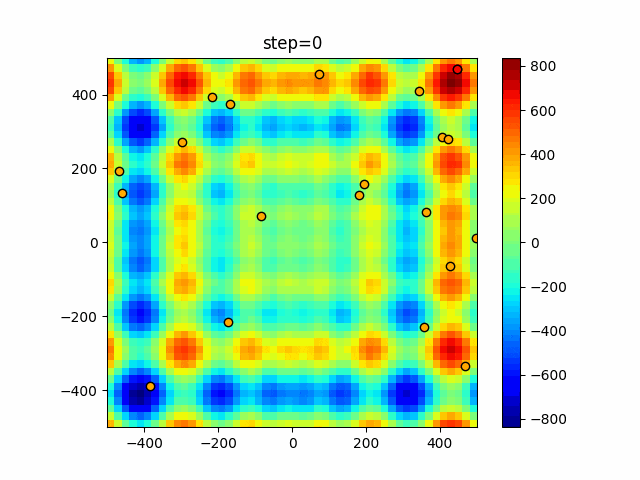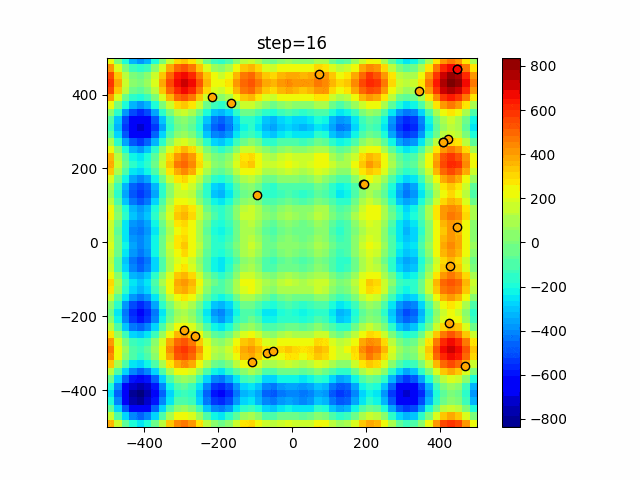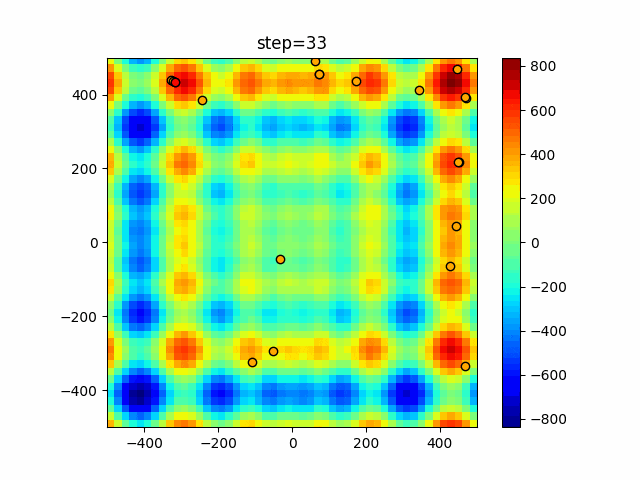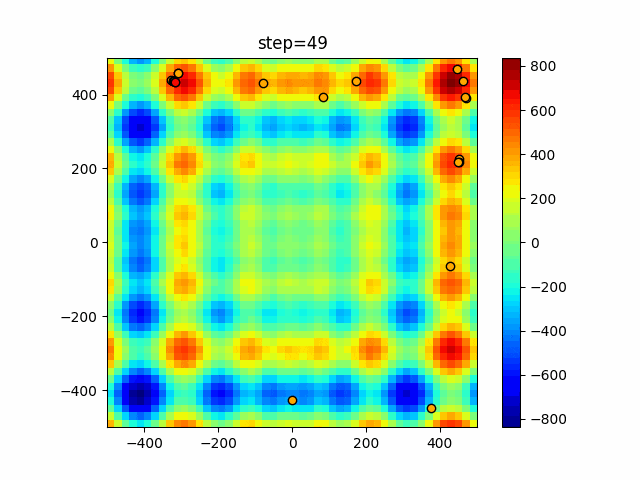
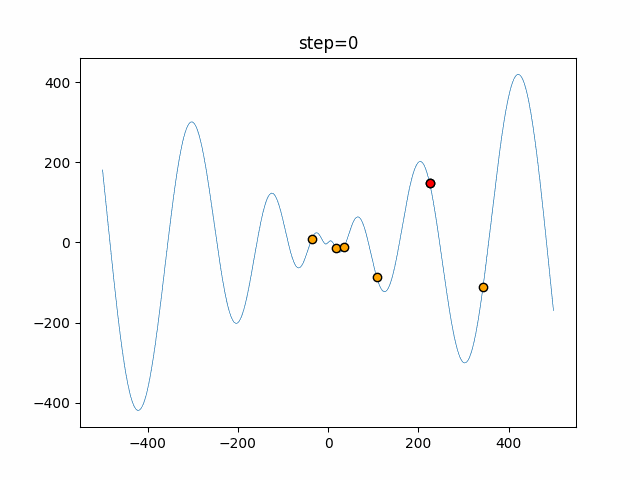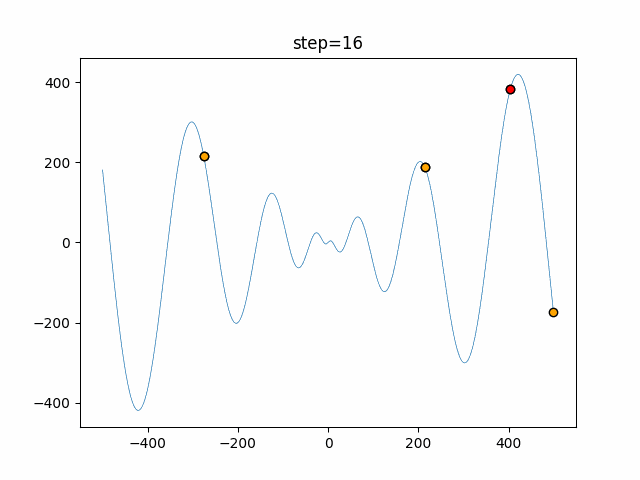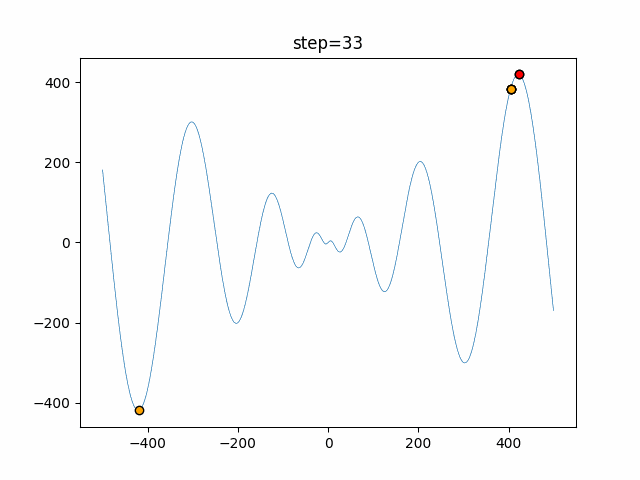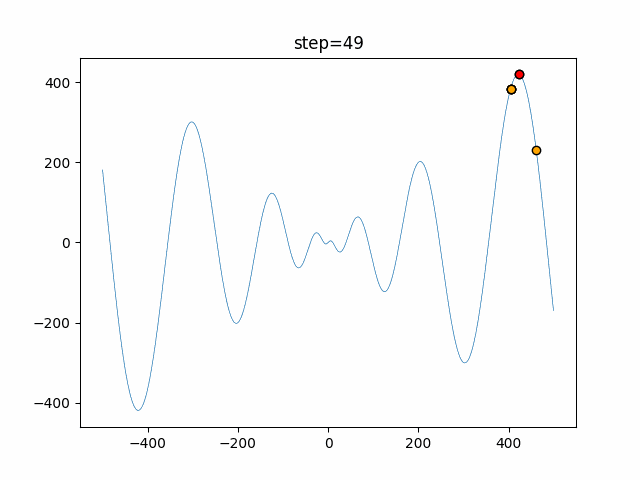
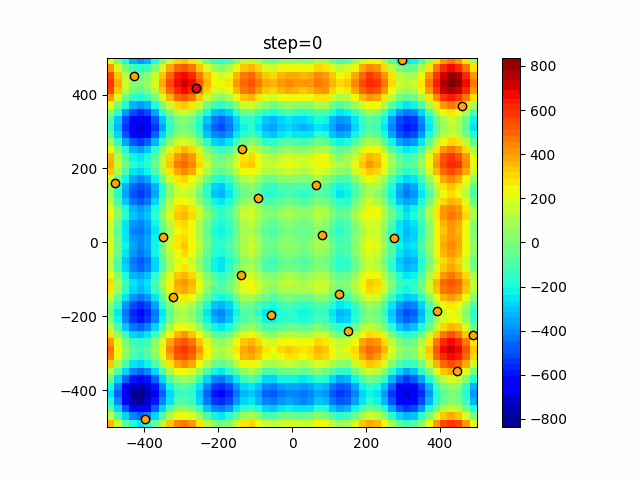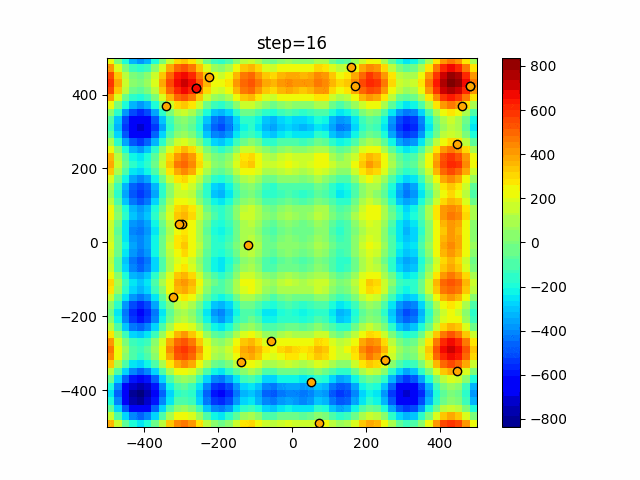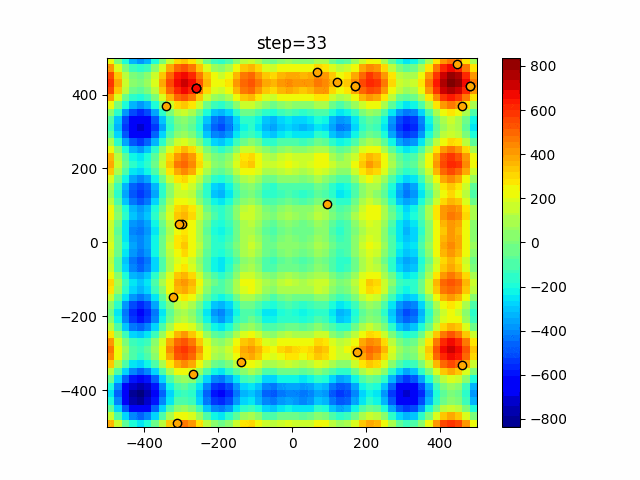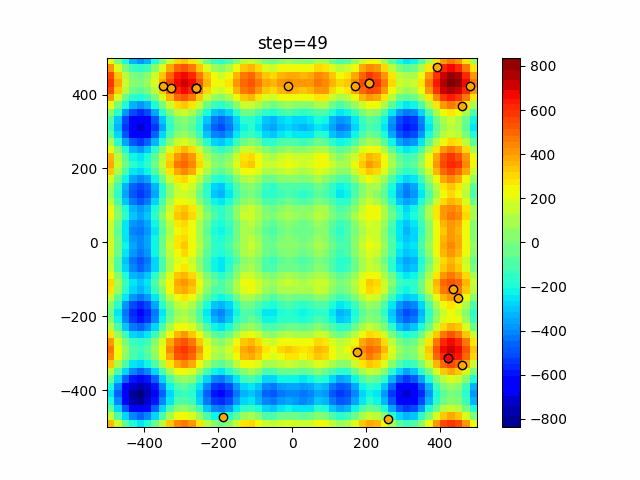
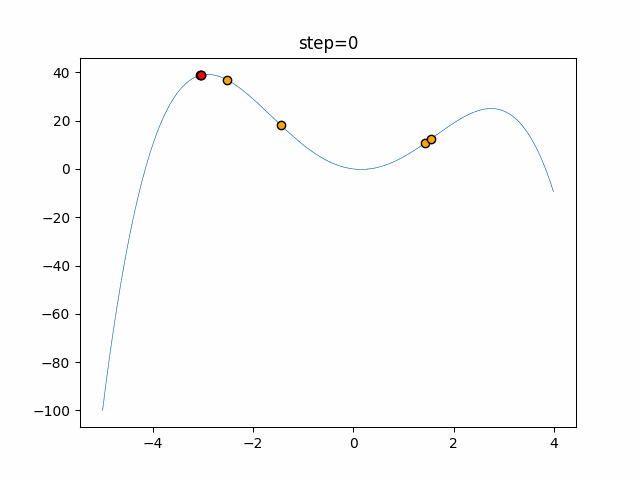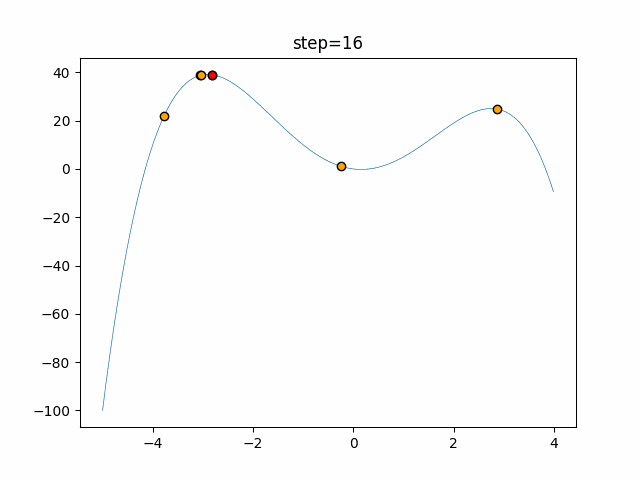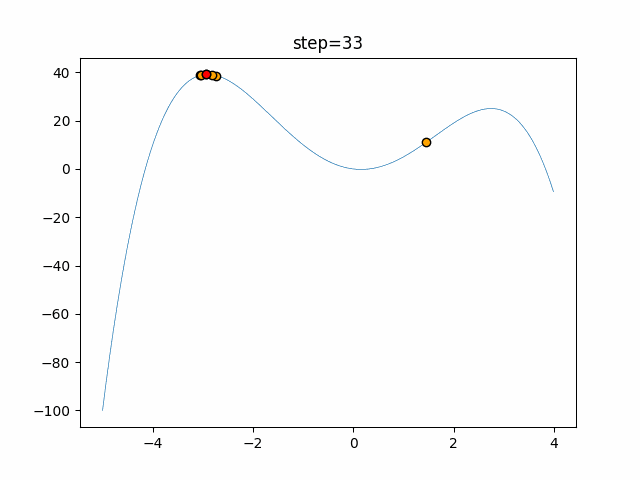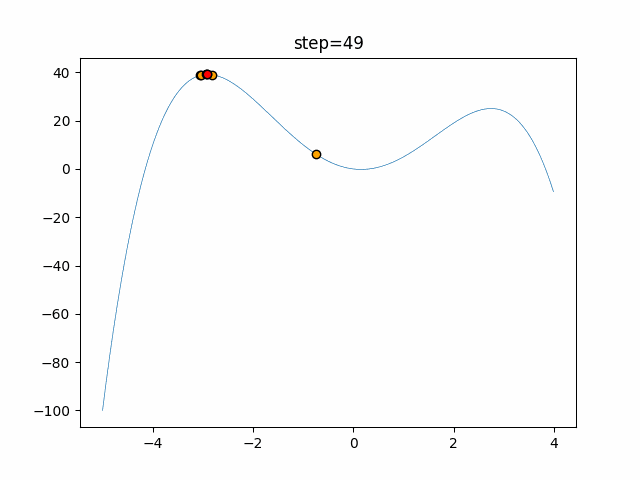
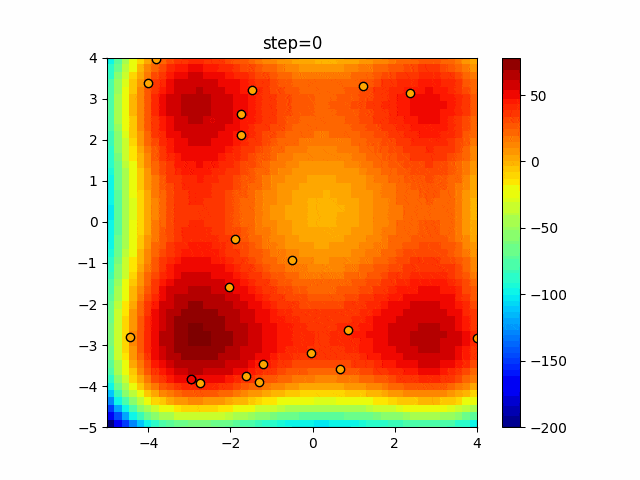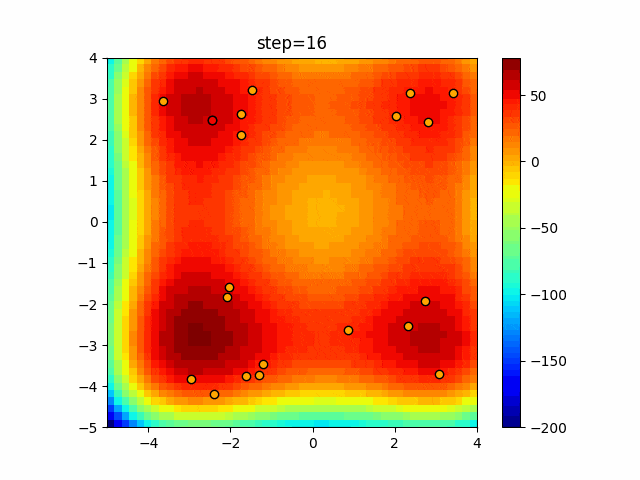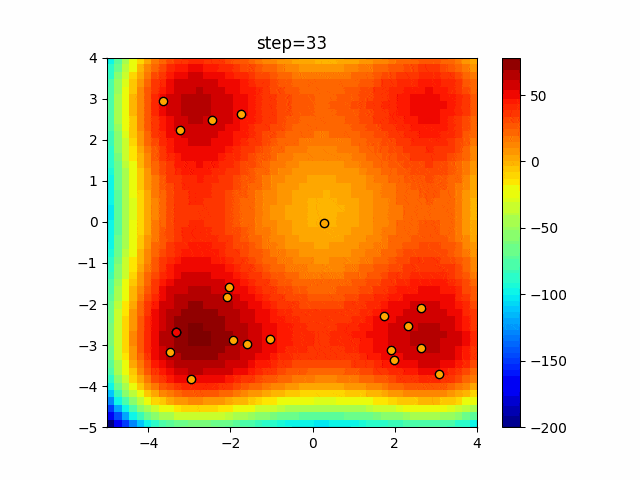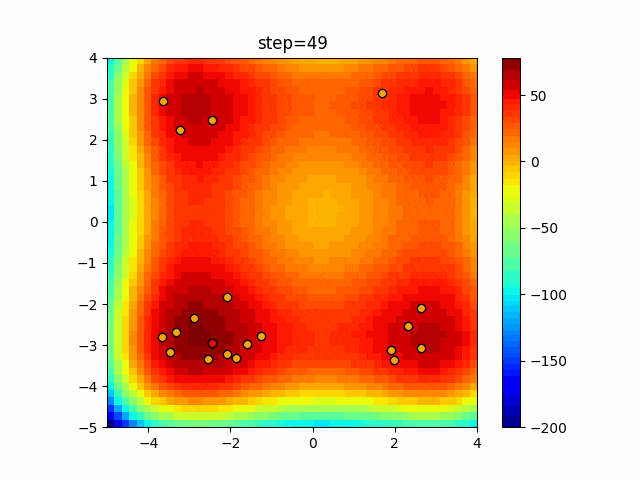
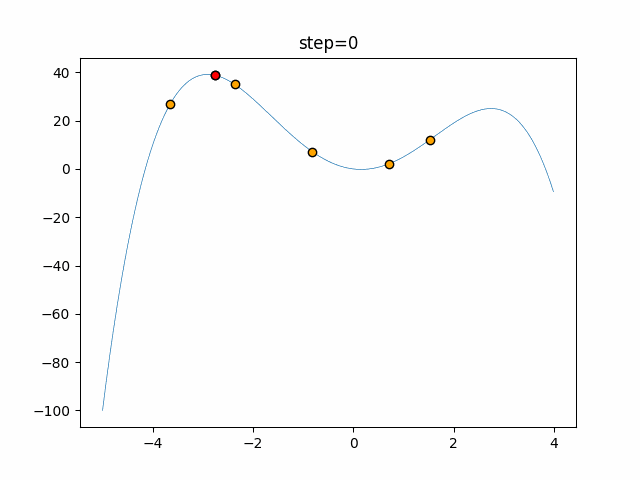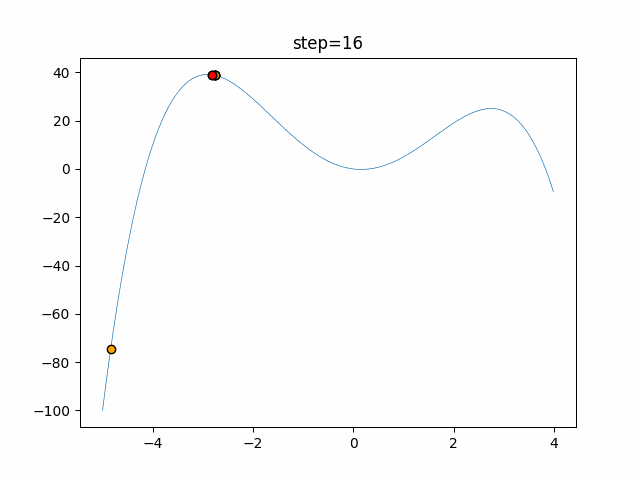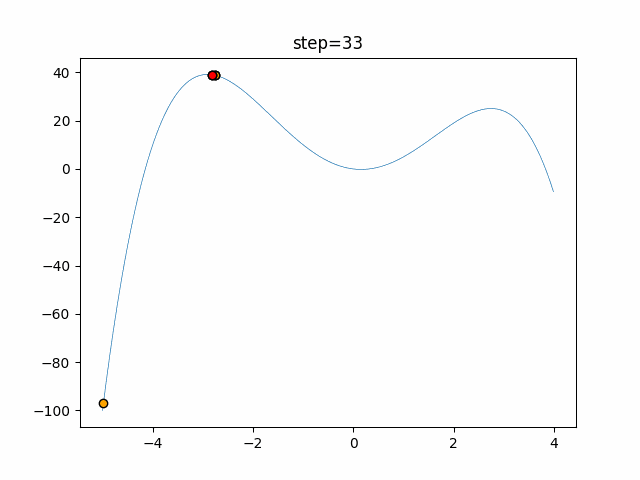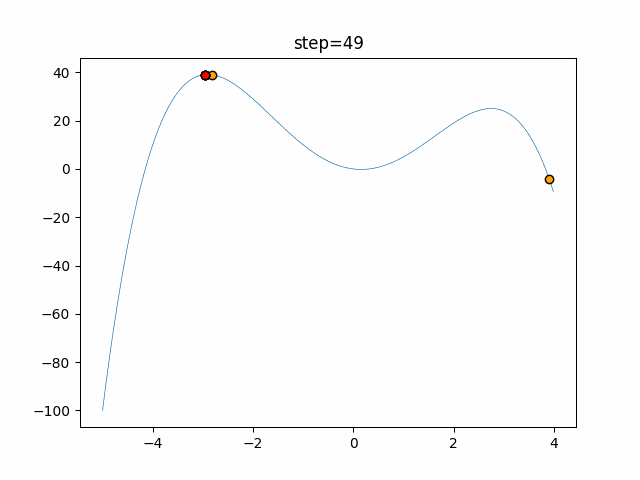
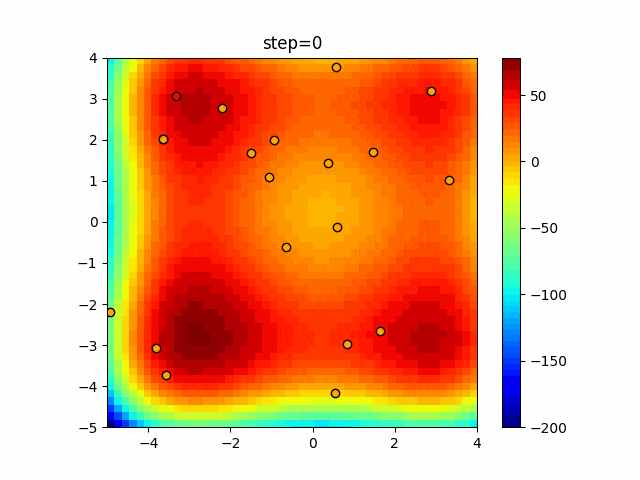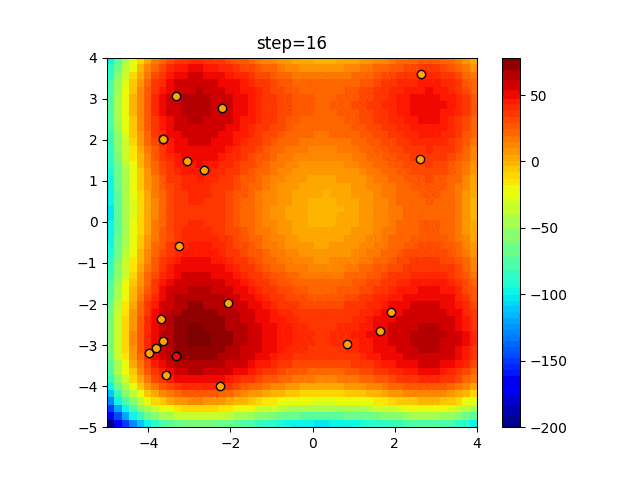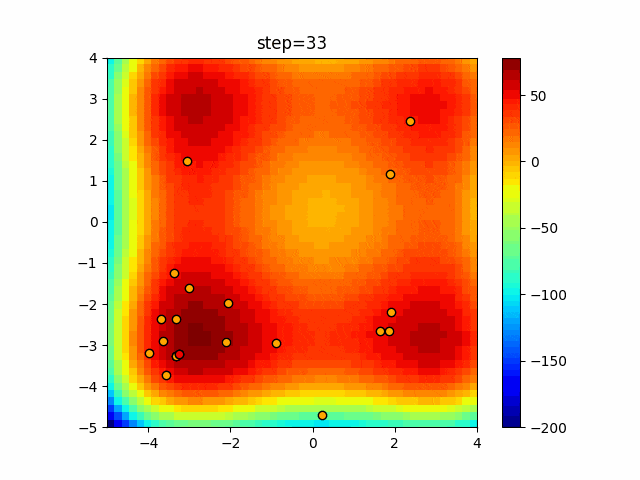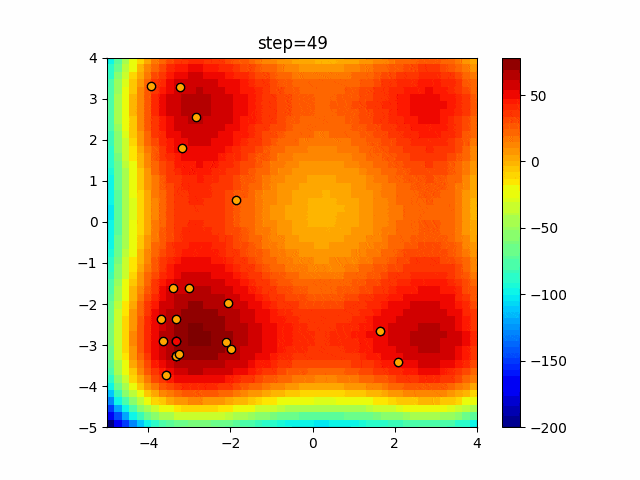
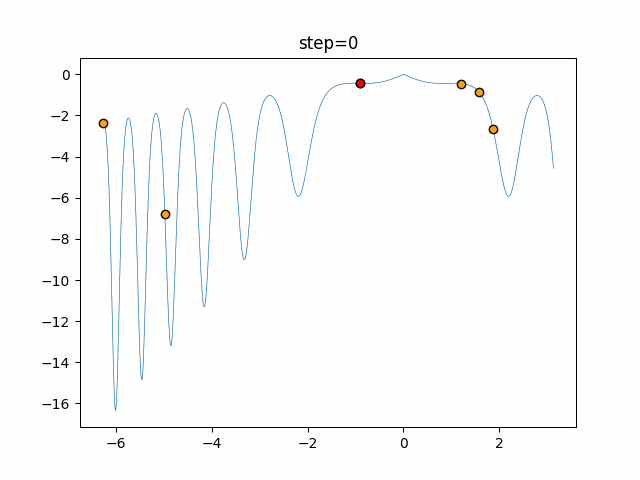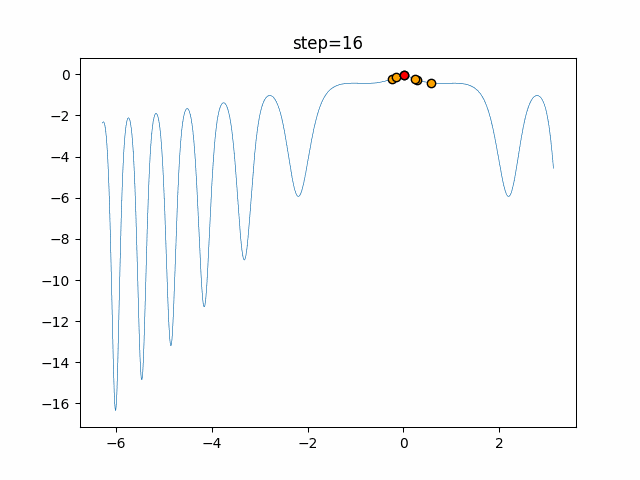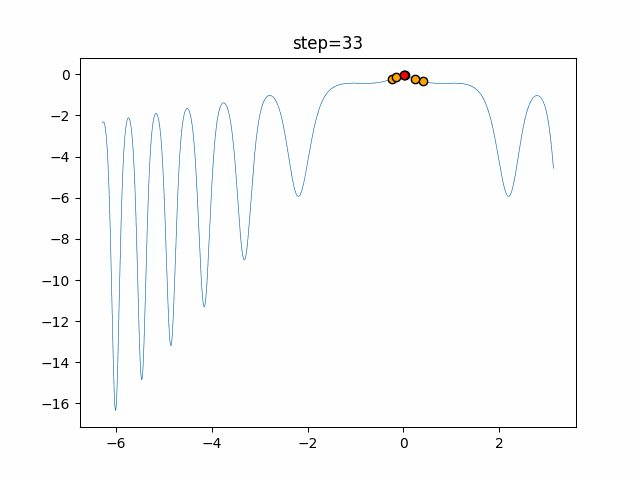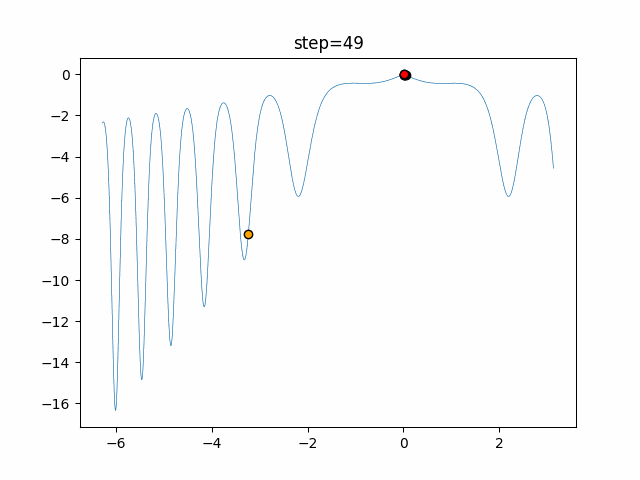
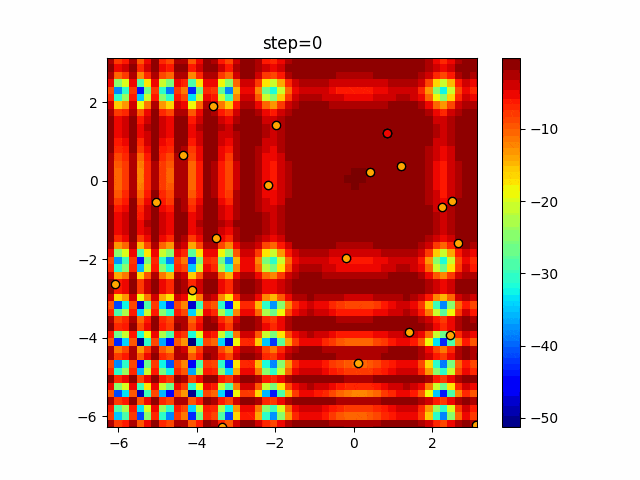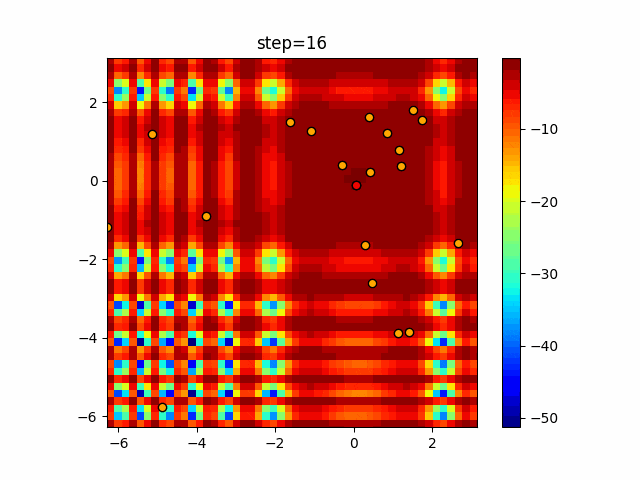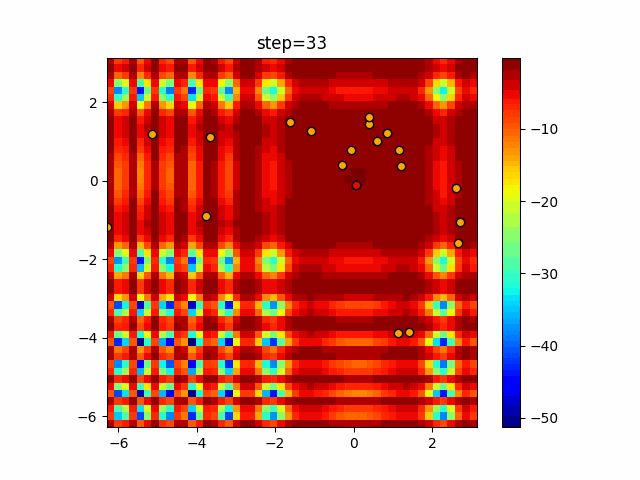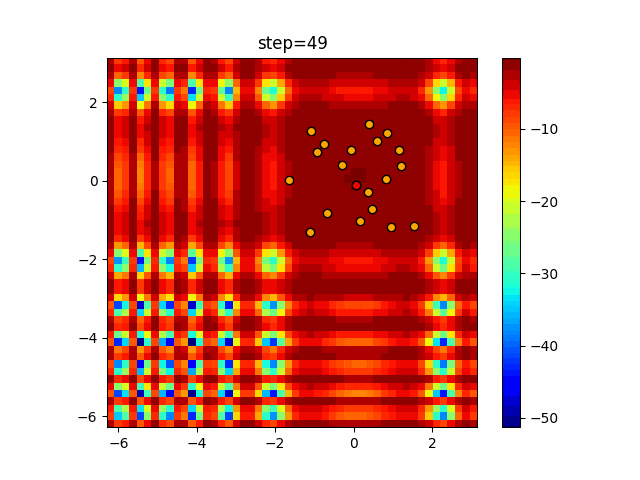
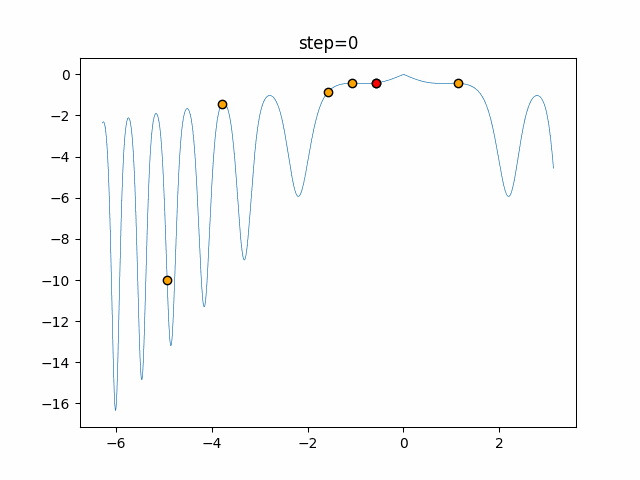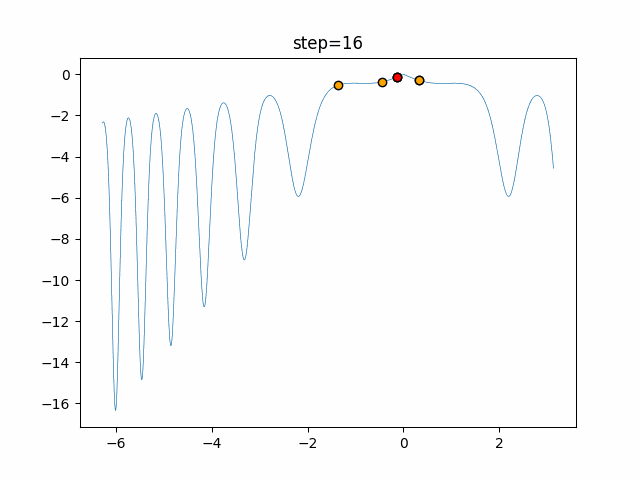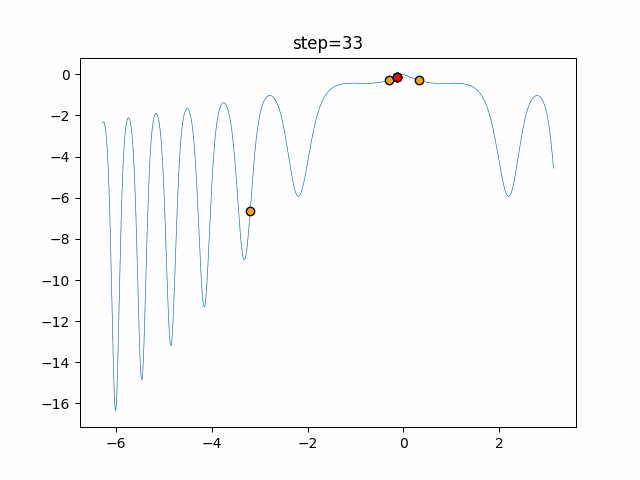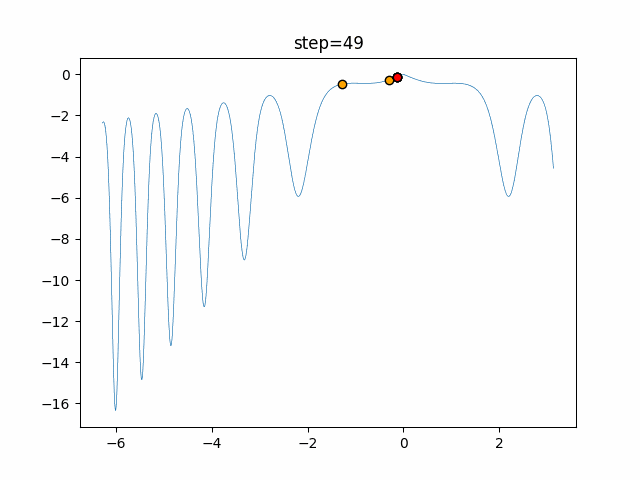
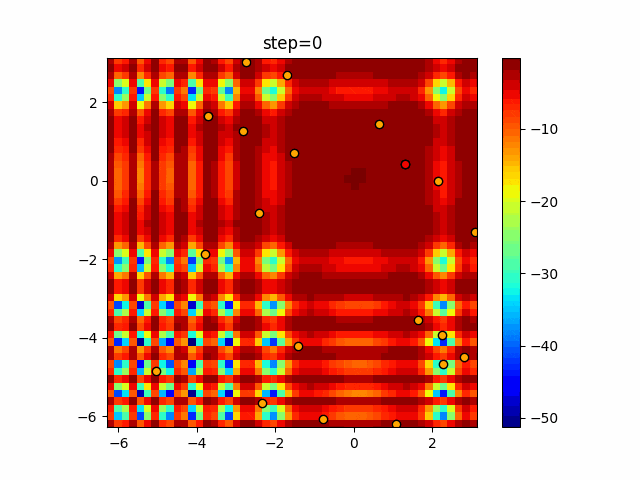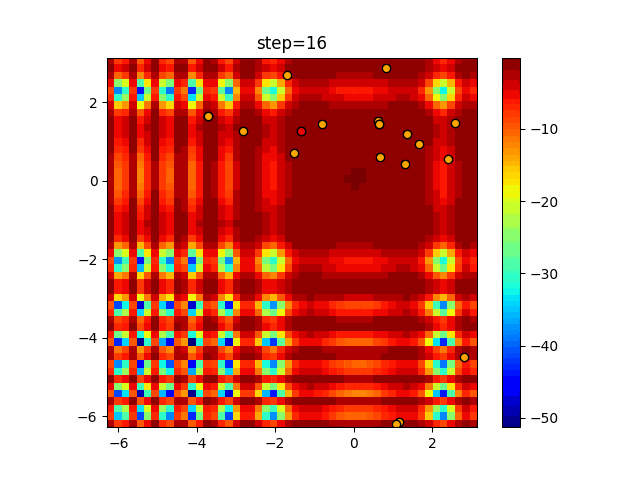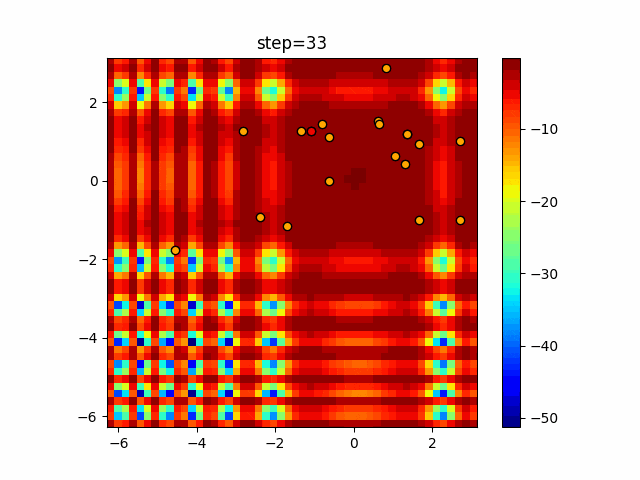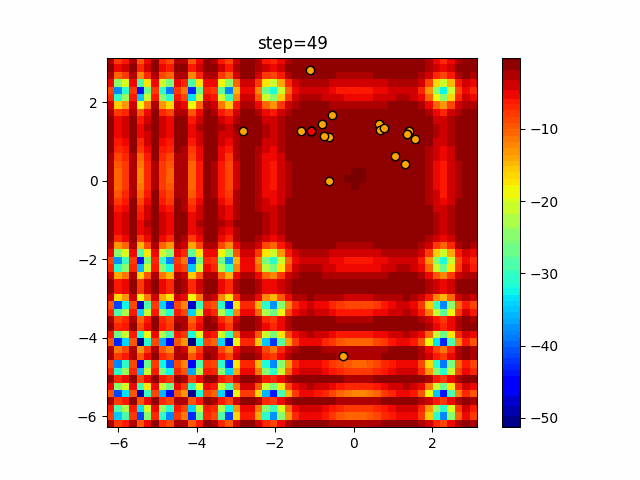
実際の動きの可視化

1次元は6個体、2次元は20個体で50step実行した結果です。
赤い丸がそのstepでの最高スコアを持っている個体となります。

パラメータは以下で実行しました。

Cuckoo(N, scaling_rate=1.0, levy_rate=1.0, bad_nest_rate=0.1)
Cuckoo_greedy(N, epsilon=0.5, bad_nest_rate=0.1)

function_Ackley

• Cuckoo
  • 1次元

• 2次元

• Cuckoo_greedy
  • 1次元

• 2次元

function_Rastrigin

• Cuckoo
  • 1次元

• 2次元

• Cuckoo_greedy
  • 1次元

• 2次元

function_Schwefel

• Cuckoo
  • 1次元

• 2次元

• Cuckoo_greedy
  • 1次元

• 2次元

function_StyblinskiTang

• Cuckoo
  • 1次元

• 2次元

• Cuckoo_greedy
  • 1次元

• 2次元

function_XinSheYang

• Cuckoo
  • 1次元

• 2次元

• Cuckoo_greedy
  • 1次元

• 2次元

あとがき

アルゴリズム自体はかなり簡単で精度もかなりいいらしいです。
レヴィ分布に従った乱数の生成が一番難しかったです…。