はじめに
最適化アルゴリズムの実装シリーズです。
まずは概要を見てください。
コードはgithubにあります。
ホタルアルゴリズム
ホタルアルゴリズム(Firefly Algorithm)はホタルの求愛行動に着目したアルゴリズムです。
以下の行動規則に従ってモデル化します。
- ホタルの光の強さは評価値
- 強い光を放っているホタルに他のホタルが近寄ってくる
- 魅力的であるほど、他のホタルが近寄ってくる
- 光っているホタルが近くにいないときはランダムに飛ぶ
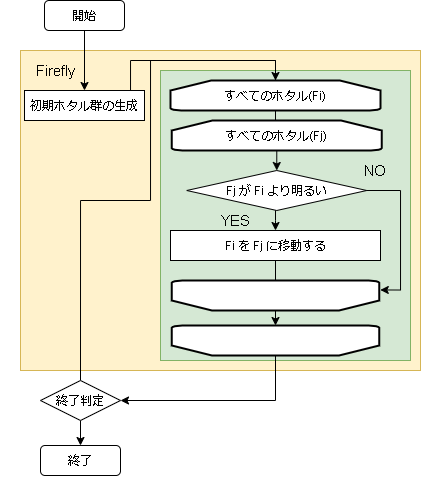
- アルゴリズムのフロー
- 用語の対応
| 問題 | ホタルアルゴリズム |
|---|---|
| 入力値の配列 | ホタルの位置 |
| 入力値 | ホタル |
| 評価値 | ホタルの位置における評価値(ホタルの光の強さ) |
- ハイパーパラメータに関して
| 変数名 | 意味 | 備考 |
|---|---|---|
| attracting_degree | 誘引度($\beta_0$)(0.0~1.0) | 大きいほどホタルに近づく割合が大きい |
| absorb | 光の吸収係数($\gamma$)(0.0~∞) | 大きいほど光の減衰が多い(遠くのホタルが見えなくなる) |
| alpha | 乱数の反映率(0.0~1.0) | 大きいほどランダムによく動く |
| is_normalization | ユークリッド距離を正規化するか | 正規化するとabsorbの値が20~100ぐらいだといい感じになる |
ホタルの移動
ホタルの移動は2個体を比較し、相手のほうの光が強かったら近づくように移動します。
移動式は以下です。
$$
d_{ij} = |\vec{x_j} - \vec{x_i}|
$$
$$
attract = \beta_0e^{-\gamma d_{ij}^2}
$$
$$
\vec{x_i}(t+1) = \vec{x_i}(t) + attract(\vec{x_j}(t) - \vec{x_i}(t)) + \alpha \vec{\epsilon}
$$
| 数式 | 意味 | ハイパーパラメータ |
|---|---|---|
| $i$ | 対象のホタル | |
| $j$ | 相手のホタル | |
| $x$ | 座標 | |
| $d_{ij}$ | 二人のホタルの距離(※1) | |
| $\gamma$ | 光の吸収係数(定数) | absorb |
| $\beta_0$ | ホタルの誘引度(定数) | attracting_degree |
| $attract$ | 相手のホタルの魅力値 | |
| $t$ | 時刻 | |
| $\alpha$ | ランダム要素を取り入れる率(定数) | alpha |
| $\vec{\epsilon}$ | 座標と同じ次元のランダム数(※2) |
※1、実装はユークリッド距離ですが、他の距離でもいいらしい
※2、実装では一様分布ですが、正規分布などでもいいらしい
import random
import numpy as np
i = 自分のホタルのindex
j = 相手のホタルのindex
# 相手のホタルの光が強かったら移動する
if fireflys[i].getScore() < fireflys[j].getScore():
pos = np.asarray(fireflys[i].getArray())
pos2 = np.asarray(fireflys[j].getArray())
d = np.linalg.norm(pos2 - pos) # ユークリッド距離
attract = attracting_degree * (math.exp(-absorb * (d ** 2)))
# 範囲+負の値の範囲で一様乱数
r = []
for _ in range(problem.size)
t = random.randint(0, 1)
if t == 0:
t = -1
r.append(problem.randomVal() * t)
r = np.asarray(r)
# 座標を計算
pos = pos + attract * (pos2 - pos) + alpha * r
# 更新
fireflys[i].setArray(pos)
ユークリッド距離の正規化
$attract$ はユークリッド距離の値にかなり影響されます。
しかし、次元数が変わるとユークリッド距離の範囲も以下のように変化します。
すべての次元で1離れている場合のユークリッド距離
1次元: $\sqrt{1^2} = 1$
2次元: $\sqrt{1^2 + 1^2} = 1.4142$
3次元: $\sqrt{1^2 + 1^2 + 1^2} = 1.7320$
ですので、どの次元でも0~1の範囲に収まるように正規化しました。
この正規化処理は本記事オリジナルで元のアルゴリズムにはありません。
import random
import numpy as np
# n次元の最大距離
t = [problem.MAX_VAL - problem.MIN_VAL for _ in range(problem.size)]
# 最大のユークリッド距離
max_norm = np.linalg.norm(t)
# iとjのホタルのユークリッド距離を出す
pos1 = np.asarray(fireflys[i].getArray())
pos2 = np.asarray(fireflys[j].getArray())
d = np.linalg.norm(pos2 - pos)
# ユークリッド距離を0~1の範囲で正規化
d = d / max_norm
ホタルの魅力値に関して
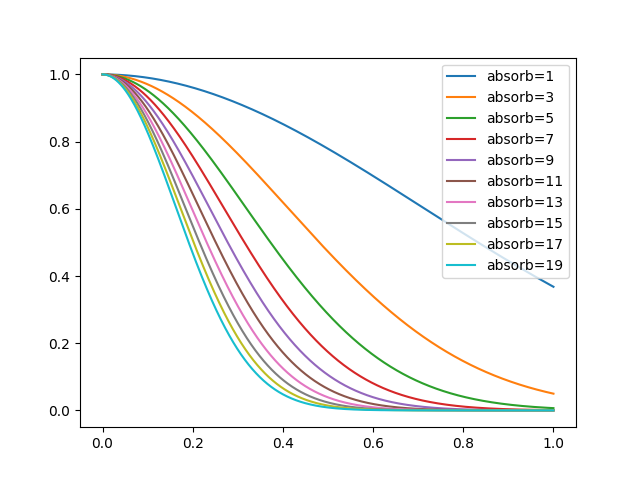
ホタルアルゴリズムで重要な $attract$ ですが、$\gamma$ (absorb)の値によってどう変化するかをグラフ化して見ました。
(attracting_degree は 1 です)
x軸が相手のホタルとのユークリッド距離で、y軸が attract 値です。
attract が大きいほど相手のホタルに近づきます。
グラフを見てわかる通りある程度離れると急激に attract の値が少なくなります。
この attract値を制御しやすくするためには正規化が必要な気がしたので実装を追加しています。
コード全体
import math
import random
import numpy as np
class Firefly(IAlgorithm):
def __init__(self,
firefly_max,
attracting_degree=1.0,
absorb=0.5,
alpha=1.0,
is_normalization=False,
):
self.firefly_max = firefly_max
self.attracting_degree = attracting_degree
self.absorb = absorb
self.alpha = alpha
self.is_normalization = is_normalization
def init(self, problem):
self.problem = problem
# ユークリッド距離正規化用
t = [problem.MAX_VAL - problem.MIN_VAL for _ in range(problem.size)]
self.max_norm = np.linalg.norm(t)
self.fireflys = []
for _ in range(self.firefly_max):
self.fireflys.append(problem.create())
def step(self):
for i in range(len(self.fireflys)):
for j in range(len(self.fireflys)):
if i == j:
continue
# 光が強かったら移動する
if self.fireflys[i].getScore() < self.fireflys[j].getScore():
pos = self.fireflys[i].getArray()
pos2 = self.fireflys[j].getArray()
d = np.linalg.norm(pos2 - pos) # ユークリッド距離
if self.is_normalization:
# 0~1の範囲で正規化する
d /= self.max_norm
# 誘引度
attract = self.attracting_degree * (math.exp(-self.absorb * (d ** 2)))
# 範囲+負の値の範囲で一様乱数
r = []
for _ in range(problem.size)
t = random.randint(0, 1)
if t == 0:
t = -1
r.append(problem.randomVal() * t)
r = np.asarray(r)
pos = pos + attract * (pos2 - pos) + self.alpha * r
# 更新
self.fireflys[i].setArray(pos)
ハイパーパラメータ例
各問題に対して optuna でハイパーパラメータを最適化した結果です。
最適化の1回の試行は、探索時間を2秒間として結果を出しています。
これを100回実行し、最適なハイパーパラメータを optuna に探してもらいました。
| 問題 | absorb | alpha | attract | firefly_max | is_normalization |
|---|---|---|---|---|---|
| EightQueen | 30.348200739383188 | 0.023361773591726337 | 0.2870040283132875 | 35 | True |
| function_Ackley | 28.535248274373334 | 0.02020150316119749 | 0.3817578607938779 | 22 | True |
| function_Griewank | 24.886474482157883 | 0.030874057659246265 | 0.2570801290508207 | 16 | True |
| function_Michalewicz | 12.85000382821637 | 0.00019928439251062913 | 0.9311223660128144 | 38 | True |
| function_Rastrigin | 12.146442425313117 | 0.0043715893301495105 | 0.6005897245267422 | 23 | True |
| function_Schwefel | 19.283223050420563 | 0.7687804405285998 | 0.09958914072852465 | 30 | False |
| function_StyblinskiTang | 22.45670196693838 | 0.040041083413524164 | 0.6313203783344563 | 8 | True |
| function_XinSheYang | 19.93462659647029 | 0.7629337202966674 | 0.7449791915452185 | 12 | False |
| g2048 | 15.50932867945044 | 0.8550076810686411 | 0.29794958618177236 | 22 | True |
| LifeGame | 9.681288121919476 | 0.46635850168820797 | 0.9893266181614047 | 42 | True |
| OneMax | 3.0779446144304785 | 0.6083197521965231 | 0.8027617234478412 | 48 | True |
| TSP | 13.999384524084206 | 0.08809615253769626 | 0.46965098629117824 | 21 | True |
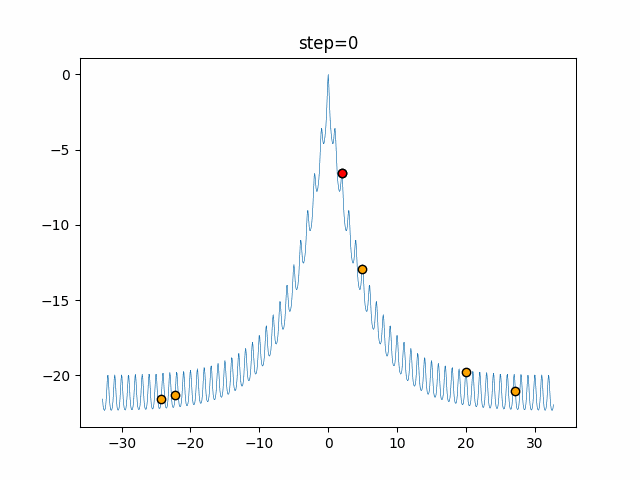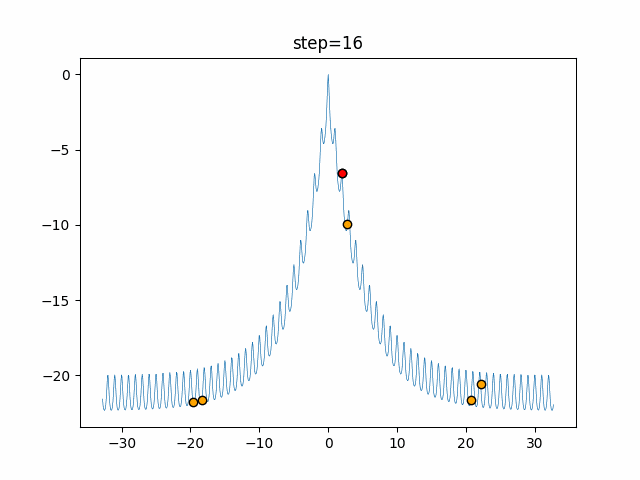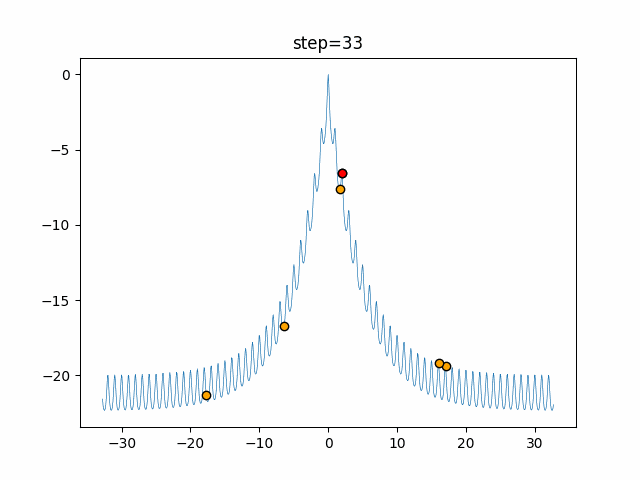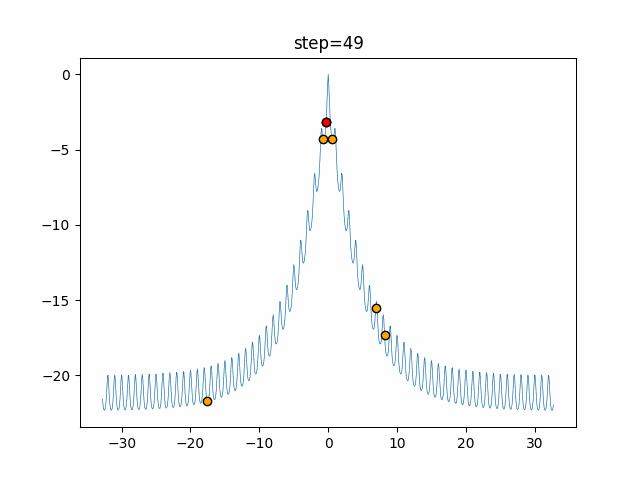
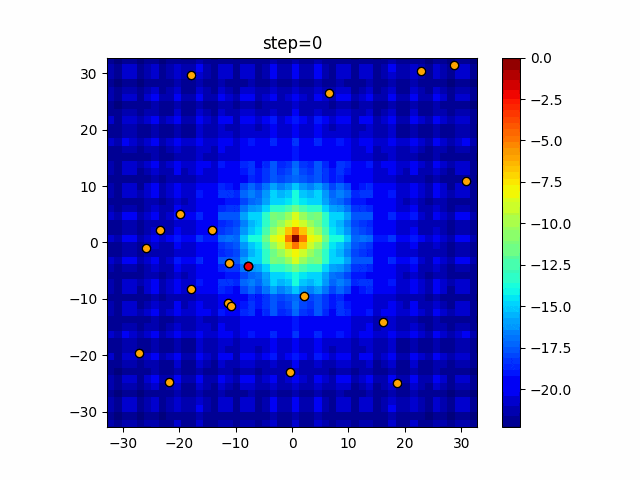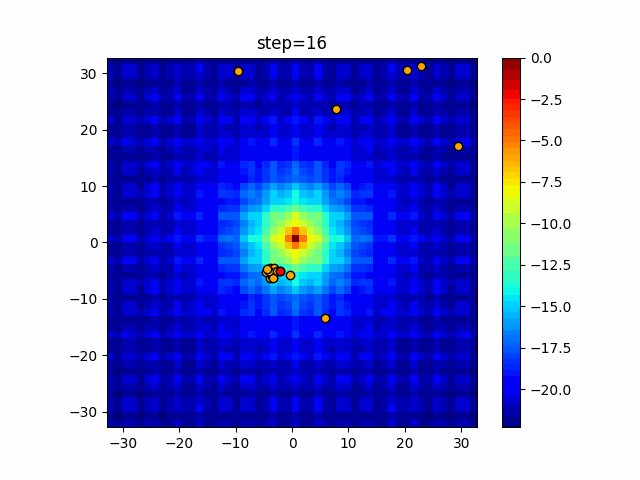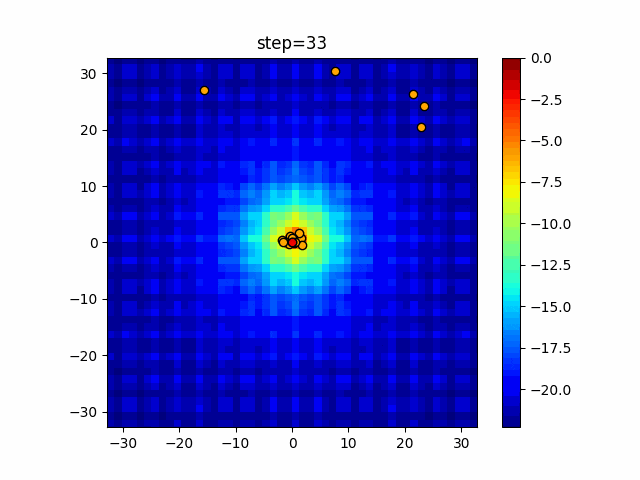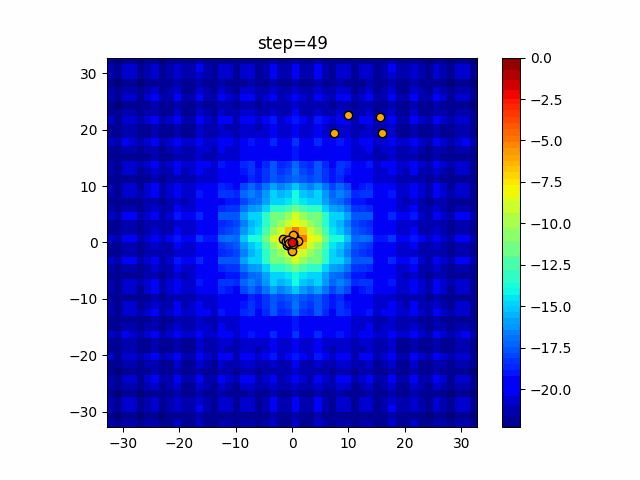
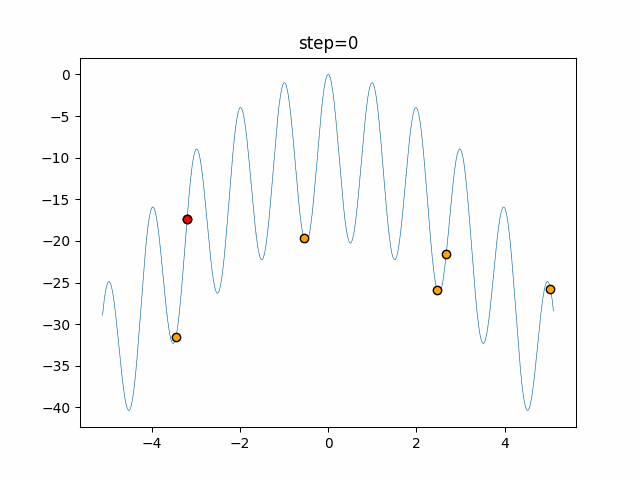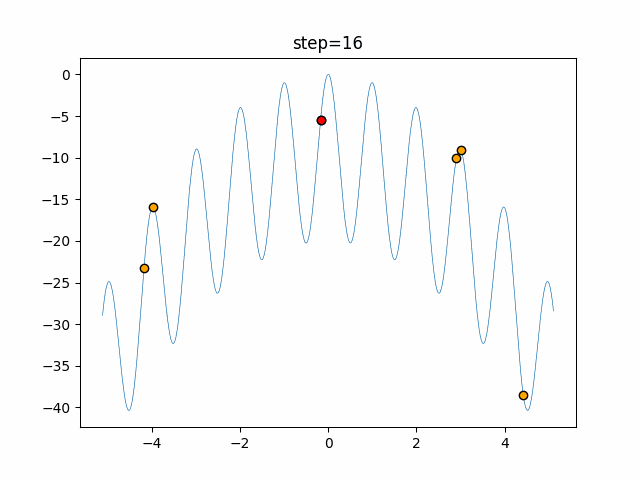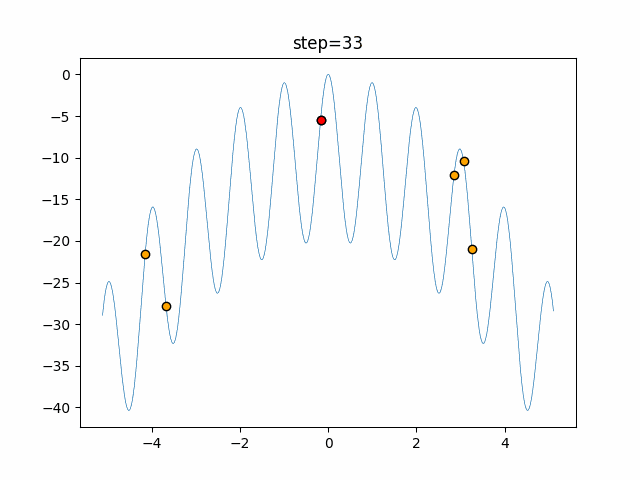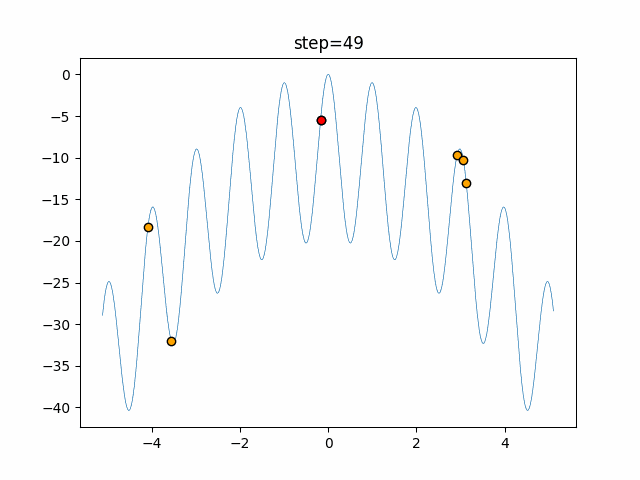
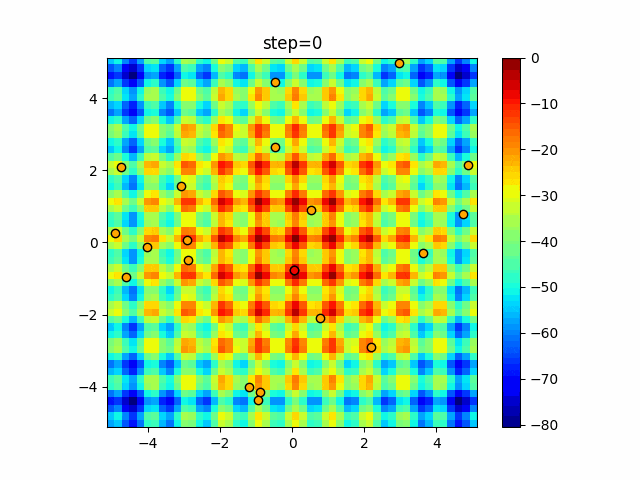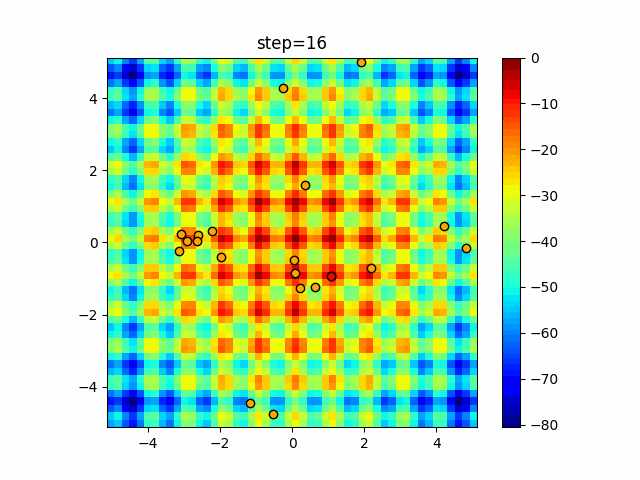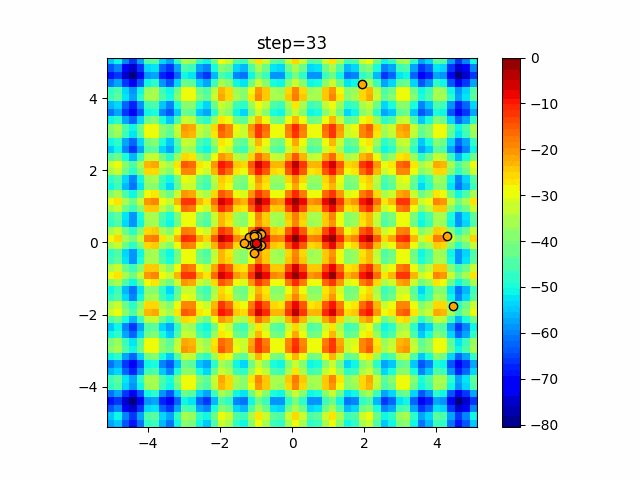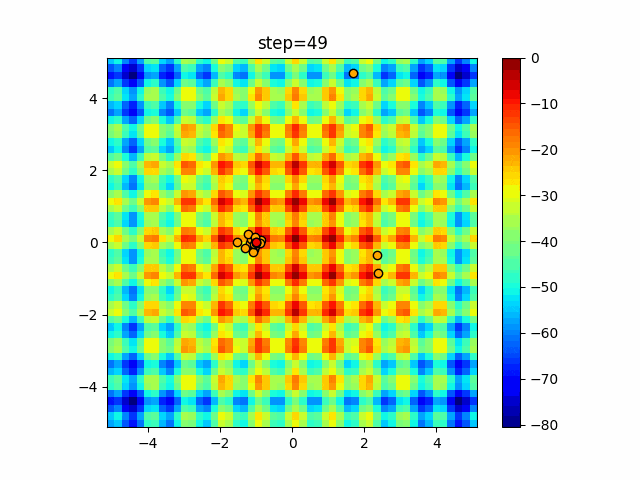
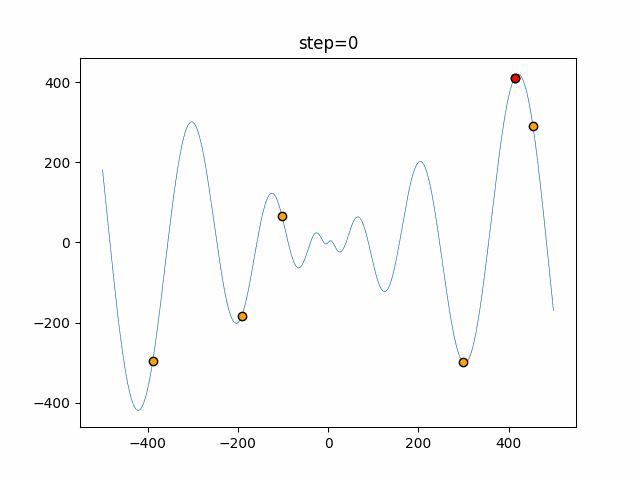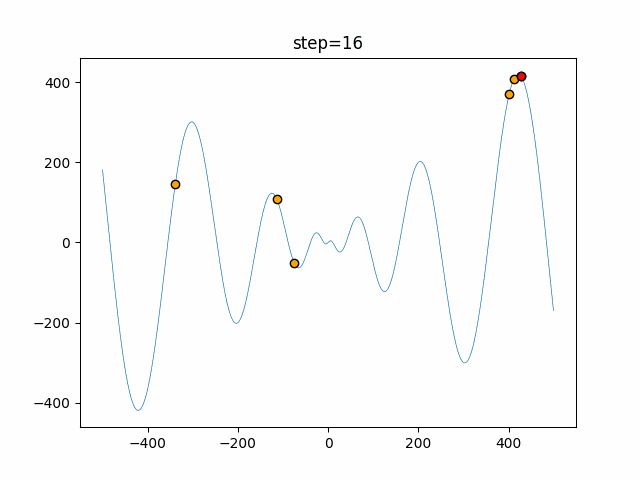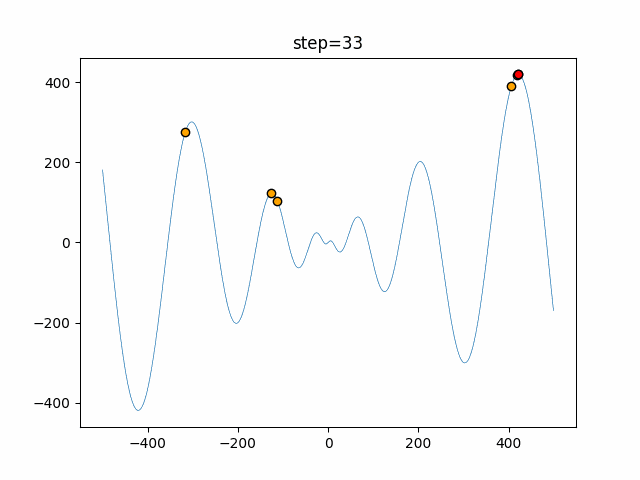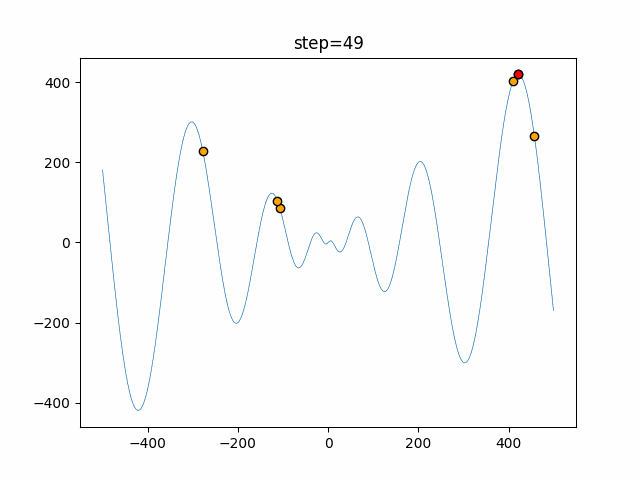
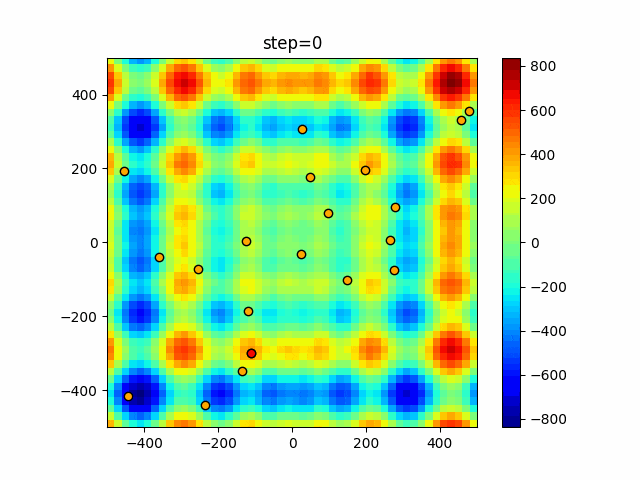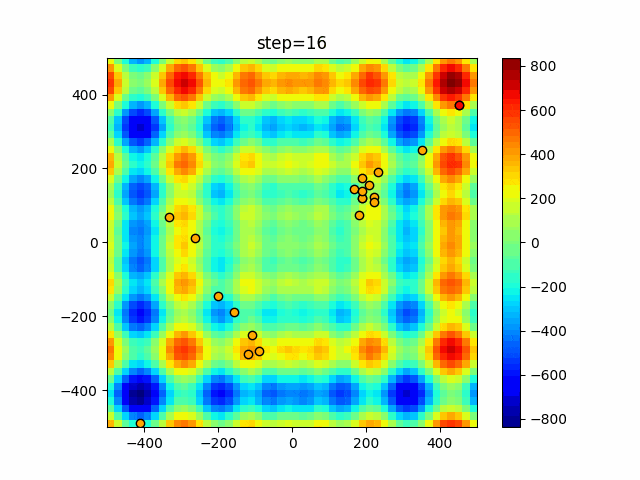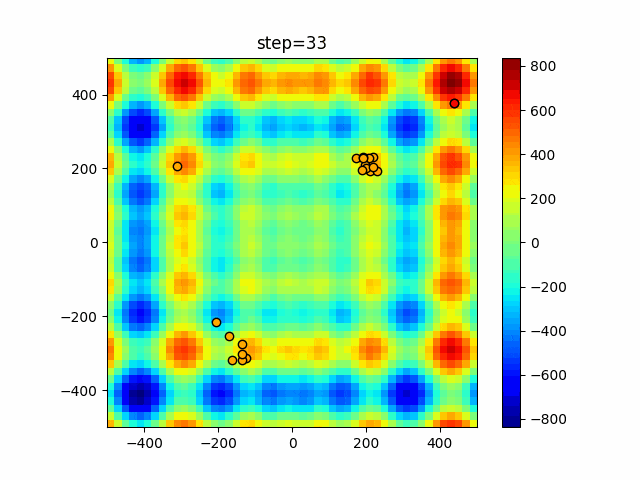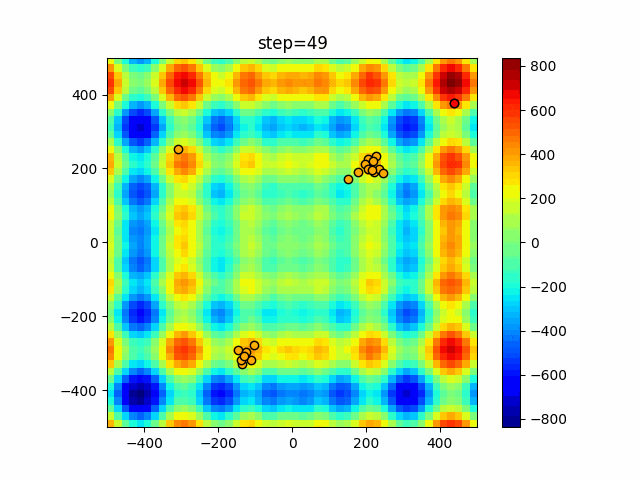
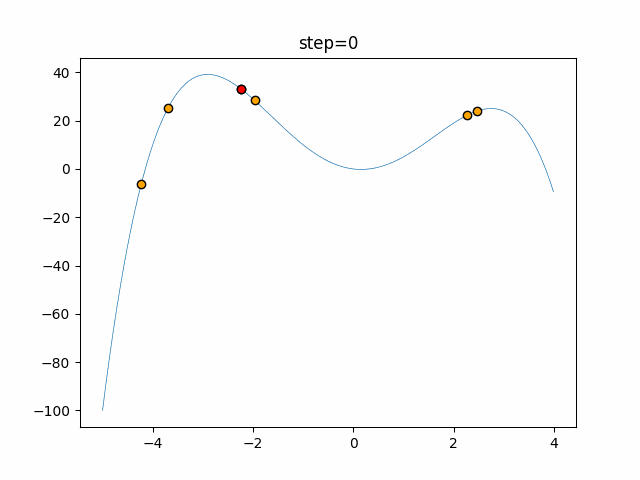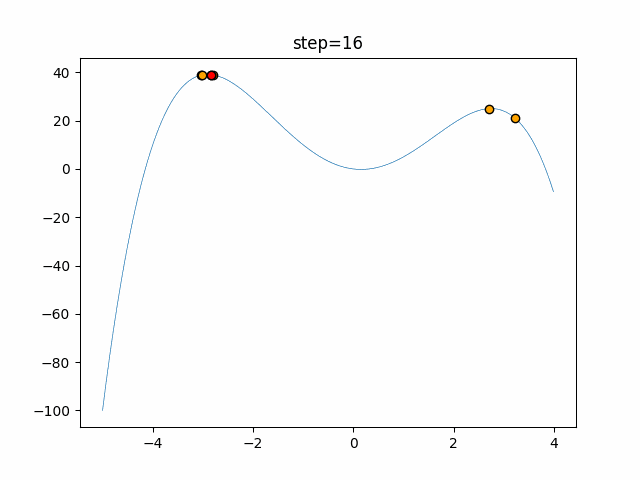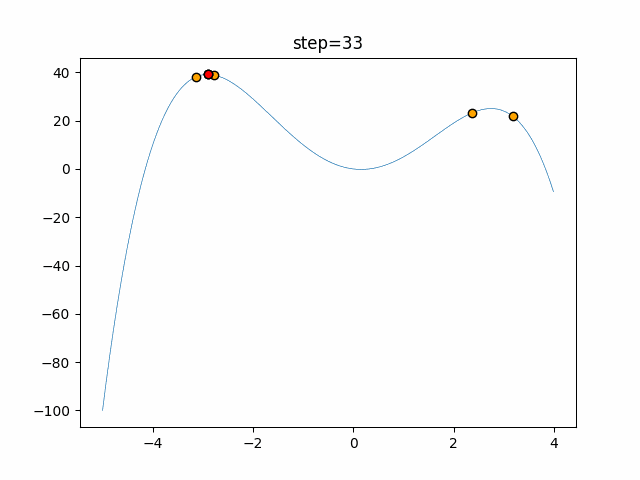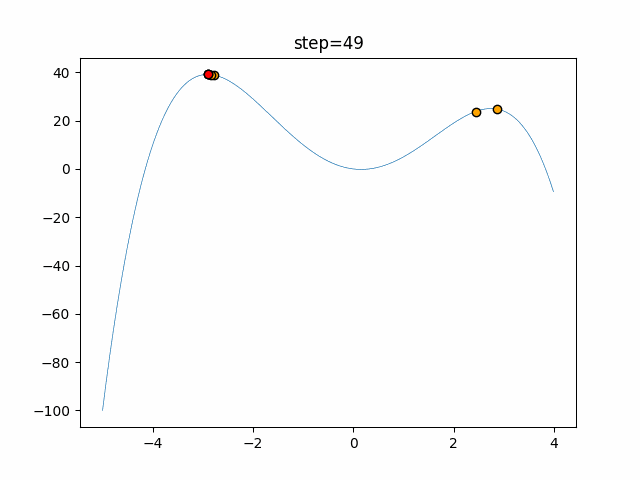
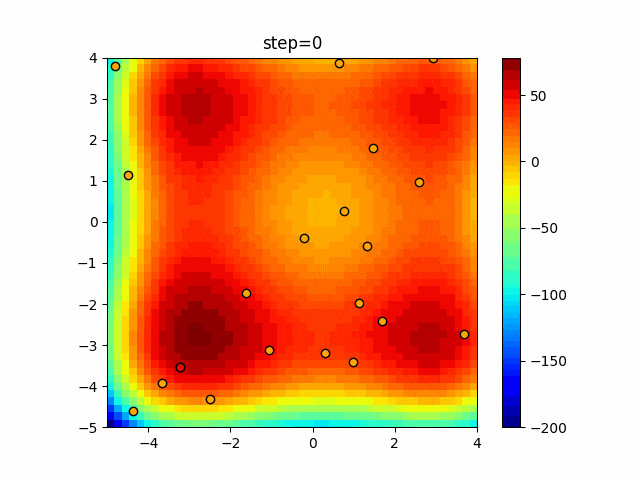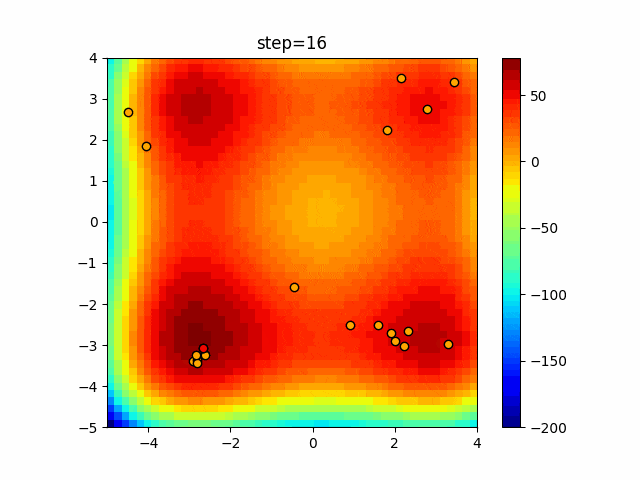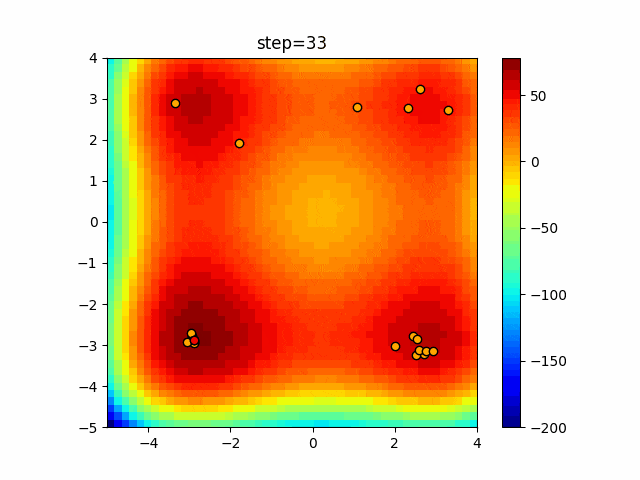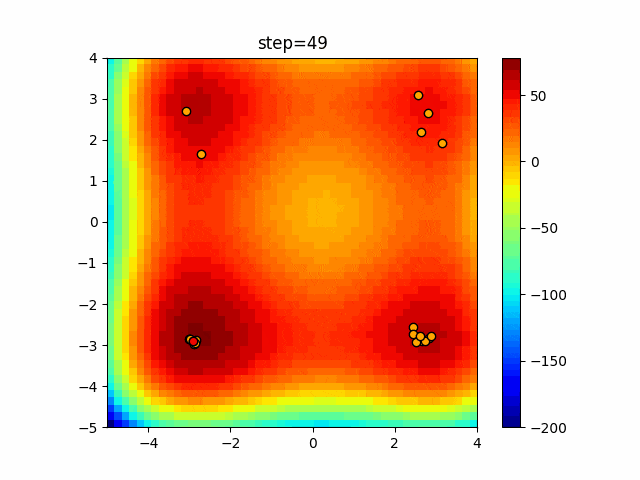
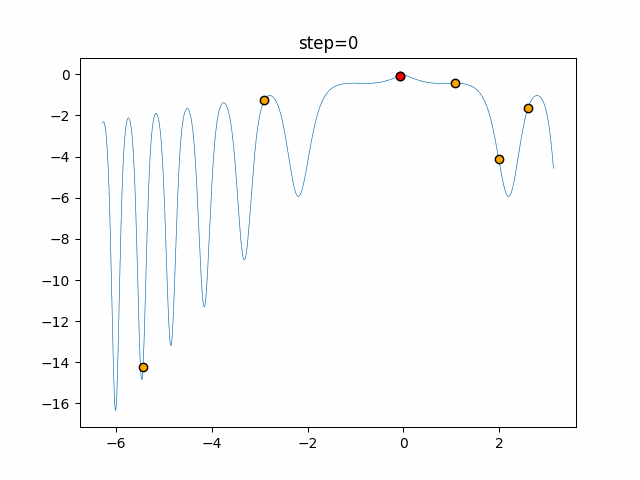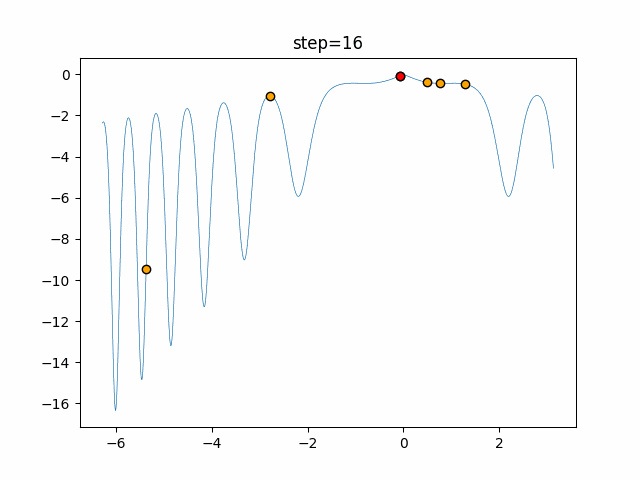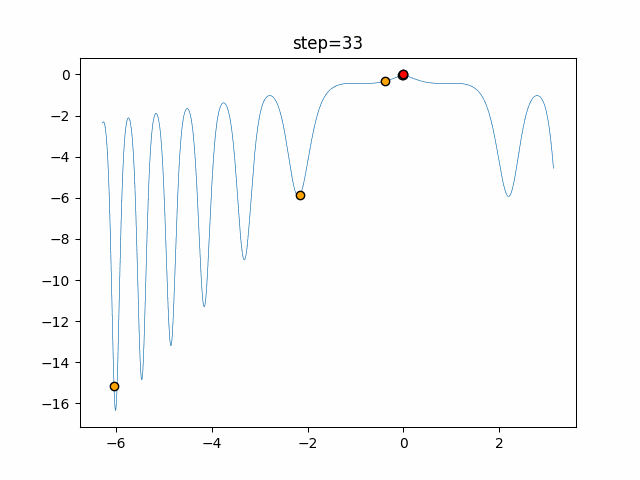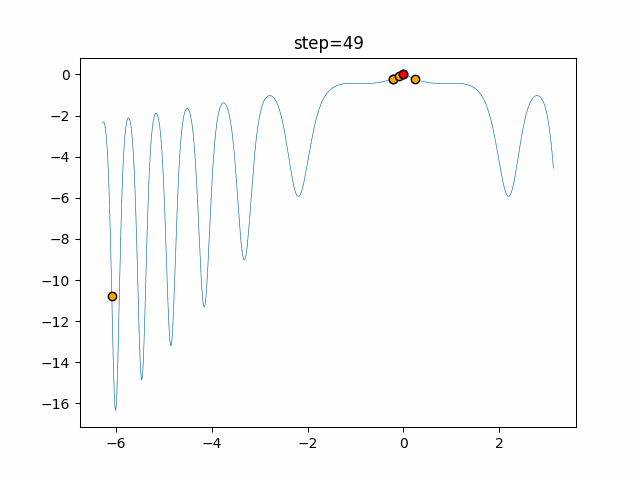
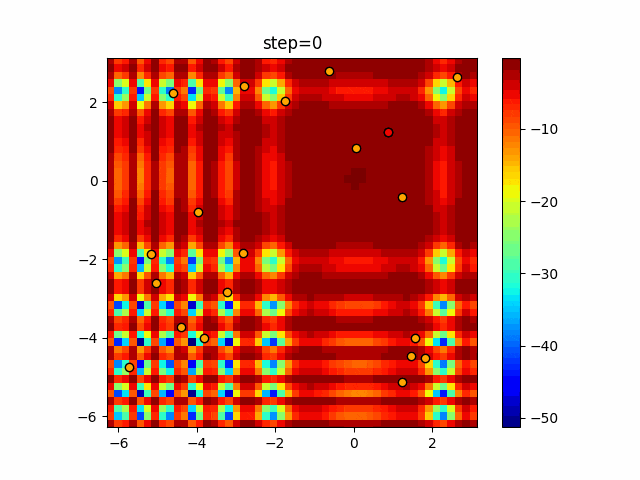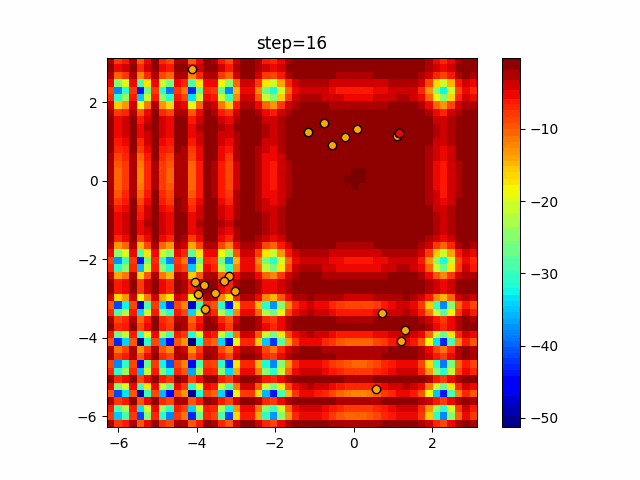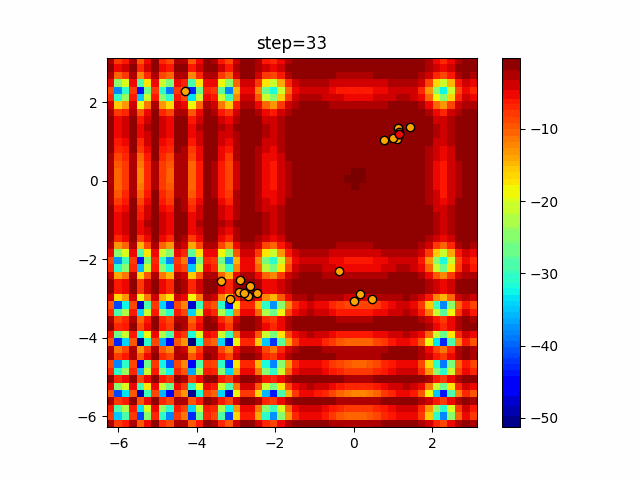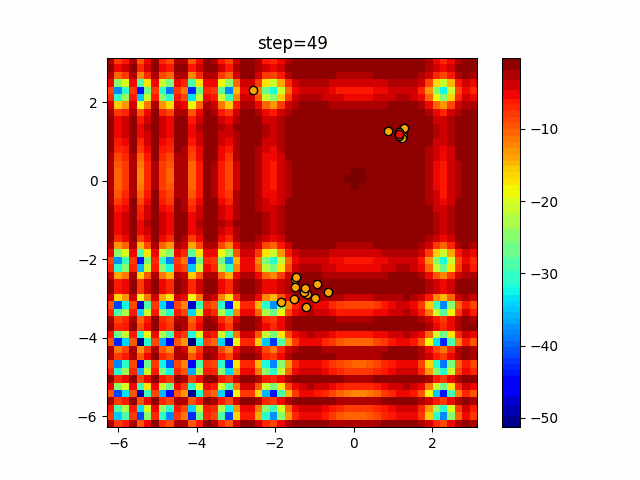
実際の動きの可視化
1次元は6個体、2次元は20個体で50step実行した結果です。
赤い丸がそのstepでの最高スコアを持っている個体となります。
パラメータは以下で実行しました。
Firefly(N, attracting_degree=0.08, absorb=50.0, alpha=0.03, is_normalization=True)
function_Ackley
- 1次元
- 2次元
function_Rastrigin
- 1次元
- 2次元
function_Schwefel
- 1次元
- 2次元
function_StyblinskiTang
- 1次元
- 2次元
function_XinSheYang
- 1次元
- 2次元
あとがき
画像はalphaを低めに設定しているので局所解からは抜け出されにくくなっています。
ふよふよ漂っている感じがホタルっぽくていいですね。