こんにちは、DeNAでデータサイエンティストをやっているまつけんです。
今回はディープラーニングのモデルの一つ、Variational Autoencoder(VAE)をご紹介する記事です。ディープラーニングフレームワークとしてはChainerを使って試しています。
VAEを使うとこんな感じの画像が作れるようになります。VAEはディープラーニングによる生成モデルの1つで、訓練データを元にその特徴を捉えて訓練データセットに似たデータを生成することができます。下記はVAEによって生成されたデータをアニメーションにしたものです。詳しくは本文をご覧ください。

本記事で紹介している内容のPythonコードはコチラにあります。
1. Variational Autoencoderとは?
まず、VAEとはどんなものであるかを説明したいと思いますが、その前に通常のオートエンコーダーについて触れたいと思います。
1-1. 通常のオートエンコーダー
オートエンコーダーとは、
- 教師なし学習の一つ。そのため学習時の入力データは訓練データのみで教師データは利用しない。
- データを表現する特徴を獲得するためのニューラルネットワーク。
といった特徴を持ちます。
MNISTを例にとると、28x28の数字の画像を入れて、同じ画像を出力するニューラルネットワークということになります。
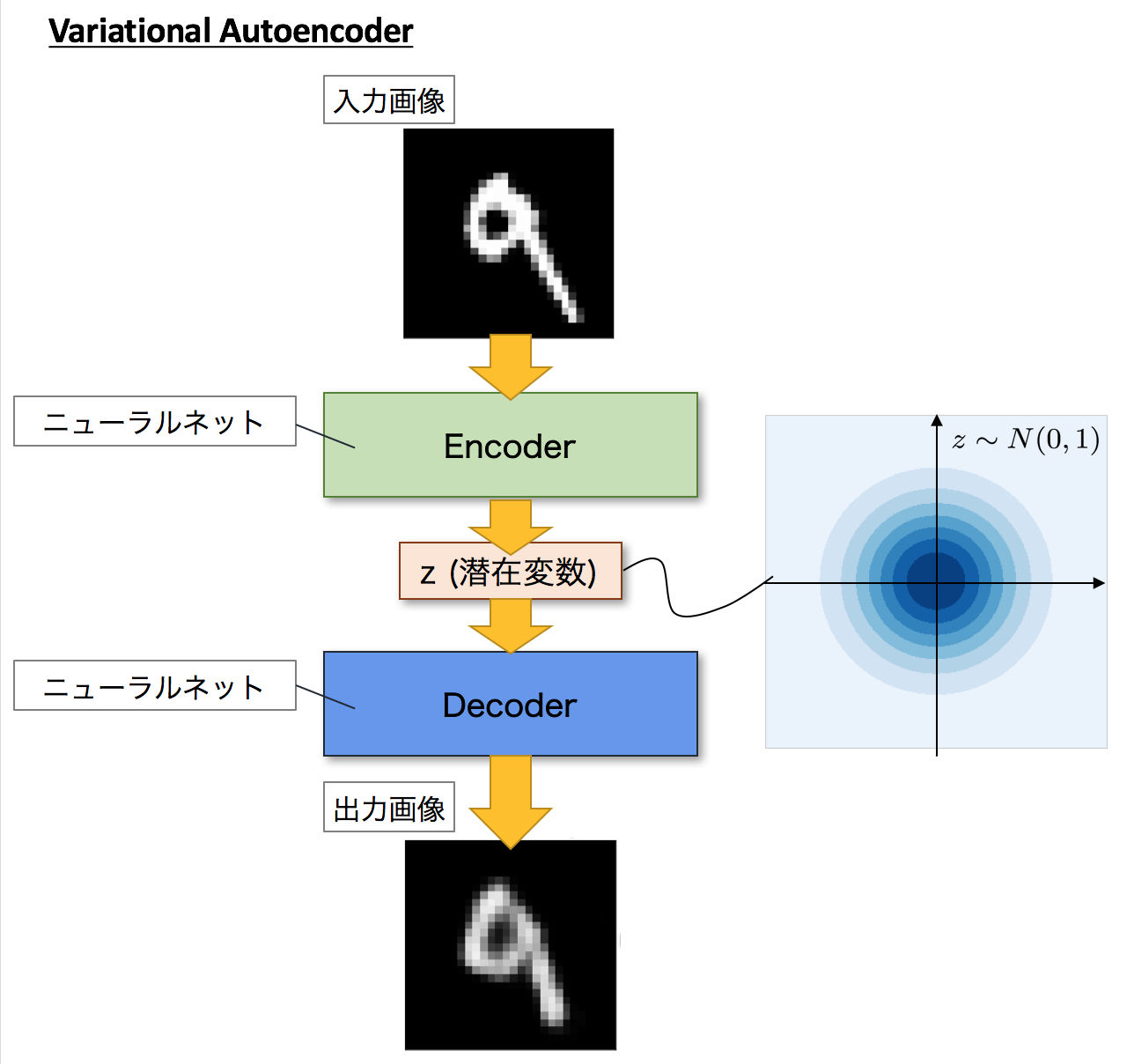
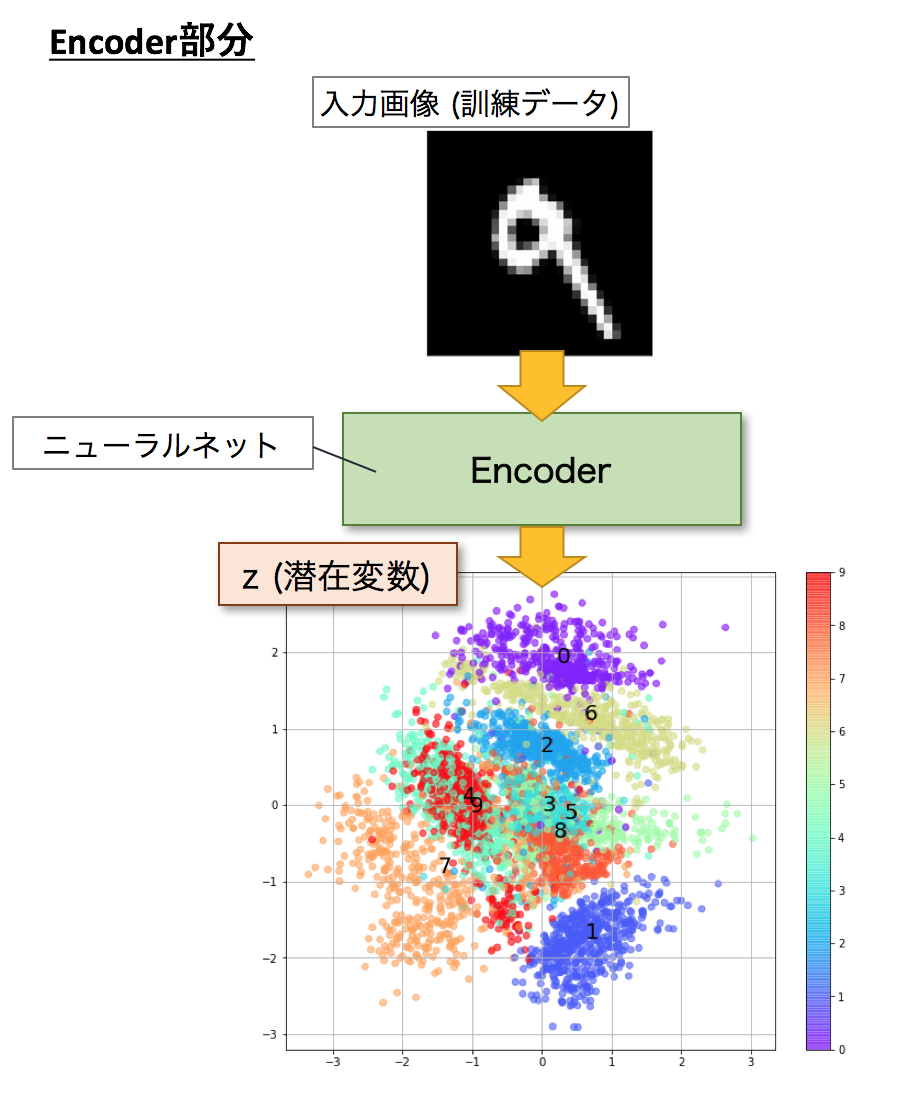
下記の図のイメージですね。 入力データ$X$から潜在変数$z$に変換するニューラルネットワークをEncoderといいます。(入力データを符号化とみなせるため、Encoderという名称が付いています)この時、$z$の次元が入力$X$より小さい場合、次元削減とみなすこともできます。
逆に潜在変数$z$をインプットとして元画像を復元するニューラルネットワークをDecoderと言います。

ニューラルネットが1層の場合を数式で表すと、
\hat{x}(x) = \hat{f}(\hat{W} f(Wx+b)+\hat{b})
です。このときロスを
Loss = \sum_{n=1}^N \|x_n - \hat{x}(x_n) \|^2
とします。これはReconstruction Errorと呼ばれます。入力したデータになるべく近くなるように誤差逆伝播法で重みの更新を行うことで学習することができます。
1-2. Variational Autoencoder(VAE)
VAEはこの潜在変数$z$に確率分布、通常$z \sim N(0, 1)$を仮定したところが大きな違いです。通常のオートエンコーダーだと、何かしら潜在変数$z$にデータを押し込めているものの、その構造がどうなっているかはよくわかりません。VAEは、潜在変数$z$を確率分布という構造に押し込めることを可能にします。
イメージは下記です。
まだよくわかりませんね。実際にプログラムを動かしたものを見ると少しイメージが湧くかと思います。
まずは入力と出力を対比させてみます。(これは$z$の次元を20に設定して学習したものです。)ちょっとぼやっとしていますが、元の形をほとんど復元できています。もともとMNISTは784次元のデータなので、次元削減した20次元にほとんどの本質的な特徴を入れ込むことができたと言えそうです。

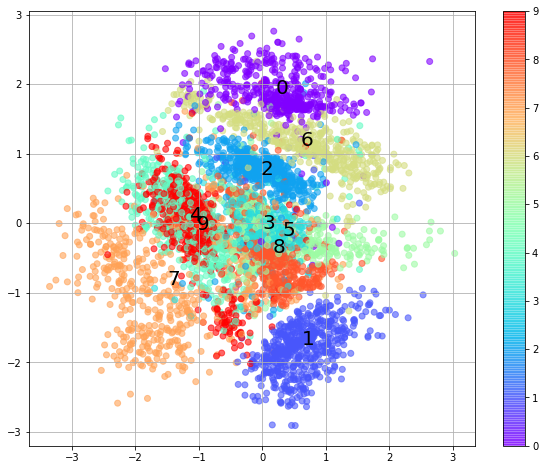
次に、Encoder部分に限ってその挙動を見てみましょう。すでに学習済みのEncoderがあったとしてそこに訓練データのデータセットを入れて潜在変数に落としてみます。可視化できるように$z$の次元は2次元にします。どうでしょう、訓練データのMNISTデータセットが2次元の正規分布に従う円の上に散らばっている様子が見て取れると思います。また、ここがミソなのですが、教師データのない教師なし学習にもかかわらず同じクラスラベルのデータが近いところに集まっていることも見て取れます。VAEは$z$が正規分布に従うように設計されており、正規分布に従う乱数を学習時に取り入れているので、この乱数によるブレによって似た形状のものを近くに寄せる効果があるためです。つまり、同じ画像を入力しても毎回ちょっとずれたところに$z$がプロットされ、その$z$からDecoderによって生成する画像を入力画像と同じようにするためです。下記の散布図で数字がテキストでプロットされている位置は、各ラベルの中央です。
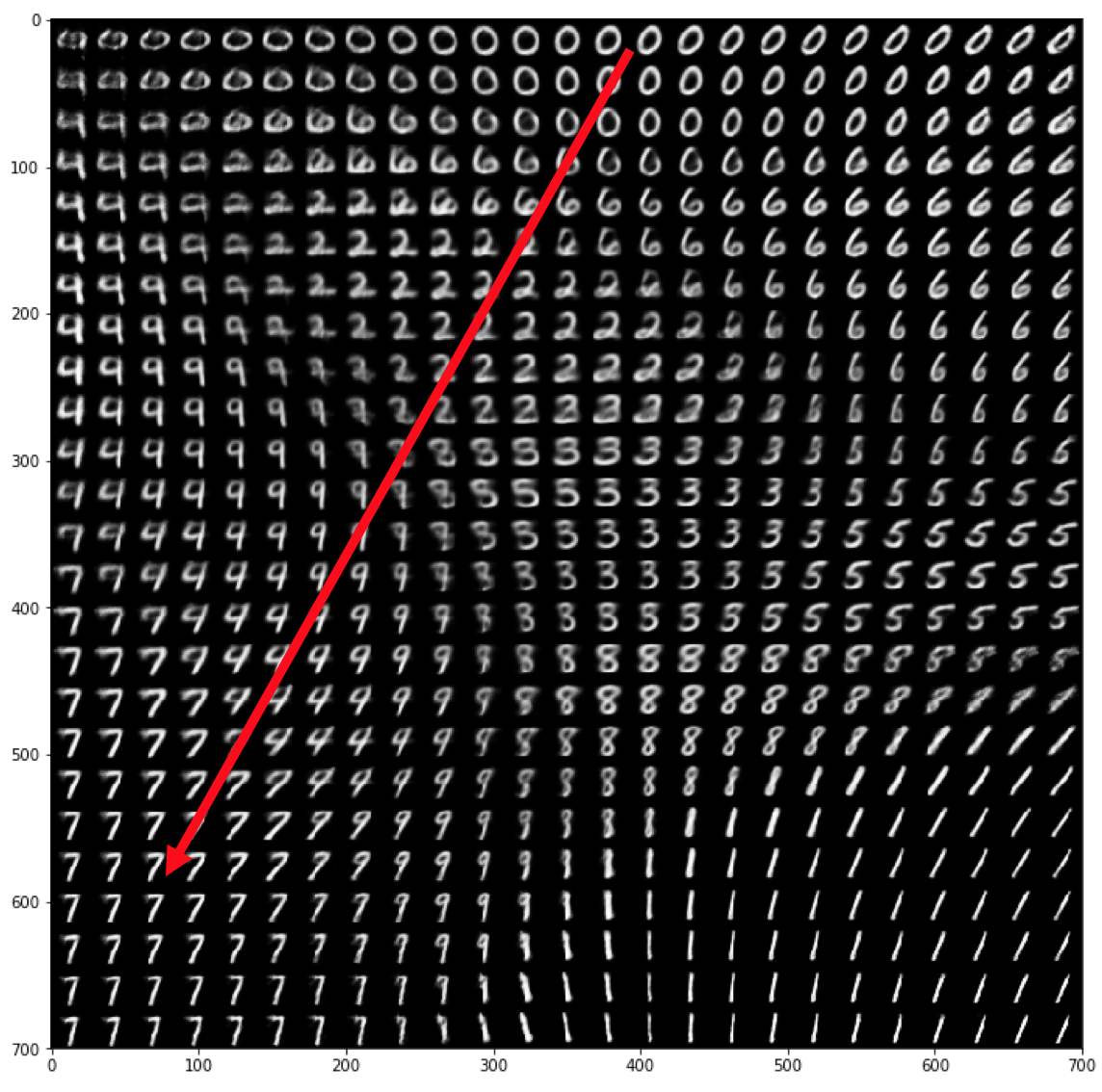
さて、それではこの"0"から"7"に向かって潜在変数の空間上に沿ってデータを少しずつずらしながらデータを生成してみたらどうなるでしょうか。

下記のアニメーションがその結果です。
t\cdot z_0 + (1-t)\cdot z_7, \ \ 0\leq t \leq 1
のように、$t$を0から1までちょっとずつ動かしたものをインプットとしてDecoderによってMNIST画像を生成したものです。0からスタートして、0-6-2-8-9-4-7とちゃんとその間にある数字を経由して7になる様子がわかりますね![]() これらは訓練データそのものではなくN(0,1)上にマッピングされているVAEが生成した画像であることがミソです。
これらは訓練データそのものではなくN(0,1)上にマッピングされているVAEが生成した画像であることがミソです。
$z$の2次元の空間から$-2 \leq z_1 \leq 2, \ -2 \leq z_2 \leq 2$を切り出してDecoderに入力し、対応する出力画像を表示したものが下記の図になります。 赤い線が先ほどの移動の軌跡です。
訓練データよりEncoderが生成した$z$のマップと位置関係がほぼ同じことも見て取れます。逆に、N(0, 1)の観点から非常に確率(密度)が低いところは元のデータセットからはかけ離れているということなので、対応する生成された画像が数字の形としては崩れていることはデータ生成の確率分布の構造を正しく表していると言えます。
各0〜9からスタートして、各0〜9までたどり着く様子を全て表示したものがしたの図です。この例は潜在変数の次元を20まで増やしています。なので、先ほどと違って途中経由する数字が少なくなります。次元が高いので表現力が上がっていますね。
1−3. 多様体仮説
Deep Learningはタスクの学習と表現学習を合わせて行えるところが特徴の1つです。画像などの高次元のデータは、実はその高次元の中でごく一部にしかデータが分布しておらず、意味のあるデータ(訓練データの本質を捉えたデータ)はその高次元の中で局所的に固まっていると考える多様体仮説(Manifold Hypothesis)というものがあります。下記のスイスロールデータの例がわかりやすいかと思います。3次元上にデータが分布しているのですが、かなりデータが局所に偏っており、実はデータのほとんどは2次元で表現できるということが見てわかるかと思います。ロールの間にデータのない隙間があります。なので、3次元での距離が近いデータが似ているとは限らず、局面に沿った方向の移動で距離を考えたほうが類似しているものが見つかる可能性が高いということになります。なので2次元に開いて距離を測ったほうが良いということですね。
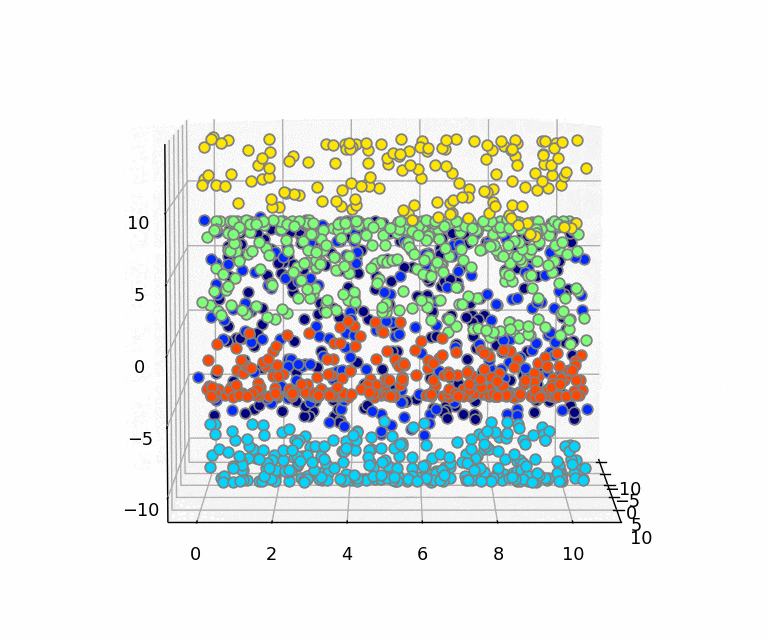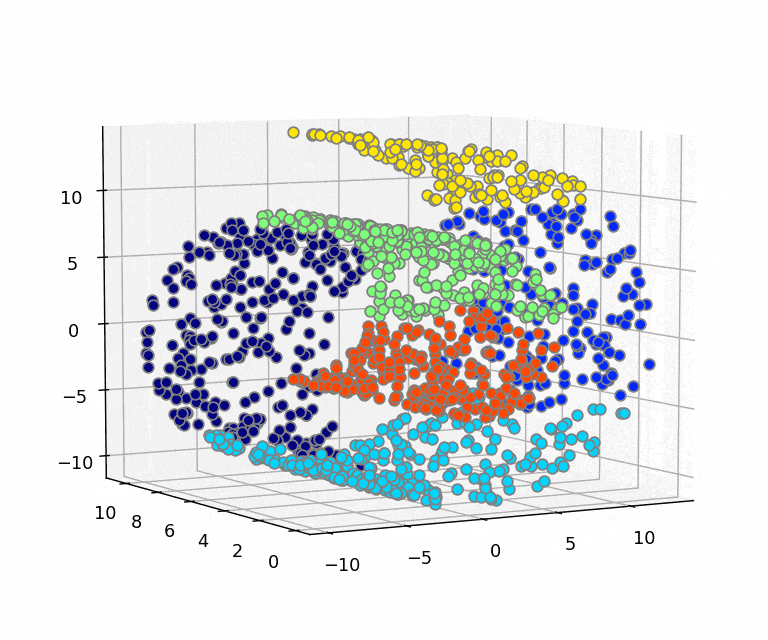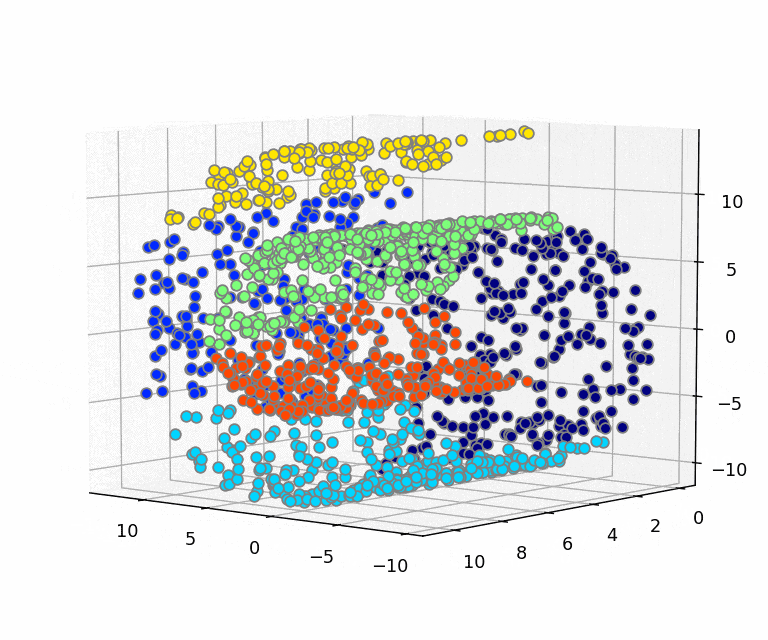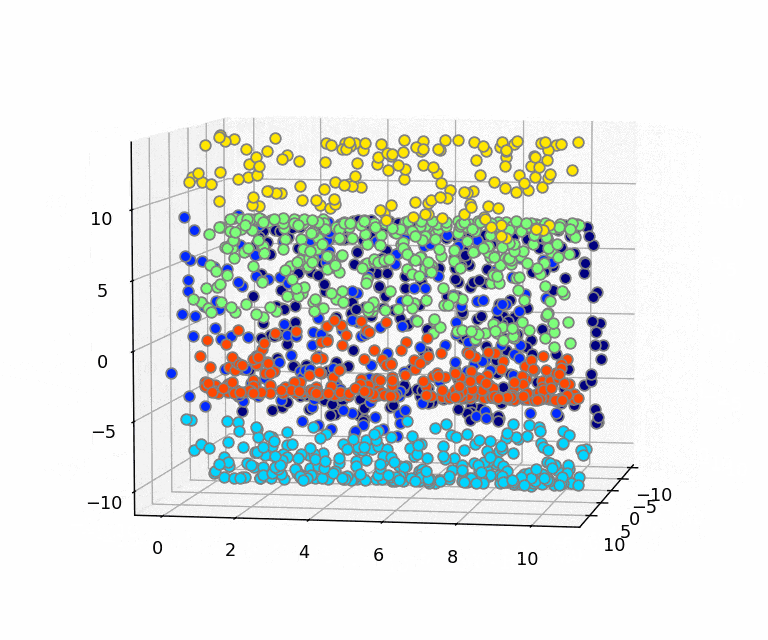
[3次元中の2次元多様体としてのスイスロール]
[スイスロールを2次元に展開してみるとこんな感じ]
話をスイスロールからMNISTのVAEに戻すと、この多様体を捉えて784次元のMNIST画像データの次元から潜在変数 $z \sim N(0, 1)$の次元にデータ押し込めるのがVAEです。表現学習と多様体仮説については[7]も参考にしてください。
2. Chainerでの実装
Chainer公式のExampleをベースにカスタマイズしたものを用いて解説します。3層のMLP(Multi Layer Perceptron)を用いてEncoderとDecoderをモデリングしています。
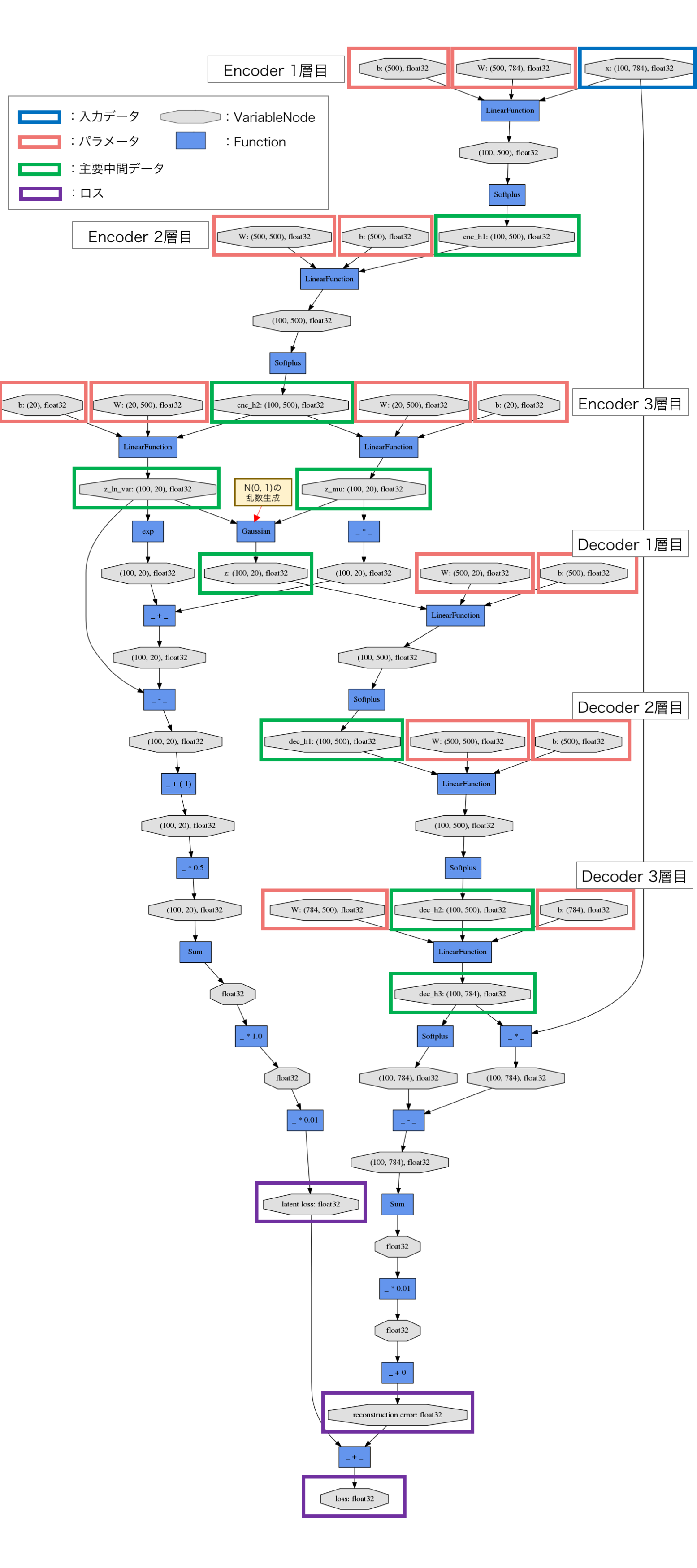
コードに先立って、Chainerが出力する計算グラフ(Computation Graph)を下記に示します。EncoderとDecoderの3層のMLP部分と、潜在変数$z$の生成にGaussianつまり正規分布に従う乱数を利用しているところが見て取れます。Encoderはこの正規分布のパラメーター$\mu$と$\sigma^2$を出力することで$z$を表現しています。
# Reference: https://jmetzen.github.io/2015-11-27/vae.html
class Xavier(initializer.Initializer):
"""
Xavier initializaer
Reference:
* https://jmetzen.github.io/2015-11-27/vae.html
* https://stackoverflow.com/questions/33640581/how-to-do-xavier-initialization-on-tensorflow
"""
def __init__(self, fan_in, fan_out, constant=1, dtype=None):
self.fan_in = fan_in
self.fan_out = fan_out
self.high = constant*np.sqrt(6.0/(fan_in + fan_out))
self.low = -self.high
super(Xavier, self).__init__(dtype)
def __call__(self, array):
xp = cuda.get_array_module(array)
args = {'low': self.low, 'high': self.high, 'size': array.shape}
if xp is not np:
# Only CuPy supports dtype option
if self.dtype == np.float32 or self.dtype == np.float16:
# float16 is not supported in cuRAND
args['dtype'] = np.float32
array[...] = xp.random.uniform(**args)
# Original implementation: https://github.com/chainer/chainer/tree/master/examples/vae
class VAE(chainer.Chain):
"""Variational AutoEncoder"""
def __init__(self, n_in, n_latent, n_h, act_func=F.tanh):
super(VAE, self).__init__()
self.act_func = act_func
with self.init_scope():
# encoder
self.le1 = L.Linear(n_in, n_h, initialW=Xavier(n_in, n_h))
self.le2 = L.Linear(n_h, n_h, initialW=Xavier(n_h, n_h))
self.le3_mu = L.Linear(n_h, n_latent, initialW=Xavier(n_h, n_latent))
self.le3_ln_var = L.Linear(n_h, n_latent, initialW=Xavier(n_h, n_latent))
# decoder
self.ld1 = L.Linear(n_latent, n_h, initialW=Xavier(n_latent, n_h))
self.ld2 = L.Linear(n_h, n_h, initialW=Xavier(n_h, n_h))
self.ld3 = L.Linear(n_h, n_in,initialW=Xavier(n_h, n_in))
def __call__(self, x, sigmoid=True):
""" AutoEncoder """
return self.decode(self.encode(x)[0], sigmoid)
def encode(self, x):
if type(x) != chainer.variable.Variable:
x = chainer.Variable(x)
x.name = "x"
h1 = self.act_func(self.le1(x))
h1.name = "enc_h1"
h2 = self.act_func(self.le2(h1))
h2.name = "enc_h2"
mu = self.le3_mu(h2)
mu.name = "z_mu"
ln_var = self.le3_ln_var(h2) # ln_var = log(sigma**2)
ln_var.name = "z_ln_var"
return mu, ln_var
def decode(self, z, sigmoid=True):
h1 = self.act_func(self.ld1(z))
h1.name = "dec_h1"
h2 = self.act_func(self.ld2(h1))
h2.name = "dec_h2"
h3 = self.ld3(h2)
h3.name = "dec_h3"
if sigmoid:
return F.sigmoid(h3)
else:
return h3
def get_loss_func(self, C=1.0, k=1):
"""Get loss function of VAE.
The loss value is equal to ELBO (Evidence Lower Bound)
multiplied by -1.
Args:
C (int): Usually this is 1.0. Can be changed to control the
second term of ELBO bound, which works as regularization.
k (int): Number of Monte Carlo samples used in encoded vector.
"""
def lf(x):
mu, ln_var = self.encode(x)
batchsize = len(mu.data)
# reconstruction error
rec_loss = 0
for l in six.moves.range(k):
z = F.gaussian(mu, ln_var)
z.name = "z"
rec_loss += F.bernoulli_nll(x, self.decode(z, sigmoid=False)) / (k * batchsize)
self.rec_loss = rec_loss
self.rec_loss.name = "reconstruction error"
self.latent_loss = C * gaussian_kl_divergence(mu, ln_var) / batchsize
self.latent_loss.name = "latent loss"
self.loss = self.rec_loss + self.latent_loss
self.loss.name = "loss"
return self.loss
return lf
3. VAEの理論的な概要
生成モデルの目的は、データの分布である $p(X)$を推定することです。PRMLの言葉を借りると下記のようになります。
陰または陽に出力の分布だけでなく入力の分布もモデル化するアプローチは、モデルからのサンプリングによって入力空間で人工データを生成できることから、**生成モデル(Generative model)**と呼ばれる」(PRML 上巻p42)
画像を対象と考えると$X$は通常非常に高次元のデータとなります。本記事ではMNISTを対象としていますので784次元のデータです。前節でご紹介した通り、この高次元のうち、実際にデータが存在する箇所は非常に限られているため、それをうまくキャプチャして低次元の因子(例えば10次元など)の潜在変数$z$で表現させることを考えます。つまり高次元データ$X$と低次元データ$z$の対応関係を構築してうまく利用しようというものです。
VAEはこの潜在変数$z$が正規分布として分布するように学習させて、$p(X)$を推定します。$p(X)$はエビデンス(Evidence)と呼ばれることもあります。
ここで、
- $p(\cdot)$:確率モデル
- $z$:潜在変数
- $X$:データ
とします。この確率分布にパラメーターがあるとすると、$p(X)$に関する最尤法を用いて最もよく$X$を表現する$p(X)$のパラメーターを求めることができます。VAEではこの確率分布を構成する要素の一部にニューラルネットワークを用い、誤差逆伝播法と確率的勾配降下法でそのパラメーターを求めていきます。
潜在変数$z$とデータ$X$の関係をグラフィカルモデルで表すとこのようになります。

データ$X$から潜在変数$z$を対応づけるニューラルネットワークをEncoderと呼びます。いわゆるjpegのように画像ファイルの圧縮のアナロジーで考えるとEncoderと呼ばれる所以がわかるかと思います。
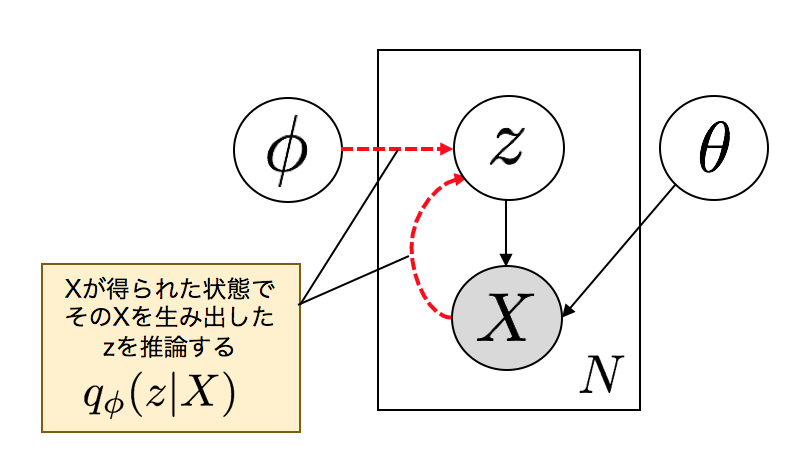
逆に潜在変数$z$からデータ$X$を復元するニューラルネットワークがDecoderです。
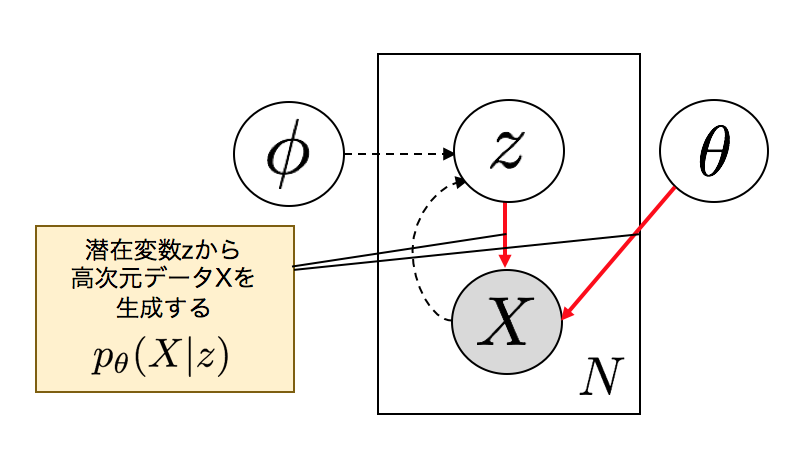
以上から、Encoder、Decoder、2つのニューラルネットで構成されるVAEが下記のようにモデル化できます。$\phi$はEncoderのパラメータ、$\theta$はDecoderのパラーメータです。
ポイントは、Encoderは直接$z$を生成するのではなく、下記のように$z$が従う正規分布のパラメーター$\mu, \sigma$を生成していることです。

推定したいモデル$p(X)$は上記のように2つのニューラルネットワークから構成されるモデルであると決定できました。あとは、データにフィットしたパラメータを求める手順です。下記のステップで考えると変分下限(Variational lower–bound)$L(X, z)$(後述)を最大にするようなパラメータを求めれば良いとわかります。変分下限はELBO(Evidence Lower BOund)と呼ばれることもあります。
パラメータを求める考え方のステップ
- $p(X)$の尤度を最大にするニューラルネットワークのパラメータ$\theta, \phi$を最尤法にて求める。
- 扱いやすいように対数尤度$\log p(X)$を最大にするターゲットとする。
- そのまま$\log p(X)$を最大にすることは積分の扱いが困難であるため、変分下限$L(X, z)$を最大にして下から抑えに行くことで対数尤度を最大にするパラメーターを求める。
さてこの変分下限とはなんでしょうか。これは下記のように求められます。
 イェンセンの不等式については[コチラ](http://qiita.com/kenmatsu4/items/26d098a4048f84bf85fb)も参考にしてください。
イェンセンの不等式については[コチラ](http://qiita.com/kenmatsu4/items/26d098a4048f84bf85fb)も参考にしてください。
不等号があるので、$L(X, z)$は$\log p(X)$の下限を表し、下記の図の「?」で表されるようなギャップが存在しています。

この「?」を求めるため対数尤度$\log p(X)$と変分下限$L(X, z)$の差を計算してみると下記の式より$D_{KL}[q(z|X) | p(z|X)]$であることがわかります。

最後の式のところ、0以上となるのはカルバックライブラーダイバージェンスはが常に0以上のためです。

よって変分下限は

となりました。第1項は固定値、第2項はパラメータに依存する項目なので、ターゲットとしていた「変分下限の最大化」はカルバックライブラーダイバージェンス$D_{KL}[q_{\phi}(z|X) || p_{\theta}(z|X)]$の最小化と同値になります。
このカルバックライブラーダイバージェンス$D_{KL}[q_{\phi}(z|X) || p_{\theta}(z|X)]$は、下記のように3つの項に分解できます。

これを変分下限の式に代入します。

これで変分下限が2つの項で表せることがわかりました。

2つめの項は $\mathbf{E}_{q(z|X)}[\log p(X|z)]$ で、これはEncoder、Decoderを表します。つまり、$q(z|X)$に関する、データ$X$の対数尤度$\log p(X|z)$の期待値を最大化したいということです。確率分布にEncoderで推論した$z$の分布を用い、対数尤度$\log p(X|z)$の期待値を取っています。
Chainerで該当する部分はこちらです。
mu, ln_var = self.encode(x)
batchsize = len(mu.data)
# reconstruction error
rec_loss = 0
for l in six.moves.range(k):
z = F.gaussian(mu, ln_var)
z.name = "z"
rec_loss += F.bernoulli_nll(x, self.decode(z, sigmoid=False)) / (k * batchsize)
$p_{\theta}(X|z)$は多変量ベルヌーイ分布に従うと仮定し([3] C.1 Bernoulli MLP as decoderより)F.bernoulli_nllで損失を計算しています。つまり、各ピクセルが0から1の間の値をとるとして、VAEの出力と、入力画像でクロスエントロピーを取っていると考えられます。この損失はReconstruction Errorと呼ばれます。

1つめの項$D_{KL}[q(z|X) | p(z)]$は正則化項で、$z$の分布が$p(z)$つまり$N(0, I)$となるように制約をかけている項になります。$q(z|X)$と$p(z)$の分布が近づけば近づくほどカルバックライブラーダイバージェンスの値は0に近づくので、変分下限が大きくなることになります。
Chainerで該当する部分はこちらです。
self.latent_loss = C * gaussian_kl_divergence(mu, ln_var) / batchsize
'gaussian_kl_divergence'のコア部分は下記の通り。
var = exponential.exp(ln_var)
mean_square = mean * mean
loss = (mean_square + var - ln_var - 1) * 0.5
これは正規分布に従う時のカルバックライブラーダイバージエンスを計算しています。([3] APPENDIX B参照)
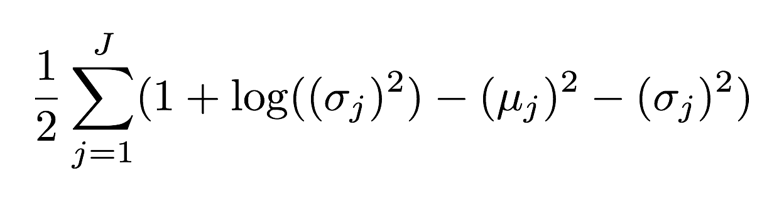
(正規分布の場合のKullback Leibler Divergenceの導出についてはコチラに解説記事を書きましたのでご参考としてください。)
これで最大化したいものが計算可能になりました。ニューラルネットワークの学習としては損失を最小化する価値で行うため、この変分下限にマイナスをかけたものを損失関数として、パラメーター$\theta, \phi$の最適化を行います。
Reparameterization Trick
最後に問題になるのが、先ほどの構造だと、$z \sim N(\mu(X), \sigma(X))$という確率分布が間に入っているため、誤差逆伝播法をそれより下に適用することができなくなってしまうことです。これを解決するためにReparameterization Trickという手法が用いられます。
$z \sim N(\mu(X), \sigma(X))$を直接扱うのではなく、$\varepsilon \sim N(0, I)$にてノイズを発生させ、$z = \mu(X) + \varepsilon*\sigma(X)$という形でつなげることで、下記の図のようにVAEを構成し、確率変数を避けて青い矢印を逆にたどって、誤差逆伝播法を適用するものです。

Chainerコードでいうと下記のあたりが該当します。
mu, ln_var = self.encode(x)
batchsize = len(mu.data)
# reconstruction error
rec_loss = 0
for l in six.moves.range(k):
z = F.gaussian(mu, ln_var)
おまけ
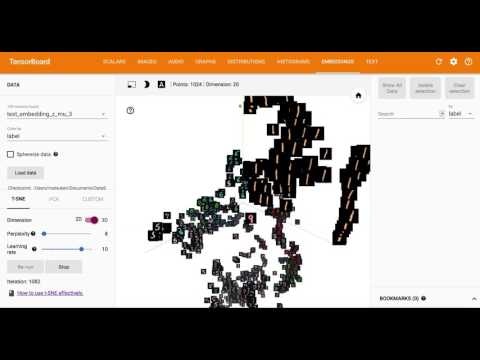
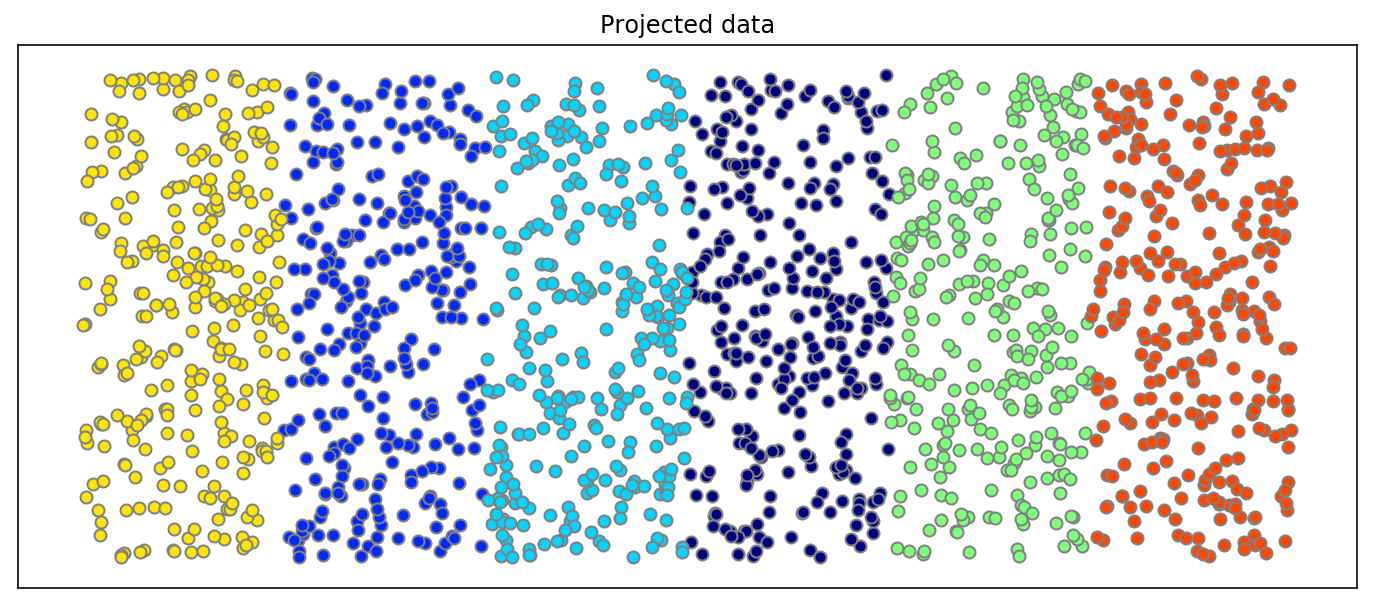
TensorFlowのTensorboardの機能の1つ、Embeddingを使って、20次元の潜在変数$z$をT-SNEで3次元二次元削減してビジュアライズしたもの。
参考
[1] 本記事のPythonコード
https://github.com/matsuken92/Qiita_Contents/tree/master/chainer-vae
[2] Tutorial on Variational Autoencoders
https://arxiv.org/abs/1606.05908
[3] Auto-Encoding Variational Bayes(Diederik P Kingma, Max Welling)
https://arxiv.org/abs/1312.6114
[4] 自然言語処理のための変分ベイズ法(Daichi Mochihashi)
http://chasen.org/~daiti-m/paper/vb-nlp-tutorial.pdf
[5] 猫でも分かるVariational AutoEncoder(Sho Tatsuno)
https://www.slideshare.net/ssusere55c63/variational-autoencoder-64515581
[6] 生成モデルの Deep Learning(Seiya Tokui)
https://www.slideshare.net/beam2d/learning-generator
[7] IIBMP2016 深層生成モデルによる表現学習
https://www.slideshare.net/pfi/iibmp2016-okanohara-deep-generative-models-for-representation-learning
[8] Variational AutoEncoder
https://www.slideshare.net/KazukiNitta/variational-autoencoder-68705109
[9] Deep Learning Chapter 17 The Manifold Perspective on Representation Learning
http://www.deeplearningbook.org/version-2015-10-03/contents/manifolds.html