2回目のリベンジです。
疑問点が晴れてなくなったのでこれでちゃんと理解できたはずです。
※ネット上の情報をかき集めて自分なりに実装しているので正確ではないところがある点はご了承ください
※数学が得意ではなく数式が間違っていたらすいません
TL;DR
- multistep lerningの話だよ
- TD誤差による伝播だよ
- On-Policyでは問題ないよ
- Off-Policyでも問題なく学習できるようにしたよ(retrace)
はじめに
Agent57系列の記事です。
過去の記事は以下となります。
本記事のコード
複数ステップの価値
おさらいです。
行動価値関数は以下です。
$$
Q_\pi(s_t, a_t) = \sum_{s \in S} T(s_{t+1}|s_t, a_t)(r_{t+1} + \gamma \sum_{a \in A} \pi (a_{t+1}|s_{t+1}) Q_\pi(s_{t+1}, a_{t+1}))
$$
話を簡単にするために状態の遷移確率は100%(一意に決まる)とします。
$$
Q_\pi(s_t, a_t) = r_{t+1} + \gamma \sum_{a \in A} \pi (a_{t+1}|s_{t+1}) Q_\pi(s_{t+1}, a_{t+1})
$$
$t$が現step、$s$が状態、$a$がアクション、$r$が即時報酬、$\gamma$が割引率、$\pi(a|s)$が状態sでアクションaを選ぶ確率です。
$\sum_{a \in A}$で全アクションに対してその先の価値を確率で掛けているので$\sum$の箇所は1step先の(状態)価値になります。
行動価値は期待値なので実際にサンプリングして求める場合を考えます。
\begin{align}
Q_\pi(s_t, a_t) &= E_{\pi}[r_{t+1} + \gamma Q_\pi(s_{t+1}, A_\pi(a_t|s_t))] \\
&\approx \frac{ \sum_N(r_{t+1} + \gamma Q_\mu(s_{t+1}, A_\mu(a_{t}|s_{t}) ) }{N} = Q_{\mu}(s_t, a_t)
\end{align}
ここで $A_\pi(a_t|s_t)$ は方策 $\pi(s_t|a_t)$ により確率的に決まるアクション、$A_\mu(a_t|s_t)$ は方策 $\mu(s_t|a_t)$ により確率的に決まるアクションです。
実際はサンプリング毎にQ値を更新するので上記の式みたいに$N$回サンプリングし、その結果から更新とはなりませんが、サンプリング結果から期待値を予測する事には変わりありません。
ここで予測する際にある次の行動価値 $Q(s_{t+1}, a_{t+1})$ を展開すると複数ステップ先の情報を元に期待値を予測できます。
+1step展開した場合は以下です。
$$
\frac{
\sum_N(r_{t+1} + \gamma
(r_{t+2} + \gamma Q(s_{t+2}, a_{t+2}))
)
}{N}
$$
TD誤差による伝播
上記は価値を伝播させていましたが、実際に求めたいのは価値の差(TD誤差:$\delta$)であり、TD誤差を伝播させても結果は変わりません。
2stepの場合は以下です。
- 価値の伝播
$$
TD_{error} = r_{t+1} + \gamma (r_{t+2} + \gamma Q(s_{t+2}, a_{t+2})) - Q(s,a)
$$
- TD誤差の伝播
\begin{align}
TD_{error} &= \delta(s_t,a_t) + \gamma \delta(s_{t+1},a_{t+1}) \\
\delta(s_t,a_t) &= r_{t+1} + \gamma Q(s_{t+1}, a_{t+1}) - Q(s_t,a_t)
\end{align}
以下の具体例で計算してみます。
- 価値の伝播
\begin{align}
TD_{error} &= 1 + \gamma (-1 + \gamma 0.5) - Q(s,a) \\
&= 1 - \gamma + 0.5 \gamma^2 - Q(s,a)
\end{align}
- TD誤差の伝播
\begin{align}
\delta(s0,a0) &= 1 + \gamma (-0.5) - Q(s,a) \\
\delta(s1,a0) &= -1 + \gamma 0.5 - (-0.5) \\
TD_{error} &= 1 + \gamma (-0.5) - Q(s,a) + \gamma(-1 + \gamma 0.5 - (-0.5)) \\
&= 1 - \gamma + 0.5 \gamma^2 - Q(s,a)
\end{align}
同じ結果になりましたね。
一般化すると以下です。
- 価値
\begin{align}
TD_{error} &= r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} + \cdots + \gamma^{t+k-1} r_{t+k} - Q(s_{t+k},a_{t+k}) \\
&= \sum_{s=1}^{k} \gamma^{t+s-1} r_{t+s} - Q(s_{t+k}, a_{t+k})
\end{align}
- TD誤差
\begin{align}
TD_{error} &= \delta(s_t,a_t) + \gamma \delta(s_{t+1},a_{t+1}) + \gamma^2 \delta(s_{t+2},a_{t+2}) + \cdots \\
&= \sum_{s=0}^{k} \gamma^{s} \delta(s_{t+s},a_{t+s}) \\
\delta(s_t,a_t) &= r_{t+1} + \gamma Q(s_{t+1}, a_{t+1}) - Q(s_t,a_t)
\end{align}
期待値を求める場合のサンプリング確率について
期待値をサンプリングの結果から求める場合(モンテカルロ法)、求めたい期待値の確率とサンプリングする際の確率は同じである必要があり、違う場合は重点サンプリングで修正する必要があります。
例としてコインを考えます。
コインの表が出る確率は50%(+2とします)、裏が出る確率は50%(+1とします)です。
期待値は以下です。
$$
0.5 \times 2 + 0.5 \times 1 = 1.5
$$
ここで実際にコインを投げて確かめてみます。
しかしコインがゆがんでおり、表が出る確率は75%、裏は25%でした。
100回投げた結果、表が75回、裏が25回出たとします。
これをそのまま計算したらもちろん期待値にはなりません。
$$
\frac{75 \times 2 + 25 \times 1}{100} = 1.75
$$
この場合、重点サンプリングとして、$\frac{実際の確率}{サンプリング時の確率}$を各サンプルに対して掛けてやる必要があります。
今回ですと以下です。
$$
\frac{75 \times 2 \times \frac{0.5}{0.75} + 25 \times 1 \times \frac{0.5}{0.25}}{100} = 1.5
$$
ちゃんと正しい期待値になりましたね。
サンプリングの方策が違う場合の安全な学習方法
On-Policy
On-Policyは探索に使う方策と求めたい方策が同じ($\mu = \pi$)なので、特に問題は起こりません。
Off-Policy
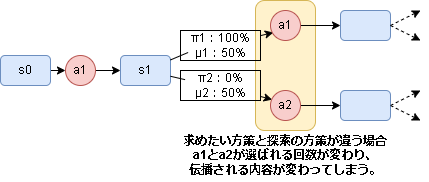
Off-Policyは $\mu \neq \pi$ な場合で、探索と求めたい確率分布が違うため期待値を正確に求めることができません。
イメージとしては以下です。
選択されるアクションの回数に差異があるため、期待値がちゃんと求められない状況になるイメージです。
ここまでが問題設定です。
retrace
上記問題を解決するために(重点サンプリングみたいに)係数を掛けて伝播を修正しようという事を考えます。
先ほど一般化したTD誤差に係数 $c$ を掛けて修正します。
\begin{align}
TD_{error} = &\delta(s_t,a_t) \\
& + c_{t} \gamma \delta(s_{t+1},a_{t+1}) \\
& + c_{t} c_{t+1} \gamma^2 \delta(s_{t+2},a_{t+2}) \\
& + c_{t} c_{t+1} c_{t+2} \gamma^3 \delta(s_{t+3},a_{t+3}) \\
& + \cdots \\
& + (\prod_{s=0}^{k-1} c_{t+s} ) \gamma^k \delta(s_{t+k},a_{t+k}) \\
TD_{error} =& \delta(s_t,a_t) + \sum_{s=1}^{k} \gamma^s (\prod_{s=0}^{k-1} c_{t+s}) \delta(s_{t+k},a_{t+k}) \\
TD_{error} =& \sum_{s=t}^{t+k-1} \gamma^{s-t} (\prod_{i=t+1}^{s} c_i) \delta(s_s,a_s) \quad ※論文の記載
\end{align}
※未来の行動は過去の行動が影響するので$c$はどんどん乗算していく必要がある
※行動価値は行動選択後の価値なので最初は$c$による修正の対象外(s=t+1の謎がやっと解けました)
ここからやっと論文の内容です。
論文の内容は係数 $c$ をどう設計するのが良いかという内容です。
重点サンプリングと同じでもいけそうな気がしますが、そのまま使うと分散が大きくなりすぎる($\prod c_s$ ここの部分のせいで値が膨大になってしまう)ので、上限を1に抑えたのが retrace です。
$$
c_s = \lambda \min(1, \frac{ \pi(a_s|s_s) }{ \mu(a_s|s_s) })
$$
$\lambda$ は任意の定数です。
確認
実際のコードは GoogleColaboratory から確認してください。
GridEnv
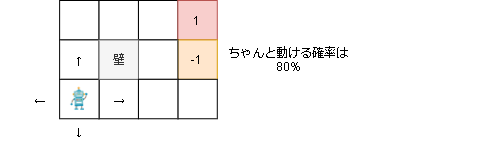
以下の環境を元に実際に見てみます。
例えば上に動こうとした場合にちゃんと上に行ける確率は80%で、10%で左、10%で右に移動します。
壁に移動した場合は動きません。
赤いマスに行くと報酬1が手に入り終了、オレンジのマスも報酬-1が手に入り終了します。
また、1step毎に-0.04の報酬が手に入ります。
行動価値(Greedy)
Q値が最大なアクションを選ぶ方策の場合の行動価値は以下となります。
動的計画法で求めているので理論値となります。(これと比較し学習できてるか確認します)
------------------------------------------------------------
0.523 | 0.650 | 0.801 | 0.000 |
0.498 0.610| 0.537 0.766| 0.648 0.928| 0.000 0.000|
0.435 | 0.650 | 0.554 | 0.000 |
------------------------------------------------------------
0.487 | 0.000 | 0.585 | 0.000 |
0.399 0.399| 0.000 0.000| 0.503 -0.686| 0.000 0.000|
0.317 | 0.000 | 0.224 | 0.000 |
------------------------------------------------------------
0.374 | 0.267 | 0.428 | -0.753 |
0.307 0.273| 0.288 0.327| 0.286 0.187| 0.189 0.017|
0.292 | 0.267 | 0.314 | 0.151 |
------------------------------------------------------------
逆ε-greedyなQ学習
探索の方策としてε以下はランダムにそうじゃない場合はQ値が最小のアクションを選択する方策を実装しました。
(学習時はQ値が最大アクションのQ値を伝播します)
コードでのイメージは以下です。
def policy(self, s):
if random.random() < epsilon:
# ランダム
return random.randint(0, nb_actions-1)
else:
# Q値が "最小" のアクションを選択
return np.argmin(self.Q[s])
Q学習(1step, Off-Policy)
普通のQ学習です。
1stepなので(探索が十分なら)方策に関係なく学習できるはずです。
------------------------------------------------------------
0.565 | 0.767 | 0.783 | 0.000 |
0.537 0.702| 0.597 0.832| 0.645 0.998| 0.000 0.000|
0.442 | 0.657 | 0.816 | 0.000 |
------------------------------------------------------------
0.549 | 0.000 | 0.773 | 0.000 |
0.395 0.439| 0.000 0.000| 0.523 -0.288| 0.000 0.000|
0.441 | 0.000 | 0.427 | 0.000 |
------------------------------------------------------------
0.442 | 0.436 | 0.625 | -0.880 |
0.368 0.345| 0.355 0.428| 0.497 0.234| 0.033 -0.381|
0.355 | 0.362 | 0.425 | 0.195 |
------------------------------------------------------------
行動価値(Greedy)と似た結果です。
ちゃんと学習できていますね。
Q学習(価値伝搬(multisteps)、10step、Off-Policy)
Rainbowで使われている手法ですね。
10step先の価値まで伝播しています。
マイナスを優先する方策なので負の値ばかり伝播してしまいうまく学習できないことが想定されます。
------------------------------------------------------------
-0.610 | -0.268 | -0.272 | 0.000 |
-0.197 0.240|-0.259 0.004|-0.689 0.926| 0.000 0.000|
-0.634 | 0.104 | 0.036 | 0.000 |
------------------------------------------------------------
-0.021 | 0.000 | -0.390 | 0.000 |
-0.425 0.025| 0.000 0.000| 0.211 -0.995| 0.000 0.000|
-0.279 | 0.000 | -0.317 | 0.000 |
------------------------------------------------------------
-0.104 | -0.688 | -0.544 | -0.911 |
-0.052 -0.442|-0.518 -0.764|-0.270 -0.764|-0.604 -0.816|
-0.001 | -0.414 | -0.657 | -0.559 |
------------------------------------------------------------
学習できていませんね。
予想通りの結果になりました。
Q学習(TD誤差、10step, Off-Policy)
TD誤差を伝播させる方法です。
retrace は使っていません。
また値が発散してしまうので他と比べて学習率を下げています。
------------------------------------------------------------
0.734 | 0.514 | 0.877 | 0.000 |
0.735 0.598| 0.487 0.675| 0.539 0.919| 0.000 0.000|
0.739 | 0.696 | 0.911 | 0.000 |
------------------------------------------------------------
0.743 | 0.000 | 0.808 | 0.000 |
0.832 0.787| 0.000 0.000| 0.583 -0.868| 0.000 0.000|
0.881 | 0.000 | 0.954 | 0.000 |
------------------------------------------------------------
0.879 | 1.239 | 0.771 | -0.784 |
0.941 1.044| 0.879 0.997| 1.116 0.672| 0.624 0.803|
0.839 | 1.124 | 0.924 | 0.590 |
------------------------------------------------------------
なぜか1を超えている場所もあったりと全然学習できていませんね。
Q学習(TD誤差+retrace、10step, Off-Policy)
retraceを適用した結果です。
------------------------------------------------------------
0.495 | 0.603 | 0.692 | 0.000 |
0.500 0.525| 0.483 0.610| 0.681 0.793| 0.000 0.000|
0.290 | 0.601 | 0.517 | 0.000 |
------------------------------------------------------------
0.410 | 0.000 | -0.532 | 0.000 |
0.334 0.329| 0.000 0.000| 0.669 -0.817| 0.000 0.000|
0.299 | 0.000 | 0.542 | 0.000 |
------------------------------------------------------------
0.351 | 0.340 | 0.562 | -0.982 |
0.301 0.379| 0.331 0.423| 0.472 -0.369|-0.368 -0.102|
0.340 | 0.422 | 0.466 | 0.193 |
------------------------------------------------------------
行動価値(ε-Greedy)の結果に近い結果になっていますね。
10step先まで見ていてもちゃんと学習できています。
(おまけ) SARSA(価値伝播(multisteps)、10step, On-Policy)
On-Policyの場合は価値伝播でもちゃんと学習できるはずなので確認してみました。
※方策はε-greedyに戻しています。
- 行動価値(ε-Greedy)
ε-Greedyな方策の場合の行動価値の理論値は以下となります。(ε=0.5)
------------------------------------------------------------
0.221 | 0.377 | 0.600 | 0.000 |
0.192 0.328| 0.238 0.537| 0.365 0.866| 0.000 0.000|
0.121 | 0.377 | 0.201 | 0.000 |
------------------------------------------------------------
0.179 | 0.000 | 0.371 | 0.000 |
0.081 0.081| 0.000 0.000| 0.114 -0.750| 0.000 0.000|
-0.002 | 0.000 | -0.151 | 0.000 |
------------------------------------------------------------
0.052 | -0.078 | 0.023 | -0.839 |
-0.012 -0.063|-0.035 -0.077|-0.068 -0.254|-0.191 -0.387|
-0.029 | -0.078 | -0.100 | -0.294 |
------------------------------------------------------------
- SARSA(ε=0.5)
学習した結果は以下です。
------------------------------------------------------------
0.146 | 0.315 | 0.516 | 0.000 |
0.135 0.340| 0.349 0.642| 0.506 0.972| 0.000 0.000|
0.209 | 0.081 | 0.589 | 0.000 |
------------------------------------------------------------
0.201 | 0.000 | -0.136 | 0.000 |
0.270 -0.131| 0.000 0.000| 0.030 -0.516| 0.000 0.000|
-0.109 | 0.000 | -0.152 | 0.000 |
------------------------------------------------------------
-0.165 | -0.328 | -0.476 | -0.900 |
-0.077 -0.168|-0.071 -0.243|-0.476 -0.571|-0.001 -0.765|
-0.262 | -0.356 | -0.686 | -0.058 |
------------------------------------------------------------
概ね同じですね。
On-Policyでは問題ない事が分かります。
おわり
retraceは難関でしたね…
multistep lerningの話だと分かった後はすぐでした。
分かればもっと理解が早かったと思います…