強化学習については全然キャッチアップしてこなかったので、強化学習のビッグウェーブに乗り遅れてしまった。「教師あり」や「教師なし学習」の手法を用いた実問題の適用は良く聞くし、私もよく使用するが、「強化学習」はそこまで使われていない気がする(ゲームへの適用例はたくさんあるけど)。最新の手法を理解するために、まずは基礎について学ぶ。できるだけ数式を使って説明できるようにしたい。
2019/3/28追記:方策勾配法追加しました。
2019/4/29追記:Thompson Sampling追加しました。
2022/2/25追記:報酬の部分を更新しました。
強化学習とは
Source: Reinforcement Learning: An Introduction 2nd Edition, Richard S. Sutton and Andrew G. Barto)
強化学習は機械学習の中でも少し取っ付きにくい感じがする。機械学習の中でも用語が独特であるのと、強化学習で使用されるモデルは価値を返すものであったり、行動を返すものであったり、通常の教師有り学習でみられるような誤差関数の与え方が異なるためである。
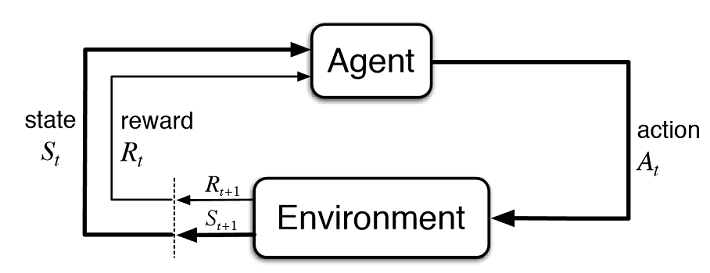
とりあえず、これらの用語について詳しく知っていく必要がある。上図はエージェントの行動のフローを表している。時刻$t$では、状態$S_t$と即時報酬$R_{t}$が環境により与えられている。行動の主体であるエージェントは、これまでの情報から最適な行動$A_t$を決定する。そして、環境は、次の状態$S_{t+1}$および報酬$R_{t+1}$を返す。これらの行動を繰り返していく中で、累積報酬が最大となるように状態価値$V(S)$や行動価値$Q(S, A)$、行動方針である方策(policy, $\pi(A|S)$)が学習されていく。
多腕バンディット問題(Mult-armed bandit problem)
強化学習において状態$S$が変化しない最も単純な問題である。スロットマシンからアームを引くと、ある確率に基づいて報酬が得られるという設定である。行動の主体であるエージェントは腕を引くという行動だけ行う。どの腕を選んだらよいか、行動を通じて探索していく。
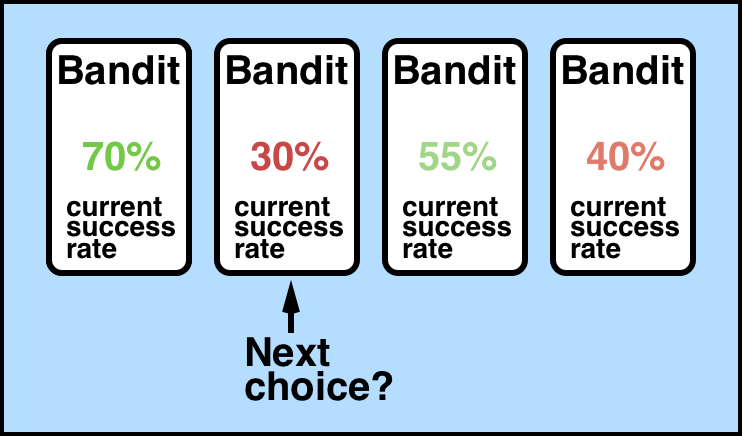
この図は4つのアームを持つスロットマシンを表しており、それぞれの確率は今までの行動に基づいて得られた報酬の平均である。
ここでの問題設定を当たりなら報酬1, 外れなら報酬0となるベルヌーイ試行とする。5本のアームのスロットの払戻(当たり設定)p=[0.1, 0.1, 0.1, 0.1 0.9]としておく(エージェントは知らないため、これを推定する)。
import random
class BernoulliArm():
def __init__(self, p):
self.p = p
def draw(self):
if random.random() > self.p:
return 0.0
else:
return 1.0
報酬について
報酬はスロットを引いて貰える即時報酬$r$(0もしくは1)と、その結果が積み重なった累積報酬$G$がある。エピソード$i$における$T$ステップ目までの累積報酬は次式となる。
$$
G_{i, t} = r_{i, t} + \gamma r_{i, t+1} + \gamma^{2} r_{i, t+1} + \dots + \gamma^{T_{i}-1} r_{i, T}
$$
ここで、$\gamma$は時間割引率であり、遠くのステップで得られる報酬ほど低くなるようする。強化学習ではある方策$\pi$における行動を通して最終的な累積報酬が何かを推定する問題となる。状態$s$から$G$の期待値を推定する式は状態価値関数と呼ばれ、価値$V(s)$と表現される。状態価値を推定する方法は複数あるが、ここではモンテカルロ法を用いて価値を推定する。
増分モンテカルロ
増分モンテカルロ(incremental Monte Carlo)では、次の更新式で価値関数を推定する。
\begin{align}
V(s) &= V(s) + \frac{1}{n}(G_t - V(s))\\
&= \frac{n-1}{n}V(s) + \frac{1}{n} r_t
\end{align}
ここで、$G_t = r_t$とした。$V(s), r_t$はそれぞれ時刻$t$における価値、即時報酬、$n$はアームを選択した回数である。この$V$は累積報酬の期待値(得られるであろう累積報酬)を表している。
これはActionSelector()のupdate()に実装している。
class ActionSelector:
def __init__(self, counts, values):
self.counts = counts
self.values = values
def initialize(self, n_arms):
self.counts = np.zeros(n_arms)
self.values = np.zeros(n_arms)
def select_arm(self):
raise NotImplementedError
def update(self, chosen_arm, reward):
self.counts[chosen_arm] = self.counts[chosen_arm] + 1
n = self.counts[chosen_arm] # 今回のアームを選択した回数
value = self.values[chosen_arm] # 更新前の平均報酬額
new_value = ((n-1) / float(n)) * value + (1 / float(n)) * reward
self.values[chosen_arm] = new_value
選択回数はself.countsに、期待報酬はself.valuesに格納するようにする。initialize()はエピソードが完了時、初期化するために用いられる。select_arm()では、探索と活用を踏まえながら、どのような方針でアームを選択すべきかを実装していく必要がある。
方策
方策は状態が与えられたときに次の行動を返す確率モデルであり、$\pi(a|s)$と表現される。とエージェントは「探索と活用」を考慮しながら行動を決定する。ここでは、代表的な3つを記載する。
ε-greedy
上図のNext choiceは一番左の70%を選んだ方がよさそうだが、30%の腕を選ぼうとしている。$\varepsilon$-greedyでは確率$\varepsilon$でランダムに探索(explore)を行い、$1-\varepsilon$で報酬の平均が最大のものを活用(exploit)するというもので探索と活用はトレードオフの関係にある。$\varepsilon$が大きいとランダムな腕を選び続けるため、少しずつ減らしていくことが良いと言われている(アニーリングと呼ばれる)。
以下コードは、標準の$\varepsilon$-greedyアルゴリズムである。
class EpsilonGreedy(ActionSelector):
def __init__(self, counts: list = [], values: list = [], epsilon: float = 0.1):
super(EpsilonGreedy, self).__init__(counts, values)
self.epsilon = epsilon
def select_arm(self):
if random.random() > self.epsilon:
return np.argmax(self.values)
else:
return random.randrange(len(self.values))
UCB1 (Upper Confidence Bound)
探索と活用をうまく行うために行動(アーム)の選択基準には様々な方法が提案されている。その中でもUCBは、Chernoff-Hoeffdingの不等式より得られた境界条件に基づいたものである。Regretを最小化、すなわち行動信頼度の上界を求めることでこの選択基準を更新していく。下式のUCBスコアに従いアーム選択をする。
\begin{align}
\hat{\mu}_{i,t} &= \frac{\sum_{s=1}^{t} r_{i, s}}{N_{i,s}} \\
\text{UCB}_{i,t} &= \hat{\mu}_{i, t} + \sqrt{\frac{2\log t}{N_{i,t}}} \\
i_{t+1} &= \arg\max_{i} \text{UCB}_{i,t}
\end{align}
ここで、$\mu_{i,t}$は$i$番目の腕で$t$ステップ目までの期待報酬を表す。これまで得られた累積報酬であり$V$に対応する。$N_{i,t}$は、これまでに腕$i$を選んだ回数である。
UCBが最大となる腕$i$を選ぶことで行動を選択する。本手法はモンテカルロ木探索やベイズ最適化などにもよく用いられる選択基準である。
class UCB1(ActionSelector):
def __init__(self, counts=[], values=[]):
super(UCB1, self).__init__(counts, values)
def select_arm(self):
n_arms = len(self.counts)
for arm in range(n_arms):
if self.counts[arm] == 0:
return arm
total_counts = sum(self.counts)
bonus = np.sqrt((2 * np.log(np.array(total_counts))) / np.array(self.counts))
ucb_values = np.array(self.values) + bonus
return np.argmax(ucb_values)
Thompson Sampling
何らかの事前分布を設定し、真の分布へ近づけるようにパラメータを更新していく方法である。armの選択にベルヌーイ分布を利用しているので、ここではベータ分布を利用する。
f(x; \alpha, \beta) = \frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha, \beta)}, \\
E(x)=\frac{\alpha}{\alpha + \beta}
alpha, betaはそれぞれarm数だけの列数がある。報酬が正ならalpha[arm]に+1を, そうでなければbeta[arm]に+1を加えていき分布の更新とサンプリングを行っていく。その中で最も大きい値のインデックスが次に選択するarmとなる。
class ThompsonSampling(ActionSelector):
def __init__(self, counts=[], values=[]):
super(ThompsonSampling, self).__init__(counts, values)
self.alpha = None
self.beta = None
def initialize(self, n_arms):
self.counts = np.zeros(n_arms)
self.values = np.zeros(n_arms)
self.alpha = np.ones(n_arms)
self.beta = np.ones(n_arms)
def select_arm(self):
return self.beta_sampling(self.alpha, self.beta)
def update(self, chosen_arm, reward):
self.counts[chosen_arm] = self.counts[chosen_arm] + 1
n = self.counts[chosen_arm]
value = self.values[chosen_arm]
new_value = ((n - 1) / float(n)) * value + (1 / float(n)) * reward
self.values[chosen_arm] = new_value
if new_value > 0:
self.alpha[chosen_arm] += 1
else:
self.beta[chosen_arm] += 1
@staticmethod
def beta_sampling(alpha, beta):
samples = [np.random.beta(alpha[i] + 1, beta[i] + 1) for i in range(len(alpha))]
return np.argmax(samples)
実装例
バンディット問題のソースコード自体は、"Bandit Algorithms for Website Optimization"のものを大部分利用している。
全体のソースコードは以下:
import random
from typing import Any, Dict, List
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from numpy import ndarray
from tqdm import tqdm
from bandit_problem.utils import (
UCB1,
BernoulliArm,
EpsilonGreedy,
ThompsonSampling,
)
def test_algorithm(
algo: Any, arms: List[BernoulliArm], num_sims: int = 200, horizon: int = 200,
) -> Dict[str, ndarray]:
"""Run an algorithm for evaluation in MAB
"""
# Initialize variables with zeros.
chosen_arms = np.zeros(num_sims * horizon)
rewards = np.zeros(num_sims * horizon)
cumulative_rewards = np.zeros(num_sims * horizon)
sim_nums = np.zeros(num_sims * horizon)
times = np.zeros(num_sims * horizon)
for sim in tqdm(range(num_sims)):
sim += 1
algo.initialize(len(arms))
for step in range(horizon):
step += 1
index = (sim - 1) * horizon + step - 1
sim_nums[index] = sim
times[index] = step
# select an arm and obtain the reward.
chosen_arm = algo.select_arm()
reward = arms[chosen_arm].draw()
# store the choice.
chosen_arms[index] = chosen_arm
rewards[index] = reward
cumulative_rewards[index] = reward if step == 1 else cumulative_rewards[index - 1] + reward
# update algorithm
algo.update(chosen_arm, reward)
return {
"sim_nums": sim_nums,
"times": times,
"chosen_arms": chosen_arms,
"rewards": rewards,
"cumulative_rewards": cumulative_rewards,
}
def run(arms: List[BernoulliArm], algo: Any, y_label: str = "rewards") -> None:
"""Run and plot results
"""
label_name = algo.__class__.__name__
print(label_name)
n_arms = len(arms)
algo.initialize(n_arms)
results = test_algorithm(algo, arms, num_sims=NUM_SIMS, horizon=HORIZON)
df = pd.DataFrame(results)
grouped = df[y_label].groupby(df["times"])
# Figure
plt.title(f"Multi-armed bandit: sims={NUM_SIMS}")
plt.plot(grouped.mean(), label=label_name)
plt.ylabel(f"{y_label} mean")
plt.xlabel("Number of steps")
plt.legend(loc="best")
if __name__ == "__main__":
NUM_SIMS = 200
HORIZON = 200
theta = [0.1, 0.1, 0.1, 0.1, 0.9]
random.shuffle(theta)
print(theta)
arms = list(map(lambda x: BernoulliArm(x), theta))
# Set Algorithms
algo_list = [
EpsilonGreedy(epsilon=0.3),
UCB1(),
ThompsonSampling(),
# "PG": PolicyGradient(len(arms))
]
plt.figure(figsize=(6, 4), dpi=300)
for algo in algo_list:
run(arms, algo)
plt.savefig("mab.png")
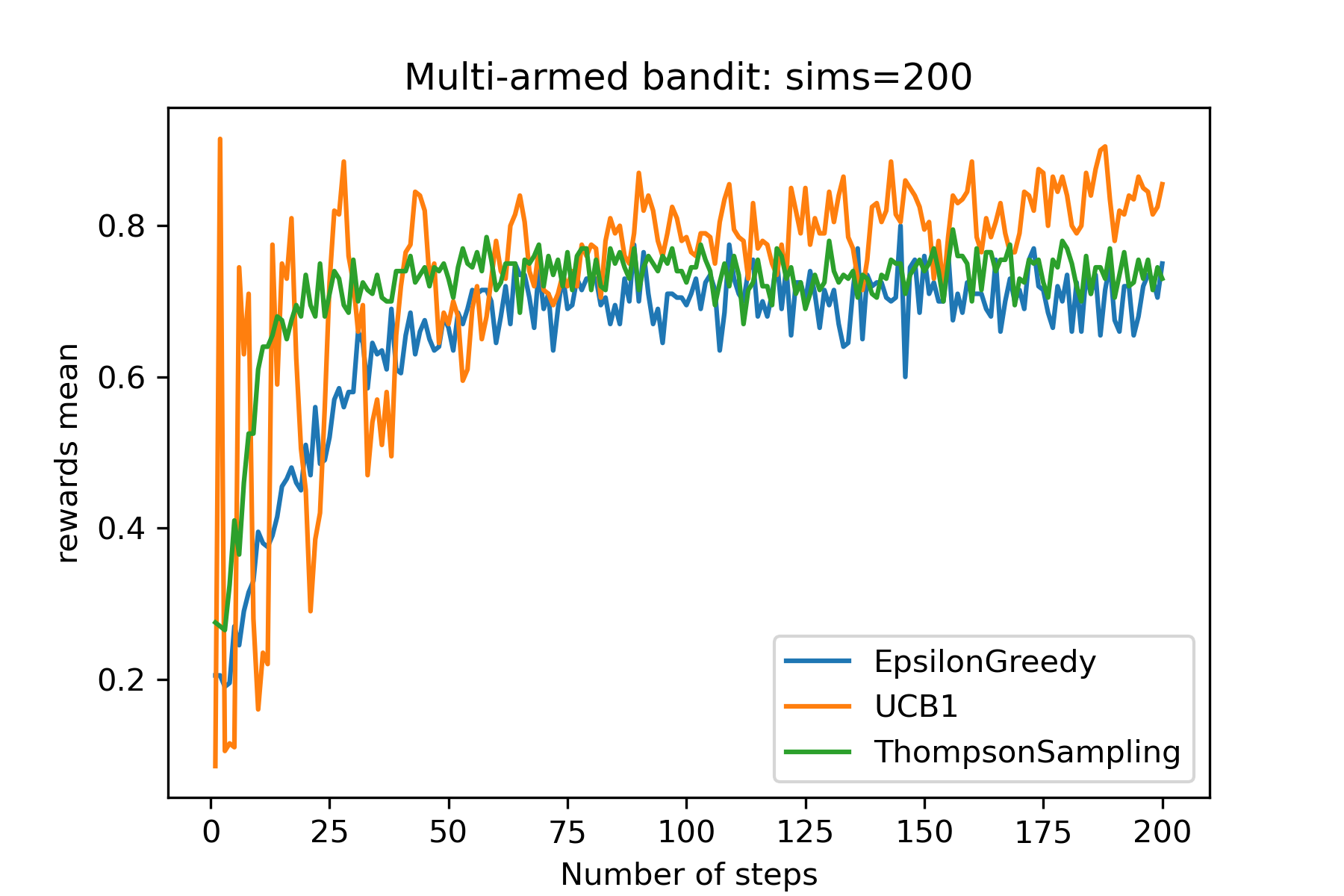
結果(1)
横軸はプレイ回数を表しており、この操作を200回繰り返した(シミュレーション(エピソード)数=200)。縦軸はその平均報酬である。epsilon=0.3としており、e-greedyアルゴリズムでは30%の確率で探索をするため、最適でない行動を選んでいる。UCB1は大きくばらついてるが、最終的には報酬が0.8前後まで到達している。UCBアルゴリズムは長期的な報酬和の理論下限を最適化しているため、平均報酬は劣っている。Thompson samplingでは平均報酬が0.7前後に落ち着いており、epsion=0.3のときと類似する結果となった。
方策勾配法
Cart-poleに行く前に、方策勾配法についても試してみた。方策は状態$s$が与えられたとき、行動確率$a$を返す確率分布である。$\theta$でパラメタライズされた方策は$\pi_{\theta}(a|s)$とかける。今回の場合は状態は変化しないため、初期状態のみからスタートすることになる。方策勾配定理を用いると以下の式が導かれる。
\begin{align}
\nabla_\theta J(\theta) = \mathbb{E}_{\pi_\theta} [\sum_{t=0}^H \nabla_\theta \log{ \pi_\theta (a_t | s_t)} \mathcal{R}(s_t, a_t)]
\end{align}
この$\mathcal{R}$をいかに近似するかで方策の更新が変わってくる。Q関数で近似すればActor Criticである。REINFORCEでは直接報酬を用いる。
\begin{align}
\nabla_\theta J(\theta) \approx \frac{1}{M}\sum_{m=1}^{M}\frac{1}{T}\sum_{t=1}^{T} \nabla_{\theta} \log \pi_{\theta} (a_t|s_t) \mathcal{R}(s_t, a_t)
\end{align}
ここで、Mはエピソード数、Tはステップ数である。ステップが完了してから方策を更新するのがポイントとなる。アーム1から5、すなわちtheta = [0.1, 0.1, 0.2, 0.1, 0.7]に設定して, horizon=200, n_sims=200で実験した。方策はソフトマックス関数を用いた。
- ソフトマックス関数
\pi_i = \frac{\exp(\beta\theta_i)}{\sum_j \exp(\beta \theta_j) }
- 微分
\dfrac{\partial \pi_i}{\partial \theta_j}=
\begin{cases}
\pi_i(1-\pi_i)&i=j \\
-\pi_i \pi_j&i\neq j
\end{cases}
- 対数微分
\begin{align}
\frac{\partial}{\partial \theta_j}\ln \pi_i &= \frac{1}{\pi_i}\frac{\partial \pi_i}{\partial \theta_j} \\ &=
\begin{cases}
(1-\pi_i) &i=j \\
-\pi_j & i\neq j
\end{cases}
\end{align}
簡単のため、$\beta=1$とした。本来は方策をニューラルネットワークで表現するのが良い。
class PolicyGradient(ActionSelector):
def __init__(self, n_arms, counts=[], values=[]):
super(PolicyGradient, self).__init__(counts, values)
self.n_arms = n_arms
self.total_values = [0 for _ in range(self.n_arms)]
self.total_counts = 1
self.episodes = 0
# soft max parameter
self.theta = np.ones(self.n_arms) + np.random.normal(0, 0.01, self.n_arms)
# policy gradient
self.grad_reward = 0
self.mean_grad_reward = 0
# hyper parameter
self.beta = 1.0
self.eta = 0.10
def initialize(self, n_arms):
self.counts = np.zeros(n_arms)
self.values = np.zeros(n_arms)
# M : episodes T : total step
# (1/M)∑(1/T)∑[∇log(π(a))* rewards]
self.total_counts = np.sum(self.counts)
if self.total_counts == 0:
self.total_counts = 1
self.mean_grad_reward = self.grad_reward / self.total_counts
self.episodes += 1
# update theta
if self.episodes % 10 == 0:
self.theta = self.reinforce(self.theta)
th = self.soft_max(self.theta)
print(f"EPISODE {self.episodes} : Update Policy Probability {th}")
# print(f"(1/T)∑∇logπ(a)R = {self.mean_grad_reward}\n"))
def select_arm(self):
# t = sum(self.counts) + 1
# beta= 1 / np.log(t + 0.0000001)
beta = 1.0
logits = beta * self.theta
probs = self.soft_max(logits)
return categorical_draw(probs)
def update(self, chosen_arm, reward):
self.counts[chosen_arm] = self.counts[chosen_arm] + 1
n = self.counts[chosen_arm]
value = self.values[chosen_arm]
new_value = ((n - 1) / float(n)) * value + (1 / float(n)) * reward
self.values[chosen_arm] = new_value
self.grad_reward += self.grad_ln_pi().dot(self.values) # new_value
def reinforce(self, theta):
# REINFORCE
nabla_J = self.mean_grad_reward / self.episodes
new_theta = theta + self.eta * nabla_J
self.mean_grad_reward += self.mean_grad_reward
return new_theta
@staticmethod
def soft_max(logits):
return np.nan_to_num(
[np.exp(var) / np.nansum(np.exp(logits)) for var in logits]
)
def grad_soft_max(self):
pi = self.soft_max(self.theta)
dpi = [i * (1 - i) if i == j else -i * j for i in pi for j in pi]
grad_pi = np.array(dpi).reshape(len(pi), -1)
return grad_pi
def grad_ln_pi(self):
pi = self.soft_max(self.theta)
dlog_pi = [(1 - i) if i == j else -j for i in pi for j in pi]
dlog_pi = np.array(dlog_pi).reshape(len(pi), -1)
return dlog_pi
結果
初期状態であるエピソード1では、方策はランダムに選ばれる。400 episodeほど経つと、下図のようになる。
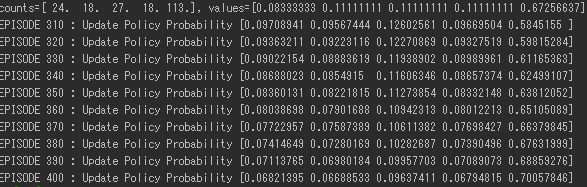
1000 episodeほど経つと、ほとんど最後のアームを選択するようになった。
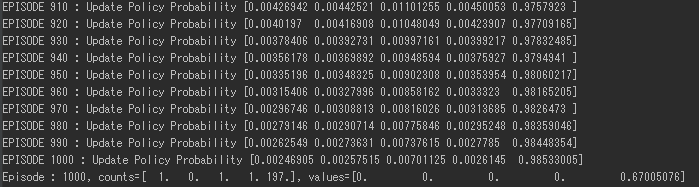
方策の更新がうまくいっていることがわかる。最終の報酬結果をみてみる。
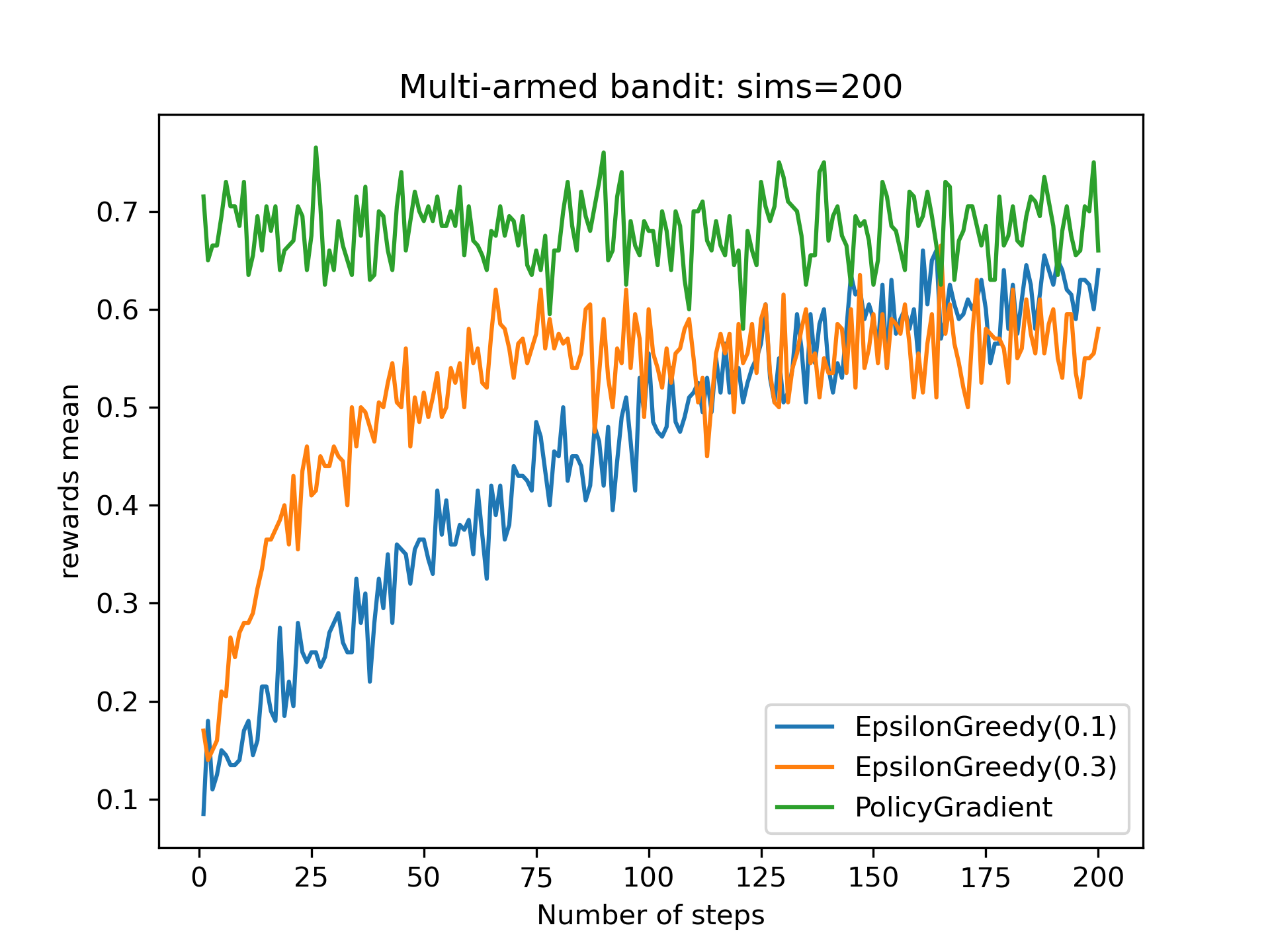
epsilon greedyでは徐々に報酬が上がっていくのに対し、REINFORCEでは最初からアーム5を選択するようになった。
他の手法
- UCB2
- Exp3
- FPL
- ベイズ最適化
色々なアルゴリズムが提案されているが、次は環境変化のある問題にいきたい。Cart-poleを見ていく。