previous post is here Lecture04
Outline
- Introduction
- On-policy monte carlo control
- On-policy Temporal Difference learning
- Off-policy learning
- summary
Contents
1. Introduction
model free control can solve the issues in MDP like,
- MDP model is unknown, but experience can be sampled
- MDP model is known, but is too big to use, except by samples
2. On and Off-policy Learning
Definition
- On-policy (on-line) Learning: updating the policy while we are following it during the process, “learn on the job”
- Off-policy learning: “look over someone’s shoulder”, learn from sample $µ$
nice explanation
http://d.hatena.ne.jp/masatoi/20060715/1152943285
Suttonの教科書に良く出てくる表現で、学習の過程で方策の評価、改善が行われるものをon-policy、そうではないものをoff-policyと呼ぶ。on-policyの手法としては動的計画法やSarsaがあり、off-policyの手法にはQ-learningがある。Q-learningは価値の更新を行うが、方策の更新は行わない。価値の学習状況により行動選択確率が変わっていくような行動選択手法を用いることができるが、これは方策を改善していくことにはならない?
on-policyの強化学習手法は価値の改善と方策の改善の両方を行い、その両方が相互依存関係にある。つまり改善された価値に基づいて新たな方策をつくり、その方策に基づいて価値を更新していくというループ構造である。これを一般化方策反復(generalized policy iteration; GPI)と呼ぶ。
$\epsilon$-Greedy Exploration
This method allows us to choose most of time optimal policies, but with the probability of $\epsilon$ we instead select an action at random.
Non Greedy action: $\frac{\epsilon}{|A(s)|}$
Greedy Action: $(1 - \epsilon) + \frac{\epsilon}{|A(s)|}$
\pi(a|s) = \left\{
\begin{array}{ll}
\frac{\epsilon}{m} + (1 - \epsilon) & (if\space a^* = argmax_{a \in A} \space Q(s,a)) \\
\frac{\epsilon}{m} & (otherwise)
\end{array}
\right.
As for greedy algorithm, we just stick to the best one, and never try finding better one.
However, regarding to $\epsilon$-Greedy Exploration, like above, with the probability $(1 - \epsilon)$, we take greedy action, and otherwise choose an action at random.
By applying this to $\epsilon$-Greedy Policy Improvement, we get this theorem.
For any $\epsilon$-Greedy policy π, the $\epsilon$-Greedy policy $\pi^`$ with respect to $q_{\pi}$ is an improvement,
v_{\pi^`}(s) \geq v_{\pi}(s)\\
on line 3, it is saying max must be equal or at least better than the weighted average of sum of greedy policy!
\begin{align}
q_{\pi}(s, \pi^`(s)) &= \sum_{a \in A} \pi^`(a|s) q_{\pi}(s, a)\\
&= \frac{\epsilon}{m} \sum_{a \in A}q_{\pi}(s, a) + (1 - \epsilon) max_{a \in A} \space q_{\pi}(s, a)\\
&\geq \frac{\epsilon}{m} \sum_{a \in A}q_{\pi}(s, a) + (1 - \epsilon) \sum \frac{\pi(a|s) - \frac{\epsilon}{m}}{1 - \epsilon} \space q_{\pi}(s, a)\\
&= \sum_{a \in A} \pi(a|s) q_{\pi}(s, a)\\
&= v_{\pi} (s)
\end{align}
GLIE(Greedy in the Limit with Infinite Exploration)
- All state-action value pairs are explored infinitely many times: $\lim_{k \to \infty} N_k(s,a) = \infty$
- The policy converges on a greedy policy:
\lim_{k \to \infty} \pi _k(a|s) = 1 \space (a = argmax_{a \in A} \space Q_k(s,a))
Monte Carlo Control
Simply saying, update $Q_t(s,a)$(action-value functions) gradually towards $R_t$.
Let $R_{total}$ be total reward.
at t = T
$R^{total} = r_t$
At t = T-1
$R_{t-1}^{total} = r_{t-1} + γr_{t}$
update $Q(s_{t-1}, a_{t-1})$ towards $R_{t-1}^{total}$
At t = T-2
$R_{t-2}^{total} = r_{t-2} + γr_{t-1} + γ^2r_{t}$
update $Q(s_{t-2}, a_{t-2})$ towards $R_{t-2}^{total}$
over and over again till the beginning!!

3. On-Policy Temporal Difference Learning
Updating Action Value Functions with SARSA

$Q(s,a) \leftarrow Q(s,a) + \alpha \space (R + \gamma \space Q(s',a') - Q(s,a))$
Convergence
Under the conditions of GLIE, this converges.
n-Step SARSA
n-step SARSA updates Q-return towards the n-step Q-return.
n = 1 => $q^1_t = R_{t+1} + \gamma Q(S_{t+1})$
n = 2 => $q^2_t = R_{t+1} + \gamma R_{t+2} + \gamma ^2 Q(S_{t+1})$
$\vdots$
n = $\infty$
q^{\infty}_t = R_{t+1} + \gamma R_{t+2} + \cdots \gamma ^n Q(S_{t+n})\\
Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \space (q^n_t \space - \space Q(S_t, A_t))
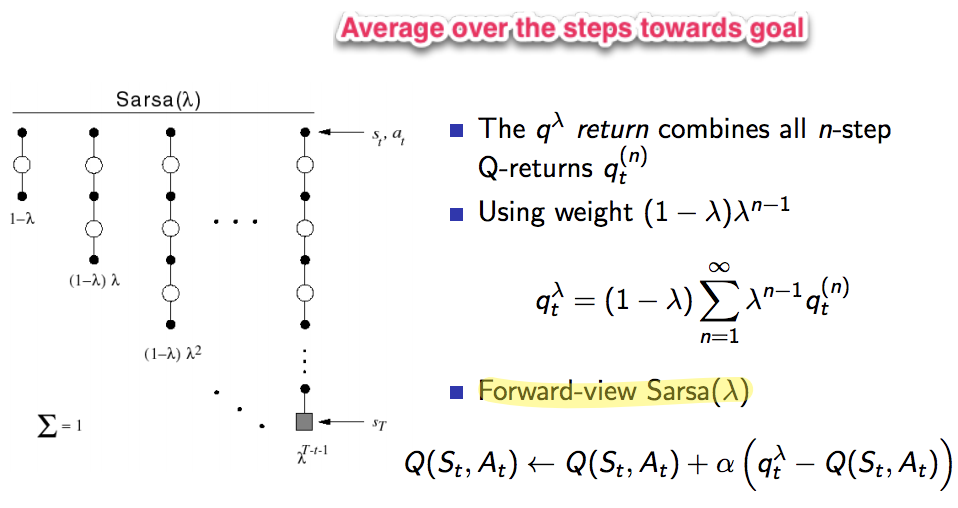
Sarsa(λ)
Off-Policy Learning
What makes off policy different from on-policy learning??
First of all, there's no reason that an agent has to do the greedy action; Agents can explore or they can follow options. This is not what separates on-policy from off-policy learning.
The reason that Q-learning is off-policy is that it updates its Q-values using the Q-value of the next state s′ and the greedy action a′. In other words, it estimates the return (total discounted future reward) for state-action pairs assuming a greedy policy were followed despite the fact that it's not following a greedy policy.
The reason that SARSA is on-policy is that it updates its Q-values using the Q-value of the next state s′ and the current policy's action a″. It estimates the return for state-action pairs assuming the current policy continues to be followed.
The distinction disappears if the current policy is a greedy policy. However, such an agent would not be good since it never explores.
Importance Sampling
Expectation Formula
$E[f(x)] = \int f(x)p(x) dx$
Importance Sampling Formula
$ ∫f(x)π(x)dx=∫f(x)\frac{π(x)}{q(x)}q(x)dx$
$q(x)$ is called proposal distribution which is approximation of original distribution.
$\frac{π(x)}{q(x)}$ is called importance weight: to modify the biases arising in the difference of $q(x)$ from original distribution($π(x)$).
*if you want study further, please check Likelihood weighted Sampling.
Importance Sampling for Off-Policy Monte-Carlo
Weighted importance sampling for off-policy learning with linear function approximation
Authors: A. Rupam Mahmood, Hado van Hasselt, Richard S. Sutton
Importance sampling is an essential component of off-policy model-free reinforcement learning algorithms. However, its most effective variant, weighted importance sampling, does not carry over easily to function approximation and, because of this, it is not utilized in existing off-policy learning algorithms. In this paper, we take two steps toward bridging this gap. First, we show that weighted importance sampling can be viewed as a special case of weighting the error of individual training samples, and that this weighting has theoretical and empirical benefits similar to those of weighted importance sampling. Second, we show that these benefits extend to a new weighted-importance-sampling version of off-policy LSTD(λ). We show empirically that our new WIS-LSTD(λ) algorithm can result in much more rapid and reliable convergence than conventional off-policy LSTD(λ) (Yu 2010, Bertsekas & Yu 2009).













