「はじめてのパターン認識」の第8章「サポートベクトルマシン」の解説です。
なんとなくで理解していたSVMをようやく深く理解しました。なんとなく理解は間違っていないのですが、数式にするととても難しい・・・ラグランジュ未定乗数などはマセマの「微分積分キャンパス・ゼミ」で復習し、不等式制約付凸計画問題は「言語処理のための機械学習入門」で新たに勉強しました。
最後の1クラスSVMに関しては力尽き、たいした解説していません。いつか必要になったときに理解し追記したいと思います。
最初は「はじパタ」よりも「Coursera機械学習入門オンライン講座」から勉強した方が絶対わかりやすくおすすめです(英語が嫌でなければ)。
※はじパタ勉強系は記事「文系社会人がはじパタで機械学習を数式含めて理解した奮闘記」にまとめました。
参考リンク
いろいろ参考にしました。
- はじめてのパターン認識 第8章 サポートベクトルマシン 前半(slideshare): 多項式カーネルまでを詳しく解説
- はじめてのパターン認識第八章(slideshare)
- はじめてのパターン認識 8章: 数式参考
- はじめてのパターン認識8章サポートベクトルマシン(slideshare): 数式詳しい
- 最初に学ぶ 2分類SVMモデルの基本: 基本がわかりやすい
- はじパタ8章 svm(slideshare): 動径基底関数カーネル以降記載
- ソフトマージンSVM: ソフトマージンSVMについてわかりやすい
- サポートベクターマシン: PDFでv-svmなどについても書かれている
内容
8.1 サポートベクトルマシンの導出
サポートベクトルマシン(support vector machine)は第7章で解説したクラス間マージンから導きます。最大マージン$D_{max}$を実現する2クラス線形識別関数の学習方法です。7章と異なり、SVMでは同次座標系ではなく標準座標系を使います。他クラス問題は(K-1)の1対多SVMで実現することが多い。
8.1.1 最適識別超平面
標準座標系の以下の前提で考えます。
| 内容 | 式 |
|---|---|
| クラスラベル付き学習データ集合 | $D_L=\{(t_i,x_i)\}(i=1, \ldots, N)$ |
| 教師データ | $t_i=\{-1, +1\}$ |
| 学習データ | $x_i \in \mathbb R^d$ |
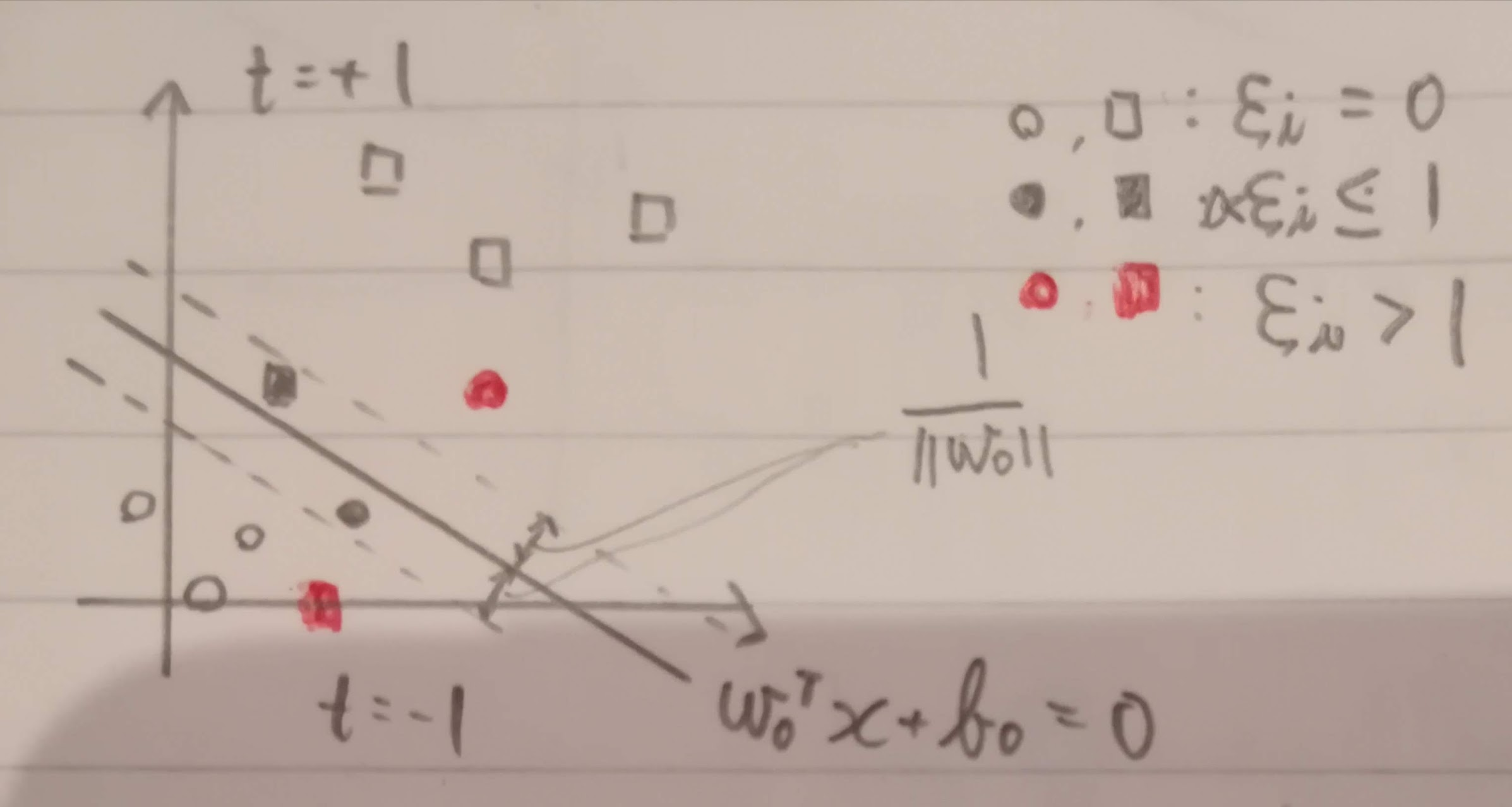
線形識別関数のマージンをkとすると全学習データで$|w^T x_i+b| \ge k$が成り立ちます。
マージンkを正規化(kで除算)して、wとbもkで除算して更新すれば、線形識別関数は以下の式。
\begin{cases}
w^T x_i + b \ge +1 (t_i = +1の場合)\\
w^T x_i + b \le -1 (t_i = -1の場合)\\
\end{cases}
場合分けをまとめると$t_i(w^T x_i + b) \ge 1$でスッキリします。
クラス間マージンは各クラスのデータをwの方向に射影した長さの差の最小値。
\begin{eqnarray}
\rho (w, b) & = & \min_{x \in C_{y = +1}} \frac{w^T x}{||w||} - \max_{x \in C_{y = -1}} \frac{w^T x}{||w||} \\
& = & \frac{1 - b}{||w||} - \frac{-1 - b}{||w||} \ \
\because w^T x + b = 1 \ or \ w^T x + b = -1\\
& = & \frac{2}{||w||}
\end{eqnarray}
最適な超平面の式を$w_0^T x + b_0 = 0$とすると、この超平面は最大クラス間マージン$\rho (w_0, b_0) = \max_{w} \rho(w, b)$を与えます。最大マージン$D_{max}$は最大クラス間マージンの半分です。つまり、最適識別超平面は$t_i(w^T x_i + b) \ge 1(i=1, \ldots, N)$の制約化でwのノルムを最小化する解$w_0=\min ||w||$として求めることができます($\frac{1}{||w||}$を最大化したいから)。
ノルム最小の係数ベクトルを求めているので、結合係数に対する正則化と同等の役割が組み込まれています。
8.1.2 KKT条件
マージン最大化する最適識別超平面は以下の不等式制約条件最適化問題の主問題を解くことで得られます。$\frac{1}{||w||}$を最大化したいので、分母のノルムを最小化させるような評価関数にします。
※これは不等式制約付凸計画問題で後続のKKT条件と併せて「言語処理のための機械学習入門」で勉強しました。「はじパタ」よりわかりやすく説明してくれています。
| 主問題内容 | 式 |
|---|---|
| 評価関数(最小化) | $L_p(w)=\frac{1}{2}w^Tw$ |
| 不等式制約条件 | $t_i(w^T x_i + b) \ge 1$ |
この問題は、次のラグランジュ関数で定式化できます。この式の$\alpha_i$はラグランジュ未定乗数といいます。
※式の右側に$g(x) \ge 0$の制約下で$f(x)$を最小化する場合の一般化した式を記載
※ラグランジュ未定乗数についてはマセマの「微分積分キャンパス・ゼミ」の勉強しました。概要を思い出すのに「ラグランジュの未定乗数法と例題」を使いました。
\begin{eqnarray}
\widetilde{L}_p (w, b, \alpha)
= \frac{1}{2} w^T w
- \sum_{i = 1}^N \alpha_i (t_i(w^T x_i + b) - 1)
& \ \ \ &一般化:L(x, \lambda)=f(x) - \lambda(x)\\
(\alpha = (\alpha_1 , \cdots , \alpha_N)^T\;\; \alpha_i \geq 0)
& \ \ \ &一般化:(\lambda \ge 0)
\end{eqnarray}
この最適化問題の解$w_0, b_0$はKKT(Karush-Kuhn-Tucker/カルーシュ・クーン・タッカー)条件を満たす解として得ることができます。
※(1)の縦棒はwに$w_0$を代入した場合、という意味です。「数学で出てくる縦棒の意味」を見て理解しました。
※$\nabla$はナブラ演算子と呼びます。複数の意味を持つ演算子で、ここでは勾配ベクトルを意味します。「ナブラ演算子∇の4つの意味と計算公式」がわかりやすい。
\begin{eqnarray}
(1)& \ & \frac{\partial \widetilde{L}_p(w, b, \alpha)}{\partial w} |_{w=w_0}
= w_0 - \sum_{i = 1}^N \alpha_i t_i x_i = 0
& \ \ \ &一般化:\nabla f(x)=0\\
(2)& \ & \frac{\widetilde{L}_p (w, b, \alpha)}{\partial b} = \sum_{i = 1}^N \alpha_i t_i = 0
& \ \ \ &一般化:\nabla g(x)=0\\
(3)& \ & t_i(w^T x_i + b) - 1 \ge 0
& \ \ \ &一般化:g(x) \ge 0\\
(4)& \ & \alpha_i \ge 0
& \ \ \ &一般化:\lambda > 0\\
(5)& \ & \alpha_i(t_i(w^T x_i + b) - 1) = 0
& \ \ \ &一般化:\lambda g(x)= 0\\
\end{eqnarray}
この(3)から(5)は相補性条件と呼びます。(3)$g(x)=t_i(w^T x_i + b)$と(4)$\lambda=\alpha_i$のどちらかが(5)の条件下で0になります(ここにはシグマなどもなく、各データごとに値が異なります)。
\begin{cases}
\alpha_i = 0 \ \ (t_i(w^T x_i + b) - 1 > 0の場合)\\
\alpha_i > 0 \ \ (t_i(w^T x_i + b) - 1 = 0の場合)\\
\end{cases}
今回は識別超平面から最近房の学習データに対してのみマージン最大化を目的とするため、$t_i(w^T x_i + b) - 1 = 0$の場合の制約が有効です。
では、最適解はKKT条件(1)から$w_0 = \sum_{i = 1}^N \alpha_i t_i x_i$です。
ここからラグランジュ関数を変形させてラグランジュ未定乗数のみの関数にします。
\begin{eqnarray}
L_d(\alpha)& = & \frac{1}{2} w_0^T w_0 - \sum_{i = 1}^N \alpha_i (t_i(w_0^T x_i + b) - 1) \\
& = & \frac{1}{2} w_0^T w_0 - w_0^T \sum_{i = 1}^N \alpha_i t_i x_i - b \sum_{i = 1}^N \alpha_i t_i + \sum_{i = 1}^N \alpha_i\\
& = & \frac{1}{2} w_0^T w_0 - w_0^T w_0 - b \times 0 + \sum_{i = 1}^N \alpha_i \ \
\because w_0 = \sum_{i = 1}^N \alpha_i t_i x_i, \ \
\sum_{i = 1}^N \alpha_i t_i=0\\
& = & -\frac{1}{2} w_0^T w_0 + \sum_{i = 1}^N \alpha_i\\
& = & -\frac{1}{2}\sum_{i = 1}^N \sum_{j = 1}^N (\alpha_i t_ix_i)^T(\alpha_j t_j x_j) + \sum_{i = 1}^N \alpha_i \ \
\because w_0 = \sum_{i = 1}^N \alpha_i t_i x_i\\
\end{eqnarray}
ここで、評価関数からwを消した双体問題(そうつい)を設定します。相対問題は$L_d(\alpha)$を最大にするαを探索します。
以下の前提で、
- ${\bf 1} = (1, \ldots, 1)^T$: N個の1を並べただけのベクトル
- ${\bf H} = (H_{ij} = t_i t_j x_i^T x_j)$: 学習データで作られた行列
- ${\bf t} = (t_1, \ldots , t_N)^T$: 教師データベクトル
こんな双体問題を設定します。制約条件はKKT条件の(2)を使っています。
| 双体問題内容 | 式 |
|---|---|
| 評価関数(最大化) | $L_d(\alpha)=\sum_{i = 1}^N \alpha_i-\frac{1}{2}\sum_{i = 1}^N \sum_{j = 1}^N (\alpha_i t_ix_i)^T(\alpha_j t_j x_j)$ $ =\alpha^T1 - \frac{1}{2}\alpha^T H \alpha$ |
| 制約条件 | $\alpha^T t = 0$ |
双対問題のラグランジュ関数$\widetilde{L}_d(\alpha)$はラグランジュ未定乗数をβとすると以下の式。
\widetilde{L}_d(\alpha, \beta) = \alpha^T{\bf 1}- \frac{1}{2} \alpha^T H \alpha - \beta \alpha^T t
\left\{ \begin{array}{ll}
t_i (w^T x_i + b) - 1 = 0 & \alpha_i > 0 \\
t_i (w^T x_i + b) - 1 \neq 0 & \alpha_i = 0 \\
\end{array} \right.
双対問題からαを求めたら$\sum_{i = 1}^N \alpha_i t_i x_i$で$w_0$を求めて、$b_0=t_s(w^T x_i + b) - 1$を求めて識別関数ができます!
※sはサポートベクトルのデータの番号
ラグランジュ乗数の最適解を$\widetilde{\alpha}=(\widetilde{\alpha}, \ldots , \widetilde{\alpha}_N)^T$とすると
\begin{align}
w_0^T w_0 & = \sum_{i = 1}^N \widetilde{\alpha}_i t_i x_i^T w_0 \\
& = \sum_{i = 1}^N \widetilde{\alpha}_i (1 - t_i b_0) \\
& = \sum_{i = 1}^N \widetilde{\alpha}_i - b_0 \sum_{i = 0}^N \widetilde{\alpha}_i t_i\\
& = \sum_{i = 1}^N \widetilde{\alpha}_i \ \
\because \sum_{i = 1}^N \alpha_i t_i = 0(KTT条件(2))
\end{align}
途中式を少し補足します。KKT条件の(5)より$\alpha_i > 0$の場合
t_i(w_0^T x_i + b_0) - 1 = 0 \\
t_i w_0^T x_i = 1- t_i b_0 \\
w_0 t_i^T x_i = 1- t_i b_0 \\
\because 積の転置は順番を交換した転置の積(AB)^T=B^TA^T
最大マージンは以下の式。
D_{max} = \frac{1}{||w||}
= \frac{1}{\sqrt{w_0^T w_0}}
= \frac{1}{\sqrt{\sum_{i = 1}^N \widetilde{\alpha}_i }}
8.2 線形分離可能でない場合への拡張
線形分離できない場合、スラック変数 $\xi_i$(「クサイ」と呼びます)を使って以下の条件にします(スラック変数は学習時には使いますが、予測時には使いません)。マージン境界を超えることを許容するのでソフトマージン識別器と言います。
t_i(w^T {\bf x}_i + b) - 1 + \xi_i \ge 0 \\
\left\{ \begin{array}{ll}
\xi_i = 0 & マージン内で正しく識別可 \\
0 < \xi_i \leq 1 & マージン境界外で正しく識別可 \\
\xi_i > 1 & 誤識別
\end{array} \right.
$\xi_i$は以下のように表現することができます。これは識別器の損失を表しているので損失関数と呼ばれます。$f_+(x)$はヒンジ関数と呼ばれます。
\xi_i = \max[0, 1-t_i(w^T x_i + b)] = f_+(1-t_i(w^T x_i + b)) \\
f_+(x)=
\begin{cases}
x \ \ (x>0の場合) \\
0 \ \ (それ以外の場合)\\
\end{cases}
全学習データのスラック変数の和$\sum_{i = 1}^N \xi_i ; (\xi_i \ge 0)$は誤識別数の上限です。
今回、ソフトマージン識別器の主問題は以下のように定義します。$\xi_i$項が追加になっています。
| 主問題内容 | 式 |
|---|---|
| 評価関数(最小化) | $L_p(w, \xi)=\frac{1}{2}w^Tw + C \sum_{i=1}^N \xi_i$ |
| 不等式制約条件 | $t_i(w^T x_i + b) \ge 1 - \xi_i, \ \ \xi_i \ge 0$ |
パラメータCは誤識別数のペナルティの強さです。Coursera機械学習入門で学習した正則化のパラメータλみたいなものですね。適切なCは交差確認法などで実験的に選ぶ必要があります。パラメータCを使うのでC-SVMと略称されています。
※Coursera機械学習入門で言っていた「C」をようやく理解しました。
制約条件が2つあるのでラグランジュ未定乗数を2つ(αとμ)使い、以下のラグランジュ関数を作ります(ここではμは平均の意味ではありません)。
\widetilde{L}(w, b, \alpha, \xi, \mu)
= \frac{1}{2} w^T w + C \sum_{i = 1}^N \xi_i - \sum_{i = 1}^N \alpha_i (t_i (w^T x_i + b) - 1 + \xi_i) - \sum_{i = 1}^N \mu_i \xi_i \\
一般化:L(x, \lambda)=f(x) - \lambda(x)
KKT条件は以下の7つです(「一般化」部分があっているか自信なし)。(6)と(7)が相補性条件です。
\begin{eqnarray}
(1)& \ & \frac{\partial \widetilde{L}_p(w, b, \alpha, \xi, \mu)}{\partial w} |_{w=w_0}
= w_0 - \sum_{i = 1}^N \alpha_i t_i x_i = 0
& \ \ \ &一般化:\nabla f(x)=0\\
(2)& \ & \frac{\widetilde{L}_p (w, b, \alpha, \xi, \mu)}{\partial b} = \sum_{i = 1}^N \alpha_i t_i = 0
& \ \ \ &一般化:\nabla g(x)=0\\
(3)& \ & \frac{\widetilde{L}_p(w, b, \alpha, \xi, \mu)}{\partial \xi_i} = C - \alpha_i - \mu_i = 0
\Rightarrow \mu_i \ge 0なので0 \ge \alpha_i \ge C
& \ \ \ &一般化:\nabla h(x) = 0\\
(4)& \ & t_i(w^T x_i + b) - 1 + \xi_i \ge 0
& \ \ \ &一般化:g(x) \ge 0\\
(5)& \ & \xi_i \ge 0, \alpha_i \ge 0, \mu_i \ge 0
& \ \ \ &一般化:\lambda > 0 とスラック変数条件 \\
(6)& \ & \alpha_i(t_i(w^T x_i + b) - 1 + \xi_i) = 0\\
(7)& \ & \mu_i \xi_i = 0\\
\end{eqnarray}
相補性条件を確認していきます。
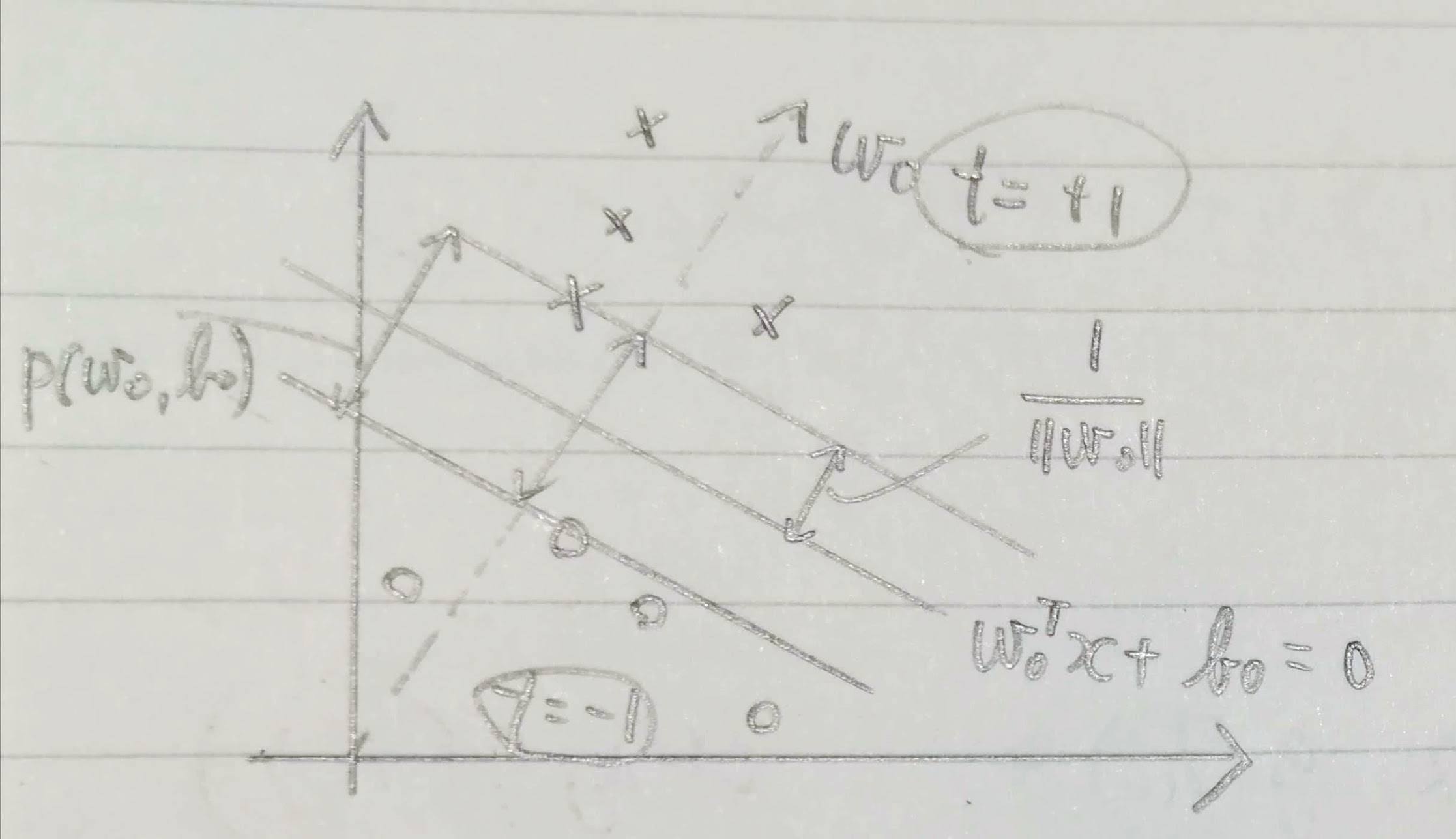
$\alpha_i < C$の場合です。このときのサポートベクトルを**自由サポートベクトル(free SV)**と呼びます。自由サポートベクトルは最適なバイアスを決めるために使用します。
\begin{eqnarray}
KKT条件(3):& C - \alpha_i - \mu_i = 0 & \Rightarrow & \mu_i > 0\\
KKT条件(7):& \mu_i \xi_i = 0 & \Rightarrow & \xi_i = 0\\
\end{eqnarray}
$\xi_i > 0$の場合です。このときのサポートベクトルを$\alpha_i$が上限値Cになるので**上限サポートベクトル(bounded SV)**と呼びます。このうち、$\xi_i > 1$は誤識別のサポートベクトルです。
\begin{eqnarray}
KKT条件(7):& \mu_i \xi_i = 0 & \Rightarrow & \mu_i = 0\\
KKT条件(3):& C - \alpha_i - \mu_i = 0 & \Rightarrow & \alpha_i = C\\
\end{eqnarray}
上限サポートべクトルと自由サポートベクトルを図にしてみました。

では、ラグランジュ関数から双対問題を求めます。結局途中からハードマージンと同じになります。
\begin{eqnarray}
\widetilde{L}(w, b, \alpha, \xi, \mu) & = & \frac{1}{2} w^T w + C \sum_{i = 1}^N \xi_i - \sum_{i = 1}^N \alpha_i (t_i (w^T x_i + b) - 1 + \xi_i) - \sum_{i = 1}^N \mu_i \xi_i \\
& = & \frac{1}{2} w^T w - \sum_{i = 1}^N \alpha_i (t_i (w^T x_i + b) - 1) + C \sum_{i = 1}^N \xi_i - \sum_{i = 1}^N \alpha_i \xi_i - \sum_{i = 1}^N \mu_i \xi_i \\
& = & \frac{1}{2} w^T w - \sum_{i = 1}^N \alpha_i (t_i (w^T x_i + b) - 1) + \sum_{i = 1}^N(C - \alpha_i - \mu_i)\xi_i\\
& = & \frac{1}{2} w^T w - \sum_{i = 1}^N \alpha_i (t_i (w^T x_i + b) - 1) \ \
\because C - \alpha_i - \mu_i = 0\\
& = & -\frac{1}{2}\sum_{i = 1}^N \sum_{j = 1}^N (\alpha_i t_ix_i)^T(\alpha_j t_j x_j) + \sum_{i = 1}^N \alpha_i \ \
\because ハードマージンと同じ\\
\end{eqnarray}
あとは制約条件$0 \ge \alpha_i \ge C$をハードマージンのときから追加してやります。その後の流れはハードマージンのときと同じです。
| 双体問題内容 | 式 |
|---|---|
| 評価関数(最大化) | $L_d(\alpha)=\sum_{i = 1}^N \alpha_i-\frac{1}{2}\sum_{i = 1}^N \sum_{j = 1}^N (\alpha_i t_ix_i)^T(\alpha_j t_j x_j)$ $ =\alpha^T1 - \frac{1}{2}\alpha^T H \alpha$ |
| 制約条件 | $0 \ge \alpha_i \ge C, \ \ \alpha^T t = 0$ |
8.3 非線形特徴写像
線形分離ができない場合に非線形特徴空間に写像して線形分離をさせる方法があります。
d次元の学習データ$x \in \mathbb R^d$と、その非線形写像の集合を考えます(d次元と同じ特徴数ではないのでMを使っています)。
\{\varphi_j({\bf x})\}_{j=1}^M
非線形写像空間のベクトルを以下で表します($\varphi_0(x)=1$はバイアス項)。
\varphi(x) = (\varphi_0(x) = 1, \varphi_1(x),\ldots , \varphi_M(x))^T
非線形特徴空間での線形識別関数を以下の式。
\begin{eqnarray}
h(\varphi(x)) & = & \sum_{j = 1}^N w_j \varphi_j(x)\\
& = & w^T \varphi(x)\\
\end{eqnarray}
この非線形特徴空間内でのSVMにおける最適識別超平面は以下の式。
w_0 = \sum_{i = 1}^M w \varphi_j(x) = w^T \varphi(x)
この最適識別超平面を先程の線形識別関数に当てはめます。
\begin{eqnarray}
w_0^T \varphi(x)\ & = & \sum_{i = 1}^N \alpha_i t_i \varphi^T(x_i)\varphi(x) \\
& = & \sum_{i = 1}^N \alpha_i t_i K(x_i, x) \\
\end{eqnarray}
このときの元の空間のベクトルの関数$K(x_i, x)$(核関数またはカーネル関数と呼びます)を使って表せれば計算が楽になって都合がいいです。
| 双体問題内容 | 式 |
|---|---|
| 評価関数(最大化) | $L_d(\alpha)=\sum_{i = 1}^N \alpha_i-\frac{1}{2}\sum_{i = 1}^N \sum_{j = 1}^N \alpha_i \alpha_j t_i t_j \varphi^T(x_i) \varphi(x_j)$ $ =\sum_{i = 1}^N \alpha_i-\frac{1}{2}\sum_{i = 1}^N \sum_{j = 1}^N \alpha_i \alpha_j t_i t_j K(x_i, x_j)$ |
| 制約条件 | $0 \ge \alpha_i \ge C, \ \ \alpha^T t = 0$ |
カーネル関数$K(x_i, x_j)=\varphi^T(x_i) \varphi(x_j)$を(i,j)要素とするN × N対称行列K(X, X)をグラム行列と言います(X=$(x_i, \ldots, x_N)^T$のデータ行列)。
K(X, X) =
\left(
\begin{array}{}
K(x_1, x_1) & \cdots & K(x_1, x_j) & \cdots & K(x_1, x_N)\\
\vdots & \ddots & & & \vdots\\
K(x_i, x_1) & \cdots & K(x_i, x_j) & \cdots & K(x_i, x_N)\\
\vdots & & & \ddots & \vdots\\
K(x_N, x_1) & \cdots & K(x_N, x_j) & \cdots & K(x_N, x_N)\\
\end{array}
\right)
グラム行列は以下の性質を持ちます。
- 対称性: $K(x_i, x_j) = K(x_j, x_i)$
- 半正定値性: $y^T K(x,x)y \ge 0$ $s.t. \ \ y \ne 0$
非線形線形空間の次元が大きくてM>>dの場合、内積計算に時間がかかり実用が難しい。核関数の計算を$x_iとx$のd次元空間での内積計算で済ませれば、高速計算ができます。そのような核関数を内積カーネルと呼びます。
8.3.1 多項式カーネル
内積カーネルのひとつである多項式カーネルです。
K_p(u, v) = (\alpha + u^T v)^p \;\;(\alpha \ge 0は実定数)
例を示します。
$u = (u_1, u_2)^T, v = (v_1, v_2)^T, \alpha=1$とした場合の2次の多項式カーネルは。
\begin{align}
K_2(u, v) & = (1 + u^T v)^2 \\
& = (1 + u_1 v_1 + u_2 v_2)^2 \\
& = 1 + u_1^2 v_1^2 + 2 u_1 u_2 v_1 v_2 + u_2^2 v_2^2 + 2 u_1 v_1 + 2u_2 v_2 \\
& = (1, u_1^2, \sqrt{2} u_1 u_2, u_2^2, \sqrt{2} u_1, \sqrt{2} u_2)^T
(1, v_1^2, \sqrt{2} v_1 v_2, v_2^2, \sqrt{2} v_1, \sqrt{2} v_2)
\end{align}
上の式の最後が$K_2(u, v) = \varphi(u)^T \varphi(v)$となっていますね。
\begin{align}
\varphi(u) & = (1, u_1^2, \sqrt{2} u_1 u_2, u_2^2, \sqrt{2} u_1, \sqrt{2} u_2)^T \\
\varphi(v) & = (1, v_1^2, \sqrt{2} v_1 v_2, v_2^2, \sqrt{2} v_1, \sqrt{2} v_2)^T
\end{align}
これで6次元空間のベクトルの内積が2次元ベクトルの内積とスカラー値(バイアス)の2乗で計算できます。この例では$u_1 v_1$などがあるように、特徴の交互作用が考慮されます。
$K_p(u, v) = (\alpha + u^T v)^p$を二項定理で展開すると以下の式。
K_p(u, v) = \sum_{i=0}^p
\left( \begin{array}
ap \\ i
\end{array}
\right)
\alpha^{p-i}(u^T v)^i
二項定理そのものはこんな感じで、「二項定理の意味と2通りの証明」が参考になります。
(a+b)^n = \sum_{k=0}^n
\left( \begin{array}
an \\ k
\end{array}
\right)
a^k b^{n-k} = \sum_{k=0}^n {}_n C_k a^k b^{n-k}
多項式カーネル$K_p(u, v)$による非線形特徴空間の次元D(d, p)は
D(d, p) =
\left(
\begin{array}{c}
d + p \\ p
\end{array}
\right)
={}_{d+p} C_p
いくつか例で計算。
| d | p | 非線形特徴空間の次元 |
|---|---|---|
| 2次元 | 2次 | $6=\frac{(2+2)!}{2!}$ |
| 2次元 | 3次 | $10=\frac{(2+3)!}{3!}$ |
| 2次元 | 4次 | $15=\frac{(2+4)!}{4!}$ |
| 3次元 | 2次 | $10=\frac{(3+2)!}{2!}$ |
| 256次元(=16*16) | 4次 | $186,043,585=\frac{(256+4)!}{4!}$ |
上の表の一番下の例だと約2億次元の高次元空間になってしまい、学習データが次元数に比較して少ないため疎な分布となります(次元数が多すぎ)。そこでカーネル法を用いて非線形特徴写像を行う学習法は、疎なカーネルマシン(sparse kernel machine)と呼ばれます。
8.3.2 動径基底関数カーネル
内積カーネルのもう一つの例に**動径基底関数カーネル(radial bases function kernel, RBFカーネル)**があります。
この辺はCoursera機械学習入門コースがとてもわかりやすいです。
K_{\sigma} (u, v) = \exp{(-\frac{1}{2\sigma^2} || u - v||^2)}
σはカーネル関数の広がりを制御するパラメータです。
σが大きければ入力データxから遠くのサポートベクトルが識別に寄与しますが、σが小さければ近傍のサポートベクトルのみが識別に寄与します。
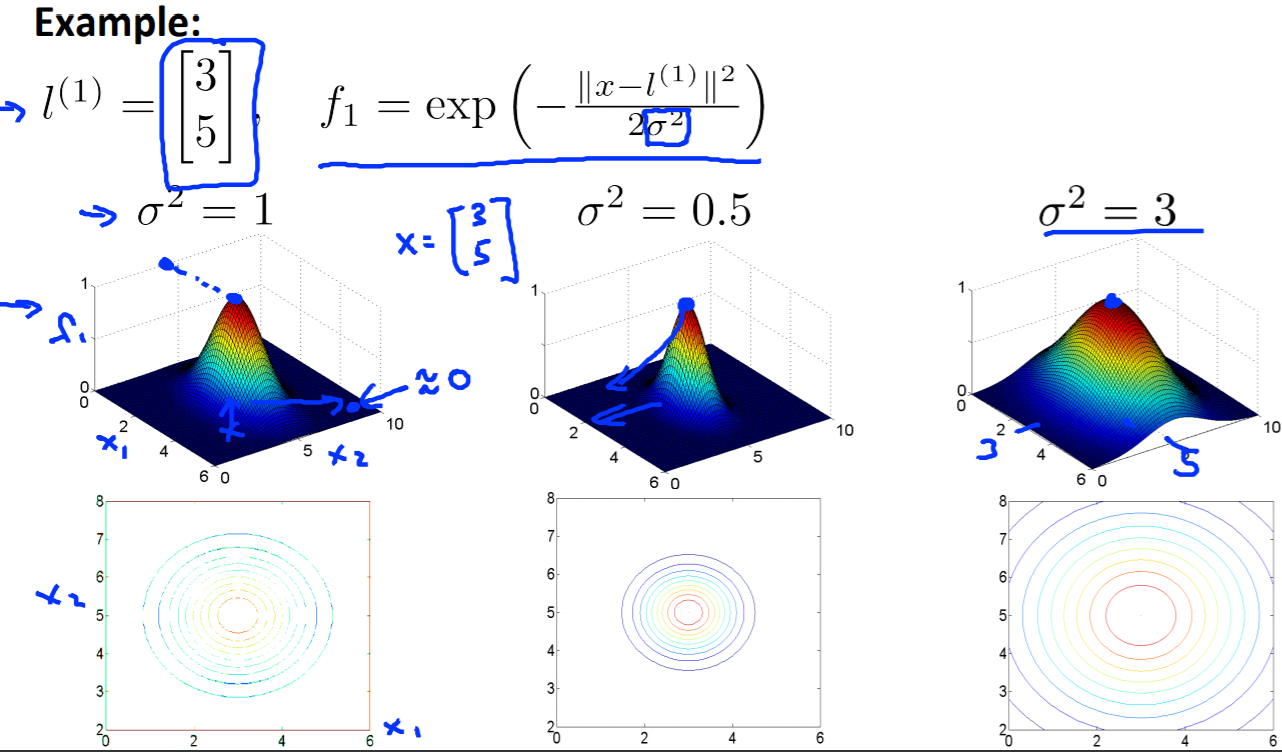
動径基底関数カーネルの非線形特徴ベクトルは、無限次元になります。これはマクローリン展開をして$u_iとv_i$を出すためです(詳細割愛)。
8.4 ν-サポートベクトルマシン
C-SVMではパラメータCを誤識別数に対するペナルティ項として入れました。誤識別数は学習データ数に影響を受けるので、誤識別数を学習データで割った誤識別率の方が一般性を持たせることができます。ただし、達成すべき誤識別率を事前に考える必要があります。
誤り率と分類器の複雑さはトレードオフの関係にあり、新しいパラメータνで明示的に取り入れたものが**ν-サポートベクトルマシン(ν-SVM)**です。
※νはアルファベットのブイ(v)かと思っていたのですが、ギリシャ文字のニューでした。
C-SVMの損失関数は以下の式でした。
\xi_i = f_+(1-t_i(w^T x_i + b)
非線形特徴空間への写像を含めて$f(x_i)=w^T \varphi(x_i)+b$とするとスラック変数は以下で表せます。
\xi_i = f_+(1-t_i f(x_i)) \\
f_+(x)=
\begin{cases}
x \ \ (x>0の場合) \\
0 \ \ (それ以外の場合)\\
\end{cases}
ここで1としていた部分をρに変えてやり最適化するための変数とします。
※ρはアルファベットのピーではなく、ギリシャ文字のロー。
\xi_i = f_+(\rho-t_i f(x_i))
C-SVMの損失関数の1の部分は、結合係数wとバイアスbをマージンで正規化したからです。1をρに変更することで最大クラス間マージンは$\frac{2}{||w_0||}$から$\frac{2 \rho}{||w_0||}$となります。
損失関数としてはρの値が小さいほど損失は小さくなります。しかし、マージンが小さいと問題が複雑になり分類器を複雑にする結果、結合係数wのノルムが大きくなります。分類器が複雑になると、汎化誤差が大きくなります(ハイバリアンス)。汎化誤差が大きくならないようマージンは小さくなりすぎない方がいいです。そこで、ρを小さくなりすぎないように、最小化対象の評価関数に-ρに比例した項νを加えて定式化します。
主問題を書きます。比較してわかりやすいようにC-SVMも載せています。
パラメータν($\ge 0$)が-ρの比例乗数で、マージンの大きさと分類器の複雑さと誤り率の間のトレードオフを調整します。
| 主問題内容 | 式 |
|---|---|
| ν-SVM: 評価関数(最小化) | $L_p(w, \rho,\xi)=\frac{1}{2}w^Tw -\nu \rho + \frac{1}{N} \sum_{i=1}^N \xi_i$ |
| C-SVM: 評価関数(最小化) | $L_p(w, \xi)=\frac{1}{2}w^Tw + C \sum_{i=1}^N \xi_i$ |
| ν-SVM: 不等式制約条件 | $t_i(w^T \varphi(x_i) + b) \ge \rho - \xi_i, \ \ \xi_i \ge 0$ |
| C-SVM: 不等式制約条件 | $t_i(w^T \varphi(x_i) + b) \ge 1 - \xi_i, \ \ \xi_i \ge 0$ |
この主問題に対するラグランジュ関数です。
\widetilde{L}(w, b, \xi, \rho,\alpha, \mu)
= \frac{1}{2} w^T w -\nu \rho + \frac{1}{N} \sum_{i = 1}^N \xi_i - \sum_{i = 1}^N \alpha_i (t_i (w^T \varphi(x_i) + b) - \rho + \xi_i) - \sum_{i = 1}^N \mu_i \xi_i \\
一般化:L(x, \lambda)=f(x) - \lambda(x) \\
\begin{eqnarray}
\end{eqnarray}
KKT条件は以下の7つです(「一般化」部分があっているか自信なし)。(6)と(7)が相補性条件です。
\begin{eqnarray}
(1)& \ & \frac{\partial \widetilde{L}_p(w, b, \xi, \rho,\alpha, \mu)}{\partial w} |_{w=w_0}
= w_0 - \sum_{i = 1}^N \alpha_i t_i \varphi(x_i) = 0
& \ \ \ &一般化:\nabla f(x)=0\\
(2)& \ & \frac{\widetilde{L}_p (w, b, \xi, \rho,\alpha, \mu)}{\partial b} = \sum_{i = 1}^N \alpha_i t_i = 0
& \ \ \ &一般化:\nabla g(x)=0\\
(3)& \ & \frac{\widetilde{L}_pw, b, \xi, \rho,\alpha, \mu)}{\partial \xi_i} = \frac{1}{N} - \alpha_i - \mu_i = 0
\Rightarrow \mu_i \ge 0なので0 \ge \alpha_i \ge \frac{1}{N}
& \ \ \ &一般化:\nabla h(x) = 0\\
(4)& \ & \frac{\widetilde{L}_pw, b, \xi, \rho,\alpha, \mu)}{\partial \rho} = -\nu + \sum_{i = 1}^N \alpha_i = 0
\Rightarrow \nu = \sum_{i = 1}^N \alpha_i
& \ \ \ &一般化:\nabla i(x) = 0\\
(5)& \ & t_i(w^T \varphi(x_i) + b) - 1 + \xi_i \ge 0
& \ \ \ &一般化:g(x) \ge 0\\
(6)& \ & \xi_i \ge 0, \alpha_i \ge 0, \mu_i \ge 0
& \ \ \ &一般化:\lambda > 0 とスラック変数条件 \\
(7)& \ & \alpha_i(t_i(w^T \varphi(x_i) + b) - \rho + \xi_i) = 0\\
& \ \ \ &相補性条件 \\
(8)& \ & \mu_i \xi_i = 0\\
& \ \ \ &相補性条件 \\
\end{eqnarray}
あとは前と同じで双対問題にします。C-SVMの制約条件を比較のため乗せています。
| 双体問題内容 | 式 |
|---|---|
| 評価関数(最大化) | $L_d(\alpha)=\sum_{i = 1}^N \alpha_i-\frac{1}{2}\sum_{i = 1}^N \sum_{j = 1}^N \alpha_i \alpha_j t_i t_j K(x_i, x_j)$ |
| 制約条件(ν-SVM) | $0 \ge \alpha_i \ge \frac{1}{N}, \ \ \sum_{i=1}^N \alpha_i t_i = 0, \ \ \nu=\sum_{i=1}^N \alpha_i$ |
| 制約条件(C-SVM) | $0 \ge \alpha_i \ge C, \ \ \alpha^T t = 0$ |
ここでνの意味がわかります。サポートベクトルは$\alpha_i > 0$となる、つまり相補性条件であるKKT条件(7)から以下の学習データです。
\alpha_i(t_i(w^T \varphi(x_i) + b) - \rho + \xi_i) = 0 \ \ and \ \ \alpha_i > 0\\
\Rightarrow t_i(w^T \varphi(x_i) + b) - \rho + \xi_i = 0
で、νは以下のようにサポートベクトルの割合の下限を示します。
\nu = \sum_{i=1}^N \alpha_i =\sum_{サポートベクトル} \alpha_i \le \frac{1}{n} \times サポートベクトル数
次に上限サポートベクトルについて考えます。上限サポートベクトルは、マージンを超えて$\xi_i > 0$(マージン誤り)となります。その場合、以下が成り立ちます。
\xi_i > 0, \ \ \mu_i \xi_i = 0 \Rightarrow \mu_i=0 \ \
(KKT条件(8)) \\
\mu_i=0, \frac{1}{N}- \alpha_i - \mu_i =0 \Rightarrow \alpha_i = \frac{1}{N} \ \
(KKT条件(3))
これで上限サポートベクトルとνの関係が出ます。
\begin{eqnarray}
\nu& = & \sum_{i=1}^N \alpha_i \\
& = & \sum_{サポートベクトル} \alpha_i \\
& = & \sum_{上限サポートベクトル} \frac{1}{N} + \sum_{上限でないサポートベクトル} \alpha_i \ \
\because \alpha_i = \frac{1}{N}(上限サポートベクトル)\\
& = & \frac{1}{N} \times 上限サポートベクトル数 + \sum_{上限でないサポートベクトル} \alpha_i \\
\end{eqnarray}
つまりνはマージン誤り、つまり上限サポートベクトルの割合の上限となります。
\therefore \nu \le \frac{1}{N} \times 上限サポートベクトル数
8.5 1クラスサポートベクトルマシン
C-SVMやν-SVMは2クラスの識別関数を構成していましたが、SVMを1クラスのみの学習に使い、入力データがそのクラスに含まれるかを判定する方法があります。異常検知などで利用されます。
1クラスSVMには以下の2つの構成法があります(ここでは、1の1クラスν-SVMのみ解説)。
- ν-SVMでのマージン境界で正例とそれ以外を識別(1クラスν-SVM)
- 精霊を超球で包み、その半径を最適化(サポートベクトル領域記述法)
基本的な考えはν-SVMです。非線形変換をし、パラメータνを使ってマージンの最大化をします。今回は1クラスなのでマージンが原点からの距離になり、パラメータρで制御します。学習データをすべて正例と思って学習しても、必ず外れ値と判断されるものが出てくるようです。
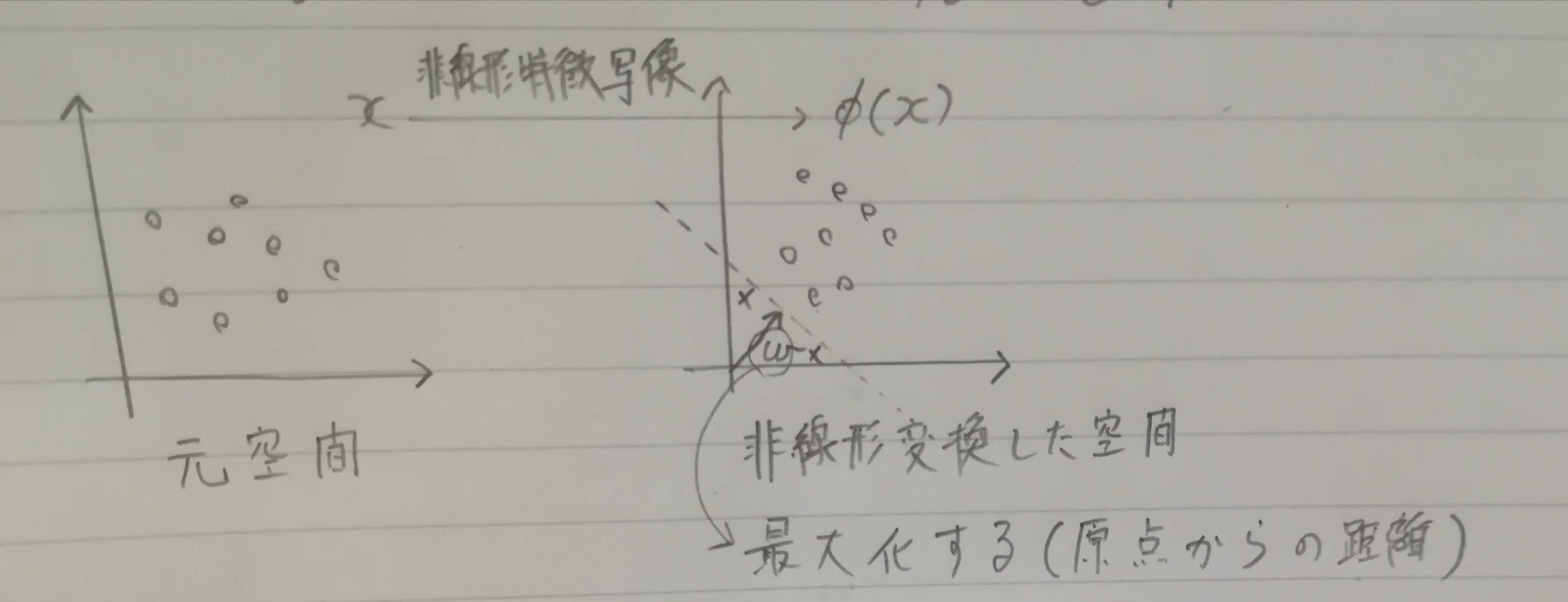
※絵が少し間違っていて、wを最大化するのではなく、マージンを最大化します。
概要は理解しましたが、主問題、双対問題などはからは完全に理解していないので省略します。ちょっとだけ思ったことをメモしておきます。
- b(バイアス)が主問題の評価関数にないのは、原点から直線が伸びているから?
- なぜνがρにくっつかずにξの分母に行く?
- 符号関数(sgn) Wikiリンク:ただ正負で±1か0とするだけ
1クラスサポートベクトルマシンについては記事「One-Class Support Vector Machine (OCSVM) で外れ値・外れサンプルを検出したりデータ密度を推定したりしよう!」がわかりやすかったです。
「はじパタ」勉強系記事リンク
| 章 | 項目 | 時間(h) | 難易度 | 学んだこと |
|---|---|---|---|---|
| 1 | はじめに | 8.9 | 特徴の型, 特徴空間, 次元の呪い | |
| 2 | 識別規則と学習法の概要 | 12 | ホールドアウト法,交差確認法 ,一つ抜き法 ,ブートストラップ法 ,バイアス・分散トレードオフ, 過学習 | |
| 3 | ベイズの識別規則 | 14.8 | ベイズ識別規則, ROC曲線 | |
| 4 | 確率モデルと識別関数 | 18 |
|
平均ベクトル, 共分散行列, 標準化, 無相関化, 白色化, 正規分布, 最尤推定 |
| 5 | k最近傍法(kNN法) | 8 |
|
最近傍法, ボロノイ境界, kNN |
| 6 | 線形識別関数(前半) | 30.4 |
|
正規方程式 |
| 6 | 線形識別関数(後半) | 前半に時間は含む |
|
フィッシャーの線形判別関数, 判別分析法, ロジスティック回帰 |
| 7 | パーセプトロン型学習規則 | 13.5 |
|
多層パーセプトロン, 誤差逆伝播法, シグモイド関数 |
| 8 | サポートベクトルマシン | 14.7 |
|
カーネルトリック, ν-SVM |
| 9 | 部分空間法 | 15.4 |
|
主成分分析, 特異値分解, CLAFIC法, カーネル主成分分析, カーネル部分空間法 |
| 10 | クラスタリング | 8.4 |
|
距離の公理, ミンコフスキー距離, K-平均法, 融合法, 混合正規分布モデル |
| 11 | 識別機の組み合わせによる性能強化 | 11.6 |
|
ノーフリーランチ定理, 決定木, バギング, アダブースト, ランダムフォレスト |