ついに「はじめてのパターン認識」の最終章である第11章「識別器の組み合わせによる性能強化」の解説です。全部読むまで半年以上かかってしまった![]()
今まで触ったことも勉強したこともなかった決定木系なのですが、そのシンプルさと異色さをようやく理解できました。基本的にはシンプルなアルゴリズムでわかりやすく短時間で理解できます。
※はじパタ勉強系は記事「文系社会人がはじパタで機械学習を数式含めて理解した奮闘記」にまとめました。
参考リンク
- はじめてのパターン認識 第11章 11.1-11.2(Slideshare)
- はじパタ11章 後半(Slideshare)
- はじめてのパターン認識 11章: 数式参考
- はじめてのパターン認識 第11章 決定木
- はじめてのパターン認識 第11章 boosting
内容
11.1 ノーフリーランチ定理
ノーフリーランチ定理は、以下を主張します。
すべての識別問題に対して、ほかの識別器より識別性能がよい識別器は存在しない
Wikipediaによると以下のように書かれています。
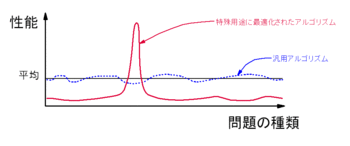
もし、データが全パターンある場合には、どのアルゴリズムを使った識別器も同じ平均性能を示しています。これは、アルゴリズムに必ず何らかの偏向があるため、データ自体がその偏向にあっていないと、性能が出ないからです。
名前の由来は以下らしい。
かつて酒場で「飲みに来た客には昼食を無料で振る舞う」という宣伝が行われたが、「無料の昼食」の代金は酒代に含まれていて実際には「無料の昼食」なんてものは有る訳がないだろう、という意味
11.2 決定木
単純な識別規則を組み合わせて複雑な識別境界を得る方法に決定木があります。下図左側のようなデータ分布があった場合、識別関数は非線形です。決定木では、特徴軸の$x_1$の値と閾値a, d, e と、$x_2$の値としきい値b, cとを比較して判断することで識別が可能です。特徴軸としきい値の大小関係を判断する過程を決定木として下図右側で表現しました。
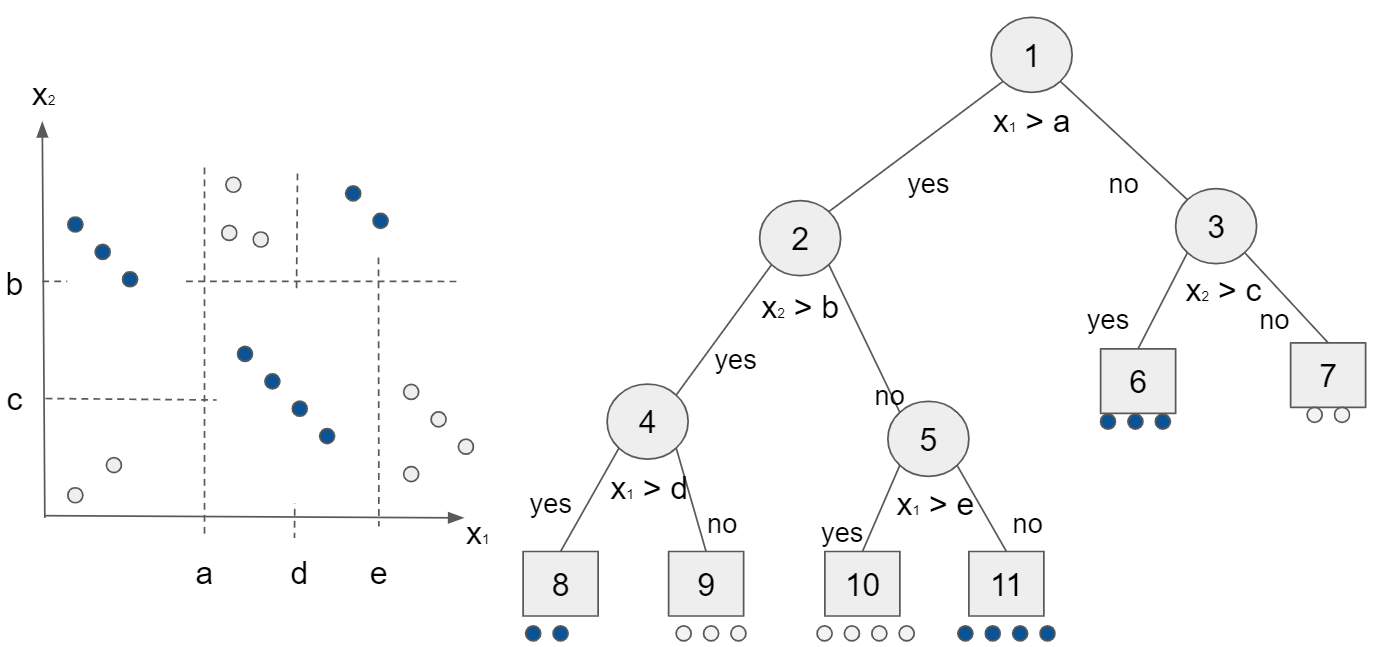
木を構成する要素はノードとノードを結ぶリンクです。ノードの呼称は下記のとおりです。
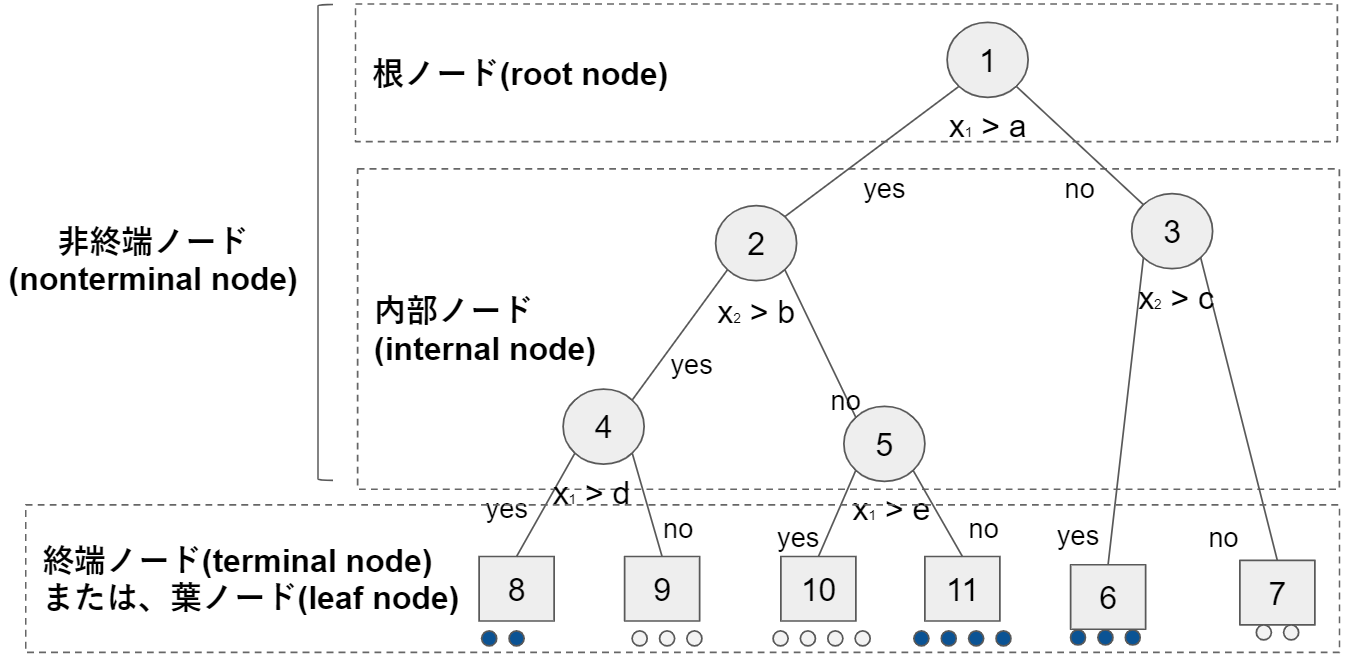
学習データから決定木を構成する方法にはボトムアップ的な手法とトップダウン的な手法があります。
ボトムアップ的な手法は、ある1つの学習データを正しく識別できる特徴の集合を探して特別な識別規則を作り、特徴に対する制約を緩めながら、他の学習データを識別できるように規則を一般化していきます。
トップダウン的な手法は、まず根ノードで全ての学習データをできるだけ誤りが少ないようにクラス分けできる特徴軸を探して特徴空間を2分割する規則を求めて、2分割された空間をさらにそれぞれ2分割する規則を求めることを繰り返して決定木を大きくする手法で、分割統治法と呼ばれます。
現在はトップダウン的な手法で決定木を構成するのが主流だそうです。
トップダウン的な手法で決定木を学習データから構成するためには、次の要素について考える必要があります。
- 各ノードで特徴分割規則を構成するための特徴軸としきい値の選択
- 終端ノードの決定。1つの終端ノードに複数クラスがあることを許容するかの選択。また、大きくなった木の剪定(pruning)をどこまで行うか。
- 終端ノードに対する多数決によるクラス割当
決定木の学習に関する代表的な方式には、CART(Classification And Regression Tree)とID3やその後継のC4.5と呼ばれるものがあります。
11.2.1 決定木に関する諸定義
決定木では以下の用語を使います。
- t: 先程の決定木の1から11までの個々のノードがt。だから「0ではない有限個の正の整数」
- T: tの集合。$t \in T$
- left(), right():左側/右側の次ノード番号を与える関数。終端ノードの場合は関数の結果が0。
木が満たす性質です。
- 各$t \in T$で、left(t) = right(t) = 0(終端ノード)か、left(t) > t かつright(t) > t (非終端ノード)のいづれかが成り立つ
- 各$t \in T$で、T内の最小数(根ノード)を除いてt = left(s)またはt = right(s)のどちらかを満たすただ1つの$s \in T$が存在する。sを親ノード、tを子ノードと言い、s=parent(t)で表す。
リンクをたどって親の親の関係にあるノードを祖先と言い、逆を子孫と言います。sがtの祖先だとtからsへ一意のパスがあり、以下の関係が成立します。
s_m(=t),s_{m-1}, \ldots, s_1, s_0(=s) \\
s_{m-1}=parent(s_m), \ldots, s_0 = parent(s_1)
その他の定義を表形式で示します。
| 式 | 内容 |
|---|---|
| $l(s,t)=m$ | パスの長さ |
| $\widetilde{T}$ | 木Tの終端ノードの集合 |
| $T-\widetilde{T}$ | 非終端ノードの集合 |
空でないTの部分集合$T_1$に対して$T_1$から$T_1 \cup {0}$への2つの関数を以下に定義します(部分集合の外に出た場合は終端ノード0に設定します)。
left_1(t) =
\begin{cases}
left(t) & (left(t) \in T_1の場合) \\
0 & (それ以外の場合)
\end{cases} \\
right_1(t) =
\begin{cases}
right(t) & (right(t) \in T_1の場合) \\
0 & (それ以外の場合)
\end{cases}
三つ組み$T_1, left_1(), right_1()$が木を構成する場合は$T_1$を部分木と言います。
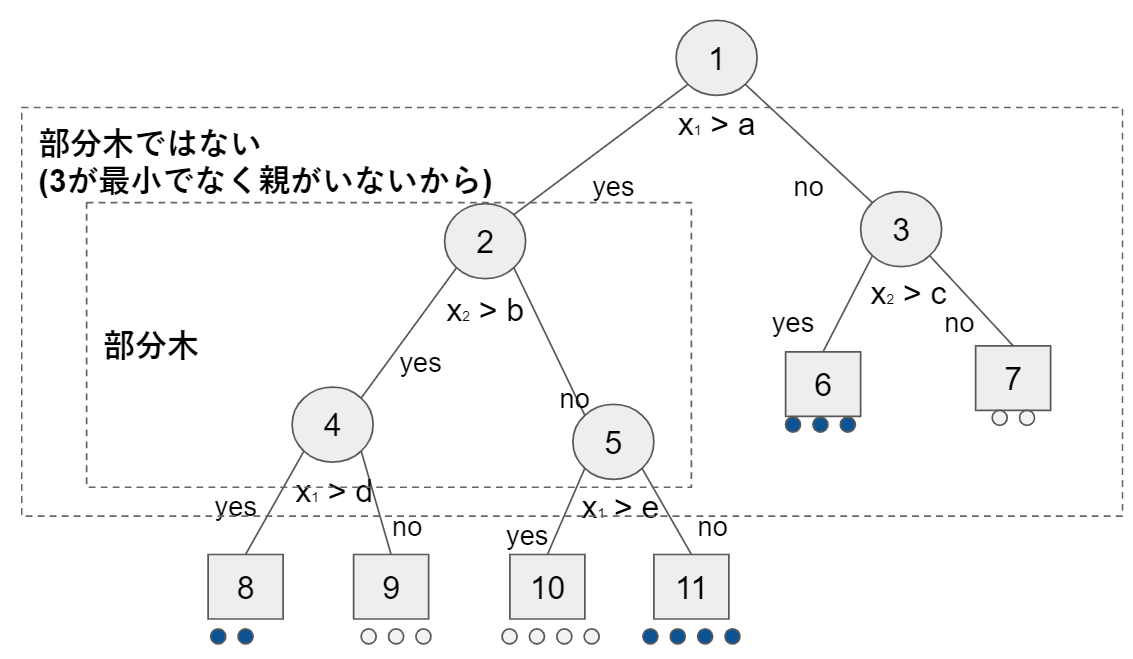
部分木$T_1$の根ノードがTの根ノードと等しい場合は剪定された部分木と言い、$T_1\preccurlyeq T$で表します。
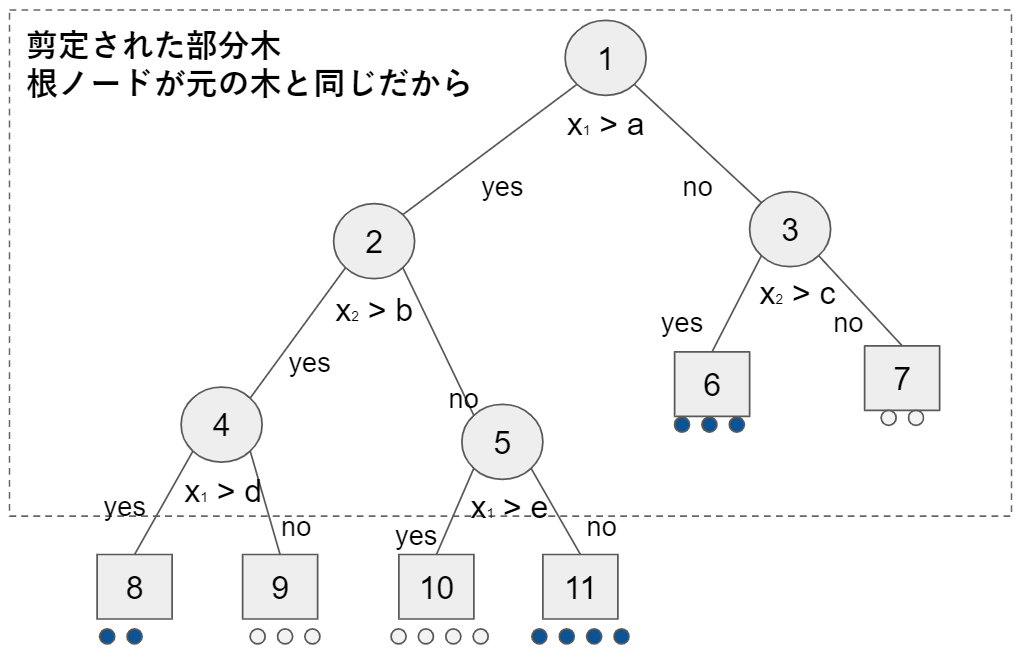
任意の$t \in T$に対して、tとその子孫全てで構成される部分木$T_t$をTの分枝(branch)と呼びます。
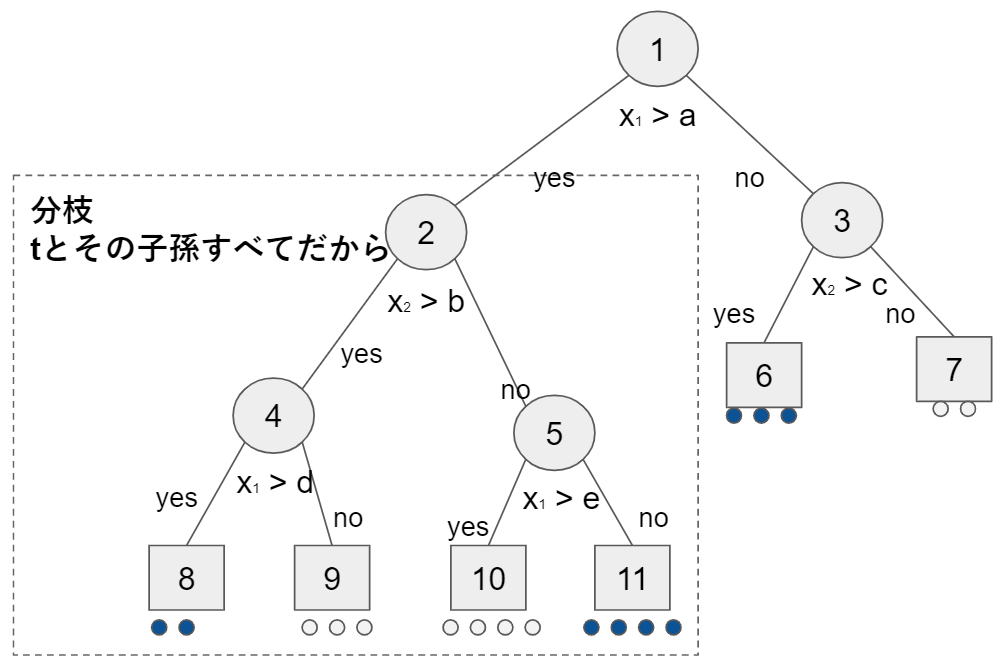
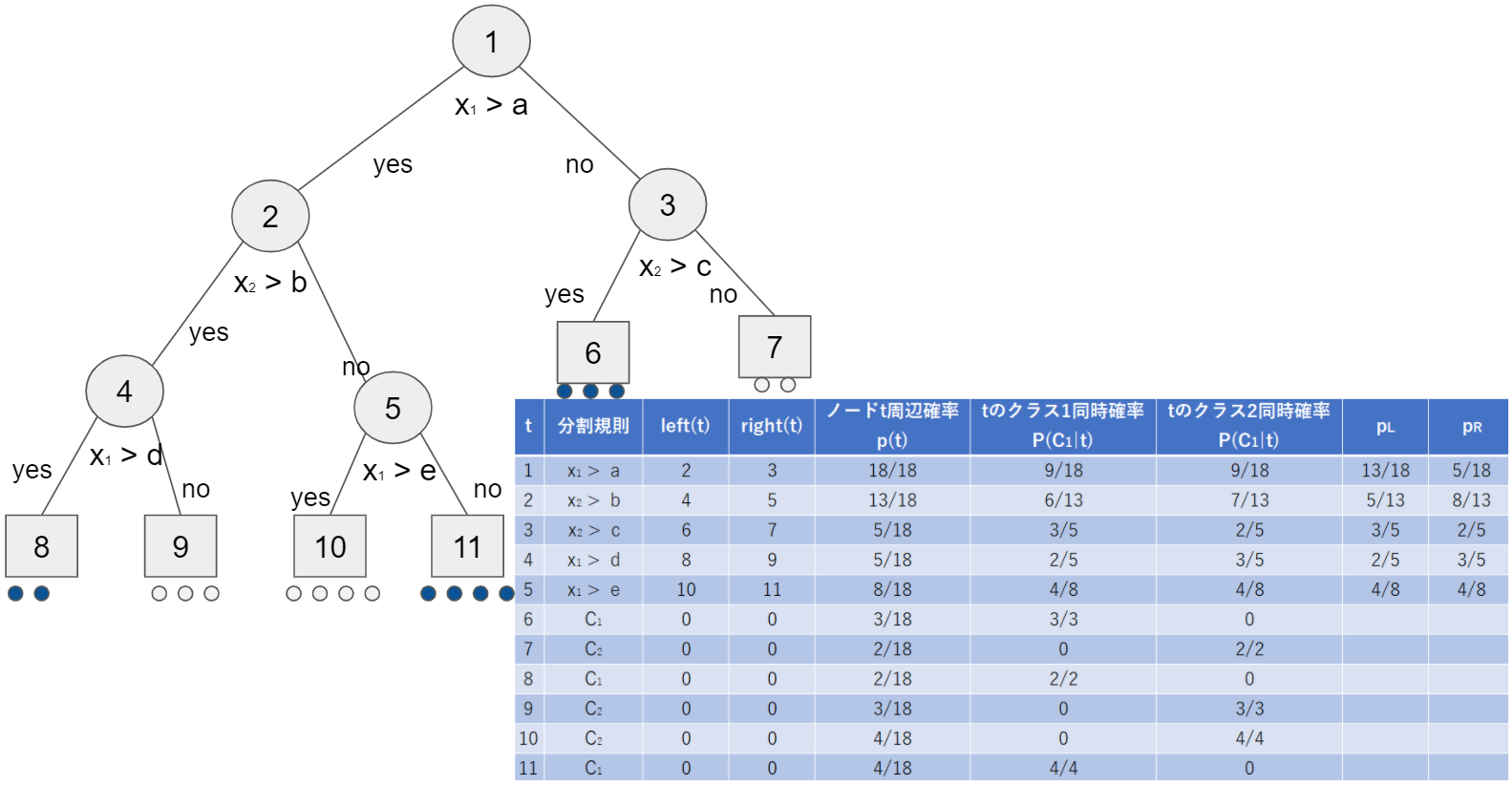
各終端ノード$t \in \widetilde{T}$はd次元特徴空間の1つの分割領域$u(t) \in \mathbb R^d$に対応しています。今までの例(2次元)で示してみます。
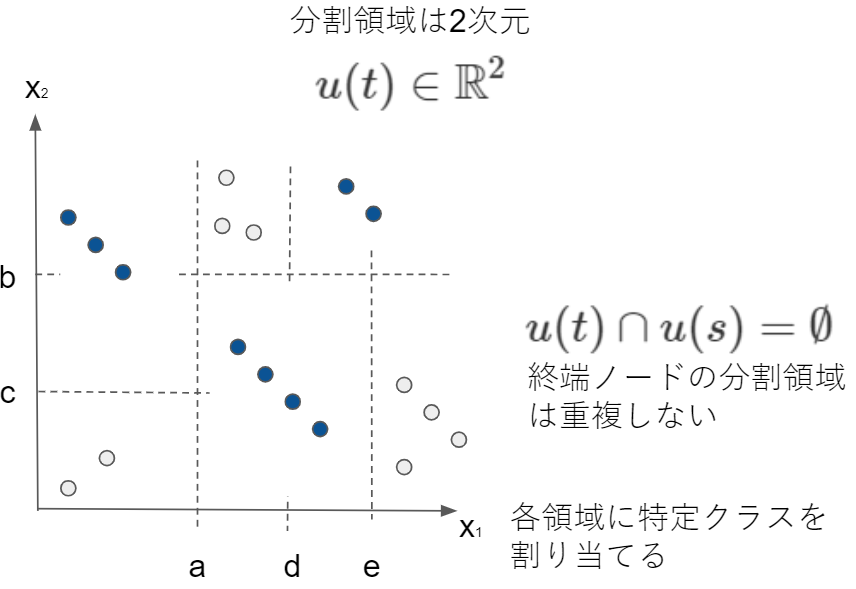
データ集合や確率系の定義です。
| 式 | 説明 |
|---|---|
| $\{(x_i,t_i)\}(i=1, \ldots, N)$ | クラスラベル付き学習データの集合 |
| $N_j$ | クラスjに属する学習データ数 |
| $P(C_j)=\frac{N_j}{N}$ | クラスjの事前確率 |
| $N(t)$ | ノードtの領域に属する学習データ数 |
| $N_j(t)$ | N(t)個のデータのうち、j番目のクラスに属するデータ数 |
| $p(t \mid C_j)=\frac{N_j(t)}{N_j}$ | クラスjの学習データがノードtに属する確率 |
上記を前提に、クラスjへの所属とノードtに属する同時確率は
p(C_j,t)=P(C_j) p(t \mid C_j)=\frac{N_j}{N} \frac{N_j(t)}{N_j}=\frac{N_j(t)}{N}
ゆえに、ノードtの周辺確率は以下の式。
p(t) = \sum_{j=1}^K p(C_j,t) = \sum_{j=1}^K \frac{N_j(t)}{N_j}=\frac{N(t)}{N}
tにおけるクラスjの事後確率。
P(C_j \mid t) = \frac{p(C_j,t)}{p(t)} =\frac{N_j(t)}{N(t)}
この事後確率が最大となるクラスを選びます。
識別クラス = \arg \max_i P(C_j \mid t)
ノードtで学習データはさらに分割され、子ノード$t_L=left(t), t_R=right(t)$が生成され、xがどちらの子ノードに属するかは以下の確率に従って決まります。
p_L = p(x \in u(t_L) \mid x \in u(t)) = \frac{p(t_L)}{p(t)} \\
p_R = p(x \in u(t_R) \mid x \in u(t)) = \frac{p(t_R)}{p(t)}
11.2.2 ノード分割規則
各ノードにおけるd次元特徴空間の最適な分割は、特徴軸ごとに可能な分割を不純度と呼ばれる評価関数で評価・選択します。特徴軸が連続値データの場合、学習データ数がNであれば、N-1の離散的な分割候補点があるだけです(例: 学習データがA, B, Cと3つあれば、分割候補点はAとBの間か、BとCの間の2(=3-1)候補あるという意味)。特徴軸が名義尺度や順序尺度の場合は、それらのカテゴリー数の分割候補点があるのみです。
あるノードtの分割規則を構成する場合は、これらのすべての候補点を不純度で評価します。選ばれる分割点は、1つの特徴軸の1つの分割点のみです。
ノードtの不純度は以下で定義します。
I(t) = \phi(P(C_1 \mid t), \ldots, P(C_K \mid t))
ここで関数$\phi(z_1, \ldots, z_K)$は、$z_i \ge 0, \sum_{i=1}^K z_i=1$に対して次の3つの性質を満たす必要があります($z_K=P(C_K \mid t)$)。
- Φ()は、すべての$i=1, \ldots, K$に対して、$z_i=\frac{1}{K}$(一様分布)のとき、最大です(最も不純)。
- Φ()は、あるiについて$z_i=1$となり、j≠iのときはすべて$z_j=0$、つまり1つのクラスに定まるとき最小です(最も不純でない)。
- Φ()は、($z_1, \ldots, z_K$)にkなして対称な関数です。
※3については、例えばK=2(二値分類)で、$z_1=0.8, z_2=0.2$でも、その逆の$z_1=0.2, z_2=0.8$でも不純度は変わらないので「対称な関数」と言っているのだと思います。
代表的な不純度
1. ノードtにおける誤り率
I(t) = 1 - \max_i P(C_i \mid t)
2. 交差エントロピーまたは逸脱度(deviance)
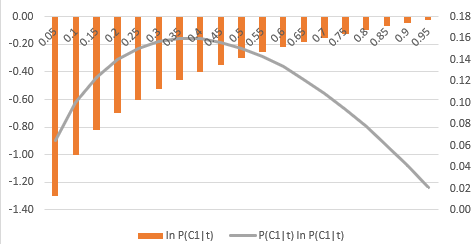
I(t) = - \sum_{i=1}^K P(C_i \mid t) \ln P(C_i \mid t)
試しにExcelで2値分類で計算しました。真ん中に行くほど損失が高くなりますね。
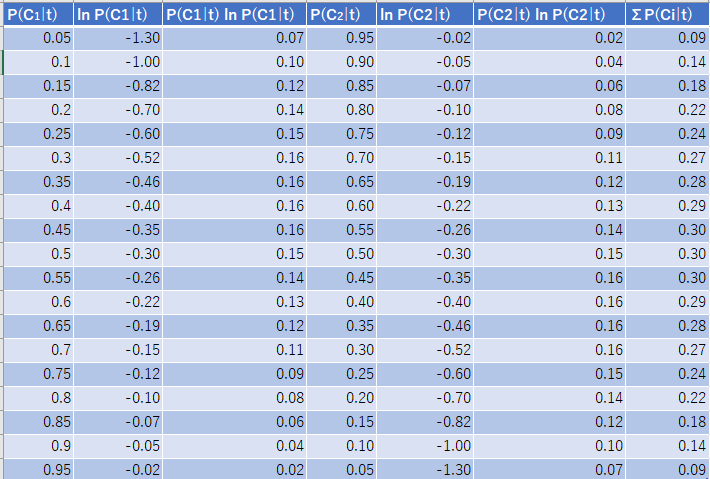
3. ジニ係数(Gini index)
\begin{eqnarray}
I(t) & = & \sum_{i=1}^K \sum_{j \ne i} P(C_i \mid t) P(C_j \mid t)\\
& = & (\sum_{i=1}^K P(C_i \mid t))^2 - \sum_{i=1}^K P^2(C_i \mid t)
\ \ \because ベルヌーイ試行の分散と考え分散 V(X)=E(X^2)-{(E(X))}^2\\
& = & 1 - \sum_{i=1}^K P^2(C_i \mid t)
\ \ \because \sum_{i=1}^K P(C_i \mid t)=1\\
& = & \sum_{i=1}^K P(C_i \mid t) - \sum_{i=1}^K P(C_i \mid t) P(C_i \mid t)\\
& = & \sum_{i=1}^K P(C_i \mid t)(1 - P(C_i \mid t))\\
\end{eqnarray}
記事「[決定木]ジニ不純度と戯れる」や「[入門]初心者の初心者による初心者のための決定木分析」を参考に理解しました。あと、ベルヌーイ試行は「ベルヌーイ分布の期待値・分散の証明」を見て思い出しています。
ノードtで分割規則を作るとき、上記の不純度の減り方最も大きい分割を選びます。分割をsとした場合$\Delta I(s,t)=I(t)-(p_L I(t_L)+p_R I(t_R))$が最大となるsを可能な分割候補から選択します。
不純度を評価関数としてノードの分割を進めていきますが、決定木が大きいとバイアスは小さくなるが汎用誤差も大きくなります。逆に分割を早い段階でとどめるとバイアスが大きくなり、再代入誤り率が大きくなる可能性があります。このトレードオフに対する1つの解決策は、終端ノードにはできるだけ1つのクラスの学習データが属するようになるまで木を成長させ、次に誤り率と木の複雑さで決まる許容範囲まで木を剪定することです。
11.2.3 木の剪定アルゴリズム
木を構成した学習データに対する再代入誤り率を定義します。
| 内容 | 前提 | ノードt | 木全体 |
|---|---|---|---|
| 再代入誤り率 | N: 総学習データ数 M(t): 総誤り数 |
$R(t)=\frac{M(t)}{N}(t \in \widetilde{T})$ | $R(T)=\sum_{t \in \widetilde{T}} R(t)$ |
| 評価関数 | |T|: ノード数 |$\widetilde{T}$|: 終端ノード数 α: 1終端ノードによる複雑さのコスト |
$R_\alpha(t)=R(t)+ \alpha$ | $R_\alpha(T)=\sum_{t \in \widetilde{T}} R_\alpha(t)$ $ = R(T) + \alpha | \widetilde{T} |$ |
上記の評価関数$R_\alpha(T)$を最小にします。ここで係数αは正則化パラメータの役割です。
任意のノードtにおける再代入誤り率は、最大事後確率から決まり、以下の式です。
r(t) = 1 - \max_i P(C_i \mid t) \ \ \
※最大事後確率は\max_i P(C_i \mid t)
ノードにおける誤り率は、ノードtに学習データが属する確率p(t)を使って以下の式です。
R(t) = r(t)p(t) \ \ \
※r(t) 誤り率 \times p(t) 属する確率
任意のノードtを根ノードとする分枝(tの全子孫による部分木)を$T_t$で表します。
もし、$R_\alpha(T_t) < R_\alpha(t)$であれば、分枝のコストの方がtを終端ノードとした場合のコストより小さいので、分枝をそのままにしておいた方が全体のコストが小さくなります。しかし、正則化パラメータα
を次第に大きくしていくと両者は等しくなり、そのときのαは以下の式です。
\alpha = \frac{R(t)-R(T_t)}{|\widetilde{T_t}|-1} \\
※ 分子は再代入誤り率の差で、分枝が効果的な場合は大きくなる\\
※ 分母は分枝終端ノード数-1で、分枝の終端ノードが多いほど大きくなり、αは小さくなる
αを上記にした場合、全体コストが変わらないので、$T_t$を剪定してもよいことになります。そこで、αをtのkの関数とみなし、ノードtのリンクの強さに関する尺度と考えます。
g(t) = \frac{R(t)-R(T_t)}{|\widetilde{T_t}|-1}
木の剪定は全ての非終端ノードについてg(t)を計算し、以下とします。
g_1(t_1) = \min_{t \in (T - \widetilde{T})}g(t)
最小値をとるすべてのノードを終端ノードとし、その子孫を削除して木を剪定します。剪定された木に対して同じ手続きを繰り返し、根ノードになるまで剪定します(最小値をとるノードが最も分枝の効果がないため)。
根ノードになるまで剪定をしますが、どこで止めればいいのかという問題が残ります。止めるところを探すためには、テストデータで汎化誤差を推定しながら剪定をすすめる必要があります。ホールドアウト法や交差確認法を用いて誤り率が最も小さくなる剪定段階を決めます。
11.3 バギング
複数の識別器を組み合わせる方法としてバギング(bagging)と呼ばれる手法があります。バギングとはBootstrap AGGRegatINGから派生した語句であり、学習データのブートストラップサンプルを用いて複数の識別器を学習させ、新しい入力データのクラスはそれらの識別器の多数決で決めるという方法です。
※ブートストラップサンプルは第2章 ブートストラップ法(bootstrap法)で学習しました。
個々の識別器の性能はランダム識別器より少し良ければよいので、弱識別器と呼ばれます。前節の決定木は、学習データの少しの変化で識別器の性能が大きく変わる不安定さがありますが、複数の決定木からの結果の多数決をとることで、1つの決定木よりも安定で性能のよい識別器を構成できます。
バギングはブートストラップサンプルによる学習なので、個々の識別器は独立して学習ができ、結果的に並列学習ができます。識別器のばらつきはブートストラップサンプルのばらつきが反映されるのみなので、決定木間の相関が高く性能が類似し、十分に性能強化できない可能性があります。この決定を補う方法がブースティングおよびランダムフォレストです。
11.4 アダブースト
ブースティング(boosting)は複数の弱識別器を用意して、学習を直列的にし、前の弱識別器の学習結果を参考にしながら1つずつ弱識別器を学習します。次の弱識別器の学習データは、それまでの学習データから次の学習にとってもっとも有益なものが選ばれます。各弱識別器は、学習データに対する誤り率が$\epsilon \leq 1/2 - \gamma$ $(\gamma > 0)$を満たすように学習されます(半分以下と考えとておけばよいのでしょうか?)。
11.4.1 アダブースト学習アルゴリズム
代表的なブースティングアルゴリズムにアダブースト(AdaBoost; adaptive boosting)があります。アダブーストは、弱識別機の学習結果に従って学習データに重みが付与されます。誤った学習データに対する重みを大きくし、正しく識別された学習データに対する重みを小さくすることで、後に学習する識別器ほど、誤りの多い学習データに集中して学習するようにします。
アダブーストは、2クラス問題の識別器であるため、多クラス問題に対応するためには、K-1個の1対多識別器を構成する必要があります。前提となるデータと式です。
| 内容 | 式 |
|---|---|
| 学習データ | $x_i \in \mathbb R^d(i=1, \ldots, N)$ |
| 教師データ | $t_i=\{-1,+1\}(i=1, \ldots, N)$ |
| 学習データの重み | $w_i^m \in \mathbb R(i=1, \ldots, N, \ \ m=1, \ldots, M)$ |
| 弱識別器 | $y_m(x)=\{-1,+1\}(m=1, \ldots, M)$ |
以下がアダブーストのアルゴリズムです。
アダブーストアルゴリズム
1. 重み初期化
重みを$w_i^1=\frac{1}{N} (i=1, \ldots, N)$に初期化します(まずは全学習データの重みを平均に設定)。
2. 個々の弱識別器ごとの繰り返し
$m=1, \ldots, M$について以下を繰り返し。
2.1. 誤差関数学習
識別器$y_m(x)$を以下の重み付き誤差関数が最小になるように学習。
E_m = \frac{\sum_{i=1}^N w_i^m I(y_m(x_i) \ne t_i)}{\sum_{i=1}^N w_i^m} \\
- $I(y_m(x_i) \ne t_i)$は識別関数の出力が正解の場合は0、不正解の場合は1となる指示関数
- 全問正解の場合は最小値0をとり、全問不正解の場合は最大値1をとる
- 誤差関数なので、誤りの場合は1×重みが積み重なる
2.2. 重み計算
識別器$y_m(x)$に対する重み$\alpha_m$を計算。誤りが多いほど小さい数(全問不正解で0)。
\alpha_m = \ln (\frac{1- E_m}{E_m})
2.3. 次識別器用データ重み更新
重み$w_i^m$を次のように更新。これはデータごとの次の識別器用重み。
w_i^{m+1}=w_i^m \exp \{\alpha_m I(y_m(x_i) \ne t_i) \}
計算例
頭の運動で「2. 個々の弱識別器ごとの繰り返し」部分の計算例です。
2.3. 重みは正解と不正解データで場合わけしていて、正解時には同じ重みを引継ぎます($\because \exp \{\alpha_m \times 0\}=1$)。不正解時には重みが増えるので、相対的に正解時の重みの値が小さくなります。また、誤差関数の結果が小さい識別器の次は誤りデータに対する重みを増やしているのもわかります。
| 内容 | 例1 | 例2 | 例3 | 例4 | 例5 |
|---|---|---|---|---|---|
| 2.1. 誤差$E_m$ | 0.01(式略) | 0.1(式略) | 0.2(式略) | 0.3(式略) | 0.4(式略) |
| 2.2. 重み$\alpha_m=\ln (\frac{1- E_m}{E_m})$ | $4.6 \simeq \ln \frac{0.99}{0.01}$ | $2.2 \simeq \ln \frac{0.9}{0.1}$ | $1.39 \simeq \ln \frac{0.8}{0.2}$ | $0.85 \simeq \ln \frac{0.7}{0.3}$ | $0.41 \simeq \ln \frac{0.6}{0.4}$ |
| 2.3. 重み(不正解時) $w_i^{m+1}=w_i^m \exp {\alpha_m I(y_m(x_i) \ne t_i) }$ |
$w_i \times 99$ | $w_i \times 9$ | $w_i \times 4$ | $w_i \times 2.33$ | $w_i \times 1.5$ |
| 2.3. 重み(正解時) $w_i^{m+1}=w_i^m \exp {\alpha_m I(y_m(x_i) \ne t_i) }$ |
$w_i^m$ | $w_i^m$ | $w_i^m$ | $w_i^m$ | $w_i^m$ |
3. 識別結果出力
入力xに対する識別結果を以下の関数に従って出力。
Y_M(x) = sign (\sum_{m=1}^M \alpha_m y_m(x)) \\
sign(a)=
\begin{cases}
+1 \ \ (a>0の場合) \\
\ \ \ 0 \ \ (a=0の場合) \\
-1 \ \ (a<0の場合)\\
\end{cases}
弱識別器の数Mはあまり大きいと過学習が生じて汎化誤差が
大きくなるので交差検証法などで選ぶ必要があります。
11.4.2 アダブースト学習アルゴリズムの導出
指数誤差関数をm=1からMまで逐次最小化により導出。目的はEを最小にする線形結合係数$\alpha_j$(木の重み)と弱識別器$y_j(x)$のパラメータを求めること。
E=\sum_{i=1}^{N}\exp(-t_{i}f_{m} (x_{i})) \ \ ※誤りの場合は-t_{i}f_{m} (x_{i})が大きくなる \\
f_{m}(\mathbf{x})=\cfrac{1}{2}\sum_{j=1}^{m}\alpha_{j}y_{j}(x) \ \ ※弱識別器y_j(x)のj=1からmまでの線形結合
逐次的最小化なので、$y_1(x), \dots, y_{m-1}(x)$とそれらの係数$\alpha_1(x), \dots, \alpha_{m-1}(x)$は決まっていると考え、$y_m(x)$と$\alpha_m$の最適化のみを考えます。
\begin{align}
E&=\sum_{i=1}^{N}\exp(-t_{i}f_{m} ( x_{i}))\\
&=\sum_{i=1}^{N} \exp ( -t_{i}f_{m-1}(x_{i}) -
\cfrac{1}{2}t_{i}\alpha_{m}y_{m}(x_{i})) \ \ ※かっこ内は最適化対象の木とそれ以外の木の合算\\
&=\sum_{i=1}^{N} w_{i}^{m} \exp (-\cfrac{1}{2}t_{i}\alpha_{m}y_{m}(x_{i}) )
\ \ \because w_{i}^{m}=\exp (-t_{i}f_{m-1}(x_{i}) ) で定数項とみなす \\
\end{align}
- $\tau_c$:$y_m(x)$で正しく識別された学習データ集合
- $\tau_e$:$y_m(x)$で誤って識別された学習データ集合
続き。
\begin{align}
E&=\sum_{i=1}^{N} w_{i}^{m} \exp (-\cfrac{1}{2}t_{i}\alpha_{m}y_{m}(x_{i}) ) \\
&=\exp(-\cfrac{\alpha_m}{2}) \sum_{i\in \tau_c}w_i^m +\exp(\cfrac{\alpha_m}{2})\sum_{i\in \tau_e} w_i^m \\
&=\exp(-\cfrac{\alpha_m}{2}) (\sum_{i=1}^{n}w_i^m - \sum_{i\in T_e} w_i^m) +\exp(\cfrac{\alpha_m}{2})\sum_{i\in T_e} w_i^m \\
&=\sum_{i\in T_e} w_i^m (\exp(\cfrac{\alpha_m}{2}) - \exp(-\cfrac{\alpha_m}{2})) + \exp(-\cfrac{\alpha_m}{2})\sum_{i=1}^{N} w_i^m\\
&= (\exp(\cfrac{\alpha_m}{2}) - \exp(-\cfrac{\alpha_m}{2}))\sum_{i=1}^{N} w_i^m I(y_m(x_i)\ne t_{i})) + \exp(-\cfrac{\alpha_m}{2})\sum_{i=1}^{N} w_i^m \\
&=\left(\exp\left(\cfrac{\alpha_{m}}{2}\right) - \exp\left(-\cfrac{\alpha_{m}}{2}\right)\right)A+\exp\left(-\cfrac{\alpha_{m}}{2}\right)B \\
&\quad\quad\left( A=\sum_{i=1}^{N} w_{i}^{m} I(y_{m}(\mathbf{x}_{i}\ne t_{i})),B=\sum_{i=1}^{N}w_{i}^{m} \right)
\end{align}
$y_m(x)$に関するEの最小化は、Bの項が定数なので、Aの最小化となります。式全体は「2.1. 誤差関数学習」の$E_m$と等しい。
\cfrac{A}{B}=\cfrac{\sum_{i=1}^{N} w_i^m I(y_m(x_i\ne t_i))}{\sum_{i=1}^{N} w_i^m}=E_m
$\alpha_m$の最小化。
\cfrac{\partial E}{\partial \alpha_m}
=\left( \cfrac{1}{2}\exp\left(\cfrac{\alpha_{m}}{2}\right) + \cfrac{1}{2}\exp\left(-\cfrac{\alpha_{m}}{2}\right) \right)A - \cfrac{1}{2}\exp\left(-\cfrac{\alpha_{m}}{2}\right)B = 0
方程式を解きます。
( \exp(\cfrac{\alpha_m}{2})+\exp(-\cfrac{\alpha_m}{2}) )A = \exp(-\cfrac{\alpha_m}{2})B \\
A\exp(\cfrac{\alpha_m}{2}) = (B-A)\exp(-\cfrac{\alpha_m}{2}) \\
\exp(\alpha_m)=\cfrac{B-A}{A} \\
\alpha_m=\ln\left(\cfrac{1-\frac{A}{B}}{\frac{A}{B}}\right)=\ln\left(\cfrac{1-E_{m}}{E_{m}}\right)
これで「2.2. 重み計算」の式が導出できました。
もう一度、指数誤差関数。
E=\sum_{i=1}^{N} w_i^m \exp (-\cfrac{1}{2}t_i \alpha_m y_m(x_i))
指数誤差関数からi番目の学習データの更新式(誤差を次の識別器の重みに反映するため)。
\begin{align}
w_{i}^{m+1}&=w_i^m \exp (-\cfrac{1}{2}t_i \alpha_m y_m(x_i) ) \\
&=\begin{cases}
w_i^m\exp(-\cfrac{\alpha_m}{2}) & (t_i y_{m}(x_i)=1) \\
w_i^m\exp(\cfrac{\alpha_m}{2}) & (t_i y_{m}(x_i)=-1)
\end{cases} \\
&=w_i^m \exp(\cfrac{\alpha_m}{2}) \exp(\alpha_m I(y_m(x_i) \ne t_i)))
\end{align}
ここで、$\exp(\cfrac{\alpha_m}{2})$はiに依存せず全データに現れるため正規化できます。正規化すると「2.3. 次識別器用データ重み更新」の$w_i^{m+1}=w_i^m \exp \{\alpha_m I(y_m(x_i) \ne t_i) \}$になります。
以上で、アダブーストの学習アルゴリズムは、指数誤差関数の逐次最適化と等価であることがわかります。
アダブーストの出力関数$f(x)=\sum_{m=1}^{M}\alpha_m y_m(x;\gamma_m)$は、f(x)をパラメータ$\gamma_m$を持つ基底関数$y_m(x;\gamma_m)$で加法展開しているとみなせるので、加法モデルと呼ばれます。$\gamma_m$は誤差関数を最小にするm番目の識別器パラメータです。
アダブーストは評価関数を逐次最適化して加法モデルを求めており、前進逐次加法モデリング(forward stagewise additive modeling)と呼びます。評価関数を変えると勾配ブースティングになります。
前進逐次加法モデリング アルゴリズム
| 内容 | 式 |
|---|---|
| 学習データ | $x_i \in \mathbb R^d(i=1, \ldots, N)$ |
| 教師データ | $t_i=\{-1,+1\}(i=1, \ldots, N)$ |
| 基底関数 | $y_m(x)=\{-1,+1\} (m=1, \ldots, M)$ |
| 基底関数にかける重み | $\alpha_m$ |
| 基底関数のパラメータ | $\gamma_m$ |
| 出力関数 | $f(x)=\sum_{m=1}^{M}\alpha_m y_m(x;\gamma_m) $ |
1. 初期値設定
初期値を$f_0(x)=0$に設定
2. 繰り返し
$m=1, \dots, M$について以下の繰り返し
2.1. 評価関数最適化
評価関数$L(t,f(x))$を(α, γ)について最適化
(\alpha_m, \gamma_m) = \arg \min_{\alpha, \gamma} \sum_{i=1}^{N} L( t_i, f_{m-1}(x_i))+\alpha y(x_i;\gamma) )
2.2. 出力関数更新
以下の式で出力関数$f_m(x)$更新。
f_m(x)=f_{m-1}(x)+\alpha_m y_m(x;\gamma_m)
記事「はじめてのパターン認識 第11章 boosting」を参照しながら理解しました。
11.5 ランダムフォレスト
バギングは、学習データに対するバイアスが小さく分散が大きな識別器に適した手法です。しかし、ブートストラップサンプリングによるため生成された決定木間の相関が高くなります。一般に分散$\sigma^2$を持つM個の独立な確率変数$X_i(i= 1, \ldots, M)$の平均$\bar{X}=(\frac{1}{M}) \sum_{i=1}^M X_i$の分散は$Var\{ \bar X \} = \frac{\sigma^2}{M}$となりますが、任意の2つの確率変数対間に正の相関$\rho$がある場合、平均の分散は以下の式となります。
Var\{ \bar X \} = \frac{1- \rho}{M} \sigma^2 + \rho \sigma^2
ブートストラップサンプル数のMを増やせば上の式の$\frac{1- \rho}{M}$は減るが、第2項が減りません。ランダムフォレストは、$\rho$をへらす仕組みを入れてバギングを強化した方法です。
11.5.1 ランダムフォレストの学習アルゴリズム
ランダムフォレスト(random forest)は、バギングを改良し決定木の各非終端ノードで識別に用いる特徴をあらかじめ決められた数だけランダムに選択することで、相関の低い多様な決定木を生成できるようにした手法です(ニューラルネットワークのドロップアウトに考え方は近いように感じました)。学習は単純ですが、SVMやアダブーストなどと同等、あるいは問題によってはそれ以上の性能を持つらしいです。
SVMやアダブーストが2クラス問題の識別器であるのに対して、ランダムフォレストは多数決により他クラス問題に自然に拡張することができます。
- m = 1からMまで以下を繰り返し
- N個のd次元学習データからブートストラップサンプル$Z_m$を生成
- $Z_m$を学習データとして、以下の手順により各ノードtを分割し、決定木$T_m$を成長させます。終端ノードのデータ数の加減は1とします。
- d個の特徴からランダムにd'個の特徴を選択($d'=\sqrt{\lfloor d \rfloor}$が推奨だが調整パラメータ)
- d'個の中から、最適な分割を与えるトク著うと分割点を求めます
- ノードtを分割点でleft(t)とright(t)に2分割
- ランダムフォレスト$\{ T_m\}_{m=1}^M$を出力
- 入力データxに対するm番目の木の識別結果を、$y_m(x) \in \{ C_1, \ldots, C_K\}$とします。ランダムフォレスト$\{T_m\}_{m=1}^M$の識別結果を
$C_i = \arg \max_j |C_j|$とします。$|C_j|$はクラス$C_j$と判断した木の数です(Latexをうまく書けず、改行して3.と別行にしました)。
11.5.2 ランダムフォレストによるデータ解析
ランダムフォレストを使うと、森のサイズによる誤り率の変化や、特徴の重要さに関する情報、学習データ間の近さに関する情報などを得ることができます。
ランダムフォレストではOut-Of-Bag誤り率(OOB誤り率)という概念を使います。ランダムフォレストは1つの木をつくるときにブートストラップにより使用する学習データを選んでおり、選択の結果、約1/3のデータは学習に使われません。その学習に使われなかった決定木のみを集めて部分森を構成し、その学習データをテストデータにして誤りを評価します。すべての学習データについてこの評価を繰り返し、平均をとることでOOB誤り率を求めます。
ランダムフォレストは森のサイズを大きくしても過学習が生じないらしいです。
特徴の重要さとして、各特徴がノード分割に使われたときの不純度(ジニ係数)の減少量を森全体で平均した量により計測できます。
ある特徴の値がクラスの識別にどのように寄与しているかを、他の特徴の寄与を加味した上で見る指標として部分依存グラフ(partial dependence plot)があります。
ランダムフォレストを用いると、学習データ間の近さを評価し視覚化できます。N個の学習データの対を考えたときに、データ間の近さを考えるのでN × N近接行列を考えることになります。i番目とj番目の学習データがOOBで、同じ終端ノードに分類される木があれば、行列のi行j列jと行i列に1を加えます。すべての学習データ対に近接行列を計算した後、多次元尺度構成法により2次元空間に写像でします。
※グラフ系は「はじパタ11章 後半(Slideshare)」で視覚的に確認しましょう。
「はじパタ」勉強系記事リンク
| 章 | 項目 | 時間(h) | 難易度 | 学んだこと |
|---|---|---|---|---|
| 1 | はじめに | 8.9 | 特徴の型, 特徴空間, 次元の呪い | |
| 2 | 識別規則と学習法の概要 | 12 | ホールドアウト法,交差確認法 ,一つ抜き法 ,ブートストラップ法 ,バイアス・分散トレードオフ, 過学習 | |
| 3 | ベイズの識別規則 | 14.8 | ベイズ識別規則, ROC曲線 | |
| 4 | 確率モデルと識別関数 | 18 |
|
平均ベクトル, 共分散行列, 標準化, 無相関化, 白色化, 正規分布, 最尤推定 |
| 5 | k最近傍法(kNN法) | 8 |
|
最近傍法, ボロノイ境界, kNN |
| 6 | 線形識別関数(前半) | 30.4 |
|
正規方程式 |
| 6 | 線形識別関数(後半) | 前半に時間は含む |
|
フィッシャーの線形判別関数, 判別分析法, ロジスティック回帰 |
| 7 | パーセプトロン型学習規則 | 13.5 |
|
多層パーセプトロン, 誤差逆伝播法, シグモイド関数 |
| 8 | サポートベクトルマシン | 14.7 |
|
カーネルトリック, ν-SVM |
| 9 | 部分空間法 | 15.4 |
|
主成分分析, 特異値分解, CLAFIC法, カーネル主成分分析, カーネル部分空間法 |
| 10 | クラスタリング | 8.4 |
|
距離の公理, ミンコフスキー距離, K-平均法, 融合法, 混合正規分布モデル |
| 11 | 識別機の組み合わせによる性能強化 | 11.6 |
|
ノーフリーランチ定理, 決定木, バギング, アダブースト, ランダムフォレスト |