「はじめてのパターン認識」の第6章「線形識別関数」の後半解説です。「線形識別なんて基礎だから簡単だろう」と甘く考えていた時期もありましたが、すごく時間がかかっています。しかし、時間をかけたかいがあったか、ようやく数式アレルギーみたいなものがなくなりました!
固有値と固有ベクトルが躓きポイントでした。もう一度「マセマ 線形代数キャンパス・ゼミ」を読んで復習しています。
※数式はほとんど「はじめてのパターン認識 第6章 後半(SlideShare)」を写経していているだけですが時間がかかります・・
※はじパタ勉強系は記事「文系社会人がはじパタで機械学習を数式含めて理解した奮闘記」にまとめました。
6.3 線形判別分析
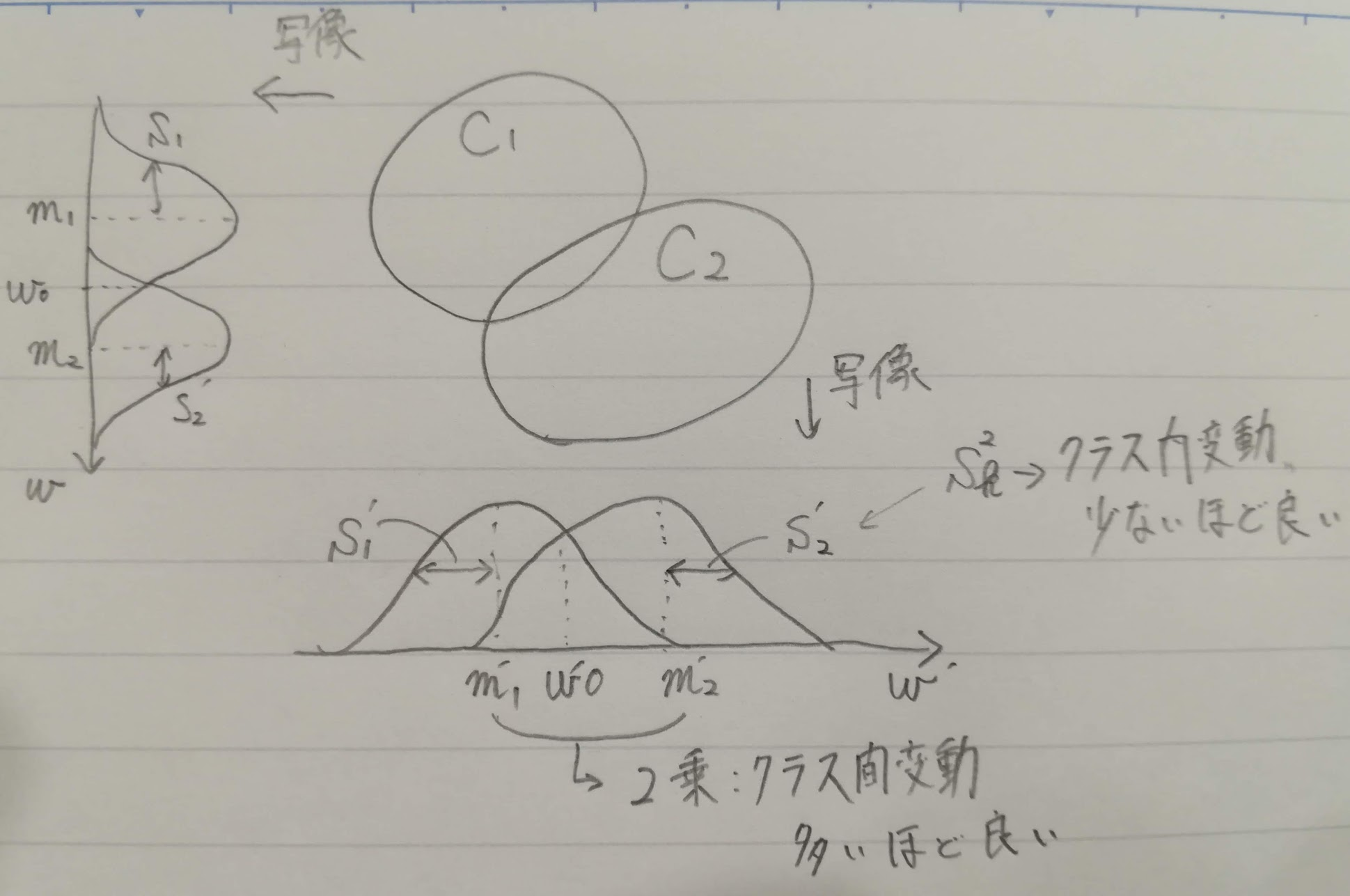
線形識別関数はd次元ベクトル$x$をベクトル$w$上のスカラ関数$f(x)$に写像しています。線形判別分析では、1次元に写像したときにクラス間の分布ができるだけ重複したにような写像方向を見つけます。線形識別関数が分類の最適な精度を目的にしているのに対して、線形判別分析はクラスのまとまりの良さを目的としています。
6.3.1 フィッシャーの線形判別関数
フィッシャーの線形判別関数は、記事「フィッシャーの線形判別分析法」およびそのリンク先や記事「Fisher の線形判別分析のベクトルwをガチで導出する」がわかりやすいです。
二値分類で、それぞれが正規分布していると仮定とした場合の写像によるクラス分離の差を絵にしました。
前提となる数値や式です。
| 項目 | 数値や式 |
|---|---|
| 各クラス | $C_1とC_2$ |
| 全学習データ数(各クラスデータ数総和) | $N=N_1+N_2$ |
| 線形識別関数 | $y=w^Tx$ |
| 平均ベクトル | $\mu_k = \frac{1}{N_k} \sum_{i \in C_k}{\textbf x}_i$ |
| クラス間変動(平均値の差の2乗) | $(m_1-m_2)^2=(w^T(\mu_1 - \mu_2))^2$ |
| クラス内変動 | $S_k^2=\sum_{i \in C_k}(y_i-m_k)^2$ |
上記の前提で以下の式(分母は全クラス内変動)を最大にする$w$を見つけることをフィッシャーの基準と呼びます。
J(w) = \frac{(m_1-m_2)^2}{S_1^2+S_2^2}
分子のクラス間変動(平均値の差の2乗)を展開します。
※多分、$S_B$のBはBetween。
\begin{eqnarray}
(m_1-m_2)^2 & = & (w^T(\mu_1-\mu_2))^2\\
& = & (w^T(\mu_1-\mu_2))(w^T(\mu_1-\mu_2))^T \ \ \because スカラの転置はスカラで、w^T(\mu_1-\mu_2)はスカラ\\
& = & w^T(\mu_1-\mu_2)(\mu_1-\mu_2)^T w \ \ \because 積の転置は順番を交換した転置の積(AB)^T=B^TA^T\\
& = & w^T S_B w\\
\end{eqnarray}
クラス内変動は以下の展開。
\begin{eqnarray}
S_k^2 & = & \sum_{i \in C_k}(y_i-m_k)^2\\
& = & \sum_{i \in C_k}(w^T({\textbf x}_i-\mu_k))^2\\
& = & \sum_{i \in C_k}(w^T({\textbf x}_i-\mu_k))(w^T({\textbf x}_i - \mu_k))^T \ \ \because スカラの転置はスカラで、w^T({\textbf x}_i-\mu_k)はスカラ\\
& = & w^T(\sum_{i \in C_k}({\textbf x}_i-\mu_k)({\textbf x}_i-\mu_k)^T)w\\
& = & w^T S_k w \ \ \because S_kは平均と学習データとの差の2乗 \\
\end{eqnarray}
これから、全クラス内変動は以下の式。
S_1^2+S_2^2 = w^T(S_1+S_2)w = w^T S_W w
よってフィッシャーの基準は以下の式。この式は一般化レイリー商と呼び、一般化固有値問題を解くことで最大化する$w$を求めます。分母と分子に$w$があるので、ノルムはどうでもよく方向だけが重要です。一般化レイリー商について、記事「レイリー商と一般化固有値問題」がわかりやすいです。
J(w) = \frac{w^T S_B w}{w^T S_W w}
一般化固有値問題に帰着するための展開
\frac{w^T S_B w}{w^T S_w w} = \lambda \ \ ※ラグランジュの未定乗数法とします\\
w^T S_B w = \lambda w^T S_w w \\
w^T S_B w = w^T \lambda S_w w \\
w^T (S_B - \lambda S_w) w = 0 \\
\frac{\partial w^T(S_B - \lambda S_w) w}{\partial w}= 0 \ \ ※極値を求める \\
((S_B - \lambda S_w) + (S_B - \lambda S_w)^T) w \\
= 2(S_B - \lambda S_w)w = 0 \ \ ※S_BとS_wは対称行列なのでS_B-\lambda S_wも対称行列\\
S_b w = \lambda S_w w
$S_W$が正則なので、両辺の左から$S_W^{-1}$をかけて通常の固有値問題にします(なぜ正則なのかを完全に理解できていないです)。
S_W^{-1} S_B w = \lambda w
ここで、$S_B w$は平均ベクトルの差に比例($\propto$)します。
S_B w = (\mu_1 - \mu_2)(\mu_1 - \mu_2)^T w \propto (\mu_1 - \mu_2) \\
\because (\mu_1 - \mu_2)^T w はスカラだから比例
ゆえに、以下の場合にフィッシャーの基準による最適な$w$となります。
w \propto S_w^{-1} S_B w \propto S_W^{-1}(\mu_1 - \mu_2)
ですが、線形識別関数のバイアス項である$w_0$は$m_1-m_2$で消えてしまい、直接求めることができません。
$w_0$を計算するために、クラス条件付き確率$p(x \mid C_k)(k=1,2)$が同じ共分散行列を持つ多次元正規分関数と仮定。
※共分散行列は第4章参照。
\Sigma_{pool} = P(C_1) \Sigma_1 + P(C_2) \Sigma_2 \\
P(C_1) = \frac{N_1}{N}, \ P(C_2) = \frac{N_2}{N} \\
\Sigma_i = \frac{1}{N} \sum^{N_i}_{j=1}({\textbf x}_j-\mu_i)({\textbf x}_j-\mu_i)^T = \frac{1}{N_i}S_i
上記の式を整理して下の共分散行列を見ると全クラスのクラス内変動行列とは$\frac{1}{N}$の違いのみです。
\Sigma_{pool} = \frac{N_1}{N} \frac{1}{N_1}S_1 + \frac{N_2}{N} \frac{1}{N_2}S_2 = \frac{S_1 + S_2}{N} = \frac{1}{N} S_W
つまり、$w$はこんな比例式になり、
w \propto S_w^{-1}(\mu_1 - \mu_2) = N \sum^{-1}_{pool}(\mu_1 - \mu_2)
最適解$w$は以下の数式です(上記に比例で定数倍部分は無視してベクトルの向きだけを考えています)。
w= \sum^{-1}_{pool}(\mu_1 - \mu_2)
これは4章で学んだベイズ誤り率最小識別規則の線形変換 ベクトルcと同じです。
c^T= \mu_j^T \sum^{-1}_j - \mu_i^T \sum^{-1}_i = (\mu_j^T - \mu_i^T) \sum^{-1}_{pool} \\
c = (\sum^{-1}_{pool})^T (\mu_j - \mu_i) = \sum^{-1}_{pool} (\mu_j - \mu_i) \ \ \because \sum_{pool}は対称行列
6.3.2 判別分析法
フィッシャーの基準は$w_0$のバイアス項を明示的に扱うことができませんでした。判別分析法ではバイアス項を明示的に合う使うような定式にしています。
まず、線形変換後のyの平均値と分散はクラスk=1,2の場合、以下のとおりです。
m_k = w^T \mu_k + w_0 \ \ (\mu_k = \frac{1}{N_k} \sum_{i \in C_k} x_i) \\
\sigma_k^2 = w^T \Sigma_k w \ \ (\Sigma_k=\frac{1}{N_k} \sum_{i \in C_k} (x_i - \mu_k)(x_i - \mu_k)^T)
クラス分離度の評価関数を$h(m_1, \sigma_1^2, m_2, \sigma_2^2)$で表します(この段階では具体的な式をまだ使わない)。評価関数を最大にする$w$と$w_0$を求めるべくhをそれぞれで微分して、0のときの解を求めます。
\frac{\partial h}{\partial w} =
\frac{\partial h}{\partial \sigma_1^2} \frac{\partial \sigma_1^2}{\partial w}
+ \frac{\partial h}{\partial \sigma_2^2} \frac{\partial \sigma_2^2}{\partial w}
+ \frac{\partial h}{\partial m_1} \frac{\partial m_1}{\partial w}
+ \frac{\partial h}{\partial m_2} \frac{\partial m_2}{\partial w} = 0 \\
\frac{\partial h}{\partial w_0} =
\frac{\partial h}{\partial \sigma_1^2} \frac{\partial \sigma_1^2}{\partial w_0}
+ \frac{\partial h}{\partial \sigma_2^2} \frac{\partial \sigma_2^2}{\partial w_0}
+ \frac{\partial h}{\partial m_1} \frac{\partial m_1}{\partial w_0}
+ \frac{\partial h}{\partial m_2} \frac{\partial m_2}{\partial w_0} = 0 \\
上の式を求めるための準備として以下の4つを計算しておきます。
\begin{eqnarray}
\frac{\partial \sigma_k^2}{\partial w} & = & \frac{\partial (w^T \Sigma_k w)}{\partial w}\\
& = & (\Sigma_k + \Sigma_k^T)w \ \ \because \frac{\partial x^T B x}{\partial x} = (B + B^T)x\\
& = & 2 \Sigma_k w\ \ \because \Sigma_kは対称行列 \\
\frac{\partial \sigma_k^2}{\partial w_0} & = & 0\\
\frac{\partial m_k}{\partial w} & = & \frac{\partial (w^T \mu_k + w_0)}{\partial w}\\
& = & \frac{\partial (\mu_k^T w + w_0)}{\partial w} \ \ \because スカラw^T \mu_kの転値はスカラ \\
& = & \mu_k \ \ \because \frac{\partial a^T x}{\partial x} = a\\
\frac{\partial m_k}{\partial w_0} & = & \frac{\partial (w^T \mu_k + w_0)}{\partial w_0}= 1\\
\end{eqnarray}
4つの中間式をクラス分離度の微分式に代入します。
\frac{\partial h}{\partial w} =
\frac{\partial h}{\partial \sigma_1^2} \frac{\partial \sigma_1^2}{\partial w}
+ \frac{\partial h}{\partial \sigma_2^2} \frac{\partial \sigma_2^2}{\partial w}
+ \frac{\partial h}{\partial m_1} \frac{\partial m_1}{\partial w}
+ \frac{\partial h}{\partial m_2} \frac{\partial m_2}{\partial w} \\
= \frac{\partial h}{\partial \sigma_1^2} 2 \Sigma_1 w
+ \frac{\partial h}{\partial \sigma_2^2} 2 \Sigma_2 w
+ \frac{\partial h}{\partial m_1} \mu_1
+ \frac{\partial h}{\partial m_2} \mu_2 \\
= 2(\frac{\partial h}{\partial \sigma_1^2} \Sigma_1 + \frac{\partial h}{\partial \sigma_1^2} \Sigma_2) w
+ (\frac{\partial h}{\partial m_1} \mu_1 + \frac{\partial h}{\partial m_2} \mu_2) = 0 \\
2 (\frac{\partial h}{\partial \sigma_1^2} \Sigma_1
+ \frac{\partial h}{\partial \sigma_2^2} \Sigma_2) w
= -(\frac{\partial h}{\partial m_1} \mu_1
+ \frac{\partial h}{\partial m_2} \mu_2) \\
\frac{\partial h}{\partial w_0} =
\frac{\partial h}{\partial \sigma_1^2} \frac{\partial \sigma_1^2}{\partial w_0}
+ \frac{\partial h}{\partial \sigma_2^2} \frac{\partial \sigma_2^2}{\partial w_0}
+ \frac{\partial h}{\partial m_1} \frac{\partial m_1}{\partial w_0}
+ \frac{\partial h}{\partial m_2} \frac{\partial m_2}{\partial w_0} \\
= \frac{\partial h}{\partial m_1} + \frac{\partial h}{\partial m_2} = 0
ここで式を簡略化するためにsを定義し、各分散をsを使って表します。
s = \frac{\frac{\partial h}{\partial \sigma_1^2}}{\frac{\partial h}{\partial \sigma_1^2} + \frac{\partial h}{\partial \sigma_2^2}} \\
\frac{\partial h}{\partial \sigma_1^2} = s(\frac{\partial h}{\partial \sigma_1^2} + \frac{\partial h}{\partial \sigma_2^2}) \\
\frac{\partial h}{\partial \sigma_2^2} = (1 - s) (\frac{\partial h}{\partial \sigma_1^2} + \frac{\partial h}{\partial \sigma_2^2}) \ \
\because 1 - s = \frac{(\frac{\partial h}{\partial \sigma_1^2} + \frac{\partial h}{\partial \sigma_2^2}) - \frac{\partial h}{\partial \sigma_1^2}}{\frac{\partial h}{\partial \sigma_1^2} + \frac{\partial h}{\partial \sigma_2^2}}
sを使って評価関数をさらに簡略化します。
\begin{eqnarray}
2 (\frac{\partial h}{\partial \sigma_1^2} \Sigma_1
+ \frac{\partial h}{\partial \sigma_2^2} \Sigma_2) w
& = &
-(\frac{\partial h}{\partial m_1} \mu_1
+ \frac{\partial h}{\partial m_2} \mu_2) \\
2 \{ s (\frac{\partial h}{\partial \sigma_1^2}
+ \frac{\partial h}{\partial \sigma_2^2}) \Sigma_1
+ (1-s) (\frac{\partial h}{\partial \sigma_1^2}
+ \frac{\partial h}{\partial \sigma_2^2}) \Sigma_2 \} w
& = &
-(\frac{\partial h}{\partial m_1} \mu_1
- \frac{\partial h}{\partial m_1} \mu_2) \\
2 (\frac{\partial h}{\partial \sigma_1^2}
+ \frac{\partial h}{\partial \sigma_2^2})
\{ s \Sigma_1 + (1-2) \Sigma_2 \} w
& = &
\frac{\partial h}{\partial m_1}(\mu_2 - \mu1) \\
\end{eqnarray}
フィッシャーの線形判別関数と同様、ノルムは興味がなくベクトル部分のみを求めたいため、スカラ部($2 (\frac{\partial h}{\partial \sigma_1^2} + \frac{\partial h}{\partial \sigma_2^2}と\frac{\partial h}{\partial m_1})$)を無視します。
w =
\{ s \Sigma_1 + (1-s) \Sigma_2 \}(\mu_2 - \mu1) \ \ \because 両辺に\{ s \Sigma_1 + (1-s) \Sigma_2 \}^{-1}を\times \\
ようやく判別分析法の具体的な評価関数です。クラス間分散とクラス内分散の比で定義します。$\bar m$は全データの平均。
h = \frac{クラス間分散}{クラス内分散} = \frac{P(C_1)(m_1 - \bar m)^2 + P(C_2)(m_2 - \bar m)^2}
{P(C_1) \sigma_1^2 + P(C_2) \sigma_2^2} \\
※ \bar m = \frac{1}{N}(N_1 m_1 + N_2 m_2)
ここでsを求めるために評価関数を分散$\sigma_k^2$で微分します。
商の微分を念頭に置きます。
商の微分公式: (\frac{f(x)}{g(x)})'=\frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)} \\
f'(x) = \frac{\partial}{\partial \sigma_k^2}(P(C_1)(m_1 - \bar m)^2 + P(C_2)(m_2 - \bar m)^2) = 0 \\
g'(x) = \frac{\partial}{\partial \sigma_k^2}(P(C_1) \sigma_1^2 + P(C_2) \sigma_2^2) = P(C_k)
\ \ \because 微分が\sigma_kなのでk側が残る\\
\frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)} = \frac{\partial h }{\partial \sigma_k^2} =
\frac{P(C_k)(P(C_1)(m_1 - \bar m)^2 + P(C_2)(m_2 - \bar m)^2)}
{(P(C_1) \sigma_1^2 + P(C_2) \sigma_2^2)^2} \\
sに上記の式を代入します。
s = \frac{\frac{\partial h}{\partial \sigma_1^2}}{\frac{\partial h}{\partial \sigma_1^2} + \frac{\partial h}{\partial \sigma_2^2}} \\
\frac{\partial h }{\partial \sigma_1^2} =
\frac{P(C_2)(P(C_1)(m_1 - \bar m)^2 + P(C_2)(m_2 - \bar m)^2)}
{(P(C_1) \sigma_1^2 + P(C_2) \sigma_2^2)^2} \\
\frac{\partial h }{\partial \sigma_2^2} =
\frac{P(C_2)(P(C_1)(m_1 - \bar m)^2 + P(C_2)(m_2 - \bar m)^2)}
{(P(C_1) \sigma_1^2 + P(C_2) \sigma_2^2)^2} \\
途中式はごちゃごちゃしているので省略。分母は共通なので分子の頭のみに注目します。これで、sの値がようやく出ました。
s = \frac{P(C_1)(\cdots)}{P(C_1)(\cdots)P(C_2)(\cdots)} = \frac{P(C_1)(\cdots)}{(P(C_1)+P(C_2))(\cdots)} \\
= P(C_1) \because P(C_1) + P(C_2) = 1
$s=P(C_1)$を$w=$の式に代入します。これでようやく判別分析法の$w$が出ます。
w = \{ s \Sigma_1 + (1-s) \Sigma_2 \}(\mu_2 - \mu_1) \\
w = \{ P(C_1) \Sigma_1 + P(C_2) \Sigma_2 \}(\mu_2 - \mu_1)
次は$w_0$を求めていきます。先ほど$\sigma_k^2$で微分した評価関数を今度は$m_k$で微分します。
h = \frac{クラス間分散}{クラス内分散} = \frac{P(C_1)(m_1 - \bar m)^2 + P(C_2)(m_2 - \bar m)^2}
{P(C_1) \sigma_1^2 + P(C_2) \sigma_2^2} \\
\frac{\partial h}{\partial m_k} = \frac{2P(C_k)(m_1-\bar m)^2}{P(C_1) \sigma_1^2 + P(C_2) \sigma_2^2}
この式を$\frac{\partial h}{\partial m_1} + \frac{\partial h}{\partial m_2} = 0$に代入します。
\frac{2P(C_1)(m_1-\bar m)^2}{P(C_1) \sigma_1^2 + P(C_2) \sigma_2^2} +
\frac{2P(C_2)(m_1-\bar m)^2}{P(C_1) \sigma_1^2 + P(C_2) \sigma_2^2} = 0 \\
P(C_1)(m_1- \bar m) + P(C_2)(m_1- \bar m) = 0 \ \
\because 分母は共通で結果が0になるので分子だけを抽出
ようやく最後です。上の式を展開して最適なバイアス項$w_0$を求めます。
P(C_1)m_1 + P(C_2)m_2 - (P(C_1)+P(C_2)) \bar m = 0 \\
P(C_1)(w^T \mu_1 + w_0) + P(C_2)(w^T \mu_2 + w_0) - \bar m = 0 \\
(P(C_1)+P(C_2)) w_0 + P(C_1)w^T \mu_1 + P(C_2)w^T \mu_2 - \bar m = 0 \\
w_0 = -w^T (P(C_1) \mu_1 + P(C_2) \mu_2) + \bar m
6.3.3 多クラス問題への拡張
フィッシャーの基準を多クラスに拡張することを考えます。多クラスの場合は、d(>K)次元のデータをK-1次元の特徴空間に写像する線形変換行列を見つけます。
各クラスのデータ数を$N_k;(k=1,\ldots,K)$とすると、各クラスのクラス内変動とクラス内平均は以下の通り。
S_k = \sum_{i \in C_k} ({\bf x}_i - \mu_k) ({\bf x}_i - \mu_k)^T \ \ ※クラス内変動 \\
\mu_k = \frac{1}{N_k} \sum_{i \in C_k} {\bf x}_i \ \ ※クラス内平均\\
全クラスのクラス内変動の和は(添字のwはwithin?)。
S_w = \sum_{k=1}^K S_k
全データの平均$\mu$は。
\mu = \frac{1}{N} \sum_{i=1}^N {\bf x}_i = \frac{1}{N} \sum_{i=1}^N N_k \mu_k
全データの変動の和である全変動$S_T$(添字のTはTotal?)。クラス内分散を含む項に分解します。
\begin{eqnarray}
S_T & = & \sum_{i = 1}^N ({\bf x}_i - \mu) ({\bf x}_i - \mu)^T\\
& = & \sum_{k = 1}^K \sum_{i \in C_k}({\bf x}_i - \mu_k + \mu_k - \mu)
({\bf x}_i - \mu_k + \mu_k - \mu)^T\\
& = & \sum_{k = 1}^K \sum_{i \in C_k}(({\bf x}_i - \mu_k) + (\mu_k - \mu))
(({\bf x}_i - \mu_k)^T + (\mu_k - \mu)^T)\\
& = & \sum_{k = 1}^K \sum_{i \in C_k}
\{ ({\bf x}_i - \mu_k)({\bf x}_i - \mu_k)^T + (\mu_k - \mu)(\mu_k - \mu)^T
+ ({\bf x}_i - \mu_k)(\mu_k - \mu)^T + (\mu_k - \mu)({\bf x}_i - \mu_k)^T \}\\
& = & \sum_{k = 1}^K \sum_{i \in C_k}({\bf x}_i - \mu_k)({\bf x}_i - \mu_k)^T
+ \sum_{k = 1}^K \sum_{i \in C_k}(\mu_k - \mu)(\mu_k - \mu)^T
+ \sum_{k = 1}^K \sum_{i \in C_k}({\bf x}_i - \mu_k)(\mu_k - \mu)^T
+ \sum_{k = 1}^K \sum_{i \in C_k}(\mu_k - \mu)({\bf x}_i - \mu_k)^T\\
& = & \sum_{k = 1}^K S_k
+ \sum_{k = 1}^K \sum_{i \in C_k}(\mu_k - \mu)(\mu_k - \mu)^T
+ 0 + 0\\
& = & S_w + \sum_{k = 1}^K \sum_{i \in C_k}(\mu_k - \mu)(\mu_k - \mu)^T\\
\end{eqnarray}
前の式の0になる項が2つの補足です。掛け合わせる項がiの影響を受けないのでこんな計算ができます。
\begin{eqnarray}
\sum_{k = 1}^K \sum_{i \in C_k}({\bf x}_i - \mu_k)(\mu_k - \mu)^T & = &
\sum_{k = 1}^K(\sum_{i \in C_k}{\bf x}_i - \sum_{i \in C_k} \mu_k)(\mu_k - \mu)^T\\
& = & \sum_{k = 1}^K(N_k \mu_k -N_k \mu_k)(\mu_k - \mu)^T = 0\\
\sum_{k = 1}^K \sum_{i \in C_k}(\mu_k - \mu)({\bf x}_i - \mu_k)^T & = &
\sum_{k = 1}^K(\mu_k - \mu)(\sum_{i \in C_k}{\bf x}_i - \sum_{i \in C_k} \mu_k)^T\\
& = & \sum_{k = 1}^K(\mu_k - \mu)(N_k \mu_k -N_k \mu_k)^T = 0\\
\end{eqnarray}
ここで全変動$S_T$の式の最後の項をクラス間変動として定義します。
S_B = \sum_{k = 1}^K \sum_{i \in C_k}(\mu_k - \mu)(\mu_k - \mu)^T
d次元 > Kクラス であれば、d次元空間からK-1次元空間への線形写像を考えます。
y_k = w_k^T {\bf x} \ \ (k=1, \ldots, K-1)
$y=(y_1, \ldots, y_{K-1})^t, W = (w_1, \ldots, y_{w-1})$とするとK-1個の線形変換は以下の式。
y= W^T {bf x}
各クラスの平均ベクトル$m_k$と全平均ベクトル$m$が以下の式。
m_k = \frac{1}{N_k} \sum_{i \in C_k} y_i = \frac{1}{N_k} \sum_{i \in C_k} W^T {\bf x}_i = W^T \mu_k \\
m = \frac{1}{N} \sum_{k=1}^K N_k m_k = \frac{1}{N} \sum_{k=1}^K W^T \mu_k = W^T \mu \\
それぞれの平均ベクトルを使って、線形変換後のクラス内変動$\widetilde S_W$を求めます。
\begin{eqnarray}
\widetilde S_W & = & \sum_{k=1}^K \sum_{i \in C_k} (y_i - m_k)(y_i - m_k)^T\\
& = & \sum_{k=1}^K \sum_{i \in C_k} (W^T {\bf x}_i - W^T \mu_k)(W^T {\bf x}_i - W^T \mu_k)^T\\
& = & \sum_{k=1}^K \sum_{i \in C_k} \{W^T({\bf x}_i - \mu_k) \}\{W^T({\bf x}_i - \mu_k) \}^T\\
& = & \sum_{k=1}^K \sum_{i \in C_k} W^T({\bf x}_i - \mu_k)({\bf x}_i - \mu_k)^T W\\
& = & W^T (\sum_{k=1}^K \sum_{i \in C_k}({\bf x}_i - \mu_k)({\bf x}_i - \mu_k)^T )W\\
& = & W^T S_W W\\
\end{eqnarray}
同様に線形変換後のクラス間変動$\widetilde S_B$です。
\begin{eqnarray}
\widetilde S_B & = & \sum_{k=1}^K N_k(m_k - m)(m_k - m)T \\
& = & \sum_{k=1}^K N_k(W^T \mu_k - W^T \mu)(W^T \mu_k - W^T \mu)^T \\
& = & \sum_{k=1}^K N_k \{ W^T(\mu_k - \mu)\}\{ W^T(\mu_k - \mu)\}^T\\
& = & \sum_{k=1}^K N_k W^T(\mu_k - \mu)(\mu_k - \mu)^T W\\
& = & W^T (\sum_{k=1}^K N_k (\mu_k - \mu)(\mu_k - \mu)^T) W\\
& = & W^T S_B W\\
\end{eqnarray}
線形変換後の全変動は$\widetilde S_T = \widetilde S_W + \widetilde S_B$とクラス内変動とクラス間変動の和となります。
2クラスの場合と同じく、最適なsy増行列$W$を求めるにはクラス間変動行列$\widetilde S_B$とクラス内変動行列$\widetilde S_W$の比を最大化することです。計算にあたり行列からスカラー量に変換する必要があります。変換方法はいろいろあるらしいですが、本の中で詳しい言及がないので省略します。
6.4 ロジスティック回帰
線形識別関数$y=w^T x$は、識別境界から離れると関数値の大きさが線形に上昇します。ここでは関数値を区間(0,1)に制限して確率的な解釈ができるようにするロジスティック回帰を解説します。ここでの「回帰」は線形関数を(0,1)の間に回帰するという意味で、分類アルゴリズムの一つです。
6.4.1 ロジスティック関数
まず、二値分類のクラス$C_1$の事後確率です。
P(C_1|{\bf x}) = \frac{p({\bf x}|C_1) P(C_1)}{p({\bf x}|C_1) P(C_1) + p({\bf x}|C_2) P(C_2)}
ここで$a = ln \frac{p({\bf x}|C_1)P(C_1)}{p({\bf x}|C_2)P(C_2)}$とおくと。
※$\ln x = \log{e} x$。
e^a = \frac{p({\bf x}|C_1)P(C_1)}{p({\bf x}|C_2)P(C_2)} \\
e^{-a} = \frac{p({\bf x}|C_2)P(C_2)}{p({\bf x}|C_1)P(C_1)}
上記を使って事後確率は以下のとおりで、**ロジスティック関数(ロジスティックシグモイド関数)**と呼びます。
※$\exp(x)=e^x$
※グラフはWikipedia「シグモイド」から

P(C_1|{\bf x}) = \frac{1}{1 + \exp(-a)} = \sigma(a)
ロジスティック関数の逆関数を考えます。
\begin{eqnarray}
\frac{1}{\sigma(a)} & = & 1 + \exp(-a) \\
\exp(-a) & = & \frac{1}{\sigma(a)} - 1 = \frac{1 - \sigma(a)}{\sigma(a)}\\
\exp(a) & = & \frac{\sigma(a)}{1 - \sigma(a)}\\
a & = & \ln (\frac{\sigma(a)}{1 - \sigma(a)})\\
& = & \ln (\frac{P(C_1 \mid {\bf x})}{1 - P(C_1 \mid {\bf x})}) \\
& = & \ln \frac{P(C_1 \mid {\bf x})}{P(C_2 \mid {\bf x})}\\
\end{eqnarray}
この最後のaをロジット関数(logit function)と言います。最後の式の事後確率の比をオッズ(odds)、その対数をログオッズ(log odds)と言います。
6.4.2 ロジスティック回帰モデル
ロジスティック回帰モデルは、事象の有無を{0,1}の二値で表し、事象の生起確率をロジスティック関数で表します。
喫煙量と肺がん発生有無を例にとリます。肺がん有無を{0,1}で表し、N人の喫煙量(本/日)を$x_i$、$i = 1, \ldots, N$とした場合の肺がんになる確率を以下で表します。
P(1 \mid x) = f(x) = \frac{1}{1+\exp(-(w_0 + w_1 x))}
ここで$a=w_0 + w_1 x=w^T {\bf x}$とします。
※${\bf x}=(1, x)^T$で、1はバイアス項用。
f(x) = \sigma(a) = \frac{1}{1+\exp(-a)}=\frac{\exp a}{1 + \exp a}
$a$は線形関数ですが、ロジスティック関数を使って非線形変換をしています。線形関数を非線形変換したも識別境界は超平面なので、ロジスティック回帰モデルは線形識別関数に分類されます。一般化線形モデル(generalized linear model)とも呼ばれます。
このとき、ロジット関数は
a = \ln \frac{P(1 \mid x)}{P(0 \mid x)} = \ln \frac{P(1 \mid x)}{1 - P(1 \mid x)} = w^t {\bf x}
オッズは
\frac{P(1 \mid x)}{1 - P(1 \mid x)} = \exp(w^t {\bf x})
ここから、$x$が1増えた場合($\widetilde x$)のオッズ比について考えます。$\widetilde x$のオッズは。
\frac{P(1 \mid \widetilde x)}{1-P(1 \mid \widetilde x)} = \exp(w^T {\bf \widetilde x})
オッズ比を計算します。
\begin{eqnarray}
\frac{\exp(w^T {\bf \widetilde x})}{\exp(w^T {\bf x})}
& = &\frac{\exp(w_0 + w_1(x+1))}{\exp(w_0 + w_1 x)}\\
& = &\frac{\exp(w_0 + w_1 x +w_1)}{\exp(w_0 + w_1 x)}\\
& = &\frac{\exp(w_0 + w_1 x) \exp(w_1)}{\exp(w_0 + w_1 x)}\\
& = & \exp(w_1)\\
\end{eqnarray}
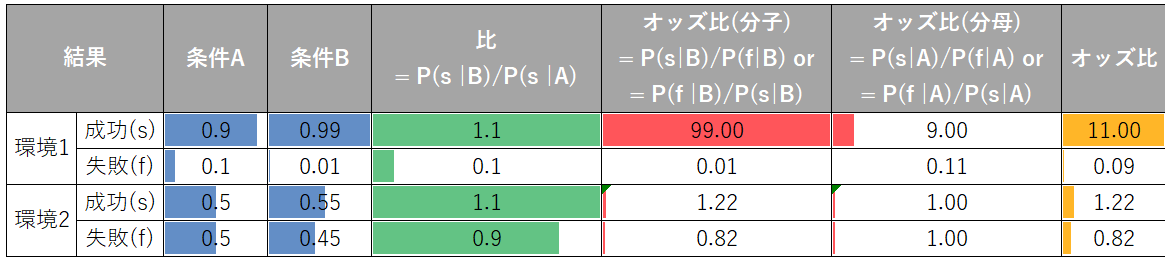
オッズ比に関する実験です。2つの異なる環境1と2において、条件をAとBで変えて実験をしたとします。環境1と2で条件をAからBに変えたことで成功確率は両者ともに1.1倍(表の「比」)になっています。しかし、オッズ比にすると環境1の場合は11倍と環境2よりもだいぶ大きいです。これは、成功確率が単純に増えただけでなく失敗確率が0に大きく近づいていることが寄与しています。
6.4.3 パラメータの最尤推定
二値分類ロジスティック回帰モデルのパラメータ最尤推定を考えます。
以下の変数で考えていきます。確率変数tはベルヌーイ試行(「二項試行」とも呼び*「取り得る結果が正確に2つである試行を繰り返し実施し、各試行が独立している」*)に従います。
| 項目 | 内容 |
|---|---|
| 確率変数t | 1 or 0 でモデルの出力 |
| tが1になる確率 | $P(t=1)=\pi$ |
| tが0になる確率 | $P(t=0)=1-\pi$ |
| tの事後確率 | $f(t \mid \pi)= \pi^t(1-\pi)^{1-t}$ |
N回試行時の尤度関数は以下の式で、尤度なのでこの値を最大化したいです。
※ここでの$\pi$は個々のデータに対するロジスティック回帰の結果です。
L(\pi_1, \ldots, \pi_N) =
\prod_{i = 1}^N f(t_i \mid \pi_i) =
\prod_{i = 1}^N \pi_i^{t_i} (1 - \pi_i)^{1 - t_i}
尤度関数をマイナスで対数化します。この値を交差エントロピー型誤差関数(cross-entropy error function)と呼び、これを最小化します。
\begin{eqnarray}
\cal{L}(\pi_1, \ldots, \pi_N) & = & - \ln L(\pi_1, \ldots, \pi_N)\\
& = & - \ln (\prod_{i=1}^N \pi_i^{t_i}(1-\pi_i)^{(1-t_i)})\\
& = & - \sum_{i=1}^N \ln (\pi_i^{t_i}(1-\pi_i)^{(1-t_i)}) \ \ \because 対数なので総乗を総和へ\\
& = & - \sum_{i=1}^N(\ln \pi_i^{t_i} + \ln(1-\pi_i)^{(1-t_i)})\\
& = & - \sum_{i=1}^N(t_i \ln \pi_i + (1-t_i)\ln(1-\pi_i))\\
\end{eqnarray}
ここで以下のロジスティック関数を代入します。
\pi_i = \sigma({\bf x}_i) = \frac{\exp(w^T {\bf x}_i)}{1 + \exp(w^T {\bf x}_i)}
\begin{eqnarray}
\cal{L}(w) & = & - \sum_{i=1}^N \{t_i \ln \frac{\exp(w^T {\bf x}_i)}{1 + \exp(w^T {\bf x}_i)} +
(1-t_i)\ln(1-\frac{\exp(w^T {\bf x}_i)}{1 + \exp(w^T {\bf x}_i)})\}\\
& = & - \sum_{i=1}^N \{t_i \ln \frac{\exp(w^T {\bf x}_i)}{1 + \exp(w^T {\bf x}_i)} +
(1-t_i)\ln(\frac{1 + \exp(w^T {\bf x}_i) - \exp(w^T {\bf x}_i)}{1 + \exp(w^T {\bf x}_i)})\}\\
& = & - \sum_{i=1}^N \{t_i \ln \frac{\exp(w^T {\bf x}_i)}{1 + \exp(w^T {\bf x}_i)} +
(1-t_i)\ln(\frac{1}{1 + \exp(w^T {\bf x}_i)})\}\\
& = & - \sum_{i=1}^N \{t_i (\ln \exp(w^T {\bf x}_i) - \ln (1 + \exp(w^T {\bf x}_i)))
+ (t_i - 1) \ln (1 + \exp(w^T {\bf x}_i)) \} \\
& = & - \sum_{i=1}^N \{t_i (\ln \exp(w^T {\bf x}_i) - \ln (1 + \exp(w^T {\bf x}_i)))
+ t_i \ln (1 + \exp(w^T {\bf x}_i)) -\ln(1 + \exp(w^T {\bf x}_i)) \} \\
& = & - \sum_{i=1}^N \{t_i w^T {\bf x}_i) - \ln(1 + \exp(w^T {\bf x}_i)) \} \\
\end{eqnarray}
上の式を最小にするパラメータ$w$を得るために微分をします。
最初に理解のために部分的に微分をしておきます。
\frac{\partial(t_i w^T {\bf x}_i)}{\partial w}
= t_i \frac{\partial(w^T {\bf x}_i)}{\partial w}
= t_i \frac{\partial({\bf x}_i^T w)}{\partial w} = t_i x_i
\begin{eqnarray}
\frac{\partial(\ln(1+\exp(w^T {\bf x}_i)))}{\partial w}
& = & \frac{1}{1+\exp(w^T {\bf x}_i)} \frac{\partial(1+\exp(w^T {\bf x}_i))}{\partial w}\\
& = & \frac{1}{1+\exp(w^T {\bf x}_i)} \frac{\partial(\exp(w^T {\bf x}_i))}{\partial w}\\
& = & \frac{1}{1+\exp(w^T {\bf x}_i)} \exp(w^T {\bf x}_i)\frac{\partial(w^T {\bf x}_i)}{\partial w}
\ \ \because u=w^T x_i, y= \exp(u)として \frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}の原理\\
& = & \frac{\exp(w^T {\bf x}_i)}{1+\exp(w^T {\bf x}_i)} \frac{\partial(w^T {\bf x}_i)}{\partial w} \\
& = & \frac{\exp(w^T {\bf x}_i)}{1+\exp(w^T {\bf x}_i)} {\bf x}_i
\ \ \because \frac{\partial(a^T x)}{\partial x}=a\\
\end{eqnarray}
ここまで準備しておけばあとは簡単。負の対数尤度関数を微分していきます。
\begin{eqnarray}
\frac{\partial \cal{L}(w)}{\partial w} & = &
- \sum_{i = 1}^N ( t_i {\bf x}_i - \frac{{\bf x}_i \exp(\textbf{$\omega$}^T {\bf x}_i)}{1 + \exp(\textbf{$\omega$}^T {\bf x}_i)}\\
& = & \sum_{i = 1}^N {\bf x}_i (\pi_i - t_i)\\
\end{eqnarray}
この式が0となるwが解です。解析的には求められないので最急降下法やニュートン-ラフソン法(Newton-Raphson法)などで求めます。
6.4.4 多クラス問題への拡張と非線形変換
他クラスへの拡張は、各クラスごとに線形変換($a_k=w_k^T {\bf x}$)をして、事後確率を計算をします。最大事後確率のクラスに分類します。この関数をソフトマックス関数(softmax関数)と言います。
P(C_k \mid x) = \pi_k(x) = \frac{\exp a_k}{ \sum_{j=1}^K \exp a_j}
線形変換でうまく分類できない場合は、入力ベクトルxを非線形関数$\varphi$(ファイ)でM+1次元に変換するとうまく分離できるようになることもあります。
\varphi({\bf x}) = (\varphi_0 = 1, \varphi_1({\bf x}), \ldots, \varphi_M({\bf x}))^T
つまりロジスティック回帰を$a_k = w_k^T \varphi({\bf x})$で計算します。その場合の空間での識別境界は超平面です。このような非線形関数を非線形基底関数と呼びます。
まず、以下のケースで考えます。
- クラス数: K
- 学習データ: ${\bf X}=({\bf x}_1, \ldots, {\bf x} _N)$
- 教師データ: ${\bf T}=({\bf t}_1, \ldots, {\bf t} _N)$
- 教師データの中身の例: ${\bf t}_i=(t_1, \ldots, t_N) = (1, \ldots, 0)$
※教師データは、対応する部分のみが1で残りが0のワンホットエンコーディング形式(ここでは$t_{11}$が1なので$C_1$に所属)
入力ベクトル$x_i$がクラス$C_k$に属する確率は以下の式です。
※左辺の$t_ik$乗部分は、所属クラスの場合は1乗でそのまま、非所属クラスでは0乗で1となります。
\prod_{k=1}^K P(C_k \mid {\bf x}_i)^{t_{ik}} = P(C_k \mid {\bf x}_i)
尤度関数は以下の式でこれを最大化します。
P({\bf T}|w_1, \cdots , w_K) =
\prod_{i=1}^N \prod_{k=1}^K P(C_k|{\bf x}_i)^{t_{ik}} =
\prod_{i=1}^N \prod_{k=1}^K \pi_{ik}^{t_{ik}} \\
※\pi_{ik} = \frac{\exp a_{ik}}{\sum_{l = 1}^K \exp a_{il}}, \ \
a_{ij} = w_j^T {\bf x}_i
上の尤度関数を負の対数化した負の対数尤度関数を最小化します。
\begin{eqnarray}
E(w_i, \cdots , w_K) & = & - \ln P({\bf T}|w_1, \cdots , w_K) \\
& = & - \ln \prod_{i=1}^N \prod_{k=1}^K \pi_{ik}^{t_{ik}}\\
& = & - \sum_{i=1}^N \sum_{k=1}^K \ln \pi_{ik}^{t_{ik}} \ \
\because \ln \prod_{n=1}^N a_i= \ln(a_1 \cdots a_N) = \ln a_0 + \cdots + \ln a_N = \sum_{i=1}^N \ln a_i\\
& = & - \sum_{i=1}^N \sum_{k=1}^K t_{ik} \ln \pi_{ik}\\
\end{eqnarray}
では、評価関数(負の対数尤度関数)Eをパラメータ$w_j$で微分して0とおいて最尤推定を求めます。
\begin{eqnarray}
\frac{\partial E}{\partial w_j} & = &
- \sum_{i=1}^N \sum_{k=1}^K t_{ik} \frac{1}{\pi_{ik}} \frac{\partial \pi_{ik}}{\partial w_j}\\
& = & - \sum_{i=1}^N \sum_{k=1}^K t_{ik}
\frac{1}{\pi_{ik}} \frac{\partial \pi_{ik}}{\partial a_{ij}}\frac{\partial a_{ij}}{\partial w_j}\\
\end{eqnarray}
まず、部分的に微分しておきます。
※途中、積の転置は順番を交換した転置の積という性質を使用。
\frac{\partial a_{ij}}{\partial w_j} =
\frac{\partial (w_j^T {\bf x}_i)}{\partial w_j} = \frac{\partial ({\bf x}_i^T w_j)}{\partial w_j} = {\bf x}_i \\
\begin{eqnarray}
\frac{\partial \pi_{ik}}{\partial a_{ij}} & = &
\frac{(\frac{\partial}{\partial a_ij} \exp a_{ik})(\sum_{l = 1}^K \exp a_{il})-
(\exp a_{ik})(\frac{\partial}{\partial a_ij}\sum_{l = 1}^K \exp a_{il})}
{(\sum_{l = 1}^K \exp a_{il})^2} (*)\\
※\pi_{ik} & = & \frac{\exp a_{ik}}{\sum_{l = 1}^K \exp a_{il}}, \ \
\frac{f(x)}{g(x)}'=-\frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}\\\
\end{eqnarray}
上の式の最後をk(正解クラス)とj(パラメータのクラス)で場合分けします。
- $k=j$のとき(所属クラス)
\begin{eqnarray}
(*) & = & \frac{(\exp a_{ij})(\sum_{l = 1}^K \exp a_{il})-
(\exp a_{ik})(\exp a_{ij})}{(\sum_{l = 1}^K \exp a_{il})^2} \\
& = & \frac{\exp a_{ij}}{\sum_{l = 1}^K \exp a_{il}}
\{ \frac{\sum_{l = 1}^K \exp a_{il}}{\sum_{l = 1}^K \exp a_{il}} -
\frac{\exp a_{ik}}{\sum_{l = 1}^K \exp a_{il}} \}
=\pi_{ij}(1-\pi_{ik}) \\
\end{eqnarray}
- $k \ne j$のとき(非所属クラス)
\begin{eqnarray}
(*) & = & \frac{0(\sum_{l = 1}^K \exp a_{il})-(\exp a_{ik})(\exp a_{ij})}{(\sum_{l = 1}^K \exp a_{il})^2}\\
& = &-\frac{\exp a_{ik}}{\sum_{l = 1}^K \exp a_{il}}
\frac{\exp a_{ij}}{\sum_{l = 1}^K \exp a_{il}} \\
& = & -\pi_{ij}\pi_{ij}=\pi_{ij}(0-\pi_{ik})\\
\end{eqnarray}
上記をクロネッカーのデルタで表現します。
※クロネッカーのデルタはに変数関数(乱暴に言うと場合分け)で、記事「クロネッカーのデルタについてわかりやすく解説する」がわかりやすいです。
(*) = \pi_{ij}(\delta_{jk} - \pi{ik}) \\
※ \delta_{jk} = \begin{cases}
1 & (j=k) \\
0 & (j \ne k)
\end{cases}
では、最後に評価関数を微分して0の場合が最小化です。
この式は解析的に解けないのでニュートン・ラフソン法などで解きます。
\begin{eqnarray}
\frac{\partial E}{\partial w_j} & = &
- \sum_{i=1}^N \sum_{k=1}^K t_{ik}
\frac{1}{\pi_{ik}} \frac{\partial \pi_{ik}}{\partial a_{ij}}\frac{\partial a_{ij}}{\partial w_j}\\
& = & - \sum_{i=1}^N \sum_{k=1}^K t_{ik} \frac{1}{\pi_{ik}}
\pi_{ij}(\delta_{jk} - \pi{ik}) {\bf x}_i \\
& = & - \sum_{i=1}^N \sum_{k=1}^K t_{ik} \frac{\pi_{ij}}{\pi_{ik}} \delta_{jk} {\bf x}_i
+ \sum_{i=1}^N \sum_{k=1}^K t_{ik} \pi_{ij} {\bf x}_i \\
& = & - \sum_{i=1}^N t_{ij} {\bf x}_i
+ \sum_{i=1}^N \pi_{ij} {\bf x}_i \sum_{k=1}^K t_{ik} \ \
\because \sum_{k=1}^K t_{ik} \frac{\pi_{ij}}{\pi_{ik}} \delta_{jk} =
t_{ij} \frac{\pi_{ij}}{\pi_{ij}} = t_{ij} \\
& = & - \sum_{i=1}^N t_{ij} {\bf x}_i
+ \sum_{i=1}^N \pi_{ij} {\bf x}_i \ \
\because \sum_{k=1}^K t_{ik} = 1 \\
& = & - \sum_{i=1}^N(\pi_{ij} -t_{ij}) {\bf x}_i = 0
\end{eqnarray}
途中式部分をちょっと補足です。
以下の式はk=jの場合だけを考えればOKなので、成り立ちます($k \ne j$の場合は0なので)。そのため、kをjに置換していて、シグマもなくすことができます。
\sum_{k=1}^K t_{ik} \frac{\pi_{ij}}{\pi_{ik}} \delta_{jk} =
t_{ij} \frac{\pi_{ij}}{\pi_{ij}} = t_{ij}
参考リンク
- はじめてのパターン認識 第6章 後半(SlideShare): このSlideShareは理解のための頼みの綱
- [Pythonによる科学・技術計算] - numpy・scipyを用いた(一般化)固有値問題の解法,ライブラリ利用: 固有値問題について参考にしました
- レイリー商と一般化固有値問題: フィッシャーの線形判別関数を理解するときに参考にしました
- はじめてのパターン認識 6章: 主にLatex数式のコピペなどに使わせてもらいました
「はじパタ」勉強系記事リンク
| 章 | 項目 | 時間(h) | 難易度 | 学んだこと |
|---|---|---|---|---|
| 1 | はじめに | 8.9 | 特徴の型, 特徴空間, 次元の呪い | |
| 2 | 識別規則と学習法の概要 | 12 | ホールドアウト法,交差確認法 ,一つ抜き法 ,ブートストラップ法 ,バイアス・分散トレードオフ, 過学習 | |
| 3 | ベイズの識別規則 | 14.8 | ベイズ識別規則, ROC曲線 | |
| 4 | 確率モデルと識別関数 | 18 |
|
平均ベクトル, 共分散行列, 標準化, 無相関化, 白色化, 正規分布, 最尤推定 |
| 5 | k最近傍法(kNN法) | 8 |
|
最近傍法, ボロノイ境界, kNN |
| 6 | 線形識別関数(前半) | 30.4 |
|
正規方程式 |
| 6 | 線形識別関数(後半) | 前半に時間は含む |
|
フィッシャーの線形判別関数, 判別分析法, ロジスティック回帰 |
| 7 | パーセプトロン型学習規則 | 13.5 |
|
多層パーセプトロン, 誤差逆伝播法, シグモイド関数 |
| 8 | サポートベクトルマシン | 14.7 |
|
カーネルトリック, ν-SVM |
| 9 | 部分空間法 | 15.4 |
|
主成分分析, 特異値分解, CLAFIC法, カーネル主成分分析, カーネル部分空間法 |
| 10 | クラスタリング | 8.4 |
|
距離の公理, ミンコフスキー距離, K-平均法, 融合法, 混合正規分布モデル |
| 11 | 識別機の組み合わせによる性能強化 | 11.6 |
|
ノーフリーランチ定理, 決定木, バギング, アダブースト, ランダムフォレスト |