はじパタ全力解説: 第6章 線形識別関数(前半)

「はじめてのパターン認識」の第6章「線形識別関数」の前半解説です。
私レベルが後から見返して理解できるレベルで数式を書いていたら長くなったので第6章を前後半に分けました。第5章までも難しく感じていたのですが、第6章はより難しく理解と整理に時間がかかりました。多分、第7章以降はもっと難しいのでしょうね。
ベクトル微分が躓きポイントでした。深く勉強まではしていませんが、「ベクトル解析」を買って読みました。
※数式はほとんど「はじパタ6章前半(SlideShare)」を写経していているだけなのですが・・・
※はじパタ勉強系は記事「文系社会人がはじパタで機械学習を数式含めて理解した奮闘記」にまとめました。

内容

線形識別関数は以下の式で表すことができ、入力データの次元が$d$とすれば、$d-1$次元の超平面となります。

f({\bf x}) = \textbf{$\omega$}^T {\bf x} + \omega_0 \\
\omega: 係数ベクトル \\
\omega_0: バイアス

6.1 線形識別関数の定義

線形識別関数は二つのクラスを区分する超平面です。

6.1.1 超平面の方程式

2クラス問題($C_1, C_2$)の線形識別関数は$f(x) = \omega^T x + \omega_0$です(中身は下表)。

項目	式
d次元入力ベクトル	$x=(x_1, \cdots, x_d)^T$
係数ベクトル	$\omega=(\omega_1, \cdots, \omega_d)^T)$
バイアス項	$\omega_0$

で、識別境界を$f(x)=0$とすると、以下の識別クラス。

識別クラス = \left\{ \begin{array} \\
C_1 \;\; (f(x) \ge 0) \\
C_2 \;\; (f(x) < 0)
\end{array} \right.

識別境界($f(x)=0$)では以下の式が成り立ち、さらに両辺を係数ベクトルのノルム$\|\omega\|$で正規化します。

\omega^T x = -\omega_0 \\
\frac{\omega^T}{\|\omega\|}x = -\frac{\omega_0}{\|\omega\|}

ここで$n= \frac{\omega}{|\omega|},\Delta_{\omega} = -\frac{\omega^T}{|\omega|}$とすると、識別境界は下式となります。

f(P) = n^T x-\Delta_{\omega} = 0

ここで、識別境界上の任意の点の位置ベクトルPを$f(P)=n^T P-\Delta_{\omega}=0$と考えます($x$をPに置き換えただけ)。

\begin{eqnarray}
f(x) & = & n^T x-\Delta_{\omega} \\
 & = & n^T x- n^T P \ \ \ \because \Delta_{\omega}=n^T P\\
 & = & n^T (x- P)=0\\
\end{eqnarray}

内積の結果が0なので、$n^Tとx-P$は直交をします。識別強化は**単位法線ベクトル$n$**を持つ超平面です。$\Delta_{\omega}$は原点から識別超平面までの距離で、正規化されたバイアスともいいます。
ここの解説は「はじパタ6章前半」が本当にわかりやすいです。

6.1.2 多クラス問題への拡張

他クラス分類にはいくつか方法があります。ここではクラス数をK個としています。

6.1.2.1. 一対多(one-versus-the-rest)

1つのクラスと他の全クラスを識別するK-1個の2クラス識別関数を使います。

識別クラス = \left\{ \begin{array} \\
                            C_j \;\; (あるjについてf_j({x}) > 0の場合) \\
                            C_K \;\; (全てのj \neq K について f_j({x}) < 0 の場合) \\
                            \end{array} \right.

識別関数$f_j(x)>1$が重複する領域が識別できないのが欠点です(3クラスでの以下のイメージ図)。

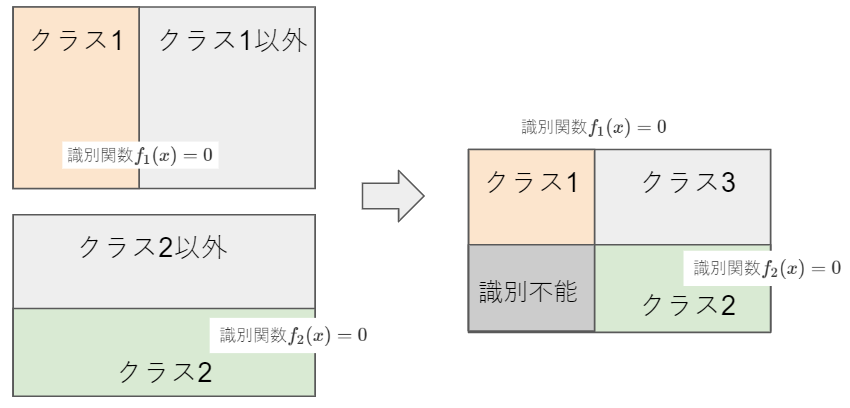
6.1.2.2. 一対一(one-versus-one)

クラス$i$と$j$を識別するK(K-1)/2個の2クラス識別関数$f_{ij}(x)$を用意し、多数決で識別クラスを決めます。この場合、多数決で同数にり決められない領域が生じるのと、識別関数が多くなるという欠点がある。

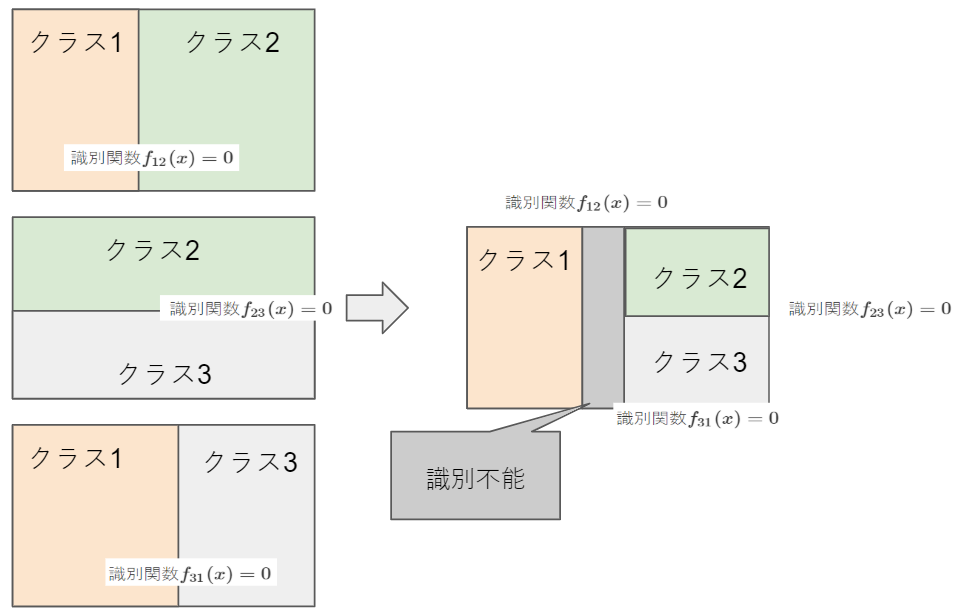
6.1.2.3. 最大識別関数法

K個の線形識別関数を用意して以下の式で識別をします(識別関数値が最大のクラスを識別クラスに決定)。

識別クラス = \arg \max_j f_j ({\bf x}) = \arg \max_j(\textbf{$\omega$}_j^T x + \omega_{j0})

**一対多・一対一と異なり、空白領域が生じません。**また、以下の性質を持っています。

1. 単連結：穴が空いていない
2. 凸：領域内の任意の2点を結ぶ直線上のすべての店がその領域に含まれている

6.2 最小2乗誤差基準によるパラメータの推定

統計でも基礎で出てくる最小2乗誤差と正規方程式についてです。
正規方程式は「Coursera 機械学習入門 2週目」で学習しました。この本より圧倒的にわかりやすいと思います(英語に抵抗なければ)。

6.2.1 正規方程式

最小2乗誤差基準は、識別関数の出力値と教師入力との差を最小にするパラメータを求める手法です。まずは二値分類で考えます。
バイアスを含めた係数ベクトルを$\omega = (\omega_0, \omega_1, \ldots , \omega_d)^T$、i番目の学習用入力ベクトルはバイアスへの対応項($x_{i0}=1$)を含めて、${\textbf x}_i = (x_{i1}, \ldots , x_{id})^T$と定義すると線形識別関数は以下の式。

f(x) = \omega_0 + \omega_1 x_1 + \cdots + \omega_d x_d = \omega^T x

入力ベクトル${\textbf x}_i$が所属するクラスは、教師入力$t_i$により以下に分類。

t_i = \left\{
       \begin{array}{l} 1\;({\textbf x}_i \in C_1) \\
             -1\;({\textbf x}_i \in C_2) \end{array}
       \right.

学習データ数をNとし、学習用の入力ベクトルを並べたデータ行列Xと、教師入力を並べた教師ベクトルtを以下に定義。

X = ({\textbf x}_1 , \cdots , {\textbf x}_N)^T, \;\; t = (t_1, \cdots , t_N)^T

識別関数の出力値と教師入力の2乗誤差で評価した評価関数$E(\omega)$は以下の式。

\begin{eqnarray}
E(\omega) & = & \sum_{i=1}^N (t_i - f({\textbf x}_i))^2\\
 & = & \sum_{i=1}^N (t_i - \omega^T {\textbf x}_i)^2\\
 & = & 
\begin{pmatrix}
t_1 - \omega^T {\textbf x}_1\\
\vdots\\
t_N - \omega^T {\textbf x}_N\\
\end{pmatrix}^T
\begin{pmatrix}
t_1 - \omega^T {\textbf x}_1\\
\vdots\\
t_N - \omega^T {\textbf x}_N\\
\end{pmatrix}
 \\
 & = & (t - X \omega)^T (t - X \omega) \\
 & = & (t^T-\omega^T X^T)(t - X \omega)\\
 & = & t^T - t^T X \omega - \omega X^T t^T + \omega^T X^T X \omega\\
 & = & t^T - 2t^T X \omega + \omega^T X^T X \omega\\
\end{eqnarray}

正規方程式 評価関数の補足

途中式でわかりにくい$X \omega$を展開するとこうなります。

\begin{eqnarray}
X \omega & = & ({\textbf x}_1, \cdots, {\textbf x}_N)^T
\begin{pmatrix}
\omega_0 \\
\vdots\\
\omega_d \\
\end{pmatrix}
= 
\begin{pmatrix}
{\textbf x}_1^T \\
\vdots\\
{\textbf x}_N^T \\
\end{pmatrix}
\begin{pmatrix}
\omega_0 \\
\vdots\\
\omega_d \\
\end{pmatrix} \\
 & = & 
\begin{pmatrix}
1 & x_{11} & x_{12} & \cdots & x_{1d}\\
\vdots &&&&\vdots \\
1 & x_{N1} & x_{N2} & \cdots & x_{Nd}\\
\end{pmatrix}
\begin{pmatrix}
\omega_0 \\
\vdots\\
\omega_d \\
\end{pmatrix} \\
 & = & 
\begin{pmatrix}
\omega_0 + \omega_1 x_{11} + \cdots & +  \omega_d x_{1d}\\
\vdots\\
\omega_0 + \omega_1 x_{N1} + \cdots & +  \omega_d x_{Nd}\\
\end{pmatrix}
=
\begin{pmatrix}
\omega^T {\textbf x}_1\\
\vdots\\
\omega^T {\textbf x}_N\\
\end{pmatrix} \\
\end{eqnarray}

また、最後の部分も少しわかりやすく展開します。
スカラの転置はスカラになり、転置行列の積の性質の1つ「積の転置は順番を交換した転置の積」から$t^T X \omega = w^T X^T t$が成り立ちます。

t^T X \omega = w^T X^T t\\
\because スカラ^T = スカラ, (AB)^T = B^T A^T

評価関数をパラメータ$\omega$で微分することにより0とすれば評価関数を最小化できます(凸関数だから)。

\frac{\partial E(\omega)}{\partial \omega} = -2X^T t + 2X^T X \omega = 0

ベクトル微分に関しては記事「ベクトルの微分」に詳しい解説があり、数学弱者にありがたいです。

評価関数の微分を解いて、パラメータの最適値$\hat \omega$を得ることが出来ます。

\hat \omega = (X^T X)^{-1} X^T t

入力データに対する予測値$\hat t$は以下の式で求めることができます。↓の行列$X(X^T X)^{-1} X^T$はハット行列と呼びます。

\hat t = X \hat \omega = X(X^T X)^{-1} X^T t

例題に標準座標系と同次座標系があります。$x_0$を1に固定して$(x_1, f(1, x_1))$平面で表現すると標準座標系で、$x_0$を１に固定せずに独立した座標として2次元空間$(x_0, x_1)$内の識別関数とする場合は同次座標系。同次座標系だと線形識別関数を$f(x)= \omega^Tx$とシンプルに表現でき、ベクトル計算がしやすくなります。
※Coursera機械学習入門コースの最初の方ですごくわかりやすく教えてくれていた記憶があります。

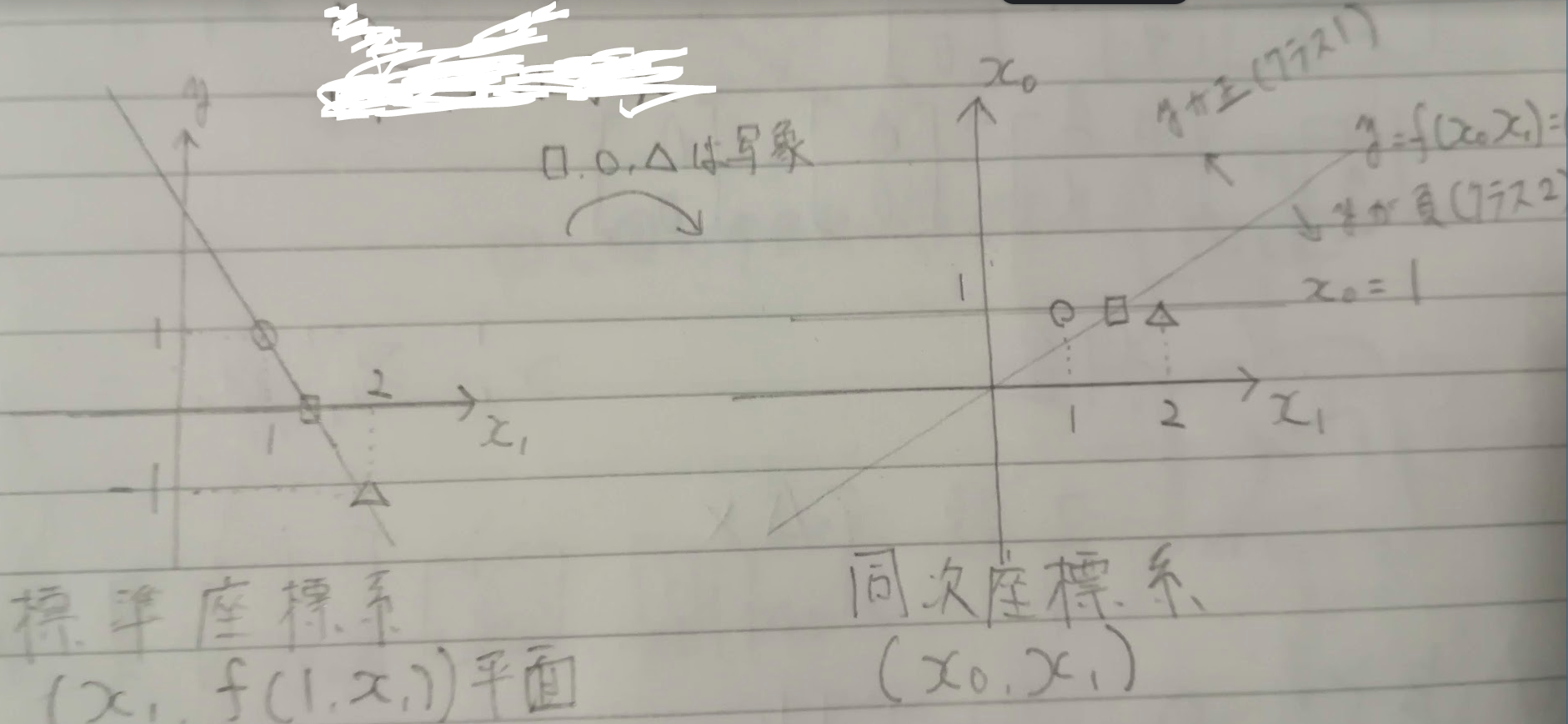
6.2.2 多クラス問題への拡張

最小2乗誤差基準の他クラス問題対応です。6.1.でやった内容と基本的には同じです。K個の識別関数を作成し、学習します。以下はその式などです。

項目	式など
N個の学習データ	${\bf X} = ({\bf x}_1, \ldots , {\bf x}_N)^T $
教師データ(i番目)	${\bf t}_i = (t_{i1}, \ldots , t_{iK})$
全教師データ	${\bf T} = ({\bf t}_1, \ldots , {\bf t}_N)^T$
2乗誤差を最小にするパラメータ	$\hat{{\bf W}} = ({\bf X}^T {\bf X})^{-1} {\bf X}^T {\bf T}$
識別関数	$f({\bf x}) = \hat{{\bf W}}^T {\bf x} = (\omega_1, \cdots , \omega_K)^T {\bf x} $ $= (f_1({\bf x}), \cdots , f_K({\bf x}))^T$
識別クラス	$\arg \max_j ; f_j({\bf x})$

線形識別の最大識別関数法は、同じクラスが同一直線上に並んでいるような場合はうまく識別できないらしいです。

参考リンク

• はじパタ6章前半(SlideShare): このSlideShareが理解のための頼みの綱
• はじめてのパターン認識 6章: 主にLatex数式のコピペなどに使わせてもらいました

「はじパタ」勉強系記事リンク

章	項目	時間(h)	難易度	学んだこと
1	はじめに	8.9		特徴の型, 特徴空間, 次元の呪い
2	識別規則と学習法の概要	12		ホールドアウト法,交差確認法 ,一つ抜き法 ,ブートストラップ法 ,バイアス・分散トレードオフ, 過学習
3	ベイズの識別規則	14.8		ベイズ識別規則, ROC曲線
4	確率モデルと識別関数	18		平均ベクトル, 共分散行列, 標準化, 無相関化, 白色化, 正規分布, 最尤推定
5	k最近傍法(kNN法)	8		最近傍法, ボロノイ境界, kNN
6	線形識別関数(前半)	30.4		正規方程式
6	線形識別関数(後半)	前半に時間は含む		フィッシャーの線形判別関数, 判別分析法, ロジスティック回帰
7	パーセプトロン型学習規則	13.5		多層パーセプトロン, 誤差逆伝播法, シグモイド関数
8	サポートベクトルマシン	14.7		カーネルトリック, ν-SVM
9	部分空間法	15.4		主成分分析, 特異値分解, CLAFIC法, カーネル主成分分析, カーネル部分空間法
10	クラスタリング	8.4		距離の公理, ミンコフスキー距離, K-平均法, 融合法, 混合正規分布モデル
11	識別機の組み合わせによる性能強化	11.6		ノーフリーランチ定理, 決定木, バギング, アダブースト, ランダムフォレスト