「はじめてのパターン認識」の第4章「確率モデルと識別関数」解説です。
20ページ弱の内容ではありますが、(私にとっては)高い前提知識を求められます。特にさらっと書かれている「固有値」と「固有ベクトル」を理解するために線形代数を復習しました。基礎的な能力大事ですね・・・
「はじめてのパターン認識」読書会 第4章が式の展開を詳しく書いてくれていて参考になりました。
※はじパタ勉強系は記事「文系社会人がはじパタで機械学習を数式含めて理解した奮闘記」にまとめました。
内容
前提知識
以下を前提知識として再学習/参照しました。
| 項目 | 備考 |
|---|---|
| 数学記号exp,ln,lgの意味 | expなど慣れなくて・・・ |
| スバラシク実力がつくと評判の線形代数キャンパス・ゼミ | 私の数学系全般バイブル |
| スバラシク実力がつくと評判の統計学キャンパス・ゼミ | 統計についてちょこちょこ見直しました |
4.1. 観測データの線形変換
4.1.1. 平均ベクトルと共分散行列
特徴間の相関を調べたいがために平均ベクトル、共分散行列、そして相関係数について学習します。
まずは平均ベクトルについて。d次元の特徴ベクトルにおける平均ベクトルは以下の通り。
\mu = (\mu_1, \cdots, \mu_d)^T \ \ ※各特徴単位での平均を並べる\\
= (E\{x_1\}, \cdots, E\{x_d \})^T \ \ ※拡特徴単位での期待値を並べる
$i$番目の特徴の平均$\mu_i$は、特徴の値と確率分布の積分で計算。
\mu_i = E\{ x_i \} = \int_{R^d} x_ip(x)dx \\
= \int^{\infty}_{-\infty}x_i p(x_i) dx_i
$i$番目の特徴である確率変数$x_i$の確率分布$p(x_i)$は、$p(x)$の周辺確率です。**「周辺」**なので以下の式には$dx_i$はありません。
p(x_i) = \int^{\infty}_{-\infty} \cdots \int^{\infty}_{-\infty}p(x_1, \cdots, x_d)dx_1 \cdots dx_{i-1} dx_{i+1} \cdots dx_d
観測データが{$x_1, \cdots, x_N$}のようにN個ある場合は平均ベクトル$\mu$は以下の算術平均で表す。※特徴数ではなく、観測データ数のことを示しています。
\mu = \bar{x} = \frac{1}{N} \sum^N_{t=1}x_i
観測データの部分を共分散行列(正確には分散・共分散行列)$\Sigma$で表す。
共分散は「共分散の意味と簡単な求め方」、共分散行列は「分散共分散行列の定義と性質」を参照ください。
\Sigma = Var\{x \} = E\{(x-\mu)(x-\mu)^T \} \\
=E \{
\begin{pmatrix}
x_1-\mu_1 \\
\vdots \\
x_d-\mu_d \\
\end{pmatrix}
(x_1-\mu_1, \cdots, x_d-\mu_d)
\} \\
=
\begin{pmatrix}
E \{ (x_1-\mu_1)(x_1-\mu_1)\} & \cdots & E \{ (x_1-\mu_1)(x_d-\mu_d)\}\\
\vdots & \ddots & \vdots \\
E \{ (x_d-\mu_d)(x_1-\mu_1)\} & \cdots & E \{ (x_d-\mu_d)(x_d-\mu_d)\} \\
\end{pmatrix} \\
=(\sigma_{ij}) =
{ \begin{cases}
i = j \ \ \ 分散\\
i \ne j \ \ \ 共分散\\
\end{cases}
}
ここで$\sigma_{ii}$は$\sigma_i^2$で、$\sigma_i$は標準偏差。
共分散行列の各要素$\sigma_{ij}$は$x$が(離散型でなく)連続量の場合、以下のように$i$番目と$j$番目の特徴の同時確率。
\sigma_{ij} = E\{(x_i-\mu_i)(x_j-\mu_j) \}=\int \int(x_i-\mu_i)(x_j-\mu_j)p(x_i, x_j)dx_i dx_j
観測データがN個ある場合の$n$番目のデータの$i$番目の特徴を$x_{ni}$、$j$番目の特徴を$x_{nj}$で表したときの共分散。
※本来は$\frac{1}{N-1}$の不偏分散を使うべきだが、機械学習の世界ではデータ数$N$が多いため大差がなくシンプルな式にしている。
\sigma_{ij} = E\{(x_i-\mu_i)(x_j-\mu_j) \}= \frac{1}{N} \sum^N_{n=1}(x_{ni}-\mu_i)(x_{nj}-\mu_j)
$i$番目と$j$番目の特徴間の相関係数$p_{ij}$は、共分散$\sigma_{ij}$を標準偏差の積で割った値で、-1から1までの値をとり、関係性がない場合は相関が0。
p_ij = \frac{\sigma_{ij}}{\sigma_i\sigma_j}
4.1.2. 観測データの標準化
データの標準化は個々の特徴を平均0、分散1にすることです。
特徴$x$を線形変換して、$y=ax+b$とします。その場合の$y$の平均と分散は以下の式。
標準化の詳細
E\{ y\} = E\{ ax + b\} = aE\{ x\} +b=a\mu+b\\
Var\{ y\}=E\{ (y-E\{ y\})^2 \} = \{ (ax+b-a\mu-b)^2 \} \\
=a^2Var\{ x\} =a^2\sigma^2
標準化で特徴$x$を変数$z$にします。これは、上記の線形変換$ax+b$で$a=\frac{1}{\sigma}$、$b=\frac{\mu}{\sigma}$としています。
z = \frac{x-\mu}{\sigma} (= \frac{1}{\sigma}x-\frac{\mu}{\sigma})
$a=\frac{1}{\sigma}$、$b=\frac{\mu}{\sigma}$を平均と分散の式に代入しています。
E\{ z\} = \frac{\mu}{\sigma} \frac{\mu}{\sigma}\\
Var\{z \} = (\frac{1}{\sigma})^2 \sigma^2 = 1
標準化については統計の基本で以前、「まずはこの一冊から 意味がわかる統計学」で勉強しました。はじパタでで理解が浅いと感じた方にはお勧めです。
4.1.3. 観測データの無相関化
線形代数前提知識
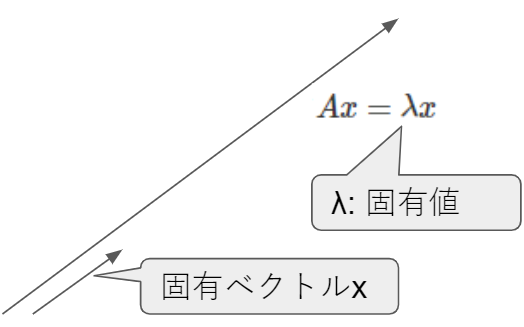
- 固有値:$\lambda$はAの固有値
- 固有ベクトル:$x$は$\lambda$に対する固有ベクトル
固有値・固有ベクトルに関する性質
- 固有ベクトル同士は線形独立
- 対称行列の固有ベクトルは直交(直角で交わるイメージ)する。対称行列は転置をしても変わらない行列($A=A^T$となる行列)のことです。
正規直交基底
そもそも**基底とは線形空間におけるベクトルからなる集合です。
このうち互いが直交する大きさが1の基底を正規直交基底**と呼びます。
ベクトル空間などを書く時間が惜しいので詳しくはリンク先を参照ください。
特徴間の相関をなくす処理である無相関化です。線形変換で特徴から相関のある情報を除去します。
詳しくは9章の主成分分析でやるそうなので軽くだけ(主成分分析では特徴数を減らしますが、無相関化は減らさない)。
4.1.3.1. 観測データの共分散行列 $\Sigma$ を作る
4.1.3.2. 固有値問題 $\Sigma s = \lambda s$ を解く($s$が固有ベクトルで、$\lambda$が固有値)
共分散行列の場合、以下の性質を持つようです。
- 固有値は実数
- 固有ベクトルは正規直行規定(ベクトルの長さが1でベクトル間は直交)
4.1.3.3. 固有ベクトルを並べて行列 $S=(s_1, s_2, \cdots, s_d)$を定義
行列$S$での線形変換は元の座標系を固有ベクトル方向に回転するため回転行列と呼びます。
例題4.2. 正規直交行列の転置は逆行列
S^TS = \left(
\begin{array}{}
s_1^T\\
\vdots\\
s_d^T
\end{array}
\right)
(s_1, \cdots, s_d) = I(単位行列)
=S^{-1}S
4.1.3.4. 観測データ$x$を$S^T$で線形変換($y=S^Tx$)。
観測データ$x$を$S^T$で線形変換したときの平均値と共分散行列は以下の式となる。
E\{ y\} = E\{S^Tx \} = S^T E\{ x\} =S^T \mu\\
\begin{eqnarray}
Var\{y \} & = & E\{ (y-E\{ y\})(y-E\{ y\})^T\} \\
& = & E\{ (S^T x- S^T \mu)(S^T x- S^T \mu)^T \} \\
& = & E\{ S^T(x- \mu)(S^T (x- \mu))^T \} \\
& = & E\{ S^T(x- \mu)((x- \mu))^T S\} \ \ \ \because(S^T)^T=S\\
& = & S^{-1}E\{ (x- \mu)(x- \mu)^T \}S = S^{-1} \Sigma S
\end{eqnarray}
分散$S^{-1} \Sigma S$は固有値$\lambda$の対角行列$\Lambda$となります。
※$\Lambda$はラムダ大文字(小文字は$\lambda$)
S^{-1} \Sigma S = S^{-1} \Sigma(s_1, s_2, \cdots, s_d) = S^{-1}(\lambda_1 s_1,\lambda_2 s_2,\ \cdots,\lambda_d s_d)\\
= S^{-1}S
\left(
\begin{array}{}
\lambda_1 & 0 & \cdots & 0\\
0 & \lambda_2 & \cdots & 0\\
\vdots & \ddots & \vdots & \vdots\\
0 & 0 & \cdots & \lambda_d\\
\end{array}
\right)
=
\left(
\begin{array}{}
\lambda_1 & 0 & \cdots & 0\\
0 & \lambda_2 & \cdots & 0\\
\vdots & \ddots & \vdots & \vdots\\
0 & 0 & \cdots & \lambda_d\\
\end{array}
\right)
= \Lambda
分散の対角成分以外がすべて0になり、無相関化したことになります。
4.1.4. 白色化
無相関化後に標準化をすることを白色化と呼びます。標準化を行っているので平均が0、分散が1です。
まずは、対角化として無相関化を行い、対角行列$\Lambda$と固有ベクトルの行列$S$を作ります。それらを使って下記の式で線形変換。
u= \Lambda^{-\frac{1}{2}}S^T(x- \mu) \\
※補足 (\Lambda^{-\frac{1}{2}})_{ij}=
\begin{cases}
\frac{1}{\sqrt{\lambda_i}}(i=j) \\
0(i \ne j)\\
\end{cases}
平均が0、分散が1になることを確認します。
\begin{eqnarray}
E \{ u\} & = & \Lambda^{-\frac{1}{2}} S^T (E\{ x\} - \mu) \\
& = & \Lambda^{-\frac{1}{2}} S^T(\mu - \mu) = 0 \\
Var\{ u\} & = & E \{ uu^T\}\\
& = & E\{ \Lambda^{-\frac{1}{2}} S^T(x-\mu)(x-\mu)^T S \Lambda^{-\frac{T}{2}}\} \\
& = & \Lambda^{-\frac{1}{2}} \{ (x-\mu)(x-\mu)^T \} \Lambda^{-\frac{T}{2}} \\
& = & \Lambda^{-\frac{1}{2}} S^{-1} \Sigma S \Lambda^{-\frac{T}{2}} \\
& = & \Lambda^{-\frac{1}{2}} \Lambda \Lambda^{-\frac{T}{2}} \\
& = & I(単位行列)
\end{eqnarray}
4.2. 確率モデル
学習データの分布表現は以下に分類できます。
- パラメトリックモデル:学習データから推定した統計量を用いて構成した確率モデルで分布を表現
- 離散的
- ポアソン分布
- 二項分布
- 他項分布
- 連続的
- 正規分布(この章のメイン)
- 一様分布
- 指数分布
- 離散的
- ノンパラメトリックモデル:学習データそのものを用いてデータの分布を表現
- ヒストグラム法
- k最近傍法(kNN法)
- パルツェン(Parzen)密度推定法
4.2.1. 正規分布関数
正規分布は以下の性質を持っています。
- 多くの観測データが正規分布に従う
- 正規分布と仮定すると解析的な解を得られる場合がよくある
- (データが正規分布していなくても)標本平均の分布は正規分布に従う(中心極限定理)
- 確率分布が平均と共分散の2つのパラメータで決まる
- 正規分布のデータを線形変換をしても正規分布に従う
- 正規分布の複数確率変数の線形和は正規分布になる(再生性がある)
- 正規分布の周辺分布も正規分布に従う
- 無相関と独立が等価(通常は無相関でも独立と言えない)
1次元正規分布関数と多次元正規分布関数は以下の通り($\mu$は平均ベクトルで$\Sigma$は共分散行列)。
N(x \mid \mu, \sigma^2 ) = \frac{1}{\sqrt{2π} \sigma}\exp{(-\frac{(x-\mu)^2}{2 \sigma^2})} \ \ ※1次元\\
N(x \mid \mu, \Sigma ) = \frac{1}{(2π)^{\frac{d}{2}} |\Sigma|^{\frac{1}{2}}} \exp{(-\frac{1}{2}(x-μ)^T \Sigma^{-1} (x-\mu))} \ \ ※d次元\\
この指数部は、任意の点$x$と平均ベクトル$\mu$との距離を表し、マハラノビス距離といいます。ユークリッド距離を共分散で割り算しており、分布の広がりが考慮されています(分散が大きければ距離が短い)。詳しくは、「マハラノビスの距離入門」を参照ください。
4.2.2. 正規分布から導かれる識別関数
「 第3章 ベイズの識別規則」で学んだことが前提です。
$i$番目のクラスのクラス条件付き確率が次の正規分布をしていると仮定。
N(x \mid C_i ) = \frac{1}{(2π)^{\frac{d}{2}} |\Sigma|^{\frac{1}{2}}} \exp{(-\frac{1}{2}(x-μ)^T \Sigma^{-1} (x-\mu))}
ベイズの誤り率最小識別規則を満たす識別関数を求めます。
まず事後確率は最後の式に比例をします(周辺確率の逆数$\frac{1}{p(x)}$は全クラス共通なので識別関数を考えるときに省略)。
※$\propto$は比例を表す記号。
\begin{eqnarray}
P(C_i \mid x) & = & \frac{p(x \mid C_i) P(C_i)}{p(x)} \\
& \propto & \frac{P(C_i)}{(2π)^{\frac{d}{2}} |\Sigma|^{\frac{1}{2}}} \exp{(-\frac{1}{2}(x-μ)^T \Sigma^{-1} (x-\mu))}
\end{eqnarray}
比例する最後の式の対数をとる。
\ln P(C_i) -\frac{d}{2} \ln(2\pi) - \frac{1}{2} \ln |\Sigma_i| - \frac{1}{2}(x-\mu_i)^T\Sigma_i^{-1}(x-\mu_i)
見やすくするために2倍をし、最小化とするために正負反転して誤り最小基準のベイズの識別規則となります。
g_i(x) = (x-\mu_i)^T\Sigma_i^{-1}(x-\mu_i) + \ln |\Sigma_i| - 2\ln P(C_i) \\
識別クラス = \arg \min_i |g_i(x)|
クラス間の識別境界は以下のように2クラスの事後確率が等しくなる点。
\begin{eqnarray}
f_{ij}(x) & = & g_i(x) - g_j(x)\\
& = & (x-\mu_i)^T\Sigma_i^{-1}(x-\mu_i) + \ln |\Sigma_i| - 2\ln P(C_i) - (x-\mu_j)^T\Sigma_i^{-1}(x-\mu_j) + \ln |\Sigma_j| - 2\ln P(C_j)\\
& = & x^T(\Sigma_i^{-1} - \Sigma_j^{-1})x \ \ ※共分散行列の差の部分が行列S\\
& + & 2(\mu_j^T \Sigma_j^{-1} -\mu_i^T \Sigma_i^{-1})x \ \ ※平均と共分散行列の内積部分がベクトルc^T\\
& + & \mu_i^T \Sigma_i^{-1}\mu_i - \mu_j^T \Sigma_j^{-1}\mu_j + \ln \frac{|\Sigma_i|}{|\Sigma_j|} -2 \ln \frac{P(C_i)}{P(C_j)} \ \ ※スカラーF\\
& = & x^TSx + 2c^Tx + F = 0\\
\end{eqnarray}
これは$x^TSx$と$x$の2次式があり、2次曲面であり2次識別関数といいます。
仮に$\Sigma_i = \Sigma_j$の場合、共分散行列の差$S$が0となり、結果として2次式部分が0になって線形識別関数になります。
さらに$Sigma = \sigma I$のように2つのクラスの共分散行列が等方的であり、事後確率が等しい($P(C_i)=P(C_j)$)場合は以下の式が成り立ちます。
\begin{eqnarray}
f_ij(x) & = & g_i(x) - g_j(x)\\
& = & 2(\mu_j^T (\sigma I)^{-1} -\mu_i^T (\sigma I)^{-1})x \\
& + & \mu_i^T (\sigma I)^{-1}\mu_i - \mu_j^T (\sigma I)^{-1}\mu_j + \ln \frac{|\sigma I|}{|\sigma I|} -2 \ln \frac{P(C_i)}{P(C_j)} \\
& = & 2 \sigma^{-1} (\mu_j^T - \mu_i^T) x + \sigma^{-1} (\mu_i^T \mu_i - \mu_j^T \mu_j) = 0 \\
\end{eqnarray}
上記の式から$\sigma^{-1}$で割って整理すると以下の式になり、入力ベクトルと平均ベクトルとのユークリッド距離が小さいクラスに識別されます。
\begin{eqnarray}
& &2 (\mu_j^T - \mu_i^T) x + (\mu_i^T \mu_i - \mu_j^T \mu_j) \\
& = & x^Tx - 2 \mu_i^T + \mu_i^T \mu_i - x^Tx + 2 \mu_j^Tx -\mu_jT\mu_j \\
& = & (x-\mu_i)^T (x-\mu_i) - (x-\mu_j)^T (x-\mu_j) = 0 \\
& \therefore & (x-\mu_i)^T (x-\mu_i) = (x-\mu_j)^T (x-\mu_j)
\end{eqnarray}
4.3. 確率モデルパラメータの最尤推定
最尤推定については、「最尤推定量とは?初めての人にもわかる解説」がわかりやすく、最初に読むことをお勧めします。
学習データ$x_i(i=1, \cdots, N)$は、真の分布から独立にサンプルされたものでi,i,d.(independently and identically distributed)標本と呼ばれます。真の分布をパラメータ$\theta$を持つ確率モデル$f(x \mid \theta)$で表します。
確率モデル$f(x \mid \theta)$に従うN個の学習データの同時分布は以下の式です。
f(x_1, \cdots, x_N \mid \theta) = \prod_{i=1}^N f(x_i \mid \theta)
上記の式は何を噛み砕くと、サイコロを2つふって1つ目が偶数になる確率を$x_1$、2つ目が5以上の目になる確率を$x_2$としたならば同時分布の確率は以下のようになるというだけです。この例では$\theta$を無視していますが、実際には$x_i$の確率分布は未知のため、$\theta$を変数と考え、確率分布を推定していきます。
f(x_1, x_2 \mid \theta) = \frac{1}{2} \times \frac{1}{3} = \frac{1}{6}
通常は$x$が変数で$\theta$が定数だが、(今回は統計の話だが)機械学習では$x$は所与の観測データで$\theta$が変数となります。$\theta$の関数であることを明示すべく$L(\theta)$で表します。
L(\theta)=f(x_i, \cdots, x_N \mid \theta)
この尤度を最大にするパラメータ$\theta$を見つけます。統計でいう最尤推定法です。**尤度関数$L(\theta)$**や対数をとった対数尤度関数$\ln L(\theta)$を微分して最適なパラメータを求めます。対数とった方が微分しやすいので便利です。
※本の中だと対数尤度関数だとLがぐにゃっとしています。私は小文字で書きました。
\frac{\partial L(\theta)}{\partial \theta_i} = 0 \ \ ※尤度関数\\
\frac{\partial \ln L(\theta)}{\partial \theta_i}= \frac{\partial l(\theta)}{\partial \theta_i} = 0 \ \ ※対数尤度関数\\
以下は正規分布の尤度関数と対数尤度関数です。対数をとった方がすっきりしています。
※$\prod$は大文字のパイ($\pi$)で総乗を示し、$\sum$(シグマ)の掛け算版です。$\prod$の展開は慣れないので理解しにくいですが、じっくりと考えればわかりました。
L(\mu, \sigma^2) = f(x_1, \cdots, x_N \mid \mu, \sigma^2)
= \prod_{i=1}^N\frac{1}{\sqrt{2 \pi} \sigma} \exp(-\frac{(x_i-\mu)^2}{2 \sigma^2}) \\
= (2 \pi \sigma^2)^{-\frac{N}{2}} \exp(-\frac{1}{2 \sigma^2} \sum_{i=1}^N(x_i - \mu)^2) \ \ ※尤度関数\\
l(\mu, \sigma^2) = -\frac{N}{2} \ln(2\pi) - \frac{N}{2} \ln \sigma^2 -\frac{1}{2\sigma^2} \sum_{i=1}^N(x_i-\mu)^2\ \ ※対数尤度関数
平均値$\mu$の推定値$\hat{\mu}$を求めるべく、対数尤度関数から$\mu$で微分した式の値を0とします。結果として算術平均の計算式となっています。
\begin{eqnarray}
\frac{\partial l(\mu, \sigma^2)}{\partial \mu} =
\frac{\partial }{\partial \mu}(\frac{1}{2\sigma^2}\sum_{i=1}^N(x_i-\mu)^2) & = & 0\\
-\frac{1}{2\sigma^2}\sum_{i=1}^N 2(x_i-\hat{\mu})(-1)) & = & 0\\
\sum_{i=1}^N x_i- \sum_{i=1}^N \hat{\mu} & = & 0\\
\therefore \hat{\mu} = \frac{1}{N}\sum_{i=1}^N x_i\\
\end{eqnarray}
今度は分散($\sigma^2$)の最尤推定をします。(不偏分散でない)分散になります。
\begin{eqnarray}
\frac{\partial l(\mu, \sigma^2)}{\partial \sigma^2} =
\frac{\partial }{\partial \sigma^2}(-\frac{N}{2} \ln \sigma^2 - \frac{1}{2 \sigma^2}\sum_{i=1}^N(x_i-\mu)^2) & = & 0\\
-\frac{N}{2} \frac{1}{\hat{\sigma}^2} -
\frac{1}{2} \frac{1}{(\hat{\sigma}^2)^2} (-1) \sum_{i=1}^N (x_i-\mu)^2& = & 0 \\
- \frac{N}{\hat{\sigma}^2} + \frac{1}{(\hat{\sigma}^2)^2} \sum_{i=1}^N (x_i-\mu)^2& = & 0 \\
\therefore \hat{\sigma}^2 = \frac{1}{N} \sum_{i=1}^N (x_i-\mu)^2\\
\end{eqnarray}
「はじパタ」勉強系記事リンク
| 章 | 項目 | 時間(h) | 難易度 | 学んだこと |
|---|---|---|---|---|
| 1 | はじめに | 8.9 | 特徴の型, 特徴空間, 次元の呪い | |
| 2 | 識別規則と学習法の概要 | 12 | ホールドアウト法,交差確認法 ,一つ抜き法 ,ブートストラップ法 ,バイアス・分散トレードオフ, 過学習 | |
| 3 | ベイズの識別規則 | 14.8 | ベイズ識別規則, ROC曲線 | |
| 4 | 確率モデルと識別関数 | 18 |
|
平均ベクトル, 共分散行列, 標準化, 無相関化, 白色化, 正規分布, 最尤推定 |
| 5 | k最近傍法(kNN法) | 8 |
|
最近傍法, ボロノイ境界, kNN |
| 6 | 線形識別関数(前半) | 30.4 |
|
正規方程式 |
| 6 | 線形識別関数(後半) | 前半に時間は含む |
|
フィッシャーの線形判別関数, 判別分析法, ロジスティック回帰 |
| 7 | パーセプトロン型学習規則 | 13.5 |
|
多層パーセプトロン, 誤差逆伝播法, シグモイド関数 |
| 8 | サポートベクトルマシン | 14.7 |
|
カーネルトリック, ν-SVM |
| 9 | 部分空間法 | 15.4 |
|
主成分分析, 特異値分解, CLAFIC法, カーネル主成分分析, カーネル部分空間法 |
| 10 | クラスタリング | 8.4 |
|
距離の公理, ミンコフスキー距離, K-平均法, 融合法, 混合正規分布モデル |
| 11 | 識別機の組み合わせによる性能強化 | 11.6 |
|
ノーフリーランチ定理, 決定木, バギング, アダブースト, ランダムフォレスト |