「はじめてのパターン認識」の第9章「部分空間法」の解説です。
前半の主成分分析や特異値分解は概要レベルで知っていましたが、部分空間法は全く知りませんでした。そして、第8章でやったカーネル法が主成分分析などでも使えるとは思ってもいませんでした。第8章のSVMが終わり、大きな山を超えたと勝手に思っていましたが、第9章も難しい・・・
※はじパタ勉強系は記事「文系社会人がはじパタで機械学習を数式含めて理解した奮闘記」にまとめました。
参考リンク
- はじめてのパターン認識 9章(前半)
- はじめてのパターン認識 第9章 9.5-9.6(slideshare): カーネル主成分分析で参考にしました。
- はじめてのパターン認識 9章: 数式参考
内容
**「部分空間」**という単語がさらっと出ていて、一見一般的な名詞に見えますが、数学的に少し勉強が必要な単語でした。私はマセマの「線形代数キャンパス・ゼミ」を使って勉強しました。「【線形空間編】部分空間と生成系」あたりは参考になります。
9.1 部分空間
d次元ベクトル空間Vの部分空間は以下のように定義されます。$x_1, \cdots, x_r(r \ge d)$をVのベクトルとし、$x_1, \cdots, x_r$の1次結合全体の集合である下記の式はVの部分空間です。
※「1次結合」の内容はリンク先が参考になります。
W = \{ a_1 x_1 + \cdots + a_r x_r | a_i \in \mathbb{R}, i = 1, \ldots , r \}
上記式の集合の縦棒の右側は、縦棒の左側で示した集合のための前提を示します(リンク先 wiki参照)。
Wが$x_1, \cdots, x_r$で貼られるr次元の部分空間であるとは、$x_1, \cdots, x_r$は1次独立(線形独立)、つまりどの$x_i$も他のr-1個の$x_j(j \ne i)$の線形独立で表すことができない、ということです。
部分空間の定義からWがVの部分空間であるための必要十分条件は以下の3つです。
(1) \ \ W \ne \emptyset \\
(2) \ \ x, y \in W \Rightarrow x + y \in W\\
(3) \ \ x \in W, \lambda \in \mathbb{R} \Rightarrow \lambda x \in W\\
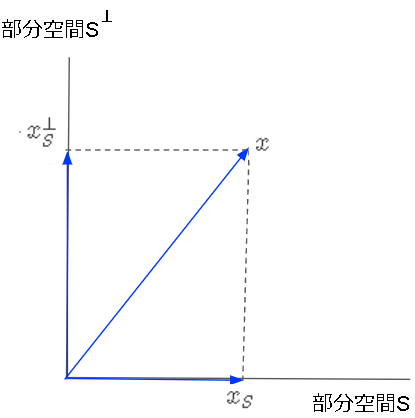
ベクトル空間Vは、部分空間Sと**直交する部分空間$S^{\perp}$**に分解でき、$V = S \cup S^{\perp}, S \cap S^{\perp} = \emptyset$が成り立ちます。
※$\perp$は直交している、という意味
任意のベクトルxは2つの直交する部分空間の成分を持ち、$x=x_S + x_S^{\perp}$のように分解できます。
以下のグラム・シュミットの正規直交化を使って部分空間の正規直交化基底を求めることができます。
(1)n_1 = \frac{x}{||x_1||} に設定 \\
(2)i > 1で順次以下の繰り返し \\
\widetilde{n}_i = x_i - \sum_{j = 1}^{i - 1} (n_j^T x_i) n_j, \;\;
n_i = \frac{\widetilde{n}_i}{|| \widetilde{n}_i||}
※本に出てくるQR分解については「ハウスホルダー(Householder)変換を用いたQR 分解(factorization) 」がわかりやすいです。
9.2 主成分分析
主成分分析は学習データの分散最大化できる方向への線形変換を求める手法です。4つのデータでイメージ図を書いてみました。
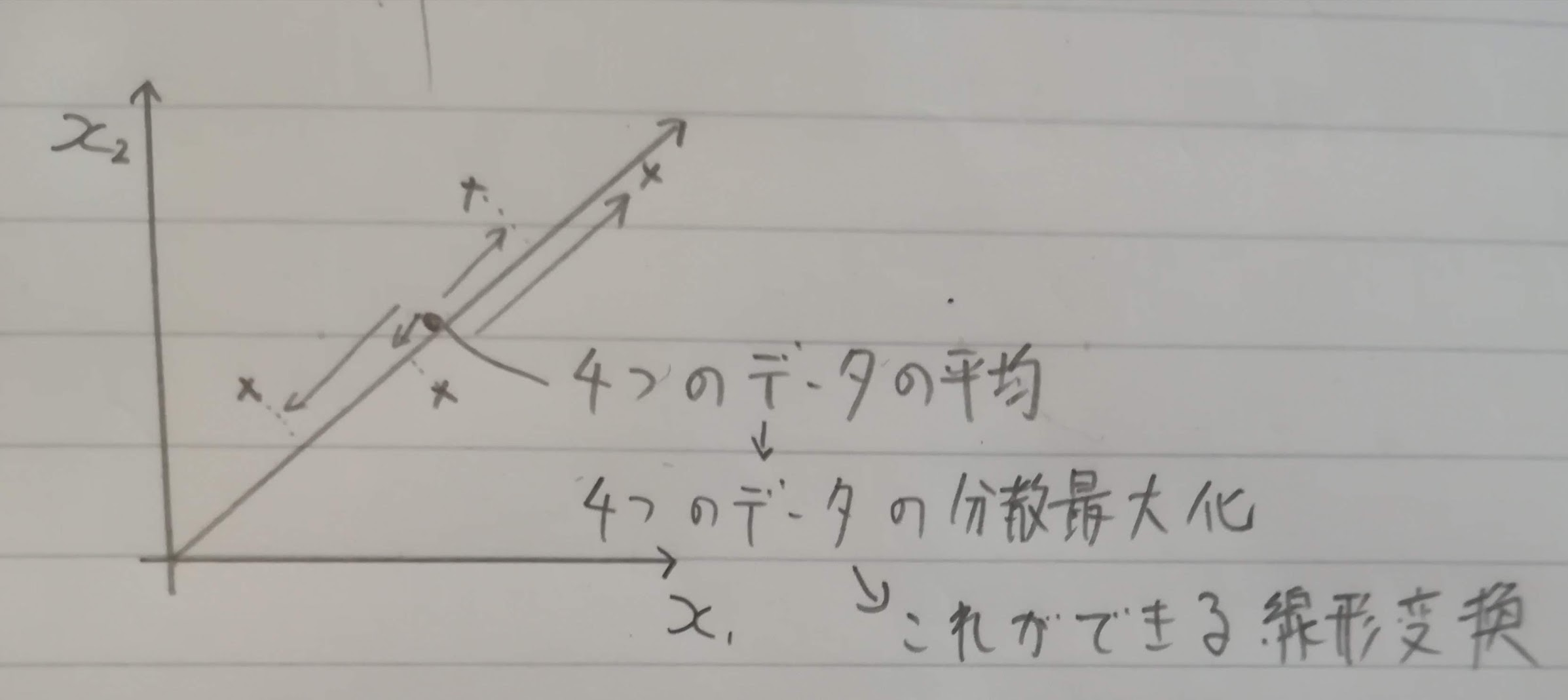
基本的には4章の無相関化と同じです(無相関化では主成分分析と異なり次元縮約はしません)。
では、主成分分析の計算方法です。前提となるデータなどの定義は以下のとおりです。
\begin{eqnarray}
学習データ:& \ \ x_i=& (x_{i1}, \ldots, x_{id})^T (i=1, \ldots, N)\\
N個のデータ行列:& \ \ X = & (x_1, \ldots, x_N)^T\\
平均ベクトル:& \ \ \overline{x}=& (\overline{x}_1, \ldots, \overline{x}_d)^T\\
データ行列-平均ベクトル:& \ \ \overline{X}=& (x_1-\overline{x}, \ldots, x_N-\overline{x})^T\\
\end{eqnarray}
共分散行列は以下の定義(不偏推定値だと分母にN-1だが、機械学習の世界ではデータ数が多く1程度は大差ないのでN)。
\Sigma = Var\{ \overline{X}\} = \frac{1}{N} \overline{X}^T \overline{X}
N個でのデータ$x_1-\overline{x}$を係数ベクトル$a_j=(a_{j1}, \ldots, a_{jd})^T(j=1, \ldots, d)$を使って線形変換をし$s_j$とします。
s_j=(s_{1j}, \ldots, s_{Nj})^T=\overline{X}a_j
この変形後のデータの分散は$s_{1j}, \ldots, s_{Nj}$の平均が0となるので以下の式で表せます。
Var\{s_j\} = \frac{1}{N}s_j^T s_j
= \frac{1}{N} (\overline{X} a_j)^T \overline{X} a_j
= \frac{1}{N} a_j^T \overline{X}^T \overline{X} a_j
= a_j^T Var\{\overline{X}\} a_j
この分散を最大にする射影ベクトルは、係数ベクトル$a_j$のノルムを1と制約した以下のラグランジュ関数を最大にする$a_j$を見つけることです(λはラグランジュ未定乗数)。
E(a_j) = a_j^T Var\{\overline{X}\} a_j - \lambda (a_j^T a_j - 1)
\frac{\partial E(a_j)}{\partial a_j}
= 2Var\{\overline{\bf X}\} a_j - 2 \lambda a_j = 0 \ \
\because \frac{\partial x^T Bx}{\partial x}=2Bx(巻末付録)\\
\therefore Var\{\overline{\bf X}\} a_j = \lambda a_j
これは元データの共分散行列に関する固有値問題を解くことで、分散が最大になる射影ベクトル$a_j$が得られることを意味しています。以下の3つのページを見ると理解できました。
- 主成分分析と固有値問題: 詳しく主成分分析と固有値問題を解説してくれている
- 主成分分析 (1) - 2変量の主成分分析: 主成分分析の基礎
- 主成分分析 (2) - 主成分の導出と意味: 主成分分析の導出
この問題を解いて得られる固有値を$\lambda_1 \ge \ldots \ge \lambda_d$とし、対応する固有ベクトルを$a_1, \ldots, a_d $とします。共分散行列は実対称行列(複素数を使っていない対称行列)なので固有ベクトルは相互に直行し、以下が成り立ちます$\delta_{ij}$はクロネッカーのデルタ)。
※クロネッカーのデルタはに変数関数(乱暴に言うと場合分け)で、記事「クロネッカーのデルタについてわかりやすく解説する」がわかりやすいです。
a_i^T a_j=\delta_{ij} = \begin{cases}
1 & (i=j) \\
0 & (i \ne j)
\end{cases}
元データの共分散行列はd×d行列なので、得られるゼロでない固有値の数は共分散行列の連絡で決まり、最大dです。最大固有値に対応する固有ベクトルで線形変換した特徴の分散は以下の式です。
\begin{eqnarray}
Var\{s_1\}& = & a_1^T Var\{\overline{X}\} a_1\\
& = & a_1^T \lambda_1 a_1 \ \ \because Var\{\overline{\bf X}\} a_j = \lambda a_j\\
& = & \lambda_1 a_1^T a_1 \ \ \because \lambda_1はスカラなので順番変更\\
& = & \lambda_1 \ \ \because クロネッカーのデルタより \\
\end{eqnarray}
つまり線形変換後の特徴の分散は最大固有値と一致します。最大固有値に対応する固有ベクトルで線形変換された特徴量を第1主成分と言い、k番目の固有値に対応する固有ベクトルで変換された特徴量を第k主成分と言います。変換後の特徴量の分散は固有値に一致するため、全分散量は以下の式で、元データの全分散量と同一です。
V_{total} = \sum_{i = 1}^d \lambda_i
第k成分の分散の全分散に対する割合を寄与率と言います。
c_k = \frac{\lambda_k}{V_{total}}
第k成分までの累積寄与率は以下の式です。
r_k = \frac{\sum_{i=1}^k \lambda_i}{V_{total}}
9.3 特異値分解
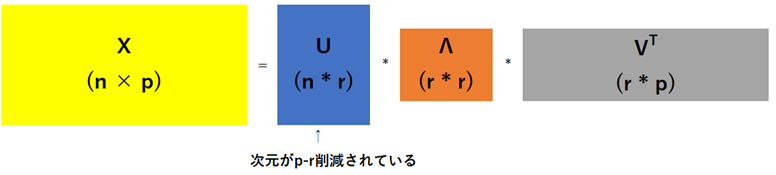
主成分分析に関連した行列分解法に**特異値分解(SVD; singular value decomposition)**があります。任意のn × p行列Xを以下のように3つの行列の積に分解します。
※Λは大文字ラムダ(大文字エーではない)
\begin{eqnarray}
X & = &U \Lambda V^T& \\
& = & (u_1 u_2 ... u_p)
{ \left(
\begin{array}{cccc}
\sqrt{λ_1} & 0 & \ldots & 0 \\
0 & \sqrt{λ_2} & \ldots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \ldots & \sqrt{λ_p}
\end{array}
\right)
\left(
\begin{array}{cccc}
\upsilon^T_1 \\
\upsilon^T_2 \\
\vdots \\
\upsilon^T_p
\end{array}
\right)
}
\end{eqnarray}
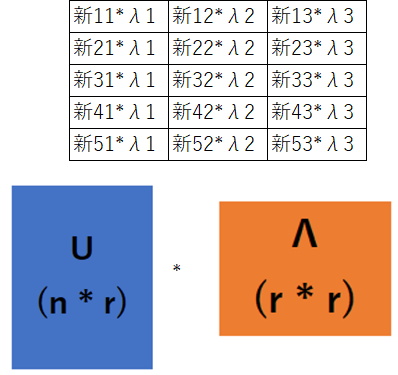
ここのUが求めるべき次元削減の結果です。はじパタ上では、まだ次元を減らす話をしていないので、下図のrの部分をpとして解説しています。
参考書によっていくつか行列の書き方があるようですが、本質的には同じです(リンク先がわかりやすい)。
$X = U \Lambda V$のVを除いて表してみました。次元(特徴)が3つに削減されたUに固有値平方根の対角行列(Λ)を掛けます。
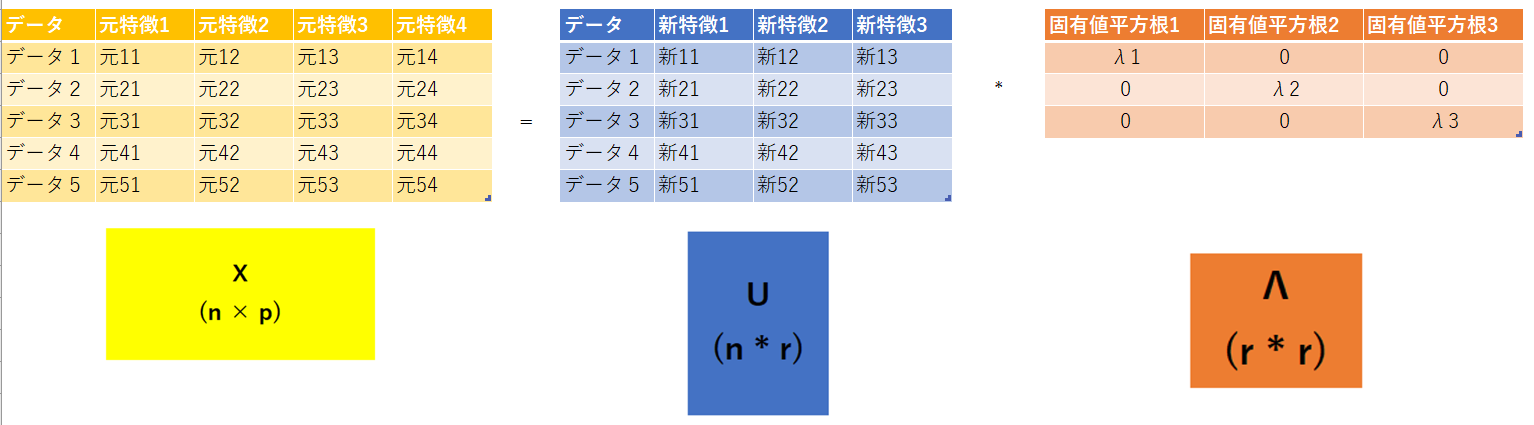
これによりUΛは新特徴と固有値平方根の乗算となりますが、Λは固有値の大きい順に並べているため、影響度の大きい特徴が残ります。
特異値分解は以下の解説がわかりやすく、詳しくここで書かないようにします。
- 特異値分解を詳しく解説: 分解方法を絵でわかりやすく解説してくれている
- SVD(特異値分解)解説: どう活用するのかをわかりやすく解説してくれている
- 特異値分解の定義,性質,具体例: シンプルな具体例があり、わかりやすい
9.4 部分空間法
9.4.1 部分空間法とは
部分空間法は、クラスごとに部分空間を構成する正規直交基底を学習データから求め、入力データを各クラスの部分空間に射影して識別します。クラスごとの独立した部分空間を構成させるので、多クラス識別が容易にできます。また、特徴数が大きくても次元の少ない部分空間へ射影計算をするので、計算量が少ないです。
部分空間法には、相関行列または共分散行列を使う方法があります。相関行列の場合は、**CLAFIC法(class-feature information compression)**があります。相関行列と共分散行列に関しては「相関行列の定義と分散共分散行列との関係」を参照ください。
相関行列の場合は原点から見たデータのばらつきを評価します。各部分空間の原点は共通してデータベクトルの原点です。一方、共分散行列の場合は各クラスの平均ベクトルとなります。下図に概念を書きました(SはSubspace(部分空間)の略っぽい)。
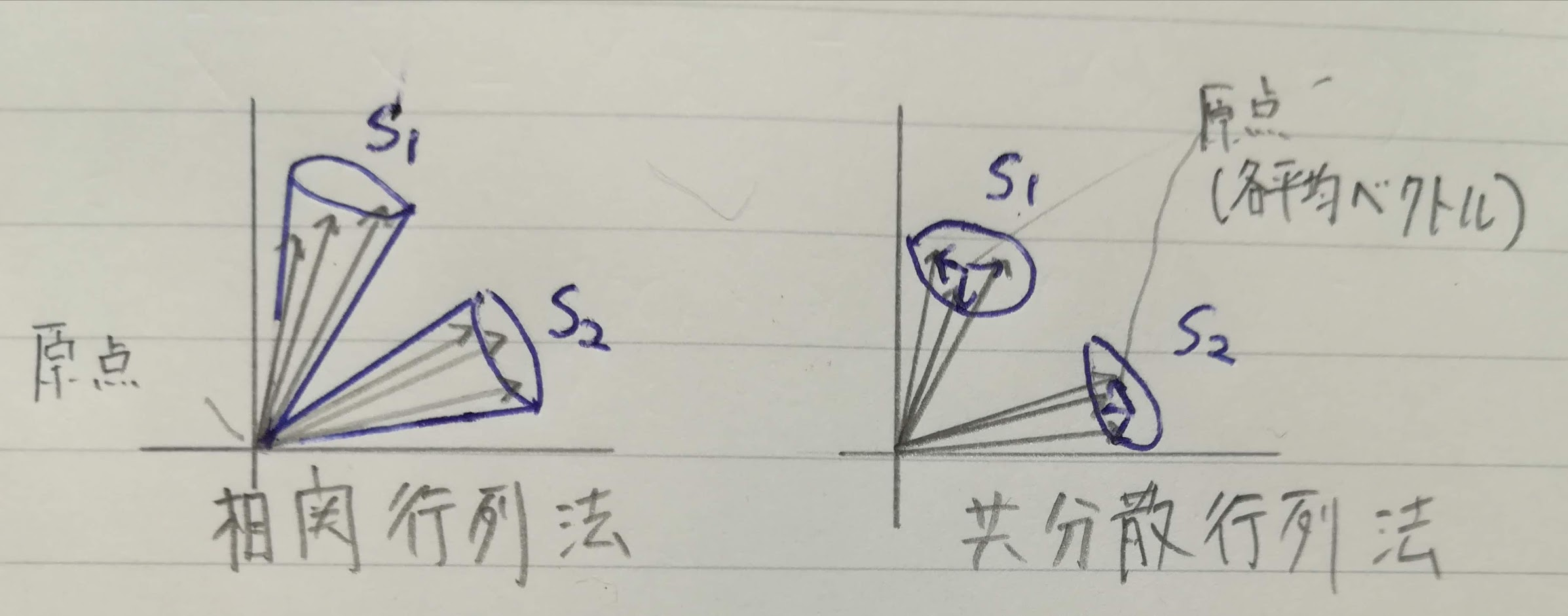
基本的な原理は同じで、識別性能もあまり変わらないらしいです。
9.4.2 CLAFIC法
まず、部分空間への正射影ということで以下のスライドを念頭に置きます(「例題ではじめる部分空間法」のスライド15)。
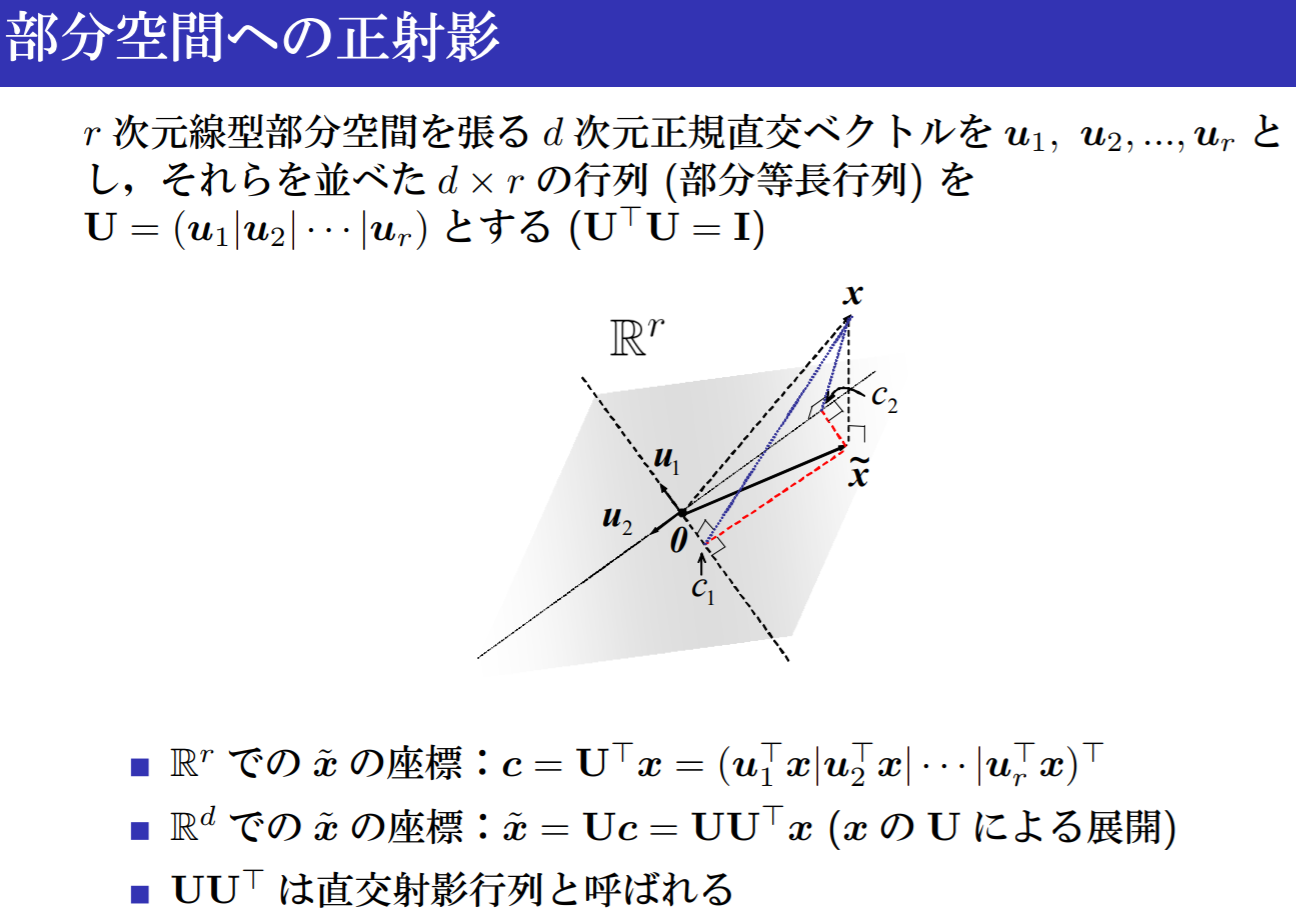
データ$x \in \mathbb R^d$はKこのクラス$C_1, \ldots, C_K$のどれかに属するもとのします。クラスごとの部分空間を$S_1, \ldots, S_k$とし、クラスiの部分空間$S_i$を張る基底ベクトルを以下で表します。
\{u_{i1}, \ldots, u_{id_i}\}
$d_i$は部分空間$S_i$の次元です。基底ベクトルは、xがi番目のクラスに属しているとき、部分空間$S_i$へ正射影した長さの期待値が最大になるように$||u_{ij}||=1$の制約下で選択します。
\begin{eqnarray}
E \{ \sum_{j = 1}^{d_i} (x^T u_{ij})^2 | x\in C_i \}
& = & E \{\sum_{j = 1}^{d_i} (x^T u_{ij}) (x^T u_{ij})^T | x \in C_i \}\\
& = & E \{ \sum_{j = 1}^{d_i} x^T u_{ij} u_{ij}^T x | x \in C_i \} \\
& = & E \{ x^T ( \sum_{j = 1}^{d_i} u_{ij} u_{ij} ) x | x \in C_i \} \\
& = & E \{ x^T P_i x | x \in C_i \} \\
\end{eqnarray}
最後の式の$P_i = \sum_{j = 1}^{d_i} u_{ij} u_{ij}^T$はクラスiの射影行列と呼びます。射影行列を使った部分空間法の識別規則は以下のとおりです。
全てのj≠iについてx^T P_j x < x^T P_i xであればx \in C_i
「例題ではじめる部分空間法」のスライド22と同じですが、以下が「期待値が最大」の場合に識別できる理由です。最も長ければ部分空間の集合と近似しているためです。
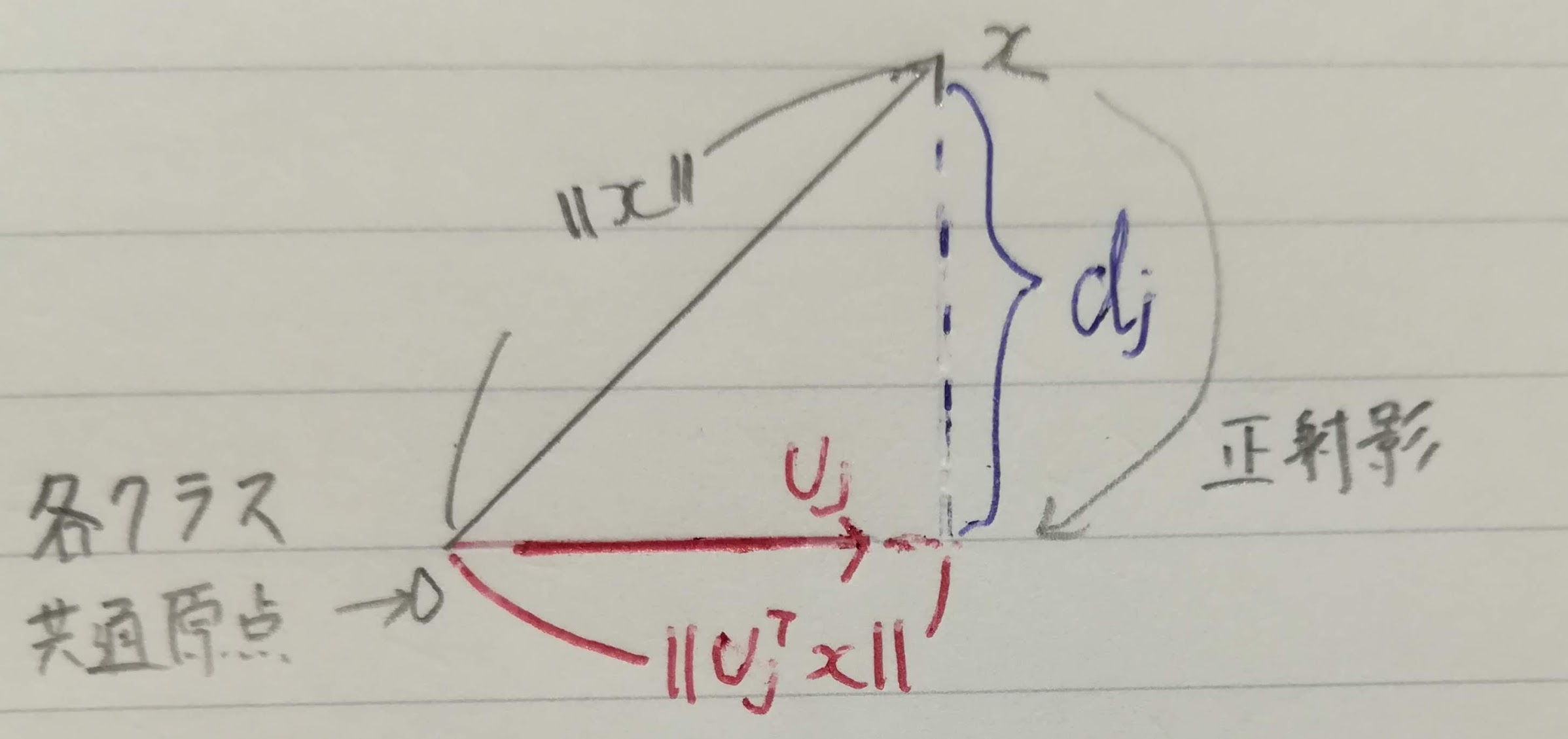
射影行列の性質は以下の3つがあります。
- べき等律: $P_i^2=P_i$
- 対称行列: $Pi^T=P_i$
- ランク1: 要素行列$u_{ij} u_{ij}^T$のランクは1
射影行列は部分空間と等しいです。なぜなら、ベクトルxの部分空間$S_i$への正射影$\widetilde{x}$は以下の式のように射影行列との積で表すことができるからです。
\widetilde{x} =
\sum_{j = 1}^{d_i} (x^T u_{ij}) u_{ij}
= \sum_{j = 1}^{d_i} (u_{ij} u_{ij}^T) x
= P_i x
xと$S_i$への正射影$\widetilde{x}$との差を残差ベクトルと言います。
\hat{x} = x - \widetilde{x}
残差ベクトルを$S_i$へ正射影すると、以下のように0となり、残差ベクトルと部分空間$S_i$は直交します。
\begin{eqnarray}
P_i \hat{x} & = & P_i (x - \widetilde{x})\\
& = & P_i x - P_i \widetilde{x}\\
& = & P_i x - P_i P_i x \ \ \because x = P_i \widetilde{x}\\
& = & P_i x - P_i^2 x\\
& = & 0 \ \ \because べき等律 P_i^2 = P_i\\
\end{eqnarray}
では、$E \{ x^T P_i x | x \in C_i \} $で制約条件を満たすi番目の部分空間の基底ベクトルをラグランジュ関数で表します。ここで$Q_i$はクラス$C_i$に属する学習ベクトルで構成された相関行列$E \{ x^T x | x \in C_i \} $です。
\begin{eqnarray}
L_i (u_{ij}) & = & \sum_{j = 1}^{d_i} E \{(x^T u_{ij})^2 \} - \sum_{j = 1}^{d_i} \lambda_{ij} (u_{ij}^T u_{ij} - 1)\\
& = & \sum_{j = 1}^{d_i} u_{ij}^T E\{ x^T x | x \in C_i \} u_{ij} - \sum_{j = 1}^{d_i} \lambda_{ij} (u_{ij}^T u_{ij} - 1)\\
& = & \sum_{j = 1}^{d_i} u_{ij}^T Q_i u_{ij} - \sum_{j = 1}^{d_i} \lambda_{ij} (u_{ij}^T u_{ij} - 1)\\
\end{eqnarray}
ラグランジュ関数を$u_{ij}$で微分して0とすることで最大化問題を解きます。これでi番目のクラス相関行列に関する固有値問題を得ることができます。
\begin{eqnarray}
\frac{\partial L_i(u_{ij})}{\partial u_{ij}} & = & 2 Q_i u_{ij} - 2 \lambda_{ij} u_{ij}
\ \ \because \frac{\partial x^T B x}{\partial x}=2Bx(巻末付録の対称行列ベクトル微分)\\
& = & 0\\
\end{eqnarray}
\\
\therefore Q_i u_{ij} = \lambda_{ij} u_{ij}
$Q_i$の固有値を$\lambda_{i1} \ge \ldots \ge \lambda_{id_i}$として、$\lambda_{ij}$に対応する固有ベクトルを$u_{ij}$とします。i番目のクラスのデータxのj番目の基底への射影の長さの2乗の期待値は以下のようにj番目の固有値と等しいです。
\begin{eqnarray}
u_{ij}^T Q_i u_{ij} & = & u_{ij}^T \lambda_{ij} u_{ij} \\
& = & \lambda_{ij} u_{ij}^T u_{ij}\\
& = & \lambda_{ij} \ \ \because ||u_{ij}|| = 1\\
\end{eqnarray}
$Q_i$から求めたi番目のクラスの固有ベクトルは正規直行規定なので、$d_i$個の規定ベクトルで張られる部分空間への$x \in C_i$の射影の長さの2乗の期待値は個々の基底への射影の和で表現でk、以下の式となります。
\begin{eqnarray}
\sum_{j = 1}^d u_{ij}^T Q_i u_{ij} & = & E\{x^T P_i x | x \in C_i \}
\ \ \because 最初に定義したの最大化する正射影した長さの期待値 \\
& = & E\{||P_i x||^2 | x \in C_i \}
\ \ \because 部分空間への射影の長さの2乗の期待値は個々の基底への射影の和\\
& = & \sum_{j = 1}^{d_i} \lambda_{ij}\\
\end{eqnarray}
つまり、部分空間の次元$d_i$をいくつとするかによって射影される長さが異なります(多いほど長くなります)。所属クラスが次元の大きさによって変えたくないので、固有値の累積値$a(d_i) = \sum_{j = 1}^{d_i} \lambda_{ij}$を使って、部分空間の次元を決める方法が提案されています。
各クラスの部分空間に共通なパラメータκを導入して、$a(d_i - 1) \leq \kappa < a(d_i)$を満たす$d_i$をi番目のクラスの部分空間の次元として採用します。κは忠実度(fidelity value)と呼ばれます。これにより、各クラスに属する学習データの射影長の期待値は一定にそろいます。κの値は交差確認法などで決める必要があります。
部分空間法のよい点は、クラスデータのみを用意すれば、そのクラスの部分空間が構成でき、識別機として使用できることです。しかし、道のパラメータに対する射影長が短ければリジェクトする必要があります。以下の値が、あるしきい値よりも小さい場合はリジェクトします。
\max_i[\frac{x^T P_i x}{x^T x}]
部分空間法はクラス間の重なりは考慮されていないので、例えば「大」と「犬」の区別に弱いです。クラス間の重なりを考慮した部分空間法として混合類似度法や差別部分空間法などがあります。また、入力をベクトルから部分空間へ拡張した相互部分空間法などがあります。
部分空間法の参考リンク
9.5. カーネル主成分分析
主成分分析を第8章で学習したカーネル法を使い、非線形特徴空間で行うことができます。学習データを$x_i \in \mathbb R^d(i=1, \ldots, N)$とし、非線形特徴変換を$\varphi(x_i): x_i \in \mathbb R^d \rightarrow \varphi(x_i) \in \mathbb R^M(M>d)$とします(カーネル関数によって特徴数が増えています)。$\sum_{i=1}^N \varphi(x_i)=0$(非線形特徴ベクトルの平均が0)が成立すればM×M共分散行列
C=\frac{1}{N} \sum_{i=1}^N \varphi(x_i) \varphi(x_i)^T
の固有値問題$C \nu_m=\lambda_m \nu_m$より、主成分$\lambda_m$と固有ベクトル$\nu_m \in \mathbb R^M$を得ることができます。
しかし、問題が2点あります。
- $\sum_{i=1}^N \varphi(x_i)=0$(非線形特徴ベクトルの平均が0)が保証されない
- カーネルトリックの内積計算で、M次元空間ではなくd次元空間の計算で、高次元非線形特徴空間の主成分を得られるか?
問題1に関しては、以下のように$\varphi(x_i)$の平均との差を取ることにより、$\widetilde{\varphi}(x_i)$の平均を0にできます。
\widetilde{\varphi}(x_i) = \varphi(x_i) - \frac{1}{N} \sum_{j=1}^N \varphi(x_j)
問題2に関して、以下で確認していきます。
問題1対応のため平均を0にした$\widetilde{\varphi}(x_i)$のN×Nグラム行列K(x, x)の(n, k)要素は以下の通り。
※グラム行列はこちらで確認しましょう。
\begin{eqnarray}
\widetilde{K}(x_n, x_k)& = & \widetilde{\varphi}(x_n)^T \widetilde{\varphi}(x_k)\\
& = & (\varphi(x_n) - \frac{1}{N} \sum_{j=1}^N \varphi(x_j))^T
(\varphi(x_k) - \frac{1}{N} \sum_{l=1}^N \varphi(x_l))\\
& = & (\varphi(x_n)^T - \frac{1}{N} \sum_{j=1}^N \varphi(x_j)^T)
(\varphi(x_k) - \frac{1}{N} \sum_{l=1}^N \varphi(x_l))\\
& = & \varphi(x_n)^T \varphi(x_k)
- \frac{1}{N} \sum_{l=1}^N \varphi(x_n)^T \varphi(x_l)
- \frac{1}{N} \sum_{j=1}^N \varphi(x_j)^T \varphi(x_k)
+ \frac{1}{N^2} \sum_{l=1}^N \sum_{j=1}^N \varphi(x_l)^T \varphi(x_j)^T\\
& = & K(x_n, x_k)
- \frac{1}{N} \sum_{l=1}^N K(x_n, x_l)
- \frac{1}{N} \sum_{j=1}^N K(x_j, x_k)
- \frac{1}{N^2} \sum_{l=1}^N \sum_{j=1}^N K(x_l, x_j)
\end{eqnarray}
つまり、$\frac{1}{N}$を全要素とするN×N行列を$1_{NN}$とすると以下の計算ができ、$\widetilde{K}$はKで表すことができます。これにより、問題2「カーネルトリックの内積計算で、M次元空間ではなくd次元空間の計算で、高次元非線形特徴空間の主成分をカーネルトリックを得ることができ」ます。
\widetilde{K} = K - 1_{NN}K - K 1_{NN} + 1_{NN} K 1_{NN}
では、品線形変換をして平均0にした学習データを並べた行列を以下とします。
X_{\widetilde{\varphi}}=(\widetilde{\varphi}(x_i), \ldots, \widetilde{\varphi}(x_N)) \in \mathbb R^{M \times N}
ここで特異値分解で$X_{\widetilde{\varphi}}=U \Lambda V^T$を求めます。
特異値分解を変形して$U=X_{\widetilde{\varphi}} V \Lambda^{-1}$にして表します。
{\begin{eqnarray}
U & = & X_{\widetilde{\varphi}} V \Lambda^{-1} & \\
(u_1, \ldots, u_r)& = & (X_{\widetilde{\varphi}} v_1, \ldots, X_{\widetilde{\varphi}} v_r)
{ \left(
\begin{array}{cccc}
\frac{1}{\sqrt{λ_1}} & 0 & \ldots & 0 \\
0 & \frac{1}{\sqrt{λ_2}} & \ldots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \ldots & \frac{1}{\sqrt{λ_r}}
\end{array}
\right)}\\
& = & (\frac{1}{\sqrt{λ_1}} X_{\widetilde{\varphi}} v_1, \ldots, \frac{1}{\sqrt{λ_r}} X_{\widetilde{\varphi}} v_r) \\
\end{eqnarray}
}
つまり、i番目の主成分要素は以下の式で表されます。
u_i = \frac{1}{\sqrt{λ_i}} X_{\widetilde{\varphi}} v_i
非線形変換と平均0化をした特徴ベクトル$\widetilde{\varphi}$を$u_i$への射影は以下の式です。
{\begin{eqnarray}
u_i^T \widetilde{\varphi}(x) & = &
(\frac{1}{\sqrt{λ_i}} X_{\widetilde{\varphi}} v_i)^T \widetilde{\varphi}(x) \\
& = & \frac{1}{\sqrt{λ_i}} v_i^T X_{\widetilde{\varphi}}^T\widetilde{\varphi}(x) \\
& = & \frac{1}{\sqrt{λ_i}} v_i^T
{ \left(
\begin{array}{cccc}
\widetilde{\varphi}(x_1)^T \widetilde{\varphi}(x) \\
\vdots \\
\widetilde{\varphi}(x_N)^T \widetilde{\varphi}(x) \\
\end{array}
\right)}\\
& = & \frac{1}{\sqrt{λ_i}} v_i^T
{ \left(
\begin{array}{cccc}
\widetilde{K}(x_1, x) \\
\vdots \\
\widetilde{K}(x_N, x) \\
\end{array}
\right)}\\
& = & \frac{1}{\sqrt{λ_i}} v_i^T \widetilde{K}(X, x)\\
\end{eqnarray}}
d次元空間での内積カーネル計算とr回のN次元ベクトルの内積計算で、すべての基底方向への射影を求めることができます。
9.6. カーネル部分空間法
CLAFIC法も内積カーネルを使って非線形特徴空間内の部分空間法へ拡張できます。流れとしては、主成分分析の内積カーネル使用と似ています。違うのは、主成分分析は中心化(平均0化)をしましたが、CLAFIC法は相関行列を使うのでその必要がない点です。
今回は詳しい解説を省略します・・・
「はじパタ」勉強系記事リンク
| 章 | 項目 | 時間(h) | 難易度 | 学んだこと |
|---|---|---|---|---|
| 1 | はじめに | 8.9 | 特徴の型, 特徴空間, 次元の呪い | |
| 2 | 識別規則と学習法の概要 | 12 | ホールドアウト法,交差確認法 ,一つ抜き法 ,ブートストラップ法 ,バイアス・分散トレードオフ, 過学習 | |
| 3 | ベイズの識別規則 | 14.8 | ベイズ識別規則, ROC曲線 | |
| 4 | 確率モデルと識別関数 | 18 |
|
平均ベクトル, 共分散行列, 標準化, 無相関化, 白色化, 正規分布, 最尤推定 |
| 5 | k最近傍法(kNN法) | 8 |
|
最近傍法, ボロノイ境界, kNN |
| 6 | 線形識別関数(前半) | 30.4 |
|
正規方程式 |
| 6 | 線形識別関数(後半) | 前半に時間は含む |
|
フィッシャーの線形判別関数, 判別分析法, ロジスティック回帰 |
| 7 | パーセプトロン型学習規則 | 13.5 |
|
多層パーセプトロン, 誤差逆伝播法, シグモイド関数 |
| 8 | サポートベクトルマシン | 14.7 |
|
カーネルトリック, ν-SVM |
| 9 | 部分空間法 | 15.4 |
|
主成分分析, 特異値分解, CLAFIC法, カーネル主成分分析, カーネル部分空間法 |
| 10 | クラスタリング | 8.4 |
|
距離の公理, ミンコフスキー距離, K-平均法, 融合法, 混合正規分布モデル |
| 11 | 識別機の組み合わせによる性能強化 | 11.6 |
|
ノーフリーランチ定理, 決定木, バギング, アダブースト, ランダムフォレスト |