SVD(Singular Value Decomposition、特異値分解)について解説します。
- SVDとは
- どう使うのか
- ちょっと証明
SVDとは
ある行列 $A$ があって、これを
A = U \Sigma V^{\mathrm{T}}
と分解します。
$U$ 、 $V$ は直交行列、 $\Sigma$ は対角行列です。
詳しく書くと、
A = (\boldsymbol{u}_1, \boldsymbol{u}_2, \cdots, \boldsymbol{u}_n)
\begin{pmatrix}
\sigma_1 & & & \\
& \sigma_2 & & \\
& & \ddots & \\
& & & \sigma_n
\end{pmatrix}
\begin{pmatrix}
\boldsymbol{v}_1^{\mathrm{T}} \\
\boldsymbol{v}_2^{\mathrm{T}} \\
\vdots \\
\boldsymbol{v}_n^{\mathrm{T}}
\end{pmatrix}
となります。
$\sigma$ は特異値といって、
\sigma_1 \geq \sigma_2 \geq \cdots \geq \sigma_n
という条件を満たすように選ぶことができます。
どう使うのか
ここの説明は、『ゼロから作る Deep Learning 2』斎藤 康毅 を参考にしています。
SVDは、主に次元削減に用いられます。
ここでは、LSA(Latent Semantic Analysis、潜在意味解析)と呼ばれる手法において、単語ベクトルを次元削減する例を考えます。
単語の特徴を表すベクトルを得たいとします。
そのために、「似たような文脈で出てくる単語は似たような特徴を持つ」という仮定をおきます。
例えば、
「彼は犬を飼っている。」
「彼は猫を飼っている。」
のように、同じような単語に挟まれて出てくる「犬」と「猫」は、似たような特徴を持つ、と考えます。
これをベクトルにしたいので、前後n単語に出てくる単語群をカウントしていきます。
ここではn=2として考えます。
例えば、「犬」に注目すると、

の前後2単語なので、「彼」「は」「を」「飼って」が1、他の単語が0、というようにベクトルを作ることができます。

これをたくさんの文章について足し合わせていくことで、同じような単語に挟まれて出てくる単語群は、ベクトルの値が近くなっていることが期待できます。
さて、このままでは「は」とか「を」のベクトルの値が大きくなりすぎて、他の単語の値の違いがほとんど見えなくなってしまうので、TF-IDFやPPMIなど、単語の出現確率で正規化したりするのですが、SVDから離れてしまうので省略。
詳しくは『ゼロから作る Deep Learning 2』斎藤 康毅 を参照してください。
こうして作ったベクトルは、文章に出てくる語彙数のぶんだけ次元を持ちます。
たとえば、10万の単語が出てくる文章でベクトルを作ったとすると、10万次元のベクトルが出来上がることになります。
ただし、実際に、10万の次元を持つベクトルを扱うというのはあまり現実的ではありません。
ほとんどの値は0になることを考えると、それぞれの次元の重要度は高くないことが推測できます。
こうした冗長な表現を削って、コンパクトなベクトルで表してやるために、SVDを使います。
得られたベクトルを並べて、表形式で書くと、

これの行が得られたベクトルだとします。
つまり、犬に対応するベクトルは、
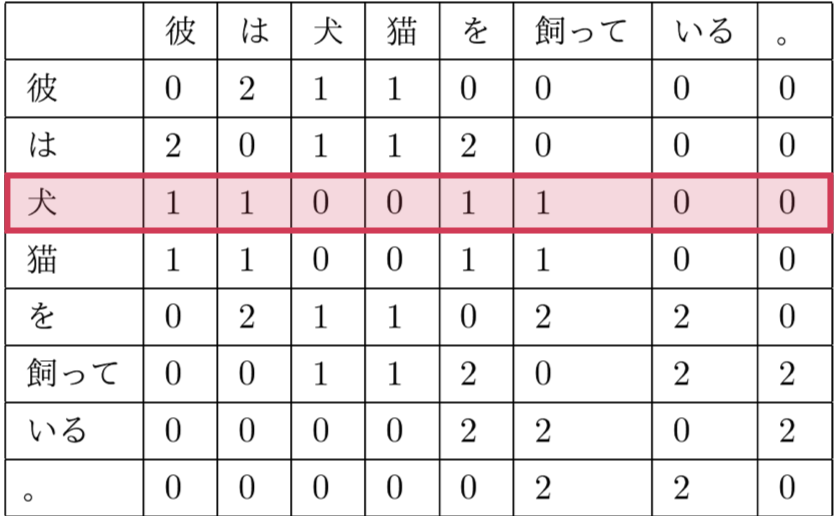
これを行列 $A$ とおいて、次元削減していきます。
$A$ にSVDを適用すると、以下のようになります。

ここで最終的に出てくるベクトル表現の行列は $U$ に相当します。

さて、特異値 $\sigma$ は、対応する軸の「重要度」みたいなものを表します。
どういうことかというと、例えば $\sigma_2$ を考えたときは、 $A$ を計算するときの貢献は、2番目の軸との掛け算で出てきます。

つまり、 $\sigma$ の値が大きければ大きいほど、その軸が $A$ を表すのに重要である、と考えることができます。
これを $\sigma$ の値の小さい順に軸を減らしていけば、得られる $U$ は、もとの $A$ のコンパクトな表現になっています。

ちょっと証明
ある行列 $A$ が、
A = U \Sigma V^{\mathrm{T}}
のように分解できることを示します。
固有値の数がどうこう、みたいなめんどくさいことは考えずに、雰囲気理解をめざします。
まず、任意の行列 $A$ について、 $AA^{\mathrm{T}}$ と $A^{\mathrm{T}}A$ の固有値が共通になることを示します。
$AA^{\mathrm{T}}$ に対応する固有ベクトルを $\boldsymbol{u}$ 、固有値を $\lambda$ と表すと、
AA^{\mathrm{T}} \boldsymbol{u}_1 = \lambda_1 \boldsymbol{u}_1 \\
AA^{\mathrm{T}} \boldsymbol{u}_2 = \lambda_2 \boldsymbol{u}_2 \tag{1}\\
\vdots
というふうに書けます。( $\boldsymbol{u}$ は単位ベクトルになるように選びます。)
これに、左から $A^{\mathrm{T}}$ を掛けて、
A^{\mathrm{T}}AA^{\mathrm{T}} \boldsymbol{u}_1 = A^{\mathrm{T}} \lambda_1 \boldsymbol{u}_1 \\
A^{\mathrm{T}}A(A^{\mathrm{T}} \boldsymbol{u}_1) = \lambda_1 (A^{\mathrm{T}} \boldsymbol{u}_1) \tag{2}
と考えると、 $\lambda_1$ が $A^{\mathrm{T}}A$ の固有値にもなっていることがわかります。
同様に繰り返すことで、 $AA^{\mathrm{T}}$ と $A^{\mathrm{T}}A$ の固有値が共通になることが示せます。
さて、 $A^{\mathrm{T}}A$ の固有ベクトルを $\boldsymbol{v}$ と書くことにすると、
A^{\mathrm{T}}A \boldsymbol{v}_1 = \lambda_1 \boldsymbol{v}_1 \tag{3}
と書けるので、 $\lambda_1$ に対応する $\boldsymbol{v}$ は、$(2)$、$(3)$から、
\boldsymbol{v}_1 = \theta_1 A^{\mathrm{T}} \boldsymbol{u}_1 \tag{4}
と書けます。
ここで、 $\boldsymbol{v}$ が単位ベクトルになるように、 $\theta_1$ という定数を掛けています。
これを順番に並べて行列にすると、
\begin{align}
(\boldsymbol{v}_1, \boldsymbol{v}_2, \cdots, \boldsymbol{v}_n) &=
(A^{\mathrm{T}}\boldsymbol{u}_1, A^{\mathrm{T}}\boldsymbol{u}_2, \cdots, A^{\mathrm{T}}\boldsymbol{u}_n)
\begin{pmatrix}
\theta_1 & & & \\
& \theta_2 & & \\
& & \ddots & \\
& & & \theta_n
\end{pmatrix} \\
&= A^{\mathrm{T}}(\boldsymbol{u}_1, \boldsymbol{u}_2, \cdots, \boldsymbol{u}_n)
\begin{pmatrix}
\theta_1 & & & \\
& \theta_2 & & \\
& & \ddots & \\
& & & \theta_n
\end{pmatrix}
\end{align}
より、
V = A^{\mathrm{T}}U
\begin{pmatrix}
\theta_1 & & & \\
& \theta_2 & & \\
& & \ddots & \\
& & & \theta_n
\end{pmatrix} \tag{5}
となります。
ここで、
\Theta =
\begin{pmatrix}
\theta_1 & & & \\
& \theta_2 & & \\
& & \ddots & \\
& & & \theta_n
\end{pmatrix}
とおいて、
V\Theta^{-1} = A^{\mathrm{T}}U \tag{6}
と書き直しておきます。
さて、$(1)$を行列にして、
AA^{\mathrm{T}}U = U
\begin{pmatrix}
\lambda_1 & & & \\
& \lambda_2 & & \\
& & \ddots & \\
& & & \lambda_n
\end{pmatrix}
が成り立つので、$(6)$を代入して、
AV\Theta^{-1} = U
\begin{pmatrix}
\lambda_1 & & & \\
& \lambda_2 & & \\
& & \ddots & \\
& & & \lambda_n
\end{pmatrix}
これを変形していくと、
AV = U
\begin{pmatrix}
\lambda_1 & & & \\
& \lambda_2 & & \\
& & \ddots & \\
& & & \lambda_n
\end{pmatrix}
\Theta \\
A = U
\begin{pmatrix}
\lambda_1 & & & \\
& \lambda_2 & & \\
& & \ddots & \\
& & & \lambda_n
\end{pmatrix}
\Theta V^{\mathrm{T}}
A = U
\begin{pmatrix}
\lambda_1 \theta_1 & & & \\
& \lambda_2 \theta_2 & & \\
& & \ddots & \\
& & & \lambda_n \theta_n
\end{pmatrix}
V^{\mathrm{T}} \tag{7}
ここで、 $V$ は実対称行列($A^\mathrm{T}A$)の固有ベクトルを並べた行列なので、それぞれの $\boldsymbol{v}$ は直交し、
V^{\mathrm{T}} = V^{-1}
と書けることを使っています。
また、対角行列同士の掛け算は、要素ごとの積になります。
これで一応SVDの形の変形ができることはわかったのですが、せっかくなので $\theta$ の値も求めておきます。
$(4)$から、
\| \boldsymbol{v}_1 \|^2 = \theta_1^2
(\boldsymbol{u}_1^{\mathrm{T}} AA^{\mathrm{T}} \boldsymbol{u}_1)
と書けて、これに$(1)$を代入すると、
\begin{align}
\| \boldsymbol{v}_1 \|^2 &= \theta_1^2
(\boldsymbol{u}_1^{\mathrm{T}} \lambda_1 \boldsymbol{u}_1) \\
&= \theta_1^2 \lambda_1 \| \boldsymbol{u}_1 \|^2
\end{align}
です。
$\boldsymbol{u}$ 、 $\boldsymbol{v}$ は単位ベクトルを選んでいるので、
\theta_1 = \frac{1}{\sqrt{\lambda_1}}
となり、$(7)$は
A = U
\begin{pmatrix}
\sqrt{\lambda_1} & & & \\
& \sqrt{\lambda_2} & & \\
& & \ddots & \\
& & & \sqrt{\lambda_n}
\end{pmatrix}
V^{\mathrm{T}}
と書くことができます。
\sigma_k = \sqrt{\lambda_k}
として、
A = U
\begin{pmatrix}
\sigma_1 & & & \\
& \sigma_2 & & \\
& & \ddots & \\
& & & \sigma_n
\end{pmatrix}
V^{\mathrm{T}}
A = U \Sigma V^{\mathrm{T}}
が導けます。