「はじめてのパターン認識」の第3章解説です。
やはり15ページ程度のくせに読み解くのに時間かかりました。 確率関連の単語が当然知っているものとして書かれているので、その辺の知識が怪しい自分にとっては復習から始めています。
SlideShare「はじパタ!輪読会 第3章前半 ベイズの識別規則」なども参考にしました(あのグラフどうやって書いているのだろう?)。
※はじパタ勉強系は記事「文系社会人がはじパタで機械学習を数式含めて理解した奮闘記」にまとめました。
内容
前提
本題に入る前にベイズの識別規則を理解する上で必要な前提知識をいくつか解説します。
条件付き確率
**条件付き確率は「ある事象 B が起こるという条件下での別の事象 A の確率」**のことで「B が起こったときの A の(条件付き)確率」「条件 B の下での A の確率」とも言えます。
数式では$P(A \mid B)$または$P_B(A)$で表します。
P(A\mid B)=\dfrac{P(A\cap B)}{P(B)}
例と詳細整理
| 記号・式 | 内容 | 上記での例 | 上記の例での確率 |
|---|---|---|---|
| $P(A)$ | Aの確率 | 偶数が出る確率 | $\frac{1}{2}(=\frac{3}{6})$ |
| $P(B)$ | Bの確率 | 3以上の目が出る確率 | $\frac{2}{3}(=\frac{4}{6})$ |
| $P(A\cap B)$ | AとBが同時に起きる確率 | 偶数(A)かつ3以上(B)の確率 | $\frac{1}{3}(=\frac{2}{6})$ |
| $P(A\mid B)=\dfrac{P(A\cap B)}{P(B)}$ | Bが起こる条件下でのAの確率 | 3以上(B)と判明時の偶数(A)の確率 | $\frac{1}{2}(=\frac{\frac{1}{3}}{\frac{2}{3}})$ |
| $P(B\mid A)=\dfrac{P(A\cap B)}{P(A)}$ | Aが起こる条件下でのBの確率 | 偶数(A)と判明時の3以上(B)の確率 | $\frac{2}{3}(=\frac{\frac{1}{3}}{\frac{1}{2}})$ |
確率変数の独立
$P(A \cap B)=P(A)P(B) $が成立するとき、確率変数$X$と$Y$は独立であると言います。$P(A \cap B)$は$P(A,B)$とも表現します。要はAとBの事象は互いに影響を与えないということです。
確率変数の独立詳細
P(A \cap B)=\frac{1}{3} \\
P(A)P(B) = \frac{1}{2} \times \frac{2}{3} = \frac{1}{3} \\
\therefore P(A \cap B)=P(A)P(B)
逆に独立でない例は、袋に黒と白の石が1つずつ入っていて、順番に取って戻さなかった場合です。1回目に黒が出る確率と2回目に黒が出る確率は独立ではありません。以下が少し整理した内容です。
| 記号・式 | 内容 | 確率 |
|---|---|---|
| $P(A)$ | 1回目に黒が出る確率 | $\frac{1}{2}$ |
| $P(B)$ | 2回目に黒が出る確率 | $\frac{1}{2}$ |
| $P(A \cap B)$ | 1回目に黒が出て、2回目にも黒が出る確率 | $0$ |
| $P(A)P(B)$ | $P(A)$と$P(B)$の乗算 | $\frac{1}{4}(=\frac{1}{2}\times\frac{1}{2})$ |
ちなみに独立の場合は無相関ですが、無相関だからといって独立とは限りません。詳しくは「独立と無相関の意味と違いについて」を参照ください。
条件付き独立
条件付き独立は、確率変数の独立に条件が付きます。確率AとBが条件Cを与えたもとで独立しているとき条件付き独立と言えます。
式にすると以下の通りで、$P(A \cap B\mid C)$は、「はじパタ」では$P(A, B\mid C)$と記載されていますが同じ意味です。
P(A \cap B\mid C)=P(A\mid C)P(B\mid C)
条件付き独立の詳細
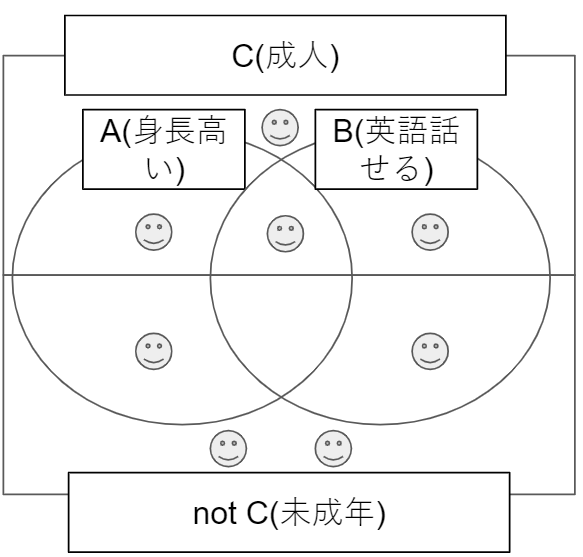
- 事象A: 身長が高い
- 事象B: 英語を話せる
- 条件C: 成人
| 記号・式 | 内容 | 確率 |
|---|---|---|
| $P(A)$ | 身長が高い確率 | $\frac{3}{8}$ |
| $P(B)$ | 英語を話せる確率 | $\frac{3}{8}$ |
| $P(A \cap B)$ | 身長が高くて英語を話せる確率 | $\frac{1}{8}$ |
| $P(A)P(B)$ | $P(A)$と$P(B)$の乗算 | $\frac{9}{64}(=\frac{3}{8}\times\frac{3}{8})$ |
| $P(A \mid C)$ | 成人という条件下で身長が高い確率 | $\frac{1}{2}(=\frac{2}{4})$ |
| $P(B \mid C)$ | 成人という条件下で英語を話せる確率 | $\frac{1}{2}(=\frac{2}{4})$ |
| $P(A \cap B \mid C)$ | 成人という条件下で身長が高くて英語を話せる確率 | $\frac{1}{4}$ |
| $P(A \mid C)P(B \mid C)$ | $P(A \mid C)$と$P(B \mid C)$の乗算 | $\frac{1}{4}(=\frac{1}{2}\times\frac{1}{2})$ |
条件がない場合は$P(A \cap B) \neq P(A)P(B)$と独立ではありませんが、C(成人)という条件をつけると$P(A \cap B \mid C) = P(A \mid C)P(B \mid C)$なり、独立の条件を満たします。
同時確率、周辺確率、条件付き確率
同時確率は複数の事象が同時に起きる確率、周辺確率は同時確率から一部の確率変数を消したもの、条件付き確率は特定の条件下での確率です。
例として、AとBが2回じゃんけんをして、Aの勝率数とBの勝利数をそれぞれ$X$と$Y$とします(あいこは両者の勝利とカウントしない)。その場合の3つの確率は以下の表のようになります。
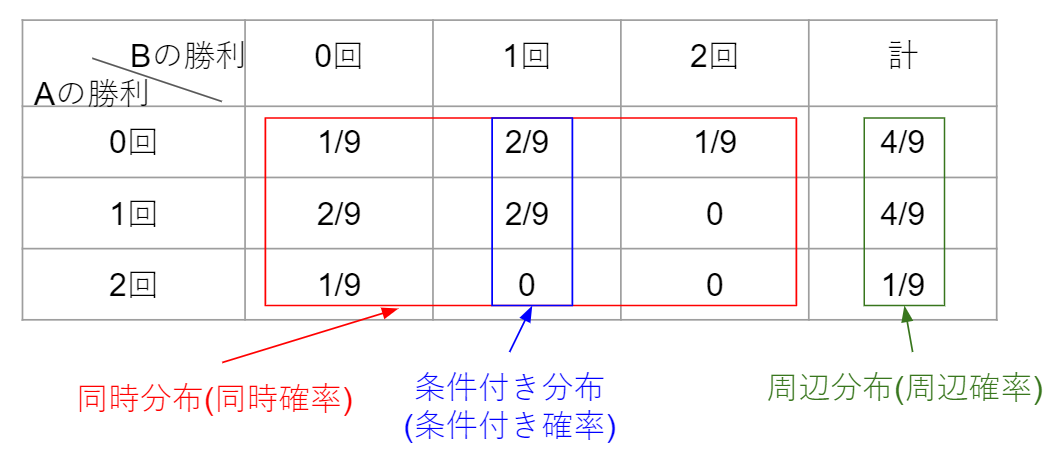
以下のサイトを参考にしました。
3.1. ベイズの識別規則
3.1.1. 最大事後確率基準
観測データを$x$、識別クラスを$C_i(i=1, \cdots, K)$としたときにベイズの識別規則は次式(ベイズの定理)の事後確率がもっとも大きなクラスに観測データを分類します。
P(C_i \mid x) = \frac{p(x \mid C_i)}{p(x)} \times P(C_i) \\
= 修正項 \times 事前確率
上記の式は以下の同時分布の式から導出できます(2項目と3項目を$p(x)$で割るだけ)。
p(C_i, x) = P(C_i \mid x)p(x) = p(x \mid C_i)P(C_i)
ベイズの定理内の単語の意味は以下のとおりです。
例の部分は、先程のAとBが2回じゃんけんをして、Aの勝率数とBの勝利数をそれぞれ$x$と$C_i$とします(あいこは両者の勝利とカウントしない)。
| 用語 | 記号・式 | 意味 | 例 |
|---|---|---|---|
| 事後確率 | $P(C_i \mid x)$ | 観測データ$x$が与えられた条件下で、クラス$C_i$に属する条件付き確率 | $x=0$(Aが0回勝った)と知っている場合の$C_i=1$(Bの勝利数が1)の確率 $P(C_1 \mid x=0)= \frac{1}{2}$ |
| クラス条件付き確率(尤度) | $p(x \mid C_i)$ | クラス$C_i$が与えられた下での観測データ$x$の確率分布 | $C_i=1$(Bの勝利数が1)の場合の$x=0$(Aの勝利数が0)の確率 $p(x=0 \mid C_1)=\frac{1}{2}$ |
| 周辺確率 | $p(x)$ | 観測データ$x$の生起確率 | $x=0$(Aの勝利数が0)の確率 $p(x=0)=\frac{4}{9}$ |
| 事前確率 | $P(C_i)$ | クラス$C_i$の生起確率 | $C_i=1$(Bの勝利数が1)の確率 $P(C_1)= \frac{4}{9}$ |
事後確率の式$P(C_i \mid x) = \frac{p(x \mid C_i)}{p(x)} \times P(C_i)$内の$p(x)$はすべてのクラス$C_i$に出てくるため省略して、識別規則は以下のようになる。
\arg \max_{i} p(x \mid C_i)P(C_i) \\
3.1.2. ベイズの識別規則の例
以下の例でベイズの識別規則を理解していきます。
| サンプル数 | 喫煙者(S=1) | 飲酒者(T=1) | |
|---|---|---|---|
| 健康(G=1) | 800人 | 320人 | 640人 |
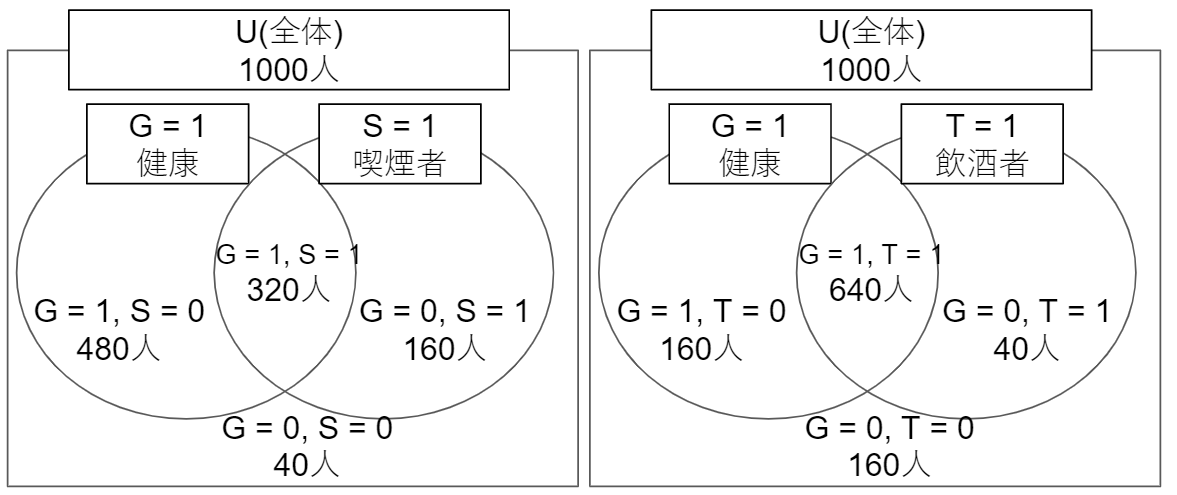
| 不健康(G=0) | 200人 | 160人 | 40人 |
上記の表をベン図にしました。GとS、GとTはそれぞれ関係性はわかりますが、SとTの関係性はわかりません。
では、ベイズの定理の構成要素の一つ一つを整理していきます。
P(C_i \mid x) = \frac{p(x \mid C_i)}{p(x)} \times P(C_i) \\
= \frac{クラス条件付き確率(尤度)}{周辺確率} \times 事前確率
事前確率
各クラスごとの事前確率$P(C_i)$を求めます。
P(G=1) = \frac{800}{1000} = \frac{4}{5}, \
P(G=0) = \frac{200}{1000} = \frac{1}{5}
クラス条件付き確率(尤度)
クラス条件付き確率(尤度)($p(x \mid C_i)$)を求めます。
| S=1(喫煙者) | S=0(非喫煙者) | T=1(飲酒者) | T=0(非飲酒者) | |
|---|---|---|---|---|
| G=1(健康) | $P(S=1 \mid G=1)$ $\frac{2}{5}(=\frac{320}{800})$ |
$P(S=0 \mid G=1)$ $\frac{3}{5}(=\frac{480}{800})$ |
$P(T=1 \mid G=1)$ $\frac{4}{5}(=\frac{640}{800})$ |
$P(T=0 \mid G=1)$ $\frac{1}{5}(=\frac{160}{800})$ |
| G=0(不健康) | $P(S=1 \mid G=0)$ $\frac{4}{5}(=\frac{160}{200})$ |
$P(S=0 \mid G=0)$ $\frac{1}{5}(=\frac{40}{200})$ |
$P(T=1 \mid G=0)$ $\frac{1}{5}(=\frac{40}{200})$ |
$P(T=0 \mid G=0)$ $\frac{4}{5}(=\frac{160}{200})$ |
SとTのクラス条件付き確率、同時確率、周辺確率
上記をクラス条件付きのSとTの同時確率にします。同時確率にする前提としてSとTが条件付き独立であると仮定しています。条件付き独立であれば$P(A \cap B\mid C)=P(A\mid C)P(B\mid C)$の式が使えます。
下表では以下の計算をしています。
- 1と2行目にあるクラス条件付き確率は$P(S\mid G)P(T\mid G)$
- 3と4行目にある同時確率は$P(S, T \mid G) \times P(G)$
- 最終行の周辺確率は同時確率(3と4行目)の和(周辺化)
| S=1, T=1 | S=0, T=1 | S=1, T=0 | S=0, T=0 | |
|---|---|---|---|---|
| クラス条件付き確率 $P(S, T \mid G=1)$ |
$\frac{8}{25}$ $(=\frac{2}{5} \times \frac{4}{5})$ |
$\frac{12}{25}$ $(=\frac{3}{5} \times \frac{4}{5})$ |
$\frac{2}{25}$ $(=\frac{2}{5} \times \frac{1}{5})$ |
$\frac{3}{25}$ $(=\frac{3}{5} \times \frac{1}{5})$ |
| クラス条件付き確率 $P(S, T \mid G=0)$ |
$\frac{4}{25}$ $(=\frac{4}{5} \times \frac{1}{5})$ |
$\frac{1}{25}$ $(=\frac{1}{5} \times \frac{1}{5})$ |
$\frac{16}{25}$ $(=\frac{4}{5} \times \frac{4}{5})$ |
$\frac{4}{25}$ $(=\frac{1}{5} \times \frac{4}{5})$ |
| 同時確率 $P(S, T, G=1)$ |
$\frac{32}{125}$ $(=\frac{8}{25} \times \frac{4}{5})$ |
$\frac{48}{125}$ $(=\frac{12}{25} \times \frac{4}{5})$ |
$\frac{8}{125}$ $(=\frac{2}{25} \times \frac{4}{5})$ |
$\frac{12}{125}$ $(=\frac{3}{25} \times \frac{4}{5})$ |
| 同時確率 $P(S, T, G=0)$ |
$\frac{4}{125}$ $(=\frac{4}{25} \times \frac{1}{5})$ |
$\frac{1}{125}$ $(=\frac{1}{25} \times \frac{1}{5})$ |
$\frac{16}{125}$ $(=\frac{16}{25} \times \frac{1}{5})$ |
$\frac{4}{125}$ $(=\frac{4}{25} \times \frac{1}{5})$ |
| 周辺確率 $P(S, T)$ |
$\frac{36}{125}$ $(=\frac{32}{125} + \frac{4}{125})$ |
$\frac{49}{125}$ $(=\frac{48}{125} + \frac{1}{125})$ |
$\frac{24}{125}$ $(=\frac{8}{125} + \frac{16}{125})$ |
$\frac{16}{125}$ $(=\frac{12}{125} + \frac{4}{125})$ |
事後確率確率
事後確率($P(C_i \mid x) = \frac{p(x \mid C_i)}{p(x)} \times P(C_i)$)を求めます。
| S=1, T=1 | S=0, T=1 | S=1, T=0 | S=0, T=0 | |
|---|---|---|---|---|
| $P(G=1 \mid S, T)$ | $\frac{8}{9}$ $(\frac{8}{25} \times \frac{125}{36} \times \frac{4}{5})$ |
$\frac{48}{49}$ $(\frac{12}{25} \times \frac{125}{49} \times \frac{4}{5})$ |
$\frac{1}{3}$ $(\frac{2}{25} \times \frac{125}{24} \times \frac{4}{5})$ |
$\frac{3}{4}$ $(\frac{3}{25} \times \frac{125}{16} \times \frac{4}{5})$ |
| $P(G=0 \mid S, T)$ | $\frac{1}{9}$ $(\frac{4}{25} \times \frac{125}{36} \times \frac{1}{5})$ |
$\frac{1}{49}$ $(\frac{1}{25} \times \frac{125}{49} \times \frac{1}{5})$ |
$\frac{2}{3}$ $(\frac{16}{25} \times \frac{125}{24} \times \frac{1}{5})$ |
$\frac{1}{4}$ $(\frac{4}{25} \times \frac{125}{16} \times \frac{1}{5})$ |
| 判断 | $G=1$ | $G=1$ | $G=0$ | $G=1$ |
3.1.3. 尤度比
ベイズの識別規則による識別境界は事後確率が等しくなるところ、$P(C_i \mid x) = P(C_j \mid x)$でした。事後確率をクラス条件付き確率と事前確率に分解して表現すると以下の式。
\begin{cases}
C_i & \Leftarrow p(x \mid C_i) P(C_i) > p(x \mid C_j) P(C_j) \\
C_j & \Leftarrow p(x \mid C_i) P(C_i) < p(x \mid C_j) P(C_j) \\
\end{cases}
これを尤度比に変形すると以下のようになり、$\frac{P(C_j)}{P(C_i)}$がしきい値の役割をします。
\begin{cases}
C_i & \Leftarrow \frac{p(x \mid C_i)}{p(x \mid C_j)} > \frac{P(C_j)}{P(C_i)} \\
C_j & \Leftarrow \frac{p(x \mid C_i)}{p(x \mid C_j)} < \frac{P(C_j)}{P(C_i)} \\
\end{cases}
3.1.4. ベイズの識別規則は誤り率最小
ベイズの識別規則は基本的に誤り率を最小にします。
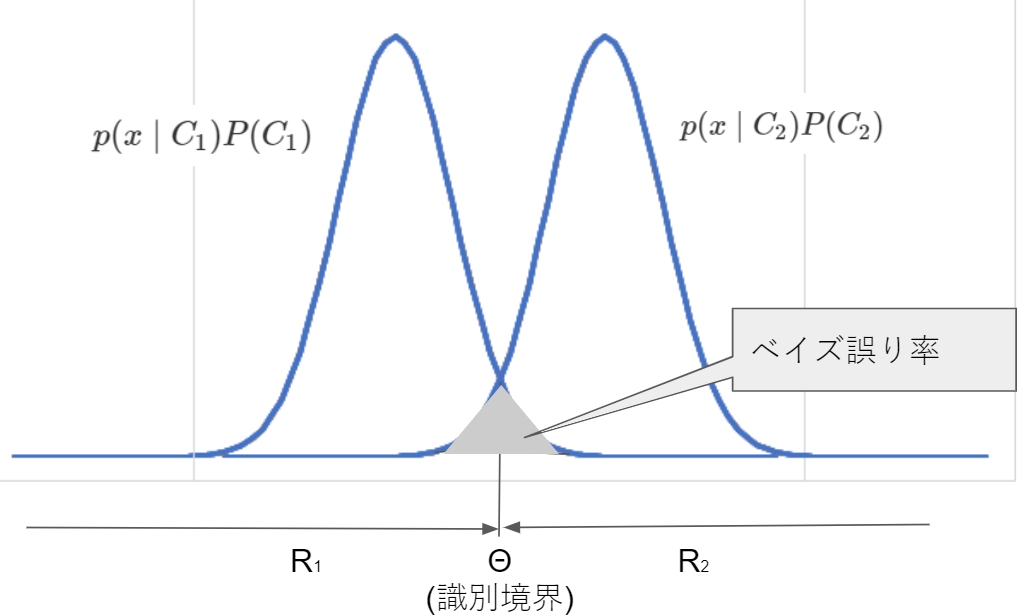
二値分類の例で、誤り率$\epsilon(x)$は事後確率が小さい方なので$\epsilon(x)=\min [P(C_1 \mid x), P(C_2 \mid x)]$となり、条件付きベイズ誤り率と呼びます。
上記の正規分布っぽい確率分布で、それぞれのクラスがとる領域を$R_1$, $R_2$とするとベイズ誤り率は以下の展開ができます。
\epsilon = E\{\epsilon(x) \} = \int_{R_1+R_2} \epsilon(x)p(x)dx \ \ \ ※ベイズ誤り率は条件付きベイズ誤り率の期待値\\
= \int_{R_1+R_2} \min[P(C_1 \mid x), P(C_2 \mid x)]p(x)dx \ \ \ ※高い方は採択されるクラス \\
= \int_{R_1+R_2} \min[\frac{p(x \mid C_1)P(C_1)}{p(x)}), \frac{p(x \mid C_2)P(C_2)}{p(x)})]p(x)dx \ \ \ ※ベイズの定理で展開 \\
= \int_{R_1+R_2} \min[p(x \mid C_1)P(C_1)), p(x \mid C_2)P(C_2))]dx \ \ \ ※p(x)を消去 \\
= \int_{R_1+R_2} (p(C_1, x \in R_2) + p(C_2, x \in R_1)) \ \ \ ※min部分を分解 \\
= \int_{R_2}p(x \mid C_1)P(C_1)dx + \int_{R_1}p(x \mid C_2)P(C_2)dx \ \ \ ※積分部分を分解 \\
※インテグラル($\int$)の下だけあるやつ($\int_{R_1+R_2}$)は(From Toではなく)範囲を示すようです。Yahoo知恵袋に書いてありました。
※$\Theta$は「シータ」の大文字
3.1.5. 最小損失基準に基づくベイズの識別規則
ベイズの識別規則に間違えの重み付けをして行きます。例えば、健康診断での2種類の間違えの損失は以下のとおりで、その場合に損失行列(コスト行列)を使って重み付けをします。
「コスト考慮型学習」のページがわかりやすいです。
本当は健康なのに病気と診断された場合の損失 < 本当は病気なのに健康と診断された場合の損失
健康を$C_1$、病気を$C_2$とした場合の損失行列$L_{ij}$は以下の通り。損失値は適当に入れています。
マトリックスのフレームは混合行列と同じですね。
| 実際は健康($C_1$) | 実際は病気($C_2$) | |
|---|---|---|
| 健康と診断($C_1$) | $L_{11}=0$ 正解 健康な人に健康と診断 |
$L_{12}=1$ 間違え 病気な人に健康と診断 |
| 病気と診断($C_2$) | $L_{21}=5$ 間違え 健康な人に病気と診断 |
$L_{22}=0$ 正解 病気な人に病気と診断 |
観測データ$x$をクラス$C_i$と判断したときの損失は以下の式。損失に事後確率をかけ合わせた総和ですね。
r(C_i \mid x) = \sum_{k=1}^K L_{ik}P(C_k \mid x)
健康$C_1$と診断する損失の場合は以下の計算です(損失値は上記のマトリックスに入れた適当な値)。
r(C_1 \mid x) = \sum_{k=1}^K L_{1k}P(C_k \mid x) \\
= L_{11}P(C_1 \mid x) + L_{12}P(C_2 \mid x) \\
= 0 + 1 \times P(C_2 \mid x) \\
= 健康な人に健康と診断する場合の損失(0) + 病気な人に健康と診断する場合の損失(P(C_2 \mid x))
識別クラスは
\arg \min_i r(C_i \mid x)
仮に二値分類の場合の損失は
r(x) = \min[r(C_1 \mid x), r(C_2 \mid x)]
損失の期待値は。
r = E\{ r(x) \} = \int_{R_1+R_2} \min[r(C_1 \mid x), r(C_2 \mid x)]p(x)d(x) \\
= \int_{R_1+R_2} \min[L_{11}P(C_1 \mid x) + L_{12}P(C_2 \mid x), L_{21}P(C_1 \mid x) + L_{22}P(C_2 \mid x)]p(x)d(x) \\
= \int_{R_1+R_2} \min[L_{11}p(x \mid C_1)P(C_1) + L_{12}p(x \mid C_2)P(C_2), L_{21}p(x \mid C_1)P(C_1) + L_{22}P(x \mid C_2)p(C_2)]d(x) \ \ \ ※p(x)を展開\\
= \int_{R_1} ( L_{11}p(x \mid C_1)P(C_1) + L_{12}p(x \mid C_2)P(C_2)) d(x) \ \ ※積分範囲R_1\\
+ \int_{R_2} ( L_{21}p(x \mid C_1)P(C_1) + L_{22}p(x \mid C_2)P(C_2)) d(x) \ \ ※積分範囲R_2 \\
識別規則は以下の式。ちなみに$L_{11}$と$L_{22}$はゼロになることが多いのでは?損失値の決め方に関する情報は、少し調べた限りでは見つかりませんでした。
\begin{cases}
C_1 & \Leftarrow L_{11} p(x \mid C_1) P(C_1) + L_{12}p(C_2 \mid x)P(C_2) < L_{21} p(x \mid C_2) P(C_2) + L_{22}p(C_2 \mid x)P(C_2) \\
C_2 & \Leftarrow L_{11} p(x \mid C_1) P(C_1) + L_{12}p(C_2 \mid x)P(C_2) > L_{21} p(x \mid C_2) P(C_2) + L_{22}p(C_2 \mid x)P(C_2) \\
\end{cases}
識別規則をすっきりと変形。
\begin{cases}
C_1 & \Leftarrow (L_{21}-L_{11}) p(x \mid C_1) P(C_1) > (L_{12}-L_{22}) p(x \mid C_2) P(C_2) \\
C_2 & \Leftarrow (L_{21}-L_{11}) p(x \mid C_1) P(C_1) < (L_{12}-L_{22}) p(x \mid C_2) P(C_2) \\
\end{cases}
これを尤度比に変形すると以下のようになり、$\frac{P(C_j)}{P(C_i)}$がしきい値の役割をします。
\begin{cases}
C_1 & \Leftarrow \frac{p(x \mid C_1)}{p(x \mid C_j)} > \frac{(L_{12}-L_{22})P(C_2)}{P(C_2)} \\
C_2 & \Leftarrow \frac{p(x \mid C_2)}{p(x \mid C_j)} < \frac{(L_{21}-L_{11})P(C_1)}{P(C_1)} \\
\end{cases}
3.1.6. リジェクト
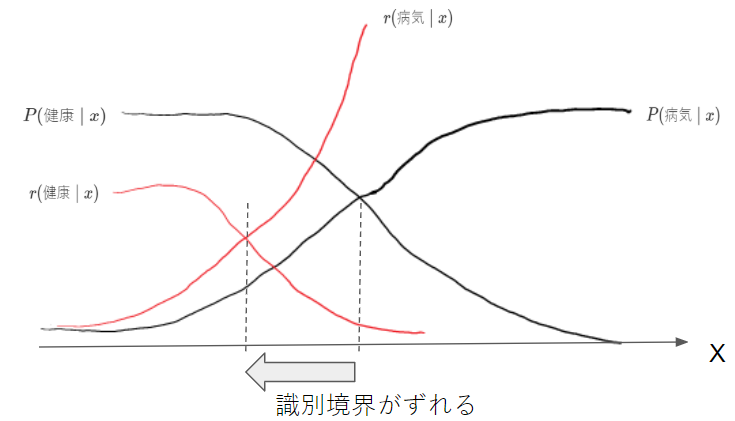
条件付きベイズ誤り率では、識別境界においては0.5となります。誤り率が大きな領域で判断を保留することをリジェクトと言います。下のグラフの真ん中部分が誤り率が$\epsilon(x) \ge t$となるリジェクト領域です。
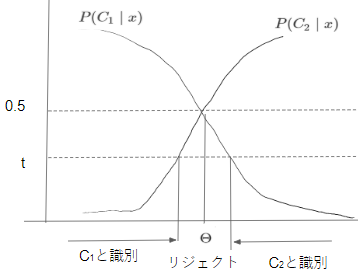
二値分類では、誤り率$\epsilon(x)$は他方のクラスに識別される確率と同じなので、その確率がしきい値$t$以上の場合をリジェクトとする。以下はクラス1での誤り率(クラス2と識別される確率)を表しています。
\epsilon(x) = \frac{p(x \mid C_2)P(C_2)}{p(x)} \ge t
これを展開・整理します。
\frac{p(x \mid C_2)P(C_2)}{p(x \mid C_1)P(C_1) + p(x \mid C_2)P(C_2)} \ge t \ \ \ ※p(x)を置換\\
\frac{p(x \mid C_2)P(C_2)}{t} \ge p(x \mid C_1)P(C_1) + p(x \mid C_2)P(C_2) \ \ \ ※左辺の分母で乗算とtで除算 \\
\frac{1}{t} \ge \frac{p(x \mid C_1)P(C_1)}{p(x \mid C_2)P(C_2)} + 1 \ \ \ ※左辺の分子で除算 \\
\frac{1-t}{t} \ge \frac{p(x \mid C_1)P(C_1)}{p(x \mid C_2)P(C_2)} \\
リジェクトを考慮した識別クラスは以下のようになります。
\begin{cases}
C_i & \Leftarrow P(C_i \mid x) = \max_j P(C_j \mid x) > 1-t \\
リジェクト & \Leftarrow すべてのクラスについてP(C_i \ x) \ge 1-t \\
\end{cases}
リジェクト率と正答率・誤識別率の関係を示すリジェクト - 誤識別率曲線は以下のグラフで表せます。
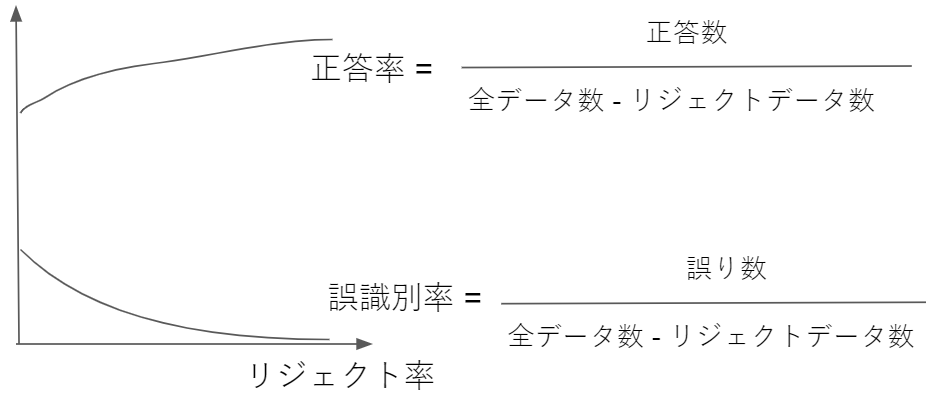
※「認識率」ではなく「正答率」と表現しています。その方が私にとってしっくりくるので。
3.2. 受動者動作特性曲線(ROC曲線)
この章では**受信者動作特性曲線(ROC曲線: Receiver Operator Characteristics Curve)**について学びます。これは、事前確率や尤度、識別境界などの情報を必要としない性能評価法です。
以前、言語処理100本ノック(2015年版)の79本目「適合率-再現率グラフの描画」でPythonを使って出力しています。
3.2.1. ROC曲線の求め方
前提となる**混合行列(Confusion Matrix)**を知る必要があります。以前、混合行列について記事「【入門者向け】機械学習の分類問題評価指標解説(正解率・適合率・再現率など)」に詳しく書いたので割愛します。
今回メインで使う2つの指標を補足。
- 偽陽性率(false positive rate) = FP/N : 全Negativeの中でPositiveと予測した誤りの率
- 真陽性率(true positive rate) = TP/P : 全Positiveの中でPositiveと予測した正解の率
まずは、$x$の値と尤度、識別境界などの関係をグラフで表します。
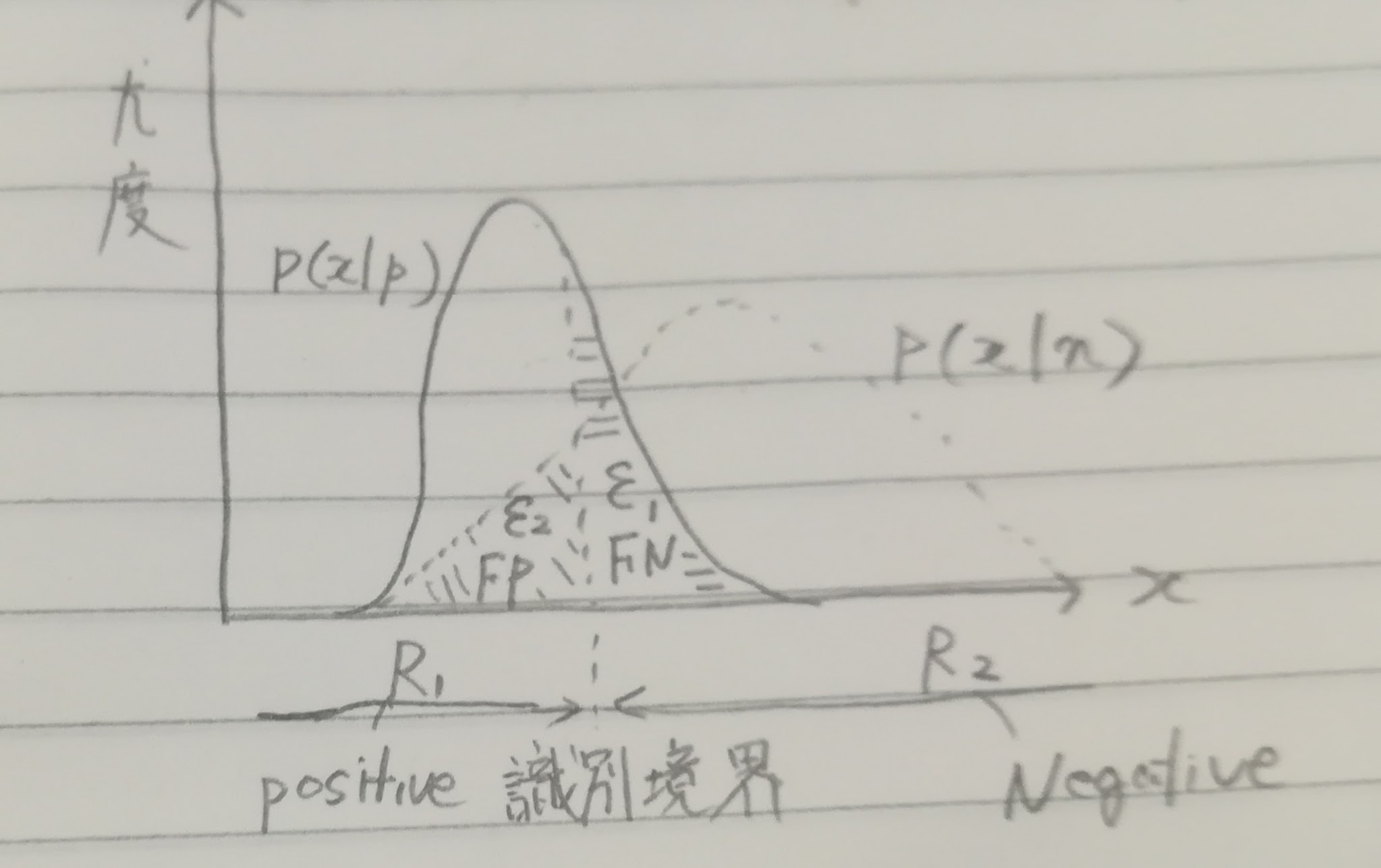
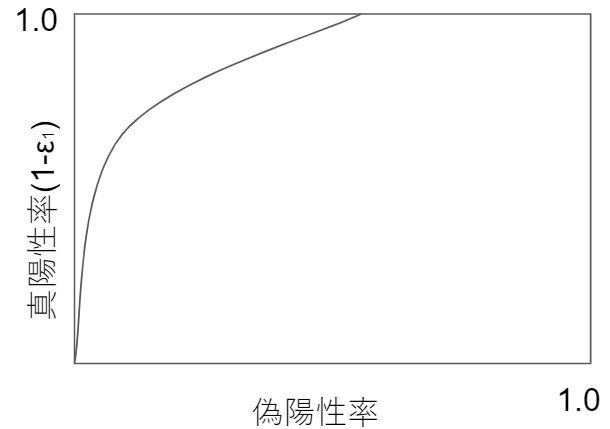
ROC曲線は縦軸が真陽性率($1-\epsilon_1=\frac{TP}{P}$)、横軸が偽陽性率($\epsilon_2=\frac{FP}{N}$)です。
自信がなくてもPositiveを多くしていくことで真陽性率(縦軸)が上がりますが、一方で横軸の偽陽性率の分子であるFP(Positiveとお手付きする間違え)も増えていきます。
3.2.2. ROC曲線による性能評価
ROC曲線の下側面積を**ROC曲線下面積(AUC: Area Under an ROC Curve)**と呼び、識別機の性能評価尺度として使われます。
完全な識別器とランダムな識別器を図で示しました。
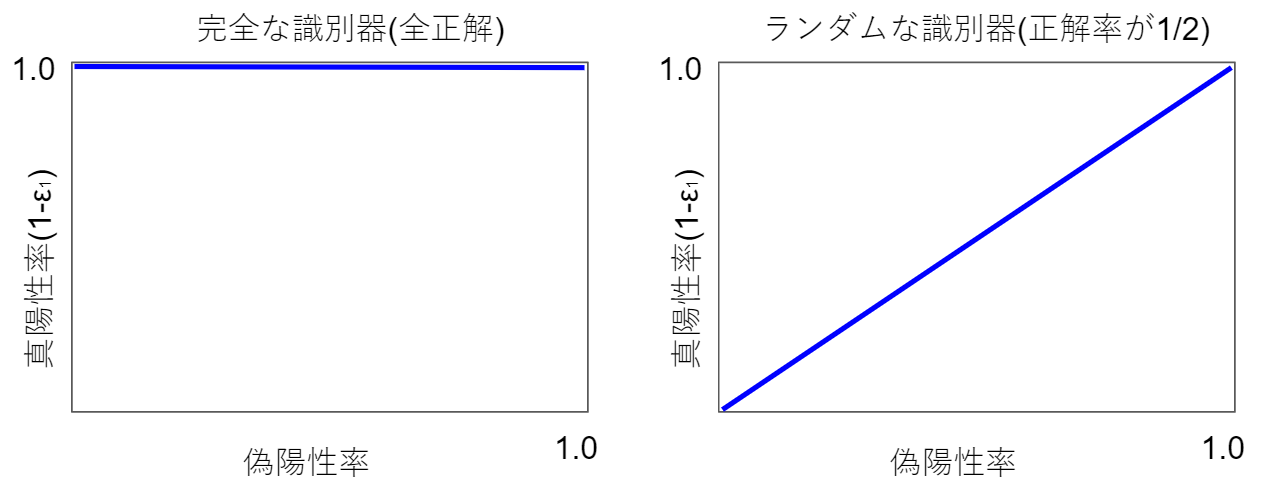
完全な識別機はAUCが1.0、ランダムな識別機はAUCが0.5です。
最小損失識別規則で、かつ$L_{11}=L_{22}=0$(正解時の損失なし)と仮定すると、損失の期待値$r$は以下の式。
r = \int_{R_1} ( L_{12}p(x \mid n)P(n)) d(x) + \int_{R_2} ( L_{21}p(x \mid p)P(p)) d(x) \\
= L_{12}P(n)\epsilon_2 + L_{21}P(p)\epsilon_1 \ \ ※\epsilon_nは真陽性/偽陽性部分
上記の式をROC曲線空間にあわせて書き直します。
L_{21}P(p) \epsilon_1 = r - L_{12}P(n) \epsilon_2 \\
\epsilon_1 = \frac{r - L_{12}P(n) \epsilon_2}{L_{21}P(p)} \\
\begin{eqnarray}
1 - \epsilon_1 & = & 1 - \frac{r - L_{12}P(n) \epsilon_2}{L_{21}P(p)} \\
& = & \frac{L_{12}P(n)}{L_{21}P(p)}\epsilon_2 + (1 - \frac{r}{L_{21}P(p)}) \\
& = & \alpha \epsilon_2 + h(r)
\end{eqnarray}
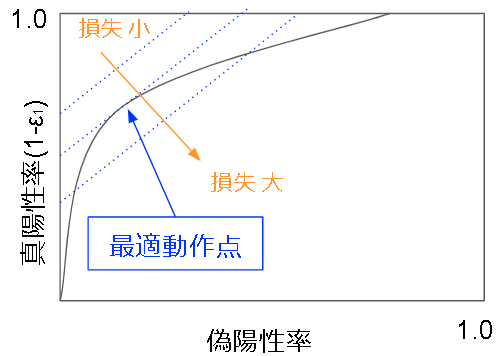
これは損失$r$によって切片が変化する1次関数で、1つの直線上では損失が一定です。等損失直線群および最適動作点は以下の図のようになります。最適動作点はROC曲線と等損失直線が接している点です。
3.2.3. ROC曲線の構成
ROC曲線の便利な点は、クラスの分布がわからなかくても各学習データの真のクラスがわかれば構成できることです。
仮に5つのp/n(positive/negative)の二値分類データがあり、識別のスコア(信頼度)を下表で記載しています。スコアの降順にしており、それぞれのスコアでの偽陽性率、真陽性率を併せて記載しています。
| No. | 真のクラス | スコア(信頼度) | 偽陽性率 | 真陽性率 |
|---|---|---|---|---|
| 1 | p | 0.9 | $\frac{0}{2}$ | $\frac{1}{3}(+\frac{1}{3})$ |
| 2 | p | 0.85 | $\frac{0}{2}$ | $\frac{2}{3}(+\frac{1}{3})$ |
| 3 | n | 0.8 | $\frac{1}{2}(+\frac{1}{2})$ | $\frac{2}{3}$ |
| 4 | p | 0.75 | $\frac{1}{2}$ | $\frac{3}{3}(+\frac{1}{3})$ |
| 5 | n | 0.7 | $\frac{2}{2}(+\frac{1}{2})$ | $\frac{3}{3}$ |
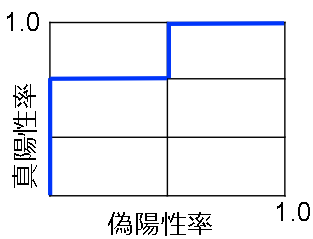
この表からROC曲線を作りました。階段状になるため、ROCグラフとも呼ばれるそうです。
「はじパタ」勉強系記事リンク
| 章 | 項目 | 時間(h) | 難易度 | 学んだこと |
|---|---|---|---|---|
| 1 | はじめに | 8.9 | 特徴の型, 特徴空間, 次元の呪い | |
| 2 | 識別規則と学習法の概要 | 12 | ホールドアウト法,交差確認法 ,一つ抜き法 ,ブートストラップ法 ,バイアス・分散トレードオフ, 過学習 | |
| 3 | ベイズの識別規則 | 14.8 | ベイズ識別規則, ROC曲線 | |
| 4 | 確率モデルと識別関数 | 18 |
|
平均ベクトル, 共分散行列, 標準化, 無相関化, 白色化, 正規分布, 最尤推定 |
| 5 | k最近傍法(kNN法) | 8 |
|
最近傍法, ボロノイ境界, kNN |
| 6 | 線形識別関数(前半) | 30.4 |
|
正規方程式 |
| 6 | 線形識別関数(後半) | 前半に時間は含む |
|
フィッシャーの線形判別関数, 判別分析法, ロジスティック回帰 |
| 7 | パーセプトロン型学習規則 | 13.5 |
|
多層パーセプトロン, 誤差逆伝播法, シグモイド関数 |
| 8 | サポートベクトルマシン | 14.7 |
|
カーネルトリック, ν-SVM |
| 9 | 部分空間法 | 15.4 |
|
主成分分析, 特異値分解, CLAFIC法, カーネル主成分分析, カーネル部分空間法 |
| 10 | クラスタリング | 8.4 |
|
距離の公理, ミンコフスキー距離, K-平均法, 融合法, 混合正規分布モデル |
| 11 | 識別機の組み合わせによる性能強化 | 11.6 |
|
ノーフリーランチ定理, 決定木, バギング, アダブースト, ランダムフォレスト |