よく機械学習初学者向けのおすすめとして紹介される「はじめてのパターン認識」。通称「はじパタ」です。
文系卒の私としてはこれが「はじめて」?状態![]()
時間をかけてでも理解してみることにしました。
第1章でまず、「超立方体」と「次元の呪い」の2つに躓きます。しかし、時間をかければなんとか理解可能。記事がとても長くなってしまった・・・・
※はじパタ勉強系は記事「文系社会人がはじパタで機械学習を数式含めて理解した奮闘記」にまとめました。
内容
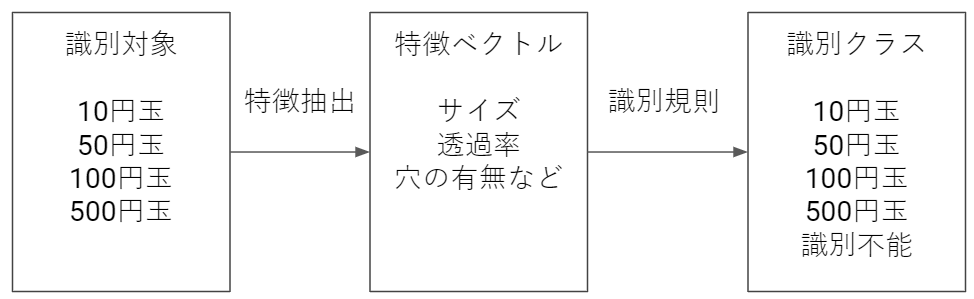
「何か」を判断することを識別といい、「有効な特徴」を抽出することを特徴抽出という。「有効な特徴」と「何か」を結びつける規則を識別規則といい、この規則を学習している。
1.1. パターン認識とは
覚える用語
| 用語 | 意味 |
|---|---|
| 特徴抽出 | 識別の手がかりとなる特徴量を測定すること |
| 特徴ベクトル | 抽出されたたくさんの特徴を並べてベクトルの形にまとめたもの |
| 識別規則 | 特徴ベクトルを用いてクラスに分類するための規則 |
| 学習データ | 入力データとクラスの対応関係を学習するための事例 |
| 汎化能力 | 学習データになかった未知のデータで正しくクラスを識別する能力 |
パターン認識の成否を決める鍵
- 識別に有効な特徴をいかに早く抽出できるか
- 識別規則の学習
パターン認識の流れ
1.2. 特徴の型
特徴の分類
- 非数値データとして抽出される定性的特徴
- 数値データとして抽出される定量的特徴
特徴尺度の分類
| 尺度名 | 特徴分類 | 定義 | 例 |
|---|---|---|---|
| 名義尺度 | 定性的特徴 | 分類のための単なる名前 | 名前・住所 |
| 順序尺度 | 定性的特徴 | 順序関係を表す。比較はできるが加減算などの演算はできない | 大中小・優良可 |
| 間隔尺度 | 定量的特徴 | 一定の単位で量られた量で等間隔性がある 原点はあっても「無」ではない 加減算が意味を持つ |
年月・試験点数 |
| 比例尺度 | 定量的特徴 | 原点が定まっている量 割り算(比)が意味を持つ |
身長・絶対零度 |
注意点・わかりにくかった点
- 順序尺度で「3(優), 2(良), 1(可)」として、各クラス間を等間隔とみなして間隔尺度とする場合もある
- 「試験点数」は原点(0)点はあるが、0点だったとしても何も知らないわけではないのでを間隔尺度
- 絶対零度は温度がないことなので比例尺度
定性的な特徴の表現
定性的な特徴を計算機上で表現するために符号(0 / 1 or -1 / +1)を用いる。
クラス数がK(>2)個以上ある場合、K個の2値変数を用意し、クラスに対応する変数のみを1として他をすべて0にする符号化を行う。このような2値変数をダミー変数と呼ぶ。以下が「大・中・小」のダミー変数の例。
| $\beta_1$ | $\beta_2$ | $\beta_3$ | |
|---|---|---|---|
| 大 | 1 | 0 | 0 |
| 中 | 0 | 1 | 0 |
| 小 | 0 | 0 | 1 |
いわゆるOne-hot Encodingですね。
1.3. 特徴ベクトル空間と次元の呪い
1.3.1. 特徴ベクトル空間
特徴数を$d$とすれば、特徴ベクトルは$d$次元線形空間を張る。読んで字の如しですが、特徴数が2次元の場合は2次元線形空間で、3次元の場合は3次元線形空間という意味ですね。
例えば縦7、横7のグレイスケール画像であれば49次元のベクトルとして表現します。つまり画像データは49次元のベクトル空間中の1点として表現します。
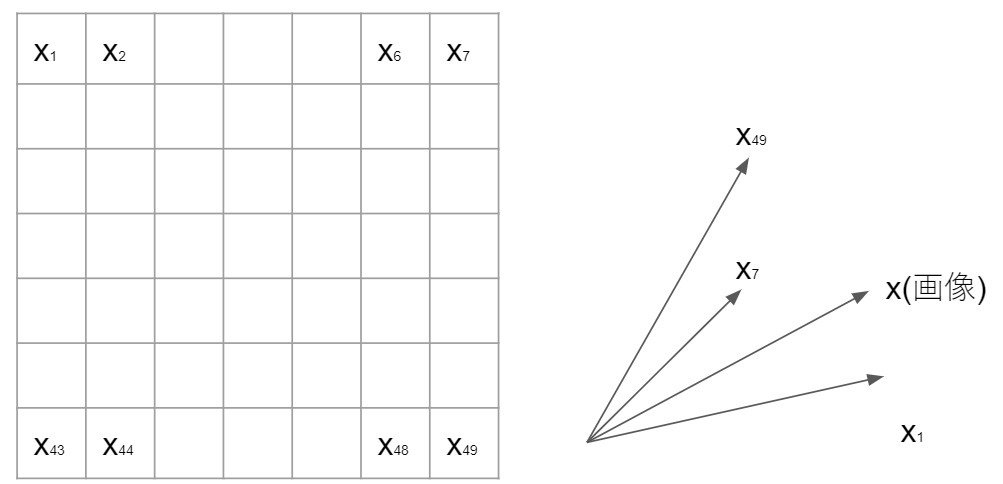
数式で表すと以下のようになります($T$は転置を表していて、縦に49個$x$を並べても同じ)。
x = (x_1, x_2, \cdots, x_{49})^T
1.3.2. 次元の呪い
通常のグレースケール画像だと、画素が256種類あります。これを先程の縦7・横7画像に当てはめると$256^{49}$通りの画像がありえます(軽く計算しましたが、1兆を軽く超えます)。未知の複雑な関数を学習するために必要なデータが、次元の増加とともに指数関数的に増加することを次元の呪いと呼びました。
次元の呪いと超立方体に関する個人的理解
「はじパタ」で最初に躓くポイントが「次元の呪い」と「超立方体」かと思います。本の中で2ページ程度の解説ですが、中々奥深い内容で、正しいか自信がないですが私なりの理解を解説。
次元
まず3次元までのそれぞれの名称です。ここまではわかりやすいです。
| 次元数 | 名称 |
|---|---|
| 0次元 | 点 |
| 1次元 | 線 |
| 2次元 | 面 |
| 3次元 | 立体 |
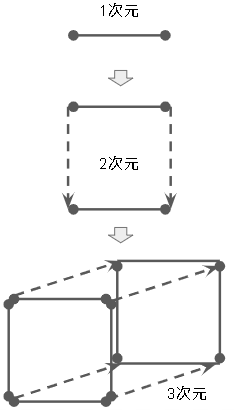
WikipediaのHypercubeにある以下の絵が0次元(点)から4次元(超立方体)まで次元が増えていく様子がわかりやすいです。

4次元以上になると、人間が知覚できる世界から離れてわからなくなってきます。理論的に次元(軸)を増やしていったものだと考えてください。
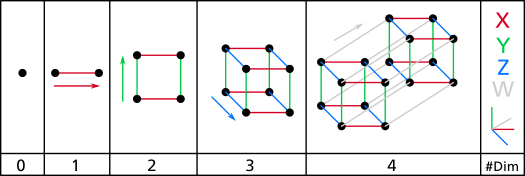
超立方体とは
$d$次元線形空間を表しているのが超立方体。2次元なら正方形で3次元なら立方体。なぜ1辺の長さが均等なのかというと、正規化をして0以上1以下の範囲にしているから(そんな解説はどこにもなかったけど、正規化していると予測)。
**4次元以上は人間は感覚的に理解することができない。**下図gifの4次元超立方体もあくまで2次元に無理矢理投影したの形なので正確ではなく理解ができない(理解の一助にくらいにはなる)。

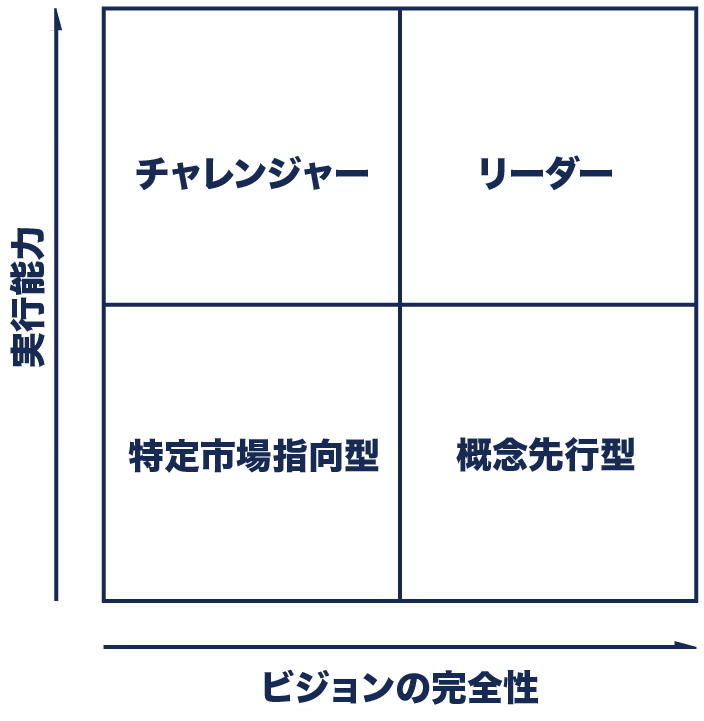
そもそも**「超立方体」が「次元の呪い」のトピックで出てくる理由は$d$次元線形空間を理解する必要がある**から。例えば有名なGartnerのマジッククアドラントは「実行能力」と「ビジョンの完全性」という2つの特徴を使って4クラスに分類しています。
2つ程度の特徴であれば簡単ですが、実際の機械学習では特徴数が非常に多いです。その際に特徴数だけの多次元線形空間で考えます。多次元線形空間内で各データを超立方体で表します。ただ、超立方体は非常に概念的な存在であるためイメージがしにくいです。ユークリッド空間でも以下のように書かれており、凡人では「超立方体」を明瞭に理解できないと諦めます。
高次元空間の可視化は、熟達した数学者でさえ難しい
超立方体の性質
緑茶思考ブログを主に読んで理解しました。また、ユークリッド空間を読んでおくと少し理解が早くなると思います。超立方体はユークリッド空間をベースに考えます。
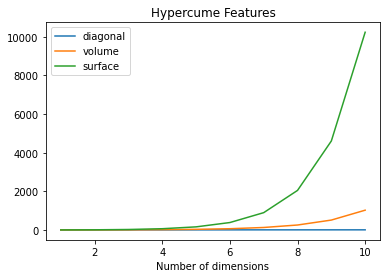
超立方体の次元数に従い、対角線の長さ(diagonal)・超体積(volume)・超表面積(surface)は以下のように変わります(出力コード)。
頂点
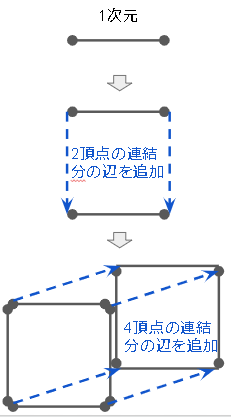
$n$次元の頂点の数は $2^n$
1次元だと線の両端(2つ)。1次元に1つ次元が増えることにより2つ(両端)が2倍に増加。あとはその連続。下の図のように考える。
| 次元 | 頂点の数 | 備考 |
|---|---|---|
| 1次元(線) | 2($=2^1$) | 直線の両端2つ |
| 2次元(正方形) | 4($=2^2$) | 正方形の四隅 |
| 3次元(立方体) | 8($=2^3$) | 立方体の各頂点 |
| $n$次元 | $2^n$ | 次元が1増えるに従い2倍になる |
辺
$n$次元の辺の数は $2^{n-1}n$
1つ前の次元の辺の数の2倍($2^{n-1}(n-1)$)と1つ前の次元の頂点数($2^{n-1}$)を足した数
| 次元 | 辺の数 | 備考 |
|---|---|---|
| 1次元(線) | 1($=2^0\times1$) | 直線なので1本 |
| 2次元(正方形) | 4($=2^1\times2$) | 四角形の4辺 |
| 3次元(立方体) | 12($=2^2\times3$) | 縦・横・高さでそれぞれ4本で計12本 |
| $n$次元 | $2^{n-1}n$ | 次元が1増えると2倍になり、さらに頂点の数分増える |
面(ファセット)
「面」という言葉ですが、3次元以外では私達が通常考える面とは違います。正確には**$n$次元超立方体に対する$n-1$次元超平面の数**です。例えば、立方体(3次元超立方体)の面(2次元超平面)は各次元(縦・横・高さ)に2つずつある。 つまり $3 \times 2=6$となる。これが、$n$次元で、そのままの式になると考えます。
| 次元 | 面の数 | 備考 |
|---|---|---|
| 1次元(線) | 2($= 2 \times 1$) | 点(0次元超平面)の数 |
| 2次元(正方形) | 4($=2 \times 2$) | 線(1次元超平面)の数 |
| 3次元(立方体) | 6($=2 \times 3$) | 面(2次元超平面)の数 |
| $n$次元 | $2n$ | 各次元に直行する面($n-1$次元超平面)が2つずつ存在する |
超体積
超「体積」という言葉ですが、3次元以外では私達が通常考える体積とは違います。1次元の場合は長さ、2次元の場合は面積を示します。**1辺の長さの$n$乗($a^n$)**が計算式です。「次元の呪い」観点では、次元が増えれば超体積が増えるということが重要。
1辺の長さを$a$で表し、仮に$a=2$とすると以下のようになります(1だとすべて次元数に関わらず同じになってしまうので2にしました)。
| 次元 | 超体積 | 備考 |
|---|---|---|
| 1次元(線) | 2($=2^1$) | 長さ |
| 2次元(正方形) | 4($=2^2$) | 面積 |
| 3次元(立方体) | 8($=2^3$) | 体積 |
| $n$次元 | $2^n(=a^n)$ | 1辺の長さの$n$乗 |
超表面積
超「表面積」という言葉ですが、3次元以外では私達が通常考える体積とは違います。
1辺の長さが$a$の$n$次元の立方体の超表面積は以下の計算式。
n-1次元立方体の超体積(a^{n-1}) \times 面(ファセット)の数(2n)
$n-1$次元立方体の超体積a^{n−1}と面(ファセット)の数$2n$を乗算して超表面積は$2na^{n−1}=(a^{n−1}\times 2n)$。
1辺の長さを$a$で表し、仮に$a=2$とすると以下のようになります。
| 次元 | 超表面積 | 備考 |
|---|---|---|
| 1次元(線) | 2$=(2 \times 1 \times 2^0$) | 0次元の点(1)が2(点) |
| 2次元(正方形) | 8$=(2 \times 2 \times 2^1$) | 1次元の線(2)が4(辺) |
| 3次元(立方体) | 24$=(2 \times 3 \times 2^2$) | 2次元の面(4)が6(面) |
| $n$次元 | $2na^{n-1}$ | $n-1$次元の超平面が面の数 |
対角線の長さ
対角線の長さは$\sqrt na$ は ユークリッド距離(ピタゴラスの公式を使う)で展開すると計算式$\sqrt {a^2 + a^2 + \cdots + a^2}$。
「次元の呪い」観点では、次元が増えれば対角線が長くなるということが重要。
※ユークリッド空間を読めば「ユークリッド距離」についての理解が深まります。
| 次元 | 対角線の長さ | 備考 |
|---|---|---|
| 1次元(線) | $1(=\sqrt 1 \times 1$) | 線の長さ |
| 2次元(正方形) | $\sqrt 2(=\sqrt 2 \times 1$) | 正方形の対角線 |
| 3次元(立方体) | $\sqrt 3(=\sqrt 3 \times 1$) | 立方体の対角線 |
| $n$次元 | $\sqrt na$ | $\sqrt {a^2 + a^2 + \cdots + a^2}$ |
m次元超平面の数
$m (0 \leq m \leq n - 1)$ 次元面の個数は 以下のとおりです。
{{2^{n-m}} {_nC_m}}
例えば3次元(立方体)に対しては、$m$次元超平面は以下の数だけあるという意味。
- 2次元超平面(面)が6面($=2^{3-2}{}_3 C _2=2^1 \times 3$)
- 1次元超平面(線)が12本($=2^{3-1}{}_3 C _1=2^2 \times 3$)
$n$次元から$m$次元超平面の選び方はn個からm個選ぶ組み合わせ分あるので${_nC_m}$個ある(例:3次元に対して1次元超平面は縦・横・高さの3通りの次元の選び方がある)。
それぞれの組み合わせに対して選ばなかった$2{n-m}$次元分だけ超平面があるので掛け合わせる(例:3次元の縦・横・高さのそれぞれに対して1次元超平面は4本ある)。
少しだけ見やすく計算すると以下の通り。
| 次元 | 1次元超平面(線)の数 | 2次元超平面(面)の数 |
|---|---|---|
| 2次元(正方形) | $4本(=2^1{}_2 C _1 $) | - |
| 3次元(立方体) | $12本(=2^2{}_3 C _1 $) | $6本(=2^1{}_3 C _2 $) |
10次元までの数値はWikipediaのHypercubeに記載されています。
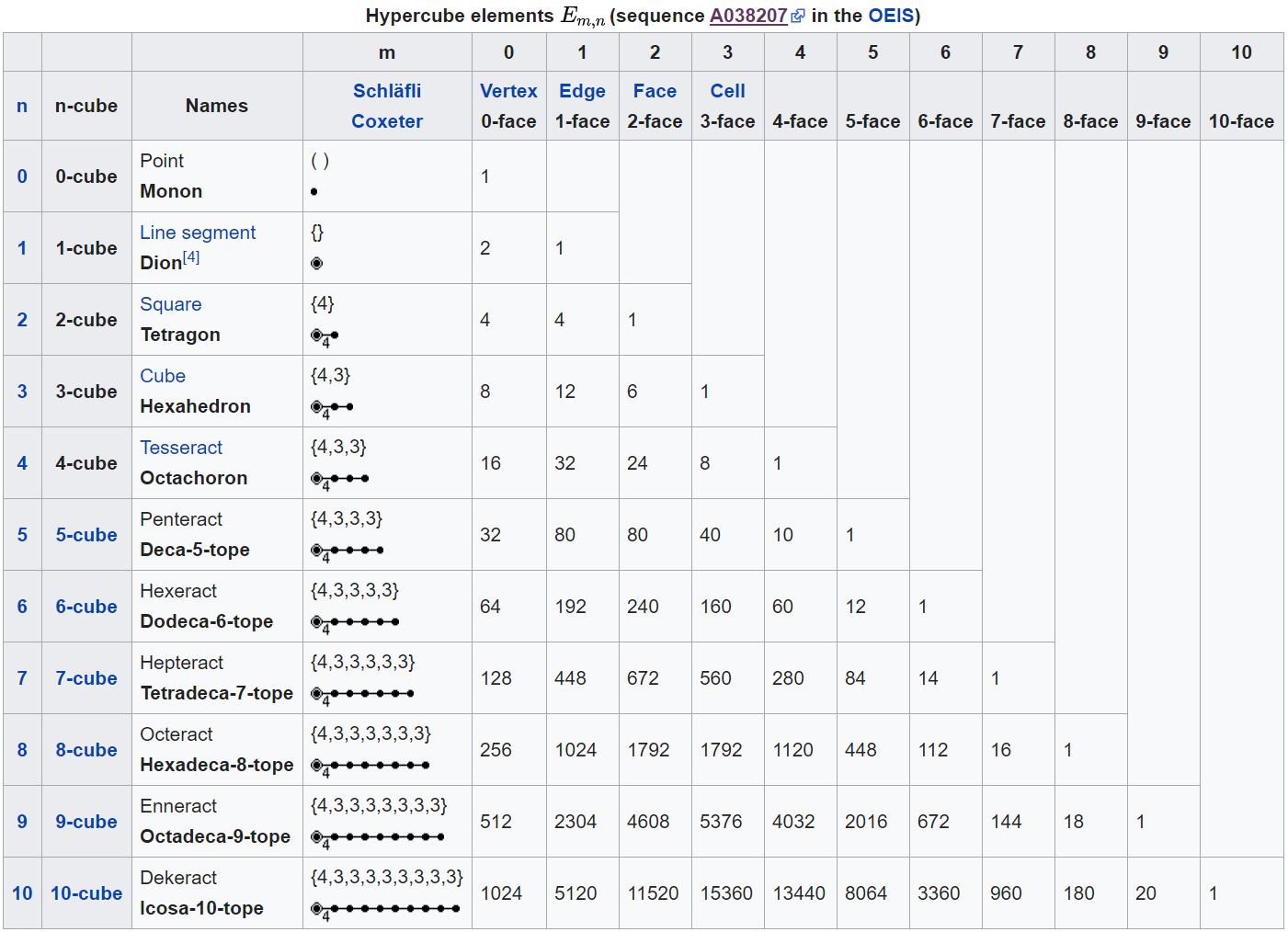
※上記2つのグラフの出力コード
次元の呪いとサンプル間の距離
When a measure such as a Euclidean distance is defined using many coordinates, there is little difference in the distances between different pairs of samples.
Wikipedia "Curse of dimensionality"の"Distance functions"では上記のように述べられています。ユーグリット距離において座標(次元)が多いとサンプル間の距離の違いが小さくなる。意味がわかりにくいですね。数式に表すと以下のようになります。
{\lim_{d \to \infty} E\left[ \frac{\mathrm{dist}_\mathrm{max}(d) - \mathrm{dist}_\mathrm{min}(d)}{\mathrm{dist}_\mathrm{min}(d)} \right] \to 0
}
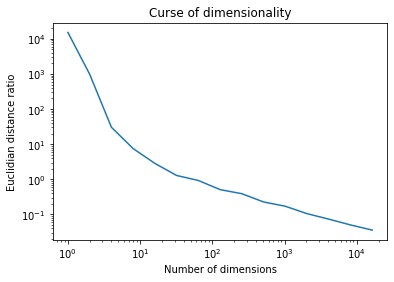
サンプル数を無限に増やすとサンプル間の最小と最大の距離の差が0に収束します。
10000サンプル数に対して次元を増やしていってサンプル間の最大・最小距離を計算・表示してみます(記事「Python 次元の呪いを可視化してみる」のコードを見て変更)。空間が広くなっているの最大の距離は逓増していますが、最小の距離はほぼ最大と同じになっていきます。次元が増えるにつれて差が小さくなっていくのがわかります。
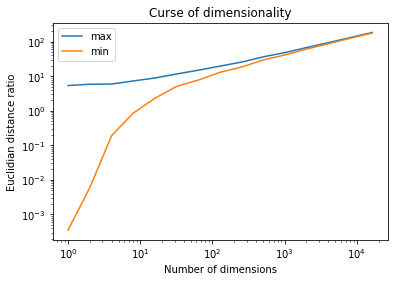
割合で表示するとこんな感じ。ゼロに収束されていき、**サンプル間の距離の差がなくなってしまいます(つまり特徴で差をつけにくくなってしまう)。**これが次元の呪いです。
次元の呪いとデータ分布
**高次元空間ではデータが空間の外側に集中して分布します。**これまた理解しにくいですね。
1から3次元までを図で示してみました。次元が増えるにつれて灰色と青で囲まれた外側部分の超体積の割合が増えていきます。仮に1割を外側とした場合、超体積のの外側の割合が次元が増えるにつれて増えていきます。
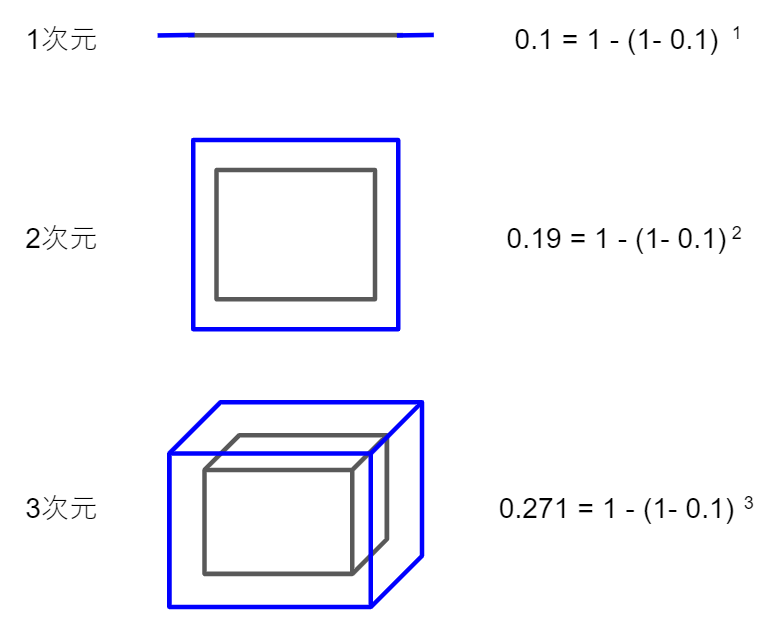
$n$次元超立方体での外側の全体に占める割合は以下の計算式です($r$は外側の厚みの割合)。
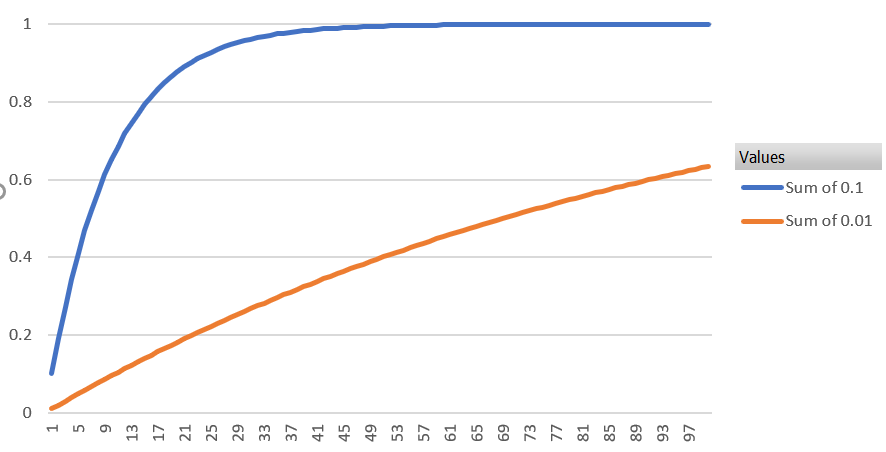
1-(1-r)^n
以下のグラフは外側の厚みを0.1または0.01とした場合の次元(x軸)に対しての外側部分の超体積の割合(y軸)です。0.01と設定しても100次元で6割を有に超えていまします。
これは俗に「サクサクメロンパン問題」とも言うようです。
この外側に集中するということで何が大事かと言うと、高次元空間においてはサンプル間の距離差がたいしてなくなるということです。
記事「次元の呪いについて」を参考にしました。
「はじパタ」勉強系記事リンク
| 章 | 項目 | 時間(h) | 難易度 | 学んだこと |
|---|---|---|---|---|
| 1 | はじめに | 8.9 | 特徴の型, 特徴空間, 次元の呪い | |
| 2 | 識別規則と学習法の概要 | 12 | ホールドアウト法,交差確認法 ,一つ抜き法 ,ブートストラップ法 ,バイアス・分散トレードオフ, 過学習 | |
| 3 | ベイズの識別規則 | 14.8 | ベイズ識別規則, ROC曲線 | |
| 4 | 確率モデルと識別関数 | 18 |
|
平均ベクトル, 共分散行列, 標準化, 無相関化, 白色化, 正規分布, 最尤推定 |
| 5 | k最近傍法(kNN法) | 8 |
|
最近傍法, ボロノイ境界, kNN |
| 6 | 線形識別関数(前半) | 30.4 |
|
正規方程式 |
| 6 | 線形識別関数(後半) | 前半に時間は含む |
|
フィッシャーの線形判別関数, 判別分析法, ロジスティック回帰 |
| 7 | パーセプトロン型学習規則 | 13.5 |
|
多層パーセプトロン, 誤差逆伝播法, シグモイド関数 |
| 8 | サポートベクトルマシン | 14.7 |
|
カーネルトリック, ν-SVM |
| 9 | 部分空間法 | 15.4 |
|
主成分分析, 特異値分解, CLAFIC法, カーネル主成分分析, カーネル部分空間法 |
| 10 | クラスタリング | 8.4 |
|
距離の公理, ミンコフスキー距離, K-平均法, 融合法, 混合正規分布モデル |
| 11 | 識別機の組み合わせによる性能強化 | 11.6 |
|
ノーフリーランチ定理, 決定木, バギング, アダブースト, ランダムフォレスト |