「はじめてのパターン認識」の第7章「パーセプトロン型学習規則」の解説です。ここまで真面目に進めていくと数式には慣れたな、とさすがに感じました。単純パーセプトロンははじめてしっかりと理解しました(理解した結果「実務で使わないな」と思いましたが・・・)。
ニューラルネットワークについても書かれていて、以前に学習したせいもあって比較的短い時間で理解しました。誤差逆伝播法は、以前理解したときに時間がかかった記憶があり、初見だったら難しかったと思います。やはり、最初は「はじパタ」よりも「Coursera機械学習入門オンライン講座」から勉強した方が絶対わかりやすいです![]()
※はじパタ勉強系は記事「文系社会人がはじパタで機械学習を数式含めて理解した奮闘記」にまとめました。
内容
7.1. パーセプトロン
線形識別関数$f(x)=w^T x$を使って二値分類を考えます。ニューラルネットワークで一世を風靡するしており、よく知っている内容なので省略。
7.1.1. パーセプトロンの学習規則
線形識別関数で二値分類をして、片方のクラスでは符号を反転させます。それにより、$f(x)<0$の場合は一律誤りと判定させます。

学習データの系列を$x_i, x_2, \ldots, x_i$とした場合、パーセプトロンの学習規則は係数ベクトル$w_{i+1}$を以下のように学習率$\eta$(「イータ」と読みます)を使って計算します。$\eta=1$の場合は固定増分誤り訂正法と呼びます。
\begin{cases}
f(x_i) \ge 0 であれば w_{i+1} = w_i \\
f(x_i) \lt 0 であれば w_{i+1} = w_i + \eta x_i\\
\end{cases}
以下のステップで学習していきます。これはバッチ学習ではなく1件ずつの学習ですね。
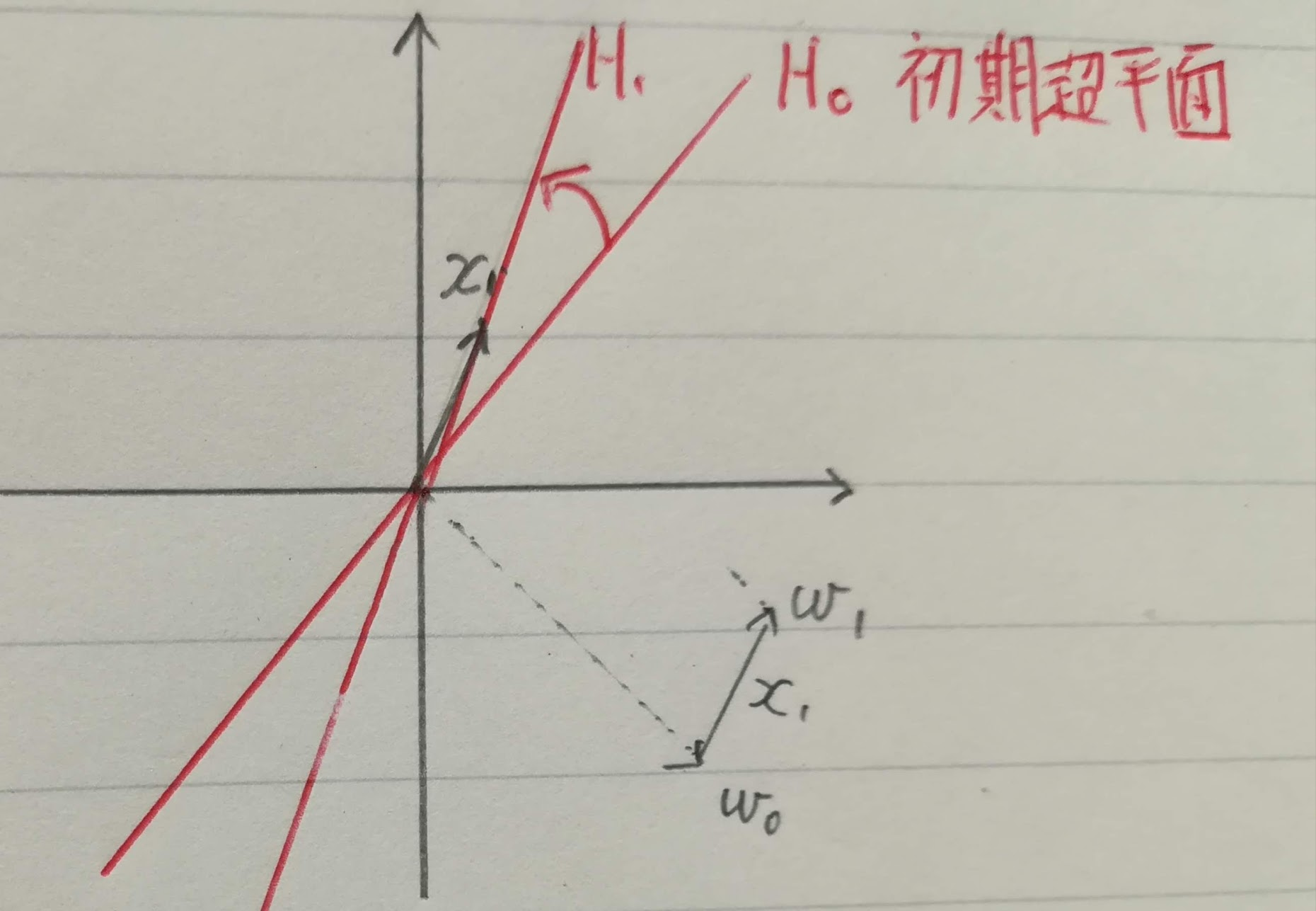
- 初期パラメータ$w_0$と初期超平面 $H_0$で$x_1$を分類
- $x_1$が誤りだったので、この図では固定増分誤り訂正法でパラメータ$w_0$を調整し、$w_1$を計算
- $w_1$から新しい超平面$H_1$を作成→この連続
7.1.2. 学習の難しさの尺度
テストデータにノイズを含んでいるとノイズのない学習データを使った識別関数はノイズの分だけ間違えやすくなります。そこで、学習データが識別超平面から近い距離(h以下の距離)の場合も誤りとしてパラメータ$w$を更新するようにします。このhをマージンと呼びます。
aにマージンとを含めた誤りを識別する式$h-\frac{w_i^Tx_i}{||w_i||}$を代入したステップ関数を使います。
f_{step}(a)=
\begin{cases}
1 (a \gt 0の場合)\\
0 (それ以外の場合)
\end{cases}
i番目の学習における$w_i$の変更量$\Delta w_i$は、符号反転をした学習データについて以下のように書けます。
\Delta w_i = \eta f_{step}(h-\frac{w_i^Tx_i}{\|w_i\|}x_i)=
\begin{cases}
\eta x_i (h > \frac{w_i^Tx_i}{\|w_i\|}の場合)\\
0 \ (それ以外の場合)
\end{cases}
$w^T x$に対して取れるマージの大きさ$D(w)$はクラス$C_1, C_2$の学習データを識別関数の法線ベクトル上に射影した長さの差の最小値の半分です。
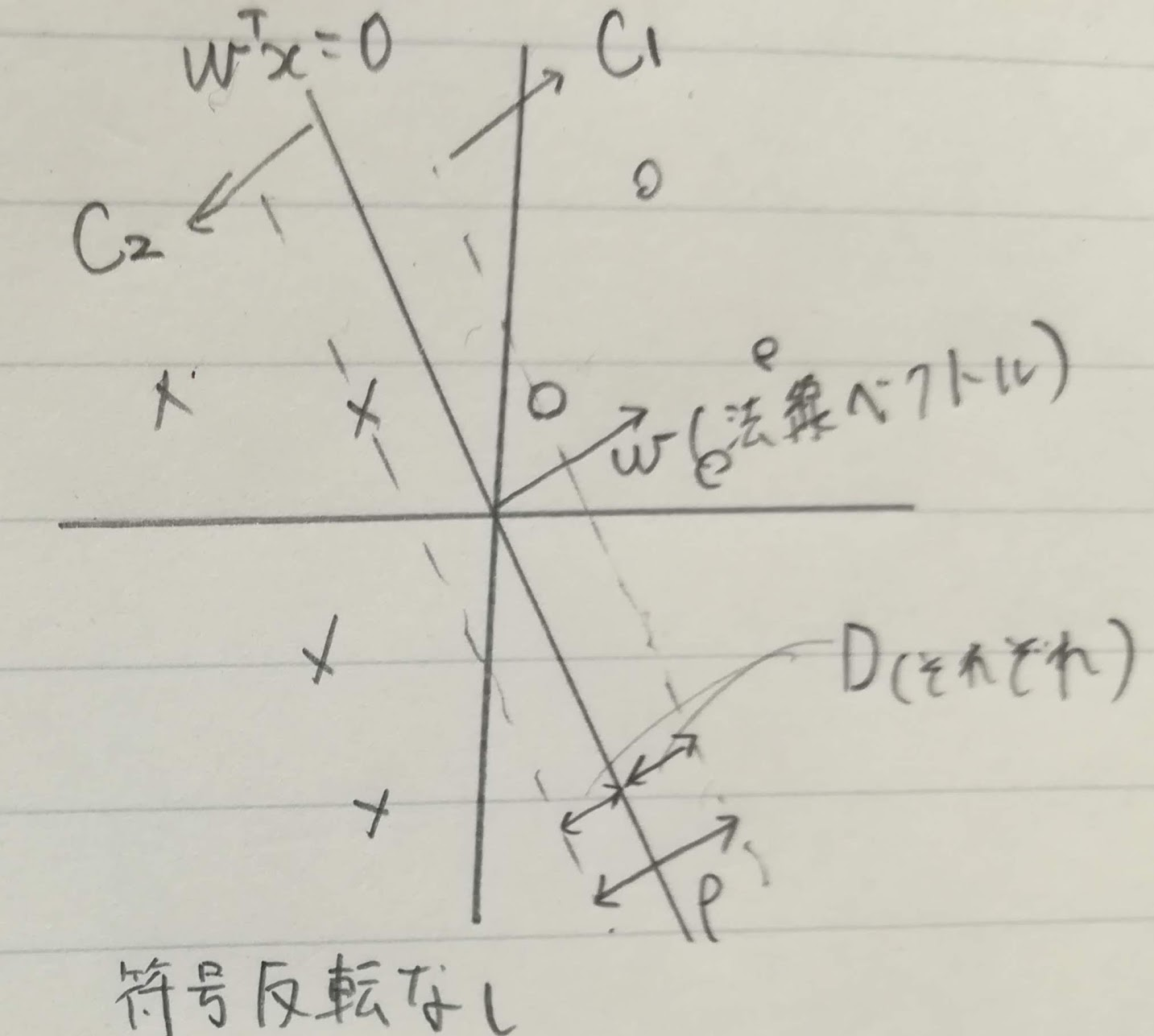
クラス2に属するデータの線形識別関数の結果は負なので、maxとしています(符号反転なしとしています)。
\rho(w) = \min_{x \in C_1} \frac{w^T x}{\|w\|} - \max_{x \in C_2} \frac{w^T x}{\|w\|}
$\rho(w)$をクラス間マージンと呼び、最大マージン$D_{max}$はクラス間マージンを使って以下で表すことができます。
D_{max} = \frac{1}{2} \rho_{max} = \max_w \rho(w)
例題7.1 2入力論理積関数の$D_{max}$
- $d_A=\frac{w^T x_A + b}{||w||}=\frac{(w_1, w_2)^T(0, 0) + b}{\sqrt{w_1^2+w_2^2}}=\frac{b}{\sqrt{w_1^2+w_2^2}} < 0$
- $d_B=\frac{w^T x_B + b}{||w||}=\frac{(w_1, w_2)^T(1, 0) + b}{\sqrt{w_1^2+w_2^2}}=\frac{w_1+b}{\sqrt{w_1^2+w_2^2}} < 0$
- $d_C=\frac{w^T x_C + b}{||w||}=\frac{(w_1, w_2)^T(0, 1) + b}{\sqrt{w_1^2+w_2^2}}=\frac{w_1+b}{\sqrt{w_2^2+w_2^2}} < 0$
- $d_D=\frac{w^T x_D + b}{||w||}=\frac{(w_1, w_2)^T(1, 1) + b}{\sqrt{w_1^2+w_2^2}}=\frac{w_1+w_2+b}{\sqrt{w_2^2+w_2^2}} > 0$
7.1.3. パーセプトロンの収束定理
2クラスの学習データが線形分類可能なら、パーセプトロンの学習規則は有限の学習回数で収束でき、これをパーセプトロンの収束定理と言います。以下の前提で証明していきます。
- $h(=\alpha d)$: マージンで「次元ごとにαの大きさを取る」としています。
- $M_i$: データ$x_i$が学習で使われた回数
- $M(=\sum_i M_i)$: 学習の総数
- $w^*$: 解ベクトル(学習)が収束した時の係数ベクトル
マージンhについて
M回の学習で獲得された係数ベクトルwは初期値を0と仮定すると以下の式です。
w=\eta \sum_{x_i \in C_1, C_2} M_i x_i
学習収束時の係数ベクトルとwとの内積を計算します。この値はMに比例して増加して、係数ベクトルが解ベクトルに近づいていきます。
\begin{eqnarray}
w^T w^* & = & (\eta \sum_{x_i \in C_1, C_2} M_i x_i)^T w^* \\
& = & \eta \sum_{x_i \in C_1, C_2} M_i x_i^T w^* \ \
\because \eta \sum_{x_i \in C_1, C_2} M_i x_iのうちx_i部分のみがベクトル\\
& \ge & \eta \min_{x_i \in C_1, C_2} M_i x_i^T w^* \\
& = & \eta M D(w^*) \|w^*\|
\because D(w)=\min_{x_i \in C_1, C_2} \frac{w^T x}{\|w\|}
\end{eqnarray}
$||w||$の上限を求めるために、各学習データの長さが$||x_i||^2 \ge d$を満たしていると仮定して、$x_i$による係数ベクトルの変更量を求めます。
\begin{eqnarray}
\Delta ||w||^2 & = & ||w + \eta x_i ||^2 - ||w||^2 \\
& = & \eta^2 ||x_i||^2 + 2\eta w^T x_i \\
& \le & \eta^2 d + 2\eta \alpha d = d \eta (\eta + 2\alpha)\\
\end{eqnarray}
\because ||x_i||^2 \ge dの仮定から \\
\because w^T x_i \le h = \alpha d(学習をしているのでマージンより小さい)
つまり、M回学習した係数ベクトルは$||w||^2 \le M d \eta(\eta + 2 \alpha)$となります。
$wとw^*$の方向余弦は$\cos \theta = \frac{w^T w^*}{||w|| ||w^*||}$です。
方向余弦を二乗すると以下のようになります。
※方向余弦の2乗の和は1なので。
\cos^2 \theta = \phi = \frac{(w^T w^*)^2}{||w||^2 ||w^*||^2} \le 1
式を展開します。
\frac{(\eta M D(w^*)||w^*||)^2}{Md \eta(\eta +2 \alpha) ||w^*||^2} \le
\frac{(w^T w^*)^2}{||w||^2 ||w^*||^2} = \phi \le 1 \\
\because w^T w^*= \eta M D(w^*)||w^*||, ||w||^2 \le M d \eta (\eta + 2\alpha) \\
\frac{\eta^2 M^2 D^2(w^*)||w^*||^2}{Md \eta(\eta +2 \alpha) ||w^*||^2} \le \phi \le 1 \\
\frac{M \eta D^2(w^*)}{d (\eta +2 \alpha)} \le \phi \le 1 \\
方向余弦の2乗をなくして展開します。
\begin{eqnarray}
\frac{M \eta D^2(w^*)}{d (\eta +2 \alpha)} & \le & 1\\
M & \le & \frac{d (\eta +2 \alpha)}{\eta D^2(w^*)}\\
& = & \frac{d(1+\frac{2 \alpha}{\eta})}{D^2_{max}}\\
\end{eqnarray}
最後の$D(w^*)=D_{max}$として計算している部分を正確に理解できていないのですが、最適解ではSVMのようにマージンを最大化できる、という意味なのでしょうか?どちらにしろ学習回数に上限があるのがわかります。
次元dとマージンαが大きいと学習に時間がかかり、逆に$D^2_{max}$2のクラス間の距離が大きければ学習が速いことがわかります。
以下を参考にしました。
7.2. 誤差逆伝播法
7.2.1. 多層パーセプトロン
線形識別関数(単純パーセプトロン)で正しく識別できない例に下表のような排他的論理和(XOR)関数があります。
| $x_1$ | $x_2$ | 出力 | 教師データ |
|---|---|---|---|
| 0 | 0 | 0 | -1 |
| 0 | 1 | 1 | +1 |
| 1 | 0 | 1 | +1 |
| 1 | 1 | 0 | -1 |
この場合は2つの入力要素を乗算して第さんの入力要素を作ることで、線形分離ができます。
| $x_1$ | $x_2$ |
|
出力 | 教師データ |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | -1 |
| 0 | 1 | 0 | 1 | +1 |
| 1 | 0 | 0 | 1 | +1 |
| 1 | 1 | 1 | 0 | -1 |
以下の図のような2種類の回路があります。先程の排他的論理和で入力要素を増やしたのが左のパターン、一般的なのは右のパターン(多層回路)です。
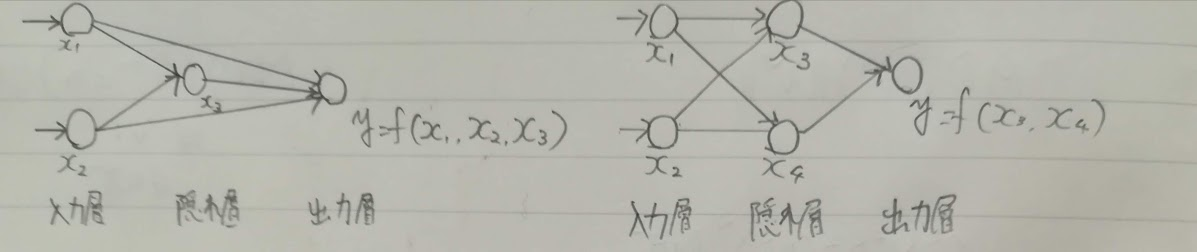
真ん中を隠れ層と呼びその素子を隠れ素子と呼びます。左の入力部分を入力層、右の出力部分を出力層と呼びます。
ここから学習するのは、多層パーセプトロンの誤差逆伝播法(バックプロパゲーション法)です。下図のような回路を学習回路と呼びます。
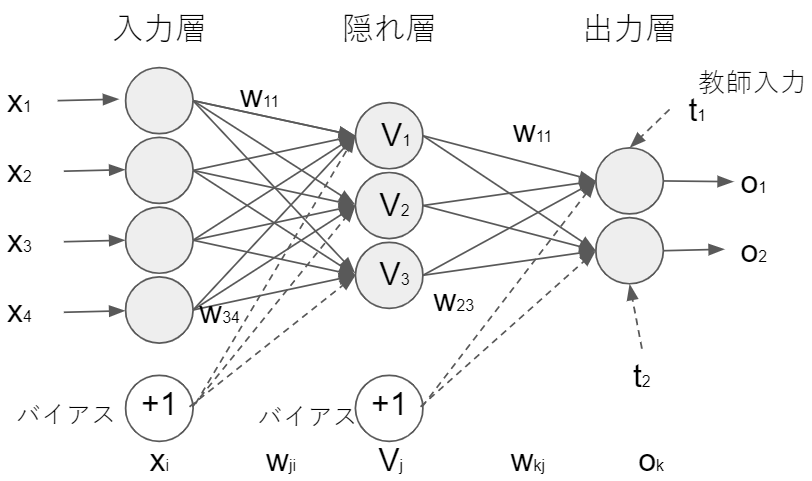
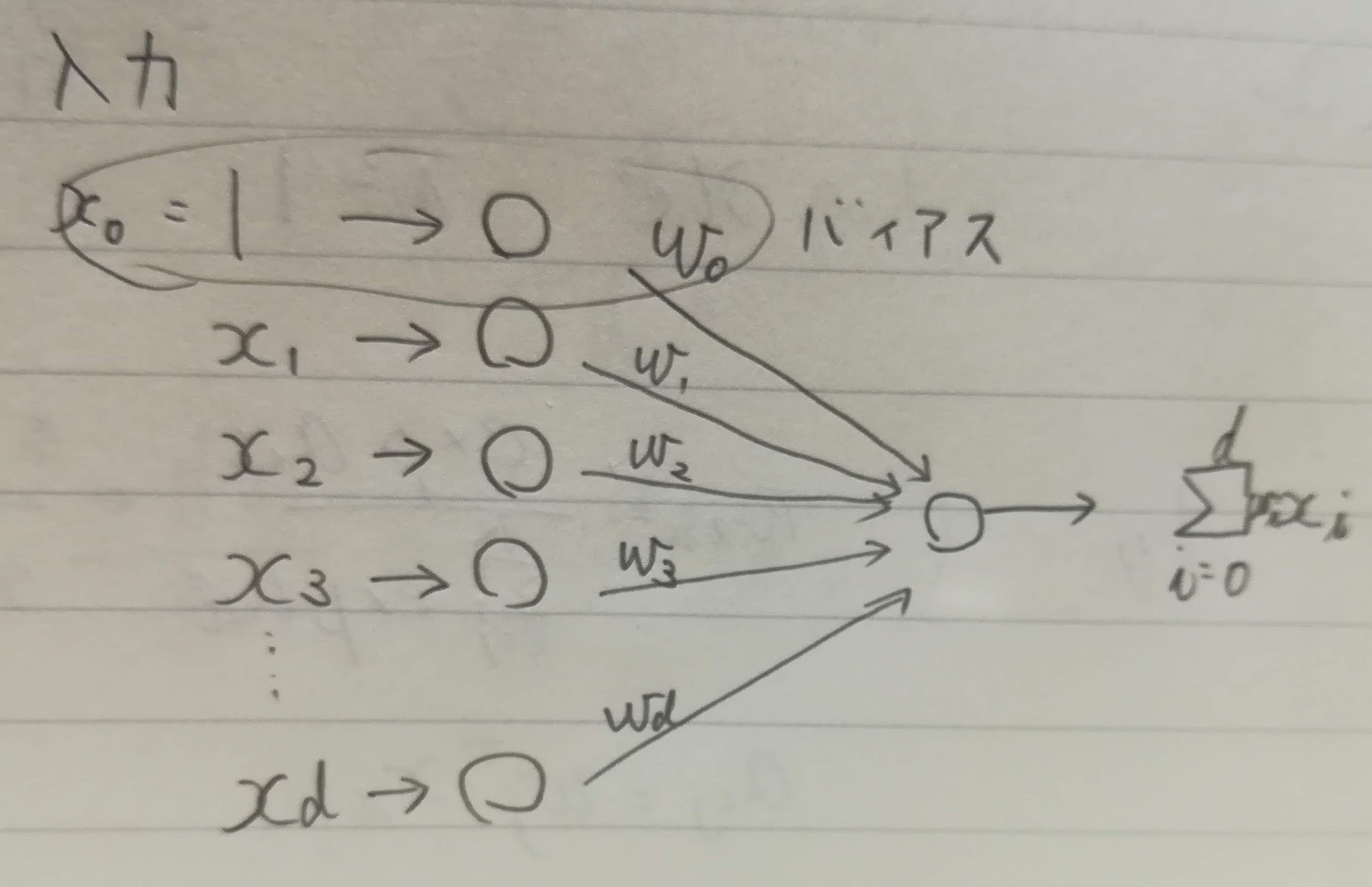
入力層で使う学習データは$x^n(n= 1, \ldots, N)$です。下付き添字は次元に使うので乗数ではないけど上付き添字を使います。学習データの次元はd。バイアス項も含めたn番目学習データの入力は$x^n=(1, x_1^n,\ldots,x_d^n)^T$ です。隠れ層の素子$V_j(j=1, \ldots, M)$へはこんな入力が来ます。
h_j^n = \sum_{i = 0}^d w_{ji} x_i^n = w_j^T x^n
上の式の結果を出力関数$g(u)$を使って$V_j^n=g(h_j^n)$として出力します。ここの隠れ素子出力関数が線形だと多層回路にしても1層の回路での表現と同じになってしまうので非線形にします。$g(u)$は非線形出力関数と呼ばれ、あらゆるuで微分可能な単調増加関数です(ニューラルネットワークでは活性化関数という単語で覚えました)。シグモイド関数をよく使う、と書かれていますが、今はReLUやソフトマックスなどほかもよく使っています。
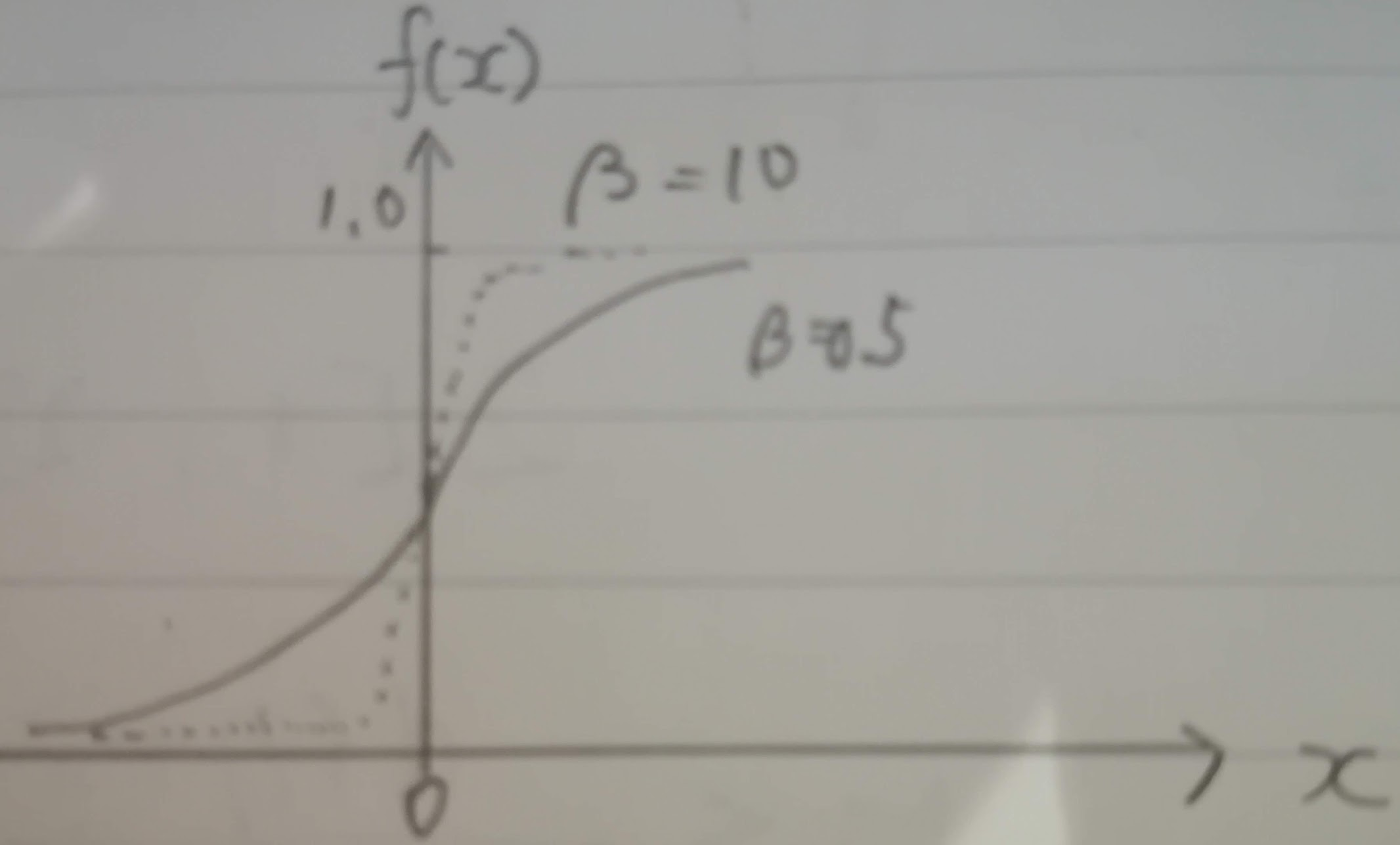
シグモイド関数は$g(u)=\frac{1}{1+\exp(-\beta u)}$で、以下のグラフのようにβの値によって傾きが異なります。
出力素子$o_k(k=1, \ldots, K)$への入力は以下。
\begin{eqnarray}
h_k^n & = & \sum_{j = 0}^M w_{kj} V_j^n \\
& = & \sum_{j = 0}^M w_{kj} g(h_j^n)\\
& = & \sum_{j = 0}^M w_{kj} g(\sum_{i = 0}^d w_{ji} x_i^n)\\
\end{eqnarray}
出力素子$o_k$に対する出力は以下の式。
\begin{eqnarray}
o_k^n & = & \widetilde{g}(h_k^n)\\
& = & \widetilde{g}(\sum_{j = 0}^M w_{kj} V_j^n)\\
& = & \widetilde{g}(\sum_{j = 0}^M \omega_{kj} g(\sum_{i = 0}^d \omega_{ji} x_i^n))\\
\end{eqnarray}
$\widetilde{g}()$は出力素子用の(非)線形出力関数で、出力素子の非線形性をソフトマックス関数で表し、
\widetilde{g}(o_k^n) = \frac{\exp(o_k^n)}{\sum_{l = 1}^K \exp(o_l^n)}
ロジスティック回帰と同様の確率的な解釈を与える場合もあります。
\widetilde{g}(o_k^n) = p(t_k^n = 1| x^n)
7.2.2. 誤差逆伝播法の学習規則
隠れ素子から出力素子への結合係数の学習です。二乗誤差最小化を最急降下法で行います。n番目の学習データによる誤差の評価関数は以下の式。
\begin{align}
E_n(w) & = \frac{1}{2} \sum_{k = 1}^K (t_k^n - o_k^n)^2 \\
& = \frac{1}{2} \sum_{k = 1}^K (t_k^n - \widetilde{g}(h_k^n))^2 \\
& = \frac{1}{2} \sum_{k = 1}^K(t_k^n - \widetilde{g}(\sum_{j = 0}^M w_{kj} V_j^n))^2 \\
& = \frac{1}{2} \sum_{k = 1}^K(t_k^n - \widetilde{g}(\sum_{j = 0}^M w_{kj} g(\sum_{i = 0}^d \omega_{ji} x_i^n)))^2
\end{align}
で、学習データ全体は$E(w) = \sum_{n = 1}^N E_n(w)$。
E(w)を評価関数とするバッチアルゴリズムでは、学習データ全体を使って結合係数の修正量を計算し更新することを1エポックと呼びます。$\tau$エポック目の修正量を$\Delta w_kj(\tau)$とすると、$w_{kj}(\tau+1)=w_{kj}(\tau)+\Delta w_{kj}(\tau)$で更新します($\tau$は「タウ」と読みます)。
※バッチアルゴリズム、確率的最急降下法、ミニバッチは「Coursera機械学習入門コース(10週目 - ビッグデータ対応)」で習いました。
$\Delta w_{kj}(\tau)$は合成微分を使って以下の式です。
\begin{align}
\Delta w_{kj}(\tau) & = \sum_{n = 1}^N(- \eta \frac{\partial E_n(w)}{\partial w_{kj}}) \\
& = - \eta \sum_{n = 1}^N (\frac{\partial E_n(w)}{\partial o_k^n} \frac{\partial o_k^n}{\partial h_k^n} \frac{\partial h_k^n}{\partial w_{kj}}) \\
& = \eta \sum_{n = 1}^N (t_k^n -o_k^n) \widetilde{g}'(h_k^n)V_j^n \\
& = \eta \sum_{n = 1}^N \delta_k^n V_j^n
\end{align}
上記の補足です。
\begin{eqnarray}
\frac{\partial E_n(w)}{\partial o_k^n}
& = & \frac{\partial}{\partial o_k^n}\frac{1}{2} \sum_{k = 1}^K (t_k^n - o_k^n)^2\\
& = & \frac{1}{2} \frac{\partial}{\partial o_k^n}((t_1^n-o_1^n)^2 + \ldots + (t_k^n-o_k^n)^2) \\
& = & -2 \times \frac{1}{2} (t_k^n - o_k^n) = -(t_k^n - o_k^n) \\
\frac{\partial o_k^n}{\partial h_k^n}
& = & \frac{\partial o_k^n}{\partial} \widetilde{g}(h_k^n)
= \widetilde{g}'(h_k^n)\\
\frac{\partial h_k^n}{\partial w_{kj}}
& = & \frac{\partial}{\partial w_{kj}}(\sum_{j=1}^J(w_{k1}^n g(h_1^n)+ \ldots + w_{kj}^n g(h_J^n))) \\
& = & g(h_j) = V_j^n\\
\end{eqnarray}
$\delta_k^n=(t_k^n -o_k^n) \widetilde{g}'(h_k^n)$を誤差信号と呼びます。出力関数がシグモイド関数の場合、微分すると出力値が0と1に近い部分で0になって学習がすすまなくなるらしいです。
一方でn番目学習データによる$w_{kj}$の修正量を$\Delta w_{kj}^n(\tau)=\eta \delta_k^n(\tau) V_j^n(\tau)$で与える方法を確率降下法(オンライン学習)または確率的最急降下法と言います。
入力素子$x_i$から隠れ素子$V_j$への結合素子$w_{ji}$の学習のための評価関数は、先ほどの出力素子の結合係数$w_{kj}$場合と同じですが、今度は$w_{ji}$で微分するので合成関数の微分を2回します。バッチ学習では以下の式。
\begin{align}
\Delta w_{ji}(\tau) & = \sum_{n = 1}^N (- \eta \frac{\partial E_n(w)}{\partial w_{ji}}) \\
& = -\eta \sum_{n = 1}^N(\frac{\partial E_n(w)}{\partial V_j^n} \frac{\partial V_j^n}{\partial w_{ji}}) \\
& = -\eta \sum_{n = 1}^N(\sum_{k = 1}^K(\frac{\partial E_n(w)}{\partial o_k^n} \frac{\partial o_k^n}{\partial h_k^n} \frac{\partial h_k^n}{\partial V_j^n})
\frac{\partial V_j^n}{\partial h_j^n} \frac{\partial h_j^n}{\partial w_{ji}}) \\
& = \eta \sum_{n = 1}^N \sum_{k = 1}^K (t_k^n - o_k^n) \widetilde{g}'(h_k^n) w_{kj} g'(h_j^n) x_i^n \\
& = \eta \sum_{n = 1}^N \sum_{k = 1}^K \delta_k^n w_{kj} g'(h_j^n) x_i^n
\end{align}
上記の補足です。
\begin{eqnarray}
\frac{\partial h_k^n}{\partial V_j^n}
& = & \frac{\partial}{\partial V_j^n} \sum_{j=1}^J w_{kj}^n V_j^N\\
& = & \frac{\partial}{\partial V_j^n}(w_{k1}^n V_1^n + \ldots + w_{kj}^n V_j^n) \\
& = & w_{kj} ^n\\
\frac{\partial h_j^n}{\partial w_{ji}^n}
& = & \frac{\partial}{\partial w_{ji}^n} (w_j^n)^T x_i^n\\
& = & \frac{\partial}{\partial w_{ji}^n} ((x_i^n)^T w_j^n)\\
& = & x_i^n \because \frac{\partial a^T x}{\partial x} = a\\
\end{eqnarray}
ここで隠れ素子jの誤差信号を$\delta_j^n = g'(h_j^n) \sum_{k = 1}^N \delta_k^n \omega_{kj}$で定義すれば$\Delta \omega_{ji}(\tau) = \eta \sum_{n = 1}^N \delta_j^n x_i^n$と表現できます。
$\sum_{k = 1}^K \delta_k^n w_{kj}$の項は、各出力素子で発生した誤差$\delta_k^n$を結合素子$w_{kj}$を介して出力素子$k(=1,\ldots, K$)から隠れ素子へ戻しているので誤差逆伝播法(error Back Propagation法)と呼ばれます。
確率降下法では以下の式です。
\Delta w_{kj}^n(\tau) = \eta \delta_k^n(\tau)V_j^n(\tau) \\
\Delta w_{ji}^n(\tau) = \eta \delta_j^n(\tau) x_i^n(\tau)
7.3. 誤差逆伝播法の学習特性
7.3.1. 初期値依存性
誤差逆伝播法は、最急降下法や共役(きょうやく)勾配法などで解くことが多いです。方法によらず、誤差評価関数は局所最小値が多く全体最適解を得ることは難しいです。どの最小値に行くかは結合係数の初期値に依存します。
※共役勾配法は記事「共役勾配法」がわかりやすかったです。
7.3.2. 隠れ素子の数
隠れ素子を増やすと過学習しやすくなるという説明。
7.3.3. 過学習と正則化
非線形性が強くなるとノイズ成分に適合して過学習が生じやすくなります。昔は早期終了規則(early stopping)が過学習対策として使われていました。最近では結合係数が大きくなることに対するペナルティ項を加える正則化がよく使われます。
正則化は、記事「Coursera機械学習入門コース(3週目 - ロジスティック回帰、正則化)」で書いたので解説を省略します。
7.3.4. 隠れ層の数と識別能力
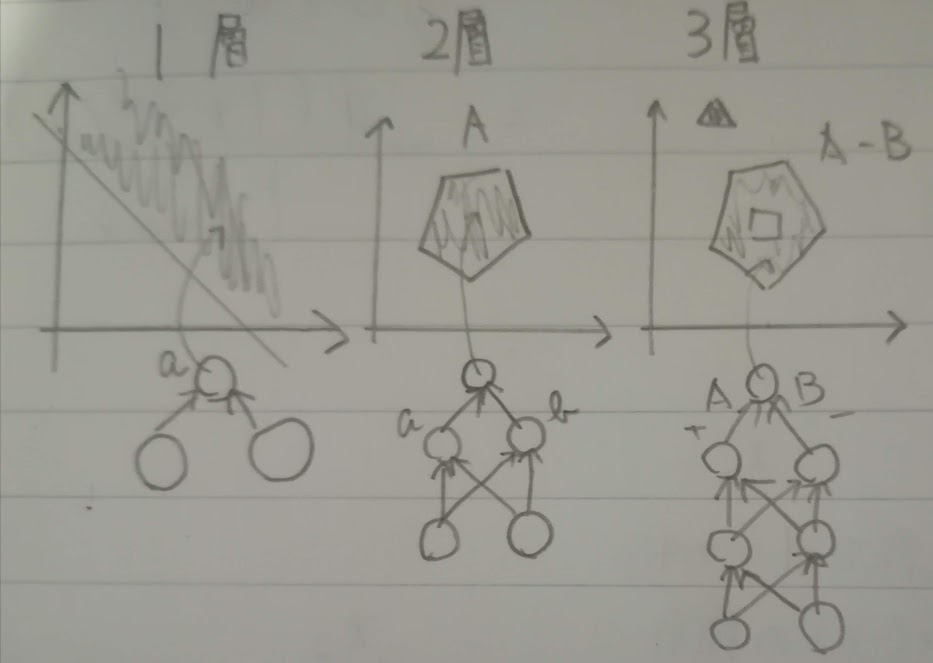
誤差逆伝播法は原理的に隠れ層がいくつあっても出力層の誤差を逆伝播できます。しかし、隠れ層は非線形出力関数なので誤差の評価関数は局所最適解を多く持つようになり大域的な最適化は難しくなります。
下の図は層に応じた表現の例です。
7.3.5. 学習回路の尤度
誤差逆伝播法の評価関数は二乗誤差最小化基準がよく使われるらしいです(今はそうでもない気もしますが・・・)。
ソフトマックス関数で出力を$\widetilde{g}(o_k)=p(t_k=1|x)$とする場合、評価関数は以下の式です。
E(w) = - \sum_{n = 1}^N \sum_{k = 1}^K t_k^n \log o_k^n \\
t_k^n: 正解以外は0 \\
\log o_k^n: 尤度
この場合はロジスティック関数と同じ表現で、最尤推定法によって結合係数の更新式を使えます(6章後半でやったベルヌーイ試行のやつですね)。
p(t|x, w) = \prod_{k=1}^K o_k^{t_k}(1-o_k)^{1-t_k}
上の式を少し解説。
{o_k^{t_k}(1-o_k)^{1-t_k}
= \left\{
\begin{array}{} o_k^1(1-o_k)^0 = o_k (t_k=1) \\
o_k^0(1-o_k)^1 = 1-o_k (t_k=0) \end{array}
\right.
}
負の対数尤度は交差エントロピー型誤差関数です。まずは、確率部分だけを負の対数尤度化。
\begin{eqnarray}
- \ln(\prod_{k=1}^K o_k^{t_k}(1-o_k)^{1-t_k}) & = &
- \sum_{k=1}^K \ln (o_k^{t_k}(1-o_k)^{1-t_k})\\
& = & - \sum_{k=1}^K (\ln o_k^{t_k}+ \ln (1-o_k)^{1-t_k})\\
& = & - \sum_{k=1}^K (t_k \ln o_k+ (1-t_k) \ln (1-o_k))\\
\end{eqnarray}
で、データ数だけ総和をして交差エントロピー型誤差関数にします。
E(w) = - \sum_{n = 1}^N \sum_{k = 1}^K (t_k^n \ln o_k^n + (1 - t_k^n) \ln (1 - o_k^n))
出力素子の学習は以下。
\begin{eqnarray}
\Delta w_{kj} & = & -\eta \frac{\partial E(w)}{\partial w_{kj}} \\
& = & - \eta \frac{\partial E(w)}{\partial O_k} \frac{\partial O_k}{\partial h_k} \frac{\partial h_k}{\partial w_{kj}}\\
& = & \eta \sum_{n=1}^N \frac{t_k^n - o_k^n}{o_k^n(1-o_k^n)} g'(\sum_{j=0}^M w_{kj} V_j^n) V_j^n\\
& = & \eta \sum_{n=1}^N \frac{t_k^n - o_k^n}{o_k^n(1-o_k^n)} \beta o_k^n(1-o_k^n) V_j^n \ \
&\because& g'(\sum_{j=0}^M w_{kj} V_j^n) = \beta o_k^n(1-o_k^n) \\
& = & \eta \sum_{n=1}^N \delta_k^n V_j^n \ \
&\because& \delta_k^n= \beta(t_k^n-o_k^n)\\
\end{eqnarray}
上記の補足です。
\begin{eqnarray}
\frac{\partial E(w)}{\partial O_k}
& = & \frac{\partial}{\partial O_k}
(- \sum_{n = 1}^N \sum_{k = 1}^K (t_k^n \ln o_k^n + (1 - t_k^n) \ln (1 - o_k^n)) )\\
& = & - \sum_{n = 1}^N (\frac{t_k^n}{o_k^n} - \frac{1-t_k^n}{1-o_k^n}) \\
& = & - \sum_{n = 1}^N \frac{(t_k^n-t_k^n o_k^n)-(o_k^n-t_k^n o_k^n)}{o_k^n(1-o_k^n)}\\
& = & - \sum_{n = 1}^N \frac{t_k^n-o_k^n}{o_k^n(1-o_k^n)}\\
\end{eqnarray}
また、例題7.2で出ていたシグモイド関数の微分も使っています。
\begin{eqnarray}
g'(\sum_{j=0}^M w_{kj} V_j^n) & = & g'(h_k^n) \\
& = & \beta g(h_k^n)(1-g(h_k^n)) \\
& = & \beta o_k^n(1-o_k^n)
\end{eqnarray}
シグモイド関数を出力関数にした場合は出力関数の微分($g'(\sum_{j=0}^M w_{kj} V_j^n)$)が消え、二乗誤差基準の場合のように非線形部分で学習が進まないことがない。
※「7.2.2 誤差逆伝播法の学習規則」に二乗誤差基準の場合について記載
出力関数がシグモイド関数の場合、微分すると出力値が0と1に近い部分で0になり学習が進まなくなる
参考リンク
- 逆伝播の仕組み: 長いですが非常に参考になります
- はじめてのパターン認識7章後半 式変形メモ〜誤差逆伝播法〜: 数式の展開が詳しい
- パーセプトロン型学習規則(Slideshare)
- はじめてのパターン認識 第7章 パーセプトロン型学習規則: 7.1.3.より後から解説
- はじぱた7章F5up(Slideshare): 7-2の途中から解説
- Coursera機械学習入門コース(5週目 - ニューラルネットワークと誤差逆伝播法): 学習前に見返しました
- はじめてのパターン認識 7章: 数式を参考にしました
「はじパタ」勉強系記事リンク
| 章 | 項目 | 時間(h) | 難易度 | 学んだこと |
|---|---|---|---|---|
| 1 | はじめに | 8.9 | 特徴の型, 特徴空間, 次元の呪い | |
| 2 | 識別規則と学習法の概要 | 12 | ホールドアウト法,交差確認法 ,一つ抜き法 ,ブートストラップ法 ,バイアス・分散トレードオフ, 過学習 | |
| 3 | ベイズの識別規則 | 14.8 | ベイズ識別規則, ROC曲線 | |
| 4 | 確率モデルと識別関数 | 18 |
|
平均ベクトル, 共分散行列, 標準化, 無相関化, 白色化, 正規分布, 最尤推定 |
| 5 | k最近傍法(kNN法) | 8 |
|
最近傍法, ボロノイ境界, kNN |
| 6 | 線形識別関数(前半) | 30.4 |
|
正規方程式 |
| 6 | 線形識別関数(後半) | 前半に時間は含む |
|
フィッシャーの線形判別関数, 判別分析法, ロジスティック回帰 |
| 7 | パーセプトロン型学習規則 | 13.5 |
|
多層パーセプトロン, 誤差逆伝播法, シグモイド関数 |
| 8 | サポートベクトルマシン | 14.7 |
|
カーネルトリック, ν-SVM |
| 9 | 部分空間法 | 15.4 |
|
主成分分析, 特異値分解, CLAFIC法, カーネル主成分分析, カーネル部分空間法 |
| 10 | クラスタリング | 8.4 |
|
距離の公理, ミンコフスキー距離, K-平均法, 融合法, 混合正規分布モデル |
| 11 | 識別機の組み合わせによる性能強化 | 11.6 |
|
ノーフリーランチ定理, 決定木, バギング, アダブースト, ランダムフォレスト |